A&A 394, 317-321 (2002)
DOI: 10.1051/0004-6361:20021139
S. Lambert - C. Bizouard
SYRTE, UMR 8630/CNRS, Observatoire de Paris, 61 avenue de l'Observatoire, 75014 Paris, France
Abstract
Resolution B1.8 adopted by the XXIV General Assembly of the International Astronomical Union (Manchester, August 2000) recommends the use of the Non-Rotating Origin (Guinot 1979) on the moving equator both in the International Celestial Reference System (ICRS) and in the International Terrestrial Reference System (ITRS). The Non-Rotating Origin (NRO) in the ITRS is designated the Terrestrial
Ephemeris Origin (TEO). Resolution B1.8 is to be implemented on 1 January 2003 by the International Earth Rotation Service (IERS) which is required to provide the position of the TEO in the ITRS. This paper is devoted to the calculation of this position. Because the TEO depends on the polar motion, which is poorly modeled, its position has been derived from observational data. This has been compared to an analytical model based on a simplified representation of polar motion. We propose then a numerical expression for the displacement of the TEO to be used in the new coordinate transformation from the Celestial Reference System to the Terrestrial Reference System according to the resolution.
Key words: reference systems - ephemerides
The study has been realized in the framework of the resolutions adopted by the XXIV General Assembly of the International Astronomical Union (Manchester, August 2000) concerning the transformation between the Celestial Reference System (CRS) and the Terrestrial Reference System (TRS), which are to be implemented in the International Earth Rotation Service (IERS) procedures on 1 January 2003.
Resolution B1.8 recommends the use of the Non-Rotating Origin (NRO) on the moving equator to reckon the angle of rotation of the Earth. The NRO (also called departure point) in the Celestial Reference System (CRS) is defined by the kinematical condition of non-rotation of this point around the rotation axis when the rotation pole moves in the CRS (Guinot 1979). Similarly, the NRO in the Terrestrial Reference System (TRS) is defined by the kinematical condition of non-rotation around the rotation axis when the rotation pole moves in the TRS. The properties of these two points have already been studied in Capitaine et al. (1986, 2000).
In practice, the determination of the Earth orientation refers to the Celestial Intermediate Pole (CIP), defined by IAU 2000 resolution B1.7, which is the pole correponding to an axis closed to the rotation axis (difference smaller than 20 mas). Therefore:
![]() The NRO as realized by taking into account the motion of the CIP in the Celestial Reference System (CRS) gives a point on the moving equator of date noted
The NRO as realized by taking into account the motion of the CIP in the Celestial Reference System (CRS) gives a point on the moving equator of date noted ![]() and designated by the Celestial Ephemeris Origin (CEO).
and designated by the Celestial Ephemeris Origin (CEO).
![]() The NRO as realized by taking into account the motion of the CIP in the Terrestrial Reference System (TRS) gives a point on the moving equator of date noted
The NRO as realized by taking into account the motion of the CIP in the Terrestrial Reference System (TRS) gives a point on the moving equator of date noted ![]() and designated as the Terrestrial Ephemeris Origin (TEO).
and designated as the Terrestrial Ephemeris Origin (TEO).
Astrometric and geodetic data analysis software involve the computation of the transformation between the CRS and the TRS. In the framework of the IAU 2000 recommendations, they need an expression for the displacement of the Terrestrial Ephemeris Origin both for the classical transformation and for transformation based on the Non-Rotating Origin representation.
The study is focused on the computation of the position of the TEO in the ITRS.
After having briefly recalled the expression of the quantity
![]() to locate the TEO (Sect. 2), we have directly computed this quantity from the observed polar motion (Sect. 3). Then a very simple analytical model of
to locate the TEO (Sect. 2), we have directly computed this quantity from the observed polar motion (Sect. 3). Then a very simple analytical model of
![]() has been derived for a better understanding of the observed variations (Sect. 4). Finally, a numerical expression of
has been derived for a better understanding of the observed variations (Sect. 4). Finally, a numerical expression of
![]() is proposed for practical use in the transformation between ICRS and ITRS (Sect. 5).
is proposed for practical use in the transformation between ICRS and ITRS (Sect. 5).
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{2747f1.ps}\end{figure}](/articles/aa/full/2002/40/aa2747/Timg8.gif) |
Figure 1: The non-rotating origin with respect to the ITRF. |
| Open with DEXTER | |
Consider a displacement of the CIP between dates t0 and t, the point ![]() along the moving equator defines the broken arc
along the moving equator defines the broken arc
![]() (see Fig. 1):
(see Fig. 1):
| (1) |
| (2) |
The computation of
![]() is based upon combined time series C04 for polar motion which is provided by the Earth Orientation Parameters Product Center of the International Earth Rotation Service (IERS EOP-PC) based at the Paris Observatory, France. Such a series is obtained by the combination of individual polar motion series from various spatial and geodetic techniques such as Very Long Baseline radio Interferometry (VLBI), Global Positioning System (GPS, GLONASS), Satellite Laser Ranging (SLR) or Lunar Laser Ranging (LLR). This series give daily averaged values for the CIP coordinates
is based upon combined time series C04 for polar motion which is provided by the Earth Orientation Parameters Product Center of the International Earth Rotation Service (IERS EOP-PC) based at the Paris Observatory, France. Such a series is obtained by the combination of individual polar motion series from various spatial and geodetic techniques such as Very Long Baseline radio Interferometry (VLBI), Global Positioning System (GPS, GLONASS), Satellite Laser Ranging (SLR) or Lunar Laser Ranging (LLR). This series give daily averaged values for the CIP coordinates ![]() ,
,
![]() ,
the values for UT1-UTC and length-of-day LOD, and the Celestial pole offsets
,
the values for UT1-UTC and length-of-day LOD, and the Celestial pole offsets
![]() and
and
![]() which are the corrections to the nutation model IAU 1980. For a sampling of one day (at 0h UTC) the data covers the period from 1962 January 1st until today. The uncertainties on
which are the corrections to the nutation model IAU 1980. For a sampling of one day (at 0h UTC) the data covers the period from 1962 January 1st until today. The uncertainties on ![]() and
and ![]() as given by the IERS EOP-PC (IERS 1999) are displayed in Table 1. The most significant improvement during the early 80's corresponds to the advent of VLBI observations in the combination. The series is plotted in Fig. 2 for the two coordinates and a FFT spectrum of these coordinates is shown in Fig. 3.
as given by the IERS EOP-PC (IERS 1999) are displayed in Table 1. The most significant improvement during the early 80's corresponds to the advent of VLBI observations in the combination. The series is plotted in Fig. 2 for the two coordinates and a FFT spectrum of these coordinates is shown in Fig. 3.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{2747f2.ps}\end{figure}](/articles/aa/full/2002/40/aa2747/Timg19.gif) |
Figure 2:
Observed polar motion during the last two decades from the IERS C04 series, amplitudes are in mas, u-component ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{2747f3.ps}\end{figure}](/articles/aa/full/2002/40/aa2747/Timg20.gif) |
Figure 3: Complex spectrum of polar motion (Fast Fourier Transform) over the total duration of the IERS C04 series (1962-2002), amplitudes are in mas, frequencies are in cycles per year (cpy). |
| Open with DEXTER | |
The GPS technique allows us to estimate directly the rates
![]() and
and
![]() .
Analysis Centers providing series of polar motion rates are mainly the Center for Orbit Determination in Europe (CODE) since 1993.5, the Jet Propulsion Laboratory (JPL, USA) since 1992.4 and the GeoForschungsZentrum (GFZ, Germany) since 1996.5.
.
Analysis Centers providing series of polar motion rates are mainly the Center for Orbit Determination in Europe (CODE) since 1993.5, the Jet Propulsion Laboratory (JPL, USA) since 1992.4 and the GeoForschungsZentrum (GFZ, Germany) since 1996.5.
The computation of
![]() has been performed by using pole coordinates
has been performed by using pole coordinates ![]() and
and ![]() of the C04 series (Sect. 3.2) and their rates
of the C04 series (Sect. 3.2) and their rates
![]() and
and
![]() ,
and by using the pole coordinates rates from the GPS series (Sect. 3.3).
,
and by using the pole coordinates rates from the GPS series (Sect. 3.3).
Let
![]() and
and
![]() be the CIP coordinates in the ITRS. From time series of u and v, we can compute numerically the quantity
be the CIP coordinates in the ITRS. From time series of u and v, we can compute numerically the quantity
![]() given by Eq. (3).
given by Eq. (3).
First, a numerical derivative of u and v has been applied by the following algorithm. For a numerical series S whose sampling is based on a time scale T, the numerical derivative D at the point number n is given by:
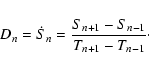 |
(4) |
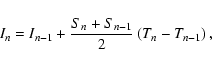 |
(5) |
| 62-67 | 68-71 | 72-79 | 80-83 | 84-95 | 95-02 | |
| 30 | 20 | 15 | 2 | 0.7 | 0.2 | |
| 30 | 20 | 15 | 2 | 0.7 | 0.2 |
We notice that the curve of
![]() shows a periodic variation with period 2334.4 days with an amplitude that reaches 1
shows a periodic variation with period 2334.4 days with an amplitude that reaches 1 ![]() as and which is also present in the polar motion (see Fig. 2). Smaller oscillations with Chandlerian and annual periods are also visible. The trend of the curve is varies during the 40 years depending on the variations of the amplitudes of the chandlerian and annual wobbles. It is a well known fact that the Chandler wobble has undergone some drastic variations in amplitude and phase during the twentieth century. For details see Guinot (1972) and Vondrák (1985).
as and which is also present in the polar motion (see Fig. 2). Smaller oscillations with Chandlerian and annual periods are also visible. The trend of the curve is varies during the 40 years depending on the variations of the amplitudes of the chandlerian and annual wobbles. It is a well known fact that the Chandler wobble has undergone some drastic variations in amplitude and phase during the twentieth century. For details see Guinot (1972) and Vondrák (1985).
Another computation has been made using direct estimates of the rates ![]() and
and ![]() from GPS observations. The use of these estimates is only possible for recent observations, but it provides an independant computation which can be compared with the previous results during the common interval. Differences between
from GPS observations. The use of these estimates is only possible for recent observations, but it provides an independant computation which can be compared with the previous results during the common interval. Differences between
![]() computed with the numerical derivative using C04 series and
computed with the numerical derivative using C04 series and
![]() computed with the estimated rates using various GPS data are plotted in Fig. 5. These differences, which never reach more than 0.1
computed with the estimated rates using various GPS data are plotted in Fig. 5. These differences, which never reach more than 0.1 ![]() as, are not significant at the present level of EOP accuracy. This validates the two independant methods of computation.
as, are not significant at the present level of EOP accuracy. This validates the two independant methods of computation.
It is well known that the polar motion, at low frequencies (periods longer than a few days), is mostly a combination of the Chandler wobble, with a period of about 433 days (Lambeck 1988), and the annual oscillation. The Fourier spectrum in Fig. 3 shows the two main peaks at 433 days and 365.25 days. The combination of these two oscillations causes a modulation of 2334.4 days (about 6.4 years) which is clearly visible in Fig. 2. In addition, we observe a linear trend in both coordinates.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{2747f4.ps}\end{figure}](/articles/aa/full/2002/40/aa2747/Timg29.gif) |
Figure 4:
Displacement
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{Image1.eps}\par\end{figure}](/articles/aa/full/2002/40/aa2747/Timg30.gif) |
Figure 5:
Differences between
|
| Open with DEXTER | |
In this section, we assume that the observed polar motion is well represented by two prograde circular waves at the above periods and by a linear trend:
| u | = | (6) | |
| v | = |
| |
= | (7) | |
| = |
| Parameter | 1962-1982 | 1972-1992 | 1982-2002 |
| 140 | 160 | 178 | |
| 92 | 87 | 80 | |
|
|
-73 | -59 | -58 |
|
|
107 | 110 | 120 |
| u0 mas | 68 | 63 | 41 |
| u1 mas per mjd | 0.006 | 0.005 | 0.000 |
| v0 mas | -378 | -364 | -341 |
| v1 mas per mjd | -0.014 | -0.013 | -0.009 |
As we mentionned above, Chandlerian and annual wobbles amplitudes have known variations. To illustrate these variations, least-squares fits of Chandler, annual and linear terms over three windows spanning twenty years were performed. Note that the data span has to be greater than the modulation period of 433-day and 365.25-day wobbles, i.e. 6.4 years for their decorellation. Table 2 displays the results. Over the complete span 1962-2002, the estimates gives
![]() 158 mas,
158 mas,
![]() 85 mas,
85 mas,
![]() -64
-64![]() ,
,
![]() 113
113![]() ,
u0= 52 mas, v0= -348 mas, u1= 0.004 mas per century and v1= -0.012 mas per century. The quantity
,
u0= 52 mas, v0= -348 mas, u1= 0.004 mas per century and v1= -0.012 mas per century. The quantity
![]() associated with this model has been computed from Eq. (8). It is compared to the previous results from C04 data in Fig. 6. The deviation is caused by changes in amplitudes of the wobbles and the changes in the trends.
associated with this model has been computed from Eq. (8). It is compared to the previous results from C04 data in Fig. 6. The deviation is caused by changes in amplitudes of the wobbles and the changes in the trends.
Now, let us evaluate the size of each term in view of having an accuracy of 1 ![]() as over a century. We take the typical values of
as over a century. We take the typical values of
![]() 200 mas,
200 mas,
![]() 100 mas, u0= 50 mas, v0= -400 mas, u1= 0.005 mas per Julian century and v1= 100 mas per Julian century. It leads to the values diplayed in Table 3. We notice that the periodic term coming from B(t) is near the level of accuracy desired and other periodic terms P(t) are totally negligible, as well as secular terms u0v1 and u1v0. Considering the least-squares estimates reported in Table 2, we have computed the amplitudes of the main terms expressed in above equations, L and B, for three periods of 20 years. Results are displayed in Table 4. The periodic term B(t) is, with these values, below the desirable accuracy, and should be neglected. At 1
100 mas, u0= 50 mas, v0= -400 mas, u1= 0.005 mas per Julian century and v1= 100 mas per Julian century. It leads to the values diplayed in Table 3. We notice that the periodic term coming from B(t) is near the level of accuracy desired and other periodic terms P(t) are totally negligible, as well as secular terms u0v1 and u1v0. Considering the least-squares estimates reported in Table 2, we have computed the amplitudes of the main terms expressed in above equations, L and B, for three periods of 20 years. Results are displayed in Table 4. The periodic term B(t) is, with these values, below the desirable accuracy, and should be neglected. At 1 ![]() as accuracy over the last 40 years, the expression for
as accuracy over the last 40 years, the expression for
![]() is reduced to a linear form:
is reduced to a linear form:
|
|
100 |
|
|
10 |
| u1v0 | 10-6 |
| v1u0 | 10-6 |
|
|
1 |
| Other terms in P | 10-8 |
| 1962-1982 | 1972-1992 | 1982-2002 | |
| L |
-38 | -44 | -51 |
| B |
0.4 | 0.4 | 0.4 |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{2747f6.ps}\end{figure}](/articles/aa/full/2002/40/aa2747/Timg61.gif) |
Figure 6:
Quantity
|
| Open with DEXTER | |
The diurnal and subdiurnal tidal variations for polar motion provided by Ray (McCarthy 1996; Ray 1994) should be added for a more rigourous study due to possible effects from their very short periods in the time integration. These high-frequency contributions are very small compared to the amplitude of the long periodic polar motion: they can reach a maximum of 0.5 mas.
We have computed analytically the contribution of these corrections ![]() and
and ![]() in
in
![]() .
The analytical model used in the IERS Conventions (McCarthy 1996) is in the form:
.
The analytical model used in the IERS Conventions (McCarthy 1996) is in the form:
| |
= | 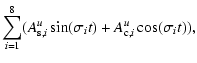 |
(13) |
| = | 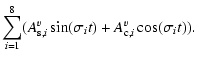 |
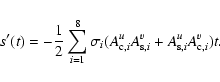 |
(14) |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{2747f7.ps}\end{figure}](/articles/aa/full/2002/40/aa2747/Timg69.gif) |
Figure 7:
Displacement of the Terrestrial Ephemeris Origin
|
| Open with DEXTER | |
As a conclusion of this study, we propose a numerical expression for the quantity
![]() .
Although such a model is limited in time because of unpredictable changes in the wobbles amplitudes, it is possible to provide a numerical expression for
.
Although such a model is limited in time because of unpredictable changes in the wobbles amplitudes, it is possible to provide a numerical expression for
![]() which represents the motion of the TEO in the ITRS with an accuracy of 1
which represents the motion of the TEO in the ITRS with an accuracy of 1 ![]() as over the last 40 years. On this span, variations in the amplitudes of the wobbles will not produce an error larger than 1
as over the last 40 years. On this span, variations in the amplitudes of the wobbles will not produce an error larger than 1 ![]() as. The following expression is fitted on the curve obtained from C04 data:
as. The following expression is fitted on the curve obtained from C04 data:
If the Chandler amplitude in the next years does not present variations larger than during the span 1962-2002, then according to Table 4, the uncertainty on the linear trend is 13 ![]() as per julian century. We can ensure that the 1
as per julian century. We can ensure that the 1 ![]() as accuracy linear model can be extended for the 10 next years.
as accuracy linear model can be extended for the 10 next years.
Figure 7 shows the linear model of
![]() corresponding to expression (15) together with the numerical computation from observations. If unexpected variations in the amplitudes of the wobbles occur in the coming years, such a model will have to be updated.
corresponding to expression (15) together with the numerical computation from observations. If unexpected variations in the amplitudes of the wobbles occur in the coming years, such a model will have to be updated.