A&A 394, 71-76 (2002)
DOI: 10.1051/0004-6361:20021134
The late-time radio spectrum of SN 1993J
M. A. Pérez-Torres1 - A. Alberdi2 - J. M. Marcaide3
1 - Istituto di Radioastronomia,
via P. Gobetti 101, 40129 Bologna, Italy
2 -
Instituto de Astrofísica de Andalucía, CSIC, Apdo.
Correos 3004, 18080 Granada, Spain
3 -
Departamento de Astronomía y
Astrofísica, Universidad de Valencia,
46100 Burjassot, Spain
Received 16 May 2002 / Accepted 30 July 2002
Abstract
We present VLA radio continuum measurements of SN 1993J in M 81
at the frequencies of 0.32 (P-band), 1.3 and 1.7 (L-band),
4.9 (C-band), 8.5 (X-band), and 14.9 (U-band) GHz
carried out on December 17 and 21, 2000, about 2820 days after
the supernova explosion.
We find that a power-law spectrum, free-free absorbed by an homogeneous,
or clumpy, distribution of ionized gas yields the best fit to
the radio data.
A combined homogeneous-clumpy model is not favored, but neither
totally excluded.
This result contrasts with the modeling
of the early (
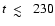 days) radio emission from SN 1993J,
where a mixture of homogeneous and clumpy absorbers appeared to be
necessary to adequately describe the behavior of the light curves.
The radio spectrum of supernova SN 1993J between 0.32 and 14.9 GHz
is well characterized by
days) radio emission from SN 1993J,
where a mixture of homogeneous and clumpy absorbers appeared to be
necessary to adequately describe the behavior of the light curves.
The radio spectrum of supernova SN 1993J between 0.32 and 14.9 GHz
is well characterized by
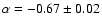 (
(
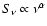 ),
typical of an optically thin radio supernova.
A fit to the radio spectra of SN 1993J from
),
typical of an optically thin radio supernova.
A fit to the radio spectra of SN 1993J from 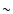 70 up to 2820 days shows
that the observed spectral index of SN 1993J
has been slowly evolving since
70 up to 2820 days shows
that the observed spectral index of SN 1993J
has been slowly evolving since 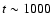 days, with
the observed spectral index changing from
days, with
the observed spectral index changing from
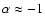 to
to
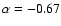 .
This spectral evolution seems to suggest that, in addition to the
radiative (synchrotron) losses,
adiabatic cooling and ionization (Coulomb) losses at the lowest frequencies
might be contributing significantly to the integrated electron spectrum.
.
This spectral evolution seems to suggest that, in addition to the
radiative (synchrotron) losses,
adiabatic cooling and ionization (Coulomb) losses at the lowest frequencies
might be contributing significantly to the integrated electron spectrum.
Key words:
techniques: interferometric -
supernovae: individual: SN 1993J -
ISM: supernova remnants -
radio continuum: stars -
galaxies: individual: M 81
1 Introduction
The most widely accepted model for the radio emission from
supernovae is the standard interaction model, in which the observed
radio (synchrotron) emission is associated with the interaction region between the
supernova ejecta and the pre-supernova wind of the progenitor star.
The radio emission shows an early rise and
a late decline due to a low-frequency absorption process.
Chevalier (1982) considered a number of mechanisms that could
account for the absorption:
(i) free-free absorption by material in front of the forward shock front,
(ii) free-free absorption by material within the emitting region,
(iii) synchrotron self-absorption, and
(iv) the Razin-Tsytovich effect.
At the beginning of the 1980's, the available radio light curves could
be well explained by synchrotron radio emission that was
partially free-free absorbed by ionized thermal material in
the circumstellar wind of the progenitor star (e.g. Weiler et al. 1986).
The availability of more complete light curves for these supernovae
(e.g. Weiler et al. 1989, 1990)
provided further support for this mechanism.
However, as new radio supernovae have been detected, the situation has become more complex.
For example, the radio light curves of SN1986J showed a
different shape in the rise to maximum, which was interpreted by Weiler et al. (1990)
as evidence for internal free-free absorption.
These authors suggested that a filamentary, clumpy-like structure of thermal absorbers
could also be the source of the slow radio turn-on.
Chevalier (1998) has recently argued that synchrotron self-absorption
is likely to be the dominant absorption mechanism for some radio supernovae,
in particular for SN1987A, and for type Ib and type Ic supernovae.
Finally, observations of SN 1993J seem to indicate that more than one
absorption mechanism plays a role
(Fransson & Björnsson 1998; Pérez-Torres et al. 2001;
Mioduszewski et al. 2001).
SN 1993J is to date the radio supernova whose evolution has been monitored
in greatest detail.
The brightness and proximity of SN 1993J in M 81
offered an unprecedented occasion for VLBI studies,
almost since the supernova explosion on 28 March 1993.
For the first time, a shell-like structure in a young
radio supernova was discovered (Marcaide et al. 1995a), in
agreement with the circumstellar interaction model.
Marcaide et al. (1995b) showed that the expansion of SN 1993J was
self-similar, and produced the first movie of an expanding supernova.
Later on, Marcaide et al. (1997) reported on the deceleration
of the SN 1993J expansion, a result recently confirmed by Bartel et al.
(2000).
The modeling of the radio light curves of SN 1993J
has also given deeper insight into the supernova phenomenon.
It seems now clear that the progenitor of SN 1993J had a substantial
mass-loss rate during the late stages of its evolution ( 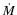
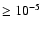
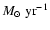 ,
e.g. van Dyk et al. 1994).
The power-law density profile
of the circumstellar medium around SN 1993J seems to be different from the standard one
(Lundqvist 1994; van Dyk et al. 1994;
Marcaide et al. 1997; Immler et al. 2001;
Mioduszewski et al. 2001), although
Fransson & Björnsson (1998) have succeeded in modeling
the SN 1993J radio light curves with an s=2 density profile for the CSM.
,
e.g. van Dyk et al. 1994).
The power-law density profile
of the circumstellar medium around SN 1993J seems to be different from the standard one
(Lundqvist 1994; van Dyk et al. 1994;
Marcaide et al. 1997; Immler et al. 2001;
Mioduszewski et al. 2001), although
Fransson & Björnsson (1998) have succeeded in modeling
the SN 1993J radio light curves with an s=2 density profile for the CSM.
Based on numerical modelings of the available radio
data for SN 1993J, Fransson & Björnsson (1998) and
Pérez-Torres et al. (2001) made predictions about its
late-time, low frequency (<1.4 GHz) radio light behaviour.
However, observational results of the low-frequency radio emission from SN 1993J were
lacking.
Thus, we carried out VLA observations between 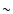 322 and
322 and 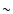 15 000 MHz
aimed at checking the above modeling efforts,
as well as a way to
discern the main absorbing processes acting in SN 1993J.
15 000 MHz
aimed at checking the above modeling efforts,
as well as a way to
discern the main absorbing processes acting in SN 1993J.
2 Observations and data reduction
We observed SN 1993J using 25 antennas of the VLA in
its most extended configuration
(A, with baseline lengths from 0.68 up to 36.4 km)
at L (18 cm) and P (90 cm) bands
from UT 13:55 to UT 15:25 on 17 December 2000,
and at U (14.9 GHz), X(8.5 GHz), C(4.9 GHz), L(1.3-1.7 GHz), and P(0.32 GHz) bands
from UT 08:40 to UT 11:40 on 21 December 2000.
Each frequency band was split into two intermediate frequencies (IFs).
Data processing was made using the Astronomical Image
Processing System (AIPS).
We first describe briefly the observations at the higher frequencies,
and then emphasize and describe in detail those at lower
frequencies, particularly those in the P-band,
deemed to be a discriminator of the dominant
absorption mechanism in SN 1993J.
Table 1 summarizes our observations.
The flux densities reported were obtained by combining the data from
both intermediate frequencies (IFs) at each frequency band,
except at L-band, for which the frequency separation was large enough
that we could use each flux density value independently.
We used a standard continuum mode at U, X, and C bands, thus covering a
bandwidth of 50 MHz per IF and frequency band. At all three bands,
we observed SN 1993J phase-referenced to 0917+624. The source
0917+624 also served as the phase reference for the system calibration.
At U- and X-band, 3C 286 was used as primary flux calibrator (assumed of constant
flux density), while at C-band 3C 147 was used instead.
At U-band, the integration times on SN 1993J
and 0917+624 were
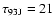 min and
min and
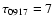 min,
while at X-band these were 11.5 and 6 min, and at C-band 12 and 7 min, respectively.
min,
while at X-band these were 11.5 and 6 min, and at C-band 12 and 7 min, respectively.
Observations were done in spectral-line mode in order to detect the
likely presence of radio frequency interference (RFI) in the data, and
also to avoid bandwidth smearing.
In addition, this observing mode allows a more careful editing.
3C 286 was used at both bands as primary flux calibrator,
as well as bandpass calibrator.
L-band observations.
Each of the two 12.5-MHz IFs at L-band (centered at 1.34 and 1.67 MHz,
respectively) were split into 8 spectral channels.
Observations of SN 1993J (
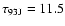 min)
were phase-referenced to 0917+624 (
min)
were phase-referenced to 0917+624 (
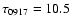 min).
0917+624 was also used as secondary flux calibrator at L-band.
Our final hybrid map at L-band (not shown here)
was made at an effective observing frequency of 1.50 GHz.
The peak of brightness of the map (97.4 mJy beam-1)
corresponds to the nucleus of M 81, and the flux density
of SN 1993J is 31.9 mJy.
The rms of the image background is 0.3 mJy/beam.
The flux density values reported
at L-band in Table 1 correspond
to each IF, 1.34 and 1.67 GHz, respectively.
Since the center frequencies in L-band are quite separated,
they can be used as independent values for the purpose of fitting a
spectral index (see below). We note that, though the distance between SN 1993J
and M 81 (2
min).
0917+624 was also used as secondary flux calibrator at L-band.
Our final hybrid map at L-band (not shown here)
was made at an effective observing frequency of 1.50 GHz.
The peak of brightness of the map (97.4 mJy beam-1)
corresponds to the nucleus of M 81, and the flux density
of SN 1993J is 31.9 mJy.
The rms of the image background is 0.3 mJy/beam.
The flux density values reported
at L-band in Table 1 correspond
to each IF, 1.34 and 1.67 GHz, respectively.
Since the center frequencies in L-band are quite separated,
they can be used as independent values for the purpose of fitting a
spectral index (see below). We note that, though the distance between SN 1993J
and M 81 (2
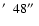 )
is much larger than the dimensions of the restoring beam
(
)
is much larger than the dimensions of the restoring beam
(
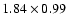 arcsec), wide field mapping is necessary
if one aims at accurate determinations of the flux densities of SN 1993J
at low frequencies.
arcsec), wide field mapping is necessary
if one aims at accurate determinations of the flux densities of SN 1993J
at low frequencies.
P-band observations.
At P-band, each of the two 3.125-MHz IFs (centered at 322 and 327 MHz,
respectively) was split into 32 spectral channels, which permitted a
detailed inspection of the data, looking for the presence of RFI.
Since 0917+624 is a relatively weak source at P-band, unlike at
higher frequencies, confusion of many strong sources in the field made it
unsuitable as secondary calibrator. Therefore, the much stronger source
J1206+6414 (3C 268.3) was used instead. The total integration times
were
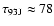 min, and
min, and
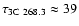 min.
We imaged 3C 268.3 to obtain an accurate value of its flux density.
We noticed that the coordinates used for 3C 268.3 at the correlator
(
min.
We imaged 3C 268.3 to obtain an accurate value of its flux density.
We noticed that the coordinates used for 3C 268.3 at the correlator
(
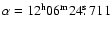 ,
,
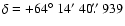 ;
J2000.0) were off from the actual ones by more than one arcmin. Indeed,
the coordinates obtained using the AIPS task JMFIT were
;
J2000.0) were off from the actual ones by more than one arcmin. Indeed,
the coordinates obtained using the AIPS task JMFIT were
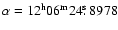 ,
,
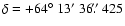 (J2000.0).
Such position offset for 3C 268.3 translated into a similar one for
SN 1993J and the whole sky around it.
We corrected the phases of 3C 268.3 for this offset.
(J2000.0).
Such position offset for 3C 268.3 translated into a similar one for
SN 1993J and the whole sky around it.
We corrected the phases of 3C 268.3 for this offset.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{ms2681fig1.eps}
\end{figure}](/articles/aa/full/2002/40/aa2681/Timg34.gif) |
Figure 1:
a) Field of of view of the VLA in A configuration (VLA-A) around SN 1993J
at P-band, on 17 and 21 December, 2000.
The image shows only the inner 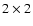 deg (rather
than the deg (rather
than the 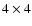 deg actually mapped), which includes
38 fields out of the 78 used in the hybrid mapping process.
The image is centered on SN 1993J.
Only contours above 20 mJy beam-1 have been drawn.
b) Hybrid map of the galaxy M 82.
The contours are (-2, 2, 3, 5, 7, 10, 15, 20, 30, 40, 50, 70, 90, 100, 110, 120) deg actually mapped), which includes
38 fields out of the 78 used in the hybrid mapping process.
The image is centered on SN 1993J.
Only contours above 20 mJy beam-1 have been drawn.
b) Hybrid map of the galaxy M 82.
The contours are (-2, 2, 3, 5, 7, 10, 15, 20, 30, 40, 50, 70, 90, 100, 110, 120) 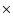 4.2 mJy beam-1, the off-source rms noise.
The peak of brightness of the map
(
4.2 mJy beam-1, the off-source rms noise.
The peak of brightness of the map
(
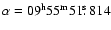 , ,
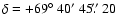 ;
J2000.0)
is 537.8 mJy beam-1. The flux density in the image above the 2-rms level is 10.49 Jy.
The dimensions of the restoring beam
are ;
J2000.0)
is 537.8 mJy beam-1. The flux density in the image above the 2-rms level is 10.49 Jy.
The dimensions of the restoring beam
are
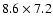 arcsec, with the beam's major axis
oriented along
arcsec, with the beam's major axis
oriented along
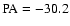 deg.
c) Hybrid map of SN 1993J and the nucleus of its host galaxy M 81.
The contours are (-3, 3, 5, 10, 15, 20, 25, 30) deg.
c) Hybrid map of SN 1993J and the nucleus of its host galaxy M 81.
The contours are (-3, 3, 5, 10, 15, 20, 25, 30) 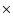 3.3 mJy beam-1,
the off-source rms noise.
The peak of brightness of the map corresponds to the supernova
and is 71.1 mJy beam-1.
The dimensions of the restoring beam
are
3.3 mJy beam-1,
the off-source rms noise.
The peak of brightness of the map corresponds to the supernova
and is 71.1 mJy beam-1.
The dimensions of the restoring beam
are
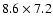 arcsec, with the beam's major axis
oriented along arcsec, with the beam's major axis
oriented along
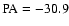 deg. deg. |
| Open with DEXTER |
With the 3C 268.3 data corrected, we imaged
SN 1993J at P-band, aimed to determine its flux density.
Since the primary beam of the VLA at P-band is so large
(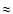
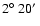 ), bright sources far from
the supernova could greatly affect our image.
Further, to obtain a good signal-to-noise ratio (SNR) in the image, one
is forced to map even distant, strong sources.
The situation is similar to that encountered
at L-band, where self-calibration was mandatory to improve the SNR
of the image, but useless unless M 81 was also included in the imaging process.
At P-band, not only the M 81 nucleus is important,
but also far away, strong sources such as
M 82 need also to be taken into account to be able to apply self-calibration
to the data.
We used the AIPS task SETFC to create a list of fields with
suspected sources in them, rather than making an enormous,
computationally unmanageable image. It is worth noticing
that the interferometric phases are initially so poorly calibrated
that the reconstructed image will show very few sources, making
very difficult the convergence of the hybrid mapping procedure.
Therefore, we used the AIPS procedure FACES,
which searches for sources in the NVSS catalog,
to supply an initial model of the sky,
and thus improve the global phase calibration.
We then applied wide-field imaging on this self-calibrated dataset:
since the array configuration looks different to sources in different
parts of the (large) primary beam, we handled this by
computing the uv-coverage differently for many small fields
within the task IMAGR.
Sources above a threshold of 33 mJy (at a frequency of 1.4 GHz)
were searched for as a priori candidates in the NVSS catalog,
within a
), bright sources far from
the supernova could greatly affect our image.
Further, to obtain a good signal-to-noise ratio (SNR) in the image, one
is forced to map even distant, strong sources.
The situation is similar to that encountered
at L-band, where self-calibration was mandatory to improve the SNR
of the image, but useless unless M 81 was also included in the imaging process.
At P-band, not only the M 81 nucleus is important,
but also far away, strong sources such as
M 82 need also to be taken into account to be able to apply self-calibration
to the data.
We used the AIPS task SETFC to create a list of fields with
suspected sources in them, rather than making an enormous,
computationally unmanageable image. It is worth noticing
that the interferometric phases are initially so poorly calibrated
that the reconstructed image will show very few sources, making
very difficult the convergence of the hybrid mapping procedure.
Therefore, we used the AIPS procedure FACES,
which searches for sources in the NVSS catalog,
to supply an initial model of the sky,
and thus improve the global phase calibration.
We then applied wide-field imaging on this self-calibrated dataset:
since the array configuration looks different to sources in different
parts of the (large) primary beam, we handled this by
computing the uv-coverage differently for many small fields
within the task IMAGR.
Sources above a threshold of 33 mJy (at a frequency of 1.4 GHz)
were searched for as a priori candidates in the NVSS catalog,
within a 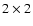 deg region around SN 1993J.
This resulted in 78 fields that were
cleaned using wide-field mapping.
Figure 1 shows
the inner 1
deg region around SN 1993J.
This resulted in 78 fields that were
cleaned using wide-field mapping.
Figure 1 shows
the inner 1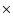 1 deg of our final, composite image of
the VLA-A field at P-band.
For clarity, only contours above 20 mJy beam-1 have been drawn.
Panel b shows the galaxy M 82,
offset about
1 deg of our final, composite image of
the VLA-A field at P-band.
For clarity, only contours above 20 mJy beam-1 have been drawn.
Panel b shows the galaxy M 82,
offset about
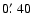 from SN 1993J.
The latter is shown in panel c along with the nucleus of its host galaxy M 81.
M 82 has a flux of
from SN 1993J.
The latter is shown in panel c along with the nucleus of its host galaxy M 81.
M 82 has a flux of 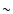 10.5 Jy, at an epoch when SN 1993J has a flux of a mere
71.1 mJy (see Table 1 for details of the observations).
10.5 Jy, at an epoch when SN 1993J has a flux of a mere
71.1 mJy (see Table 1 for details of the observations).
3 The radio spectrum of SN 1993J
We fitted the radio spectrum of SN 1993J obtained
on 17 and 21 December 2000 using three models for its radio emission.
These models are described by the equations
where
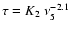 ,
and
,
and
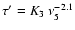 .
These equations represent a simple power-law spectrum (model 1),
a power-law spectrum free-free absorbed by a screen of homogeneously
distributed ionized gas (model 2),
and
a power-law spectrum free-free absorbed by a "clumpy'' medium (model 3).
To facilitate comparisons with the modeling of van Dyk et al. (1994),
we have used here their notation:
.
These equations represent a simple power-law spectrum (model 1),
a power-law spectrum free-free absorbed by a screen of homogeneously
distributed ionized gas (model 2),
and
a power-law spectrum free-free absorbed by a "clumpy'' medium (model 3).
To facilitate comparisons with the modeling of van Dyk et al. (1994),
we have used here their notation:
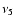 is the frequency, in units of 5 GHz;
is the frequency, in units of 5 GHz;
 is the observed spectral index;
K1 is the flux density at 5 GHz, in mJy;
and K2 and K3 are the optical depths at 5 GHz of the
homogeneous and "clumpy'' external absorbing media, respectively,
at the epoch of our observations.
Table 2 summarizes our results, and Fig. 2
shows the best fits to models 1 through 3.
A simple power-law spectrum (model 1) yields a good fit to the data
from 14.94 GHz down to 1.34 GHz, but departs significantly from the
actual flux density at frequencies below 400 MHz, and can
be ruled out.
The best fits are given by models 2 (homogeneous absorbing
medium) and 3 (clumpy absorbing medium), which yield an observed
spectral index
is the observed spectral index;
K1 is the flux density at 5 GHz, in mJy;
and K2 and K3 are the optical depths at 5 GHz of the
homogeneous and "clumpy'' external absorbing media, respectively,
at the epoch of our observations.
Table 2 summarizes our results, and Fig. 2
shows the best fits to models 1 through 3.
A simple power-law spectrum (model 1) yields a good fit to the data
from 14.94 GHz down to 1.34 GHz, but departs significantly from the
actual flux density at frequencies below 400 MHz, and can
be ruled out.
The best fits are given by models 2 (homogeneous absorbing
medium) and 3 (clumpy absorbing medium), which yield an observed
spectral index
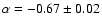 .
The frequency at which the free-free optical depth becomes unity
is very similar for both model 2 (
.
The frequency at which the free-free optical depth becomes unity
is very similar for both model 2 (
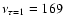 MHz) and
model 3 (
MHz) and
model 3 (
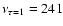 MHz).
Note, however, that the very-low radio frequency behavior of the spectrum
is significantly different (see Fig. 2).
While model 2 (solid line) predicts a sharp fall-off below frequencies
of
MHz).
Note, however, that the very-low radio frequency behavior of the spectrum
is significantly different (see Fig. 2).
While model 2 (solid line) predicts a sharp fall-off below frequencies
of  200 MHz, model 3 (dashed line) predicts
a much milder flux density decrease.
Unfortunately, the absence of radio measurements below 322 MHz
does not allow us to rule out either of these models.
Thus, from Table 2 we cannot exclude, or prefer, either of the
two alternative models.
200 MHz, model 3 (dashed line) predicts
a much milder flux density decrease.
Unfortunately, the absence of radio measurements below 322 MHz
does not allow us to rule out either of these models.
Thus, from Table 2 we cannot exclude, or prefer, either of the
two alternative models.
To model the early-time (
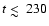 days) radio light curves
of SN 1993J,
van Dyk et al. (1994) invoked a combined
"homogeneous-clumpy'' model of the form
days) radio light curves
of SN 1993J,
van Dyk et al. (1994) invoked a combined
"homogeneous-clumpy'' model of the form
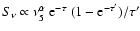 .
For such model, we can also obtain acceptable solutions
(e.g.
.
For such model, we can also obtain acceptable solutions
(e.g.
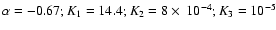 )
at the expense of increasing
)
at the expense of increasing
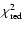 by
by 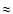 50%.
If the fitting parameters are left unconstrained, this model yields an even
better fit than models 2 and 3, but at the unaffordable price of a
negative - hence unphysical - value for K2, or K3.
Clearly, the combined "homogeneous-clumpy'' model cannot be preferred over
models 2 or 3, but we also feel we cannot exclude it
solely on the basis of a 50% increase of the reduced
50%.
If the fitting parameters are left unconstrained, this model yields an even
better fit than models 2 and 3, but at the unaffordable price of a
negative - hence unphysical - value for K2, or K3.
Clearly, the combined "homogeneous-clumpy'' model cannot be preferred over
models 2 or 3, but we also feel we cannot exclude it
solely on the basis of a 50% increase of the reduced 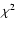 .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{ms2681fig2.eps}
\end{figure}](/articles/aa/full/2002/40/aa2681/Timg88.gif) |
Figure 2:
Fits to the continuum radio spectrum of SN 1993J on 17 and 21 December 2000.
As indicated in the figure, the dotted, solid, and dashed lines correspond to
models 1, 2, and 3, respectively, as described in the text.
Note that the size of each data point but the one at 0.324 GHz, is larger than
its associated error bar. |
| Open with DEXTER |
For a power-law relativistic electron distribution,
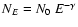 ,
the spectral index of the electron distribution
,
the spectral index of the electron distribution 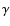 is related to the observed spectral index:
is related to the observed spectral index:
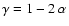 .
From our value of
.
From our value of 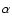 ,
it then follows that
,
it then follows that
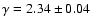 .
This value of
.
This value of 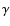 agrees well with that predicted by Fransson &
Björnsson (1998) for SN 1993J at epochs
agrees well with that predicted by Fransson &
Björnsson (1998) for SN 1993J at epochs
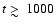 days.
We should note that synchrotron self-absorption could play a role in the
radio emission from SN 1993J (Chevalier 1998; Fransson & Björnsson
1998; Pérez-Torres et al. 2001; Mioduszewski et al. 2001).
In particular, the modeling of Fransson & Björnsson (see their Fig. 12),
predicted a flux density of
days.
We should note that synchrotron self-absorption could play a role in the
radio emission from SN 1993J (Chevalier 1998; Fransson & Björnsson
1998; Pérez-Torres et al. 2001; Mioduszewski et al. 2001).
In particular, the modeling of Fransson & Björnsson (see their Fig. 12),
predicted a flux density of 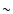 70 mJy at 0.32 GHz and for
the approximate epoch of our observations, while the modeling of Pérez-Torres et al. predicted
at that frequency a flux density larger than 100 mJy.
Such an excess in flux of the latter modeling is likely related to
the different spectral evolution obtained for the electron spectrum.
70 mJy at 0.32 GHz and for
the approximate epoch of our observations, while the modeling of Pérez-Torres et al. predicted
at that frequency a flux density larger than 100 mJy.
Such an excess in flux of the latter modeling is likely related to
the different spectral evolution obtained for the electron spectrum.
Figure 3 shows the evolution of the observed spectral
index of SN 1993J from 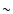 70 up to 2820 days after the explosion.
For each epoch, we fitted the available radio continuum data
(van Dyk, private communication) using model 2 as described above.
While at early epochs the fits are not superb,
they seem to be compatible with
70 up to 2820 days after the explosion.
For each epoch, we fitted the available radio continuum data
(van Dyk, private communication) using model 2 as described above.
While at early epochs the fits are not superb,
they seem to be compatible with
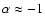 .
However, for epochs
.
However, for epochs
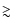 1000 days, there seems to be a clear trend:
the observed spectral index,
1000 days, there seems to be a clear trend:
the observed spectral index, 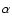 ,
becomes progressively less steep.
This spectral evolution could be explained assuming significant energy losses,
mainly associated with synchrotron, as well as Coulomb and expansion losses.
Fransson & Björnsson (1998) proposed a model
that reproduces reasonably well the observed spectral evolution
of SN 1993J.
In their model, a constant fraction of the shocked thermal electrons
- characterized by a constant spectral index - are injected and accelerated.
These electrons lose their energy mainly due to synchrotron losses,
thus steepening the integrated electron spectrum.
Moreover, these authors predict that, for the physical
parameters they are considering, radiative (synchrotron) losses
start to become less important at
,
becomes progressively less steep.
This spectral evolution could be explained assuming significant energy losses,
mainly associated with synchrotron, as well as Coulomb and expansion losses.
Fransson & Björnsson (1998) proposed a model
that reproduces reasonably well the observed spectral evolution
of SN 1993J.
In their model, a constant fraction of the shocked thermal electrons
- characterized by a constant spectral index - are injected and accelerated.
These electrons lose their energy mainly due to synchrotron losses,
thus steepening the integrated electron spectrum.
Moreover, these authors predict that, for the physical
parameters they are considering, radiative (synchrotron) losses
start to become less important at
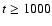 days at frequencies below
days at frequencies below
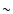 2.3 GHz, whereas energy losses of the electrons due to
adiabatic and Coulomb cooling contribute significantly below 2.3 GHz,
which seems consistent with the observational results.
We note that a multi-frequency monitoring of SN 1993J at radio frequencies down to
2.3 GHz, whereas energy losses of the electrons due to
adiabatic and Coulomb cooling contribute significantly below 2.3 GHz,
which seems consistent with the observational results.
We note that a multi-frequency monitoring of SN 1993J at radio frequencies down to 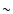 70 MHz,
would likely prove to be very useful to further constrain the population of electrons
responsible for the emission, as well as to better understand the late-time
radio evolution of SN 1993J.
70 MHz,
would likely prove to be very useful to further constrain the population of electrons
responsible for the emission, as well as to better understand the late-time
radio evolution of SN 1993J.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{ms2681fig3.eps}\end{figure}](/articles/aa/full/2002/40/aa2681/Timg96.gif) |
Figure 3:
Evolution of the observed spectral index, 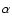 ,
for SN 1993J,
as obtained from fitting the radio continuum data at each epoch
to model 2 (see text for details). ,
for SN 1993J,
as obtained from fitting the radio continuum data at each epoch
to model 2 (see text for details). |
| Open with DEXTER |
Figure 4 shows the fits of model 2
to all data points (solid line), and
to all but the P-band data point (dashed line).
Because any absorption model will obviously fit
by turning down sharply below the lowest frequency data point,
the availability of radio continuum measurements at the lowest
possible frequencies is important,
in particular as a radio supernova ages.
Had the P-band data not been available, we could
have wrongly concluded that the peak of the SN 1993J spectrum is
at 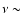 0.8 GHz at a level of
0.8 GHz at a level of 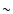 35 mJy.
Having the P-data point available, we conclude
that the peak is around, or below 0.3 GHz,
and at least at a level of 70 mJy.
(We note that a similar fit to all data, but using
model 3 rather than model 2,
would not change this result.)
Similarly, the best fit to our SN 1993J radio data using models 2 or 3
as described above, but not including the P-band measurement,
yields
35 mJy.
Having the P-data point available, we conclude
that the peak is around, or below 0.3 GHz,
and at least at a level of 70 mJy.
(We note that a similar fit to all data, but using
model 3 rather than model 2,
would not change this result.)
Similarly, the best fit to our SN 1993J radio data using models 2 or 3
as described above, but not including the P-band measurement,
yields
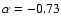 ,
a somewhat steeper
value than is obtained if all data points are used,
,
a somewhat steeper
value than is obtained if all data points are used,
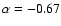 ,
but within 2
,
but within 2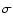 of it.
of it.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{ms2681fig4.eps}
\end{figure}](/articles/aa/full/2002/40/aa2681/Timg100.gif) |
Figure 4:
Fits to the continuum radio spectrum of SN 1993J on 17 and 21 December 2000.
Although both fits correspond to model 2, in one case (solid line) all radio measurements
are used, while in the other case (dashed line) all but the P-band data point are used.
This results in a turnover frequency much higher than actually observed.
See text for details. |
| Open with DEXTER |
4 Summary
We present VLA radio continuum measurements of SN 1993J in M 81
taken on 17 and 21 December, 2000, about 2820 days after the supernova
explosion, spanning the frequency range from 0.32 to 14.9 GHz.
We discuss in detail the P-band (322-327 MHz) observations, since
the task of obtaining the flux density at these frequencies is much harder
than at higher frequencies, due to confusion from many nearby and far away,
strong sources, e.g. M 82.
We also point out the importance of having a radio spectral coverage
that extends down to P-band as the supernova ages, since otherwise the
conclusions can be wrong.
We discuss three models for the late radio emission of SN 1993J:
(i) a simple power-law spectrum,
(ii) a power-law spectrum
free-free absorbed by a screen of homogeneously distributed ionized gas,
and (iii) a power-law spectrum free-free absorbed by a "clumpy'' medium.
We find that the best fit to the data is yielded by a power-law spectrum
free-free absorbed by either a homogeneous, or a clumpy, distribution of ionized gas.
However, a mixture of homogeneous and
clumpy absorbers, while not preferred, cannot be totally ruled out.
The radio spectrum between 0.32 and 14.94 GHz
is well characterized by
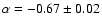 (
(
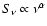 ),
typical of an optically thin radio supernova, and
is significantly different from that obtained at epochs
),
typical of an optically thin radio supernova, and
is significantly different from that obtained at epochs
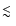 1000 days
between 1.4 and 14.9 GHz, which indicates an ongoing spectral evolution
in the radio emission from SN 1993J.
Since the spectral index
1000 days
between 1.4 and 14.9 GHz, which indicates an ongoing spectral evolution
in the radio emission from SN 1993J.
Since the spectral index 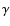 of the electron distribution
(
of the electron distribution
(
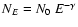 ), is related to the observed spectral index
by
), is related to the observed spectral index
by
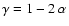 ,
our value of
,
our value of 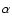 translates into
translates into
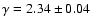 ,
which agrees well with that predicted by
Fransson & Björnsson (1998)
for
,
which agrees well with that predicted by
Fransson & Björnsson (1998)
for
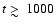 days.
We also fit the available radio continuum data of SN 1993J for
the period from
days.
We also fit the available radio continuum data of SN 1993J for
the period from 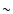 70 up to 2820 days since the explosion,
using a power-law spectrum free-free
absorbed by a screen of homogeneously distributed ionized gas.
The fit shows that the observed spectral index of SN 1993J
has been slowly evolving since
70 up to 2820 days since the explosion,
using a power-law spectrum free-free
absorbed by a screen of homogeneously distributed ionized gas.
The fit shows that the observed spectral index of SN 1993J
has been slowly evolving since
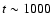 days on, with
days on, with
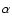 increasing from a value close to -1 to the current -0.67.
This spectral evolution seems to suggest that, in addition to the
radiative (synchrotron) losses,
adiabatic cooling and ionization (Coulomb) losses at the lowest frequencies
might be contributing significantly to the integrated electron spectrum.
An extension of the low frequency observations further down to
increasing from a value close to -1 to the current -0.67.
This spectral evolution seems to suggest that, in addition to the
radiative (synchrotron) losses,
adiabatic cooling and ionization (Coulomb) losses at the lowest frequencies
might be contributing significantly to the integrated electron spectrum.
An extension of the low frequency observations further down to 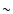 70 MHz should
help to fine tune the physical parameters of SN 1993J, and discern between
the homogeneous or clumpy nature of its circumstellar medium.
From a technical point of view, such observations will be challenging.
70 MHz should
help to fine tune the physical parameters of SN 1993J, and discern between
the homogeneous or clumpy nature of its circumstellar medium.
From a technical point of view, such observations will be challenging.
Acknowledgements
We thank Lucas Lara for his help with some aspects of the data
reduction process, and Gianfranco Brunetti for discussions.
We thank Kurt Weiler for making the VLA data publicly available.
We are also grateful to an anonymous referee for a careful
and constructive review of our manuscript.
MAPT is grateful to the Instituto de Astrofísica de Andalucía
for its hospitality during a short visit.
This research has been supported by a Marie Curie Fellowship
of the European Community (contract IHP-MCFI-99-1),
and by the Spanish DGICYT grants AYA2001-2147-C02-01
and AYA2001-2147-C02-02.
The VLA is an instrument of the National Radio Astronomy Observatory,
which is a facility of the National Science Foundation operated under
cooperative agreement by Associated Universities, Incorporated.
-
Bartel, N., Bietenholz, M. F., Rupen, M. P., et al.
2000, Science, 287, 112
In the text
NASA ADS
-
Chevalier, R. A.
1982a, ApJ, 259, 302
In the text
NASA ADS
-
Chevalier, R. A.
1998, ApJ, 499, 810
In the text
NASA ADS
-
Fransson, C., & Björnsson, C.-I.
1998, ApJ, 509, 861
In the text
NASA ADS
-
Immler, S., Aschenbach, B., & Wang, Q. D.
2001, ApJ, 561, L107
In the text
NASA ADS
-
Lundqvist, P. 1994, in
Circumstellar Media in the Late Stages of Stellar Evolution,
ed. R. E. S. Clegg, I. R. Stevens, & W. P. S. Meikle
(Cambridge: Cambridge University Press), 213
In the text
-
Marcaide, J. M., Alberdi, A., Ros, E., et al.
1995a, Nature, 373, 44
In the text
NASA ADS
-
Marcaide, J. M., Alberdi, A., Ros, E., et al.
1995b, Science, 270, 1475
In the text
NASA ADS
-
Marcaide, J. M., Alberdi, A., Ros, E., et al.
1997, ApJ, 486, L31
In the text
NASA ADS
-
Mioduszewski, A. J., Dwarkadas, V. V., & Ball, L.
2001, ApJ, 562, 869
In the text
NASA ADS
-
Pérez-Torres, M. A., Alberdi, A., & Marcaide, J. M.
2001, A&A, 374, 997
In the text
NASA ADS
-
Van Dyk, S. D., Weiler, K. W., Sramek, R. A., et al.
1994, ApJ, 432, L115
In the text
NASA ADS
-
Weiler, K. W., Sramek, R. A., Panagia, N., et al.
1986, ApJ, 301, 790
In the text
NASA ADS
-
Weiler, K. W., Panagia, N., Sramek, R. A., et al.
1989, ApJ, 336, 421
In the text
NASA ADS
-
Weiler, K. W., Panagia, N., & Sramek, R. A.
1990, ApJ, 364, 611
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=17cm,clip]{ms2681fig1.eps}
\end{figure}](/articles/aa/full/2002/40/aa2681/Timg34.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{ms2681fig2.eps}
\end{figure}](/articles/aa/full/2002/40/aa2681/Timg88.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{ms2681fig3.eps}\end{figure}](/articles/aa/full/2002/40/aa2681/Timg96.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{ms2681fig4.eps}
\end{figure}](/articles/aa/full/2002/40/aa2681/Timg100.gif)