A&A 394, 285-297 (2002)
DOI: 10.1051/0004-6361:20021106

Solar ${\vec p}$-modes from 1979 days of the GOLF experiment

B. Gelly1 - M. Lazrek1,2,3 - G. Grec3 - A. Ayad 1,4 - F. X. Schmider1 - C. Renaud3 - D. Salabert1 - E. Fossat1


1 - Laboratoire d'Astrophysique, UMR 6525 du CNRS, Université de Nice-Sophia Antipolis, 06108 Nice Cedex 2, France
2 - C.N.R., 52 Charii Omar Ibn El Khattab, BP 8027, Rabat, Morocco
3 - Département Cassini, UMR 6529 du CNRS, Observatoire de la Côte d'Azur, 06304 Nice, France
4 - Laboratoire de Physique des Hautes Énergies et Astrophysique, Université Cadi Ayyad, Marrakech, Morocco

Received 26 March 2002 / Accepted 10 July 2002

Abstract
With the GOLF instrument onboard the SoHO observatory, 1979 days of full-disc Doppler velocity observations have been compiled into a study of p-mode properties. We develop a multi-step iterative method (MSIM) algorithm to access all p-mode parameters while minimizing any perturbating effect or cross-talk between parameters during their determination. We present frequency and splitting tables, amplitudes, linewidths, line asymmetries, pseudo-modes, and background noise determinations. We have a first look at the changes induced by the transition from the low-activity to the high-activity part of solar cycle 23: we have recorded frequency shifts with a downturn at 3.7 mHz followed by a possible higher upturn, and linewidth changes to a good accuracy. We detect an effect on the noise background at 3 mHz possibly related to an interaction between noise and the modes and connected to the asymmetry of the profiles.

Key words: Sun: oscillations - Sun: helioseismology


1 Introduction

The GOLF helioseismology instrument was launched onboard the SoHO spacecraft on December 2, 1995 (Gabriel et al. 1995). After a commissioning phase which ended on April 1, 1996, GOLF has been running continuously, except for an interruption due to the spacecraft loss on June 25, 1998 followed by its recovery on August 8, 1998, and a much shorter period in January 1999. Altogether, the duty cycle of GOLF is close to 95% of possibly the finest data available for the helioseismic investigation. A number of important topics have already been addressed using the GOLF data, including the validation of the solar models against sound-speed inversions (Turck-Chièze 2001; Brun et al. 1999), the solar neutrino production puzzle (Turck-Chièze et al. 2001), the solar internal rotation through splitting measurements (Bertello et al. 2000a), the effect of the asymmetry of the modes on the p-mode parameters, and the effect of such changes in the inversions (Thiery et al. 2000; Basu et al. 2000), and of course the search for g-modes (Gabriel et al. 2002; Grec & Renaud 2002). Most of the GOLF science so far is based upon p-mode studies, from the pioneering paper of Lazrek et al. (1997) to recent attempts in the detection of the very low frequency modes (Bertello et al. 2000b; García et al. 2001b). Solar activity effects have already been reported using GOLF data (Lazrek et al. 2001; Thiery 2000) on shorter time-series. The present work uses 1979 days of observations, and we are confident that some solar activity effects must be present, because the beginning of the mission was at the solar minimum of cycle 22 to 23, and that the current data corresponds to the maximum of cycle 23. This paper focuses on making a running analysis along the duration of this experiment to determine the p-mode parameters to the highest accuracy allowed by the quality and the duration of the selected data. We then check for changes in these parameters, and find out how much of those can be attributed to solar-cycle effects.

2 Data preprocessing and calibration


  \begin{figure} \par\includegraphics[width=17.5cm,clip]{MS2512f01.eps} \end{figure} Figure 1: GOLF data calibration overview: each point represents 18 days of data. a) and b) Granulation and supergranulation magnitude versus time. c) Sum of the spectral density of the calibrated signal in the p-mode range (2 to 4 mHz). d) The photon noise in the experiment with the clearly visible yearly modulation. All ordinates are m2 s-2 UpsymnmHz-1.
Open with DEXTER

  
2.1 The helioseismic signal

GOLF is an instrument dedicated to the monitoring of the global solar velocity field and has been operated onboard the spatial observatory SoHO (Domingo et al. 1995) since 1996. GOLF is a spectrophotometer using optical resonance of Na atoms. A permanent magnet separates the Zeeman components and allows the creation of 2 narrow bandpasses ($ \simeq $0.02 Å) centered on the wings of the Fraunhofer D lines (Gabriel et al. 1995). The rotation of a polarizer is added to alternatively tune the 2 bandpasses.

The motor used to rotate the polarizer during the flight has shown poor reliability and was used only briefly during the P2 period (Table 1). The later observations were made in a back-up photometric mode in a single optical bandpass. During P3, GOLF was tuned on the blue wing of the Na lines. At the start of P4, GOLF was tuned on the red wing of the Na lines and is still working in this configuration. The observations used for this study cover the period from April 1996 to December 2001 (this is an arbitrary choice, more measurements being now available). There are 2 significant gaps in 1998 due to temporary loss of SoHO and a gyro failure.

The relation of the GOLF single-band signal to the average across the solar disc of the solar velocity field has been estimated for the p-modes (Pallé et al. 1999; Renaud et al. 1999). Other velocity components are present and are related to several sources of variation of the monochromatic intensity, to the instrumental noise and to the photon noise.


   
Table 1: Time coverage for the analyzed data.
Period P2 P3 P4
begin Feb. 18, 1996 Apr. 10, 1996 Oct. 15, 1998
end Mar. 31, 1996 Jun. 24, 1998 Dec. 31, 2001
days 43 805 1174
coverage 79% 99.35% 94.09%
photometry differential blue wing red wing

2.2 Normalization of experimental parameters

The data acquisition involves 2 photometric chains, experiencing different performances and data coverage. In order to remain in a well defined condition for the signal to noise ratio, we use only the channel having higher efficiency, referred to as PM2. The conversion of the GOLF measurement to the variation of the disc-averaged solar velocity depends on a calibration procedure. A method is proposed in Ulrich et al. (2000). The basis are found in the instrumental laboratory calibrations, together with additional studies of the solar D lines. Nevertheless one of the purposes of our work is to study the dynamic properties of the solar atmosphere, which could be interdependent with the line profile used in this complex calculation. We decided not to follow this calibration procedure in order to avoid any model fitting and to check the dependency of the results on several critical steps of the data reduction. Our computation of the Doppler shift is made in 2 major steps, allowing the conversion of the raw photometric signal I(t) to a "velocity'' signal $ \xi (t) $ related to the disc-averaged surface velocity:

The first step is to normalize intensities to a reference photometric condition as the measurements include components related to the distance from the Sun, the radial component of the orbital velocity, and the decay of the measured light due to the aging of the optical components. SoHO moves around the Sun on a halo orbit circling the Lagrange point L1, that is a perturbated elliptic solar orbit. The parameters of this trajectory are computed to great accuracy. The solar intensity is first computed for a constant distance to the Sun. The instrumental drifts give also proportional photometric factors. A second order modulation is then detected at low frequency and can originate either from changes of the magnetic pattern or from changes in the average over the solar disc of the velocity field. This modulation is clearly related to the solar rotation (Grec et al. 1999). The effects of such a modulation on the p-mode signal are proportional only if, due to a change in the magnetic pattern, there is a change of the global monochromatic solar flux: we consider this as the most likely situation to happen. Both effects can be removed simultaneously from the signal: by using a low-pass filter with a cutoff at 23 UpsymnmHz, we can extract the photometric "carrier'' <I(t)>.

The second step is to normalize to a reference sensitivity for the small velocity changes. The seasonal changes of the orbital velocity give an additive component of <I(t)>, so far a perturbating term in the photometric analysis. i is the intensity collected at the $\lambda_{\rm S}$ solar wavelength. As $\lambda_{\rm S}$ depends on the orbital Doppler shift, the line slope ${\rm d}i/{\rm d}\lambda_{\rm S}$ is related to the solar lines and varies accordingly to the seasonal change in the orbital velocity V(t). This results in a variable sensitivity $s={\rm d}i/{\rm d}V$. Those 2 effects can be regarded as a linear departure from linearity and the slope is simply $s(t)\propto (~ 1+\gamma_{P_n}~V ~ )$, where $\gamma_{P_n}$ is a constant number.

The observational function $ \xi (t) $ for the p-mode study is then given in Eq. (1), in which the constant factors $\sigma_{P_n}$ and $\gamma_{P_n}$ depend on the optical bandpass selected.

 
$\displaystyle % \xi(t)=\sigma_{P_n}\frac{I(t)}{<I(t)>} \ \left ( ~ 1+\gamma_{P_n}~V(t) ~ \right ).$     (1)

The Einstein effect results in an asymmetry of the working points on respectively the blue and red wings, hence we have to use specific constants for each period (or line wing).

2.3 Calibration of instrumental parameters

We describe in Sect. 3.1 the method used to study the p-mode properties. As a by-product, we have computed 4 basic parameters from 18-day independent time-series. The key parameter of the calibration method is the result obtained for the integrated value $ \mathcal{E}_{5} $ of the power spectrum in the 5 min spectral range. The coefficients $\sigma_{P_n}$ and $\gamma_{P_n}$ are adjusted to the following conditions:

This results mainly in different values for the slope-dependent coefficients $ \gamma _{P_{3}} $ and $ \gamma _{P_{4}} $. With these coefficients, $ \mathcal{E}_{5} $ (Fig. 1c) decreases for the second part of P4. The noise (Fig. 1d) is mainly due to the quantum photon noise depending on the observed flux, then the distance to the Sun, and the decay of the photometric efficiency.

3 Analysis: modeling of the power spectrum

  
3.1 Fitting procedure

Our model of the spectral profiles takes into account all the identified components in the low degree solar velocity spectrum:


  \begin{figure} \includegraphics[width=8.8cm,clip]{fig2.ps} \end{figure} Figure 2: Visual flowchart of the current MSIM procedure.
Open with DEXTER

Doing so, we aim to account for every spectral feature of the power spectrum, and such that the residuals, if any, could be tracked to either some un-modeled physical phenomenon, or to some numerical problem. The flowchart of our fitting procedure is summarized in Fig. 2. It is an iterative algorithm that never attempts to solve all the unknown parameters at once but find them step by step and gradually includes the fresh estimates in the target parameters vector. For example we start by the estimation of all the central frequencies, while amplitudes linewidths and splittings remain set to their input table values; then, using these "fresh'' frequencies kept constant until the next iteration, we estimate the amplitudes and the linewidths. Finally, setting these 3 parameters, we estimate the splitting as a single number for a given multiplet. This process is iterated 4 times at most. It must start initialized to some realistic p-mode parameter table, and stops whenever convergence in the parameters is achieved but usually 4 iterations are sufficient. The convexity of function to minimize is quite different for parameters such as the frequency, where it is rather simple, and the splitting where it is usually very tricky (Fierry-Fraillon 1999). Thus, we think that this iterative approach is efficient in avoiding the cross-talk arising from the simultaneous fit of parameters. At each stage, the minimization of the cost function is done using a maximum likelihood criterion based on a $ \chi _{2}^{2} $ spectral probability density function (PDF). Techniques consisting of fitting the entire spectrum at once (modes and background, "WSF'') have already been successfully implemented (Roca Cortés et al. 1998). This requires the minimization of a vector of at least 250 parameters just for mode amplitudes, frequencies and linewidths, possibly much more if one wants to go into asymmetry and splitting. It was tested successfully on small time-series but would be extremely time-consuming in our case. Our procedure, to be referred as Multi-Step Iterative Method (MSIM) is distinct from the so-called WSF method because:

The main advantage in using MSIM is that, being a "global fit'', it allows us, within certain limits, to test the model of the power spectrum used and possibly to improve it. Another important feature is that it is a automated procedure that does not require an operator input: once the initial parameter table has been given, it will proceed to the end. All the a priori are either written in the program or in the input parameter table.

Finally, we have been making this analysis at 3 typical time scales using a running window:

As a consequence, only 1/4th of any of the computed power spectra are fully independent, but reciprocally, we smooth out any solar trend at periods lower than 1/8 of the window length. Having different lengths for the individual time-series is also useful because some parameters do change over short time scales during the activity cycle (certainly shorter than one year), so that we need some flexibility between the possibility of sampling properly these variations, and the convenience of having a very good spectral resolution when parameters do not change noticeably.

  
3.2 Solar noise and photon noise fits

The solar noise model we used is derived from the classical "Harvey model'', except that instead of a 4-component model of the solar noise which includes noise from the active regions, the supergranulation, the mesogranulation and the granulation, we use only the two most relevant contributions, which, in our case, are the granulation (in the 600-1200 UpsymnmHz range) and the supergranulation (in the 20-600 UpsymnmHz range). Active regions are at very low frequency and their effects are filtered out in the calibration process (Eq. (1)) so we do not consider them. We also found that using a mesogranulation component does not improve the result of the model for our purpose. Finally our noise model is:

 
$\displaystyle % N_{{\rm sun}}(\nu ) = 4~ v_{{\rm g}}^{2}~ \tau _{{\rm g}}/(1+2\... ...} + 4~ v_{{\rm sg}}^{2}~ \tau _{{\rm sg}}/(1+2\pi ~ \tau _{{\rm sg}}~ \nu )^{2}$     (2)

where $ v_{{\rm g}},~ \tau _{{\rm g}} $ and $ v_{{\rm sg}},~ \tau _{{\rm sg}} $are the amount and threshold of granulation and supergranulation respectively. While Fig. 3 gives an example of such a fit, Fig. 1 shows the temporal behavior of the noise over the P3 and P4 periods. The solar granulation (Fig. 1a) and supergranulation (Fig. 1b) amplitude values are estimated as in Eq. (2). Both are modulated, but the granulation level is more affected than the supergranulation by the changes in the line depth of the working point of the instrument (yearly modulation). We also notice an increase in the supergranulation when switching from the P3 to the P4 period. These results are quite comparable with the results from García et al. (2001a) using a different calibration process.
  \begin{figure} \includegraphics[width=8.8cm,clip]{MS2512f03.eps}\par \end{figure} Figure 3: Global background noise fit, using 2 components for the solar noise and a constant level for the photon noise (not represented here). The top curve is the sum of the 3 components and is the reference background level used in the p-mode fit. The extra noise component discussed in Sect. 3.3 is visible as the superimposed "bump'' peaking at 3000 UpsymnmHz. The bump curve here is a model of the average of the determination of the component over all our subseries.
Open with DEXTER

Concerning the estimation of photon noise level, the 40 s sampling time used in this analysis gives a cutoff frequency of 12.5 mHz. Although the solar acoustic cutoff is at about 5.4 mHz, we know that the range 6 to 10 mHz does contain so-called HIPs (or pseudo-modes, García et al. 1998), and some p-mode wings, so that the photon noise cannot be safely estimated there. Finally, our photon noise $ B_{\rm phot} $ is computed as a constant level in the 10 to 12.5 mHz range.

   
3.3 "Extra'' noise component

In determining p-mode parameters using our former model for the background noise, we noticed that an extra component was needed to ensure a correct determination of amplitudes and linewidths. This extra component has a specific frequency behavior which is shown in Fig. 3. An error in the background determination results in a truncation in the mode amplitude which is also fairly well reflected in the linewidth. It is the checking of the coupling between the amplitudes and the linewidths that allows one to find and address this problem. This effect is easier to track on the linewidths, which are very well defined, and without this new noise component, they can be changed by as much as 15% in the 3 mHz range. Changes in this quantity between the P3 and P4 periods are being investigated, but we currently have no answer to this point. Our model of the velocity background noise in the spectra relies on the hypothesis of independence of the sources of noise we have listed, e.g. granulation, supergranulation, and photon noise level, with the oscillation. This extra noise component may come from the weakness of this hypothesis: if there were some correlation between the modes and the solar noise, this would possibly explain the non-random spectral shape of this new component.

  
3.4 P-mode fit


  \begin{figure} \includegraphics[width=7.8cm,clip]{MS2512f04a.eps}\hspace*{1.5cm} \includegraphics[width=8.2cm,clip]{MS2512f04b.eps} \end{figure} Figure 4: a) -$ \bullet $- is the average relative frequency difference for an $\ell =1$ between the known value and the output of the fit. b) is the average relative linewidth difference for the same modes. - - $ \blacklozenge $- - is the standard deviation of the value (frequency difference or linewidth difference) computed over 30 realizations, and - - $ \blacktriangledown $- - is the average of the error-bars we estimate in the MSIM process for these values.
Open with DEXTER

For the p-mode parameter extraction, we have been testing two options, either assuming a pure Lorentz profile for each p-mode component, or assuming asymmetrical profiles, (Nigam & Kosovichev 1999a) better representing the physics of the excitation of the modes. Neither of these formulae did actually suit our needs:

Finally our choice was to compute the line parameters using a modified asymmetrical formula in which we drop the asymmetry away from the central frequency:
 
                                 $\displaystyle L(\nu )=A\frac{\left(1+Bx\right)^{2}+B^{2}}{1+x^{2}} \ \mbox{for}\ \left\vert \nu -\nu _{0}\right\vert <k\Gamma$ (3)
    $\displaystyle L(\nu )=\frac{A}{1+x^{2}} \ \mbox{for}\ \left\vert \nu -\nu _{0}\right\vert \geq k\Gamma$ (4)

where $ x=(\nu -\nu _{0})/\Gamma $ is the centered scaled frequency, and $ A,~ \Gamma ,~ \nu _{0},~ B $ are the mode amplitude, linewidth, central frequency and asymmetry coefficient respectively. $k\Gamma$ depends on the frequency and its value ranges from 30 to 50 $\mbox{{\usefont{U}{psy}{m}{n}m}}$Hz, allowing the asymmetry to be well taken into account when fitting the parameters (inside a 135 $\mbox{{\usefont{U}{psy}{m}{n}m}}$Hz slice of the power spectrum). To model the effect of the neighbouring peak profiles, where most of the expected effect is far away from the central frequency, we use the classical symmetric expression. In the absence of a correct formulation, and in the framework of this study, this approximative mixed solution gives better results than selecting either the classical or the Nigam expression.

Also, note that given the difficulty in determining properly the value of B for frequencies higher than 3.7 mHz, all modes profiles were taken symmetric above this value. This problem is similar to the determination of the splitting: the increase in the linewidths and the decrease in the distance between modes of even or odd $\ell$ greatly bias the result and decrease its confidence, so that at that point we prefer to return to a simpler scheme.

  
3.5 Pseudo-modes fit

We fit the pseudo-modes in the 5800 to 7000 UpsymnmHz frequency range using the following 6-parameter model:

 
                         $\displaystyle % H(\nu )$ = $\displaystyle P_{{\rm hips}}~ \exp \left(-\left(\nu -\nu _{0{\rm h}}\right)/\beta _{{\rm h}}\right).$ (5)
    $\displaystyle \left[ 1+C_{{\rm h}}~ \cos \left(\left(\nu -\nu _{0{\rm h}}\right) /T_{{\rm hips}} +\Phi _{{\rm h}}\right)\right]$  

where $ P_{{\rm hips}} $ is the maximum amplitude of the pseudo-modes, $ \beta _{{\rm h}} $ is their exponential decay, $ T_{{\rm hips}} $ is the pseudo-modes period (in frequency units), $ \Phi _{{\rm h}} $ is the pseudo-modes phase, $ \nu _{0{\rm h}}=5800 $ UpsymnmHz, and $ C_{{\rm h}} =0.1$is a constant contrast factor that should be estimated separately, otherwise its determination interferes with the determination of $ P_{{\rm hips}} $. We have checked that setting $C_{{\rm h}}$ to a constant value does not impact significantly the results for the other parameters.

4 Method assessment on simulated spectra

We have checked for the reliability of our parameter extraction technique by synthesizing artificial oscillation spectra and feeding them into the extraction routines.

  
4.1 Artificial spectra

Artificial spectra are created using a known p-mode parameters table, and known solar and photon noise characteristics which allow us to generate a complete power spectrum from 20 UpsymnmHz up to the sampling cutoff frequency. The randomness of the excitation is introduced using a normal noise distribution pattern in the complex Fourier spectrum as in Fierry Fraillon et al. (1998). The resulting square modulus (spectral density) is then used as the input of the peak-finding routines. Given the duration of the extraction process, we had to limit the number of realizations providing the statistics of the results to 30 spectra. There are two underlying physical assumptions to this simulation process:

We certainly do not believe the first statement, given that some of us have been able to show evidence for correlation between m-components (Ferrari et al. 1999) of a given $\ell$, although the difficulty of giving a correct formulation and the little which is quantitatively known of this correlation makes it impossible to introduce it in this simulation.

We have reasons to believe the second assumption poorly justified, because of the fact that modes are asymmetric, and that the explanation of this asymmetry suggests that some noise has to be correlated with the mode to explain the reversal of the sign of the asymmetry parameter between velocity and intensity measurements (Nigam et al. 1998; Nigam & Kosovichev 1999b; Severino et al. 2001).

However, our goal here was to test the MSIM algorithm for its accuracy, and our artificial spectra, representing only some of the best known properties of the signal, provide enough features to perform this test.


  \begin{figure} \includegraphics[width=8.8cm,clip]{MS2512f05.eps} \end{figure} Figure 5: Experimental splitting restitution. -$ \bullet $- is the average splitting difference between the known value and the output of the fit, for an $\ell =1$ mode. - - $ \blacklozenge $- - is the standard deviation of this value computed over 30 realizations, and - - $ \blacktriangledown $- - is the average of the error-bars we estimate in the program.
Open with DEXTER

4.2 Simulation results

Figure 4a shows the average frequency difference between 30 realizations of an artificial spectrum computed as in Sect. 4.1 and differing only by their random noise. Results are divided by the input value, so that we actually plot the average relative difference. The retrieval of the input frequency is quite good: the largest errors are of about 10-4 at 4300 UpsymnmHz which means about 0.5 UpsymnmHz at worst, and the magnitude of the error is always less than the size of the corresponding $1\sigma$error-bars. Above 4400  $\mbox{{\usefont{U}{psy}{m}{n}m}}$Hz the combination of the increase in the linewidths and the decrease in the separation of the modes degrades seriously the quality of the frequency restitution, although it is important to note that there is no obvious bias, even above that point. Figure 4b is the same for the linewidths: there is a hint of a bias at the lowest and highest frequencies, which means that the fit would slightly underestimate the linewidths at those points, but for most of the range the linewidths are correct and the error is inside the error-bars.

Finally, Fig. 5 represents our capability to correctly fit the splitting of an $\ell =1$ mode with realistic input values, taken from previous determinations. We never miss the splitting value by more than $ 10\% $, and again our error-bars are coherent with this error. We note that 3000  $\mbox{{\usefont{U}{psy}{m}{n}m}}$Hz appears as a quality boundary for the splitting determinations.

Concerning the error-bars, we have plotted in Figs. 4 and 5 two curves with identical meaning: one is the average of the error-bars given by the fitting program, corresponding to the inversion of the numerical Hessian of the system, and the other is the standard deviation for our 30 realizations (i.e. $1\sigma$). The similarity between the two curves makes us confident in the robustness of our fits.

Another key point is that we did not introduce the extra noise component of Sect. 3.3 in our simulation. However, in forcing the software to fit, we never succeed in getting anything other than random amplitudes at a very low level. This is an a contrario evidence that our result on real spectra was not a spurious effect created by some hidden numerical error.

This work on artificial spectra has proven that the process of automatically extracting the parameters with error-bars from the power spectra has reached a high level of reliability, provided that our hypothesis on the nature of all the contributions to the signal are valid.

5 Results using the MSIM software

   
5.1 Frequencies

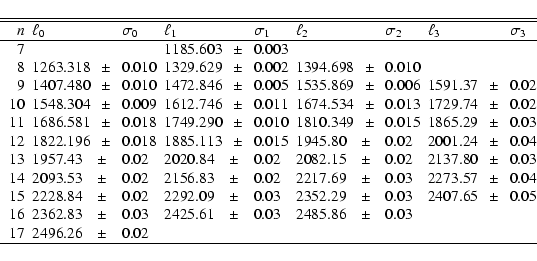
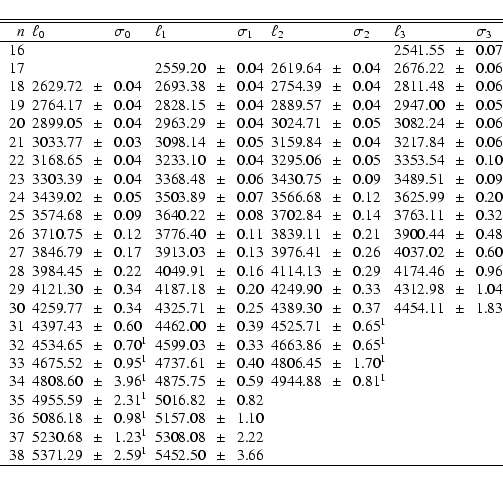
Tables A.1-A.3 are p-mode frequencies computed as described in Sect. 3.4 on 16-month time-series. Following our variability study (see below in the same section), the frequencies below 2500 UpsymnmHz seem little affected by solar cycle effects, so in Table A.1 we have averaged these frequencies over the P3 and P4 periods in order to increase their precision. For $\nu > 2500$ UpsymnmHz, Table A.2 is the weighted average of our determinations over 16 months (with a 12-month overlap) over the P3 period ("blue wing'' period). Table A.3 is the same determination over the P4 period ("red wing'' period). Above 4.4 mHz, we have tagged the frequencies for $ \ell =0$ and $ \ell =2$ because the increase in their linewidths combined with the decrease in the separation of these modes affects very much their determination, as previously mentioned in Sect. 4.2. The situation is quite different for the group of odd peaks, because although they are also indistinguishable, their difference in amplitude suggests that we are measuring mostly energy from the $\ell =1$.


  \begin{figure} \includegraphics[width=8.8cm,clip]{MS2512f06.eps} \end{figure} Figure 6: Frequency changes vs. frequency for 4 low-degree modes; -$ \bullet $- : $ \ell =0$, - $ \blacklozenge $- : $\ell =1$, - $ \blacktriangledown $- : $ \ell =2$, - $ \blacktriangle $- : $ \ell =3. $
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.6cm,clip]{MS2512f07a.eps}\hspace*{7mm} \includegraphics[width=8.5cm,clip]{MS2512f07b.eps} \end{figure} Figure 7: a) Linewidths vs. frequencies, determined over 16-month time-series. $ \blacksquare $ represents all the individual determinations over all the available data. - $ \blacklozenge $- is the 16-month average of the P3 period determination, and - $ \blacktriangle $- is the 16-month average for the P4 period. b) Linewidth changes vs. frequency. - $ \blacklozenge $- : $\ell =1$ and 3 (simultaneously), -$ \bullet $- :$ \ell =$ 0 and 2 (simultaneously).
Open with DEXTER

Each frequency value $ f_{\rm m} $ in Tables A.1, A.2, or A.3 is the weighted average of n measurements $ f_{i}~ (i=1,\ldots n) $:

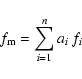\begin{displaymath}% f_{\rm m}=\sum ^{n}_{i=1}a_{i}~ f_{i} \end{displaymath} (6)

where ai are the weighting coefficients:

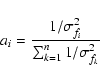\begin{displaymath}% a_{i}=\frac{1/\sigma _{f_{i}}^{2}}{\sum ^{n}_{k=1}1/\sigma ^{2}_{f_{k}}} \end{displaymath} (7)

and $ \sigma _{f_{i}} $ are the individual error-bars for each frequency measurement fi. This means that the better the individual determinations, the more they influence the final result. Because we have such overlapping data, we compute $ \sigma _{f_{\rm m}} $, the error-bar on the non-independent determinations of the frequencies, using the formula for non-independent random variables:

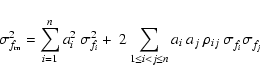\begin{displaymath}% \sigma ^{2}_{f_{\rm m}}=\sum ^{n}_{i=1}a^{2}_{i}~ \sigma ^{... ...a_{i}~ a_{j}~ \rho _{ij}~ \sigma ^{}_{f_{i}}\sigma ^{}_{f_{j}} \end{displaymath} (8)

and the correlation coefficients $ \rho_{ij} $ between the $ i{\rm th} $ and the $ j{\rm th} $ determination are taken proportional to the amount of overlap between the fractional time-series sections, i.e. $ \rho _{ij}=$ 0.75, 0.50, 0.25, 0.0.

We have computed the frequency differences between P4 and P3 periods. Figure 6 shows the frequency changes versus frequency. There is an obvious effect that can be separated in several features:

5.2 Linewidths, and linewidths changes

Figure 7a shows our determination of the p-mode linewidths on 16-month sections, using asymmetrical profiles and forcing $\Gamma _0= \Gamma _2$ and $\Gamma _1=\Gamma _3$. We emphasize that we have checked that using asymmetrical profiles (Nigam & Kosovichev 1998) as described in Sect. 3.4 instead of simple Lorentz profile helps very much in increasing the coherence of the result, as was previously shown by Thiery et al. (2000). The general shape of the linewidths is in good agreement with former determinations like Chaplin et al. (1997) or Fierry Fraillon et al. (1998). An interesting feature of Fig. 7a is the clear change in the linewidth slopes at $ \simeq $3.9 mHz, both for $\ell=0,2$ and $\ell=1,3$. It is not a fitting artifact due, for instance, to the $\ell=0,2$ separation being of the same magnitude than the linewidths, otherwise the $\ell=1,3$ measurement would not display the same trend. In addition, such a bias, if present, would have been detected in Sect. 4.1. This leads us to think that whatever damping effect is producing the "plateau'' level is still efficient up to 3.9 mHz, where possibly there is a return to another damping rate.

Also, one can already see that the linewidths determined on the P4 period are slightly higher than those determined on P3. There is more p-mode damping at high-activity than at low activity, or the coherence-time of the oscillation is shortened. Figure 7b shows the relative amount of change for the linewidths. They do change by 20% at most at about 3500 UpsymnmHz. Linewidths at higher frequencies do not appear to change significantly in time. Although not obvious, this plot also supports the possibility of some increase in the coherence time of the oscillations below 2000 UpsymnmHz.

5.3 Amplitudes and SNR

Figure 8 compares the amplitude determinations of modes $ \ell =0,1,2,3 $, computed over 4-month time-series, to the noise levels at the same frequencies. All modes show a quite broad dispersion in their SNR, up to a factor 3, even over 4-month spans. The thickness of the noise baseline reflects as much changes in the experiment as changes in the solar noise of various origins, but mostly modulation due to the excursion in the line wings, and solar activity. As to the modes $ \ell =0$ and $\ell =1$they appear to have roughly the same amplitudes.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2512f08.eps} \end{figure} Figure 8: Amplitudes and noise background in 1979 days of GOLF data for low-degree modes. From top to bottom: $ \ell =0$  and $\ell =1$, almost superimposed, then $ \ell =2$, and then $ \ell =3. $ Finally the bottom line is the background noise (the extra noise component of Sect. 3.3 is not plotted here).
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS2512f09.eps} \end{figure} Figure 9: Ratio $ \widehat{R}_{43}$ of the low resolution power spectra for the "red'' (P4) and the "blue'' (P3) periods. The "blue wing'' signal clearly dominates the "red wing'' one (in log scale).
Open with DEXTER

The visible subdivision of the amplitudes in two domains for the high-frequency end of the curves comes mostly from the switching of the experiment from the blue to the red slope of the Na lines (from P3 to P4 period). This effect is mainly present for $ \ell =0$ and $\ell =1$, and is fainter, although real, on $ \ell =2$. To check this feature, we have computed the ratio $ \widehat{R}_{43}$:

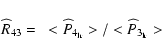\begin{displaymath}% \widehat{R}_{43}=~<\widehat{P}_{4_{\rm lr}}>/<\widehat{P}_{3_{\rm lr}}> \end{displaymath} (9)

of the average of the low-resolution 1-day spectra for P3 and P4 (Fig. 9). This ratio indicates an excess of power for the P3 period, starting at about 3 mHz and increasing to a maximum at about 5.5 mHz. This ratio then goes slowly down to 1 when both spectra get to their respective photon noise levels. In other words, from the maximum of the p-mode power to the cutoff frequency, the blue wing appears to oscillate more than the red wing of the Na line by a maximum value of 2.5 in power at the cutoff frequency. Of course this result relies on the quality of the data calibration. While confident in our calibration procedure, we think that no error would possibly produce such a physically significant ratio. On the other hand, Robillot (2000) has been advocating for the existence of this effect in the data from his MR5 spectrophotometer (Ambroz et al. 1995). He finds an average value of 1.85 in oscillatory power in favor of the blue wing of the NaD1 line. Given the small amount of data in his case (a few non-continuous days), we did not find any very significant frequency dependence when we re-analyzed them. Still, we confirm his former analysis and we find an average value of 2.2 in power in favor of the blue wing.


  \begin{figure} \includegraphics[width=8.8cm,clip]{MS2512f10.eps} \end{figure} Figure 10: Amplitudes change between P3 and P4 versus frequency for 3 low-degree modes; -$ \bullet $- :$ \ell =0$, - $ \blacklozenge $- : $\ell =1$, - $ \blacktriangle $- : $ \ell =2$.
Open with DEXTER

Finally, we computed the same kind of ratio as $ \widehat{R}_{43}$on the P2 period when the experiment was still potentially a differential one. Instead of calibrating a differential velocity, we calibrated separately both the blue and red wings of P2 and we computed $ \widehat{R}_{2r2b}=<\widehat{P}_{2r_{\rm lr}}>/<\widehat{P}_{2b_{\rm lr}}> $. The result is very similar to Fig. 9, indicating that a large majority if not all of the effect seen in this figure is not due to solar activity changes, and probably not due either to experimental changes having occurred between P3 and P4. Its explanation may just be the selective response of the solar atmosphere to the oscillations at different wavelengths inside the same absorption line, giving different levels in the photosphere. For the same reason, the weighting functions of the integration across the solar disc differs and that may be responsible for some of this effect.

Figure 10 shows the amplitude differences computed on 16-month spectra averaged over P3 and over P4. Of course it looks very much like Fig. 9, particularly in its frequency signature, except that the information is coming only from p-mode peaks in high-resolution spectra. No solar cycle information in p-mode amplitudes can usefully come from comparing P3 and P4 in the GOLF data, so far.


  \begin{figure} \includegraphics[width=8.8cm,clip]{MS2512f11.eps} \end{figure} Figure 11: $ \square $ : individual determinations of the B parameter on 16-month time series. - $ \blacklozenge $- : Average of the 16 month asymmetries for the P3 period. - $ \blacktriangle $- : Average of the 16 month asymmetries for the P4 period.
Open with DEXTER

5.4 Peak skewness

Figure 11 is our determination of the asymmetry parameter B defined in Eq. (3). This figure has a few characteristic features like:

Negative values for the B asymmetry parameter are nominal in the case of radial velocity measurements. The BiSON and MDI measurements also show the same pattern, with a minimum of the skewness at n=21 (e.g. $ \approx $3100 UpsymnmHz) for BiSON (Chaplin & Appourchaux 1999), and a general parabolic shape rather comparable. They have values -0.05<B<0.01 matching closely our numbers. Thiery et al. (2000) analyzed the GOLF data and they have a quite comparable result on a shorter frequency range. Finally Thiery (2000) has results on the skewness of the MDI low-degree modes which again are in perfect agreement with our result. Concerning the changes in the value of B from P3 to P4, they have been extensively studied in Thiery (2000) and Thiery et al. (2001). In comparing the changes in the asymmetry parameter in the GOLF data and in the MDI data (GOLF proxy) for periods matching closely our P3 and the P4 periods, they reach the conclusion that it is the level of correlated intensity signal in the GOLF velocity data during P3 which is responsible for the lower (in absolute value) value of the B parameter. Our result fully supports this conclusion, and we interpret this change as an effect of the changes in the physics of the oscillation between the red and the blue wings of the line, and not as a solar cycle effect.


  \begin{figure} \includegraphics[width=17.3cm,clip]{MS2512f12.eps} \end{figure} Figure 12: Per-mode splitting determination plotted against $ (\ell +1/2)/\nu $ which is comparable to the lower turning point of the modes (only the sound speed value is missing in the numerator): a) GOLF splittings from Bertello et al. (2000a), b) BiSON splittings from Chaplin et al. (2001b), c) our determination.
Open with DEXTER

5.5 Splitting


   
Table 2: Splitting values in nHz and averaged per-mode.
n$ \ell _{1} $  $ \sigma _{1} $$ \ell _{2} $  $ \sigma _{2} $$ \ell _{3} $  $ \sigma _{3} $
7432$ \pm $2      
8432$ \pm $2433$ \pm $5   
9432$ \pm $6437$ \pm $10435$ \pm $8
10444$ \pm $12430$ \pm $16429$ \pm $17
11432$ \pm $16438$ \pm $9430$ \pm $15
12442$ \pm $28422$ \pm $26428$ \pm $25
13453$ \pm $42429$ \pm $22438$ \pm $13
14431$ \pm $42425$ \pm $14436$ \pm $28
15447$ \pm $66425$ \pm $21437$ \pm $22
16406$ \pm $38436$ \pm $24448$ \pm $29
17449$ \pm $57462$ \pm $22437$ \pm $28
18450$ \pm $66430$ \pm $20442$ \pm $14
19467$ \pm $31433$ \pm $20458$ \pm $13
20455$ \pm $28425$ \pm $28440$ \pm $14
21449$ \pm $47417$ \pm $47444$ \pm $18
22457$ \pm $50429$ \pm $35456$ \pm $25
23460$ \pm $60410$ \pm $50465$ \pm $40
24   437$ \pm $60440$ \pm $50
25      450$ \pm $52


   
Table 3: Mean splittings comparisons (nHz).
  BiSON ($ \sigma - $weighted) Bertello et al. ($ \sigma - $weighted) This work ($ \sigma - $weighted)
$\ell =1$ 435.4$~~\pm~~$3.6

over

$ 9\leq n\leq 22 $

 436$ \pm $9

over

$ 9\leq n\leq 20 $

 433$ \pm $2

over

$ 7\leq n\leq 23 $
$ \ell =2$ 436.0$~~\pm~~$3.1

over

$ 9\leq n\leq 23 $

 426$ \pm $11

over

$ 10\leq n\leq 19 $

 434$ \pm $4

over

$ 8\leq n\leq 24 $
$ \ell =3$ 435.4$~~\pm~~$3.6

over

$ 11\leq n\leq 23 $

 459$ \pm $14

over

$ 12\leq n\leq 19 $

 440$ \pm $6

over

$ 9\leq n\leq 25 $

Splittings of the low-order p modes are important because they are the only piece of information we have on the current rotation rate of the solar core, addressing a fundamental problem of angular momentum conservation in this star. Figure 12 shows our determination of the individual rotational splittings for $ \ell =1,~ 2,~ 3 $. In our fitting strategy, splittings are computed separately after all other parameters have passed satisfactorily each round of estimation. This ensures a minimum of cross-talk between the splitting computation and the frequency computation. Each point in Fig. 12 is the average of all the individual determinations over 16 months. The error-bars that are shown are compiled from the individual error-bars as in Sect. 5.1. We limit the frequencies where we give the splitting to $ \nu <3500 $ UpsymnmHz for $\ell =1$ and 2, and to $ \nu <3700 $ UpsymnmHz for $ \ell =3$. Above those limits the error-bars increase dramatically because of the increase in the linewidths which become of the same magnitude as twice the splitting separation, hence making these data irrelevant for core rotation studies. It is important to stress that the higher the frequency of a given $ \ell , $ the deeper its internal turning point. The deepest "samples'' of the integrated rotation are then provided by the highest frequency splittings of the $\ell =1$ mode which, unfortunately, are the least accurate that we can provide.

Nevertheless, if we compare Fig. 12 to Fig. 5 in Lazrek et al. (1997), which was also made from GOLF data, we can tell that a lot of improvements come from the much longer available time-series, and that the error-bars have decreased quite significantly.

Comparing this study to the equivalent work of Chaplin et al. (2001b) on BiSON data, we can tell that there is an impressively good agreement between those two independent splitting determinations: only three values (of 69) formally disagree. We can also compare our determination with the work of Bertello et al. (2000a) on GOLF data. The agreement is good, although not as good as for BiSON, some mid-range $ \ell =2$ and $ \ell =3$ modes having a splitting higher than 460 nHz, and that impacts also the $ \ell - $averaged values found in Table 3. The agreement is the best at low frequencies for $\ell =1$.

Finally, we have looked for splitting changes between the P3 and P4 periods and found none significant, to our current level of accuracy.

5.6 Pseudo-modes

Traveling waves above the solar photospheric cutoff frequency have been known to exist as early as the late seventies, but the existence of a regularly spaced peak structure above 5.4 mHz in the p-mode spectrum was first observed by Libbrecht (1988). Kumar & Lu (1991) interpreted it as an interference pattern and proposed the name HIPs (High-frequency Interference Peaks). They showed that the value of the recurrence of the peaks is an indicator of the depth of the acoustic source within the photosphere. HIPs are a remarkable feature of the GOLF signal (García et al. 1998). We find them above the acoustic cutoff frequency, between 5.8 and 7.0 mHz. Figure 13 shows the results of the fit on overlapping 16-month sequences for the P3 and P4 periods, and following Sect. 3.5 specifications. The spectral recurrence of the pseudo-modes peaks (we prefer the term recurrence to the term period in this case) we have measured is (cf. Eq. (6)) $ T_{{\rm hips}}\simeq 70 \pm 0.5 $ UpsymnmHz. It matches quite well the value of $ \simeq $$70 \pm 2 $ Upsymnm Hz given by García et al. (1998) over the same data computed on a shorter time-series. Nevertheless, their amplitude (the $ P_{{\rm hips}} $ parameter in Eq. (6)) was cut off by more than a factor 2 between P3 and P4, until they are barely distinguishable from noise. The coherence in $ T_{{\rm hips}} $ makes us confident that, although weaker, HIPs are still present during P4.


  \begin{figure} \includegraphics[width=8.8cm,clip]{MS2512f13.eps} \end{figure} Figure 13: Pseudo-modes recurrence in frequency and amplitude for the P3 and P4 periods.
Open with DEXTER

6 Conclusion

The frequency dependence of the frequency shifts below 4 mHz associated with solar activity has been known for a long time (Woodard & Noyes 1985; Gelly et al. 1988; Palle et al. 1989; Libbrecht & Woodard 1990; Howe et al. 1999). Its sign, and its regular increase in magnitude up to 4 mHz, can be very well fitted by an inverse mode mass model (Chaplin et al. 2001a; Jiménez-Reyes et al. 2001), and there is a general agreement on the interpretation of this effect as changes taking place in the superadiabatic layer at the top of the convection zone (Balmforth et al. 1996). Still, this explanation does not account properly for the changes that affect the Sun luminosity along its activity cycle. The slope and sign reversal of the p-mode frequency shifts have been previously noticed on intermediate $\ell$ by Ronan et al. (1994) and Jefferies (1998), and this effect was already visible (although unnoticed) in the work of Libbrecht (1988). The analysis is more convincing at higher $\ell$ because the power in the modes is higher and the effect is then obvious. Then, we are left with a challenge: whatever physical effect mentioned to explain the change in the frequencies at 3.5 mHz will possibly have some trouble in explaining the opposite changes at 5. mHz. Several authors have been aware of this problem: Goldreich et al. (1991) explained a frequency decline above 4 mHz because of an entropy increase in the optically thin layers of the solar atmosphere. They suggest a chromospheric resonance to account for the "precipitous nature of the decline [...] at 4.4 mHz'', a statement which is very much in agreement with our results. Jain & Roberts (1993, 1996) propose a model of the convection zone and solar atmosphere in which a uniform horizontal magnetic field is able to reproduce both the downturn and the upturn of the frequency shifts. The key point here is the horizontal nature of the field, which otherwise would require too important changes to be realistic. If we assume that this trend reversal is rather $\ell$-independent, as suggested by various observations, then the effect will probably be still coming from or even above the surface layers of the Sun: one must start to question the possible influence of the chromosphere on the frequency shifts as suggested by the above-mentioned works.

Theories explain pseudo-modes using the acoustic path difference between downward and upward propagating waves to build interferences above the photospheric cutoff frequency (Kumar & Lu 1991). Changes in the reflectivity of the surface layers because of changing magnetic effects would affect the amplitude of those modes, while changes in the source position of the waves would affect the value of the spectral recurrence of the HIPs (Kumar 1993). We observe a very important change in the amplitudes when switching from P3 to P4, but we have a very good stability in the recurrence of the HIPs spectral pattern during the whole run. We conclude that HIPs visibility in the spectra should be sensitive to the wavelength, or rather to the level in the photosphere to which they are observed. Also, from the steadiness of the recurrence, we can infer that the position of the acoustic source remained the same to our precision level on $ T_{{\rm hips}} $, e.g. within a few kilometers.

We have measured linewidth differences between P3 and P4 and found them changing: between 2 and 3.3 mHz, we see a positive dependence (linewidths increase with activity), and between 3.3 and 4.5 mHz the trend is reversed, although the shift is still positive. We believe that this is a true solar activity signature. Komm et al. (2000a) and Komm et al. (2000b) have reported linewidth shifts in intermediate-$\ell$ and high-$\ell$ in the GONG network data, showing that p-modes are broader with increasing magnetic activity. We agree with them on the frequency dependence and on the sign of the effect. Recently, Houdek et al. (2001) have given an interpretation of the linewidth shifts measured in the BiSON network data in terms of changes in the shape of the convective eddies. They model the shifts in linewidths by changing the eddy shape parameter by 6% between 1991 and 1997. While this is a very interesting way of connecting the p-mode linewidths to some physical phenomenon, we think that the fit of the model giving this result does not account very convincingly for their data, and would not match our own results of Fig. 7b. Anyway, the few available observational results of linewidth shifts all indicate a decrease in the coherence time of the p-modes at high solar activity.

Starting with Roxburgh & Vorontsov (1997), several authors have discussed the possibility of correlation between the modes and the background noise. Such a correlation would explain the reversal of asymmetry of the p-modes between intensity and velocity observations (Toutain et al. 1998; Nigam et al. 1998). Our approach in Sect. 3.3 (i.e. the tentative model of an extra noise component), has been so far purely empirical, and only guided by numerical considerations on the quality of the results on the modes amplitudes and linewidths. Whether asymmetry reversal between intensity and velocity is the only effect of this possible correlation, or some other effects like the one we present here can happen is a problem that we shall be investigating in depth. If confirmed, the amount of correlation would probably be quite significant.

Finally, the p-mode amplitudes and the SNR of the GOLF experiment do change significantly between P3 and P4, and we can state that p-mode radial velocities were better seen on the blue wing of the Na line for a large part of the high frequency domain up to the cutoff frequency. We are careful in saying that our velocities here are rather "scaled intensities'' than pure Doppler shifts converted to radial velocities. However, the blue side of the Na lines looks very different to the red side, and this prevents us from concluding whether there are solar-cycle effects in our amplitudes determinations. This difference not only concerns the modes, but the background seems also implicated up to and even above the cutoff frequency. What progress can be made on the response of the solar photosphere to the p-mode oscillations, or to the dependence of the modes SNR on the experimental wavelength inside a spectral line are questions that would require more observations of an "enhanced GOLF'' instrument.

Acknowledgements
The auhors wish to thank P. Boumier from IAS, Université Paris Sud, for many constructive remarks and helpful suggestions in the final writing of this paper.

The GOLF instrument is due to a team from a consortium of institutes. SOHO is a space solar observatory from a common project between ESA and NASA.

Appendix A: Frequency tables


  
Table A.1: Low-frequency table and associated error-bars. Frequencies below 2500 UpsymnmHz are very little affected by the solar activity cycle, hence they have been averaged over the P3 and P4 periods in order to increase their precision.

\begin{displaymath}\begin{tabular}{r@{\ \ }l@{}c@{}l@{\ \ }l@{}c@{}l@{\ \ }l@{}c... ... $\!\!\! \pm $& 0.02 & & & & & & & & & \\ \hline \end{tabular}\end{displaymath}



  
Table A.2: Frequency table for $ \ell =0$ to $ \ell =3$ with associated error bars. Frequencies listed in here are the average of determinations over 16-month data spans for the P3 period. 1 Above 4400 Upsymnm Hz, $ \ell =0$ and $ \ell =2$cannot be separated clearly, and the frequencies may be affected (see text).

\begin{displaymath}\begin{tabular}{r@{\ \ }l@{}c@{}l@{\ \ }l@{}c@{}l@{\ \ }l@{}c... ...452.50 & $~~ \pm ~~$& 3.66 & & & & & & \\ \hline \end{tabular}\end{displaymath}



  
Table A.3: Same as Table A.2 but for the P4 period. 1same as in Table A.2.

\begin{displaymath}\begin{tabular}{r@{\ \ }l@{}c@{}l@{\ \ }l@{}c@{}l@{\ \ }l@{}c... ...452.31 & $~~ \pm ~~$& 2.98 & & & & & & \\ \hline \end{tabular}\end{displaymath}


References

 

Copyright ESO 2002