A&A 394, 323-328 (2002)
DOI: 10.1051/0004-6361:20021144
E. A. Perdios - V. S. Kalantonis
Department of Engineering Sciences, University of Patras, 26500 Patras, Greece
Received 22 March 2002 / Accepted 23 July 2002
Abstract
This paper concerns the numerical determination of
doubly asymptotic orbits at the collinear equilibrium
points of the general three-body problem. To compute a doubly
asymptotic orbit we use a linear analysis to determine
the relevant outgoing eigenvector and a combined iterative method
based on the characteristic bisection and Newton's method to solve
the resulting system of equations for the mass parameters of the
problem. Many such orbits are presented.
Key words: celestial mechanics - methods: numerical
Asymptotic orbits are an interesting case of motion in
dynamical systems, when the moving particle remains in the
vicinity of unstable equilibrium points for an infinitely long
time, and they can be used as reference orbits. Asymptotic orbits
to equilibrium points were first studied by Str
![]() mgen
(1935), and were associated with families of periodic
orbits as their terminations with infinite period. These were
spiralling asymptotics to the equilateral triangle equilibrium
points of the restricted three-body problem. Str
mgen
(1935), and were associated with families of periodic
orbits as their terminations with infinite period. These were
spiralling asymptotics to the equilateral triangle equilibrium
points of the restricted three-body problem. Str
![]() mgen's
work was extended by Markellos et al.
(1995), Perdios (1996,
1997), within the framework of the photogravitational
restricted problem (see also Szebehely & Nacozy
1967; Danby 1967, 1984;
Markellos 1991, among others, for the classical
case). Non-spiralling asymptotic orbits to the collinear
equilibrium points were studied by Deprit & Henrard
(1965), Perdios & Markellos (1990),
Perdios (1993) and Perdios et al.
(2001). These orbits correspond to period
discontinuities in the evolution of orbits within the families to
which they belong. Asymptotic orbits to the collinear points
and to the associated Lyapunov orbits around them were also studied
in detail, both analytically and numerically, by Llibre et al.
(1985) and Koon et al. (2000).
mgen's
work was extended by Markellos et al.
(1995), Perdios (1996,
1997), within the framework of the photogravitational
restricted problem (see also Szebehely & Nacozy
1967; Danby 1967, 1984;
Markellos 1991, among others, for the classical
case). Non-spiralling asymptotic orbits to the collinear
equilibrium points were studied by Deprit & Henrard
(1965), Perdios & Markellos (1990),
Perdios (1993) and Perdios et al.
(2001). These orbits correspond to period
discontinuities in the evolution of orbits within the families to
which they belong. Asymptotic orbits to the collinear points
and to the associated Lyapunov orbits around them were also studied
in detail, both analytically and numerically, by Llibre et al.
(1985) and Koon et al. (2000).
In this paper we compute non-spiralling doubly asymptotic orbits at the collinear equilibrium points of the general three-body problem. Analytical results for the existence of such orbits in the general three-body problem, such as those of Llibre et al. (1985) and Koon et al. (2000) in the restricted problem, are not available, to our knowledge. In the present paper we provide numerical evidence for their existence. We find several such orbits at each of the three collinear equilibrium points for both possible directions of the outgoing eigenvector. The determination of a doubly asymptotic orbit proceeds through a linear analysis to determine the relevant outgoing eigenvector, and a combination of the characteristic bisection and Newton's method to solve numerically the resulting system of equations for the mass parameters of the problem.
In the next section we give the equations of motion of the general three-body problem. In Sect. 3 we describe the procedure employed to determine doubly asymptotic orbits. Finally, in Sect. 4 we present the doubly asymptotic orbits computed.
In a coordinate system ![]() ,
rotating with angular velocity
,
rotating with angular velocity
![]() ,
the equations of motion of three particles with masses m1,
m2 and m3, attracting each other according to the Newtonian law
of gravitation, are expressed in the form (Hadjidemetriou
& Christides 1975):
,
the equations of motion of three particles with masses m1,
m2 and m3, attracting each other according to the Newtonian law
of gravitation, are expressed in the form (Hadjidemetriou
& Christides 1975):
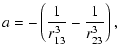 |
|||
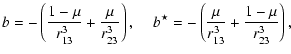 |
|||
![$\displaystyle \displaystyle r_{13} = \displaystyle\left[\left(x+\frac{\mu}{1-\mu}x_2\right)^2+y^2
\right]^{1/2},$](/articles/aa/full/2002/40/aa2503/img11.gif) |
|||
| |
|||
| |
(2) |
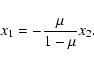 |
(3) |
| (4) |
To compute a doubly asymptotic orbit we first have to
determine, for each pair of values of the mass parameters
![]() ,
the collinear equilibrium points Li, i=1,2,3 on the rotating
X1-axis. To this end we set Xi(t)=0, i=2,5,6,7and X8(t)=1 in the system of the equations of motion and the following
system arises:
,
the collinear equilibrium points Li, i=1,2,3 on the rotating
X1-axis. To this end we set Xi(t)=0, i=2,5,6,7and X8(t)=1 in the system of the equations of motion and the following
system arises:
For motion in the vicinity of an equilibrium point L we
transfer the origin of the coordinate system by
means of the translation:
| (6) |
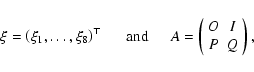 |
(8) |
![\begin{displaymath}P=\left(
\begin{array}{cccc}
c_5^1 & 0 & c_5^3 & 0 \\ [1mm]
...
... 0 & 0 & c_7^8 \\ [1mm]
0 & 0 & c_8^7 & 0
\end{array}\right),
\end{displaymath}](/articles/aa/full/2002/40/aa2503/img28.gif) |
(9) |
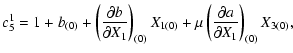 |
|||
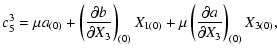 |
|||
| |
|||
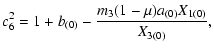 |
|||
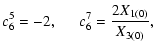 |
|||
![$\displaystyle \displaystyle c_7^1= m_3\Bigg[(1-\mu)a_{(0)}+(1-\mu)\left(\frac{\...
...1(0)}
+\left(\frac{\partial b^\star}{\partial X_1}\right)_{(0)}X_{3(0)}
\Bigg],$](/articles/aa/full/2002/40/aa2503/img34.gif) |
|||
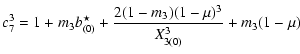 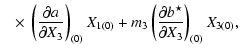 |
|||
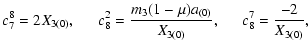 |
(10) |
| (12) |
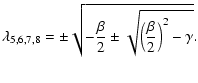 |
(13) |
| (15) |
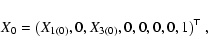 |
(16) |
To solve this system we employ a combination of the characteristic
bisection and Newton's methods. The characteristic bisection method
is based on the characteristic polyhedron concept. It amounts
to constructing another refined characteristic polyhedron containing
the solution, by "bisecting"
a known one in order to calculate the solution with the desired accuracy
(for details we refer to Vrahatis 1995).
Although this method computes the solution of
a system such as (17) with certainty, its convergence is slow compared
to that of Newton's method, which is known to be quadratic.
Newton's method is applied here as follows.
Since System (17) is not satisfied initially we consider
corrections ![]() and
and
![]() of
of ![]() and m3such that:
and m3such that:
The procedure employed here is the following.
First, the characteristic bisection method is applied to compute a
doubly asymptotic orbit with a predetermined mild accuracy
![]() ,
typically
,
typically
![]() .
Then we
utilize the previous estimate of the orbit as an initial approximation
for Newton's method. In case a better approximation is not accomplished
after one iteration of Newton's method, we reapply the
characteristic bisection, starting from its previous stage,
in order to achieve a superior estimate, say
.
Then we
utilize the previous estimate of the orbit as an initial approximation
for Newton's method. In case a better approximation is not accomplished
after one iteration of Newton's method, we reapply the
characteristic bisection, starting from its previous stage,
in order to achieve a superior estimate, say
![]() .
Then we apply again Newton's method and continue with the same
procedure until the solution of (17) is obtained with the
desired accuracy. This procedure ensures both certainty and speed of
convergence (see for details Perdios et al. 2002).
.
Then we apply again Newton's method and continue with the same
procedure until the solution of (17) is obtained with the
desired accuracy. This procedure ensures both certainty and speed of
convergence (see for details Perdios et al. 2002).
We have used the above analysis and numerical procedure,
for a suitably small value of the orbital parameter
![]() ,
to compute doubly asymptotic orbits to all three collinear
equilibrium points for both directions of the outgoing
eigenvector in each case, i.e. for both signs of the orbital
parameter
,
to compute doubly asymptotic orbits to all three collinear
equilibrium points for both directions of the outgoing
eigenvector in each case, i.e. for both signs of the orbital
parameter
![]() .
The results are presented in
Table 1.
.
The results are presented in
Table 1.
In Figs. 1-6 the asymptotic orbits of
Table 1 marked by asterisks are shown.
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{2503f1a.EPS}\\ [5mm]
\includegraphics[width=5.7cm,clip]{2503f1b.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg77.gif) |
Figure 1:
a) Doubly asymptotic orbit at L1 with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{2503f2a.EPS}\\ [5mm]
\includegraphics[width=5.7cm,clip]{2503f2b.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg78.gif) |
Figure 2:
a) Doubly asymptotic orbit at L1 with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{2503f3.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg79.gif) |
Figure 3:
Doubly asymptotic orbit at L2 with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{2503f4.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg80.gif) |
Figure 4:
Doubly asymptotic orbit at L2 with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{2503f5.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg81.gif) |
Figure 5:
Doubly asymptotic orbit at L3 with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{2503f6.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg82.gif) |
Figure 6:
Doubly asymptotic orbit at L3 with
|
| Open with DEXTER | |
We have also found some asymptotic orbits of the restricted three-body
problem when within the framework of the general three body problem
our numerical procedure converged to a pair of mass parameter
values such that ![]() but m3=0. For example at L1 for
but m3=0. For example at L1 for
![]() and
and
![]() we found an asymptotic orbit
with initial conditions:
we found an asymptotic orbit
with initial conditions:
![\begin{figure}
\par\includegraphics[width=5cm,clip]{2503f7a.EPS}\\ [2mm]
\inclu...
...2503f7b.EPS}\\ [2mm]
\includegraphics[width=5cm,clip]{2503f7c.EPS} \end{figure}](/articles/aa/full/2002/40/aa2503/Timg87.gif) |
Figure 7:
Doubly asymptotic orbits of the restricted
problem a) at L1 with
|
| Open with DEXTER | |
Acknowledgements
Thanks are due to Prof. V. V. Markellos for valuable discussions during this work. V. S. Kalantonis acknowledges financial support under a University of Patras "K. Karatheodory" research grant.