A&A 394, 89-96 (2002)
DOI: 10.1051/0004-6361:20021128

Vertical scaleheights in a gravitationally coupled, three-component Galactic disk

C. A. Narayan - C. J. Jog

Department of Physics, Indian Institute of Science, Bangalore 560 012, India

Received 29 January 2002 / Accepted 25 July 2002

Abstract
The vertical scaleheight of the atomic hydrogen gas shows a remarkably flat distribution with the galactocentric radius in the inner Galaxy. This has been a long-standing puzzle (Oort 1962) because the gas scaleheight should increase with radius when treated as responding to the gravitational potential of the exponential stellar disk. We argue that the gravitational force of the molecular and atomic hydrogen gas should also be brought into the picture to explain this. We treat the stars, the HI and H2 gas as three gravitationally coupled components in the Galactic disk, and find the response of each component to the joint potential and thus obtain their vertical distribution in a self-consistent fashion. The effect of the joint potential is different for the three components because of their different velocity dispersions. We show that this approach cohesively and naturally explains the observed scaleheight distribution of all the three components, namely, the HI and H2 gas and the stars, in the region studied (2-12 kpc). This includes the constant scaleheight for the HI seen in the inner Galaxy. The effect of H2 dominates in the molecular ring region of 4-8.5 kpc, while that due to HI is dominant in the outer Galaxy.

Key words: galaxies: kinematics and dynamics - galaxies: structure - Galaxy: structure - hydrodynamics - galaxies: ISM


1 Introduction

The constancy of HI vertical scaleheight in the inner region of our Galaxy (<8.5 kpc) has been well-known for a long time and has not been explained so far (Oort 1962; Dickey & Lockman 1990; Heiles 1991). This behaviour is surprising since the atomic hydrogen gas, in the presence of the stellar disk potential alone, should have a scaleheight which increases exponentially with radius. Physically, the scaleheight of a component is a measure of the equilibrium between the local vertical gravitational force and the gas pressure as given by the equation of hydrostatic equilibrium (e.g., Rohlfs 1977). Thus, an increase in the gravitational force in the disk would reduce the scaleheight. We show in this paper that the gas gravity needs to be taken into account, to get the correct physical description for the observed vertical scaleheights of all the disk components.

The interstellar gas in the Galaxy contains $\sim$15% of the total disk surface density (Binney & Merrifield 1998). About half of it is in the form of atomic hydrogen and the other half is in the form of molecular hydrogen but with widely different radial distributions (Scoville & Sanders 1987; Bronfman et al. 1988). A large fraction of mass of atomic hydrogen is located in the outer Galaxy (with R, the galactocentric radius >8.5 kpc), which is also the region where the force due to the stellar disk becomes weak. Hence we expect the gravity of atomic gas to play a significant role in the determination of the scaleheights of stars and gas in the outer Galaxy. In contrast, most ($\sim$80%) of the molecular hydrogen gas is concentrated in the form of a ring between 4-8.5 kpc. The molecular hydrogen gas is known to exist in the form of self-gravitating clumps called molecular clouds and several such clouds segregate to form a cloud complex (Rivolo et al. 1986). It has been shown recently that such complexes (of a few 100 pc in size each) with mass densities $\sim$6 times that of Oort limit dominate the local gravitational field, and this leads to a redistribution of the nearby disk matter resulting in smaller scaleheights of the disk components (see Jog & Narayan 2001). On a larger scale, the average H2 distribution will affect the scaleheight distribution of all the disk components in the inner Galaxy. Because of its low velocity dispersion the gas forms a thin layer, and hence can dominate the in-plane dynamics and affect the net vertical distribution of the disk components even though its contribution to the total surface density is small.

In this paper, we treat the stars, the HI and H2 gas as three gravitationally coupled disk components and obtain their vertical scaleheights as a function of radius under the new joint potential. A similar study showing the importance of gravitational coupling between stars and gas for the local stability of a two-component galactic disk has been shown earlier by Jog & Solomon (1984) and Jog (1996). The importance of including the HI self-gravity was pointed out in the past to mainly study the vertical distribution of HI at large radii in galaxies (van der Kruit 1988; Olling 1995). However, these earlier papers do not include H2 gas and also they do not treat a coupled three-component disk as we do in this paper.

The formulation of equations is discussed in Sect. 2. Section 3 describes the method of solving them and the parameters used. The results obtained and a comparison with observations are discussed in Sect. 4. The discussion and conclusions follow in Sects. 5 and 6 respectively.

2 Formulation of equations

We consider the atomic and molecular hydrogen gas layers to be very thin disks embedded in the stellar disk. We use the galactic cylindrical co-ordinates ( $R, \phi, z$), and consider their distribution from R = 2-12 kpc. For the sake of simplicity, all the three disks are taken to be axisymmetric and coplanar. The gravitational force due to these embedded layers would modify the steady-state density distribution of all the three components and along all the three axes. However, we can neglect the effect along the azimuthal direction because of the assumed axisymmetry and along the radial direction because the disk is thin. Therefore, we need to consider the modification of the steady-state density distribution only along the z-axis.

The force equation along the z-axis or the equation of hydrostatic equilibrium is given by (e.g., Rohlfs 1977):

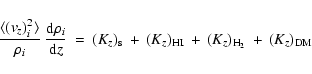\begin{displaymath}{\frac {\langle{({\mathit v}_z)^2_i}\rangle}{\rho_i} \: \frac... ...\mathit K}_z)_{\rm H_2}} \: + \: {({\mathit K}_z)_{\rm DM}} } \end{displaymath} (1)

where $\rho$ is the mass density, $(K_{z}) \: = \: - {{\partial}{\psi}}/ {{\partial}z} $ is the force per unit mass along z-axis, $\psi$ is the corresponding potential, and the subscript i = s, HI, and H2 denotes these quantities for stars, HI and H2 respectively. The last term on the right hand side denotes the force along the z-axis due to the dark matter (DM) halo. Due to the disk being thin, its effect on the vertical distribution within the halo can be neglected. We take the root mean square of the vertical velocities of a component ${{\langle{({\mathit v}_z)^2_i} \rangle }{1}/{2}}$ or the random velocity dispersion at a radius R and treat the component as being isothermal along z. The right hand side of Eq. (1) gives the total vertical force due to all the components. The dark matter halo has been included for the sake of completeness, and also because it helps us to quantify the role played by the halo in defining the vertical density distribution in the region of interest ($R \leq 12$ kpc).

For a thin axisymmetric disk, the joint Poisson equation reduces to:

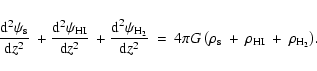\begin{displaymath}{{\rm\frac {d^2{\psi_{\rm s}}}{d{\mathit z^2}} \: + \frac {d^... ...rm s} \: + \: {\rho}_{HI} \: + \: {\rho}_{H_2} \right )}}. \end{displaymath} (2)

Combining Eqs. (1) and (2), the density distribution of a component at a radius R, can be defined by:

$\displaystyle \frac{{\rm d}^2{\rho_i}}{{\rm d}{z^2}} = \frac{\rho_{i}}{\langle(... ... ] + \frac{1}{\rho_{i}} \left( \frac {{\rm d}{\rho_{i}}}{{\rm d} z} \right)^{2}$     (3)

where the square brackets contain terms that arise due to the joint potential of the three disk components and the halo, and the same total potential is experienced by all the components. The vertical velocity dispersion, on the other hand, varies with each component. Thus, despite a common gravitational potential, the density distribution of each component will be different due to the difference in their random velocity dispersions.

3 Solution and parameters

3.1 Solution of equations

We need to solve the three coupled equations (represented by Eq. (3)) simultaneously to obtain the vertical density distribution of each component. Each second order ordinary differential equation can be split into two first order differential equations for the sake of simplicity. They can be solved numerically as an initial value problem, using the fourth-order Runge-Kutta method of integration (Press et al. 1986). The two boundary conditions required at the mid-plane, z = 0 are:

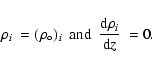\begin{displaymath}{\rho_i \: = (\rho_\circ)_i \: \: {\rm and} \: \: \frac {{\rm d}\rho_i}{{\rm d}{\mathit z}} \: = 0. } \end{displaymath} (4)

For a realistic distribution, the density along the vertical axis is homogeneous very close to the mid-plane, thus ${{{\rm d}{\rho_i}}/{{\rm d}{\mathit z}} = 0 \: {\rm at} \: {\mathit z} = 0 }$. We are then left with ${(\rho_{\circ})_i}$, the modified midplane density which is not known a priori. The distribution of matter can be treated as a one dimensional problem along the z-axis and hence the surface density $\Sigma_{i}(R)$ will not vary even when the joint gravitational potential is considered. The surface density is twice the area under the curve $\rho_{i}(z)$ versus z. Given a value of $\Sigma_{i}(R)$ (see Sect. 3.2 for the values used), the value of ${(\rho_{\rm\circ})_i}$ can be found by trial and error. Once this is fixed, the distribution $\rho_{i}(z)$ follows easily. All the three components, stars, HI and H2 affect each other's density distribution via Eq. (3) so that the Galactic disk is actually a coupled system. At each R, the three density functions are solved simultaneously by taking account of the effect of the other components in an iterative fashion. First, $\rho_{\rm s}(z)$ is evaluated using Eq. (3) with null values for the corresponding gas densities. $\rho_{{\rm HI}}(z)$ is then obtained by using the known stellar density distribution and null values for $\rho_{\rm H_2}(z)$. Knowing $\rho_{\rm s}(z)$ and $\rho_{{\rm HI}}(z)$, $\rho_{\rm H_2}(z)$ can be found easily. However, these results do not describe the real coupled disk distribution because $\rho_{\rm s}(z)$ has been evaluated here in the absence of HI and H2. Knowing the non-zero values for gas densities, $\rho_{\rm s}(z)$ is re-evaluated incorporating the gas gravity. The above cycle is repeated four times until each of the distribution converges with a fifth decimal accuracy. We obtain a sech2-like distribution for each component and we use its HWHM (half-width-half-maximum) to define the vertical scaleheight. In comparison, for a one-component self-gravitating disk, the vertical distribution obeys a sech2 distribution (Spitzer 1942). Repetition of the above calculation at regular intervals of R enables us to plot the scaleheights versus radius, provided the surface density $\Sigma_{i}(R)$ is known at all radii.

3.2 Parameters used

For each disk component, we need to specify the surface density and the random velocity dispersion at each radius R in the disk. Table 1 gives values of all the observed parameters used. The observed values are used for all the gas parameters, whereas all the stellar parameters except for the velocity dispersion are taken from models in the literature. The HI gas surface density is negligible at the Galactic centre, slowly increases to $\sim$5 $M_{\odot}$ pc-2 by 4 kpc and remains roughly constant till about 16 kpc (Scoville & Sanders 1987). A similar HI profile was obtained by Dame (1993), also based on the HI data by Burton & Gordon (1978). The molecular hydrogen gas is concentrated in the form of a ring with the peak surface density of $\sim$20 $M_{\odot}$ pc-2 at $\sim$5 kpc from the centre (Scoville & Sanders 1987). The vertical velocity dispersions of HI and H2 gas are 8 km s-1 (Spitzer 1978) and 5 km s-1 (Clemens 1985; Stark 1984) respectively and they remain constant with radius. These values agree fairly well with the determination based on a tangent-point analysis by Malhotra (1994) for H2, and by Malhotra (1995) for HI.


 
Table 1: Input parameters from observations
Parameters Value Reference
Surface density 5 $M_{\odot}$ pc-2 Scoville & Sanders (1987)
of HI    
Surface density radially Scoville & Sanders (1987)
of H2 varying  
Velocity dispersion 8 km s-1 Spitzer (1978)
of HI    
Velocity dispersion 5 km s-1 Clemens (1985),
of H2   Stark (1984)
Vertical velocity exponentially Lewis & Freeman (1989)
dispersion of stars decreasing  


Lewis & Freeman (1989) have measured the stellar radial velocity dispersion at different points between 1-17 kpc along the galactocentric radius towards the Baade's window in the Milky Way. Assuming the ratio of the vertical to the radial random velocity dispersion at all radii to be equal to its value at the solar neighbourhood, namely 1/2(Binney & Merrifield 1998), we get the corresponding vertical velocity dispersions. The method of least square fit to the data gives an exponential fit with a scalelength of 8.7 kpc, and a value of 18 km s-1 at the solar neighbourhood.

The two key parameters required to find the entire stellar disk surface density distribution are the local stellar surface density and the exponential radial disk scalelength, $h_{\rm R}$. The stellar disk mass surface density at the solar point has the following range of observed values. For example, from a set of distance and velocity data, Kuijken & Gilmore (1991) obtain the total disk plus halo surface density to be $ 48 \pm 9$ $M_{\odot}$ pc-2for the region very close to the midplane. More recent observations point to a value of $ 52 \pm 13$ $M_{\odot}$ pc-2 (Flynn & Fuchs 1994). Dehnen & Binney (1998) use a lower limit of 40 $M_{\odot}$ pc-2 for the total disk surface density as a constraint for four models involving a range of values for the stellar disk scalelength.

The determination of the radial disk scalelength $h_{\rm R}$ has attracted much attention in the literature in recent years. A wide range of values is obtained for $h_{\rm R}$ ranging from 2.3 kpc (Drimmel & Spergel 2001) to 6 kpc (Mendez & van Altena 1998). Most of the recent papers tend towards a lower value in this range: Fux & Martinet (1994): 1.9-3.3 kpc; Ruphy et al. (1996): 2.3 kpc; Dehnen & Binney (1998): 2-3.2 kpc; Mera et al. (1998): 3.2 kpc; Porcel et al. (1998): 2.1 kpc; Drimmel & Spergel (2001): 2.3 kpc.


 
Table 2: Model-dependent input parameters
  Stellar disk Velocity dispersion
Model Parameters of HI
  $(\Sigma_{\circ})_{\rm s}$ $h_{\rm R}$  
  ($M_{\odot}$ pc-2) (kpc) (km s-1)
       
Standard model 640.9 3.2 8
(Sect. 3.2)      
Varying stellar 200.0 6.0 8
disk parameters      
Varying velocity 640.9 3.2 8 (at R = 8.5 kpc) with
dispersion of HI     slope = -0.8 km s-1 kpc-1


We adopt the model of Mera et al. (1998) (see Table 2) as the standard mass model for the Galaxy for the following reasons. First, it is modern and simple and also allows us to study the gravitational effect of various components. Second, their choice of the total surface density of 52 $M_{\odot}$ pc-2 at the solar neighbourhood from a recent paper in the literature (Flynn & Fuchs 1994) and their choice of $h_{\rm R} = 3.2$ kpc fall within the acceptable range as can be seen from the discussion above. Third, for the sake of internal consistency, we prefer to use the parameters from a single mass model as opposed to choosing them in an ad hoc manner. Finally, they use a screened halo-density profile which is sufficient to determine the dynamical effect of the spherical halo. Its contribution to the local surface density is negligible but it gives rise to a non-zero force term along the z-axis. Subtracting the total gas surface density of 7 $M_{\odot}$ pc-2 (Scoville & Sanders 1987) from the above value of the local total surface density, we get the local stellar surface density to be 45 $M_{\odot}$ pc-2. This gives the central extrapolated stellar surface density, ${\rm (\Sigma_{\circ})_{\rm s}} = 640.9~M_{\odot}$ pc-2 as given in Table 2.

In spherical co-ordinates, the density profile for the halo is (Mera et al. 1998):

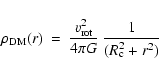\begin{displaymath}{\rho_{{\rm DM}}}(r) \: = \: \frac {v^2_{{\rm rot}}}{4 \pi G} \: \frac {1}{(R^2_{\rm c} + r^2)} \end{displaymath} (5)

where ${\rho_{{\rm DM}}}$ is the dark matter halo mass density; $R_{\rm c}$, the core radius = 5 kpc; and $v_{{\rm rot}}$, the circular velocity = 220 km s-1.

By inverting the Poisson equation for the dark matter halo, we calculate the halo potential to be the following:

\begin{displaymath}{\psi_{{\rm DM}}}(r) \: = \: {v^2_{{\rm rot}}} \: \left [ 1 \... ...{-1}} \left (\frac {r}{R_{\rm c}} \right ) \: \right ]\cdot \end{displaymath} (6)

Rewriting the above equation in cylindrical co-ordinates and taking the second derivative of the halo potential with respect to z, we get

$\displaystyle \frac {{\partial}^2 \psi_{{\rm DM}}}{{\partial} z^2} = \frac {v^2... ...t{R^2 + z^2}} {R_{\rm c}} \right ) \: \left [ 1 - \frac{3z^2}{R^2+z^2} \right ]$      
$\displaystyle +\frac {z^2 R^2_{\rm c} v^2_{{\rm rot}}}{(R^2 + z^2)^2 (R^2_{\rm ... ...rm rot}}} {(R^2 + z^2)} \: \left [ \frac {2z^2}{(R^2 + z^2)} - 1 \right ] \cdot$     (7)

Thus, ${{\rm d}({\mathit K}_z)_{DM}/{\rm d}{\mathit z} = -{\partial}^2\psi_{DM}/{\partial} {\mathit z}^2}$, is the halo contribution used in the right hand side of Eq. (3).

4 Results

4.1 Results for vertical scaleheight: Standard model

The results for the vertical scaleheight are obtained as a function of the galactocentric radius using the Galactic mass model of Mera et al. (1998), as explained in Sect. 3.1. The sampling is done at every 420 pc which is set by the bin-size of the H2 data given by Scoville & Sanders (1987).

4.1.1 HI scaleheight
Figure 1a shows the plot of vertical scaleheight versus radius for HI with the dashed line obtained using the stellar potential and the solid line obtained using the joint potential approach. The observed values are shown as crosses and are taken from Lockman (1984) for the inner Galaxy (R < 8.5 kpc), and Wouterloot et al. (1990) for the outer Galaxy (R > 8.5 kpc) - see Burton (1992) for details. The curve obtained using the stellar potential alone increases exponentially and thus deviates strongly from the observed curve beyond 8 kpc. On using the joint potential, the scaleheights reduce significantly at large radii and show a better overall agreement with observations. Thus our model explains the old puzzle (Oort 1962) of nearly-constant scaleheight observed in the inner Galaxy.

At 10 kpc, the scaleheight reduces by about $34\%$ to give a value of 187 pc, which is very close to the observed value of 193 pc (Wouterloot et al. 1990). In the outer Galaxy, the HI surface density is either comparable to or more than that of stars because of the exponential fall-off of the stellar surface density. Thus the joint self-gravitating disk extends well beyond the stellar disk and the HI gravity is mainly responsible for the scaleheight determination in that region. In the inner Galaxy (R < 8.5 kpc), the combined gravity of HI and H2is responsible for the reduced scaleheights. Unlike the smooth dashed line, the response to the joint potential has many small-scale dents on it. This is also seen later in the plots for H2 and stars. The appearance of these dents is not due to an undersampling of data points but rather is due to the gravity of H2 gas which shows a non-smooth radial distribution, as seen from the fact that the locations of the dents coincide with the surface density peaks of molecular hydrogen gas. This is analogous to the local effect of a molecular cloud complex on the disk shown by Jog & Narayan (2001).


 \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=8.8cm,clip]{fig1a.E... ....4cm}\subfigure[]{\includegraphics[width=8.8cm,clip]{fig1c.EPS} }}\end{figure} Figure 1: a) A plot of HI vertical scaleheight versus galactocentric radius. The joint potential approach gives a theoretical curve (solid line) which is in a better agreement with observations than the curve obtained using the stellar potential alone (dashed line), particularly in the range of 5-10 kpc. b) A plot of H2 scaleheight versus radius. The scaleheight obtained on using the joint potential (solid line) agrees well with observations over the entire radial range. c) The stellar disk scaleheight versus radius obtained with the stellar potential alone (dashed line) and for the joint potential (solid line). The joint potential approach gives a much more moderate flaring and these results match with the observational data of Kent et al. (1991).
Open with DEXTER

A more subtle point is that in the range R = 0-5 kpc both the approaches predict lower values than observed, implying that some other factors must be affecting the scaleheight. There could be additional physical processes that increase the scaleheight in the region such as, the heating due to the bar (Binney & Merrifield 1998) within the central 4 kpc. On the other hand, beyond 10 kpc, the predicted scaleheights are larger than the observed values in spite of incorporating the HI gas gravity. Thus, the dominant role played by the HI gas gravity is still not sufficient to bring about a complete agreement between the two. One would then expect that, inclusion of the halo potential would resolve the disagreement between the observed and theoretical curves. However, Fig. 1c already includes the halo potential and it brings about less change in the disk density distribution than expected. A possible reason as to why the halo contribution may not be very important is due to its extended z distribution and this is discussed in detail in Sect. 5. Thus, the agreement of the theoretical vertical scaleheights for HI with observations is best seen in the middle galactic range of 5-10 kpc. A small radial variation of HI velocity dispersion leads to a better agreement with observations over a larger radial range as shown in Sect. 4.2.

4.1.2 H2 scaleheight

Figure 1b shows the plot of scaleheight vs. radius for H2, with the dashed line obtained using the stellar potential and the solid line obtained using the joint potential approach. The observed scaleheight values from Sanders et al. (1984) for R < 8.5 kpc and Wouterloot et al. (1990) for R > 8.5 kpc are shown as crosses. Neglecting the self-gravity of HI and H2 once again yields scaleheights much larger than the observed values. On the other hand, the curve predicted by treating the galactic disk as a coupled, three-component system, agrees very well with observations. This agreement continues further upto 14 kpc though Fig. 1b shows results upto only 12 kpc. Both the theoretical results are in good agreement with the observations in the inner few kpc from the Galactic centre because, this region is entirely dominated by the stellar potential so that the joint potential differs very little from it.

4.1.3 Stellar scaleheight
Figure 1c shows the vertical scaleheight curves for the stellar disk, obtained using the potential of stellar disk alone (shown as a dashed line), and that obtained using the joint potential (shown as a solid line). The stellar disk potential gives an exponentially increasing curve, while the joint potential results in a nearly flat curve. The resulting scaleheight curve exhibits the following detailed behaviour. In the region of 0-5 kpc the scaleheight is almost constant at 300 pc. In the middle region of 5-10 kpc it shows a linear increase with a slope of $\sim$24 pc kpc-1, while beyond 10 kpc it remains a constant at $\sim$420 pc. Without gas gravity (the dashed line, Fig. 1c), the stellar scaleheight in the solar neighbourhood is = 550 pc. With the gas gravity (the solid line, Fig. 1c), this comes down to a reasonable 380 pc. This agrees well with the local observed characteristic half thickness of 350 pc (Binney & Tremaine 1987, Chap. 1). We would like to stress that the near constancy of the stellar scaleheight upto 5 kpc (Fig. 1c) in our model comes about naturally by incorporating the gravity of HI and H2 in a standard exponential galactic disk.

Unfortunately, these results cannot be compared with the optically deduced scaleheights in the non-local regions of our own Galaxy due to the high optical depth in the visible band. Hence, one has to compare the trend in the predictions with the data from external galaxies. van der Kruit & Searle (1981a,b) first showed from a study of edge-on spirals that these exhibit a remarkably constant stellar scaleheight with radius. However, recent data by de Grijs & Peletier (1997) show a moderate increase in the stellar scaleheight with radius, in agreement with the trend shown by our results in Fig. 1c. This moderate increase is shown to be a general result for spiral galaxies (Narayan & Jog 2002).

A linear increase beyond 5 kpc with a small slope of 20 pc kpc-1 has been argued for by Kent et al. (1991). This is obtained from a best fit to the near-IR data from the $\it Spacelab 2$ mission for the Galaxy. This is in very good agreement with our results. A similar conclusion, based on the COBE/DIRBE data was reached by Drimmel & Spergel (2001). Kent et al. (1991) however do not mention whether the behaviour continues farther into the outer Galaxy or not. Their motivation for using such a slope was purely to get the best fit to the observed data and involved no dynamics whereas we get it physically due to the inclusion of gas gravity in the study.

4.2 Variation in input parameters

In Sect. 4.1, we saw that the results for H2 and stars using the joint potential approach are in very good agreement with the observations in the region studied (2-12 kpc). In the case of HI, the best agreement is limited to a small region of 5-10 kpc (see Fig. 1a). To improve the agreement with HI observations over the entire region studied, the predicted scaleheights should increase in the region 0-5 kpc and decrease in the region beyond 10 kpc. We try to obtain this by two different approaches by varying the input parameters as described below.

4.2.1 Variation in the stellar disk parameters
We have used the mass model of Mera et al. (1998) in Sect. 4.1 as a realistic mass model to bring out the importance of gas gravity. In this section, we vary the stellar disk parameters namely ${\rm ({\Sigma}_{\circ})_{\rm s}}$, the central surface density, and hR, the disk scalelength, freely and study the resulting variation in the HI scaleheight. For an overall agreement, the gravitational force should be weaker in the region below 5 kpc and stronger in the region beyond 10 kpc. This can be brought about by a lower value of central surface density along with a larger radial scalelength as compared to the model of Mera et al. (1998). We find that the best mathematical fit to the observed data is obtained by using ${\rm ({\Sigma}_{\circ})_s} = 200$ $M_{\odot}$ pc-2 and hR = 6 kpc (see Table 2). Note that these parameters are far from the typical values of ${\rm ({\Sigma}_{\circ})_s} \sim 640$ $M_{\odot}$ pc-2 and $h_{R} \sim$3 kpc (see Sect. 3.2). Also, we find that the results obtained for H2 and stars in this case deviate to a large degree from the observed behaviour. Thus the above attempted change in the parameters is unrealistic. Hence this is not the correct way to explain the observed radial variation of the HI scaleheight.
4.2.2 Variation in HI velocity dispersion

Yet another way of improving the agreement between the scaleheight curve of HI and the observations is by varying the HI velocity dispersion with radius instead of using a constant value of 8 km s-1 as done earlier in Sect. 4.1. We find that a simple linear variation (between R = 2-12 kpc) with a slope of -0.8 km s-1 kpc-1 is required to obtain the least $\chi^2$ value. The value of HI gas velocity at R = 8.5 kpc is taken to be 8 km s-1 (see Table 2) and is used as a constraint in determining the slope. In Fig. 2a, we plot the results for HI obtained using the joint potential plus the variation in velocity dispersion (as a solid line) and the observed data as crosses (see Sect. 4.1.1 for details of observed data). The results agree well with observations over the entire radial range studied. On comparing with Fig. 1a, it is clear that the variable HI velocity dispersion leads to a better overall agreement with the observed data.

A plausible physical mechanism to explain this varying HI gas dispersion could be the energy input via supernovae. As Mckee & Ostriker (1977) proposed, the kinetic energy of the HI clouds is regulated by the rate of supernovae. Hence we expect the HI velocity to increase in the molecular ring region where a higher star formation rate and a higher rate of formation of supernovae is expected. Kamphuis (1993) has shown that the increase in velocity dispersion at smaller radii is also observed in a number of external galaxies.

 \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=8.8cm,clip]{fig2a.E... ...}\subfigure[]{\includegraphics[width=8.8cm,clip]{fig2c.EPS} }} \par \end{figure} Figure 2: a) The HI scaleheight versus radius obtained for the joint potential, and where a linear variation of HI velocity dispersion with a slope of -0.8 km s-1 kpc-1 has been introduced. This gives results that are in good agreement with observations in the entire radial region studied, and the fit is better than in Fig. 1a (solid line). b) The vertical scaleheight versus radius for H2 gas (solid line), obtained using a linearly varying HI velocity dispersion as in Fig. 2a. The agreement with observations (crosses) seen here is very close to that in Fig. 1b. This implies that the introduced variation in the HI velocity dispersion does not affect the H2 scaleheight noticeably. c) A plot of the predicted stellar scaleheight of our Galaxy versus radius, obtained using a linearly varying HI velocity dispersion as in Fig. 2a. The results are similar to that in Fig. 1c. Thus the introduced variation in the HI velocity dispersion does not affect the stellar scaleheight noticeably.
Open with DEXTER

Interestingly, Oort (1962) had proposed a similar increase in the velocity dispersion of HI at smaller radii as a possible way for obtaining the observed constant scaleheight, though he did not give a physical reason for this trend. This idea was also proposed by de Boer (1991). Oort (1962) had suggested a linear variation in HI velocity dispersion with a slope of about -2 km s-1 kpc-1 (varying from 13 to 5 km s-1 between R = 4-8 kpc), where the HI distribution is defined by the stellar potential alone. Note that the slope that we require is smaller and is equal to -0.8 km s-1 kpc-1. This is because we have included the effect of the gas gravity, and hence a smaller radial variation in HI velocity dispersion is sufficient to give a constant vertical scaleheight for HI.

Figure 2b contains the resulting H2 scaleheight versus radius (solid line) and the observed data for H2 (see Sect. 4.1.2 for details on observations of H2). Figure 2c contains the resulting stellar scaleheight versus radius (solid line). On varying the HI velocity dispersion the scaleheights of H2 and stars are not affected to a noticeable extent (compare Figs. 2b and 2c respectively with Figs. 1b and 1c), because the change in the HI velocity dispersion will not directly affect the vertical distribution of the other components. Thus the joint potential plus a slightly varying HI gas dispersion seems like a plausible physical scenario which can self-consistently explain the scaleheight distribution of all the three galactic disk components for realistic input parameters.

5 Discussion

(1) It is interesting that the maximum impact of the different components is seen to occur in different galactocentric radial regions. With the stellar surface density peaking at the centre of the Galaxy, the stellar disk alone determines the scaleheights of all the components in the central few kpc. The maximum effect due to H2 is seen in the region of 4-8.5 kpc, with a peak at 5 kpc. Finally, the maximum effect due to HI is seen only beyond 8.5 kpc, despite the fact that the HI surface density is constant between 4-16 kpc. This is because, the inner Galaxy is entirely dominated by stars and H2 and it is only in the outer Galaxy that the HI becomes important. Thus the three components seem to conspire to give a nearly constant scaleheight for each of them in the inner Galaxy.

(2) We have included the dark matter halo potential to evaluate its contribution in reducing the scaleheight quantitatively. We find that the presence of the halo reduces the HI scaleheight at 12 kpc only by $13\%$. This is contrary to the general expectation in the literature that the outer Galaxy structure is dominated and defined by the dark halo. This is because the dark matter and visible disk matter dominate at entirely different range of z values. For a self-gravitating stellar disk (Eq. (1)), we find that more than 99 percent of its matter lies within $ z \leq 1 $ kpc, within radius of 12 kpc. Whereas, a standard massive spherical dark matter halo of a mass of 1012 $M_{\odot}$ and core radius = 5 kpc (as defined in Sect. 3.2) has less than $6\%$ of its entire mass in the column at 12 kpc, within the same z limit. Therefore, the disk matter distribution along z is not strongly dependent on the presence of halo upto the highest radius studied here, namely R = 12 kpc.

(3) We have only considered the turbulent gas pressure associated with the vertical velocity dispersion of HI as being responsible for its vertical support. We have not included the pressure support due to magnetic fields and cosmic rays. This is for simplicity, and also because these may not be important for supporting neutral hydrogen as argued by Lockman & Gehman (1991). It is interesting that our resulting scaleheights for a three-component, gravitationally coupled galactic disk using the support of turbulent gas pressure alone match well with observations, this confirms the argument of Lockman & Gehman (1991).

6 Conclusions

In this paper we show that the gas gravity is crucially important in the determination of the vertical scaleheights of all the disk components in a galactic disk. We treat the galactic disk as a gravitationally coupled, three-component system consisting of stars, atomic gas and molecular gas, and also include the effect of the dark matter halo. The model developed is general and is applied to the Galaxy in this paper. We obtain the self-consistent vertical distribution for each component responding to the joint potential for a radial region of 2-12 kpc. Our approach leads naturally to a better agreement with observations of all the three components:

(1) The radial variation of the HI vertical scaleheight matches fairly well with observations and the best agreement is seen between R = 5-10 kpc. The inclusion of gas gravity can explain the 40-year old puzzle of the observed nearly-constant HI scaleheight.

The overall agreement over the entire region studied is even better if a small linear variation with radius in the HI velocity dispersion with a slope of -0.8 km s-1 kpc-1 between 2-12 kpc is introduced. The physical justification for this increase at smaller radii is the higher expected supernova rate in the inner Galaxy.

(2) The radial variation of H2 scaleheight obtained matches very well with observations upto a radius of 14 kpc. Our model gives the physical origin of the H2 vertical scaleheight distribution, which has not been studied in the literature so far.

(3) The stellar scaleheight is found to be nearly constant with radius at $\sim$300 pc in the central region of 0-5 kpc of our Galaxy and shows a slow linear increase beyond 5 kpc. This agrees well with the result obtained by fitting the near-IR data in the Galaxy by Kent et al. (1991).

We have applied the above general model to two external galaxies, NGC 891 and NGC 4565, and we find that these also show a similar moderate flaring with radius (Narayan & Jog 2002).

Acknowledgements
We would like to thank the anonymous referee for useful comments.

References

 

Copyright ESO 2002