A&A 394, 47-57 (2002)
DOI: 10.1051/0004-6361:20021100

Magnetic fields in the absence of spiral density waves - NGC 4414

M. Soida1 - R. Beck3 - M. Urbanik1 - J. Braine2


1 - Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Kraków, Poland
2 - Observatoire de Bordeaux, UMR 5804 CNRS/INSU, BP 89, 33270 Floirac, France
3 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 20 September 2001 / Accepted 29 July 2002

Abstract
We present three-frequency VLA observations of the flocculent spiral galaxy NGC 4414 made in order to study the magnetic field structure in absence of strong density wave flows. NGC 4414 shows a regular spiral pattern of observed polarization $\vec B$-vectors with a radial component comparable in strength to the azimuthal one. The average pitch angle of the magnetic field is about 20 $\hbox{$^\circ$ }$, similar to galaxies with a well-defined spiral pattern. This provides support for field generation by a turbulent dynamo without significant "contamination'' from streaming motions in spiral arms. While the stellar light is very axisymmetric, the magnetic field structure shows a clear asymmetry with a stronger regular field and a smaller magnetic pitch angle in the northern disk. Extremely strong Faraday rotation is measured in the southern part of the disk, becoming Faraday thick at 6 cm. The distribution of Faraday rotation suggests a mixture of axisymmetric and higher-mode magnetic fields. The strong Faraday effects in the southern region suggest a much thicker magnetoionic disk and a higher content of diffuse ionized gas than in the northern disk portion. An elongation of the 20 cm total power emission is also seen towards the South. Although NGC 4414 is currently an isolated spiral, the asymmetries in the polarized radio emission may be sensitive tracers of previous encounters, including weak interactions which would chiefly affect the diffuse gas component without generating obvious long-term perturbations in the optical structure.

Key words: galaxies: magnetic fields - galaxies: individual: NGC 4414 - radio continuum: galaxies - polarization


1 Introduction

The relative role of small-scale velocity perturbations and galaxy-scale gas flows in determining the evolution and structure of galactic magnetic fields is one of the most hotly debated questions in studies of the evolution and structure of galactic magnetic fields (e.g. Zweibel 1996; Zweibel & Heiles 1997; Beck et al. 1996). Large-scale galactic magnetic fields are known to display a coherent spiral-like pattern of polarization $\vec B$-vectors (see Beck et al. 1996 for a review), indicating a substantial radial component capable of resisting the shear due to differential rotation. The spiral magnetic field pattern could be produced by the dynamo mechanism (Wielebinski & Krause 1993; Beck et al. 1996) in which the small-scale motions are constantly feeding the large-scale poloidal (i.e. radial and vertical) field. The radial field could also be produced by continuous field stretching by large-scale flows due to density waves or bars (e.g. Otmianowska-Mazur & Chiba 1995). In choosing a flocculent spiral, where flocculent means without large-scale spiral structure, density waves and bars should play no significant role in determining the magnetic field orientation.

In well-studied nearby spiral galaxies it is extremely difficult to discern the effects of the turbulent dynamo from those due to processes in spiral arms. These objects have well-developed grand-design patterns with strong density wave compression and/or a high concentration of star formation in spiral arms. The first process may strongly modify the magnetic field by effects of compression and gas flows along the arms (Otmianowska-Mazur & Chiba 1995). In some galaxies like M 83 spiral-like compression regions (as traced by aligned dust filaments) fill the whole interarm space. Strong star formation in spiral arms acts destructively on regular fields (Beck et al. 1996). Differences in turbulent activity between the arms and the interarm region may give rise to strong concentration of regular magnetic fields between the stellar arms, thereby strongly influencing the global field structure (Rohde & Elstner 1998).


 

 
Table 1: Basic properties of NGC 4414.
Other names PGC 40692 Reference
  UGC 7539  
RA1950 $\rm 12^h23^m57\hbox{$.\!\!^{\rm s}$ }8$ de Vaucouleurs et al. (1991)
Dec1950 $31\hbox{$^\circ$ }29\hbox{$^\prime$ }58\hbox{$.\!\!^{\prime\prime}$ }0$ de Vaucouleurs et al. (1991)
Inclination 55 $\hbox{$^\circ$ }$ LEDA
Position Angle 155 $\hbox{$^\circ$ }$ LEDA
Distance 19.2 Mpc Thim (2000)
Morphol. Type Sc LEDA


Knapik et al. (2000) first reported that flocculent galaxies may possess regular fields with a strong radial component. Their study was made at low resolution and only at one frequency. In this paper we present a high-resolution multifrequency polarization study of the flocculent galaxy NGC 4414 (Thornley & Mundy 1997). The velocity field shows no evidence for non-circular gas flows (Braine et al. 1993; Sakamoto 1996; Thornley & Mundy 1997). NGC 4414 has a high surface gas density and is forming stars fairly intensively, much like in our own galaxy, but is in no way a starburst. All this ensures good conditions for building up a global magnetic field by turbulent processes in a way unaffected by large-scale gas flows and compressions.

2 Observations and data reduction

The maps of total power and linearly polarized radio emission of NGC 4414 at three frequencies were obtained using the Very Large Array (VLA) of the National Radio Astronomy Observatory (NRAO)[*]. At 8.44 GHz and 4.86 GHz the compact D-array configuration has been used. At 1.415 GHz and 4.86 GHz observations were made with C-array. The on-source time was 1.3 hours and 1.7 hours in the C-array at 1.415 GHz and 4.86 GHz, respectively. In the D-array the observing time was 14 hours at 8.44 GHz and 13 hours at 4.86 GHz. The receiver bandwidth was 50 MHz.

The intensity scale was determined by observing 3C286 and calibrating with the flux densities taken from Baars et al. (1977). The position angle of the linearly polarized emission was calibrated using the same source with an assumed position angle of 33 $\hbox{$^\circ$ }$. The phase calibrator 1219+285 was also used to determine telescope phases and the instrumental polarization.

The data reduction has been performed using the AIPS data reduction package. The edited and calibrated visibility data were Fourier transformed to obtain maps of the Stokes parameters I, Q and U at all three frequencies. At 4.86 GHz the visibilities from both array configurations were combined. The maps were weighted with $\rm ROBUST=0$ for the best resolution and sensitivity compromise, yielding synthesized half-power beam widths (HPBW) of 7 $\hbox {$^{\prime \prime }$ }$ and 11 $\hbox {$^{\prime \prime }$ }$ at 8.44 GHz and 4.86 GHz, respectively. At 1.415 GHz our C-array map also weighted with $\rm ROBUST=0$, has an original HPBW of 14 $\hbox {$^{\prime \prime }$ }$. The naturally weighted maps, more sensitive to extended structures, have HPBWs of 11 $\hbox {$^{\prime \prime }$ }$ and 16 $\hbox {$^{\prime \prime }$ }$ at 8.44 GHz and 4.86 GHz, respectively. The Qand U maps were combined to get maps of the linearly polarized emission (corrected for the positive zero level offset) and of the position angle of apparent magnetic vectors ($\vec B$-vectors).

NGC 4414 has been also observed using the Effelsberg 100-m MPIfR telescope to determine the total power flux at 2.695 GHz. Several small maps of the galaxy scanned either in RA or in declination were made, then the maps were averaged and the flux density was determined by integrating the final map in concentric rings.

3 Results

3.1 Total power emission


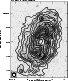  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F01.ps}}\end{figure} Figure 1: Total power map of NGC 4414 at 8.44 GHz with polarization $\vec B$-vectors superimposed onto the H$\alpha $ image from Pogge (1989 and priv. comm.). Uniform weighting yielding a resolution of 7 $\hbox {$^{\prime \prime }$ }$ and rms noise of 9 $\mu $Jy/ba has been applied. Contour levels are 30, 70, 110, 150, 250, 400, 550,...$\mu $Jy/ba.
Open with DEXTER


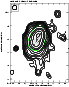  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F02.ps}}\end{figure} Figure 2: The contour map of total power emission from NGC 4414 at 1.415 GHz. The contour levels are 2, 3, 4, 5, 7, 9, 13, 20, 40, 60, 100, 150, $200 \times 170~\mu$Jy/b.a. The map has been smoothed to a resolution of $20\hbox {$^{\prime \prime }$ }$. The map is overlaid upon the distribution of CO(1-0) emission (Braine et al. 1993) shown as white contours on a grayscale background.
Open with DEXTER


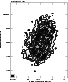  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F03.ps}}\end{figure} Figure 3: The total power map of NGC 4414 at 4.86 GHz with a resolution of $4\hbox {$^{\prime \prime }$ }$ with a greyplot of the same quantity. The contour levels are 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, $27 \times 7~\mu$Jy/ba.
Open with DEXTER

The contour map of the total power brightness of NGC 4414 at 8.44 GHz is presented in Fig. 1. The total power emission shows a ring-like distribution with a central depression roughly at the position of the hole in the CO and H$\alpha $emission (Thornley & Mundy 1997; Sakamoto 1996; Braine et al. 1993). Our total power map also shows two maxima. The southern maximum coincides roughly with an optically bright clump and with a group of three large H II regions (Pogge 1989). The peanut-shaped northern peak extends eastwards from the major axis and forms a bridge between two groups of H II regions. These brightness maxima have almost the same amplitude relative to the rest of the disk in our total power maps at 1.415 GHz and at 8.44 GHz. They are thus certainly nonthermal. In the outermost disk the radio emission in our total power maps at 8.44 and 4.86 GHz is asymmetric with a steeper brightness gradient along the western disk boundary (Fig. 1). A small peak north of the centre coincides with a bright star-forming region and is not visible in our 1.415 GHz map so we suspect that it has an increased fraction of thermal emission. A faint radio ridge extends eastwards from the southern end of the major axis. It coincides with weak optical and H$\alpha $ extensions. At low frequencies, the total power map at 1.415 GHz also shows a clear tail extending to the south (Fig. 2).

Our C-array map of NGC 4414 at 4.86 GHz shows the brightest total power peaks with a resolution of $4\hbox {$^{\prime \prime }$ }$(Fig. 3). The total power hole in the disk centre is very deep at this resolution with no trace of any nuclear source. In the southern disk there is a good agreement between the total power peaks and bright H II regions. In the outer parts of the NE disk a large H II region at RA $_{1950}=\rm 12^h 23^m 57\hbox{$.\!\!^{\rm s}$ }9$ Dec $_{1950}=+31\hbox{$^\circ$ }30\hbox{$^\prime$ }50\hbox{$^{\prime\prime}$ }$corresponds to a local radio emission maximum as well. However, in the bright peanut-shaped feature the association is less obvious: its radio-brightest part lies between nearby H$\alpha $ peaks.

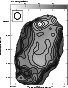  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F04.ps}}\end{figure} Figure 4: The spectral index distribution over the disk of NGC 4414 fitted to all three frequencies. The contour levels start from 0.55 with a step of 0.05. All the maps are convolved to a beam of 14 $^{\prime \prime }$.
Open with DEXTER

The spectral index distribution in the disk of NGC 4414 is shown in Fig. 4. The flattening of the spectrum in the NE disk corresponds to a bright complex of H II regions at RA $_{1950}=\rm 12^h 23^m 57\hbox{$.\!\!^{\rm s}$ }9$Dec $_{1950}=+31\hbox{$^\circ$ }30\hbox{$^\prime$ }50\hbox{$^{\prime\prime}$ }$. The mean spectral index in the inner disk (within the radius of $1\hbox{$^\prime$ }$) is about $\alpha \approx 0.82$ ( $S_{\nu}\propto \nu^{-\alpha}$) to the North $\alpha \approx 0.79$ to the South. The difference is insignificant (rms variations are about 0.02) and may be due to the flattening to $\alpha \approx 0.76$ at the position of large H II regions in the southern disk. Thus, there is no clear evidence for a flatter spectrum of total power emission in the southern disk region.

3.2 High-frequency polarized intensity


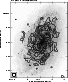  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F05.ps}}\end{figure} Figure 5: Contour map of the polarized intensity of NGC 4414 at 8.44 GHz with a resolution of 7 $\hbox {$^{\prime \prime }$ }$ (uniform weighting for highest resolution) and rms noise of 8 $\mu $Jy/ba with $\vec B$-vectors proportional to the polarization degree, overlaid upon the optical image from HST (permission from Dr W. Freedman from Carnegie Institution). Contours are drawn every 25 $\mu $Jy/ba.
Open with DEXTER

The high resolution map of the polarized intensity at 8.44 GHz is presented in Fig. 5. The brightest peak of polarized emission is located in the northern half of the disk, east of the bright ensemble of H II regions. An elongated polarized feature is also located in the southern disk, just outside of the optically bright arm-like patch. The peaks of high polarized intensity do not clearly avoid nor correspond to bright star-forming regions. Diffuse, more smoothly distributed polarized emission is visible as well.

Despite the lack of organized optical or H$\alpha $ spiral structure the polarization $\vec B$-vectors form a clear spiral pattern. Our 8.44 GHz polarization map at high resolution (Fig. 5) shows that the magnetic field orientation does not fluctuate from place to place, being coherent even at the scale of our smallest beam (650 pc). The global magnetic spiral pattern becomes fully visible when natural weighting is applied, lowering the resolution to 11 $\hbox {$^{\prime \prime }$ }$ but allowing smooth, low-brightness regions to be seen (Fig. 6). The $\vec B$-vectors are nearly azimuthal (pitch angle near 0 $\hbox{$^\circ$ }$) close to the northern semi-axis but show a strong radial component (pitch angle up to 45 $\hbox{$^\circ$ }$) in the southern disk. In the very inner disk the polarization $\vec B$-vectors cross the galaxy's centre along the minor axis, forming an S-shaped pattern. On each side of the centre polarization minima are visible, presumably caused by beam depolarization of strongly twisted magnetic fields, seen perpendicular in sky projection.

The highest degrees of polarization (up to some 30% at 8.44 GHz) were found along the western disk boundary and in the faint eastern tail. The inner disk shows a significant north-south asymmetry. The mean polarized brightness at 8.44 GHz and the mean polarization fraction are about 40% higher in the North than the South, where the H$\alpha $ emission is slightly stronger. In particular, the H$\alpha $ map (Pogge 1989 and priv. comm.) convolved to the beam of 23 $^{\prime \prime }$  (the resolution of the CO(1-0) map) shows the brightest peak in the southern disk. The mean H$\alpha $ brightness, within the area delineated by the level of 30% of the peak value, is some 10% higher in the southern disk than in the northern one. In this respect NGC 4414 resembles nearby galaxies in which the highly polarized emission tends to avoid regions of high star formation (Beck et al. 1996).

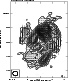  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F06.ps}} \end{figure} Figure 6: Contour map of the polarized intensity of NGC 4414 at 8.44 GHz with $\vec B$-vectors proportional to the polarization degree of NGC 4414. Natural weighting yielding an rms noise of 7 $\mu $Jy/ba, a beam of 11 $\hbox {$^{\prime \prime }$ }$ and a higher sensitivity to extended structures has been applied. Contours are plotted every 25 $\mu $Jy/ba. The vector of $10\hbox {$^{\prime \prime }$ }$ length corresponds to the polarization degree of 50%.
Open with DEXTER

3.3 Faraday rotation and depolarization


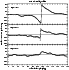  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F07.ps}} \end{figure} Figure 7: Azimuthal profiles of the Faraday rotation measures of NGC 4414 between 4.86 GHz and 8.44 GHz integrated in sectors of azimuthal width of $5\hbox {$^\circ $ }$ along rings 15 $\hbox {$^{\prime \prime }$ }$wide with the same inclination and position angle as the galaxy. The azimuthal angle runs counterclockwise from the northern end of major axis. The naturally weighted maps were convolved to a common beam of 16 $\hbox {$^{\prime \prime }$ }$. Angles have been corrected to face-on.
Open with DEXTER

NGC 4414 lies very close to the North Galactic Pole where the foreground Faraday rotation measure (RM) is smaller than 30 rad/m2 (Simard-Normandin & Kronberg 1980). Using the polarized background source found in our maps at about $4\hbox{$^\prime$ }$ NE from NGC 4414 we determined the foreground rotation to be $-4\pm8$ rad/m2. For this reason no correction for the foreground rotation was applied to our data.

The changes of RM with azimuthal angle in the disk (Fig. 7) do not show clearly any simple singly-periodic or doubly-periodic variations traditionally attributed to axisymmetric (ASS) or bisymmetric (BSS) global field symmetry (Beck et al. 1996). Instead, the azimuthal profiles show a sudden jump at an azimuthal angle of about 200 $\hbox{$^\circ$ }$ with RM values in the inner disk changing abruptly from +600 rad/m2 to -600 rad/m2. The rapid sign change occurs almost throughout the southern half of the disk. Such a jump usually means that the Faraday rotation angle exceeds 90 $\hbox{$^\circ$ }$, corresponding at 4.86 GHz to ${RM} = \pi/2\lambda^2$ $\simeq$600 rad/m2. It does not imply any reversal of the magnetic field in NGC 4414 but signifies a "Faraday-thick regime'' when the rotation angle exceeds 90 $\hbox{$^\circ$ }$ (Sokoloff et al. 1998). Such strong Faraday rotation is exceptional at 4.86 GHz and has not been observed in moderately inclined nearby galaxies which become "Faraday-thick'' much below this frequency (Beck et al. 1996). The jump is most conspicuous at small galactocentric radii, becoming smoother and of smaller amplitude in the outer disk. The azimuthal profiles shown in Fig. 7 also show that RM values in the northern half of the disk are of order of 50-70 rad/m2, much smaller than in the southern half, especially at the galactocentric radii < $45\hbox{$^{\prime\prime}$ }$.

Details of the distribution of Faraday rotation between 8.44 GHz and 4.86 GHz are shown in Fig. 8. The rotation measure (RM) forms large intermixed domains of positive and negative values which do not correspond to any of the known global field symmetries. Generally, positive values dominate in the SW and western disk part with a small spot at the northern tip of the major axis. In large parts of the southern and SW disk the RM exceeds +100 rad/m2. A narrow region of very strong Faraday rotation, reaching +600 rad/m2 is located in the southern disk close the depolarized region south of the centre, jumping on its other side down to -600 rad/m2. The negative rotation measures occupy the SE and eastern disk regions, extending to northwest. In the northern disk the rotation measures are small ($\leq$100 rad/m2) with interspersed domains of positive and negative sign. This region is also substantially polarized at 1.415 GHz, yielding similar values of RM determined between this frequency and 8.44 GHz. The above picture only weakly depends on the assumption concerning small (<30 rad/m2) foreground Faraday rotation.

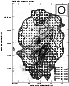  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F08.ps}} \end{figure} Figure 8: The distribution of rotation measures of NGC 4414 between 4.86 GHz and 8.44 GHz, overlaid on the greyscale H$\alpha $image (Pogge 1989 and priv. comm.) showing the brightest H II regions. Circles denote positive and crosses negative RM. The symbol sizes depend on the absolute value of RM as shown in the legend. The contours show negative (dashed) and positive (solid) values of RM with a step of 50 rad/m2. The naturally weighted maps at both frequencies were convolved to a common beam of 16 $\hbox {$^{\prime \prime }$ }$.
Open with DEXTER

The map of Faraday depolarization (DP) between 8.44 and 4.86 GHz (defined as the ratio of polarization degree between the lower and higher frequencies) is shown in Fig. 9. In the southern disk a region strongly depolarized at 4.86 GHz is present, with a depolarization factor $DP \le 0.2$. It is associated with a jump in RM, as expected for a depolarization due to strong Faraday rotation inside the emitting region (see Burn 1966; Sokoloff et al. 1998) and extends to the SE disk region. The southern disk is completely depolarized at 1.415 GHz which confirms the strong Faraday effects. Another moderately depolarized region was found NW of the centre, close to the major axis. The DP there is about 0.45, rising to 0.5-0.6 when a correction for depolarization due to RMgradients across the beam is applied. On average, the DPbetween 4.86 and 8.44 GHz in northern disk is about 0.7. This region was even detected in polarization at 1.415 GHz thus, it is definitely Faraday-thin at 4.86 GHz.

The regions of strong Faraday rotation or depolarization show some association with the ionized gas, as traced by the H$\alpha $ line. Both the Faraday rotation jump and the depolarized area lie close to the complex of three large H II regions and the jump south of the centre coincides with the strongest peak of H$\alpha $ emission. The area depolarized by more than 50% close to the northern major semi-axis lies close to two large H II regions. However, a similar complex of ionized gas NW of the disk centre (around RA $_{1950}=\rm 12^h 23^m 56\hbox{$.\!\!^{\rm s}$ }3$Dec $_{1950}=+31\hbox{$^\circ$ }30\hbox{$^\prime$ }13\hbox{$^{\prime\prime}$ }$) shows a rather low RM and is not strongly depolarized at 4.86 GHz.

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F09.ps}}\end{figure} Figure 9: The distribution of Faraday depolarization (DP) in NGC 4414 between 4.86 GHz and 8.44 GHz determined from naturally weighted maps convolved to 16 $\hbox {$^{\prime \prime }$ }$. The contour levels are 0.2, 0.4, 0.6, 0.8, 1.0.
Open with DEXTER

4 Discussion

4.1 Total magnetic field strength


 

 
Table 2: The integrated radio spectrum of NGC 4414.
Frequency Flux error References
  density    
[GHz] [mJy] [mJy]  
0.408 560 $\pm$ 25 Gioia & Gregorini (1980)
1.490 231 $\pm$   2 Condon et al. (1990)
2.695 134 $\pm$ 30 This work.
4.800 76 $\pm$   5 Gioia et al. (1982)
4.850 78 $\pm$   5 Condon et al. (1991)
4.860 83 $\pm$   5 This work.
10.55 58 $\pm$   5 Niklas et al. (1995)
10.70 43 $\pm$   7 Gioia et al. (1982)


The flux densities of NGC 4414, compiled from data available in the literature are shown in Table 2. The value at 2695 MHz has been obtained by integrating our Effelsberg map in circular rings (the galaxy was only barely resolved) out to a radius of $6\hbox{$^\prime$ }$. The flux density at 4.86 GHz was obtained from the integration of our VLA naturally weighted total power map in elliptical rings with the inclination and position angle from Table 1 out to a radius of $3\hbox{$^\prime$ }$.

The best power-law fit to this data yields $\alpha = 0.77$. Using this value and assuming energy equipartition, a lower limit to the cosmic-ray spectrum to be 300 MeV (see Beck 1991), a ratio of proton-to-electron energy density of 100 (Pacholczyk 1970), and a nonthermal disk thickness of 2 kpc (full thickness corrected to face-on), we compute the mean magnetic field strength within the radius delineated by 5% of the maximum brightness at 4.86 GHz to be $<B_{\rm t}>~=15\pm 4~\mu$G. The uncertainty takes into account factor two variations in the proton-to-electron ratio, the disk thickness and the lower energy cutoff as well as, a variation in the thermal fraction at 4.86 GHz between 0 and 10% (allowed by spectral fits to the data in Table 2). The total magnetic field in NGC 4414 is comparable to that of actively star-forming (non-starburst) spiral galaxies (Beck et al. 1996). Assuming the regular field to be parallel to the disk plane we obtain its mean strength $<B_{\rm reg}>~ =~ 4\pm 1\mu$G. The average ratio $<B_{\rm reg}>/<B_{\rm t}>$ is 0.25.

4.2 Distribution of the nonthermal emission


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{1924F10.eps}}\end{figure} Figure 10: Azimuthal variations of the total power brightness of NGC 4414 at 4.86 GHz, compared to those of CO(1-0) (Braine et al. 1993) and H$\alpha $(Pogge 1989) averaged in sectors with $5\hbox {$^\circ $ }$azimuthal width along concentric rings 15 $\hbox {$^{\prime \prime }$ }$ wide. All the data were convolved to a common beam of 23 $\hbox {$^{\prime \prime }$ }$. The profiles were normalized to the mean value in each ring. The disk was rectified to face-on. Horizontal bars denote the beam size.
Open with DEXTER

Significant correlations between the gas density, star formation rate and magnetic fields were established by Berkhuijsen et al. (1993). In grand-design objects these quantities are affected by processes in spiral arms, like the accumulation of molecular gas in dust lanes followed by massive star formation and the magnetic field enhancement in compression regions.

Azimuthal distributions of the 4.86 GHz total power brightness of NGC 4414 (showing a smaller contamination by thermal emission than that at 8.44 GHz and less affected by the zero-spacing problem than the C-array map at 1.415 GHz) are compared to the H$\alpha $ and CO(1-0) emission in Fig. 10. At all radii there is a reasonable correspondence between the maxima of emission at 4.86 GHz and those in the H$\alpha $ and CO lines. In the innermost disk region the correlation is less obvious and the maxima shifted, possibly because of severe beam-smearing effects. At larger radii the azimuthal variations of the total power brightness follow well those in CO and in H$\alpha $. The maximum of the total power brightness at the azimuthal angle of about $45\hbox{$^\circ$ }$is visible both in CO and H$\alpha $. However, instead of a second maximum visible in CO and H$\alpha $ at the azimuth of $\simeq$ $120\hbox{$^\circ$ }$ the radio emission shows only an asymmetric extension. It is possible that the CO and H$\alpha $ minimum at the azimuth of $90\hbox{$^\circ$ }$ has been smoothed out by cosmic-ray propagation effects. All profiles exhibit a similar rise for azimuthal angles > $180\hbox{$^\circ$ }$. However, the CO peak at an azimuthal angle of about 340 $\hbox{$^\circ$ }$ in the rings outside a radius of $30\hbox{$^{\prime\prime}$ }$ does not correspond to a similar feature in the H$\alpha $ line. It has no counterpart in the radio domain so the H$\alpha $ emission is not caused by strong absorption of the optical radiation from hidden star-forming regions. Thus, the interrelations between gas density, star formation rate and magnetic fields also exist in flocculent galaxies, in which the distributions of gas, young stars and magnetic field are not strongly modulated by density waves. They have a global character, while small-scale details may show substantial place-to-place differences.

The central depression in the radio emission, gas density and star formation deserves attention. The gas in this region is depleted during the early strong star formation necessary for the high stellar densities found in galaxy nuclei. In density wave galaxies the gas is replenished by radial flows in spiral arms, which feed star-forming processes in the centre and inner disk. Some flocculent galaxies show an accumulation of CO gas in the central region (Regan et al. 2001) but this is not the case for NGC 4414 (Sakamoto 1996). The central minimum of all species in NGC 4414 is an argument for the absence of dynamically important radial gas flows.

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F11.ps}}\end{figure} Figure 11: Azimuthal variations of the thermal emission of NGC 4414 at 8.44 GHz, averaged in sectors with $5\hbox {$^\circ $ }$ azimuthal width along concentric rings 15 $\hbox {$^{\prime \prime }$ }$ wide. All the data were convolved to a common beam of 16 $\hbox {$^{\prime \prime }$ }$. A nonthermal spectral index of 1 has been assumed. The disk was rectified to face-on. Thick horizontal bars denote the beam size.
Open with DEXTER


  \begin{figure} \par\resizebox{11cm}{!}{\includegraphics{MS1924F12.ps}}\hfill \parbox[b]{55mm}{ } \end{figure} Figure 12: $\vec B$-vectors of polarized intensity of NGC 4414 overlaid upon the optical image from HST (permission from Dr W. Freedman from Carnegie Institution), both rectified to face-on view. The optical image was digitally filtered to enhance the spiral pattern. The spiral armlets discussed in Thornley & Mundy (1997) are marked by symbols.
Open with DEXTER

4.3 Distribution of the thermal emission


  \begin{figure} \par\resizebox{12cm}{!}{\includegraphics{MS1924F13.ps}}\hfill \parbox[b]{55mm}{ } \end{figure} Figure 13: Top: the distribution of absolute values of pitch angles as a function of azimuthal angle and $\ln(r)$, r being the galactocentric distance in arcmin. The azimuthal angle runs counterclockwise from the northern major semi-axis. Circles denote negative and stars positive values. The dashed line marks the radius beyond which NGC 4414 rotates differentially (Sakamoto 1996). Middle: the orientations of magnetic $\vec B$-vectors for a mixture of m=0, m=1and m=2 modes as described in the text, compared to the observed orientations of magnetic $\vec B$-vectors in NGC 4414 at 8.44 GHz (bottom panel). Crosses on the right side of the graph show the beam size for two different distances from the galaxy's centre. Solid lines show the spiral armlets discussed by Thornley & Mundy (1997).
Open with DEXTER

The interpretation of our Faraday rotation data needs information on the distribution of thermal electron density independent of the H$\alpha $ data which suffer from extinction effects. The azimuthal distribution of thermal emission from NGC 4414 at 8.44 GHz (Fig. 11) was determined from our spectral index map (Fig. 4) assuming the nonthermal spectral slope $\alpha_{\rm nt}$ constant over the whole disk and equal to 1.0 - the mean observed value of $\alpha $ in the disk outskirts. The detailed value of $\alpha_{\rm nt}$ has little meaning for our discussion as it can only shift vertically the curves shown in Fig. 11 without changing the shape of azimuthal variations of the thermal flux.

The distribution of the thermal emission shows two maxima of similar amplitude at both ends of the major axis. The northern maximum at an azimuthal angle of about $30\hbox{$^\circ$ }$ coincides well with a similar peak of total radio power, CO and H$\alpha $. The southern maximum is only slightly stronger and roughly corresponds to a second peak of all these species at an azimuth $\simeq$ $220\hbox{$^\circ$ }{-}240\hbox{$^\circ$ }$. We do not find any strong excess of thermal emission in the southern disk which would naturally explain why the Faraday effects are so much stronger than in the northern disk.

The lack of much higher thermal emission in the southern disk also means that this region does not exhibit strong star formation hidden by absorption in the H$\alpha $ line. Thus we cannot explain the lower degree of polarization at high-frequency of the southern region by stronger magnetic field tangling generated by star-formation. The depolarization by differential Faraday rotation at 8.44 GHz reaches 0.68 at the RM jump. However, such strong depolarization occupies a small fraction of the disk and cannot account for the systematically lower mean polarization degree of the southern disk.

4.4 The magnetic field structure

The CO velocity field observed by Sakamoto (1996) does not show any perturbations similar to density wave streamings (Visser 1980), which would cause radial stretching of magnetic field lines. As also stated by Thornley & Mundy (1997) the optical filaments or armlets which they detected in the near infrared do not cause strong departures from otherwise smooth HI and CO velocity fields. Though the armlets are likely to be dynamical features, they do not constitute a well-organized grand-design spiral pattern (Thornley & Mundy 1997). Small-scale phenomena like chaotic, turbulent gas motions may play an important role in the dynamics and star-forming processes in NGC 4414.

Despite the lack of organized spiral arms, the $\vec B$-vectors (rectified to face-on) (Fig. 12) form a very regular spiral pattern. The magnetic pitch angle $\psi$ observed in NGC 4414 is about zero in the northern disk, increasing to about $40\hbox{$^\circ$ }{-}45\hbox{$^\circ$ }$ over the rest of the disk. This is also visible in the azimuth-$\ln(r)$ frame (Fig. 13) in which a logarithmic spiral would form a straight line inclined by the pitch angle. The infrared armlets detected by Thornley & Mundy (1997) show only limited similarity to the magnetic field structure. They generally have smaller pitch angles in the northern disk and larger ones in the remaining disk portions. However, the magnetic field is aligned only with some portions of armlets while the polarization $\vec B$-vectors apparently run across other armlet segments in all parts of the disk (Figs. 12 and 13). For the deprojection to face-on, we assumed that both the armlets and magnetic vectors lie in the galaxy plane. As demonstrated by Knapik et al. (2000) the presence of a three-dimensional magnetic field geometry as generated by the dynamo does not strongly affect the orientation of deprojected $\vec B$-vectors even at inclinations as high as $60\hbox{$^\circ$ }$. Thus, while the armlets may still have some influence upon the magnetic field structure, local processes like field amplification by the turbulent dynamo process need to be considered.

The magnetic vectors crossing the disk centre are very suggestive of an admixture of non-axisymmetric magnetic field components, especially as the field running through the centre along the minor axis cannot be explained by the limited angular resolution (see Knapik et al. 2000). The hypothesis of a mixture of modes is supported by an analysis which simultaneously uses position angles of $\vec B$-vectors at 8.44 GHz and 4.86 GHz (thus involving Faraday rotation effects), made kindly for us by Dr Andrew Fletcher (priv. comm). The azimuthal variations of magnetic pitch angles are best reproduced by a mixture of axisymmetric (the azimuthal magnetic wavenumber m=0), bisymmetric (m=1) and m=2 fields (Fig. 13 middle panel). Because the magnetic field is a vector (in contrast to e.g. density), for the BSS configuration m=1 is required to get opposite signs of magnetic field components at azimuthal angles differing by $180\hbox{$^\circ$ }$. The amplitudes of the higher modes relative to the axisymmetric field are 0.6 (m=1) and about 0.3-0.5 (m=2, varying with the radius). The axisymmetric field used in this analysis forms a trailing spiral with a pitch angle $\psi$ of about $22\hbox{$^\circ$ }$, the bisymmetric one has $\psi$ of only $2\hbox{$^\circ$ }$ while the m=2component has a large pitch angle whose absolute value varies between $40\hbox{$^\circ$ }$ and $80\hbox{$^\circ$ }$. This mixture of modes well explains the highest polarization extending from the northern major semi-axis along the western disk edge (see Fig. 6) and the weakest polarized intensity in the SE disk. It also yields two asymmetric regions of a constant sign of magnetic field along the line of sight (responsible for Faraday rotation) with the sign reversal at the azimuthal angles of about $180\hbox{$^\circ$ }$ and  $270\hbox{$^\circ$ }$. This bears some resemblance to the RM sign distribution in NGC 4414 at radii < $1\hbox{$^\prime$ }$(Fig. 14).

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1924F14.ps}}\end{figure} Figure 14: Distribution of the sign of the line-of-sight magnetic field (responsible for Faraday effects) in our model a) assuming a mixture of m=0, m=1 and m=2 modes compared to b) the sign of Faraday rotation between 8.44 GHz and 4.86 GHz for NGC 4414. The Q and U data were convolved to a beam of $21\hbox {$^{\prime \prime }$ }$ and restricted to signal stronger than $2\sigma $rms.
Open with DEXTER

As suggested by Chiba (1993) and Moss (1996a) the generation of bisymmetric magnetic fields may be boosted by the parametric resonance in strong density waves. In this work we show the evidence for higher modes of the field structure without strong effects of spiral arms. The apparent contribution of an m=2 mode may indicate a modulation of the lower modes e.g. due to the non-axisymmetric distribution of thermal gas (see Fig. 11) and Faraday effects. Furthermore, the models discussed assume only a two-dimensional magnetic field parallel to the disk. Their further development requires a three-dimensional divergence-free magnetic field, computed using elaborate MHD models.

Though NGC 4414 is currently an isolated spiral (e.g. Braine et al. 1997), the observed magnetic field asymmetries may also signify external interactions. Asymmetric total power gradients, smaller magnetic and optical pitch angles and a higher polarization degree on one side of the disk were observed in the wind-swept spirals NGC 2276 (Hummel & Beck 1995) and NGC 4254 (Soida et al. 1996; Chyzy et al., in prep.). NGC 2276 also has a radio tail noted by Condon (1983). Pitch angle asymmetries and an enhancement of the polarization on one side of the disk by field compression are found in the tidally interacting spiral NGC 3627 (Soida et al. 2001 and references therein). We note also that the large-scale distribution of H I presented by Thornley & Mundy (1997) shows at intermediate radii a slightly larger gas extent and slower density decrease with radius along the southern semi-axis, where we find larger magnetic pitch angles. A similar coincidence is found in interacting spirals (Chyzy et al. in prep.).

Isolated objects often show signs of past weak interactions, like retrograde stellar orbits or H I warps (e.g. Jore et al. 1996). Multiple "minor merging'' effects may occur during the galaxy lifetime (Haynes et al. 2000), sometimes producing large-scale asymmetries in spiral structure (Zaritsky & Rix 1997) or short low-brightness stellar or molecular tails (Aalto et al. 2001). Recently Kornreich et al. (2001) found that while the optical morphology returns quickly to a symmetric appearance, the gas dynamics constitutes a long-lasting memory of past, weak perturbations.

NGC 4414 may be an example in which a distant interaction is remembered by its magnetic field. The inner disk is relatively unperturbed (see Sect. 4.2) and no central starburst nor a nuclear source are present. NGC 4414 could have accreted diffuse gas, perturbing only its outer disk. As demonstrated using numerical models of galaxies interacting with ambient gas clouds (Otmianowska-Mazur & Vollmer 2002), asymmetries in the polarized intensity, magnetic pitch angles and H I may last for more than 1 Gyr. The magnetic field of NGC 4414 may thus "remember'' a perturbation which could have occurred 1 Gyr ago. We note finally that the asymmetries found in the H$\alpha $, H I distribution and kinematics are very weak and only visible in low-surface brightness features. They are more obvious in the magnetic field properties like the pitch angle variations by $45\hbox{$^\circ$ }$ and the dramatic asymmetry in Faraday effects between the northern and southern disk. Multifrequency polarization observations may thus serve as a complementary tracer of weak perturbations, poorly visible in other domains.

External influences could in principle explain the present-time radial magnetic field component. However, a single event cannot explain the observed strength of the regular magnetic fields (see Sect. 4.1) which require stable, continuous reproduction of their radial component over long timescales (e.g. Brandenburg & Urpin 1998). Without constant replenishment, the magnetic fields would diffuse out of the galaxy in a timescale of 108 yrs (Parker 1979). Although one can still imagine a quasi-continuous set of merging events which permanently regenerate the radial magnetic field, the turbulent dynamo seems a more reasonable alternative. The observations presented here are evidence for dynamo action with much less contamination from spiral arms than in grand-design spirals, using a considerably better resolution than in our earlier work (Knapik et al. 2000).

To reproduce the strength of the Faraday rotation is by far a more complex issue. In the northern disk we got reasonable agreement between our estimate of the regular magnetic field and standard assumptions concerning the ionized gas properties. We assume that about 80% of the observed thermal flux originates in H II regions making a small contribution to the Faraday rotation because of their small volume filling factor. Taking 20% of the thermal flux to be due to a diffuse component (Walterbos & Braun 1994) with a face-on full thickness of 700 pc and a volume filling factor of 0.04 (Fletcher et al. in prep.) we obtain for the equipartition regular field (assumed parallel to the disk plane) RM values of $\simeq$100 rad/m2, in reasonable agreement with observations. In the southern disk the apparent RM jump signifies a Faraday-thick regime and thus an intrinsic RM in excess of 500 rad/m2. We can reproduce this taking the observed thermal flux and assuming the same regular magnetic field but assuming that 50% (a factor 2.5 higher) of the observed thermal emission comes from the diffuse gas. We also require a filling factor of the diffuse ionized gas 2.5 times higher, equal to 0.1. Additionally we need a much thicker magnetoionic disk, with a face-on thickness of 3 kpc.

The observed magnetic field structure in NGC 4414 may be the result of the following processes:

We have found that the magnetic field may be a very sensitive indicator of the behaviour of the diffuse component of the interstellar gas. In particular, it may trace signs of interactions which would pass unnoticed when observing the stellar or H$\alpha $ emission. Studying their magnetic fields together with deep mapping of their environment in H I, X-rays and in low-excitation spectral lines like C II, N II, O I or O III provides an important clue to their physics and evolution.

5 Summary and conclusions

We have performed a three-frequency VLA study of the flocculent galaxy NGC 4414 known to have extremely weak traces of optical spiral structure and no evidence for non-axisymmetric gas flows. The data were analyzed together with CO(1-0) and H$\alpha $ maps, yielding the following results:

In this work we show that the regular spiral magnetic pattern observed in all nearby galaxies does not require strong density wave action. We propose that the magnetic pattern in NGC 4414 is due to the dynamo process free from contamination by flows occurring in grand-design spiral arms. On the other hand, the picture of the magnetic field in NGC 4414 is still far from being clear and no good description of the three-dimensional magnetic field geometry is yet available, except for some rough and very qualitative guesses. We suggest that observing the galactic magnetic field may provide a clue to the properties of rarefied ionized gas, contributing greatly to the Faraday rotation but little to the H$\alpha $ emission. This gas phase may be more sensitive to external interactions than either the molecular gas or H II regions associated with recent star formation. Thus, we propose to use the magnetic fields as an indicator of past external interactions working even in cases when the optical information does not indicate significant perturbations. We note finally that a more quantitative magnetic field description in NGC 4414 may come from extensive modeling using more sophisticated multi-component field topologies and realistic distributions of thermal gas and relativistic electrons. A deep study of its environment in H I line and X-ray is highly desirable. Such a study is planned for the near future.

Acknowledgements
The Authors wish to express their thanks to Dr Richard W. Pogge from Dept. of Astronomy, Ohio State University for providing us with his H$\alpha $ map of the whole disk on NGC 4414 in a numerical format and to Dr Wendy L. Freedman from Carnegie Institution for her permission to use the unpublished optical image. We express our thanks to Dr Andrew Fletcher, University of Newcastle, for performing for us the analysis of magnetic field modes in NGC 4414. We are grateful to numerous colleagues from the Max-Planck-Institute für Radioastronomie (MPIfR) in Bonn for their valuable discussions during this work. M.U. and M.S. are indebted to Professor R. Wielebinski from the MPIfR for the invitations to stay at this Institute, where substantial parts of this work were done. We wish to express our thanks to Professor Alexei Bykov from Moscow State University for providing for us his program DEPOLARM and his assistance in its use. We are also grateful to colleagues from the Astronomical Observatory of the Jagiellonian University in Kraków for their comments. We wish to express our gratitude to the anonymous referee for the critical reading of our manuscript. This work was supported by a grant from the Polish Research Committee (KBN), grants No. 962/P03/97/12 and 4264/P03/99/17.

References

 

Copyright ESO 2002