A&A 393, 1035-1051 (2002)
DOI: 10.1051/0004-6361:20021062

1-2.5 $\mu $m spectra of jets from young stars: Strong Fe  II emission in HH111, HH240-241 and HH120[*]

B. Nisini - A. Caratti o Garatti - T. Giannini - D. Lorenzetti

INAF-Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio Catone, Italy

Received 4 June 2002 / Accepted 19 July 2002

Abstract
As part of a 1-2.5 $\mu $m spectroscopic survey of jets and molecular outflows, we present the spectra of three Herbig Haro chains (HH111, HH240/241, HH120) characterized by strong emission from several Fe II  transitions originating from the first 13 fine structure levels. Such emission is correlated with optical S II emission and appears to decrease moving away from the driving source. From the analysis of the Fe II  lines we have derived electron densities values in the range $3\times 10^3$- $2\times 10^4$ cm-3, which are systematically larger than those inferred from optical S II line ratios. We suggest that Fe II  lines, having critical densities higher than the optical S II transitions, trace either regions of the post-shock cooling layers with higher compression, or a section of the jet axis at a higher degree of ionization. Strong H2  emission lines are also detected along the three flows and their analysis indicates that a combination of different shocks can be responsible for their excitation in the different objects. Consequently the Fe II  line emission, which requires the presence of fast dissociative shocks, is completely independent from the excitation mechanism giving rise to the molecular emission. In addition to the Fe II  and H2  lines, emission from other species such as C I, S II, N I as well as recombination lines from the Paschen series are detected and have been used as a reference to infer the gas-phase iron abundance in the observed HH objects. We estimate a grain destruction efficiency of about 30-60%: the highest value is found for HH240A, which also shows the highest degree of excitation among the observed objects.

Key words: stars: circumstellar matter - infrared: ISM - ISM: Herbig-Haro objects - ISM: jets and outflows


1 Introduction

Violent shocks originated in the interaction between protostellar jets and the ambient medium are extremely efficient in disrupting the dust grains, allowing the release into the interstellar medium of heavy elements which are usually strongly depleted in normal conditions (Savage & Sembach 1996). Iron is a typical example of such elements and in fact strong optical iron transitions are observed in Herbig-Haro (HH) objects showing velocities larger than $\sim$100 km s-1(e.g. Beck-Winchatz et al. 1996).

Although several studies have been performed on the optical Fe spectrum in HHs, mainly aimed at understanding the degree of iron depletion in these objects (e.g. Böhm & Matt 2001; Beck-Winchatz et al. 1996), less attention has been given to the Fe near infrared spectrum. This consists of many forbidden transitions of single ionized Fe in the range from 0.9 to 5 $\mu $m, coming from the first 16 fine structure levels. With respect to the optical lines, these transitions have the important following advantages/peculiarities which make them a valuable and independent diagnostic tool; i) they come from the low lying Fe+ multiplets and thus have excitation energies lower than the corresponding optical lines, consequently, they are easy populated at low temperatures (i.e. 2000 < T < 15 000 K); ii) they come from levels with high critical densities ( $n_{\rm cr} > 10^4$ cm-3) and thus trace shocks denser than those presenting the Fe optical emission; iii) finally, being in the infrared, they are able to signal the presence of high velocity dissociative shocks even in highly extincted shock spots, like those traced only by the H2 emission (H2 jets).


 \begin{figure} \par\includegraphics[width=16cm,clip]{Figure1.eps} \end{figure} Figure 1: Position of the SOFI slit adopted in HH111 superimposed on a H2 2.12 $\mu $m image of the jet (from Davis et al. 1994). Individual knots along the jet are identified following the nomenclature from Gredel & Reipurth (1994). Knot ZV, which is not covered by the image, lies at about 80 $\hbox {$^{\prime \prime }$ }$ from knot ZO. The position of the IRS source indicated in the figure is $\alpha _{2000}=5^{\rm h}$52$^{\rm m}$46.1$^{\rm s}$, $\delta _{2000}=+2\hbox {$^\circ $ }$48 $\hbox {$^\prime $ }$31 $\hbox {$^{\prime \prime }$ }$, while the jet driving source, HH111 VLA, lie at about 3 $\hbox {$^{\prime \prime }$ }$ to the east.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=16cm,clip]{Figure2.eps} \end{figure} Figure 2: Position of the SOFI slits in the L1634 region superimposed on an H2 2.12 $\mu $m image of the HH240 and HH241 chains, taken at the NTT telescope. Individual knots are identified following the nomenclature from Davis et al. (1997). The two chains belong to the same outflow excited by the FIR source IRAS05173-0555, ( $\alpha _{2000}=5^{\rm h}$19$^{\rm m}$48.9$^{\rm s}$, $\delta _{2000}=-5\hbox {$^\circ $ }$52 $\hbox {$^\prime $ }$05 $\hbox {$^{\prime \prime }$ }$) indicated by an open circle.
Open with DEXTER

So far, the detection of Fe NIR lines in HH objects has been limited to the two strongest transitions at 1.25 and 1.64 $\mu $m in few objects (see e.g. Gredel 1994). These transitions originate from the same upper level and therefore can be efficiently used to measure the reddening towards the object; they however are not able to give indications about the physical conditions pertaining to the emitting region. The availability of sensitive NIR spectrometers gives now the possibility to study the properties and the occurrence of Fe emission towards HH objects and H2 jets in a more systematic way.

We have recently performed a NIR spectroscopic (from 0.95 to 2.5 $\mu $m) survey of a sample of HH and H2 jets, based on the observations gathered with the SOFI spectrometer at the ESO-NTT. This survey offers the database to investigate over the Fe NIR spectrum in more details. In particular, we present here the results on three HH flows: the highly collimated jet HH111 in Orion (Reipurth 1989), the extended chains of HH objects HH240 and HH241 in the dark cloud L1634 (Davis et al. 1997) and the compact jet HH120 in the Cometary Globule CG30 (Hodapp & Ladd 1995). In spite of the different morphological characteristics and degree of excitation presented by the investigated sources, they show a similar strong Fe II  spectrum, thus allowing to examine the issue of the gas-phase Fe abundance in shocks on different observational basis with respect to the optical studies. In addition, the considered spectral range covers many transitions of molecular hydrogen, coming from vibrational levels up to $T_{\rm ex} \sim 35~000$ K, whose emission can be spatially correlated with the Fe II  emission (Gredel 1994; Lorenzetti et al. 2002). We will therefore have the possibility to investigate in more details whether there is any relation among the excitation conditions pertaining to these two species.

The paper is structured as follow: in the next section we will describe our observations summarizing the results. In Sect. 3 we report the analysis performed on the Fe II  and H2  lines observed in the different objects, from which we were able to derive physical parameters of the ionized and molecular shocked regions. In Sect. 4 we will discuss the implications of our observations and analysis specifically addressing both the conditions for the Fe II  excitation along the observed flows and the Fe gas-phase abundance determinations. Finally, in Sect. 5 we give some general conclusions of this work.

2 Observations and results


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure3.eps} \end{figure} Figure 3: Position of the SOFI slit in HH120 superimposed on a H2 2.12 $\mu $m image taken at the NTT telescope. IRS 3 and IRS 4 are the two infrared sources identified by Pettersson (1984). The position of IRS4, the jet driving source, is $\alpha _{2000}=8^{\rm h}$09$^{\rm m}$32.8$^{\rm s}$, $\delta _{2000}=-$36 $\hbox {$^\circ $ }$05 $\hbox {$^\prime $ }$00 $\hbox {$^{\prime \prime }$ }$.
Open with DEXTER

The observations were obtained during two runs conducted in January 2001 and 2002 with SOFI (Lidman & Cuby 1999) at the ESO-NTT 3.5 m telescope (La Silla). Long-slit spectra with different orientations were acquired using the blue and red grisms, which cover the spectral ranges from 0.95 to 1.64 $\mu $m and from 1.53 to 2.52 $\mu $m, respectively. The instrument uses an array of $1024 \times 1024$ pixels, with a pixel scale of 0.29 $\hbox {$^{\prime \prime }$ }$. The observations were performed with a slit width of 1 $\hbox {$^{\prime \prime }$ }$, corresponding to a spectral resolution $\lambda$/ $\Delta \lambda \sim 600$. For HH111, a single slit position aligned with the jet (PA =  $97\hbox{$^\circ$ }$), was acquired. This is depicted in Fig. 1 over the H2 2.12 $\mu $m image by Davis et al. (1994), and it covers the majority of the H2 emission knots previously identified along the jet (Gredel & Reipurth 1993). In the L1634 dark cloud, three different slit positions were obtained, whose orientation is shown in Fig. 2. The various slits comprise the bright HH knots A, B, C and D identified by Davis et al. (1997) along the two Herbig-Haro chains HH240-HH241, which are the blue-shifted (HH240) and red-shifted (HH241) lobes of a single bipolar outflow emanated by IRAS05173-0555 (Lee et al. 2000). Finally, the compact HH120 jet was observed with a single slit oriented at PA =  $91\hbox{$^\circ$ }$ (Fig. 3). The observations were performed in the usual ABBA configuration, for a total integration time of 1200 s per slit. Each observation was flat fielded and sky subtracted, while the atmospheric spectral response was removed dividing the object spectra by the spectrum of a O9 telluric star observed during the nights, corrected by a blackbody curve at the star effective temperature and by the star intrinsic hydrogen recombination lines in absorption. Wavelength calibration is obtained with a xenon-argon lamp. The estimated uncertainty is smaller than the spectral resolution element (2 pixels $\sim$ 20 Å), which corresponds to 300 km s-1; no shifts greater than such a limit have been observed. Flux calibration of the red grism was performed using photometric standard stars from the Carter & Meadow (1995) catalogue. Inter-calibration between the blue and the red grisms has been obtained by using the [Fe II]1.644 $\mu $m line, which is detected in both the ranges.


 \begin{figure} \par\includegraphics[width=13.8cm,clip]{Figure4.eps} \end{figure} Figure 4: Spectrum between 0.95 and 2.5 $\mu $m of the F knot in HH111.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=13.6cm,clip]{Figure5.eps} \end{figure} Figure 5: Spectrum between 0.95 and 2.5 $\mu $m of HH240 A.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=13.7cm,clip]{Figure6.eps} \end{figure} Figure 6: Spectrum between 0.95 and 2.5 $\mu $m of HH120.
Open with DEXTER

Figures 4-6 show the spectra of the HH111 F, HH240 A and HH120 knots, respectively, which are the knots where the richest [Fe II] spectrum is observed. Tables 1-3 list all the detected lines (uncorrected for extinction) in the various knots with their integrated fluxes. Line fluxes are computed by fitting the profile with a single or double Gaussian in case of blending. The resulting linewidths are always comparable with the width of the instrumental profile. The line flux errors given in the tables are only those resulting from the rms of the local baseline multiplied by the instrumental profile width. An additional flux calibration error of the order of 10%, resulting from the uncertainty associated with the calibration standard reduction, should be added to the total uncertainty of the lines in the red grism. In the blue grism, this total uncertainty is larger, of the order of 20%, since the additional error on the [Fe II]1.644 $\mu $m line, used for inter-calibration among the two grisms, needs also to be propagated.

The obtained line fluxes can be compared with previously published fluxes on the same objects. Flux values derived by Gredel (1994) on several H2 lines and on the [Fe II]1.25, 1.64 $\mu $m transitions in HH120 are consistent with our derived values inside the calibration errors. The H2 2.12 $\mu $m line flux in the different knots of the HH240-241 chains are systematically lower (by about a factor of two at the worst) than the fluxes derived by Davis et al. (1997) from their narrow band images. Also the H2 2.12 $\mu $m line fluxes derived by Gredel & Reipurth (1993) along the blue-shifted lobe of HH111 are about a factor of two larger than our derived values. These discrepancies can be explained by the extendness of the considered objects with respect to our 1 $\hbox {$^{\prime \prime }$ }$ aperture and considering that Gredel & Reipurth (1993) have used a larger slit aperture of 2.2 $\hbox {$^{\prime \prime }$ }$. This is supported by the fact that our flux values in the red-shifted knots HH111 ZL-ZV, which are more compact than the knots in the blue-shifted portion of the jet, are in agreement with the values derived by Gredel & Reipurth (1994) with the 2.2 $\hbox {$^{\prime \prime }$ }$ slit.

An inspection of Tables 1-3 shows that in all the considered objects several [Fe II] lines are observed involving transitions between the first 13 fine structure levels, i.e. the levels connecting the terms a6D, a4F and a4D. H2 emission lines involving vibrational bands from v=1 to v=4 are detected in both HH240 and HH120, while in HH111 only transitions up to v=2 are observed. In addition to [Fe II] and H2  emission several ionic lines are also detected in different knots, whose presence is always associated with the presence of [Fe II] lines. The strongest of these features is the [C I] doublet at 0.98 $\mu $m, while at a lower S/N we also observe the two [S II] doublets at 1.032 and 1.037 $\mu $m and the [N I] doublets at 1.041 $\mu $m and 1.040 $\mu $m (not resolved at our resolution). The [S III] line at 0.953 $\mu $m has been detected only in HH240A. A feature at 1.083 $\mu $m observed in HH240A, HH241A and HH120 can be attributed to both He I (1.0833 $\mu $m) and [S I] (1.0824 $\mu $m) which are not resolved by our instrumental setup. Hydrogen recombination lines from the Paschen series are also detected, while the Br$\gamma$ transition remains below the 3$\sigma $ detection limit. Finally, few features are detected at $S/N > 3\sigma$ whose identification remain unclear. Two features at 2.017 $\mu $m, detected in HH111 F and HH240 A, and at 1.739 $\mu $m, detected in HH111 F, lie at the same wavelengths of two [Fe I] quadrupole transitions, but the spectra do not show any other line of [Fe I] with higher transition probabilities, which should be present between 1.2 and 1.4 $\mu $m. A feature at 1.147 $\mu $m in HH120 could be attributable to [P II]: in this case, also the [P II] at 1.188 $\mu $m should be observed at the same intensity level, considering that these two lines originate from the same upper level and have similar transition probabilities. However at this wavelength we detect only a fainter feature which is more likely due to the H2 2-0 S(0) transition.


 \begin{figure} \par\includegraphics[width=12.7cm,clip]{Figure7.eps} \end{figure} Figure 7: Predicted 1.644 $\mu $m/1.600 $\mu $m, 1.644 $\mu $m/1.533 $\mu $m and 1.644 $\mu $m/1.678 $\mu $m [Fe II] line ratios as a function of the electron density $n_{\rm e}$. The two curves in each diagram correspond to values of $T_{\rm e}=4000$ K (solid line) and $T_{\rm e}=15~000$ K (dashed line). The hatched areas (between the horizontal lines) show the range of ratios observed in each object. The intersection between the curves and the hatched areas indicate the range of $n_{\rm e}$ allowed by the ratios observed in the different objects.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=7.5cm,clip]{Figure8.eps} \end{figure} Figure 8: Diagnostic diagram exploiting a density (1.644 $\mu $m/1.533 $\mu $m) and temperature (1.644 $\mu $m/0.947 $\mu $m) sensitive [Fe II ] line ratios. The grid has been constructed for electron densities of 103, 104 and 105 cm-3 (dashed lines) and for electron temperatures of 2000, 6000, 8000 and 15 000 K (solid lines). The right arrows represent 3$\sigma $ upper limits to the 1.644 $\mu $m/0.947 $\mu $m ratio, due to the non-detection of the 0.947 $\mu $m line.
Open with DEXTER


 
Table 1: (a) Observed unreddened lines in HH111: ionic lines.
[Fe II] lines
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
    ZL IRS F H J-L P
 a4D 7/2-a6D9/2 1.257 3.6(0.1) 2.6(0.3) 14.2(0.2) 10.8(0.2) 6.3(0.2) $\cdots$
 a4D 1/2-a6D1/2 1.271 $\cdots$ $\cdots$ 1.7(0.1) 0.6(0.1) $\cdots$ $\cdots$
 a4D 3/2-a6D3/2 1.279 $\cdots$ $\cdots$ 1.1(0.1) 1.1(0.2) $\cdots$ $\cdots$
 a4D 5/2-a6D5/2 1.295 $\cdots$ 0.8(0.2) 2.0(0.2) 1.6(0.2) $\cdots$ $\cdots$
 a4D 7/2-a6D7/2 1.321 1.7(0.3) 1.2(0.3) 6.3(0.1) 5.0(0.2) 3.5(0.4) $\cdots$
 a4D 5/2-a6D3/2 1.328 $\cdots$ $\cdots$ 1.3(0.2) 1.8(0.1) 0.9(0.2) $\cdots$
 a4D 5/2-a4F9/2 1.534 2.4(0.4) 1.4(0.2) 3.7(0.2) 1.8(0.2) 1.6(0.3) $\cdots$
 a4D 3/2-a4F7/2 1.600 1.9(0.3) 1.1(0.2) 2.9(0.5) 2.2(0.2) 1.5(0.3) $\cdots$
 a4D 7/2-a4F9/2 1.644 8.1(0.3) 9.8(0.7) 25.7(0.3) 18.8(0.3) 9.8(0.4) 1.9(0.4)
 a4D 1/2-a4F5/2 1.664 $\cdots$ $\cdots$ 1.7(0.3) 0.8(0.3): $\cdots$ $\cdots$
 a4D 5/2-a4F7/2 1.677 $\cdots$ 1.4(0.5): 3.5(0.5) 1.9(0.5) 1.4(0.2) $\cdots$
 a4D 7/2-a4F7/2 1.810 $\cdots$ $\cdots$ 23(2) 18(2) $\cdots$ $\cdots$
Other lines
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
    ZL F H J-L
 [C I] 1D2-3P1 0.983 $\cdots$ $\cdots$ 2.3(0.4) 2.3(0.4)
 [C I] 1D2-3P2 0.985 2.1(0.5) 5.1(0.4) 5.8(0.2) 5.6(0.4)
 [S II] 2P3/2-2D3/2 1.029 $\cdots$ 1.1(0.5): 1.0(0.2) $\cdots$
 [S II] 2P3/2-2D5/2* 1.032 $\cdots$ 1.5(0.5) 1.2(0.2) $\cdots$
 [S II] 2P1/2-2D3/2* 1.034        
 [S II] 2P1/2-2D5/2 1.037 $\cdots$ $\cdots$ 0.5(0.1) $\cdots$
 [N I] 2P3/2-2D5/2* 1.040 $\cdots$ 1.3(0.5): 0.7(0.2) $\cdots$
       2P1/2-2D5/2          
 [N I] 2P3/2-2D3/2* 1.041        
       2P1/2-2D3/2          
 Pa$\beta $ 1.282 $\cdots$ 1.0(0.3) 0.6(0.2) $\cdots$
 [Fe I] a5P2-a3F4? a 1.739   0.7(0.2)    
 [Fe I] a5P1-a3F2? a 2.017   1.6(0.5)    
$\textstyle \parbox{16cm}{ * Blend of the two indicated lines.\\ $^a$\space Tentative identification.}$



 
Table 1: (b) Observed unreddened lines in HH111:H2 lines.
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
    ZV ZO ZL IRS F H J-L P V
 1-0 S(8) 1.714 $\cdots$ $\cdots$ $\cdots$ $\cdots$ 1.1(0.2) 1.0(0.3) $\cdots$ $\cdots$ 1.2(0.2)
 1-0 S(7) 1.748 1.1(0.4): 2.1(0.8): 1.3(0.2) $\cdots$ 2.9(0.5) $\cdots$ 4.5(0.7) 5.4(0.4) 4.1(0.4)
 1-0 S(6) 1.788 $\cdots$ $\cdots$ $\cdots$ $\cdots$ 1.6(0.3) 1.3(0.6): $\cdots$ 1.8(0.7): 3.2(0.7)
 1-0 S(3) 1.958 9(3) 9(3) $\cdots$ $\cdots$ 17(2) 15(3) 17(4) 18(2) $\cdots$
 2-1 S(4) 2.003 $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ 2.2(0.8): $\cdots$ $\cdots$ $\cdots$
 1-0 S(2) 2.034 2.2(0.8): 2.2(0.4) 3.4(0.8) $\cdots$ 5.3(0.7) 4.3(0.4) 4(1) 4.2(0.6) 8.1(0.5)
 2-1 S(3) 2.073 $\cdots$ $\cdots$ 2.1(0.7) $\cdots$ 1.3(0.3) 2.0(0.5) $\cdots$ $\cdots$ 2.1(0.8):
 1-0 S(1) 2.122 2.9(0.9) 4.3(0.4) 5.9(0.4) 3(1) 7.4(0.5) 8.7(0.3) 8.1(0.4) 7(3): 16.6(0.6)
 2-1 S(2) 2.154 $\cdots$ $\cdots$ 1.1(0.3) $\cdots$ 1.5(0.4) 1.5(0.2) $\cdots$ $\cdots$ $\cdots$
 1-0 S(0) 2.224 2.3(0.9): 1.2(0.4) 2.4(0.7) $\cdots$ 3.7(0.4) 3.7(0.5) 3.5(0.8) 2.2(0.6) 6.7(0.9)
 2-1 S(1) 2.248 $\cdots$ $\cdots$ 1.8(0.7): $\cdots$ 3.0(0.8) 2.4(0.6) 4(1) $\cdots$ $\cdots$
 1-0 Q(1) 2.407 $\cdots$ 12(3) 16(3) $\cdots$ 9(1) 13(2) 22(4) 17(2) 32(2)
 1-0 Q(2) 2.414 $\cdots$ 7(3): $\cdots$ $\cdots$ 3(1) 12(4) $\cdots$ $\cdots$ 10(1)
 1-0 Q(3) 2.423 $\cdots$ 8(2) 18(8): $\cdots$ 14(2) 13(3) 20(5) 11(2) 37(4)



 
Table 2: (a) Observed unreddened lines in L1634: ionic lines.
[Fe II] lines
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
    HH240 A HH241 A
 a4D 3/2-a6D5/2a 1.248 11.3(0.7) 3.1(0.6)
 a4D 5/2-a6D7/2a 1.249    
 a4D 7/2-a6D9/2 1.257 259.0(1.0) 21.0(0.5)
 a4D 1/2-a6D1/2 1.271 12(1) $\cdots$
 a4D 3/2-a6D3/2 1.279 20(1) $\cdots$
 a4D 5/2-a6D5/2 1.295 35(2) $\cdots$
 a4D 3/2-a6D1/2 1.298 7(1) $\cdots$
 a4D 7/2-a6D7/2 1.321 88(2) 8.3(0.5)
 a4D 5/2-a6D3/2 1.328 11.2(0.7) $\cdots$
 a4D 5/2-a4F9/2 1.534 51(3) 2.9(0.4)
 a4D 3/2-a4F7/2 1.600 31(2) 3(1):
 a4D 7/2-a4F9/2 1.644 245(2) 25.8(0.8)
 a4D 1/2-a4F5/2 1.664 12(1) $\cdots$
 a4D 5/2-a4F7/2 1.677 31(3) $\cdots$
 a4D 5/2-a4F5/2 1.800 51(8) $\cdots$
 a4D 7/2-a4F7/2 1.810 151(23) 27(6)
Other lines
       
 [S III] 1D2-3P2 0.953 16(3) 4.0(1.4):
 [C I] 1D2-3P1 0.983 15.6(0.9) 1.9(0.6)
 [C I] 1D2-3P2 0.985 77(5) 10.2(0.8)
 Pa$\delta$ 1.005 6(1) $\cdots$
 [S II] 2P3/2-2D3/2 1.029 15(2) 2.8(0.3)
 [S II] 2P3/2-2D5/2* 1.032 33(4) 2.3(0.4)
 [S II] 2P1/2-2D3/2* 1.034    
 [S II] 2P1/2-2D5/2 1.037 5.1(0.7) $\cdots$
 [N I] 2P3/2-2D5/2* 1.040 7(1) $\cdots$
       2P1/2-2D5/2      
 [N I] 2P3/2-2D3/2* 1.041    
       2P1/2-2D3/2      
 He Ib 1.083 52(1) 7(1)
 [S I] 1D2-3P2b 1.082    
 Pa$\gamma$ 1.094 9.5(0.9) $\cdots$
 Pa$\beta^c$ 1.282 16(1) 1.2(0.4)
 [Fe I] a5P1-a3F2? d 2.017 6(1) ...
Lines observed in other knots: [C I] 0.985 $\mu $m: 4.2(1.3) in HH240 C, 6.0(1.6) in HH240 D: [Fe II] 1.64 $\mu $m: 8.8(1.8) in HH240 C.
* Blend of the two indicated lines.
a Blend of [Fe II] and H2 2-0 Q(3).
b Blend of He I, [S I] and H2 2-0 S(5).
c Blend of Pa$\beta $ and H2 4-2 S(2).
d Tentative identification.


3 Fe  II and H2 analysis

The most prominent features observed in all the spectra are the Fe II  and H2  lines, and we have therefore used these transitions to derive some physical parameters of the emitting regions. Since we consider only ratios between different lines, our analysis is unaffected by the absolute flux calibration uncertainties, and only the rms error given in Tables 1-3 will be considered. We put the attention on the fact that it is very unlikely that H2  and Fe II  originate from the same shocked gas. Significant Fe II  emission is in fact expected from high velocity dissociative shocks ( $v_{\rm s} > 50$ km s-1, Hollenbach & Mc Kee 1989) which would easily dissociate the H2  molecule. H2 emission is, on the other hand, preferentially expected from non-dissociative shocks either mediated or not by the presence of a magnetic field (C-shocks or slow ( $v_{\rm s} < 20$ km s-1) J-shocks, Draine 1980; Smith 1995). Therefore, the spatial association of Fe II  and H2  is probably due to the simultaneous presence of shocks with different strengths in the same beam. The physical parameters derived from the analysis of the two species may be related to different regions with differing excitation conditions, seen either in projection or unresolved within the same beam. This point will be discussed in more details in Sect. 4.

3.1 Fe  II

In order to exploit the potential of the near IR Fe II  lines, we have developed a NLTE model which considers the first 16 fine structure levels of Fe II  and which therefore comprises transitions among the a6D, a4F, a4D and a4P terms. Transition probabilities were taken from Nussbaumer & Storey (1988), while the energy of the levels and the rate coefficients for electron collisions were adopted from Zhang & Pradhan (1995).

The Fe II  lines observed in the investigated wavelength range involve transitions between the first 13 levels; moreover,the upper level of each transition is one of the four fine structure levels constituting the a4D term (for a detailed energy level diagram see Oliva et al. 1990). For this reason all the observed lines have very similar excitation energies, ranging from $\sim$11 000 to $\sim$12 000 K and thus their ratio is poorly sensitive to the gas temperature. On the other hand, having different critical densities (between 104 and 105 cm-3), these lines can be effectively used to diagnose the electron density. In addition, some of the observed lines originate from the same upper level, and thus their ratio is insensitive to the local physical conditions depending only on the differential extinction and on the atomic parameters. The two brightest transitions at 1.644 and 1.257 $\mu $m have this property, and have been used in the past to derive the reddening EJ-H in several HH objects (e.g. Gredel 1994). The 1.32 $\mu $m line that we observe here for the first time can also be effectively used for this purpouse, coming from the same level of the other two. The visual extinction values derived in our objects adopting the Rieke & Lebofsky (1985) extinction law are listed in Table 4. These have been used to correct all the observed lines for the effect of the interstellar reddening. We note that, as expected, the derived extinction values increase towards the source along the HH111 jet, and in the red-shifted lobes are higher than in the blue-lobes in both the HH111 and HH240/241 flows. Table 4 also lists literature AV values derived for the same objects from optical lines. These estimates give values systematically lower than those measured from the infrared iron lines, an evidence which can be due to the capability of the IR lines to penetrate more inside the emitting region. To see if this can be a reasonable hypothesis, we can estimate what should be the difference in extinction if we suppose that the Fe II  emission lines come from the rear surface of each emission knot while the optical lines trace only the front surface. Assuming a ionization fraction of about 0.1 (this will be discussed in Sect. 4.2) the derived electron density of $\sim$104 cm-3 translates in a total (H+H2) density of $\sim$105 cm-3. Assuming moreover that the observed knot has a physical dimension of about 0.01 pc (about 5 $\hbox {$^{\prime \prime }$ }$ at a distance of 450 pc), the column density through the knot should be about $3\times 10^{21}$ cm-2, which corresponds to an AV value of about 2 mag given a standard gas-to-dust ratio (N(H+H $_2)=1.9\times 10^{21}A_{V}$, Bohlin et al. 1978). The observed difference between AV(optical) and AV(NIR) ranges from 1.1 (in HH120) to 5.7 (the average along HH111), which we can consider reasonably close to the estimated value. In this calculation we are implicitly assuming that the dust is not totally destroyed by the shock, a statement which we will discuss in Sect. 4.2.

To derive the electron density, we used three different line ratios, namely 1.644 $\mu $m/1.600 $\mu $m, 1.644 $\mu $m/1.533 $\mu $m and 1.644 $\mu $m/1.677 $\mu $m, which involve the brightest transitions which are sensitive to density variations. Figure 7 plots the considered line ratios as a function of the electron density and for temperature values between 4000 and 15 000 K; as anticipated, the ratios appear insensitive to temperature variations while their value changes by a factor from 4 to 10 for densities between 103 and 105 cm-3. For densities larger than 105 cm-3, i.e. larger than the critical densities of the considered transitions, the lines become thermalized and thus insensitive to the density values.

For each of the considered HH knots where at least one of these ratios can be computed, the range of $n_{\rm e}$ values allowed by the observed ratios is rather well constrained and listed in Table 4. The $n_{\rm e}$ values range between 104 and 105 cm-3; noticeably these values are always larger than the corresponding $n_{\rm e}$ determinations derived from the [S II] doublet at 6700 Å. The trend for the Fe II  lines to give electron densities larger than the values derived from optical lines has been also found in supernova remnants (Oliva et al. 1989) and indicates that in presence of strong density gradients, Fe II  always traces the densest and most extincted regions of ionized gas. This evidence will be further discussed in Sect. 4.1.

As already mentioned, the detected transitions do not allow us to derive the gas temperature. The investigated spectral range, however, includes also transitions coming from the a4P term, which, being at excitation temperatures of the order of $2\times 10^4$ K, could in principle be used for temperature determinations. Unfortunately those having the most favourable radiative rates, either lie in regions of poor atmospheric transmission, like the lines at 1.811 and 1.813 $\mu $m, or are blended with other strong transitions, like the line at 1.748 $\mu $m which, at the present resolution, cannot be separated by the H2 1-0 S(7) transition. In sources poorly affected by reddening, few lines in the z-band (between 0.86 and 0.96 $\mu $m) could also be used as termometers. Among these latter lines, the one at 0.947 $\mu $m is covered by our instrument and we have therefore calculated the corresponding upper limit with the aim of constrain the gas temperature. In Fig. 8, the theoretical line intensity ratios 1.644 $\mu $m/0.947 $\mu $m and 1.644 $\mu $m/1.533 $\mu $m are plotted as functions of both density and temperature. This diagram can in principle be very useful as a diagnostic diagram for the physical conditions of the iron emitting region. However, the sensitivity of the present observations does not allow to set significant constraints on the temperature as can be seen by the 3$\sigma $ upper limits given in the figure: only in the case of HH240A can a temperature smaller than $\sim$15 000 K be inferred. Much more sensitive instrumentation, able to detect a 0.947 $\mu $m line of at least 2 order of magnitudes fainter than the 1.644 $\mu $m line, should be used to give a measure of the temperature of the iron emitting region.

3.2 H2

The observed H2 transitions have been used to construct rotational diagrams which can be exploited both to derive the temperature of the molecular gas and to infer the excitation mechanism for the H2 molecule. For this purpouse, the extinction corrected line strengths are used to plot the ln N(v,J)/g value (where N(v,J) is the column density of the upper level of the transition and g its degeneracy) against the excitation energy E(v,J). To correct for the reddening, one could in principle make an independent measure of the AV value by using couples of transitions coming from the same upper level, such as the 1-0S(1)2.12 $\mu $m/1-0Q(3)2.42 $\mu $m. This method, however, relies for the majority of the cases on the use of the 1-0 Q transitions at $\lambda > 2.4~\mu$m, where the poor atmospheric response does not allow a good flux determination. We have therefore considered the AV values derived from the Fe II  lines and given in Table 4, adopting the value within the estimated error which is closer to the AVderived from H2 line analysis.

The excitation diagrams for the different knots observed in the three sources are presented in Figs. 9-11. In the figures, the lines coming from different vibrational levels are indicated with different symbols, to better show the behaviour of different rotational series inside the same vibrational level. In these diagrams only the transitions with a S/N larger than three and not affected by blendings with other lines are reported. In almost all the cases, the 1-0 Q transitions are shown in the diagrams but not used in the analysis due to their relative higher noise.

We see clear differences in the excitation of H2 in the three sources, which we will discuss separately. In HH111, only transitions coming from the v=1 and 2 levels are observed and they are consistent with thermal excitation at a single temperature. The best fit straight line through the observative data, indicates that the temperature is mantained roughly constant and equal to $\sim$3000 K through knots from F to P, while knot V, which is the knot furthest from the exciting source, has a lower temperature of $\sim$2300 K. Gredel & Reipurth (1994) found a lower temperature of T=2100 K for the H, L and P knots. The discrepancy with our derived values may rise from both the different assumed reddening (AV=5-6 mag against our AV from 9 to 7) and from a higher noise in their observed lines at high excitation which are essential to correctly determine the slope of the line. In the red-shifted section of the flow, the relatively low number of detected lines, expecially at high excitation, prevents us from accurately determining the gas temperature in all the knots. For the knot ZL we derive T=2600 K, and upper limits of about the same value may be given for knots ZO and ZV. It therefore appears that the H2 emission in the red-shifted lobe originates from a gas at a sligthly lower temperature with respect to the blue-shifted gas.

Also along the L1634 flow the H2  lines are thermalized at a single temperature, but at variance with HH111, transitions from vibrational states up to v=4 are observed in the knots closest to the IRAS source, i.e. HH240 A and HH241 A. The temperatures are consequently higher than those in the HH111 flow and appear to decrease going away from the central source from values of 3400-3700 K in knots A to values of 2300-2600 K in knots D. Therefore, as in HH111, we see some evidence for decreasing temperature with distance from the source. The knots in the HH241 chain present higher temperature values with respect to the HH240 chain.

The lines from the higher vibrational states do not significantly deviate with respect to the straight line defined by the other transitions. Since the critical densities of the H2 levels increase with the vibrational quantum number, this evidence suggests that the H2  density of the post-shocked gas along the L1634 jet can be as high as 107 cm-3 (Giannini et al. 2001).

Finally, the HH120 rotational diagram is different from those of the other observed sources. As in HH241 A, transitions with v up to 4 are detected tracing excitation temperatures up to 34 000 K. Here, however, thermal equilibrium is not mantained by all the observed lines and different vibrational states are excited at different temperatures. This behaviour is very similar to that found in HH43 (Giannini et al. 2002; Schwartz et al. 1995) and it may indicate a stratification of the gas temperature inside the considered emission knots. As in the L1634 case, there is no separation in the diagram among transitions coming from different vibrational states, indicating also in this case a high density of compressed gas. The H2 exitation temperature of $\sim$2200 K derived by Gredel (1994) is consistent with the value we derive by fitting the v=1 transitions only. The limited sensitivity of the Gredel's observations together with the fact that he did not cover the J spectral band where the most excited lines are sitting, prevented him from tracing the components at higher temperature.

4 Discussion

4.1 Fe  II and H2 excitation along the flows

Although the observed HH objects show similar Fe II  spectra, they represent three jets with very different characteristics in terms of extent, collimation and excitation conditions and we will therefore discuss their individual properties separately.

4.1.1 HH111

HH111 is an extremely collimated jet driven by a low mass ( $L_{\rm bol} \sim 25~L_{\odot}$) VLA source (Reipurth 1999), characterized by an optically visible blu-shifted lobe and by a red-shifted infrared (H2) lobe where only the ZL knot has been detected in [S II] optical emission (Reipurth 1989). The chain of knots from F to V which are detected in our long-slit spectra appear to have a bow shock structure when observed at high spatial resolution, and their symmetry with respect to the corresponding red-shifted knots (from ZH to ZV), strongly suggests that they may be originated as intermittent events driven by periodic source eruptions (Reipurth 1989). Near infrared images and spectroscopy of the jet have been reported by Gredel & Reipurth (1993, 1994) and Davis et al. (1994) who pointed out the good spatial correlation between optical, NIR Fe II  and H2 emission.

Figure 12 compares the spatial distribution and the relative intensities of the [Fe II]1.64 $\mu $m and H2 2.12 $\mu $m emission along the jet. Fe II  emission is peaked on the F knot and tends to gradually decrease moving at larger distances from the central source. In the redshifted lobe, Fe II  emission is observed only on the ZL position. Recent HST [Fe II]1.64 $\mu $m observations obtained in the innermost region of the HH111 jet by Reipurth et al. (2000), detected different knots very close to the outflow source and apparently not associated with any optical or H2emission. These knots remain undetected at our limited spatial resolution and sensitivity with respect to the NICMOS instrument.

H2  emission is observed at almost the same flux level along the main body of the jet (from knot F to P), while there is an increase of the molecular emission at the bow shock Vwhich is only partially attributable to the smaller suffered extinction. In the redshifted lobe, the local maximum of H2  emission is observed on the knot ZL. At the present resolution, there is not a clear spatial separation between the Fe II  and H2 peaks. As we have already mentioned Fe II  and H2  trace shocked regions at completely different degree of excitations. Since all the knots along the jet present a bow-like morphology (Reipurth 1989) it is expected to have shocks at different velocities in different positions on the bow. In this configuration, Fe II, together with the optical emission is coming from the high velocity shocks at the apex of the jet, while H2  emission may be interpreted as due to tranverse shocks waves at lower velocities with respect with the main jet velocity. C-shocks with velocities as low as $\sim$20 km s-1are needed to prevent H2  dissociation and produce thermal excitation at about 3000 K as observed (Kaufman & Neufield 1996). With respect to this view, the decrease of the Fe II/H2  observed ratio moving away from the central source can be interpreted as a progressively increasing prevalence of the slow shock components in the outer bows P and V. This may for example occurs when the ambient density encountered by the jet becomes higher or comparable to the jet density, as it may be the case for more external shocks events (Hollenbach 1989). That the overall shock velocity, and thus the excitation, is decreasing with the distance from the central source is also testified by the H2 echelle observations by Davis et al. (2001), which show that the 2.12 $\mu $m line width is decreasing moving away from the central source.


 
Table 2: (b) Observed unreddened lines in L1634: H2 lines.
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
    HH240 A HH240 B HH240 C HH240 D HH241 A HH241 B HH241 C HH241 D
 2-0 S(9) 1.053 11.1(0.8) $\cdots$ 5.2(0.7) $\cdots$ 6(1) 7(1) $\cdots$ $\cdots$
 2-0 S(8) 1.057 $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ 3.8(0.8) $\cdots$ $\cdots$
 2-0 S(7) 1.064 11.3(0.7) $\cdots$ 4(1) $\cdots$ 7(1) 5(1) $\cdots$ $\cdots$
 2-0 S(6) 1.073 7(2) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 2-0 S(5)a 1.085 52(1) $\cdots$ 4.4(0.5) $\cdots$ 7(1) 11(1) $\cdots$ $\cdots$
 2-0 S(4) 1.099 7(1) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 2-0 S(3) 1.117 23(1) $\cdots$ 5.5(0.8) $\cdots$ 7.6(0.8) 17.2(0.9) $\cdots$ $\cdots$
 3-1 S(9) 1.120 5(1) $\cdots$ $\cdots$ $\cdots$ 5(1) 6(1) $\cdots$ $\cdots$
 3-1 S(7) 1.130 16(4) $\cdots$ $\cdots$ $\cdots$ 2.7(0.7) 12(3) $\cdots$ $\cdots$
 2-0 S(2)* 1.138 12(3) $\cdots$ $\cdots$ $\cdots$ $\cdots$ 8.1(0.8) $\cdots$ $\cdots$
 3-1 S(6)* 1.139                
 3-1 S(5) 1.151 8(2) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 2-0 S(1) 1.162 10(1) $\cdots$ 2.6(0.7) $\cdots$ 4(1) 6.2(0.5) $\cdots$ $\cdots$
 3-1 S(3) 1.185 6.0(0.6) $\cdots$ 3.9(0.6) $\cdots$ 3.4(0.7) 5.4(0.4) $\cdots$ $\cdots$
 2-0 S(0) 1.189 11.8(0.8) $\cdots$ $\cdots$ $\cdots$ 1.9(0.7): 3(1) $\cdots$ $\cdots$
 4-2 S(5) 1.226 4.2(0.6) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 3-1 S(1) 1.233 7.2(0.6) $\cdots$ 2.4(0.7) $\cdots$ $\cdots$ 4(1) $\cdots$ $\cdots$
 2-0 Q(1) 1.238 7.0(0.6) $\cdots$ 2.1(0.5) $\cdots$ $\cdots$ 4(1) $\cdots$ $\cdots$
 2-0 Q(2)* 1.242 5.4(0.6) $\cdots$ 1.7(0.6): $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 4-2 S(4)* 1.242                
 2-0 Q(3)b 1.247 11.3(0.7) $\cdots$ 3(1): $\cdots$ 3.1(0.6) 5(1) $\cdots$ $\cdots$
 4-2 S(3)* 1.261 6.6(0.9) $\cdots$ $\cdots$ $\cdots$ 3.7(0.5) $\cdots$ $\cdots$ $\cdots$
 3-1 S(0)* 1.262                
 2-0 Q(5)* 1.263                
 4-2 S(2)c 1.284 16(1) $\cdots$ $\cdots$ $\cdots$ 1.2(0.4) $\cdots$ $\cdots$ $\cdots$
 2-0 O(3) 1.335 8(2) $\cdots$ $\cdots$ $\cdots$ 2.3(0.3) 5(1) $\cdots$ $\cdots$
 4-2 S(0) 1.342 5(1) $\cdots$ $\cdots$ $\cdots$ $\cdots$ 3.8(0.3) $\cdots$ $\cdots$
 1-0 S(10) 1.666 7(2) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 1-0 S(9) 1.687 18(4) $\cdots$ 15(3) $\cdots$ 8.9(0.9) 17(4) $\cdots$ $\cdots$
 1-0 S(8) 1.714 16(2) $\cdots$ 16(2) $\cdots$ $\cdots$ 8(2) $\cdots$ $\cdots$
 1-0 S(7) 1.748 72(2) 9(4): 40(2) 11(3) 28(2) 53(3) 18(2) 14(3)
 1-0 S(6) 1.788 47(2) $\cdots$ 43(5) $\cdots$ 21(2) 35(2) 14(1) 12(1)
 1-0 S(3) 1.958 67(2) $\cdots$ 78(3) $\cdots$ 37(8) 91(3) $\cdots$ $\cdots$
 2-1 S(4) 2.003 18(2) $\cdots$ 22(4) 0.6(0.2) $\cdots$ $\cdots$ $\cdots$ $\cdots$
 1-0 S(2) 2.034 83(2) 15(7): 54(3) 11(2) 35(3) 67(2) 18(2) 15(1)
 2-1 S(3) 2.073 26(2) $\cdots$ 21(1) $\cdots$ 12(1) 21(5) 12(3) $\cdots$
 1-0 S(1) 2.122 223(2) 31(1) 148(3) 23.5(0.8) 92(2) 173(1) 47(1) 95(1)
 2-1 S(2) 2.154 12(2) $\cdots$ 11(2) $\cdots$ $\cdots$ 7(2) $\cdots$ $\cdots$
 3-2 S(3) 2.201 8(3): $\cdots$ 6(2) $\cdots$ $\cdots$ 4(2): $\cdots$ $\cdots$
 1-0 S(0) 2.224 57(1) 7(3): 31(2) $\cdots$ 17(1) 38(2) 16(4) 10(1)
 2-1 S(1) 2.248 25(1) $\cdots$ 25(1) $\cdots$ 8(2) 19(1) 5(1) 7(2)
 2-1 S(0) 2.355 5(2): $\cdots$ 7(1) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
 3-2 S(1) 2.386 7(2) $\cdots$ 6(2) $\cdots$ $\cdots$ 9(2) $\cdots$ $\cdots$
 1-0 Q(1) 2.407 102(4) 23(4) 63(3) 17(4) 19(2) 26(6) $\cdots$ 18(2)
 1-0 Q(2) 2.414 51(3) 10(3) 24(6) 13(4) 18(2) 45(3) $\cdots$ $\cdots$
 1-0 Q(3) 2.423 50(4) 18(8): 39(5) 11(3) 19(2) 30(2) $\cdots$ 12(3)
 1-0 Q(4) 2.438 73(4) 9(1) 41(8) 12(4) 27(4) 59(8) $\cdots$ 18(3)
 1-0 Q(5) 2.455 40(10) 8(2) 78(6) 18(3) 84(6) 106(4) $\cdots$ 26(9)
 1-0 Q(6) 2.476 56(5) $\cdots$ 11(2) $\cdots$ $\cdots$ $\cdots$ $\cdots$ $\cdots$
$\textstyle \parbox{16.2cm}{ $^*$\space Blend of the indicated two or more H$_2$... ...--0 Q(3) with [Fe {\sc ii}].\\ $^c$\space Blend of 4--2 S(2) with Pa$\beta$ .}$


We can also compare the Fe II  emission with the emission of optical lines excited in similar conditions. In this respect, the [S II] $\lambda\lambda$6717,6731 Å doublet is the most suitable for such a comparison. Sulfur has a ionization potential of 10.36 eV, against the 7.87 eV needed to have single ionized iron, and we therefore expect to have all the iron ionized where sulfur is in S+ form. Furthermore, the excitation temperature of the 6700 Å doublet is about 21 000 K, against the $\sim$11 000 K of the near IR Fe II  lines, i.e. the S II emitting region should have conditions favourable for the excitation of the NIR Fe II  lines. An analysis of the S II emission as well as of the change in the excitation conditions and physical parameters along the HH111 flow has been done by different authors and at different degrees of spatial resolution (Reipurth 1989; Morse et al. 1993a; Riera et al. 2001; Raga et al. 2002). S II emission is observed in all the knots of the blueshifted lobe, tends to decrease going from knot H to knot P and has again another local peak at the V bow-shock. The jet velocity and the electron density derived from the S II doublet ratio follow the same path, decreasing with the distance from the IRS source up to the knot P and having another local maximum at knot V. The observed spatial behaviour of the Fe II  emission is well correlated with the S II emission and with a general decrease of the jet excitation conditions moving far from the central source. Such a decrease of excitation is also testified by the detection of near infrared S II and N I only in the internal knots. We fail however to detect Fe II  emission on knot V despite the favourable conditions. One possibility is that the electron density here is well below the critical density of the Fe II  NIR lines. $n_{\rm e}$ values of the order of 500 cm-3 are indeed derived here from the optical lines by Reipurth (1989), but we have seen from the Fe II  analysis that this can be considered a lower limit to the actual density of the NIR Fe II  emission region. A different possibility is that we have aligned our slit with a less excited section of the extended V bow shock, since the high excitation conditions are restricted at the apex of the bow (Morse et al. 1993b). This would also explain the lack of C I emission on knot V, with an upper limit significantly below the values detected in the other knots.


 
Table 3: (a) Observed unreddened lines in HH120: ionic lines.
[Fe II] lines
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
 a4D 3/2-a6D5/2a 1.248 4(1)
 a4D 5/2-a6D7/2a 1.249  
 a4D 7/2-a6D9/2 1.257 67.2(0.3)
 a4D 1/2-a6D1/2 1.271 8(1)
 a4D 3/2-a6D3/2 1.279 7(1)
 a4D 5/2-a6D5/2 1.295 10(2)
 a4D 7/2-a6D7/2 1.321 25.0(0.8)
 a4D 5/2-a6D3/2 1.328 4.3(0.6)
 a4D 5/2-a4F9/2 1.534 12.6(0.4)
 a4D 3/2-a4F7/2 1.600 6.5(0.5)
 a4D 7/2-a4F9/2 1.644 68(1)
 a4D 1/2-a4F5/2 1.664 9(2)
 a4D 5/2-a4F7/2 1.677 7(2)
 a4D 5/2-a4F5/2 1.800 24(3)
 a4D 7/2-a4F7/2 1.810 66(18)
Other lines
 [C I] 1D2-3P1 0.983 21(1)
 [C I] 1D2-3P2 0.985 61.0(0.3)
 [S II] 2P3/2-2D5/2* 1.032 12(2)
 [S II] 2P1/2-2D3/2* 1.034  
 [S II] 2P1/2-2D5/2 1.037 4(1)
 [N I] 2P3/2-2D5/2* 1.040 7(3):
       2P1/2-2D5/2    
 [N I] 2P3/2-2D3/2* 1.041  
       2P1/2-2D3/2    
 He Ib 1.083 30(2)
 [S I] 1D2-3P2b 1.082  
 [P II] 1D2-3P1?d 1.147 8(3):
 Pa$\beta $c 1.282 4(1)
$\textstyle \parbox{8cm}{ $^*$\space Blend of the two indicated lines.\\ $^a$\s... ...beta$\space and H$_2$\space 4--2 S(2).\\ $^d$\space Tentative identification.}$



 
Table 3: (b) Observed unreddened lines in HH120: H2 lines.
Line $\lambda$($\mu $m) $F(\Delta~F)$(10-15 erg cm-2 s-1)
 2-0 S(9) 1.053 14.1(0.7)
 2-0 S(7) 1.064 17(1)
 2-0 S(6) 1.073 11(1)
 2-0 S(5)a 1.085 31(2)
 2-0 S(4) 1.099 11(1)
 2-0 S(3) 1.117 24(2)
 3-1 S(9) 1.121 7(2)
 3-1 S(8) 1.124 6(2)
 3-1 S(7) 1.130 18(2)
 2-0 S(2)* 1.138 16(3)
 3-1 S(6)* 1.139  
 3-1 S(5) 1.151 23(1)
 2-0 S(1) 1.162 28(2)
 3-1 S(3) 1.185 13.0(0.6)
 2-0 S(0) 1.189 5.0(0.9)
 4-2 S(9) 1.196 7(2)
 4-2 S(7) 1.204 7(2)
 3-1 S(2) 1.207 10(2)
 4-2 S(6) 1.214 6(1)
 4-2 S(5) 1.226 8(1)
 3-1 S(1) 1.233 9(1)
 2-0 Q(1) 1.238 12(0.9)
 2-0 Q(2)* 1.242 6.5(0.9)
 4-2 S(4)* 1.242  
 2-0 Q(3)b 1.247 14(1)
 4-2 S(3)* 1.261 14(1)
 3-1 S(0)* 1.262  
 2-0 Q(5)* 1.263  
 4-2 S(2)c 1.284 4(1)
 2-0 Q(7) 1.287 6(1)
 3-1 Q(1)* 1.311 7(3):
 4-2 S(1)* 1.314  
 3-1 Q(3) 1.324 4.3(0.6)
 2-0 O(3) 1.335 14(2)
 4-2 S(0)* 1.342 11(2)
 3-1 Q(5)* 1.342  
 1-0 S(9) 1.687 23(2)
 1-0 S(8) 1.714 13(3)
 1-0 S(7) 1.748 82(2)
 1-0 S(6) 1.788 60(3)
 1-0 S(3) 1.958 704(3)
 2-1 S(4) 2.003 15(3)
 1-0 S(2) 2.034 115(2)
 2-1 S(3) 2.073 27(1)
 1-0 S(1) 2.122 309(1)
 2-1 S(2) 2.154 13(2)
 3-2 S(3) 2.201 9(2)
 1-0 S(0) 2.224 76(2)
 2-1 S(1) 2.248 30(2)
 3-2 S(2) 2.287 7(3):
 1-0 Q(1) 2.407 297(3)
 1-0 Q(2) 2.414 125(4)
 1-0 Q(3) 2.423 272(5)
 1-0 Q(4) 2.438 87(4)
 1-0 Q(5) 2.455 66(5)
 1-0 Q(6) 2.476 50(10)
$\textstyle \parbox{7cm}{ $^*$\space Blend of the two or more H$_2$\space indica... ...--0 Q(3) with [Fe {\sc ii}].\\ $^c$\space Blend of 4--2 S(2) with Pa$\beta$ .}$


Finally, we would like also to comment on the fact that the electron density derived from the Fe II  analysis is larger than the values derived from the optical lines. In particular, while we derive a value of about 104 cm-3, almost constant from knots F to L, the optical derived electron densities are always between a factor of 2 and 5 lower. Towards ZL the difference between the two determinations is even higher, since we infer a lower limit of about 105 cm-3 to the density value. Riera et al. (2001) have obtained long slit spectra in the direction perpendicular to the jet axis, showing that the HH111 jet has indeed a transverse structure where the velocity and the excitation decrease going from the central axis of the jet outwards. This evidence can led to the suggestion that the Fe II  lines may trace regions along the jet axis at higher ionization and therefore higher electron density with respect to the sulfur emission region. A density stratification in the direction perpendicular to the jet axis has been indeed inferred from HST observations of T Tauri jets (Bacciotti 2001) and it is predicted by models of magnetically driven jets (i.e. Garcia et al. 2001).


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure9a.eps}\\ [5mm] \includegraphics[width=8.8cm,clip]{Figure9b.eps} \end{figure} Figure 9: H2 rotational diagram for the different knots of the HH111 flow. Different symbols indicate lines coming from different vibrational levels, as explained in the upper panel of each figure. Straight lines represent the best fit through the data. The corresponding temperatures and the adopted extinction value are indicated in each panel.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure10a.eps}\\ [5mm] \includegraphics[width=8.8cm,clip]{Figure10b.eps} \end{figure} Figure 10: As in Fig. 9 for the HH240 and HH241 knots.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure11.eps} \end{figure} Figure 11: H2 rotational diagram for HH120. Different symbols indicate lines coming from different vibrational levels, as explained in the upper corner of the figure. The three straight lines represt the best fit through the v=1, v=2 and v=3, 4 data. The corresponding temperatures are indicated in the upper corner of the figure.
Open with DEXTER

4.1.2 L1634

The extended HH objects HH240/HH241, located inside the dark cloud L1634 in Orion, consist of a series of extended bow shocks symmetrically distributed with respect to the driving source. This has been identified in a low luminosity ( $L_{\rm bol} \sim 17~L_{\odot}$) Class 0 source associated with IRAS05173-0555. In the optical, only the bright HH knot closer to the driving source is visible (HH240 A), which is also known as RNO40 from the original designation by Cohen (1980) (see also Bohigas et al. 1993). Our near infrared observations seem to confirm that the knots closer to the driving source are those having the highest excitation conditions, as shown by the detection of Fe II  emission as well as ionic emission in form of C I, N I, S II and S III only towards knots HH240 A and HH241 A. In these knots the detection of S III and the C I/Pa$\beta $ value significantly lower than the value observed in HH111 ($\sim$4 in HH240 A and 10 in HH111) testify to excitation conditions higher than in the HH111 jet. Noticeably HH240A also shows an electron density higher than the 241A HH object, although 240A lies in the blueshifted section of the outflow associated with this HH chain (Lee et al. 2000) and presents a lower extinction value. This indicates that the high electron density derives from an actual larger degree of ionization and not from an higher total density in the medium.


 
Table 4: Physical parameters derived from Fe II  lines.
HH knot AV AV(optical)a Ref. $n_{\rm e}$ $n_{\rm e}$(optical)b Ref.
    (mag) (mag)   (104 cm-3) (104 cm-3)  
HH111 F $9.1\pm0.4$ 2.7 [1] 0.8-2 0.45 [2]
  H $8.7\pm0.5$ 2.7 [1] 0.5-1 0.45 [2]
  J+L $7.6\pm1.1$ 2.7 [1] 0.8-2 0.3 [2]
  ZL $11.1\pm1.3$ ...   >10 0.2 [2]
HH240 A $2.5\pm0.8$ 1.4 [3] 3 0.16 [3]
HH241 A $5.2\pm0.8$ ..   0.3-0.5 ..  
HH120   $3.2\pm1.3$ 0.9 [4] 0.5-1 0.2 [4]
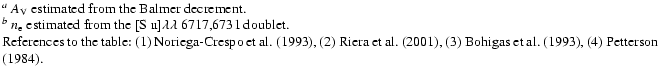
$\textstyle \parbox{16.5cm}{ $^{a}$\space $A_{\rm V}$\space estimated from the B... ...e{Riera2001}), (3) Bohigas et~al. (\cite{Bohigas1993}), (4) Petterson (1984).}$


The derived electron density in HH240 A is about 15 times the value derived from the S II optical doublet. Bohigas et al. (1993) already pointed out that densities as high as $2.2\times 10^4$ cm-3 can be inferred in this object if different tracers, like the O III lines, are used. Since HH240 A has not a jet like structure as HH111, but it represents an extended bow of shocked material, we can interpreted the higher density shown by the Fe II  lines with the presence of a density stratification in the post-shocked layers of compressed gas, where Fe II  lines trace preferentially the layers of the shocked front of high electron density.

At variance with HH111, the knots having strong Fe II  emission also show a prominent H2  spectrum excited at relatively high temperature ($\sim$3500 K). On the other hand, not only the more external knots show a spectrum basically void of any ionic lines indicating a sharp decrease of the excitation conditions, but also the temperature of the H2  gas seems to decrease moving away from the central source. This suggests that the shock velocity is diminishing with the distance from the exciting source: this evidence contrasts with the results obtained along other flows showing an H2  temperature increasing outwards (Lorenzetti et al. 2002; Herbst et al. 1997), suggesting that different velocity structures in the flows may be created by periodic events of mass ejection.

We finally remark that with our long slit spectra we do not sample all the large bow structure of the individual knot and therefore we are not able to infer if the physical properties derived are representative of all the shocked regions.


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure12.eps} \end{figure} Figure 12: Upper panel: spatial distribution of the observed H2 2 2.12 $\mu $m and [Fe II]1.64 $\mu $m lines along the HH111 axis. Offsets are with respect to the source HH111 IRS. Lower panel: extinction corrected ratio [Fe II]1.64 $\mu $m/H2 2.12 $\mu $m for the individual emission knots.
Open with DEXTER

4.1.3 HH120

The Herbig Haro object HH120 is located inside the cometary globule CG30 (belonging to the Gum Nebula) and excited by a young source (IRS4 from Pettersson 1984) associated with the FIR source IRAS 08076-3556. Several H2 jets are present in the globule (Hodapp & Ladd 1995) which are identifiable in Fig. 3. None of them however appear physically correlated with the HH120 object and they probably belong to outflows excited from other young sources of the region.

Gredel (1994) has imaged HH120 both in Fe II  and in H2, showing that the two emissions are spatially correlated although not precisely coincident. The H2  spectrum we have observed is similar to the spectrum of HH43 (Giannini et al. 2002), where it was interpreted in terms of slow J-shock excitation mechanism (Smith 1995). At variance with HH43, however, the simultaneus presence of strong Fe II  transitions is indicative that both slow and fast J shocks should be present at similar strength in the same region.

4.2 Gas-phase Fe abundance

The Fe II  gas-phase abundance in Herbig-Haro objects is expected to be regulated by the efficiency of the shock to disrupt the core of the dust grains by sputtering of energetic particles, releasing most of the metals in gas phase (e.g. Seab 1987; Jones 1999). From an observational point of view, this expectation has however given contrasting results. From one side, there are works where the iron abundance, inferred from the observed ratios of optical lines, results always close to the solar value, irrespective on the strength of the shock (Beck-Winchatz et al. 1996; Böhm & Matt 2001). On the other side, other works, by comparing the ratio among Fe and O I lines with simple shock models, derive in all the cases an iron depletion factor of about 80%, concluding that the shocks are actually not efficient in disrupting the dust grains (Mouri & Taniguchi 2000). Similar high depletion factors are also found in supernova remnants and in starburst galaxies (Oliva et al. 1989; Mouri et al. 2000). Up to now near infrared Fe II  lines have not be used to estimate the iron abundance in HH objects since any abundance determination requires a comparison of the Fe line intensity with that of another reference element, emitted in the same region, of known abundance. The comparison of near infrared Fe II  lines with optical lines introduces too much uncertainties, due to the different instrumentation adopted, the assumptions that optical and infrared lines come from the same regions and the significantly different reddening corrections in the two wavelength ranges. The presented observations have allowed to detect, together with the iron lines, also other transitions emitted from the same gas, which can be used to infer the iron abundance on a different basis with respect to the previous works. In particular, the gas-phase Fe abundance can be in principle directly derived from the [Fe II]1.25 $\mu $m/Pa$\beta $ ratio. In practice, to do that one needs to assume that iron is all in Fe+ form and estimate the ionization degree of the emitting region, given the different ionization potential of Fe and H (7.87 and 13.6 eV respectively). In computing the [Fe II]1.25 $\mu $m/Pa$\beta $ ratio of our observations, and in particular for HH120, HH240A and HH241A, we have to deal with the problem that at our resolution, Pa$\beta $ is blended with the H24-2S(2) transition. The intensity of this latter has been estimated from the intensity of the 4-2S(5) line (the closer H2 line of the series not blended with other transitions) and assuming a 4-2S(2)/4-2S(5) ratio expected at the temperature derived from the H2  excitation diagrams. It results that the 4-2S(2) intensity is negligible with respect to the observed value in HH240A and HH241B, while it contributes to about 80% of the flux in HH120.


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure13.eps} \end{figure} Figure 13: Expected intensity ratio [Fe II]1.25 $\mu $m/Pa$\beta $ plotted as function of the electron temperature, for different values of the ratio (f) between the percentage of Fe in gas-phase ( $\delta _{\rm Fe}$) and the ionization fraction ($x_{\rm e}$). The observed ratios for the different objects are indicated as straight lines. Relative uncertainties associated with each ratio are 8% for HH240 A, 20% for HH111 F, 35% for HH111 H and HH241 A, and 50% for HH120.
Open with DEXTER

The expected [Fe II]1.25 $\mu $m/Pa$\beta $ relative intensity can be estimated from our Fe II  statistical equilibrium model and assuming that the Pa$\beta $ is emitted under case B recombination. The Fe II  intensity per unit volume can be expressed as:

\begin{displaymath}\epsilon_{\rm [FeII]}(T_{\rm e},n_{\rm e})~n_{\rm Fe^+}~n_{\rm e}~~{\rm erg~cm^{-3}~s^{-1}} \end{displaymath} (1)

where

\begin{displaymath}\epsilon_{\rm [FeII]} = \frac{hc}{\lambda}~A_{\lambda}\frac{f_{\rm up}}{n_{\rm e}}~~{\rm erg~cm^{3}~s^{-1}} \end{displaymath} (2)

with $A_{\lambda}$ the radiative coefficient for the 1.25 $\mu $m transition, and $f_{\rm up}$ the fractional population in the upper level. The Pa$\beta $ intensity per unit volume is also expressed as:

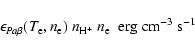\begin{displaymath}\epsilon_{\it Pa\beta}(T_{\rm e},n_{\rm e})~n_{\rm H^+}~n_{\rm e}~~{\rm erg~cm^{-3}~s^{-1}} \end{displaymath} (3)

where the $\epsilon_{Pa\beta}$ values are tabulated by Storey & Hummer (1995). The intensity ratio is therefore given by:

\begin{displaymath}\frac{[Fe {\sc II}]}{Pa\beta} = \frac{\epsilon_{\rm [FeII]}}{\epsilon_{Pa\beta}}~ \frac{n_{\rm Fe^{+}}}{n_{\rm H^+}}\cdot \end{displaymath} (4)

Assuming that the iron is all single ionized, such a ratio can be expressed as follow:

\begin{displaymath}\frac{[Fe {\sc ii}]}{Pa\beta} = \frac{\epsilon_{\rm [FeII]}}{... ...eta}}~ \frac{\delta_{\rm Fe}}{x_{\rm e}}~({\rm Fe/H})_{\odot}, \end{displaymath} (5)

where $x_{\rm e}=n_{\rm e}/n_{\rm H}$ is the hydrogen ionization fraction and $\delta _{\rm Fe}$ is the gas-phase iron fraction with respect to the total solar Fe abundance ((Fe/H)$_{\odot}$) which has been taken equal to $3.2\times 10^{-5}$ (Savage & Sembach 1996). Figure 13 plots the derived intensity ratio as function of the electron temperature and for different values of the parameter $f=\delta_{\rm Fe}/{x_{\rm e}}$. The observed values are indicated as straight lines: the associated uncertainties, ranging between 8% (for HH240A) and 50% (for HH120), are such that the [Fe II]1.25 $\mu $m/Pa$\beta $ values are basically equal for HH120, HH111 and HH240A, while HH241A shows a lower value which is outside the error bars. This figure shows that, although the observed ratio is not too much dependent on the value of the density, it is impossible to establish an accurate value for $f=\delta_{\rm Fe}/{x_{\rm e}}$, and therefore the gas-phase iron abundance without knowledge of the electron temperature and on the ionization fraction. If we assume that the electron temperature is in the range $\sim$8000-10 000 K values of the f parameter between $\sim$1.5-3 can be inferred from the majority of the observations while a lower value $\sim$0.5-1 is more appropriate for HH241A. Values of the f parameter larger than 1 indicate that the observed gas cannot be fully ionized, and indeed ionization fractions ranging from 0.05-0.4 are derived for Herbig-Haro jets (Bacciotti & Eislöffel 1999). In particular, an average value of the order of $x_{\rm e} \sim 0.1$ has been estimated in HH111 by Bacciotti et al. (1995), and in HH120 by Pettersson (1984). Taking this value, we estimate a grain destruction efficiency between $\sim$20 and 60%. HH240 A may have an higher degree of ionization, as evidenced by its higher excitation spectrum, in which case a larger efficency close to unity can be expected. On the other hand, for HH241A, either a ionization fraction larger than 0.1 or a $\delta _{\rm Fe}$ value smaller than 20% need to be considered to explain the [Fe II]1.25 $\mu $m/Pa$\beta $ ratio smaller than in the other HHs.


 \begin{figure} \par\includegraphics[width=8.8cm,clip]{Figure14.eps} \end{figure} Figure 14: Line ratios [Fe II]1.25 $\mu $m/Pa$\beta $ and [Fe II]1.25 $\mu $m/[C I]0.98 $\mu $m predicted by the fast dissociative shock model of Hollenbach & McKee (1989) for different values of the shock velocity (30-150 km s-1) and for a pre-shock density of 104 cm-3. The two curves are obtained adopting two different values of the gas-phase Fe abundance: 10-6 is the standard value adopted by Hollenbach & McKee (1989) and $3.2\times 10^{-5}$ is the total iron solar abundance. Starred symbols indicate the extinction corrected values observed in different HH knots (1-HH240 A, 2-HH111 F, 3-HH120, 4-HH111 H, 5-HH241 A).
Open with DEXTER

More constraints on the gas-phase iron abundance can be derived by comparing the observed ratios with models for fast dissociative shocks. For this comparison, in addition to the [Fe II]1.25 $\mu $m/Pa$\beta $ ratio we consider the [Fe II]1.25 $\mu $m/[C I]0.98 $\mu $m ratio, which has the advantage both to use two lines detected at a relatively high signal to noise, and to have a behaviour opposite with respect to the [Fe II]1.25 $\mu $m/Pa$\beta $ ratio. This is due to the fact that carbon has a ionization potential of only 10 eV and therefore the fraction of carbon in atomic form tends to decrease with the increasing of the ionization fraction. The [Fe II]1.25 $\mu $m/[C I]0.98 $\mu $m and the [Fe II]1.25 $\mu $m/Pa$\beta $ ratios can therefore be used together to indicate the excitation degree of the HH objects: high/low excited objects will have low/high values of [Fe II]1.25 $\mu $m/Pa$\beta $ and high/low values of [Fe II]1.25 $\mu $m/[C I]0.98 $\mu $m. These observed ratios have been compared with the results of the dissociative shock model of Hollenbach & McKee (1989). Figure 14 plots the line ratios predicted by the model for different values of the shock velocities and for a pre-shock density of 104 cm-3. In the original model a gas-phase abundance $n_{\rm Fe}$/ $n_{\rm H}=10^{-6}$ is assumed. In Fig. 14 we also show where the expected ratios would move assuming a solar Fe abundance ( $n_{\rm Fe}/n_{\rm H}=3.2\times 10^{-5}$). As expected, the increase of the shock velocity produces a decrease of the [Fe II]1.25 $\mu $m/Pa$\beta $ratio and an increase of the [Fe II]1.25 $\mu $m/[C I]0.98 $\mu $m ratio.

The predicted ratios can be compared with our reddening corrected observations. The observed values always lie in between the two curves, and result consistent with models of shocks with $v_{\rm s} \sim 50$-80 km s-1, and $\sim$30%-40% of Fe in gaseous form. HH240A is the most extreme case, with a shock velocity of about 80 km s-1 and a gas-phase abundance $\sim$60% of the total. We remark that adopting a lower pre-shock density of 10-3 cm-3 will not significantly change these results. We therefore find conclusions which are consistent with the [Fe II]1.25 $\mu $m/Pa$\beta $ ratio analysis done above and which indicates that the shock events we are observing are capable of only partially disrupting the dust grains, while between 40 and 70% of the iron still remains in solid form.

5 Conclusions

We have presented the spectra from 0.95 to 2.5 $\mu $m obtained along three chains of Herbig-Haro jets (HH111, HH240/241 and HH120) and which are characterized by prominent emission of both Fe II  and H2  transitions. Most of the Fe II  lines here detected have never been observed before in these objects. In addition, some of these spectra also present emission from other ionic lines such as C I, S II, N I, and hydrogen recombination lines of the Paschen series. The analysis of the observed features and their spatial distribution along the jets have given the following results:

1.
Spectra obtained at different positions along the extended jets HH111 and HH240-241 show that the intensity of the Fe II  lines is decreasing moving away from the driving source. Qualitatively the Fe II  emission is correlated with optical S II emission while no optical invisible emission line regions are revealed in Fe II  at our sensitivity limit.
2.
Different Fe II  transitions have been used to derive the electron density $n_{\rm e}$ and the extinction in the different observed knots. $n_{\rm e}$ values in the range $3\times 10^3$- $2\times 10^4$ are found, which are sistematically larger by a factor of about 2 to 15 than the values inferred from optical S II line ratios for the same emission knots. Also the extinction values derived from NIR Fe II  line ratios turn out to be larger than the values determined in the optical by means of the Balmer decrement. Fe II  lines, having critical densities higher than the optical S II transitions, are able to evidence the presence of regions with density gradients, and we suggest that the higher derived density comes either in zones of the post-shock cooling layers subject to the higher compression (HH240 A), or from the inner section of the jet axis at higher degree of ionization (in HH111).
3.
Strong H2  emission lines are also detected and in HH240-241A and HH120 transitions up to $T_{\rm ex} \sim 35~000$ K are observed. The three flows show different H2 excitation characteristics. In HH111 the H2 emission is consistent with a thermalized gas at a single temperature of about 2900 K and no significant temperature variations are evidenced along the flow with the exception of the farest knot HH111-V, where a lower temperature of about 2300 K is derived. A single temperature LTE gas gives a good fit through the H2 lines also in each individual knot of the HH240/241 chain, but here temperatures as high as $\sim$3500 K are estimated in the closer HH knots, while the H2  temperature sharply decreases moving away from the driving source. This behaviour can be interpreted in terms of excitation in a planar non-dissociative (C-type) shock where the shock velocity is decreasing moving outwards. A different excitation diagram is presented by HH120, which consist of multiple temperature components, and which can be interpreted as due to a slow-J type shock.

No correlation seems to exist between the relative strength of the Fe II  and H2  emission and the H2  excitation characteristics. Consequently the Fe II  line emission, which requires the presence of fast dissociative shocks, is completely independent from the excitation mechanism giving rise to the molecular emission.

4.
Pa$\beta $ and [C I]0.98 $\mu $m lines have been used as a reference to infer the gas-phase iron abundance in the observed HH objects. We estimate a grain destruction efficiency of about 30-60%: the highest value is found for HH240A, which also shows the highest degree of excitation among the observed objects. We therefore conclude that even in presence of a shock with very prominent Fe II  NIR spectrum, a part of the available iron can still be depleted onto grains.

Acknowledgements
We enjoyed fruitful discussions with Francesca Bacciotti about jet excitation. We thank the referee, Chris Davis, for making useful comments which helped to clarify some aspects of the paper, and also for providing the H2 image of the HH111 jet. We also thank Malcolm Walmsley for his critical reading of the manuscript. The present work was supported by a grant of the MIUR on the project "Evolution of young circumstellar regions: dust and gas". This research has made use of NASA's Astrophysics Data System Bibliographic Services and the SIMBAD database, operated at CDS, Strasbourg, France.

References

 

Copyright ESO 2002