The emission of asteroids beyond ![]() 5
5 ![]() m is
dominated by radiation thermally emitted from their
surface.
A blackbody fit and the Standard Thermal Model (STM)
have been applied to the obtained infrared data to determine the
range of surface (blackbody and sub-solar) temperatures.
m is
dominated by radiation thermally emitted from their
surface.
A blackbody fit and the Standard Thermal Model (STM)
have been applied to the obtained infrared data to determine the
range of surface (blackbody and sub-solar) temperatures.
To determine the black-body temperature of the observed asteroids we fitted the infrared data with a Planck function multiplied by the solid angle of the objects. Both the solid angle and the black-body temperature were treated as free parameters.
The sub-solar temperature of the observed objects was computed
by applying the STM
(Lebofsky & Spencer 1989), already
used by Tedesco et al. (1992) in the IRAS asteroid
survey.
It assumes a non-rotating spherical asteroid, in
instantaneous equilibrium with solar insolation, observed at 0![]() solar phase angle.
In this ideal situation, in which the thermal inertia is neglected,
and the asteroid nightside emission is thus not taken into
account, the sub-solar temperature is given as:
solar phase angle.
In this ideal situation, in which the thermal inertia is neglected,
and the asteroid nightside emission is thus not taken into
account, the sub-solar temperature is given as:
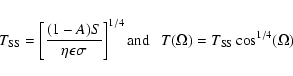 |
(1) |
In Table 2 the sub-solar and
black-body temperatures, and
the albedo and diameter values
estimated by applying STM to our data
are reported.
The table shows also the absolute magnitude H and the slope parameter G
used as input, and diameters and albedos obtained
by Tedesco et al. (1992) on the basis of
IRAS data.
Our estimations of diameters and albedos are in agreement with the
values given by Tedesco et al. (1992), with the exception
of the albedos of
511 Davida and 914 Palisana which deviate from the IRAS results.
This can be due to differences in the viewing geometry
between the IRAS and ISO observations.
In the simplified STM the real shape of the asteroid is not taken into
account:
this can influence the albedo and diameter calculations.
To model the thermal continuum of previous ISO observations, Dotto et al. (2000) and Barucci et al. (2002) used the advanced thermophysical model
(TPM) developed by Lagerros (1996, 1997, 1998). To properly apply this
advanced model we need the knowledge of several physical parameters of
the analysed asteroids. Unfortunately, we do not have a good estimation of
the pole direction, shape, infrared beaming
and thermal inertia of the five asteroids
here discussed.
A comparison between the diameter and albedo values obtained by STM and
TPM has been possible only for 77 Frigga, for which an estimation of
the rotational state is available (Erikson 2000).
We applied TPM, considering the wavelength dependent
emissivity as stated by Müller & Lagerros (1998), and default values for
thermal inertia
and beaming parameters ![]() and f,
and we obtained results similar to those computed by STM.
Since the
rotational and physical parameters of the asteroids here discussed
are not sufficiently well
known, we preferred to apply the simplest STM, with the
minimum number of free parameters, without introducing new possible
sources of error.
and f,
and we obtained results similar to those computed by STM.
Since the
rotational and physical parameters of the asteroids here discussed
are not sufficiently well
known, we preferred to apply the simplest STM, with the
minimum number of free parameters, without introducing new possible
sources of error.
Using STM we computed the expected flux at the time of ISO observations.
Then we divided the observed spectra for the STM expected flux,
obtaining the "Relative Obs/Mod''.
| Object | H | G | Diameter | Albedo | Black-body | Sub-solar | IRAS | IRAS | IRAS | IRAS |
| temp. | temp. | D | pH |
|
||||||
| (mag) | (km) | (K) | (K) | (km) | (km) | |||||
| 77 Frigga | 8.52 | 0.16 |
|
223 | 259 | 69.25 | 2.1 | 0.144 | 0.009 | |
| 114 Kassandra | 8.26 | 0.15 |
|
228 | 265 | 99.64 | 1.9 | 0.0884 | 0.003 | |
| 308 Polyxo | 8.17 | 0.21 |
|
232 | 265 | 140.69 | 3.8 | 0.0482 | 0.003 | |
| 511 Davida | 6.22 | 0.16 |
|
232 | 268 | 326.07 | 5.3 | 0.054 | 0.0023 | |
| 914 Palisana | 8.76 | 0.15 |
|
220 | 257 | 76.61 | 1.7 | 0.0943 | 0.004 |
Copyright ESO 2002