A&A 393, 749-756 (2002)
DOI: 10.1051/0004-6361:20020929
M.-A. Miville-Deschênes1 - G. Lagache2 - J.-L. Puget2
1 - Laboratoire de Radioastronomie, École Normale Supérieure, 24 rue Lhomond, 75005 Paris, France
2 - Institut d'Astrophysique Spatiale, Université Paris-Sud, Bât. 121, 91405 Orsay, France
Received 29 January 2002 / Accepted 17 June 2002
Abstract
Based on a power spectrum analysis of the IRAS ISSA maps, we present
the first detection of the Cosmic far-Infrared Background (CIB) fluctuations at 60 and 100 ![]() m.
The power spectrum of 12 low cirrus emission regions is
characterized by a power excess at spatial frequencies higher than
m.
The power spectrum of 12 low cirrus emission regions is
characterized by a power excess at spatial frequencies higher than
![]() arcmin-1.
Most of this excess is due to noise and to nearby point sources with a flux stronger than 1 Jy.
But we show that when these contributions are carefully removed, there is still a power excess that is
the signature of the CIB fluctuations.
The power spectrum of the CIB at 60 and 100
arcmin-1.
Most of this excess is due to noise and to nearby point sources with a flux stronger than 1 Jy.
But we show that when these contributions are carefully removed, there is still a power excess that is
the signature of the CIB fluctuations.
The power spectrum of the CIB at 60 and 100 ![]() m is
compatible with a Poissonian distribution,
at spatial frequencies between 0.025 and 0.2 arcmin-1.
The fluctuation level is
m is
compatible with a Poissonian distribution,
at spatial frequencies between 0.025 and 0.2 arcmin-1.
The fluctuation level is ![]()
![]() Jy2/sr and
Jy2/sr and
![]()
![]() Jy2/sr at 60 and 100
Jy2/sr at 60 and 100 ![]() m respectively.
The levels of the fluctuations are used in a larger framework, with other observationnal
data, to constrain the evolution of IR galaxies (Lagache et al. 2002). The detections reported here,
coupled with the level of the fluctuations at 170
m respectively.
The levels of the fluctuations are used in a larger framework, with other observationnal
data, to constrain the evolution of IR galaxies (Lagache et al. 2002). The detections reported here,
coupled with the level of the fluctuations at 170 ![]() m,
give strong constraints on the evolution of the IR luminosity function.
The combined results at 60, 100 and 170
m,
give strong constraints on the evolution of the IR luminosity function.
The combined results at 60, 100 and 170 ![]() m for the CIB and its fluctuations
allows, on the CIB at 60
m for the CIB and its fluctuations
allows, on the CIB at 60 ![]() m, to put a firm upper limit of 0.27 MJy/sr
and to give an estimate of 0.18 MJy/sr.
m, to put a firm upper limit of 0.27 MJy/sr
and to give an estimate of 0.18 MJy/sr.
Key words: cosmology: diffuse radiation - infrared: ISM - infrared: general
The Cosmic Far-Infrared Background (CIB) was detected
by Puget et al. (1996), exploiting COBE-FIRAS data, and has now been firmly
established over a range of wavelengths (e.g. Dwek et al. 1998; Gispert et al. 2000; Hauser & Dwek 2001).
The intensity is quite high with respect
to predictions based on evolutionary models of star formation in galaxy
populations inferred from optical data. Source counts obtained with SCUBA
at 850 ![]() m and ISO at 170 and 15
m and ISO at 170 and 15 ![]() m have partly
resolved the CIB and shown a strong cosmological evolution.
In the future, far-IR and sub-millimeter telescopes
from ground and space will perform deep surveys over small
areas, aimed at resolving a substantial fraction of the CIB and to shed
light on the number density, luminosity and spectral evolution of the
infrared galaxy populations. However, investigation of the clustering of these
populations requires surveys over much larger areas.
One way to tackle the limitation on the number of detected galaxies
per field is to search for CIB fluctuations.
So far, CIB fluctuations has only been observed at 170
m have partly
resolved the CIB and shown a strong cosmological evolution.
In the future, far-IR and sub-millimeter telescopes
from ground and space will perform deep surveys over small
areas, aimed at resolving a substantial fraction of the CIB and to shed
light on the number density, luminosity and spectral evolution of the
infrared galaxy populations. However, investigation of the clustering of these
populations requires surveys over much larger areas.
One way to tackle the limitation on the number of detected galaxies
per field is to search for CIB fluctuations.
So far, CIB fluctuations has only been observed at 170 ![]() m
in the FIRBACK fields (Lagache & Puget 2000) and at 90 and 170
m
in the FIRBACK fields (Lagache & Puget 2000) and at 90 and 170 ![]() m in the Lockman hole
(Matsuhara et al. 2000) surveys. These detections
were probably dominated by the Poissonian contribution.
By analyzing larger FIRBACK fields, power spectra seem to reveal correlated fluctuations, well
above the cirrus contribution (Puget & Lagache 2002).
These results are currently under further investigation.
Above
m in the Lockman hole
(Matsuhara et al. 2000) surveys. These detections
were probably dominated by the Poissonian contribution.
By analyzing larger FIRBACK fields, power spectra seem to reveal correlated fluctuations, well
above the cirrus contribution (Puget & Lagache 2002).
These results are currently under further investigation.
Above ![]() m, only SCUBA
observations might currently be able to give information on the
fluctuations. However, no significant CIB correlations have been detected in
the SCUBA maps (Peacock et al. 2000).
The CIB anisotropies are mainly contributed by moderate to
high redshift star-forming galaxies, whose clustering properties and
evolutionary histories are currently unknown.
Since the clustering strength depends on the bias at the relevant redshift,
observing the CIB correlated fluctuations will provide valuable informations
on bulge and elliptical formation, as well as potentially QSOs,
thereby providing clues on the physical relations between dark matter and
starburst galaxies.
m, only SCUBA
observations might currently be able to give information on the
fluctuations. However, no significant CIB correlations have been detected in
the SCUBA maps (Peacock et al. 2000).
The CIB anisotropies are mainly contributed by moderate to
high redshift star-forming galaxies, whose clustering properties and
evolutionary histories are currently unknown.
Since the clustering strength depends on the bias at the relevant redshift,
observing the CIB correlated fluctuations will provide valuable informations
on bulge and elliptical formation, as well as potentially QSOs,
thereby providing clues on the physical relations between dark matter and
starburst galaxies.
In this paper we present the results of a power spectrum analysis of the
IRAS 60 and 100 ![]() m emission of 12 regions in the sky with very low interstellar emission.
All these regions are characterized by an excess of power at high spatial frequencies
with respect to the interstellar emission.
We will show that this excess is not of instrumental origin and may be attributed to the CIB.
The discovery of the CIB fluctuations at 60 and 100
m emission of 12 regions in the sky with very low interstellar emission.
All these regions are characterized by an excess of power at high spatial frequencies
with respect to the interstellar emission.
We will show that this excess is not of instrumental origin and may be attributed to the CIB.
The discovery of the CIB fluctuations at 60 and 100 ![]() m could give
constraints on the number counts below the IRAS point source detection limit.
However, instead of extrapolating the number counts at 60 and 100
m could give
constraints on the number counts below the IRAS point source detection limit.
However, instead of extrapolating the number counts at 60 and 100 ![]() m
using the level of the fluctuations, which is of limited cosmological
interest, we prefer to use the two detections in a more general
framework of the modelisation of the IR galaxy evolution that combines
all existing number counts, redshift distributions, and observations of the CIB and its
fluctuations, in the whole IR and submm range Lagache et al. (2002).
m
using the level of the fluctuations, which is of limited cosmological
interest, we prefer to use the two detections in a more general
framework of the modelisation of the IR galaxy evolution that combines
all existing number counts, redshift distributions, and observations of the CIB and its
fluctuations, in the whole IR and submm range Lagache et al. (2002).
The paper is organized as follow.
After a presentation (Sect. 2) of the data used for this
analysis we describe in Sect. 3 the power spectrum
at 60 and 100 ![]() m of the 12 fields selected. In Sect. 4 we
present the method used to separate the Galactic and extra-Galactic
contributions to the power spectrum and we discuss our results in Sect. 5.
m of the 12 fields selected. In Sect. 4 we
present the method used to separate the Galactic and extra-Galactic
contributions to the power spectrum and we discuss our results in Sect. 5.
The IRAS mission was originally designed to measure
point sources but it also provided spectacular images of the
Galactic dust diffuse emission. These images,
constituted of
![]() pixels with a pixel size of
1.5' (i.e. the size of the field is
pixels with a pixel size of
1.5' (i.e. the size of the field is
![]() ),
are gathered in the IRAS Sky Survey Atlas (ISSA).
Each ISSA map is the result of the combination of up to three
individual maps (named HCON for Hours CONfirmation).
The HCON images were constructed from different
observations of the same region separated by several months.
The angular resolution of the 60 and 100
),
are gathered in the IRAS Sky Survey Atlas (ISSA).
Each ISSA map is the result of the combination of up to three
individual maps (named HCON for Hours CONfirmation).
The HCON images were constructed from different
observations of the same region separated by several months.
The angular resolution of the 60 and 100 ![]() m band images are
respectively
m band images are
respectively
![]() and
and
![]() .
To study the power spectrum of the CIB emission at 60 and 100
.
To study the power spectrum of the CIB emission at 60 and 100 ![]() m, we have
worked on 12 ISSA maps with particularly low cirrus emission.
m, we have
worked on 12 ISSA maps with particularly low cirrus emission.
Special care has been
taken to have a consistent diffuse emission calibration through the Atlas.
But, as the IRAS mission was designed to provide absolute
photometry only for point sources,
the ISSA images give only relative photometry and cannot be used
to determine the absolute surface brightness for diffuse emission.
Based on a comparison with the DIRBE data, it has been shown
(Wheelock et al. 1993; Schlegel et al. 1998) that, at large scale (> a few degrees), the
amplitude of the fluctuations are overestimated in the ISSA maps by a
factor 1.15 at 60 ![]() m and 1.39 at 100
m and 1.39 at 100 ![]() m. We have thus applied these
factors to our maps prior to the analysis.
m. We have thus applied these
factors to our maps prior to the analysis.
There is also an uncertainty on the zero level of the ISSA maps,
for which the zodiacal emission has been subtracted (Wheelock et al. 1993).
This uncertainty is dominated at 60 and 100 ![]() m by an imperfect knowledge of the detector offsets
and of the zodiacal emission. As we are looking at fluctuations of the signal,
a global additive offset has no impact on the power spectrum.
On the other hand, an imperfect zodiacal emission correction applied to the ISSA maps
will have an impact on the large scale structure of the maps and then on
the power spectrum (for low k values). To restore appropriately the
large scale structure of the selected fields we have compared each ISSA map
with the DIRBE data (for which the zodiacal emission correction was better done).
The ISSA maps, multiplied by the appropriate gain value (0.87 at 60
m by an imperfect knowledge of the detector offsets
and of the zodiacal emission. As we are looking at fluctuations of the signal,
a global additive offset has no impact on the power spectrum.
On the other hand, an imperfect zodiacal emission correction applied to the ISSA maps
will have an impact on the large scale structure of the maps and then on
the power spectrum (for low k values). To restore appropriately the
large scale structure of the selected fields we have compared each ISSA map
with the DIRBE data (for which the zodiacal emission correction was better done).
The ISSA maps, multiplied by the appropriate gain value (0.87 at 60 ![]() m and 0.72 at 100
m and 0.72 at 100 ![]() m)
were convolved by the DIRBE beam and then subtracted from the DIRBE data.
This offset map is then added to the ISSA map.
Note that we do not use the Schlegel et al. (1998) IRAS rescaled maps, constructed
in a similar manner, for which it is impossible to recover the associated instrumental noise.
m)
were convolved by the DIRBE beam and then subtracted from the DIRBE data.
This offset map is then added to the ISSA map.
Note that we do not use the Schlegel et al. (1998) IRAS rescaled maps, constructed
in a similar manner, for which it is impossible to recover the associated instrumental noise.
In this paper we present a power spectrum analysis of
twelve high latitude fields. These fields were selected on the
basis of their low cirrus emission (mean brightness ![]() 1 MJy/sr at 100
1 MJy/sr at 100 ![]() m)
but also on their redundancy; we have selected only
fields for which each sky position has been observed at least twice
in order to be able to estimate the contribution of the noise to the power spectrum.
The typical stripping of the ISSA maps is very efficiently removed from
the signal power spectrum by the noise estimate procedure using the difference
between observations of the different HCON as will be shown in Sect. 3.3 and Fig. 2.
m)
but also on their redundancy; we have selected only
fields for which each sky position has been observed at least twice
in order to be able to estimate the contribution of the noise to the power spectrum.
The typical stripping of the ISSA maps is very efficiently removed from
the signal power spectrum by the noise estimate procedure using the difference
between observations of the different HCON as will be shown in Sect. 3.3 and Fig. 2.
The 60 and 100 ![]() m ISSA maps of the twelve selected fields, gain and offset corrected,
are shown in Figs. A.2 to A.9 and their central coordinates are
gathered in Table 1.
Five fields are located in the southern hemisphere,
most of them in the neighborhood of the Marano field (Marano et al. 1988), and
seven are spread over the northern hemisphere (ISSA map number 376 contains the Lockman Hole).
m ISSA maps of the twelve selected fields, gain and offset corrected,
are shown in Figs. A.2 to A.9 and their central coordinates are
gathered in Table 1.
Five fields are located in the southern hemisphere,
most of them in the neighborhood of the Marano field (Marano et al. 1988), and
seven are spread over the northern hemisphere (ISSA map number 376 contains the Lockman Hole).
| ISSA |
|
|
l | b |
| 47 | 4h 1m 24.8s | -49 |
258.32 |
-47.41 |
| 66 | 23h 2m 53.8s | -49 |
338.21 |
-59.30 |
| 69 | 1h 46m 9.0s | -39 |
264.42 |
-73.02 |
| 71 | 3h 29m 49.5s | -39 |
244.45 |
-54.96 |
| 97 | 1h 34m 18.6s | -29 |
230.96 |
-80.22 |
| 322 | 13h 4m 23.3s | 29 |
76.14 |
86.14 |
| 323 | 13h 50m 16.1s | 29 |
47.86 |
76.81 |
| 348 | 9h 35m 7.0s | 39 |
182.59 |
47.71 |
| 349 | 10h 26m 56.1s | 39 |
180.70 |
57.59 |
| 356 | 16h 29m 42.1s | 39 |
63.41 |
43.50 |
| 375 | 10h 3m 12.9s | 49 |
166.14 |
50.80 |
| 376 | 11h 2m 53.8s | 49 |
158.21 |
59.30 |
For a given image, the power spectrum P(k) is
the absolute value of the Fourier Transform (we use
the Fast Fourier Transform (FFT) function of IDL)
of the image, averaged over constant values of
![]() .
To make sure that map boundaries are not
contaminating the computed power spectrum, we apodize the image with a
cosine function before computing the Fourier Transform. This prevents
the introduction of strong discontinuities when the image is periodized
in the FFT algorithm (see Appendix A).
.
To make sure that map boundaries are not
contaminating the computed power spectrum, we apodize the image with a
cosine function before computing the Fourier Transform. This prevents
the introduction of strong discontinuities when the image is periodized
in the FFT algorithm (see Appendix A).
![\begin{figure}
\par\includegraphics[width=17.2cm,clip]{H3453F1.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg21.gif) |
Figure 1:
Top left: the 100 |
| Open with DEXTER | |
The power spectrum of the 100 ![]() m ISSA map of one of our fields is shown in Fig. 1.
Since the zodiacal emission has been subtracted in the ISSA maps,
there are four main contributions to the power
spectrum at these wavelengths:
the cirrus emission, point sources,
the CIB (resolved and unresolved) and the noise.
Therefore, and if the noise and the signal are not correlated,
the power spectrum P(k)
can be expressed in the following manner:
m ISSA map of one of our fields is shown in Fig. 1.
Since the zodiacal emission has been subtracted in the ISSA maps,
there are four main contributions to the power
spectrum at these wavelengths:
the cirrus emission, point sources,
the CIB (resolved and unresolved) and the noise.
Therefore, and if the noise and the signal are not correlated,
the power spectrum P(k)
can be expressed in the following manner:
One of the main limitation of the component separation to the power spectrum is the estimate of the noise contribution. For ISSA maps, this contribution can be estimated accurately as they are the combination of up to three HCON maps. Indeed the noise power spectrum of the HCON maps, and therefore of the ISSA map, can be estimated by subtracting two HCON maps of the same region. An example of the difference between two HCON maps for a typical low brightness ISSA map is shown in Fig. 1 (top-right). The characteristic stripping of the IRAS data is seen in this difference map. The distribution of difference values is symmetric (when there is no strong point sources) and well fitted by a sum of two Gaussian functions (see Fig. 1, bottom-right).
As the distribution of the difference values is the sum of two Gaussian functions with
an equivalent width
![]() and assuming that the noise in the IRAS survey
is stationary to a good approximation (as tested below), we can conclude that the noise
of an individual HCON can also be characterized by an equivalent width:
and assuming that the noise in the IRAS survey
is stationary to a good approximation (as tested below), we can conclude that the noise
of an individual HCON can also be characterized by an equivalent width:
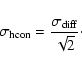 |
(2) |
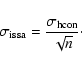 |
(3) |
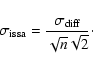 |
(4) |
In general three HCON maps were averaged but parts of them may be undefined.
Therefore, for each ISSA map we looked at the three corresponding HCON maps and
built a mask n(x,y) that gives the number of defined values that were averaged at each positions.
Then, the noise map of a given ISSA map is estimated by subtracting
two HCON maps and divide the result by
![]() .
.
The power spectra of the ISSA map and of its noise map are shown in Fig. 1 (bottom-left).
Both power spectra meet at small scales (
![]() pixel-1)
where the signal is noise dominated. The noise map is characterized by a
pixel-1)
where the signal is noise dominated. The noise map is characterized by a ![]() k-0.8 power spectrum.
We have investigated the variations of the statistical properties of the noise
on ISSA maps where three complete HCONs exists. By looking at the three possible
difference maps built from three HCONs, we found that
the shape of the power spectrum
of the noise is rather constant with time and that the absolute level of the noise varies
by less than 15% from one HCON to the other.
This is equally true at 60 and 100
k-0.8 power spectrum.
We have investigated the variations of the statistical properties of the noise
on ISSA maps where three complete HCONs exists. By looking at the three possible
difference maps built from three HCONs, we found that
the shape of the power spectrum
of the noise is rather constant with time and that the absolute level of the noise varies
by less than 15% from one HCON to the other.
This is equally true at 60 and 100 ![]() m.
m.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3453F2.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg34.gif) |
Figure 2:
Power spectrum (black solid line) of a typical bright ISSA field with no strong point sources.
The cirrus contribution to the power spectrum has been fitted by a
power law (
|
| Open with DEXTER | |
The multiplicative factor ![]() in Eq. (1) represents
the effective instrumental filter function of the system
(telescope, focal plane assembly, sky scanning and map making).
For some ISSA maps the instrumental function can be estimated directly from the power
spectrum of the map. This is the case for maps where the brightness fluctuations are dominated by the cirrus
emission and where the power spectrum is simply:
in Eq. (1) represents
the effective instrumental filter function of the system
(telescope, focal plane assembly, sky scanning and map making).
For some ISSA maps the instrumental function can be estimated directly from the power
spectrum of the map. This is the case for maps where the brightness fluctuations are dominated by the cirrus
emission and where the power spectrum is simply:
| (5) |
To estimate ![]() directly on the power spectrum of ISSA maps, we have selected 20 relatively bright
regions (mean brightness greater than 8 MJy/sr) where the noise and CIB contributions are negligible.
To make sure that the fluctuations are dominated by the cirrus emission, point sources were filtered
out using a median filtering. An example of the power spectrum of such
an ISSA map is shown in Fig. 2.
We found that the effective IRAS instrumental filter function in Fourier space is well describe
by a Gaussian function both at 60 and 100
directly on the power spectrum of ISSA maps, we have selected 20 relatively bright
regions (mean brightness greater than 8 MJy/sr) where the noise and CIB contributions are negligible.
To make sure that the fluctuations are dominated by the cirrus emission, point sources were filtered
out using a median filtering. An example of the power spectrum of such
an ISSA map is shown in Fig. 2.
We found that the effective IRAS instrumental filter function in Fourier space is well describe
by a Gaussian function both at 60 and 100 ![]() m.
To determine the width of the instrumental function,
the power spectrum of the 20 fields were fitted by the following equation:
m.
To determine the width of the instrumental function,
the power spectrum of the 20 fields were fitted by the following equation:
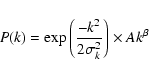 |
(6) |
The cutoff seen in Fig. 2 at frequencies larger than 0.05 arcmin-1
is where the effect of the instrumental filter function is expected.
When the power spectrum is divided by the Gaussian instrumental function (grey line)
one sees that this modeling does not stand
for scales smaller than 4.5 arcmin (k > 0.22 arcmin-1).
This is due to the effective resolution of the IRAS data.
The power spectrum has to be cut at the Nyquist frequency
corresponding to the 1.5' pixel ISSA map.
However, the effective resolution of the IRAS data is
about 3.8' and 4.25' respectively at 60 and 100 ![]() m. For that reason,
all the power spectrum at frequency above 0.1 arcmin-1, which corresponds
to the Nyquist frequency of the effective resolution, has to be taken
with cautious.
m. For that reason,
all the power spectrum at frequency above 0.1 arcmin-1, which corresponds
to the Nyquist frequency of the effective resolution, has to be taken
with cautious.
In Figs. A.2 to A.9 we present
the power spectrum of the 60 and 100 ![]() m ISSA maps of our twelve fields (black line).
For all these fields, the power spectrum of the noise has been subtracted
and the result has been divided by the PSF
m ISSA maps of our twelve fields (black line).
For all these fields, the power spectrum of the noise has been subtracted
and the result has been divided by the PSF ![]() .
At large scale, all the power spectra follow a power law typical of cirrus emission
(Gautier et al. 1992). But at
.
At large scale, all the power spectra follow a power law typical of cirrus emission
(Gautier et al. 1992). But at
![]() arcmin-1 we notice
a break in the spectra and an excess from the cirrus power law at
small scales. This power excess is observed for all our fields, at 60 and 100
arcmin-1 we notice
a break in the spectra and an excess from the cirrus power law at
small scales. This power excess is observed for all our fields, at 60 and 100 ![]() m.
m.
The power excess observed at small scales reveals the
presence of a component with a flatter power spectrum,
like what would be expected from noise or randomly distributed point sources.
At this stage, a noise contribution is unlikely as it has been well estimated and
removed accordingly.
On the other hand, in fields with such low cirrus emission, several extra-galactic point
sources were detected. In each of our fields, between 200 and 300 point sources are
listed in the IRAS Point Source Catalog (PSC), the vast majority of them being extra-galactic objects.
We remove the contribution of all point sources with flux greater than 1 Jy
at 100 ![]() m (and the same sources at 60
m (and the same sources at 60 ![]() m).
The cut at 1 Jy is chosen such that the PSC above this limit will be nearly complete.
This gives a well define separation between the sources contributing to the unresolved CIB
and the resolved sources. This is necessary for any quantitative use of our results.
We choose this cut in flux as low as possible to remove the contribution of the
nearby and resolved galaxies that dominate the power spectrum at scales k > 0.01 arcmin-1
(for those galaxies, the spatial distribution is indistinguishable from
a Poissonian distribution). Moreover, according to recent simulations, the cut of 1 Jy at 100
m).
The cut at 1 Jy is chosen such that the PSC above this limit will be nearly complete.
This gives a well define separation between the sources contributing to the unresolved CIB
and the resolved sources. This is necessary for any quantitative use of our results.
We choose this cut in flux as low as possible to remove the contribution of the
nearby and resolved galaxies that dominate the power spectrum at scales k > 0.01 arcmin-1
(for those galaxies, the spatial distribution is indistinguishable from
a Poissonian distribution). Moreover, according to recent simulations, the cut of 1 Jy at 100 ![]() m
almost corresponds to the flux where the non-Euclidean part appears in the number counts.
To remove the contribution of strong point sources (
m
almost corresponds to the flux where the non-Euclidean part appears in the number counts.
To remove the contribution of strong point sources (
![]() Jy) to the power spectrum,
they were filtered out from the ISSA map.
For each ISSA map, we have extracted the point sources of the IRAS
Point Source Catalog with a flux greater or equal to 1 Jy.
Then we have applied a median filtering to the ISSA map to estimate the background level and,
at each point source position,we have removed the points in a
Jy) to the power spectrum,
they were filtered out from the ISSA map.
For each ISSA map, we have extracted the point sources of the IRAS
Point Source Catalog with a flux greater or equal to 1 Jy.
Then we have applied a median filtering to the ISSA map to estimate the background level and,
at each point source position,we have removed the points in a
![]() window
that were more than 4 times the noise level (
window
that were more than 4 times the noise level (
![]() )
above the background.
Finally, the missing points were replaced by a bilinear interpolation.
)
above the background.
Finally, the missing points were replaced by a bilinear interpolation.
The power spectrum of the filtered ISSA maps is the blue line in Figs. A.2 to A.9.
A power excess at small scales (k>0.02 arcmin-1) is still apparent on all power spectra, at 60 and 100 ![]() m.
This excess is likely to be the signature of the unresolved cosmic far-infrared background.
To characterize it, the contribution of the cirrus emission has to be removed.
m.
This excess is likely to be the signature of the unresolved cosmic far-infrared background.
To characterize it, the contribution of the cirrus emission has to be removed.
As we do not have any independent tracers of the cirrus emission at the IRAS scales for the whole fields, the only way to derive the cirrus contribution is to use the statistical properties of their spatial distribution. Following Gautier et al. (1992) and Miville-Deschênes et al. (2002) the power spectrum of interstellar dust emission is well describe by a power law. To remove this contribution to the power spectrum of the filtered ISSA maps, we have fitted a power law on the large scale part of the power spectrum of the filtered maps. The best compromise between the number of point on which to fit the power law and the contamination from the CIB was to fit on k < 0.02 arcmin-1. The point corresponding to the largest scale was not used for the fitting as it suffers from a large statistical error. The result of the fitting, and its associated uncertainty, are shown for each ISSA map in Figs. A.2 to A.9. The uncertainty on the slope reflects the dispersion of the points around the fit. The red line in these figures is the result of the subtraction of the cirrus power law from the power spectrum of the filtered map (blue line); it is the signature of the CIB.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H3453F3.ps}\hspace*{5mm}\includegraphics[width=7.5cm,clip]{H3453F4.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg47.gif) |
Figure 3:
CIB contributions to the 60 (left) and 100 |
| Open with DEXTER | |
The average of the 12 CIB contributions is shown in Fig. 3 (black lines).
The blue lines in this figure indicate the 1![]() uncertainty on the determination, including
the PSF and the estimate of the cirrus contribution errors.
The 1
uncertainty on the determination, including
the PSF and the estimate of the cirrus contribution errors.
The 1![]() uncertainty is very close to the rms variations of the 12 averaged values.
The dispersion between the fields is thus dominated by the PSF and cirrus contribution
errors, we do not see any significant variation from field to field.
Moreover, it is important to note that the detected excess at small scales
is uncorrelated with the cirrus emission (the excess disappears when
the cirrus contribution increases). Therefore, our fields being
spread over the sky, the excess at small scale
is compatible with isotropic properties. This is an other
argument in favor of an extra-galactic origin
for the excess.
uncertainty is very close to the rms variations of the 12 averaged values.
The dispersion between the fields is thus dominated by the PSF and cirrus contribution
errors, we do not see any significant variation from field to field.
Moreover, it is important to note that the detected excess at small scales
is uncorrelated with the cirrus emission (the excess disappears when
the cirrus contribution increases). Therefore, our fields being
spread over the sky, the excess at small scale
is compatible with isotropic properties. This is an other
argument in favor of an extra-galactic origin
for the excess.
We can note in Figs. A.2-A.9 that the power spectrum
of the resolved IRAS sources is varying by factor up to 10
from field to field. The CIB (resolved and unresolved) fluctuations
are dominated by the brightest sources in ISSA maps.
The number of such sources is quite small, leading to a high
cosmic variance, and thus large variation from field to field.
On the contrary, for the unresolved CIB fluctuations,
as sources above 1 Jy (about 300 per field) are removed,
the cosmic variance is lower than 6![]() ,
which is negligible
with respect to the 1
,
which is negligible
with respect to the 1![]() uncertainty.
uncertainty.
The CIB is detected over one decade in scales, from 5 to 50 arcmin.
The power spectrum of the CIB at 60 and 100 ![]() m is compatible with
a Poissonian distribution at spatial frequencies between 0.025 and 0.2 arcmin-1.
The fluctuation level is
m is compatible with
a Poissonian distribution at spatial frequencies between 0.025 and 0.2 arcmin-1.
The fluctuation level is ![]()
![]() Jy2/sr and
Jy2/sr and
![]()
![]() Jy2/sr at 60 and 100
Jy2/sr at 60 and 100 ![]() m respectively.
m respectively.
We have shown here that the power spectrum
of high latitude fields at 60 and 100 ![]() m is characterized by a
break at small scales (near 0.02 arcmin-1).
As indicated by Gautier et al. (1992), the power spectrum of the dust emission
is usually well described by a power law proportional to
m is characterized by a
break at small scales (near 0.02 arcmin-1).
As indicated by Gautier et al. (1992), the power spectrum of the dust emission
is usually well described by a power law proportional to
![]() .
A more detailed study of the statistical properties of the
interstellar cirrus HI 21 cm emission has been carried out by Miville-Deschênes (1999).
In this analysis it is shown that
there are limited variations of the spectral index of the power law
from field to field but, what is most important for the present work,
the power spectrum of cirrus emission for scales smaller
than
.
A more detailed study of the statistical properties of the
interstellar cirrus HI 21 cm emission has been carried out by Miville-Deschênes (1999).
In this analysis it is shown that
there are limited variations of the spectral index of the power law
from field to field but, what is most important for the present work,
the power spectrum of cirrus emission for scales smaller
than
![]() is always characterized by a single power law
with no break. Therefore, it is unlikely that the power excess
observed here at small scales is of interstellar origin.
is always characterized by a single power law
with no break. Therefore, it is unlikely that the power excess
observed here at small scales is of interstellar origin.
We could also wonder if this break is of instrumental origin. It was shown by Wheelock et al. (1993) that the response of the IRAS detectors are affected by memory effects. This produces variations of the detector response as a function of scale. This effect is more important at small scales (under a few tens of arcminutes) but Wheelock et al. (1993) have shown that the amplitude of the fluctuations at these scales were underestimated. This effect will thus produce a drop of the power spectrum at small scale and cannot explain the power excess observed here.
On the other hand, instrumental noise could produce such an excess in the power spectrum. But, as the IRAS ISSA maps result from redundant individual observations, we were able to estimate the contribution of the noise to the power spectrum. We are aware that our estimate of the noise rely on the fact that the individual HCONs are independant. This is not perfectly true as, in the construction of the HCONs, an offset was added to each scan to minimize the difference between different observations of the same position. Therefore the noise level estimated by subtracting HCONs may be underestimated at the scale of a scan, which is a few degrees. But at this angular scale the signal is completely dominated by the cirrus emission, even in the low brightness regions selected for our analysis. At the scale of a few arcminutes where the CIB is detected, the noise contribution to the power spectrum has been removed accurately.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{H3453F5.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg51.gif) |
Figure 4:
Redshift distribution of the sources
making the CIB and the fluctuations at 60, 100 and 170 |
| Open with DEXTER | |
In fact it appears that most of the power excess can be attributed to the
numerous extra-galactic point sources that are present in such a low
cirrus emission field. When the strong (
![]() Jy) point sources are removed from the
ISSA maps, we recover a power spectrum typical of cirrus emission
at low spatial frequencies but with
still a power excess at small scales (k > 0.02 arcmin-1) that can be attributed
to the unresolved cosmic infrared background.
Moreover, the residue has homogeneous properties over the sky,
consistent with CIB.
Jy) point sources are removed from the
ISSA maps, we recover a power spectrum typical of cirrus emission
at low spatial frequencies but with
still a power excess at small scales (k > 0.02 arcmin-1) that can be attributed
to the unresolved cosmic infrared background.
Moreover, the residue has homogeneous properties over the sky,
consistent with CIB.
Knox et al. (2001) computed the expected power spectrum of the CIB at several
frequencies (
![]() GHz), exploiting the far-IR volume emissivity derived from the
count models of Guiderdoni et al. (1998) and assuming a bias b=3, constant with
redshift. They concluded that the clustering-induced fluctuations
can match those of the CMB at
GHz), exploiting the far-IR volume emissivity derived from the
count models of Guiderdoni et al. (1998) and assuming a bias b=3, constant with
redshift. They concluded that the clustering-induced fluctuations
can match those of the CMB at
![]() .
They also predict a shape of the CIB power spectrum peaking
around scales of 1-3 degrees. This broad maximum, if present, is at the limit of our frequency range
where the noise is becoming large,
making the detection of the clustering very difficult.
The power spectra of the CIB at 60 and 100
.
They also predict a shape of the CIB power spectrum peaking
around scales of 1-3 degrees. This broad maximum, if present, is at the limit of our frequency range
where the noise is becoming large,
making the detection of the clustering very difficult.
The power spectra of the CIB at 60 and 100 ![]() m are compatible with a
Poissonian distribution with levels
m are compatible with a
Poissonian distribution with levels ![]()
![]() Jy2/sr and
Jy2/sr and
![]()
![]() Jy2/sr respectively.
Jy2/sr respectively.
The CIB rms fluctuations in the IRAS maps
corresponding to the white noise power spectra are:
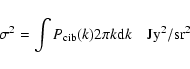 |
(7) |
This is illustrated more quantitatively in Fig. 4
on the panels showing the redshift distribution of sources
contributing to the CIB intensity and the fluctuations (Lagache et al. 2002).
It is clear from these figures that the z-distribution of the fluctuations
is bimodal, with one contribution at redshift lower than 0.25
and the other one centered at redshift around 1.
For all sources the ratio of nearby to moderate-redshift
source contribution to the fluctuations is equal to
3.8, 1.8 and 1.3 at 60, 100, 170 ![]() m
respectively, illustrating that fluctuations at larger wavelengths
are dominated by more distant sources.
When the brightest sources are removed the ratio
of nearby to moderate-redshift
contribution becomes equal to 1.7, 1 and 0.74
at 60, 100, 170
m
respectively, illustrating that fluctuations at larger wavelengths
are dominated by more distant sources.
When the brightest sources are removed the ratio
of nearby to moderate-redshift
contribution becomes equal to 1.7, 1 and 0.74
at 60, 100, 170 ![]() m. In this case, at 100
m. In this case, at 100 ![]() m
the contribution to the fluctuations
of nearby and moderate-redshift sources
is the same, becoming lower at higher wavelength.
At 60
m
the contribution to the fluctuations
of nearby and moderate-redshift sources
is the same, becoming lower at higher wavelength.
At 60 ![]() m, the fluctuations are still dominated by
the nearby objects.
m, the fluctuations are still dominated by
the nearby objects.
For the three wavelengths, the CIB is mainly due to sources
at redshift around 1. A detailed analysis of
the CIB fluctuations at 100 and 170 ![]() m (which is beyond the scope of this paper)
will give information on the distribution of sources at
m (which is beyond the scope of this paper)
will give information on the distribution of sources at ![]() making
the bulk of the CIB.
This is particularly true at 170
making
the bulk of the CIB.
This is particularly true at 170 ![]() m
where sources with flux lower than 4
m
where sources with flux lower than 4
![]() mJy
can be removed (Dole et al. 2001), leading fluctuations highly
dominated by the moderate-z sources.
mJy
can be removed (Dole et al. 2001), leading fluctuations highly
dominated by the moderate-z sources.
We can compute the ratio of CIB fluctuations to intensity
(
![]() )
at 100
)
at 100 ![]() m and compare it with the previous determination at 170
m and compare it with the previous determination at 170 ![]() m.
To compute R100 and R170, we use:
m.
To compute R100 and R170, we use:
This work suggests that the high latitude IRAS maps, in the lowest cirrus regions,
cannot be used as a tracer of the interstellar extinction structure as proposed
by (Schlegel et al. 1998). In fact it should be noted that it is only above
an intensity of order of 10 MJy/sr at 100 ![]() m that the CIB fluctuations
are lower than the cirrus contribution at the smallest scales (
m that the CIB fluctuations
are lower than the cirrus contribution at the smallest scales (
![]() arcmin-1).
arcmin-1).
Present and future CMB observations, above 100 GHz, with high sensitivity bolometers
need to remove foreground contributions (cirrus and CIB fluctuations). The CIB spectrum
being significantly "colder'' than the cirrus spectrum (
![]() ;
;
![]() ), the relative contribution
of the CIB will increase with wavelength. It is thus expected that at 1 mm
the range in l space dominated by the CIB will be much more extended than sees at
100
), the relative contribution
of the CIB will increase with wavelength. It is thus expected that at 1 mm
the range in l space dominated by the CIB will be much more extended than sees at
100 ![]() m. This question will be dealt in a forthcoming paper.
m. This question will be dealt in a forthcoming paper.
Acknowledgements
The Fond FCAR du Québec provided funds to support this research project.
The power spectrum of an image f(x,y) of Fourier Transform
![]() is computed from the
amplitude
A(kx, ky) defined as
is computed from the
amplitude
A(kx, ky) defined as
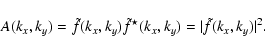 |
(A.1) |
makes an "infinite pavement'' with the image prior to compute the Fourier Transform. As the ISSA images are not periodic objects, this operation produces discontinuities where the left (top) meets the right (bottom) side of the image. These horizontal and vertical discontinuities are responsible for the cross seen in the amplitude image. The main problem with this cross is that it increases artificially the power when the average over k is done. Furthermore, the power increase is not constant as a function of k which modify the slope of the spectrum as well as the normalization.
The usual method to get rid of this effect is to apodize the image so that
the left (top) and right (bottom) sides of the image have a similar flux level.
Another method which do not modify the image but acts on the amplitude image itself is to
compute P(k) by taking the median value at constant k. For ![]() 85% of
the ISSA maps we have inspected, these two methods give very
similar results (see Fig. A.1). But when the cross is very strong,
the power at small scales is still overestimated by the "median'' method.
Furthermore, at small k values, there are less points to average and
a large fraction of them are affected by the cross effect;
at these frequencies, the median value may not be significant.
For all these reasons, we have adopted the "apodization'' method.
85% of
the ISSA maps we have inspected, these two methods give very
similar results (see Fig. A.1). But when the cross is very strong,
the power at small scales is still overestimated by the "median'' method.
Furthermore, at small k values, there are less points to average and
a large fraction of them are affected by the cross effect;
at these frequencies, the median value may not be significant.
For all these reasons, we have adopted the "apodization'' method.
![\begin{figure}
\par\includegraphics[angle=90,width=13.3cm,clip]{H3453F10.ps}\\ [...
...}\\ [4mm]
\includegraphics[angle=90,width=13.3cm,clip]{H3453F12.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg68.gif) |
Figure A.3: See Fig. A.2. |
![\begin{figure}
\par\includegraphics[angle=90,width=13.3cm,clip]{H3453F13.ps}\\ [...
...}\\ [4mm]
\includegraphics[angle=90,width=13.3cm,clip]{H3453F15.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg69.gif) |
Figure A.4: See Fig. A.2. |
![\begin{figure}
\par\includegraphics[angle=90,width=13.3cm,clip]{H3453F16.ps}\\ [...
...}\\ [4mm]
\includegraphics[angle=90,width=13.3cm,clip]{H3453F18.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg70.gif) |
Figure A.5: See Fig. A.2. |
![\begin{figure}
\par\includegraphics[angle=90,width=13.3cm,clip]{H3453F22.ps}\\ [...
...}\\ [4mm]
\includegraphics[angle=90,width=13.3cm,clip]{H3453F24.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg72.gif) |
Figure A.7: See Fig. A.6. |
![\begin{figure}
\par\includegraphics[angle=90,width=13.3cm,clip]{H3453F25.ps}\\ [...
...}\\ [4mm]
\includegraphics[angle=90,width=13.3cm,clip]{H3453F27.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg73.gif) |
Figure A.8: See Fig. A.6. |
![\begin{figure}
\par\includegraphics[angle=90,width=13.3cm,clip]{H3453F28.ps}\\ [...
...}\\ [4mm]
\includegraphics[angle=90,width=13.3cm,clip]{H3453F30.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg74.gif) |
Figure A.9: See Fig. A.6. |