1 - Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400005, India
2 - Department of Physics, University of Mumbai, Mumbai 400098, India

Abstract
Primary inversions of accurately measured solar oscillation frequencies coupled with the equations of thermal equilibrium and other input physics, enable us to infer the temperature and hydrogen abundance profiles inside the Sun. These profiles also help in setting constraints on the input physics as well as on heavy element abundance in the solar core. Using different treatments of plasma screening for nuclear reaction rates, limits on the cross-section of proton-proton nuclear reaction as a function of heavy element abundance in the solar core are obtained and an upper limit on heavy element abundance in the solar core is also derived from these results.

The precisely measured frequencies of solar oscillations have been used to probe the solar interior. The primary inversions of these observed frequencies yield the sound speed and density profiles inside the Sun. In order to infer the temperature and chemical composition profiles, we also need to know the input physics such as opacities, equation of state and nuclear energy generation rates (Gough & Kosovichev 1988; Kosovichev 1996; Shibahashi & Takata 1996; Takata & Shibahashi 1998; Antia & Chitre 1998). In all these works the heavy element abundance profile is assumed to be known; attempts to determine heavy element abundance profile from helioseismic data have not been particularly successful (Antia & Chitre 1999; Takata & Shibahashi 2001) as the resulting inverse problem becomes extremely ill-conditioned. Fukugita & Hata (1998) have obtained limits on heavy element abundance in the solar core using observed solar neutrino fluxes. It would be interesting to enquire if such limits can be independently obtained from helioseismic data.

In general, the computed luminosity in a seismically computed solar model is not expected to match the observed solar luminosity. By applying the observed luminosity constraint it is possible to constrain the input physics, particularly, the cross-section of proton-proton (pp) nuclear reaction. Antia & Chitre (1998) estimated this cross-section to be $S_{11}= (4.15\pm0.25)\times10^{-25}$ MeV barns. Similar values have been obtained by comparing the computed solar models with helioseismic data (Degl'Innocenti, Fiorentini & Ricci 1998; Schlattl, Bonanno & Paterno 1999). The main source of error in these estimates is the uncertainty in the Z profile and, therefore, Antia & Chitre (1999) attempted to find the pp reaction rate as a function of Z in the solar core. In all these works the plasma screening of nuclear reaction cross-sections was calculated using intermediate screening formulation of Graboske et al. (1973). The treatment of screening in stellar nuclear reaction rates is not yet adequately understood (Dzitko et al. 1995; Gruzinov & Bahcall 1998). Wilets et al. (2000) have done a sophisticated treatment of plasma screening and compared their results with earlier prescriptions. Their results indicate that for the solar core the intermediate screening treatment due to Mitler (1977) is better than that due to Graboske et al. (1973). It would thus be interesting to study the effect of different treatment of plasma screening on the helioseismically estimated pp reaction cross-section.

Antia & Chitre (1999) included the effect of heavy element abundance Z only on the opacity of the solar material. If we make the reasonable assumption that the abundances of C, N, O also increase with Z, then the CNO cycle will become more effective in contributing to the nuclear energy generation in the solar core. At normally accepted values of Z it is estimated that less than 2% of energy generated in the central region is produced by the CNO cycle (Bahcall et al. 2001). But if Z value is increased, this proportion will clearly increase and consequently, the pp reaction rate needs to be reduced to maintain the observed solar luminosity. In this work we demonstrate that this effect can be exploited to set an upper limit on Z in the solar core.

2 The technique

With the use of accurately measured p-mode frequencies from the first year of operation of MDI instrument (Rhodes et al. 1997) we infer the sound speed and density profiles adopting a Regularised Least Squares technique (Antia 1996). The determination of thermal and chemical composition profiles, however, necessitates the use of equations of thermal equilibrium (Antia & Chitre 1998) with the supplementary input of the equation of state, opacities and nuclear energy generation rates, provided we have a knowledge of the heavy element abundance profile inside the Sun. There is no guarantee for the resultant seismic model to yield the observed solar luminosity, $L_\odot=3.846\times 10^{33}$ ergs s^-1, unless we adjust the nuclear reaction rates slightly. This turns out to provide a valuable tool for constraining the nuclear reaction rates, in particular, the cross-section of the pp nuclear reaction which has not been measured in the laboratory because of the slow weak interaction rate. The pp reaction cross-section has only been calculated theoretically and it would be instructive to test the validity of calculated results using the helioseismic constraints.

There is an uncertainty of about 2% in evaluating the luminosity of seismic models because of possible errors in primary inversions (including an estimate of systematic errors), solar radius, equation of state, opacity, nuclear reaction rates for other reactions. Possible error due to uncertainties in treatment of plasma screening of nuclear reactions is not included in this error estimate. This can be estimated by using different treatments of plasma screening. The uncertainty arising from errors in Z profiles is, however, much larger (cf., Antia & Chitre 1998). We, therefore, estimate for each Z profile, the range of cross-section of pp nuclear reaction, which reproduces the luminosity to within 2% of the observed value. The computed luminosity in the seismic models will, of course, depend on the metallicity, $Z_{\rm c}$ in the solar core; we therefore, attempt to delineate the region in the $S_{11}{-}Z_{\rm c}$ plane which gives the correct solar luminosity. In order to obtain the thermal structure we adopt the OPAL opacities (Iglesias & Rogers 1996), the OPAL equation of state (Rogers et al. 1996) and the nuclear reaction rates from Adelberger et al. (1998). The plasma screening effects are calculated using either weak screening (Salpeter 1954) or intermediate screening (Mitler 1977). The effect of variation of $Z_{\rm c}$ on nuclear energy generation rate is incorporated in the computations by assuming the abundances of all heavy elements to increase in the same ratio for obtaining the abundances of C, N, O.

3 Results

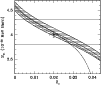$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{Eh053_f1.eps}}\end{figure}$

Figure 1: The region in $Z_{\rm c}{-}S_{11}$ plane that is consistent with helioseismic data is marked by horizontal shading. The continuous line defines the values obtained using intermediate plasma screening, where the seismic model matches the observed solar luminosity. The point with error bars shows the current best estimates for $Z_{\rm c}$ and S₁₁. The short-dashed line shows the central value obtained using weak screening, while the long-dashed line shows the central value obtained using intermediate screening and also including the effect of Z on nuclear energy generation. The two horizontal lines mark the limits of theoretically calculated values of S₁₁.

Open with DEXTER

With the help of the inverted profiles for sound speed and density, along with a homogeneous Z profile, covering a wide range of Zvalues, we first calculate a seismic model by employing the equations of thermal equilibrium. For each central value of Z we estimate the range of cross-section of pp nuclear reaction, which reproduces the luminosity to within 2% of the observed value. The numerical results are shown in Fig. 1, which delineates the region in $Z_{\rm c}{-}S_{11}$ plane that is consistent with helioseismic and luminosity constraints. This figure shows the results obtained using intermediate screening (Mitler 1977). For comparison the central value obtained using weak screening is also shown in this figure. In order to compare these results with the earlier work of Antia & Chitre (1999), in these calculations the effect of Z on nuclear energy generation rate is not included. Thus the difference is mainly due to treatment of plasma screening. It is clear that with these treatments of screening the current estimate of pp reaction cross-section (Adelberger et al. 1998) is consistent with helioseismic estimate within the expected error bars, though the best value is about 1.5% higher than the theoretical estimates. Further, there is not much difference between results obtained using the two different treatments of plasma screening. In general, the estimated value of S₁₁ using weak screening is smaller than that obtained using intermediate screening by about 1%.

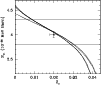$\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{Eh053_f2.eps}}\end{figure}$

Figure 2: The seismically estimated value of S₁₁ as a function of $Z_{\rm c}$ the heavy element abundance at the centre for different Z profiles. The solid line shows the value obtained with homogeneous Z profile and is the same as the long-dashed line in Fig. 1. The short-dashed and long-dashed lines show the results obtained using Z profile given by Eqs. (1) and (2), respectively. The dotted line shows the results using Z profile of Eq. (1), but with the reaction rate of $^{14}{\rm N}+p$ reaction reduced by 40%. The point with error bars shows the current best estimates for $Z_{\rm c}$ and S₁₁.

Open with DEXTER

With a view to study the effect of Z on energy generation through CNO cycle, we repeat the calculations by varying the abundances of all heavy elements in the same proportion as Z in the nuclear reaction network. These results are shown by long-dashed line in Fig. 1. We do not expect much difference at low values of $Z_{\rm c}$ , since CNO cycle produces a tiny fraction of energy in the Sun. But with augmented $Z_{\rm c}$ , this fraction becomes larger due to increased Z as well as due to the resulting increase in the temperature, since the CNO reactions are more sensitive to temperature. As a consequence, in order to maintain the solar luminosity constraint we need to reduce S₁₁, with the result that around $Z_{\rm c}= 0.035$ the estimated value of S₁₁ decreases very sharply. This is because a significant fraction of the luminosity is then accounted for by the CNO reactions with seismically inferred temperature and composition profiles. For $Z_{\rm c}= 0.035$ , CNO cycle accounts for about 8% of solar luminosity and this fraction, in fact, increases rapidly with $Z_{\rm c}$ . Thus, we can consider this as the upper limit on $Z_{\rm c}$ , which is somewhat larger than that inferred by Fukugita & Hata (1998). A lower limit on $Z_{\rm c}$ can also be obtained from this figure if we accept the range of theoretically computed values of S₁₁(Bahcall & Pinsonneault 1995; Turck-Chiéze & Lopes 1993) as representing the acceptable range of S₁₁. Assuming an upper limit of $4.3\times10^{-25}$ MeV barns for S₁₁ we get a lower limit of $Z_{\rm c}=0.006$ , which is again comparable to the lower limit obtained by Fukugita & Hata (1998). If we adopt a lower limit of $3.8\times10^{-25}$ MeV barns for S₁₁, the resulting upper limit on $Z_{\rm c}=0.032$ . The exact limits on $Z_{\rm c}$ will of course, depend on the assumed limits on S₁₁, but because of the sharp fall in the long-dashed curve in Fig. 1, the upper limit is not particularly sensitive to the assumed lower limit on S₁₁and any value $Z_{\rm c}>0.035$ would certainly be difficult to reconcile with seismic models.

In the foregoing calculations we have adopted a homogeneous Z profile, which is perhaps not too realistic. Since most of the energy generation occurs in the solar core ( $r\le0.25~R_\odot$ ) our results are unaffected by the Z profile in the outer radiative region. To demonstrate this we also use the following Z profiles:

$\begin{displaymath}% Z=\cases{Z_{\rm c}& if $r<0.25~R_\odot$ ,\cr Z_{\rm c}+{(Z_{\rm s}-Z_{\rm c})\over 0.463}(r/R_\odot-0.25)& otherwise,\cr} \end{displaymath}$

(1)

Apart from uncertainties in Z profile the nuclear reaction rate for the CNO cycle reactions are also rather uncertain and these may affect the inferred upper limit. To estimate this uncertainty we repeat the calculations using the profile given by Eq. (1) for Z, but with the reaction rate of the $^{14}{\rm N}+p$ reaction reduced by 40%, which is the estimated uncertainty in this reaction rate (Adelberger et al. 1998). These results are also shown by the dotted line in Fig. 2. From the figure it is clear the uncertainties in CNO reaction rates will not particularly affect the upper limit on $Z_{\rm c}$ in a significant way.

Table 1: Neutrino fluxes in a seismic model using the Z profile from model N0 of Brun et al. (2002).
Source Flux (cm^-2 s^-1)

pp $(6.05\pm0.06)\times10^{10}$

pep $(1.42\pm0.02)\times10^8$

hep $2.09\times10^3$

⁷Be $(4.76\pm0.48)\times10^9$

⁸B $(4.83\pm0.88)\times10^6$

¹³N $(5.27\pm0.79)\times10^8$

¹⁵O $(4.48\pm0.80)\times10^8$

¹⁷F $(2.76\pm0.30)\times10^6$

Total Cl $7.27\pm1.14$ SNU

Total Ga $127.8\pm7.2$ SNU

**Table 1:** Neutrino fluxes in a seismic model using the Z profile from model N0 of Brun et al. (2002).
Source	Flux (cm^-2 s^-1)
pp	$(6.05\pm0.06)\times10^{10}$
pep	$(1.42\pm0.02)\times10^8$
hep	$2.09\times10^3$
⁷Be	$(4.76\pm0.48)\times10^9$
⁸B	$(4.83\pm0.88)\times10^6$
¹³N	$(5.27\pm0.79)\times10^8$
¹⁵O	$(4.48\pm0.80)\times10^8$
¹⁷F	$(2.76\pm0.30)\times10^6$
Total Cl	$7.27\pm1.14$ SNU
Total Ga	$127.8\pm7.2$ SNU

Table 1 lists the neutrino fluxes in a seismic model obtained using the Z-profile of a model including tachocline mixing of Brun et al. (2002), with the use of intermediate screening, for calculating the nuclear energy generation rates. In this case we need to increase S₁₁ by 1.6% over the currently accepted value. As noted by Brun et al. (2002), an increase in S₁₁ leads to a better agreement between solar models and the seismically inferred sound speed and density profiles. Thus a small increase in S₁₁may still be required, but it is within the errors in helioseismic estimates and those in theoretically computed values. These neutrino fluxes are generally larger than those in seismic model of Antia & Chitre (1998), presumably because of reduction in S₁₁. The ⁸B neutrino flux in the seismic model is consistent with the current estimate of $(5.09\pm0.65)\times10^6$ cm^-2 s^-1 using the neutral current channel of Sudbury Neutrino Observatory (SNO) (Ahmad et al. 2002).

4 Discussion and conclusions

With the help of inverted sound speed and density profiles, it is possible to infer the T,X profiles in the solar interior, provided the Z profile and the input physics are known. The resulting seismic models have the correct solar luminosity, provided the heavy element abundance $Z_{\rm c}$ in the solar core and the cross-section for pp nuclear reaction are within the shaded region shown in Fig. 1. It appears that the currently accepted values of $Z_{\rm c}$ or S₁₁ need to be increased marginally to make them consistent with helioseismic constraints. The required increase is within the error estimates. The higher estimates for S₁₁ obtained earlier were due to differences in treatment of plasma screening. With the use of weak (Salpeter 1954) or intermediate screening due to Mitler (1977) the theoretically estimated value of S₁₁ is in reasonable agreement with seismically estimated value. With a Z profile in a standard solar model N0 of Brun et al. (2002), the seismically estimated value of S₁₁ is $4.07\times10^{-25}$ MeV barns with the use of intermediate screening and $4.02\times10^{-25}$ MeV barns for weak screening used while calculating the nuclear energy generation rate.

If the value of heavy element abundance in the solar core, $Z_{\rm c}$ , is increased beyond 0.035 the CNO cycle generates a good fraction of solar luminosity and it is not possible to get any consistent seismic model unless S₁₁ is decreased substantially below the accepted value. This puts a clear upper limit on the heavy element abundance in the solar core, which is comparable to that independently obtained by Fukugita & Hata (1998). This upper limit is not very sensitive to the Z profile or to the uncertainties in the CNO reaction rates. Even if the additional heavy elements in solar core do not include CNO, the effect of opacity alone will also put an upper limit on $Z_{\rm c}$ , but in that case the limit will depend on the assumed lower limit on S₁₁. For currently accepted theoretical limits, the upper limit in this case turns out to be around 0.035.

Note that the seismic model satisfies the normal stellar structure equations, though the inferred X profile may not match that given by an evolutionary solar model. Further, since the seismic model is confined to the radiative interior, it will not be possible to match it to an acceptable convection zone model, unless the heavy element abundance at the top of the radiative region is close to the known surface value. Thus a relatively high value of Z in the solar core can be realised only if the Z profile has a significant gradient in the radiative region. From experiments with varying Z or S₁₁ in evolutionary solar models also it is known that an increase in Z can be compensated for by a reduction in S₁₁ to match the seismically inferred sound speed and density profiles (Brun et al. 2002). Thus it is quite possible that a comparable upper limit on $Z_{\rm c}$ may be obtained from these models if we restrict the range of S₁₁, provided the initial Z profile at the zero age main sequence stage is not homogeneous.

Helioseismic limit on heavy element abundance

1 Introduction

2 The technique

3 Results

4 Discussion and conclusions

References