In this section we discuss the relative importance of 2p-, 2s- and 3s-photoionization, then analyze in detail the first-step decays of the states produced by photoionization. The following decay steps are analyzed in the configuration-average approximation. Finally, we estimate relative intensities of the lines emitted at various incident photon energies.
Calculated L-shell photoionization cross sections are presented in Fig. 1.
Relative probabilities of the monopole shake up, shake off and double shake processes are listed in Table 1. It should be noted that the monopole SU processes probabilities calculated using the SPT and R-matrix approximations differ, the latter quantities being somewhat smaller. In the following discussion, we choose to use the SPT results for the SU probabilities since they are obtained without any parameterization.
The relative probabilities of 2p/cSU are shown in Fig. 2.
The partial widths of radiationless decays for relevant aluminium inner-shell hole states are presented in Tables 2 to 4.
Table 5 represents the relative intensities of emission lines produced at various incident photon energies
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2515f2.eps}\end{figure}](/articles/aa/full/2002/39/aa2515/Timg6.gif) |
Figure 2:
Relative probability of conjugate shake up processes (3s
|
| Initial vacancy | Process | Relative probability* |
| 2s | 2s/SU 3s
|
0.0752 |
| 2s/SU 3s
|
0.0067 | |
| 2s/SO 3s
|
0.0190 | |
| 2s/SU 3p
|
0.1216 | |
| 2s/SU 3p
|
0.0088 | |
| 2s/SO 3p
|
0.0164 | |
| 2s/dS 3s3s
|
0.0021 | |
| 2s/dS 3s3p
|
0.0116 | |
| 2p | 2p/SU 3s
|
0.0817 |
| 2p/SU 3s
|
0.0073 | |
| 2p/SO 3s
|
0.0161 | |
| 2p/SU 3p
|
0.1194 | |
| 2p/SU 3p
|
0.0086 | |
| 2p/SO 3p
|
0.0162 | |
| 2p/dS 3s3s
|
0.0025 | |
| 2p/dS 3s3p
|
0.0126 |
Consider the L-shell photoionization cross sections presented in Fig. 1. Lines and symbols in Fig. 1 represent the cross sections, vertical bars show the positions of the thresholds for SU, cSU and SO processes upon 2s- and 2p- ionization.
Configuration-average one-electron results are represented with lines, while the R-matrix results are shown with symbols. Note that the results obtained in those two approximations compare well.
The cross section of 2p-photoionization (dash line and squares) dominates the
2s one (solid line and circles) over a wide energy range. It is about ten
times greater than 2s at the 2s threshold, however, descending more rapidly
than the 2s cross section, it is about twice the 2s at X=3.2 (![]() 400 eV) and becomes equal to 2s at X=7 (
400 eV) and becomes equal to 2s at X=7 (![]() 900 eV).
900 eV).
Also shown in Fig. 1 is the cross section of 3s-photoionization calculated using the one-electron approximation (dash-dot line). Single 3s-photoionization is responsible for the production of the Al II emission. One can see that 3s-photoionization is not negligible in the energy range of interest.
Relative probabilities of the monopole shake processes (SU, SO and dS) upon 2s and 2p sudden vacancy creation are presented in Table 1. One can see that the effect of the initial inner-shell vacancy is small, which is what one would have expected (Kochur et al. 2002). The SU processes dominate both for the shakes from 3s and from 3p subshells having relative probability of about 8% and 13%, respectively. The probabilities of the SO processes are smaller, 1.6 to 2%.
For monopole double shake processes the approximation used does not allow
one to distinguish accurately between up and off processes, therefore the
values presented in Table 1 combine all possible contributions, i.e.
SU+SU, SU+SO, SO+SO. However, rough estimates show that the relative
importance of those contributions are the following: (SU+SU):(SU+SO):(SO+SO)
![]() 0.6:0.2:0.2.
0.6:0.2:0.2.
The R-matrix relative probability of conjugate shake up processes upon 2p
photoionization is shown in Fig. 2 as a function of incident photon energy.
The 3p
![]() 3d excitation dominates. The whole cSU effect is
extremely dependent on the 3d excited orbital definition since the CI
between the n= 3 states is significant. In contrast to the monopole shake
processes whose probability comparatively rapidly (for outermost shells)
reach a constant limit, the relative probability of the cSU processes
decreases with energy. However, it is evident from Fig. 2 that over quite a wide energy range the cSU excitations are important.
3d excitation dominates. The whole cSU effect is
extremely dependent on the 3d excited orbital definition since the CI
between the n= 3 states is significant. In contrast to the monopole shake
processes whose probability comparatively rapidly (for outermost shells)
reach a constant limit, the relative probability of the cSU processes
decreases with energy. However, it is evident from Fig. 2 that over quite a wide energy range the cSU excitations are important.
Since both monopole and conjugate shake probabilities in Table 1 and
Fig. 2 are relative to their respective main processes, one can easily
obtain the cross sections for the shake processes by multiplying
the relative probabilities by the respective main processes cross
sections. For example, the cross section for the 2p/SU 3s
![]() 4s process
at X=1.5 is P(2p/SU 3s
4s process
at X=1.5 is P(2p/SU 3s
![]() 4s)
4s)![]()
![]() (1.5) =
0.817
(1.5) =
0.817![]() 1.9 = 1.55 Mb.
1.9 = 1.55 Mb.
It is evident from Fig. 1 that within the energy range of interest, 3s-photoionization is not negligible, making up about 2% of L-ionization. Photoionization of the 3s-subshell directly produces the line emitting states Al II 3s3p1,3P. This is the only mechanism of the Al II emission in this incident photon energy range.
Single 2p-ionization produces a single inner-shell hole Al 2p-1 state which in the one-configuration approximation can decay non-radiatively via two Auger transitions, i.e. L23M1M1 and L23M1M23 giving rise to the states 2p63p 2P and 2p63s 2S. The processes of additional excitations during the Auger transitions may lead to formation of additional decay channels leading to the states 2p63d, 2p64s, 2p64p (see Table 2). The ionic 2p63s ground state can decay no further, while all other states are line-emitting.
| Initial states | Final states1 | |||||
| Term | E2 | 3s | 3p | 3d | 4s | 4p |
| 3S | 4.291 | 0.84 | 0.043 | 0.003 | 0.006 | 0.001 |
| 3D | 4.304 | 0.0505 | 0.0609 | 0.0049 | 0.0019 | 0.0015 |
| 1D | 4.384 | 0.134 | 0.194 | 0.0075 | 0.0042 | 0.0018 |
| 1P | 4.388 | 0.0 | 0.0326 | 0.0004 | 0.0 | 0.0003 |
| 3P | 4.390 | 0.0 | 0.264 | 0.013 | 0.0 | 0.011 |
| 1S | 4.706 | 51.08 | 2.65 | 0.27 | 0.36 | 0.12 |
Our calculation showed that the population of final states during
2p-photoionization is proportional to their statistical weights.
Then using the partial widths
![]() of Table 2 it is
easy to calculate the branching ratios for the decays from initial
state i= 2p53s23p into each of the final states f= 3s, 3p, 3d, 4s, 4p:
of Table 2 it is
easy to calculate the branching ratios for the decays from initial
state i= 2p53s23p into each of the final states f= 3s, 3p, 3d, 4s, 4p:
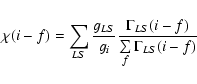
The decay process for single 2p-vacancy state can be illustrated with the following decay scheme:
| 2p53s23p | (1) |
![]() (0.607)2p63p
(0.607)2p63p
![]() 2p63s
2p63s
![]() (0.033)2p63d
(0.033)2p63d
![]() 2p63p
2p63p
![]() 2p63s
2p63s
![]() (0.009)2p64s
(0.009)2p64s
![]() 2p63p
2p63p
![]() 2p63s
2p63s
![]() (0.016)2p64p
(0.016)2p64p
![]() (0.420)2p63s
(0.420)2p63s
![]() (0.580)2p63d
(0.580)2p63d
![]() 2p63p
2p63p
![]() 2p63s.
2p63s.
Here the branching ratios (given in parentheses) are calculated for the first decay step using the data of Table 2, and for the following decays, in a configuration-average one-electron approximation. Radiationless transitions are shown with arrows while radiative transitions are shown with double arrows. These denotations will be preserved in the following discussion.
One can see from the scheme (1) that the decay of the states produced by single 2p-photoionization gives rise to five Al III lines of which the strongest is Al III 3p-3s. In about 60% of cases when 2p photoionization happens this line will be emitted.
The SO processes upon 2p-photoionization do not lead to line emission. Indeed, if either a 3s or 3p electron is shaken off, then the consequent L23MM Auger transition will end up in the ground state of Al IV.
The channel for the 2p/SU 3s
![]() 4s process is opened at 1.01 Ryd
above the 2p threshold. Its relative probability reaches its SPT limit of
0.0817 at about twice this energy above the SU threshold, i.e. at
about X=0.85. The shake-up state thus produced decays via the
following scheme:
4s process is opened at 1.01 Ryd
above the 2p threshold. Its relative probability reaches its SPT limit of
0.0817 at about twice this energy above the SU threshold, i.e. at
about X=0.85. The shake-up state thus produced decays via the
following scheme:
| 2p53s3p4s | (2) |
![]() (0.002)2p63p
(0.002)2p63p
![]() 2p63s
2p63s
![]() (0.129)2p63s.
(0.129)2p63s.
The channel for the 2p/SU 3p
![]() 4p is opened at 0.695 Ryd above
the 2p-threshold, the probability of the process reaching its SPT limit of
0.119 at about X= 0.78. The state produced by the 2p/SU 3p
4p is opened at 0.695 Ryd above
the 2p-threshold, the probability of the process reaching its SPT limit of
0.119 at about X= 0.78. The state produced by the 2p/SU 3p
![]() 4p
process decays via the following scheme:
4p
process decays via the following scheme:
| 2p53s24p | (3) |
![]() (0.032) 2p64p
(0.032) 2p64p
![]() (0.420)2p63s
(0.420)2p63s
![]() (0.580)2p63d
(0.580)2p63d
![]() 2p63p
2p63p
![]() 2p63s.
2p63s.
One can see from Fig. 2 that the conjugate shake-up process occurs with significant probability upon 2p-photoionization. The decays of the states thus produced are shown in the following schemes.
After 2p/cSU 3p
![]() 3d:
3d:
| 2p53s23d | (4) |
![]() (0.020)2p63d
(0.020)2p63d
![]() 2p63p
2p63p
![]() 2p63s.
2p63s.
After 2p/cSU 3s
![]() 3p:
3p:
| 2p53s3p2 | (5) |
![]() (0.487)2p63p
(0.487)2p63p
![]() 2p63s.
2p63s.
As discussed above, monopole double shake processes upon 2p-photoionization are rather weak, 1.5% in total upon 2p ionization, 2p/dS
3s3p dominating (1.3%). Analysis of the decay processes showed that the
states produced by SU+SU dS do not give any lines different from those
produced by single photoionization process, and the states produced by the
SU+SO decay non-radiatively into ionic ground states giving no emission.
The SO+SO dS, however weak, produce an Al IV 2p53s
![]() 2p6doublet. The thresholds for the 2p/dS processes lie at about X=1.
2p6doublet. The thresholds for the 2p/dS processes lie at about X=1.
Table 3 lists the widths of radiationless decays of the single 2s-vacancy state produced by photoionization. Single 2s vacancy in aluminium decays through two Coster-Kronig (L1L23M1, L1L23M23) and two Auger (L1M1M1, L1M1M23) transitions. Among the states produced at the first decay step only the state 2p63p reached by the L1M1M1 Auger transition is obviously line emitting (Al III 3p-3s). The state 2p53s2 decays further non-radiatively into 2p6 and gives no emission, and 2p63s is the ionic ground state.
| Initial state1 | |||||
| Transition | Final state | 1P |
3P |
||
| L1L23M1 | 2p53s3p | 2S | upper | 1.0 | 15.8 |
| 2P | 18.0 | 40.9 | |||
| 2D | 17.0 | 37.3 | |||
| 2S | lower | 51.2 | 12.6 | ||
| 2P | 73.6 | 51.8 | |||
| 2D | 118.3 | 95.8 | |||
| 4P | 0.0 | 2.7 | |||
| 4D | 0.0 | 6.6 | |||
| 4S | 0.0 | 1.3 | |||
| L1L23M23 | 2p53s2 | 2Po | 33.3 | 41.5 | |
| L1M1M1 | 2p63p | 2Po | 2.4 | 1.3 | |
| L1M1M23 | 2p63s | 2S | 0.6 | 4.2 | |
| Level width in a.u. | 0.0315 | 0.0312 | |||
| Final states | |||||||||||
| 2p6 | 2p53s | 2p53p | |||||||||
| Initial state | E1 | 3P |
1P |
3S | 3D | 1D | 3P | 1P | 1S | ||
| 2s2p63s2 | 2S | 6.57 | 3.0 | 32.0 | 226.0 | 0.6 | 3.6 | 0.2 | 0.0 | 0.0 | 0.1 |
| 2s2p63s3p | 4Po | 6.96 | 0.0 | 47.2 | 0.0 | 19.3 | 109.5 | 0.0 | 80.6 | 0.0 | 0.0 |
| 2Po | 7.07 | 1.9 | 21.0 | 21.0 | 9.78 | 47.1 | 14.2 | 29.4 | 11.3 | 2.6 | |
| 2Po | 7.36 | 5.16 | 11.0 | 8.4 | 0.82 | 4.78 | 88.0 | 2.02 | 46.1 | 24.2 | |
The state 2p53s3p is produced by the Coster-Kronig L1L23M1 transition; its quadruplet terms and both 2P terms have a zero radiationless decay width in the LS-coupling approximation. One might then expect to have emission from those states. However, the presence of the 2p-vacancy leads to noticeable spin-orbital interaction, which makes radiationless decays of those states possible. Our intermediate-coupling calculation using Badnell's code (Badnell 1985) showed that respective decays dominate radiative ones.
Having found that the singlet and triplet terms are populated proportionally to their statistical weights and using the widths listed in Table 3 we find that the decay process for the single 2s hole state can be summarized in the following way:
| 2s2p63s23p | (6) |
![]() (0.125)2p53s2
(0.125)2p53s2
![]() 2p6
2p6
![]() (0.010)2p63s
(0.010)2p63s
![]() (0.005)2p63p
(0.005)2p63p
![]() 2p63s.
2p63s.
| Transition | Incident photon energy in units of X | ||||||
| 0.60 | 0.66 | 0.98 | 1.04 | 1.40 | 2.00 | 4.00 | |
| Al II 3s3p-3s2 | 0.112 | 0.099 | 0.058 | 0.052 | 0.034 | 0.019 | 0.006 |
| Al III 3p-3s | 2.504 | 3.195 | 2.909 | 1.642 | 0.773 | 0.100 | |
| Al III 3d-3p | 0.161 | 0.190 | 0.173 | 0.098 | 0.043 | 0.007 | |
| Al III 4s-3p | 0.034 | 0.329 | 0.300 | 0.176 | 0.152 | 0.012 | |
| Al III 4p-3s | 0.254 | 0.280 | 0.255 | 0.150 | 0.065 | 0.010 | |
| Al III 4p-3d | 0.035 | 0.047 | 0.043 | 0.025 | 0.011 | 0.002 | |
| Al IV 2p53s-2p6 | 0.046 | 0.023 | 0.005 | ||||
| Al IV 2p53p-2p53s | 0.006 | 0.004 | 0.001 | ||||
| L-photoionization cross section | 3.804 | 4.093 | 4.048 | 2.572 | 1.203 | 0.226 | |
One can see that single 2s-photoionization produces a single Al III line with a rather weak probability of 0.005.
The states produced by 2s/SU, 2s/cSU, and 2s/dS decay via consecutive radiationless transition into 2p6 giving no emission.
The partial widths for the decay of the states produced by the 2s/SO processes, i.e. 2s2p63s2 and 2s2p63s3p, are listed in Table 4. Note that from 2s2p63s2, reaching 2p53p is possible due to CI, and those transitions correspond to additional excitations during Coster-Kronig decay.
The decay of the 2s/SO states give rise to a set of states emitting Al IV lines according to the following decay schemes:
After 2s/SO 3p
![]() p:
p:
| 2s2p63s2 | (7) |
![]() (0.012) 2p6
(0.012) 2p6
![]() (0.017) 2p53p
(0.017) 2p53p
![]() 2p53s
2p53s
![]() 2p6.
2p6.
After 2s/SO 3s
![]() s:
s:
| 2s2p63s3p | (8) |
![]() (0.178) 2p53s
(0.178) 2p53s
![]() 2p6
2p6
![]() (0.015) 2p6.
(0.015) 2p6.
One can see from (7, 8) that the 2s/SO processes lead to emission of additional lines, i.e. Al IV 2p53p 1,3SDP-2p63s 1,3P. Of these, the most intense ones should be the lines originating from 3D and 1D terms (see Table 4)
To be able to compare the probabilities of emission for various lines, let
us define the partial cross section for L-photoionization ending in the
emission of a specific line in the following manner:
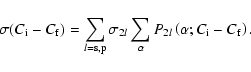 |
(9) |
Here ![]() and
and ![]() are the initial and final configuration of a
line-emitting transition,
are the initial and final configuration of a
line-emitting transition,
![]() is either the 2s- or
2p-photoionization cross section,
is either the 2s- or
2p-photoionization cross section,
![]() is the relative (to respective single ionization process) probability of emitting
the
is the relative (to respective single ionization process) probability of emitting
the
![]() line via the process
line via the process ![]() ,
,
![]() is one of
the processes leading to line emission, i.e. single
2p/2s-ionization, 2p/SU 3s
is one of
the processes leading to line emission, i.e. single
2p/2s-ionization, 2p/SU 3s
![]() 4s, etc.
4s, etc.
The values
![]() when multiplied by spectral photon flux at
certain photon energies give line emission rates per unit incident photon
energy interval. On the other hand, the values
when multiplied by spectral photon flux at
certain photon energies give line emission rates per unit incident photon
energy interval. On the other hand, the values
![]() /(
/(
![]() +
+
![]() )
are the probabilities of line emission upon the
condition that L-photoionization took place at certain energy.
)
are the probabilities of line emission upon the
condition that L-photoionization took place at certain energy.
For the Al II 3s3p-3s2 doublet, it is clear that its partial cross section coincides with the 3s-photoionization cross section.
We calculated the partial emission cross sections (9) for emission lines discovered for the following incident photon energies (in units of X): 0.60 (below 2p-threshold), 0.66 (right above the 2p-threshold, all shake channels are closed), 0.98 (2p/shake channels are opened, 2s-ionization is closed), 1.04 (right above the 2s-threshold, 2s/shake and 2p/dS channels are closed), 1.40 (2s/shake and 2p/dS channels are opened), 2.00, 4.00.
Calculated partial emission cross sections are listed in Table 5. The bottom line of Table 5 lists the total Al L-photoionization cross section.
Copyright ESO 2002