A&A 393, 757-764 (2002)
DOI: 10.1051/0004-6361:20021048

Probing the dark energy with strong lensing by clusters of galaxies

M. Sereno1,2


1 - Dipartimento di Scienze Fisiche, Università degli Studi di Napoli "Federico II", via Cinthia, Compl. Univ. Monte S. Angelo, 80126 Napoli, Italia
2 - Istituto Nazionale di Fisica Nucleare, Sez. Napoli, via Cinthia, Compl. Univ. Monte S. Angelo, 80126 Napoli, Italia

Received 19 June 2001/ Accepted 27 June 2002

Abstract
Observations of clusters of galaxies that gravitationally lens faint background galaxies can probe the amount and the equation of state, $w_{\rm X}$, of the dark energy (quintessence) in the universe. Provided that the mass profile and the mass normalization of the cluster are determined, it is possible to constrain the cosmological parameters that enter the lensing equations by means of the angular diameter distances, by locating (either by observations of giant arcs and magnification bias effect) the critical lines corresponding to known redshift source populations of galaxies. This method can help to distinguish between accelerating and decelerating models of the universe. Furthermore, since the position of critical lines is affected, especially in low-matter density universes, by the properties of quintessence, the observations of a suitable number of lensing clusters at intermediate redshifts can determine the equation of state. A very preliminary application of the method to the cluster CL 0024+1654 seems to support a flat accelerating universe dominated by dark energy.

Key words: cosmology: theory - cosmology: dark matter - gravitational lensing - galaxies: clusters: individual: CL 0024+1654


1 Introduction

Observational cosmology has devoted large efforts in the last years to characterize the energy content of the universe. Galaxy clustering (Bachall & Fan 1998; Carlberg et al. 1999) and large-scale structure (Peacock et al. 2001; Verde et al. 2001) observations favour models of a universe with a subcritical matter energy density $\Omega_{\rm M}$ (Turner 2000). Since, according to balloon-based measurements of the anisotropy of the Cosmic Microwave Background Radiation (de Bernardis et al. 2000; Balbi et al. 2000), the total of energy content of the universe nearly equals the critical density (Jaffe et al. 2001; Pryke et al. 2002), we expect that about 2/3 of the critical density is in form of dark energy (also called quintessence). Furthermore, evidence coming from type Ia supernovae that the universe is accelerating its expansion (Riess et al. 1998; Perlmutter et al. 1999a) demands a strongly negative pressure for the dark energy ( $w_{\rm X} \equiv p_{\rm X} /\rho_{\rm X} < -1/3$, where $p_{\rm X}$ and $\rho_{\rm X}$ are, respectively, the pressure and energy density of the dark energy). These observations, together with other constraints coming from the age of the universe, gravitational lensing statistics and Ly$\alpha$ forest, support a geometrically flat universe (Harun-or-Rashid & Roos 2001) ( $\Omega_{\rm M} + \Omega_{\rm X} =1$, where $\Omega_{\rm X}$ is the dark energy density parameter of the universe) with $\Omega_{\rm M} \sim 0.3$-0.4 and a constant equation of state $-1 \leq w_{\rm X} \la -0.4$ (Waga & Miceli 1998; Wang et al. 2000) at the $68\%$ confidence level or better according to a concordance analysis (Wang et al. 2000). A less conservative maximum likelihood analysis suggests a smaller range for the equation of state, $-1 \leq w_{\rm X} \la -0.6$ (Perlmutter et al. 1999b; Wang et al. 2000; Bean & Melchiorri 2002). According to these results, in what follows, without being explicitly stated, we will assume a flat universe.

After the first proposal of dark energy (the cosmological constant, $w_{\rm X}=-1$), many other candidates have been suggested. One interesting idea is that the energy density is provided by a scalar field rolling down an almost flat potential (Caldwell et al. 1998; Ratra & Peebles 1998; de Ritis et al. 2000; Rubano & Scudellaro 2002). Other possibilities are represented by a fluid with a constant equation of state, called X-matter (Chiba et al. 1997; Turner & White 1997), or by a network of light non-intercommuting topological defects (Vilenkin 1984; Spergel & Pen 1997) ( $w_{\rm X} =-m/3$ where m is the dimension of the defect: for a string, m=1; for a domain wall, m=2). Generally, the equation of state $w_{\rm X}$ evolves with the redshift, and the feasibility of reconstructing its time evolution has been investigated (Cooray & Huterer 1999; Chiba & Nakamura 2000; Saini et al. 2000; Goliath et al. 2001; Huterer & Turner 2001; Maor et al. 2001; Nakamura & Chiba 2001; Wang & Garnavich 2001; Yamamoto & Futamase 2001; Corasaniti & Copeland 2002). Since in flat Friedmann-Lemaître-Robertson-Walker (FLRW) models the distance depends on $w_{\rm X}$ only through a triple integral on the redshift (Maor et al. 2001), $w_{\rm X} (z)$ can be determined only given a prior knowledge of the matter density of the universe (Goliath et al. 2001; Weller & Albrecht 2001; Gerke & Efstathiou 2002). In what follows, we will consider only the case of a constant equation of state.

Although the listed results are really compelling, it is still useful to develop new tools for the determination of the cosmological parameters. Many of the discussed methods are affected by shortcomings, like poorly controlled systematic errors or large numbers of model parameters involved in the analysis. An independent constraint can improve the statistical significance of the statement about the geometry of the universe and can disentangle the degeneracy in the space of the cosmological parameters.

Gravitational lensing systems have been investigated as probes of dark energy. Gravitational lensing statistics (Waga & Miceli 1998; Cooray & Huterer 1999; Wang et al. 2000; Zhu 2000), effects of large-scale structure growth in weak lensing surveys (Benabed & Bernardeau 2001) and Einstein rings in galaxy-quasar systems (Futamase & Yoshida 2001; Yamamoto & Futamase 2001) are very promising ways to test quintessence. Here, we propose to investigate clusters of galaxies acting as lenses on background high redshift galaxies. The feasibility of these systems to provide information on the universe is already known (Paczynski & Gorski 1981; Breimer & Sanders 1992; Fort et al. 1997; Link & Pierce 1998; Lombardi & Bertin 1999; Gautret et al. 2000). Provided that the modeling of the lens is constrained, once both arc positions and its redshift are measured, it is possible to gain an insight into second-order cosmological parameters contained in angular diameter distances ratios (Chiba & Takahashi 2002; Golse et al. 2002). In addition to observations of arcs, a statistical approach based on magnification bias (Broadhurst et al. 1995; Fort et al. 1997; Mayen & Soucail 2000) can as well locate the critical lines (locations of maximum amplification) corresponding to background source populations.

In this paper, we will explore the feasibility of clusters of galaxies acting as lenses in probing both the amount and the equation of state of quintessence in the universe, assumed to be flat. In Sect. 2, we outline the method. Section 3 is devoted to an application to the cluster of galaxies CL 0024+1654. In Sect. 4, we discuss some systematics affecting the method. Some final considerations are presented in Sect. 5.

2 How critical lines depend on dark energy


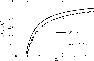  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{1598f1.eps}} \end{figure} Figure 1: The ratio of distances $D_{\rm ds}/D_{\rm s}$ as a function of the source redshift for a deflector at $z_{\rm d} =0.3$, for different sets of cosmological parameters. The thick lines correspond to ${\Omega _{\rm M} }=0.3$; the thin lines to ${\Omega _{\rm M} }=0.5$. The full and dashed lines correspond to, respectively, $w_{\rm X}=-1$ and $w_{\rm X}=-1/3$.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{1598f2.eps}} \end{figure} Figure 2: Contours of equal $D_{\rm ds}/D_{\rm s}$ on the $(\Omega _{\rm M},w_{\rm X})$ plane for $z_{\rm d} =0.3$ and $z_{\rm s} =1$. Each contour is drawn with a step of 0.01. The value of the contours increases from the top right corner to the bottom left corner. The thin dashed lines correspond to lines of constant q0.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{1598f3.eps}} \end{figure} Figure 3: The derivative of the ratio of distances $D_{\rm ds}/D_{\rm s}$ with respect to $w_{\rm X}$ for a lens at $z_{\rm d} =0.3$ as a function of the source redshift, for different values of the equation of state. The full lines correspond to $w_{\rm X}=-1$; the dashed lines to $w_{\rm X}=-2/3$; the long-dashed lines to $w_{\rm X}=-1/3$. The thick (thin) lines are for $\Omega _{\rm M}=0.3(0.5)$.
Open with DEXTER


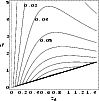  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{1598Serenof4.eps}} \end{figure} Figure 4: The relative variation between the ratio of distances $D_{\rm ds}/D_{\rm s}$ for two cosmological models, ( ${\Omega _{\rm M} }=0.3,w_{\rm X}=-1$) and ( ${\Omega _{\rm M} }=0.3,w_{\rm X}=-1/3$), in the $(z_{\rm d},z_{\rm s})$ plane. Each contour is drawn with a step of 0.01.
Open with DEXTER

The study of critical lines in a gravitational lensing system is a potentially important tool to probe the content of dark energy in the universe and to constrain its equation of state, as already shown in the case of galaxy-quasar lensing in Futamase & Yoshida (2001) and Yamamoto & Futamase (2001). This type of cosmological investigations requires an accurate modeling of the lens, the observation of a critical line and the knowledge of the redshifts of both the lens and the deflected source (Breimer & Sanders 1992; Fort et al. 1997; Link & Pierce 1998).

As an example for our quantitative considerations, let us consider as deflecting cluster a singular isothermal sphere (SIS). The projected density mass $\Sigma$ of the SIS is

 \begin{displaymath} \Sigma (\theta)=\frac{\sigma^2}{2G}\frac{1}{D_{\rm d}\theta}, \end{displaymath} (1)

where G is the Newtonian constant of gravitation, $\sigma $ the velocity dispersion, $D_{\rm d}$ the angular diameter distance to the deflector and $\theta$ the angular position in the sky. For a spherically symmetric lens, the tangential critical line is determined by (Schneider et al. 1992)

 \begin{displaymath} \theta_{\rm t}=\sqrt{ \frac{4 G M(\theta_{\rm t})}{c^2} \frac{D_{\rm ds}}{D_{\rm d} D_{\rm s}}}, \end{displaymath} (2)

where c is the velocity of the light and $M(\theta)$ is the lens mass within the radius $\theta$; $D_{\rm ds}$ and $D_{\rm s}$ are the angular diameter distances to the source from, respectively, the lens and the observer. For the SIS, Eq. (2) reduces to

 \begin{displaymath} \theta_{\rm t}=4 \pi \left( \frac{\sigma}{c}\right)^2 \frac{D_{\rm ds}}{D_{\rm s}}\cdot \end{displaymath} (3)

Once $\theta_{\rm t}$ and $\sigma $ are known, the ratio of distances $D_{\rm ds}/D_{\rm s}$ can be determined.

The dependence on the cosmological parameters is contained in the angular diameter distance. In a flat FLRW universe, the angular diameter distance between an observer at $z_{\rm d}$ and a source at $z_{\rm s}$is

 
$\displaystyle D(z_{\rm d}, z_{\rm s})=\frac{c}{H_0}\frac{1}{1+z_{\rm s}} \int_{... ...m d}z}{\sqrt{\Omega_{\rm M} (1+z)^3+(1-\Omega_{\rm M})(1+z)^{3(w_{\rm X}+1)}}};$     (4)

H0 is the today Hubble parameter. At high redshift, the pressureless matter density overcomes the dark energy; for large $z_{\rm d}$and small $w_{\rm X}$, $D_{\rm ds}$ is nearly insensitive to the equation of state. For the expression of the distance in inhomogeneous universes, we refer to Sereno et al. (2001, 2002).

Let us go, now, to examine the feasibility of determining $w_{\rm X}$ with observations of strong lensing events in clusters of galaxies by the study of the ratio of distances $D_{\rm ds}/D_{\rm s}$. Once the lens redshift is fixed, $D_{\rm ds}/D_{\rm s}$ first increases rapidly with the source redshift and, then, for $z_{\rm s}$ greater than 2.5, is nearly constant (Asada 1997; Fort et al. 1997), as can be seen in Fig. 1. The change with the cosmological parameters can be significant. The ratio increases with decreasing $\Omega_{\rm M}$ and with dark energy with large negative pressure, i.e. it is maximum in the case of the cosmological constant. The variations with $\Omega_{\rm M}$ and $w_{\rm X}$ are comparable. Changing $\Omega_{\rm M}$ from 0.3 to 0.5 has the same effect of increasing $w_{\rm X}$ from -1 to -1/3, so that $D_{\rm ds}/D_{\rm s}$ is nearly indistinguishable in a universe with ${\Omega _{\rm M} }=0.3$ filled in with string networks and in a model with ${\Omega _{\rm M} }=0.5$ and cosmological constant.

To quantify the dependence of $D_{\rm ds}/D_{\rm s}$ with the cosmological parameters, we consider fixed redshifts for the lens and the source, see Fig. 2. The ratio is quite sensitive to $\Omega_{\rm M}$. The variations due to changes in $\Omega_{\rm M}$ for $w_{\rm X}=\rm const.$ are greater than in the case of the constant deceleration parameter  $q_0 \equiv (1+3w_{\rm X}(1-{\Omega_{\rm M} }))/2$. For $z_{\rm d} =0.3$, $z_{\rm s} =1$, and $\Omega_{\rm M}$ ranging from 0 to 0.6, when q0=0 the variation is $\sim $4%; when $w_{\rm X}=-1$, the variation is $\sim $15%. The dependence on the cosmological parameters is maximum for high negative values of q0, i.e. the region today preferred by observations. For some particular pairs $(z_{\rm d},z_{\rm s})$, i.e. for low lens redshifts and sources very near to the deflector, the ratio is nearly constant on lines of constant deceleration parameters; these properties suggest that the method of the critical line can help to distinguish between accelerating and decelerating universes. The dependence of $D_{\rm ds}/D_{\rm s}$ on the equation of state increases for low matter density universes and the sensitivity nearly doubles for small changes in $\Omega_{\rm M}$: for $z_{\rm d} =0.3$and $z_{\rm s} =1$, the relative variation from $w_{\rm X}=-1$ to $w_{\rm X}=-1/3$ is $1.9\%$ ($3.4\%$) when ${\Omega _{\rm M} }=0.5$ (0.3). The sensitivity is maximum for intermediate $w_{\rm X}$; for large negative pressure ( $w_{\rm X} \la -0.9$), the ratio is nearly independent of variations of the equation of state.

In Fig. 3, the derivative of the ratio $D_{\rm ds}/D_{\rm s}$with respect to $w_{\rm X}$ is plotted as a function of the redshift of the source once the redshift of the deflector is fixed. The derivative is negative for a large range of redshifts of both source and deflector. Transitions from negative to positive values occur for very negative $w_{\rm X}$. The source redshift where the derivative cancels out decreases with increasing $\Omega_{\rm M}$ and $z_{\rm d}$: for $z_{\rm d} =0.3$ (0.6), ${\Omega _{\rm M} }=0.3$ and $w_{\rm X}=-1$, the derivative is null at $z_{\rm s} \simeq 7.0$ (2.1). The sign of the derivative determines, when the equation of state changes, as the angular position of the critical lines moves: when the derivative is negative (positive), as the equation of state increases (i.e. as $w_{\rm X}$ moves from -1 to 0), the angular radius in the sky of the critical line, for fixed source and deflector redshifts, decreases (increases).

The modulus of the derivative is an estimate of the dependence of the ratio on $w_{\rm X}$. Independently of the value of $z_{\rm d},\ \Omega_{\rm M}$ and $w_{\rm X}$, the dependence on $w_{\rm X}$ first increases and takes its maximum at an intermediate source redshift, and then decreases quite slowly. For dark energy in the form of a cosmological constant ( $w_{\rm X}=-1$), $z_{\rm d} =0.3$ and ${\Omega _{\rm M} }=0.3$, the maximum is at $z_{\rm s} \sim 0.75$. For increasing $w_{\rm X}$, the maximum moves to higher redshifts: for domain walls ( $w_{\rm X}=-2/3$), the maximum is at $z_{\rm s} \sim 1.02$. From Fig. 3, we see that for a large range of $w_{\rm X}$and  $\Omega_{\rm M}$ the maximum is at $z_{\rm s} \la 2$. This trend of the derivative is connected to the properties of the ratio $D_{\rm ds}/D_{\rm s}$, that flattens at higher source redshifts.

Now, we want to search for the optimal lens and source configuration in order to discriminate among quintessence models. For illustration, we choose two universes with the same content of matter ( ${\Omega _{\rm M} }=0.3$) but different $w_{\rm X}$; we consider a cosmological constant ( $w_{\rm X}=-1$) and string networks ( $w_{\rm X} =-1/3)$. In Fig. 4, we scan the $(z_{\rm d},z_{\rm s})$ plane plotting the relative variation between the two pairs of cosmological parameters. For a given lens redshift, the best $z_{\rm s}$ is very close to the deflector, i.e. a couple of redshifts corresponding to the rising part of the ratio $D_{\rm ds}/D_{\rm s}$; the sensitivity decreases for larger and larger source redshifts. So, the configurations with high sensitivity to the quintessence are those with very low cross section for strong lensing events. On the other hand, given a background population at $z_{\rm s} \ga 1$, the optimal lens is a quite high redshift cluster at $z_{\rm d} \sim 0.7$; however, the dependence on the quintessence is nearly constant for lenses at $z_{\rm d} \ga 0.6$

In order to estimate the accuracy of the determination of the equation of state, the variation induced on $D_{\rm ds}/D_{\rm s}$ by $w_{\rm X}$ must be compared to the error within which the parameters of the lens are known. For the SIS, the error in the estimate of the ratio of distances is

 \begin{displaymath} \left\vert \Delta \left( \frac{D_{\rm ds}}{D_{\rm s}} \right... ...ht\vert^2} \left\vert \frac{D_{\rm ds}}{D_{\rm s}}\right\vert, \end{displaymath} (5)

where $\Delta \sigma$ and $\Delta \theta_{\rm t}$ are the errors, respectively, on the velocity dispersion and $\theta_{\rm t}$. Usually, the largest uncertainty in the modeling of a lens comes from the error in the measurement of the velocity dispersion. Catalogues of galaxy velocities in lensing clusters are of the order of 50, so that the uncertainty on $\sigma $ is $\sim $15%. $\Delta \theta_{\rm t}$ comes from the accuracy of the location of the arc and its radial thickness and from the uncertainty on the geometrical properties of the lens, i.e. the accuracy of the location of the center, typically chosen to coincide with the brightest cluster galaxy, and the ellipticity of the mass distribution. For tangential arcs at $\theta_{\rm t} \sim 20 \hbox{$^{\prime\prime}$ }$ (Williams et al. 1999), an error as large as $\sim $1 $\hbox{$^{\prime\prime}$ }$ can contribute a $5 \%$ error. The error on $\theta_{\rm t}$ is generally negligible with respect to the error in the mass normalization and will not be considered in the rest of this section. The variation on $D_{\rm ds}/D_{\rm s}$ connected to changes in the equation of state can be expressed as

 \begin{displaymath} \left\vert \frac{\partial}{\partial w_{\rm X}} \left( \frac{D_{\rm ds}}{D_{\rm s}} \right) \right\vert\Delta w_{\rm X} , \end{displaymath} (6)

and so, comparing Eqs. (5) and (6), for Nclusters we have a statistical error of
 
                $\displaystyle \Delta w_{\rm X}$ $\textstyle \ga$ $\displaystyle \frac{2}{\sqrt{N}}\left\vert \frac{\Delta \sigma}{\sigma} \right\... ...X}} \left( \frac{D_{\rm ds}}{D_{\rm s}} \right) \right\vert^{-1} \right \rangle$  
  = $\displaystyle \frac{2}{\sqrt{N}}\left\vert \frac{\Delta \sigma}{\sigma} \right\... ...n \left( \frac{D_{\rm ds}}{D_{\rm s}} \right) \right\vert^{-1} \right \rangle ,$ (7)

where the average is on the redshifts of the critical lines. The error in the determination of $w_{\rm X}$ increases with $\Delta \sigma$ and decreases with the derivative. Since the error induced by the velocity dispersion is proportional to the ratio of distances $D_{\rm ds}/D_{\rm s}$, see Eq. (5), and the variation induced by $w_{\rm X}$ is proportional to the derivative, see Eq. (6), the uncertainty in the estimate of $w_{\rm X}$ is inversely proportional to the logarithmic derivative of $D_{\rm ds}/D_{\rm s}$, i.e. to the relative variation of $D_{\rm ds}/D_{\rm s}$. The properties of the logarithmic derivative with respect to the cosmological parameters $\Omega_{\rm M}$ and $w_{\rm X}$ are the same of the ordinary derivative; the main difference is the disappearance of the minimum. As we have seen before, the uncertainty in the equation of state, given a deflector redshift, increases with zs and decreases for quintessence with $w_{\rm X}$ far away from -1.

The case of the cosmological constant is the more problematic one since the derivative can cancel out (when  ${\Omega _{\rm M} }=0.3$ and $z_{\rm s}=1.5 $, the derivative is null at $z_{\rm d} \simeq 1.13$). However, clusters at intermediate redshift $(z_{\rm d} \sim 0.4)$ are quite stable with respect to the error in the equation of state.

As we shall see in the next section, it is possible to obtain information from a single cluster of galaxies on more than one critical line. So, using in Eq. (7) the number N of clusters, the lower limit on $\Delta w_{\rm X}$ is overestimated. Given a typical error of $\sim $15% on $\sigma $, we can use Eq. (7) to estimate the number of deflectors necessary for estimating $w_{\rm X}$within a given uncertainty. For mean redshifts of $\langle z_{\rm d} \rangle =0.4$ and $\langle z_{\rm s} \rangle =1.2$, an uncertainty of $\Delta w_{\rm X} \simeq 0.25$ needs $\sim $75 ($\sim $120) lensing clusters in a universe with ${\Omega _{\rm M} }=0.3$and $w_{\rm X}=-1/3$ (-0.5). N increases with dark energy with large negative pressure and large values of $\Omega_{\rm M}$. As discussed, the method is unable to constrain the equation of state in the extreme case of a cosmological constant, when $\Delta w_{\rm X} \simeq 0.25$ needs $\sim $800 clusters and $\Delta w_{\rm X} \simeq 0.5$ needs $\sim $200 clusters. In general, to distinguish dark energy with an intermediate value of $w_{\rm X}$ from a cosmological constant at $95\%$ confidence level, in a low matter density universe, we need 100-200 strong lensing events. These simple estimates are in agreement with the results in Yamamoto & Futamase (2001).

Together with spectroscopic analyses, X-ray observations of a lensing cluster can help to estimate the absolute mass of the deflector. The projected X-ray cluster mass, under the hypotheses of isothermal and hydrostatic equilibrium, is proportional to the cluster gas temperature, $T_{\rm X}$, and $D_{\rm d}$ (Wu 2000): X-ray data alone cannot determine the mass without a prior knowledge of cosmological parameters. However, it has been shown that the relation between $\sigma $ and $T_{\rm X}$ is not affected by cosmic evolution and is consistent with the isothermal scenario, $\sigma \propto T_{\rm X}^{0.5}$(Wu et al. 1998). Once calibrated this relation, X-ray observations obtained with the new generation of telescopes can considerably enlarge the data sample of lensing clusters with known mass and help to disentangle the effect of cosmology and mass normalization of the deflector.

3 CL 0024+1654

Now, let us consider the application of the method outlined in Sect. 2 to a well studied cluster of galaxies, CL 0024+1654, in order to test the feasibility of what we are proposing, and how good the results can be.

CL 0024+1654 is one of the best investigated lenses in the universe. It is an optically rich cluster of galaxies, with a relaxed structure without a single central dominant cluster galaxy, at z=0.395 and with a velocity dispersion of $\sigma =1050 \pm 75$ km s-1(Dressler et al. 1999; Czoske et al. 2001; Czoske et al. 2002). This is the formal velocity dispersion estimated with the assumptions of virial equilibrium and random galaxy velocities, so that the reported error is a purely statistical one. We will consider the effect of some possible systematics in the next section. This value of $\sigma $ is consistent with lensing observations (Shapiro & Iliev 2000). X-ray data (Soucail et al. 2000; Böhringer et al. 2000) also support a regular morphology with no significant substructures. The measured value of $T_{\rm X} =5.7^{+4.9}_{-2.1}$ is compatible with the observed velocity dispersion. A single background galaxy behind CL 0024+1654, at spectroscopic redshift z=1.675 (Broadhurst et al. 2000), is imaged in a well known multiple arc at $\theta_{\rm t} = 30.5\hbox{$^{\prime\prime}$ }$ (Kassiola et al. 1992; Wallington et al. 1995; Smail et al. 1996; Tyson et al. 1998). Images are characterized by a bright elongated knot, surrounded by a low surface brightness halo. The knot comprises two peaks, with separations ranging from $0.5\hbox{$^{\prime\prime}$ }$ to  $1.1\hbox{$^{\prime\prime}$ }$, roughly consistent with the relative lengths of the various arc components (Smail et al. 1996). Given this peculiar morphology, we assume an indetermination on the critical radius $\Delta \theta_{\rm t} \sim 0.7\hbox{$^{\prime\prime}$ }$. We do not take into account the error on the position of the centre; in the analyses considered here, it is determined as a free parameter in the lensing reconstruction. Based on deep images with the Hubble Space Telescope, Tyson et al. (1998) performed a multi-parameter fit, including a number of small deflecting "mascons", to the mass profile. Each mascon was parameterized with a power-law model (Schneider et al. 1992),

 \begin{displaymath} \Sigma (\theta ) \propto \frac{1+\gamma \left( \frac{\theta}... ...(\frac{\theta}{\theta_{\rm c}}\right)^2 \right]^{2-\gamma}}\ , \end{displaymath} (8)

where $\theta_{\rm c}$ is the core radius and $\gamma$ is the slope. Remarkably, they found that more than $98\%$ of the cluster matter is well represented by a single power-law model centred near the brightest cluster galaxies with $\theta_{\rm c} =10.0\pm 0.9\hbox{$^{\prime\prime}$ }$ and $\gamma =0.57 \pm 0.02$, slightly shallower than an isothermal sphere ( $\gamma_{\rm SIS}=0.5$). To disentangle the effect of cosmology and absolute mass, we have to fix the central density $\Sigma_0$independently of lensing data. It is (Bonnet et al. 1994),

 \begin{displaymath} \Sigma_0=\frac{8\alpha \sigma^2}{3 \pi G \theta_{\rm c}} \frac{I^2_{(1+\alpha)/2}}{I_{\alpha}} \frac{1}{D_{\rm d}}, \end{displaymath} (9)

with $\alpha=2(1-\gamma)$ and $I_\beta=\int_{0}^{\infty}(1+u^2)^{-\beta}{\rm d}u$. For a power-law model, the angular position $\theta_{\rm t}$ of the tangential critical line is related to the angular diameter distances and the parameters of the lens by

 \begin{displaymath} \left( \frac{\theta_{\rm t}}{\theta_{\rm c}}\right)^2=\left(... ...{\rm d} D_{\rm ds}}{D_{\rm s}}\right)^{\frac{1}{1-\gamma}} -1. \end{displaymath} (10)

Substituting in Eq. (10) for $\Sigma_0$ and using the fit parameters, we get an estimate for the ratio $D_{\rm ds}/D_{\rm s}$. It is

 \begin{displaymath} \frac{D_{\rm ds}}{D_{\rm s}}(z_{\rm d}=0.395,z_{\rm s}=1.675)=0.76^{+0.18}_{-0.12}. \end{displaymath} (11)

The main term in the error budget comes from the indetermination in the velocity dispersion which contributes $\sim $75% of the total error. In Fig. 5, we show the dependence of $D_{\rm ds}/D_{\rm s}$ on the cosmological parameters for a lens-source configuration as in CL 0024+1654; the values of $(\Omega _{\rm M},w_{\rm X})$compatible with the estimate in Eq. (11) are also plotted. Low matter density universes ( ${\Omega_{\rm M} } \la 0.55$), which are accelerating their expansion, are favoured. We find $-1 \leq w_{\rm X} \la -0.2$, with the lower values of  $\Omega_{\rm M}$corresponding to the higher values of the equation of state.

The method of the depletion curves, i.e. the variation along the radial direction in the surface density of background galaxies around a massive cluster of galaxies, has been employed to further study CL 0024+1654 (Fort et al. 1997; van Kampen 1998; Rögnvaldsson et al. 2001; Dye et al. 2002). Observations of the magnification bias have been obtained in the B- and I-band (Fort et al. 1997) and in the U- and R-band (Rögnvaldsson et al. 2001; Dye et al. 2002). Extrapolating Hubble Space Telescope data to their detection limit, Dye et al. (2002) obtained, for the background R-galaxies, a mean redshift of $\langle z_{\rm s} \rangle =1.2 \pm0.3$. From a fit to the SIS profile of the depletion curve in the R-band, the location of the critical curve comes out at $15\pm10 \hbox{$^{\prime\prime}$ }$ (Dye et al. 2002). Using these estimates in Eq. (3), we can obtain a second constraint on the ratio $D_{\rm ds}/D_{\rm s}$; unfortunately, as can be seen in Fig. 6, the uncertainties completely hide the second order effect of the cosmological parameters on the ratio of distances $D_{\rm ds}/D_{\rm s}$.

A more interesting result can be obtained from the I-band. As discussed in Fort et al. (1997), the angular radius where the depletion curve starts to increase locates the last critical line, that is the critical line corresponding to the farther source population. The last critical line at $\sim $60 $\hbox{$^{\prime\prime}$ }$ in the I-band corresponds to background galaxies at redshift 2.5< z < 6.5; however, about $20\%$ of the very faint I selected galaxies should be above z=4. As noted in van Kampen (1998), given the very low density of the background I-galaxies, an appropriate radial binning to study the radial profile of the magnification bias is $30 \hbox{$^{\prime\prime}$ }$. So, we will consider an error of $15 \hbox{$^{\prime\prime}$ }$. This estimate of the location of the last critical line is independent of the assumed mass profile, and can be used in Eq. (10) to obtain a new constraint on $D_{\rm ds}/D_{\rm s}$, see Fig. 6. Since $D_{\rm ds}/D_{\rm s}$ is nearly flat for $z_{\rm s} \ga 2.5$, the value of the ratio of distances is quite insensitive to the value of $z_{\rm s}$ corresponding to the last critical line.

Some interesting considerations are obtained from the variation of the ratio $D_{\rm ds}/D_{\rm s}$ with the redshift of the source. Figure 6 shows $D_{\rm ds}/D_{\rm s}$ for a lens at z=0.395 and for various cosmological models. Models without dark energy are rejected, with no regard to the value of the pressureless matter density: both open ( $\Omega_{\rm M} <1$) and flat (the Einstein-de Sitter model, with ${\Omega _{\rm M} }=1$) dark matter models are very poorly consistent with the experimental points. On the other hand, flat universes with quintessence are in agreement with the data. In particular, the data from the I-band analysis are marginally compatible (at the $68\%$confidence level) with a flat de Sitter universe ( ${\Omega _{\rm X}}=1$ and $w_{\rm X}=-1$). Given the large uncertainties, we cannot draw definitive conclusions on this multi-band analysis. However, even if the data from the R-galaxies have not information on the cosmology, the data from the multiple arc and the last critical line in the I-band prefer accelerating universes with subcritical matter density.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{1598f5.eps}} \end{figure} Figure 5: Contours of equal $D_{\rm ds}/D_{\rm s}$ on the $(\Omega _{\rm M},w_{\rm X})$ plane for CL 0024+1654 ( $z_{\rm d}=0.395$) and its multiple arc ( $z_{\rm s}=1.675$). Each contour is drawn with a step of 0.01. The value of the contours increases form 0.61 in the top right corner to 0.76 in the lower left corner. The thick lines correspond to the data in Eq. (11). The thick full line corresponds to the best parameters; the dashed one to the lower limit. The thin dashed line separates accelerating universes (below) from decelerating ones (above).
Open with DEXTER


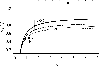  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{1598f6.eps}} \end{figure} Figure 6: $D_{\rm ds}/D_{\rm s}$ as a function of the source redshift for CL 0024+1654 ( $z_{\rm d}=0.395$) for different cosmological models. The thick lines are for flat models with quintessence. The full thick line for ${\Omega _{\rm X}}=1$ and $w_{\rm X}=-1$ (de Sitter universe); the dashing thick line is for ${\Omega _{\rm M} }=0.3$ and $w_{\rm X}=-1$. The thin lines are for universes with pressureless matter alone. The full line is for an Einstein-de Sitter universe ( ${\Omega _{\rm M} }=1$); the thin dashed line is for an open universe ( $\Omega _{\rm M} =0.1$). "R-band" indicates the data derived from Dye et al. (2002) (the error in $\sigma $ is not considered); "ARC" is the data in Eq. (11); "I-band" indicates the data from the depletion curve in Fort et al. (1997).
Open with DEXTER

4 Systematics

In the previous section, we performed a statistical analysis based on the data found in the literature. We want now to address some systematics that can affect our results. A very accurate knowledge of the mass distribution of the lens is required to put meaningful constraints on cosmological parameters. One of the more important source of indetermination comes from the modeling of the mass profile of the lens (Chiba & Takahashi 2002). In Eq. (5), we have considered only the error coming from a not very accurate mass normalization but, in general, we have also to face the indetermination on the cluster mass profile. As a general feature, the three-dimensional mass density of a clump, $\rho$, is proportional to a typical length scale, $r_{\rm s}$, so that, with respect to the angular diameter distance, $\rho \propto D_{\rm d}^{-2}$. The mass enclosed within an angular radius $\theta$ comes out

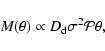
\begin{displaymath}M(\theta ) \propto D_{\rm d} \sigma^2 {\cal P} \theta, \end{displaymath}

where $D_{\rm d}$ contains the cosmological dependence and $\sigma^2$ stands for an overall normalization. ${\cal P}$ is a factor accounting for the deviations of the cluster mass profile from the SIS; ${\cal P}$ is a function of $\theta$ and of some parameters, such as a core radius. Substituting in Eq. (3), we get, for a spherically symmetric lens,

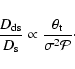
\begin{displaymath}\frac{D_{\rm ds}}{D_{\rm s}} \propto \frac{\theta_{\rm t}}{ \sigma^2 {\cal P} } \cdot \end{displaymath}

To consider the uncertainty in the profile, we have to add in quadrature to the right hand side of Eq. (5) an additional relative error of $\Delta {\cal P}/{\cal P}$. Usually, the main contribution to the error budget comes from the mass normalization but, in some extreme cases, the indetermination in the mass profile can be of the same order. $\Delta {\cal P}$ is maximum when calculated between a lens with a soft core and a halo with a singular density steeply rising towards the center, as predicted by numerical simulations in the standard cold dark matter framework of structure formation and approximated by a Navarro-Frenk-White profile (NFW, Navarro et al. 1995,1996).

A NFW model can match the mass distribution of CL 0024+1654 (Broadhurst et al. 2000). The required mass inside the arc's radius for such a model, reproducing the projected mass distribution outside the core radius, is $40\%$ higher than the prediction of a power-law model (Tyson et al. 1998). Without an independent information, $\Delta {\cal P}$ would be a really large error. Fortunately, the NFW profile is discarded since it implies a velocity dispersion much higher than the measured value (Shapiro & Iliev 2000). Once we can discard models with singular central density, the indetermination in the model can be accounted for by the errors within which we constrain the parameters of the mass profile ( $\Delta \gamma$ and $\Delta \theta_{\rm c}$ in the power-law model used in Sect. 3). In general, an uncertainty in the cluster mass profile can significantly weaken the results on the cosmological parameters; but, in the case of CL 0024+1654, the degeneracy in the fit is not the main error.

Together with the overall mass profile, sub-structures must be considered. In the case of a lens with a rather regular morphology, even if a "not correct" potential shape is used in the reconstruction or the contribution of small sub-structures is neglected, the cosmological parameters are still retrieved, although with larger errors (Golse et al. 2002). On the contrary, neglecting a sub-structure as large as $20\%$ of the total mass in a bi-modal cluster completely hides the effect of cosmology (Golse et al. 2002). Adding the contribution of individual galaxy masses is also useful to tighten the confidence levels and can become critical in some extreme cases, as a galaxy strongly perturbing the location of multiple-images (Golse et al. 2002). Deep imaging of CL 0024+1654 has made it possible to construct a high-resolution map of the projected mass distribution of the cluster and to take into account the effect of perturbing galaxies. Kassiola et al. (1992) and Wallington et al. (1995) considered the perturbing potentials of two galaxies near the middle segment of the arc. Tyson et al. (1998) assigned one or more mascons to each of the 118 cluster galaxies and 25 free mascons for the remaining cluster mass. However, all these studies in literature agree on a overall representation as the one in Eq. (8).

Some features in the 3-D space, as a possible merger scenario, can invalidate our estimation of the cosmological parameters. A recent analysis of the distribution of the galaxies in the redshift space (Czoske et al. 2001,2002) suggests a fairly complicated structure. A group of galaxies lying just in front of the main cluster could be the result of a high speed collision of two smaller clusters with a merger axis very nearly parallel to the line of sight (Czoske et al. 2002). In particular, a bulk velocity component present in the central velocity distribution would over-estimate the mass obtained from the formal central velocity dispersion. Furthermore, galaxies at large projected distance from the centre are also affected by the collision and cannot be used to derive $\sigma $(Czoske et al. 2002). The consequences on the dark energy constraint are quite dramatic since such a scenario could entail a systematic error on the estimation of the velocity dispersion of the same order of the statistical one. As can be seen from Fig. 5, this additional error would completely hide any dependencies on the cosmological parameters.

Even if, together with strong lensing observations, both a weak lensing analysis out to 10 arcmin (Bonnet et al. 1994) and X-ray observations (Soucail et al. 2000; Böhringer et al. 2000) favour a regular morphology, the points just discussed suggest caution in the interpretation of the results obtained in the previous section.

5 Some final considerations

We have explored the feasibility of reconstructing the properties of the dark energy in the universe by using strong lensing systems in which a cluster of galaxies acts as deflector. With respect to other lensing systems, for the one discussed in this paper it is possible to determine the position of the critical lines in two independent ways: with giant arcs or with the radial shape of the depletion curves. This circumstance allows to study the ratio of angular diameter distances that characterizes the angular position of the critical lines over a large range of source redshifts, just for a single lensing cluster. Provided that the properties of the background populations are well constrained, it is possible in principle to use multi-band depletion measurements to obtain several independent estimates of the ratio of distances, each one probing a different source redshift.

For a flat universe, the sensitivity of the angular positions of the critical lines on quintessence becomes higher in low-density pressureless matter universes and for dark energy with intermediate equation of state. While the analysis of only a few lensing clusters suffices to distinguish between accelerating and decelerating models of universe (also without a prior knowledge of $\Omega_{\rm M}$), a considerably larger sample ( $N \sim 200$) and an accurate estimate of $\Omega_{\rm M}$ are needed to constrain the equation of state within an uncertainty of $\Delta w_{\rm X} \sim 0.25$ and discriminate, at the $95\%$ confidence limit, between a cosmological constant and an evolving quintessence.

In our opinion, a first application of the method to the cluster CL 0024+1654 has given interesting results. A combined analysis of both the multiple arc and the depletion curves disfavours models of a universe without dark energy. On the other hand, flat accelerating universes are in agreement with the data. These preliminary estimates agree with the currently favoured constraints from other independent measurements. However, some features in the redshift space of CL 0024+1654, as a possible merger scenario, could invalidate our results. Indeed, a very accurate knowledge of the absolute mass distribution of the deflector and a correct understanding of the pattern of sub-structures are necessary to obtain secure constraints on the cosmological parameters.

The method we have discussed is quite general and can be applied to several strong lensing systems. For example, a single galaxy, whose stellar velocity dispersion can be accurately measured, can multiply image a background quasar. Clusters of galaxies need an accurate modeling of the pattern of substructures and present a quite problematic measurement of $\sigma $ but allow one to study the ratio $D_{\rm ds}/D_{\rm s}$ at different source redshifts. Furthermore, a multiple image system of galaxies with known redshift makes possible an absolute calibration of the total mass of the cluster (Golse et al. 2002). We have shown how analyses of magnification bias in multi-band photometry can be combined with observations of giant arcs to obtain some insight on cosmological parameters.

Acknowledgements
I am very grateful to E. Piedipalumbo, C. Rubano, M. V. Sazhin and P. Scudellaro for useful discussions and S. Refsdal for the reading of the manuscript. I also thank the referee, J.-P. Kneib, for his reports which helped to improve the paper.

References

 
Copyright ESO 2002