We have carried out simulations of supersonic light jets in order to model the features observed in optical and radio images of the western hot-spot in the radio galaxy Pictor A. We have considered jets with density ratios
A&A 393, 765-792 (2002)
DOI: 10.1051/0004-6361:20021004
C. J. Saxton 1,2 - R. S. Sutherland 2 - G. V. Bicknell 1,2 - G. F. Blanchet 1,2,3 - S. J. Wagner 4
1 - Department of Physics & Theoretical Physics, Australian National
University, Canberra, Australia
2 -
Research School of Astronomy & Astrophysics, Australian
National University, Canberra, Australia
3 -
INSA, 135 avenue de Rangueil, 31077 Toulouse Cedex 4, France
4 -
Landessternwarte Heidelberg-Konigstuhl, Konigstuhl, 69117
Heidelberg, Germany
Received 16 March 2001 / Accepted 28 June 2002
Abstract
We have carried out simulations of supersonic light jets in order
to model the features observed in
optical and radio images of the western hot-spot
in the radio galaxy Pictor A.
We have considered jets with density ratios
![]() ,
and Mach numbers ranging between 5 and 50.
From each simulation,
we have generated ray-traced maps of radio surface brightness
at a variety of jet inclinations,
in order to study the appearance of time-dependent luminous structures
in the vicinity of the western hot-spot.
We compare these rendered images with observed features of Pictor A.
A remarkable feature of Pictor A observations
is a bar-shaped "filament'' inclined almost at right angles
to the inferred jet
direction and extending 24'' (
,
and Mach numbers ranging between 5 and 50.
From each simulation,
we have generated ray-traced maps of radio surface brightness
at a variety of jet inclinations,
in order to study the appearance of time-dependent luminous structures
in the vicinity of the western hot-spot.
We compare these rendered images with observed features of Pictor A.
A remarkable feature of Pictor A observations
is a bar-shaped "filament'' inclined almost at right angles
to the inferred jet
direction and extending 24'' (
![]() )
along its longest axis.
The constraints of reproducing the appearance of this structure
in simulations indicate that the jet of Pictor A
lies nearly in the plane of the sky.
The results of the simulation are also consistent
with other features found in the radio image of Pictor A.
This filament arises
from the surging behaviour of the jet near the hot-spot; the surging is
provoked by alternate compression and decompression of the jet by the
turbulent backflow in the cocoon.
We also examine the arguments for the jet
in Pictor A being at a more acute angle to the line of sight and find that
our preferred orientation is just consistent with the limits on the
brightness ratio of the X-ray jet and counter-jet.
We determine from our simulations,
the structure function of hot-spot brightness and also
the cumulative distribution of
the ratio of intrinsic hot-spot brightnesses.
The latter may be used to quantify the use of hot-spot ratios for the
estimation of relativistic effects.
)
along its longest axis.
The constraints of reproducing the appearance of this structure
in simulations indicate that the jet of Pictor A
lies nearly in the plane of the sky.
The results of the simulation are also consistent
with other features found in the radio image of Pictor A.
This filament arises
from the surging behaviour of the jet near the hot-spot; the surging is
provoked by alternate compression and decompression of the jet by the
turbulent backflow in the cocoon.
We also examine the arguments for the jet
in Pictor A being at a more acute angle to the line of sight and find that
our preferred orientation is just consistent with the limits on the
brightness ratio of the X-ray jet and counter-jet.
We determine from our simulations,
the structure function of hot-spot brightness and also
the cumulative distribution of
the ratio of intrinsic hot-spot brightnesses.
The latter may be used to quantify the use of hot-spot ratios for the
estimation of relativistic effects.
Key words: galaxies: jets - galaxies: general
The FR II radio galaxy Pictor A (z=0.0342)
consists of two lobes dominated by hot-spots separated by
4' (
![]() )
from the flat spectrum nucleus.
Near the western hot-spot, there is a faint, 24''(
)
from the flat spectrum nucleus.
Near the western hot-spot, there is a faint, 24''(
![]() )
long radio and optical filament,
"upstream of the hot-spot'' first detected by
Röser & Meisenheimer (1987).
Wagner et al. (2002)
found the filament to be
highly polarised, confirming that
it radiates via optical synchrotron emission.
)
long radio and optical filament,
"upstream of the hot-spot'' first detected by
Röser & Meisenheimer (1987).
Wagner et al. (2002)
found the filament to be
highly polarised, confirming that
it radiates via optical synchrotron emission.
The filament has been studied in detail at several radio frequencies by Perley et al. (1997). The radio emission at 8415 MHz, Fig. 1, which bears a striking correspondence to the optical emission, also reveals a knot further upstream from the filament. This is of particular interest since at various timesteps throughout our simulation such a morphology is captured.
The discovery of optical synchrotron radiation, emitted by electrons with radiative life-times of about 100 yr (for magnetic fields of the order of equipartition), in a filament which extends several thousand light years perpendicular to the jet strongly indicates that the electrons are accelerated in situ. The crossing time from the hot-spot to the filament is much longer than the cooling time-scale, and efficient acceleration to optical emitting energies is required.
Our objective here is to ascertain whether purely hydrodynamical simulations can qualitatively reproduce the radio and optical morphology. Indeed on the basis of our simulations we suggest below that the filament is the result of a quasi-periodic pulsing behaviour of the terminal jet shock.
Before discussing the simulations, we summarise relevant aspects of the observations and in the following sections we point out the relevance of the features in the simulations to the observational data.
A total intensity radio map (Perley et al. 1997), displayed in Fig. 1 shows the high-surface brightness western hot-spot; a bar-shaped region (the filament) east of the hot-spot, extends perpendicular to the inferred direction of the jet. The region between the hot-spot and the ridge line of the bar shows a "pedestal'' of lower surface brightness.
High S/N observations were obtained with the VLT (UT1)
during commissioning of FORS1.
Figure 2 shows total intensity emission at 450 nm.
Wagner et al. (2002)
presented polarization maps derived from these data,
showing up to ![]() polarization in the hot-spot,
and up to
polarization in the hot-spot,
and up to ![]() polarization in the filament.
Such a high degree of polarization cannot be the result of
scattering and strongly suggests that
the filament radiates optical synchrotron emission.
Moreover, in the optical image, the bar-shaped filament is quite bright,
and spatially coincides with a similar in the radio images.
The eastern edge of the bar is very pronounced,
but the surface brightness gradient in the western direction
is more gradual.
The filament is brightest at its ends and near the centre,
where it overlaps the inferred jet direction.
In the optical image there are
faint extensions from the hot-spot extending
in the direction of the ends of the filament.
polarization in the filament.
Such a high degree of polarization cannot be the result of
scattering and strongly suggests that
the filament radiates optical synchrotron emission.
Moreover, in the optical image, the bar-shaped filament is quite bright,
and spatially coincides with a similar in the radio images.
The eastern edge of the bar is very pronounced,
but the surface brightness gradient in the western direction
is more gradual.
The filament is brightest at its ends and near the centre,
where it overlaps the inferred jet direction.
In the optical image there are
faint extensions from the hot-spot extending
in the direction of the ends of the filament.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS1285f01_figrad.eps}\end{figure}](/articles/aa/full/2002/39/aa1285/Timg36.gif) |
Figure 1:
Radio image.
VLA 8415 MHz map of the western lobe,
with contour levels at multiples of
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS1285f02_figopt.eps}\end{figure}](/articles/aa/full/2002/39/aa1285/Timg37.gif) |
Figure 2: Optical image. Total intensity emission at 450 nm with polarization map overlay. |
| Open with DEXTER | |
The earliest simulations of astrophysical jets were published by Norman et al. (1982) and Smith et al. (1985). Their simulations revealed hot-spot morphologies that were different from the simple one-shock structure envisaged by Blandford & Rees (1974). These papers were seminal in leading to a good physical understanding of the properties of supersonic extragalactic jets.
In this work we have carried out similar simulations with a view to addressing in detail the time variability of hot-spot morphology. In particular we address the question of whether the Pictor A morphology could arise naturally in a light supersonic jet. Our simulations were conducted using the VH-1 code (Blondin & Lukfin 1993) which is an implementation of the Piecewise Parabolic Method (PPM) (Colella & Woodward 1984). An advantage of PPM for this type of simulation is its excellent resolution of shocks.
|
|
The simulations were computed on an axisymmetric grid,
with
![]() cells
in the axial and radial directions.
We performed calculations
with nine different cases of the jet parameters,
i.e. jet Mach number
M=5, 10, 50and the ratio of jet to background densities,
cells
in the axial and radial directions.
We performed calculations
with nine different cases of the jet parameters,
i.e. jet Mach number
M=5, 10, 50and the ratio of jet to background densities,
![]() .
In each case the jet density and pressure were
normalized by the respective values,
.
In each case the jet density and pressure were
normalized by the respective values,
![]() ,
in the background medium.
If we take
,
in the background medium.
If we take
![]() to be the temperature of the external medium,
then the normalising value of the velocity is
to be the temperature of the external medium,
then the normalising value of the velocity is
![]() .
The unit of length, x0, is defined by the
value of the
.
The unit of length, x0, is defined by the
value of the
![]() ,
in numerical units.
If we take the observed western hot-spot
,
in numerical units.
If we take the observed western hot-spot
![]() ,
for
,
for
![]() ,
as indicative of the jet diameter, then
,
as indicative of the jet diameter, then
![]() and the unit of time,
and the unit of time,
![]() .
As with simulations of this type,
the exact physical parameters of velocity and density are not recovered.
However, a high Mach number and low
density ratio serve to reproduce,
at least qualitatively, many of the features found in real jets.
.
As with simulations of this type,
the exact physical parameters of velocity and density are not recovered.
However, a high Mach number and low
density ratio serve to reproduce,
at least qualitatively, many of the features found in real jets.
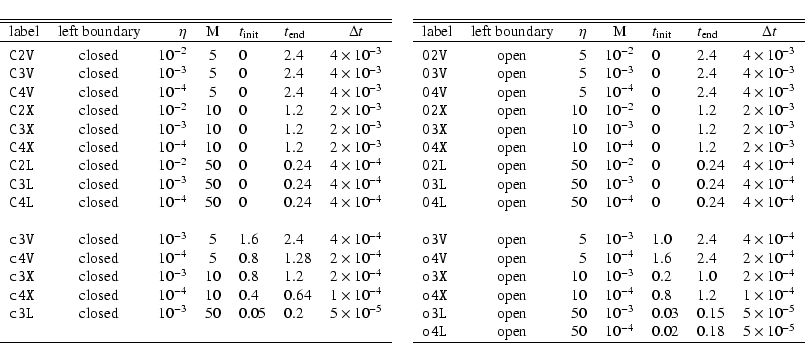
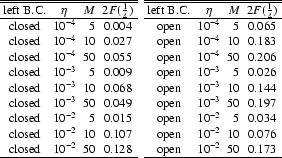
Table 1
lists the jet parameters, time resolution
and left boundary condition of our simulations.
We define the grid to be 10 units in the z direction
and 5 units in the radial direction.
Table 2
indicates the jet's total mass flux, force and power
for each choice of the basic parameters,
in terms of fiducial values of the temperature, T7,
and the number density of the background medium,
![]() .
For a jet with Mach number M,
density contrast
.
For a jet with Mach number M,
density contrast ![]() ,
adiabatic index
,
adiabatic index ![]() (assumed equal to the ambient medium),
and cross-sectional area
(assumed equal to the ambient medium),
and cross-sectional area
![]() ,
the initial flow velocity,
mass flux, force and kinetic power are
,
the initial flow velocity,
mass flux, force and kinetic power are
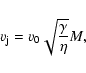 |
(1) |
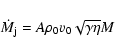 |
(2) |
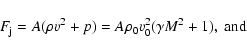 |
(3) |
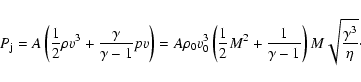 |
(4) |
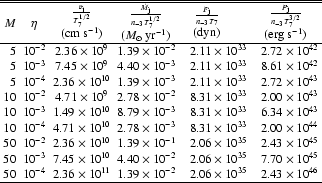 |
Each simulation is initialised with the high-velocity, low-density jet material extruding a small distance into the ambient medium. At every subsequent time step the conditions of the initial jet are recreated in the cells at the base of the jet on the left (inner z) boundary of the grid, and thus the jet's injected fluxes of mass, momentum and energy remain constant in time. We performed simulations with two different choices for the condition applied at the left boundary outside the radius of the jet. (1) A reflecting ("closed'') boundary condition represents the effects of the symmetry plane through the nucleus, felt by a jet that is close to its origin and counterjet. (2) An "open'' boundary allows free outflow of mass, momentum and energy, thereby representing systems where the hot-spot and bow shock are distant from the nucleus and not directly influenced by the opposite lobe. The outer z and r boundaries are open to outflow.
In our simulations, a scalar variable ![]() ,
as introduced in
Saxton et al. (2001), is passively advected with the gas.
Cells occupied purely by jet material are initially assigned the value
,
as introduced in
Saxton et al. (2001), is passively advected with the gas.
Cells occupied purely by jet material are initially assigned the value
![]() ;
and the ambient medium initially has
;
and the ambient medium initially has ![]() .
Thus
.
Thus ![]() traces the local fraction of matter originating in the jet.
traces the local fraction of matter originating in the jet.
We adopt the approximation of using the pressure field to trace the emissivity
of the relativistic particles within jet plasma
(e.g. Saxton et al. 2001).
This approximation is based on the fact that the synchrotron emissivity,
![]() is proportional to
is proportional to
![]() where p is the pressure,
B is the magnetic field and
where p is the pressure,
B is the magnetic field and ![]() is the spectral index.
If the magnetic
pressure,
is the spectral index.
If the magnetic
pressure, ![]() tracks the particle pressure,
then
tracks the particle pressure,
then
![]() ,
and
,
and
![]() typically.
Even if the magnetic pressure does not track the pressure faithfully,
it is likely that regions of high pressure still correspond to
regions of high emissivity.
typically.
Even if the magnetic pressure does not track the pressure faithfully,
it is likely that regions of high pressure still correspond to
regions of high emissivity.
We revolve the hydrodynamic data frames of ![]() and pto form 3D cylindrical structures.
Using
and pto form 3D cylindrical structures.
Using ![]() to distinguish synchrotron-emitting jet material
from gas originating in the background medium,
the weighted emissivity is then
to distinguish synchrotron-emitting jet material
from gas originating in the background medium,
the weighted emissivity is then
![]() .
By integrating
.
By integrating ![]() along rays through the 3D volume
we generate surface brightness images of the jet and cocoon
at a selected orientation.
The resulting images are compared with observations
in Sect. 5.
along rays through the 3D volume
we generate surface brightness images of the jet and cocoon
at a selected orientation.
The resulting images are compared with observations
in Sect. 5.
The density distribution and velocity fields of representative frames
from six of the simulations are shown in Fig. 3.
At the beginning of each simulation,
a bow shock is quickly established around the jet.
The regions just downstream and inside the bow shock
are dominated by the shocked dense interstellar medium (ISM).
The innermost regions immediately surrounding the jet
are occupied by a cocoon of low-density gas
moving in a turbulent backflow opposite the jet direction.
Flow velocities in some regions are comparable to
the initial jet velocity ![]() ,
and are much larger than the bow shock velocity
(see Fig. 4).
Turbulent velocities are typically lower in the outer parts of the cocoon,
further from the jet.
The scalar tracer
,
and are much larger than the bow shock velocity
(see Fig. 4).
Turbulent velocities are typically lower in the outer parts of the cocoon,
further from the jet.
The scalar tracer ![]() (see Fig. 5)
reveals that jet-derived matter dominates
the inner regions of the backflow,
whereas the outer regions just downstream of the bow shock
are entirely composed of background gas.
(see Fig. 5)
reveals that jet-derived matter dominates
the inner regions of the backflow,
whereas the outer regions just downstream of the bow shock
are entirely composed of background gas.
The evolution of the backflow depends upon the left boundary condition.
When the left boundary of the grid is open to outflow,
the backflow occupies a cylindrical "sheath''
surrounding and flowing opposite the jet,
ultimately flowing off the grid.
This "sheath'' has a radius a few times that of the jet.
It increases gradually as the jet progresses across the grid,
but is insensitive to ![]() .
Very little of the surrounding gas mixes with
backflowing jet plasma:
most of the fast-moving backflow
still exhibits high concentrations of jet plasma (
.
Very little of the surrounding gas mixes with
backflowing jet plasma:
most of the fast-moving backflow
still exhibits high concentrations of jet plasma (
![]() )
when it exits the left boundary
(see right column of Fig. 5).
)
when it exits the left boundary
(see right column of Fig. 5).
In simulations with a closed, reflecting boundary,
cocoon eddies accumulate inside a roughly conical volume,
which is widest near the left boundary,
and tapers towards the head of the jet.
This "wake'' cocoon
expands laterally as the jet progresses forwards,
and jet material accumulates and mixes with
the shocked ISM.
The eddies are typically smaller
and have lesser concentrations of jet matter (lower ![]() )
with increasing distance from the head of the jet
(see upper panels of Fig. 5).
)
with increasing distance from the head of the jet
(see upper panels of Fig. 5).
The density contrast of the jet, ![]() ,
affects the gross structure of
the surrounding radio emitting regions.
If the left boundary is closed,
jets with lower
,
affects the gross structure of
the surrounding radio emitting regions.
If the left boundary is closed,
jets with lower ![]() produce wider bow shocks and wider "wake'' cocoons
(see left panels of Fig. 3).
However in cases with an open boundary
the high-
produce wider bow shocks and wider "wake'' cocoons
(see left panels of Fig. 3).
However in cases with an open boundary
the high-![]() ,
fast backflowing "sheath'' cocoon
has approximately the same width,
,
fast backflowing "sheath'' cocoon
has approximately the same width,
![]()
![]() ,
for all the values of
,
for all the values of ![]() we have studied:
we have studied:
![]() and 10-4(see right panels of Fig. 5).
In such systems the bow shock widens marginally with decreasing
and 10-4(see right panels of Fig. 5).
In such systems the bow shock widens marginally with decreasing ![]() .
.
The amount of mixing between jet and ISM also shows a dependence upon ![]() .
For the open boundary mixing per unit length is more pronounced in the backflow
for the larger values of
.
For the open boundary mixing per unit length is more pronounced in the backflow
for the larger values of ![]() (see the right panels of
Fig. 5).
(see the right panels of
Fig. 5).
There is a similar dependence for the case of the closed boundary with some
additional features.
For
![]() ,
the cocoon widens almost linearly from the head of the jet
(radius
,
the cocoon widens almost linearly from the head of the jet
(radius ![]()
![]() )
and the degree of mixing in the backflow
increases more or less gradually with distance from this point.
However in cases with
)
and the degree of mixing in the backflow
increases more or less gradually with distance from this point.
However in cases with
![]() ,
the head of the jet is persistently surrounded by
a broad (radius
,
the head of the jet is persistently surrounded by
a broad (radius ![]()
![]() ), low-density, high-
), low-density, high-![]() ellipsoidal
region that is essentially the first turbulent cell in the backflow
(see upper-left panels of
Figs. 3, 5).
There is a lot of mixing at the trailing edge of this cavity
and average
ellipsoidal
region that is essentially the first turbulent cell in the backflow
(see upper-left panels of
Figs. 3, 5).
There is a lot of mixing at the trailing edge of this cavity
and average ![]() values decline rapidly
to the left of that region.
Cases with
values decline rapidly
to the left of that region.
Cases with
![]() show an intermediate behaviour:
the cavity is more extended in the z direction
and includes more fingers of entrained dense gas.
show an intermediate behaviour:
the cavity is more extended in the z direction
and includes more fingers of entrained dense gas.
In the ultra-light (
![]() )
jets with an enduring cavity,
the head of the jet surges back and forth along the axis
between the front and back ends of the cavity.
Similar surging behaviour occurs in most of the simulations,
to different extents and at different frequencies.
This cyclic process begins when
turbulence in the backflow briefly compresses and constricts the jet
at one point
(see Fig. 7, panels 2 and 3).
A portion of the front of jet is cut off,
and its remnant mixes into the front of the cocoon.
Jet plasma accumulates upstream of the obstruction
(Fig. 7, panel 4),
until it is able to surge through to a point much closer to the bow shock
(Fig. 7, panels 5 and 6).
Thus the terminal shock of the jet is not a constant feature:
it may occur close to the bow shock
(when the jet has just undergone a surge),
or it may occur many jet diameters further upstream
(when the jet is being disturbed by turbulence).
The extent and frequency of surging depends on the jet parameters
and the condition of the left boundary.
In the closed-boundary,
)
jets with an enduring cavity,
the head of the jet surges back and forth along the axis
between the front and back ends of the cavity.
Similar surging behaviour occurs in most of the simulations,
to different extents and at different frequencies.
This cyclic process begins when
turbulence in the backflow briefly compresses and constricts the jet
at one point
(see Fig. 7, panels 2 and 3).
A portion of the front of jet is cut off,
and its remnant mixes into the front of the cocoon.
Jet plasma accumulates upstream of the obstruction
(Fig. 7, panel 4),
until it is able to surge through to a point much closer to the bow shock
(Fig. 7, panels 5 and 6).
Thus the terminal shock of the jet is not a constant feature:
it may occur close to the bow shock
(when the jet has just undergone a surge),
or it may occur many jet diameters further upstream
(when the jet is being disturbed by turbulence).
The extent and frequency of surging depends on the jet parameters
and the condition of the left boundary.
In the closed-boundary,
![]() cases,
the strong, persistent, frontal eddy
frequently pinches off the jet at the back end of the cavity,
where the backflow converges back towards the surface of the jet.
Cases with
cases,
the strong, persistent, frontal eddy
frequently pinches off the jet at the back end of the cavity,
where the backflow converges back towards the surface of the jet.
Cases with
![]() exhibit unusually extreme surging behaviour,
because the relatively violent turbulence throughout the entire cocoon
can pinch this ultra-light jet at almost any point along its length.
exhibit unusually extreme surging behaviour,
because the relatively violent turbulence throughout the entire cocoon
can pinch this ultra-light jet at almost any point along its length.
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\begin{array}{c}\includegraphics[...
...cm,clip]{MS1285f03_exit-2mx_flow0500.eps}\end{array}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg77.gif) |
Figure 3:
Snapshots of flow velocity vectors superimposed on a |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\begin{array}{c}\includegraphics[...
...cm,clip]{MS1285f04_exit-2mx_velm0500.eps}\end{array}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg78.gif) |
Figure 4:
Linearly scaled snapshots of the velocity magnitude,
with the initial jet velocity |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\begin{array}{c}\includegraphics[...
...cm,clip]{MS1285f05_exit-2mx_scal0500.eps}\end{array}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg79.gif) |
Figure 5:
Scalar tracer |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\begin{array}{c}\includegraphics[...
...cm,clip]{MS1285f06_exit-2mx_pres0500.eps}\end{array}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg80.gif) |
Figure 6: Pressure maps corresponding to the frames in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\begin{array}{c}\includegraphics...
...cs[width=5cm,clip]{MS1285f07_surge_6.eps}\end{array}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg82.gif) |
Figure 7:
Snapshots of the scalar tracer, |
| Open with DEXTER | |
As discussed above (Sect. 3.2),
the regions of strongest emission are
high pressure shock features with
a significant concentration of jet plasma
(i.e. large ![]() ).
In agreement with past studies
(Norman et al. 1982),
we find several types of shocks
characterising particular regions of the jet and its surroundings.
The plots of
).
In agreement with past studies
(Norman et al. 1982),
we find several types of shocks
characterising particular regions of the jet and its surroundings.
The plots of
![]() in Fig. 16 show the shocks
appearing as intense lines, in several regions of the flow.
in Fig. 16 show the shocks
appearing as intense lines, in several regions of the flow.
We classify the different shocked regions as follows:
In summary, allowing for the axial symmetry of our simulations, the kinds of bright three-dimensional structures that are possible include: bright point-like, disk-like and cone-like shocks within the jet; in the backflow there may occur a diversity of rings and circular ribbons, with potentially flat, curved or solid cross-sections. In the following section, we consider how these structures may appear in two-dimensional projections onto the sky, and how these images may compare with observations.
In this section we compare rendered images with the morphology of bright structures evident in the observations of Pictor A. The optical observations (Fig. 2) are a guide to the current positions of the shocks. Because of the longer lifetime of radio emitting electrons the radio image (Fig. 1) is indicative of the overall distribution of jet plasma within the cocoon.
In the rendering of our simulations we seek physical configurations that show a bright hot-spot at the front of the jet and a transverse bar upstream of the hot-spot. As refinements, we prefer images in which the bar appears brightened at its edges. The optical image (Fig. 2) also suggests faint arcs connecting the ends of the bar to the hot-spot. We also have in mind (in the optical data) the bright knot of emission at the intersection of the jet axis and the bar, and the faint tail of emission leading from that knot to the east.
We generated ray-traced images of each frame of each simulation,
with the jet oriented at a variety of inclinations,
![]() (
(![]() is the angle between the jet and the line of sight).
We inspected and compared all the resulting
images and sorted them somewhat subjectively
according to their consistency with the topology, proportions
and brightness ratios seen in the Pictor A observations.
In the following we consider the effects of orientation
upon the quality of the matching rendered images,
and the effects of the jet parameters.
We also inspect the underlying physical nature of the bright features
and their temporal evolution.
is the angle between the jet and the line of sight).
We inspected and compared all the resulting
images and sorted them somewhat subjectively
according to their consistency with the topology, proportions
and brightness ratios seen in the Pictor A observations.
In the following we consider the effects of orientation
upon the quality of the matching rendered images,
and the effects of the jet parameters.
We also inspect the underlying physical nature of the bright features
and their temporal evolution.
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...hics[width=5cm,clip]{MS1285f08_jet-2mx_045f0357.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg86.gif) |
Figure 8:
|
| Open with DEXTER | |
The orientation of the jet has a substantial effect on the projected appearance of the axially symmetric luminous features surrounding the jet.
The hot-spot and knot are not decisive characteristics, since diamond and terminal shocks appear at numerous instances and their appearance is virtually independent of orientation. However the transverse bar in the Pictor A observations provides a tight constraint on the selection of appropriate rendered images. This elongated feature must be the projection of at least one luminous structure that is three-dimensionally extended. Therefore it is necessary but not sufficient to select snapshots that contain extended high-pressure features. When projected onto the sky at some orientation, only a subset of these configurations produce images similar to the observations.
When the jet is at a large angle to the plane of the sky,
e.g.
![]() ,
very few frames show the desired topology and brightness:
typically a few times
,
very few frames show the desired topology and brightness:
typically a few times ![]() of frames
have a subjective resemblance to the images.
The best images of jets at
of frames
have a subjective resemblance to the images.
The best images of jets at ![]() inclinations
are shown in Fig. 8.
In these cases,
the appearance of a straight "bar,'' if any,
is a coincidence due to the visual superposition of the near and far edges
of unconnected rings in the backflow;
it is not a single physical structure.
One of the positive features of the better renderings at
inclinations
are shown in Fig. 8.
In these cases,
the appearance of a straight "bar,'' if any,
is a coincidence due to the visual superposition of the near and far edges
of unconnected rings in the backflow;
it is not a single physical structure.
One of the positive features of the better renderings at
![]() is the abundance of snapshots in which
the hot-spot is projected in front of
an edge of a bright ring in the backflow,
thereby resembling the faint arcs
connecting the hot-spot to the bar in the optical observations.
However the occurence of conspicuously elliptical features
throughout the image tends to ruin the overall resemblence,
and the accidental bars appearing by superposition
are never much wider than the hot-spot.
Indeed the least-bad matches have small features
compared to the initial jet,
is the abundance of snapshots in which
the hot-spot is projected in front of
an edge of a bright ring in the backflow,
thereby resembling the faint arcs
connecting the hot-spot to the bar in the optical observations.
However the occurence of conspicuously elliptical features
throughout the image tends to ruin the overall resemblence,
and the accidental bars appearing by superposition
are never much wider than the hot-spot.
Indeed the least-bad matches have small features
compared to the initial jet,
![]() ,
and we speculate that the resemblences might be even less convincing
if these structures could have been resolved more finely
by the simulations.
,
and we speculate that the resemblences might be even less convincing
if these structures could have been resolved more finely
by the simulations.
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...hics[width=5cm,clip]{MS1285f09_jet-2ml_030f0461.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg90.gif) |
Figure 9:
Some of the best examples of raytraced images
of a jet inclined at
|
| Open with DEXTER | |
When the system is viewed at inclinations
![]() ,
the matches are more abundant and better in quality.
Approximately
,
the matches are more abundant and better in quality.
Approximately ![]() of all frames rendered at
of all frames rendered at
![]() show features qualitatively similar to
the Pictor A observations.
Approximately
show features qualitatively similar to
the Pictor A observations.
Approximately ![]() of the frames at
of the frames at
![]() show the same quality of resemblance.
Inclinations of
show the same quality of resemblance.
Inclinations of
![]() produce images with a straight, bright transverse bar
behind the hot-spot.
Lower inclinations, progressively down to
produce images with a straight, bright transverse bar
behind the hot-spot.
Lower inclinations, progressively down to
![]() ,
yield more images in which arcs appear to connect the ends of the bar
with the hot-spot.
However the trade-off is that the apparent bar
may be less straight and distinct.
,
yield more images in which arcs appear to connect the ends of the bar
with the hot-spot.
However the trade-off is that the apparent bar
may be less straight and distinct.
At inclinations as low as
![]() ,
frames that discernibly resemble observation
are as rare as
,
frames that discernibly resemble observation
are as rare as ![]() 0.6%.
Some of the best examples are presented in Fig. 9,
but they are not compelling matches.
Like the best morphological matches at
0.6%.
Some of the best examples are presented in Fig. 9,
but they are not compelling matches.
Like the best morphological matches at
![]() ,
their bar radii are
,
their bar radii are ![]()
![]() ,
and they tend to involve coincidental superposition of
the far side of an annulus behind the hot-spot.
There are instances showing a favourable "pedestal'' or "arcs''
near the hot-spot,
but the best simulated "bar'' features
are plainly elliptical rather than straight.
,
and they tend to involve coincidental superposition of
the far side of an annulus behind the hot-spot.
There are instances showing a favourable "pedestal'' or "arcs''
near the hot-spot,
but the best simulated "bar'' features
are plainly elliptical rather than straight.
At a given inclination,
good morphologies appear with roughly equal abundance
for all choices of the jet parameters,
with the exception of the extreme case
![]() where the turbulent backflow and the jet behave abnormally
(see Sect. 5.2).
For example renderings,
see Figs. 10-15,
and a selection of corresponding plots of
where the turbulent backflow and the jet behave abnormally
(see Sect. 5.2).
For example renderings,
see Figs. 10-15,
and a selection of corresponding plots of
![]() in
Fig. 16,
which indentify the principal intense linear features with shocks.
We display more examples for cases where
in
Fig. 16,
which indentify the principal intense linear features with shocks.
We display more examples for cases where
![]() but this is only because these simulations produced more frames of data,
and the emission features evolve more rapidly compared to
the jet's advance across the grid
(see Sect. 5.3 below).
but this is only because these simulations produced more frames of data,
and the emission features evolve more rapidly compared to
the jet's advance across the grid
(see Sect. 5.3 below).
As implied by the distribution of ![]() and the commonplace occurrence of annular shocks
throughout the backflow,
the rendered snapshots include
bright bars of diverse widths,
(up to approximately
and the commonplace occurrence of annular shocks
throughout the backflow,
the rendered snapshots include
bright bars of diverse widths,
(up to approximately
![]() in cases with
in cases with
![]() ).
The observed filament
(Figs. 1, and 2)
has a radius four times that of the hot-spot.
If the observed hot-spot corresponds to the width of the jet,
then all of our simulations are in principle
able to produce bright shocks in the backflow
that are consistent in size with the observed filament.
).
The observed filament
(Figs. 1, and 2)
has a radius four times that of the hot-spot.
If the observed hot-spot corresponds to the width of the jet,
then all of our simulations are in principle
able to produce bright shocks in the backflow
that are consistent in size with the observed filament.
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...ics[width=5cm,clip]{MS1285f10_fine-4m5_010f0307.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg98.gif) |
Figure 10:
A selection of morphological matches to Pictor A,
from ray-traced renderings in a
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...ics[width=5cm,clip]{MS1285f11_fine-4mx_000f0878.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg99.gif) |
Figure 11:
Morphological matches as in Fig. 10
but with jet parameters
|
| Open with DEXTER | |
| |
Figure 12:
Morphological matches as in Fig. 10
but with jet parameters
|
| Open with DEXTER | |
| |
Figure 13:
Morphological matches as in Fig. 10
but with jet parameters
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...graphics[width=5cm,clip]{MS1285f14_jet-2mx_000f0389.eps}\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg102.gif) |
Figure 14:
Morphological matches as in Fig. 10
but with jet parameters
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...hics[width=5cm,clip]{MS1285f15_jet-2ml_000f0547.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg103.gif) |
Figure 15:
Morphological matches as in Fig. 10
but with jet parameters
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...graphics[width=5cm,clip]{MS1285f16_jet-2mx_grap0389.eps}\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg104.gif) |
Figure 16:
Plots of
|
| Open with DEXTER | |
Let us now consider the overall brightness distribution of various features
in the image.
This includes the brightness distribution of the filament,
its brightness relative to the hot-spot and
the overall brightness of the hot-spot and bar relative to the lobe.
Note that in the observations, the brightest part of the filament
is approximately ![]() of the peak brightness in the hot-spot,
in the radio and about
of the peak brightness in the hot-spot,
in the radio and about ![]() in the optical.
in the optical.
Some frames rendered from the simulations have shapes
that are consistent with the observations of Pictor A,
in terms of qualitative topology and approximate proportions,
but may differ from the observations in terms of brightness.
For instance, in some imperfect examples,
the bar is dim on the edges rather than being edge-bright,
e.g.
![]() (in centre panel, upper row of Fig. 11,
and right column, Fig. 23)
and
(in centre panel, upper row of Fig. 11,
and right column, Fig. 23)
and
![]() (centre panel, lower row of Fig. 11).
In these cases,
the bar is the image of a disk-like (rather than annular) shock
that cuts the jet and a high-
(centre panel, lower row of Fig. 11).
In these cases,
the bar is the image of a disk-like (rather than annular) shock
that cuts the jet and a high-![]() transverse stream
diverging from the jet.
transverse stream
diverging from the jet.
In some cases in which the morphology is approximately correct,
the ratio of filament to hot-spot brightness is larger than observed:
e.g.
![]() shown in the central panel of Fig. 14;
and
shown in the central panel of Fig. 14;
and
![]() (right column, Fig. 22),
in which the wide bar is a shock cutting through
both the jet and cocoon.
However, we cannot rule out cases with overly bright bars
since relativistic beaming may be important in the hot-spot.
There are also examples in
which the ratio of filament to hot-spot brightness
is approximately correct, e.g. the
three examples in the uper row of Fig. 15.
Here the brightness ratios are approximately
(right column, Fig. 22),
in which the wide bar is a shock cutting through
both the jet and cocoon.
However, we cannot rule out cases with overly bright bars
since relativistic beaming may be important in the hot-spot.
There are also examples in
which the ratio of filament to hot-spot brightness
is approximately correct, e.g. the
three examples in the uper row of Fig. 15.
Here the brightness ratios are approximately ![]() ,
,
![]() and
and ![]() (ordered from left to right).
The appropriate ratios are preferentially found
in the highest Mach number cases.
A filament at the
(ordered from left to right).
The appropriate ratios are preferentially found
in the highest Mach number cases.
A filament at the ![]() level
is generally more difficult to find in a low Mach number
lobe because of the lack of contrast with the background cocoon.
The physics of the contrast between hot-spot and cocoon
is discussed further below.
level
is generally more difficult to find in a low Mach number
lobe because of the lack of contrast with the background cocoon.
The physics of the contrast between hot-spot and cocoon
is discussed further below.
The observed filament is extended more to the south of the inferred jet than the north. Because of the axisymmetry of the simulations, this feature is not replicated. However, an axisymmetric approximation is justified in view of the very straight jet evident in the X-ray image (Wilson et al. 2001). Nevertheless, in most of the matches that we have presented in Figs. 10-15, the simulated filament is seen to be brighter towards the ends. This is the result of the annular shocks arising in the region of the hot-spot.
A feature of the observations that is replicated
in approximately ![]() of the matches in
Figs. 10-15
is a small "knot'' of emission at the centre of the bar.
Such a feature is often the result of the superposition
the bright annulus with a section of the jet that is also bright,
such as a shock upstream of and related to the terminal shock
of the hot-spot.
of the matches in
Figs. 10-15
is a small "knot'' of emission at the centre of the bar.
Such a feature is often the result of the superposition
the bright annulus with a section of the jet that is also bright,
such as a shock upstream of and related to the terminal shock
of the hot-spot.
Yet another observational feature that appears in almost every panel in Figs. 10-15 is the radio knot south-east of the bar along the inferred direction of the jet. These knots correspond to diamond shocks in the jet; their exact location depends stochastically upon the details of the turbulence in the cocoon.
In the radio observations (Fig. 1),
diffuse emission from the radio lobe in regions near the bar and hot-spot
is ![]() 0.5% of the maximum surface brightness of the hot-spot.
As Perley et al. noted,
such a large contrast is highly unusual for a radio galaxy.
Ideally, our ray-traced images should produce a similar contrast
between the brightness of bar and hot-spot
and the wispy rings and dim emission pervading the rest of the cocoon.
0.5% of the maximum surface brightness of the hot-spot.
As Perley et al. noted,
such a large contrast is highly unusual for a radio galaxy.
Ideally, our ray-traced images should produce a similar contrast
between the brightness of bar and hot-spot
and the wispy rings and dim emission pervading the rest of the cocoon.
Ideally, higher Mach number jets produce hot-spots
with a higher contrast to the lobe.
In simple terms, if the jet terminates in a single steady shock,
the pressure contrast between the hot-spot
and the cocoon is given by
![]() .
This aspect of jet physics lead Perley et al.
to suggest that the Mach number may be as high as 40.
In terms of a realtivistic jet,
this is equivalent to a Lorentz factor of 24.
However, the inferred parameters of the hot-spot
(especially the pressure)
could be significantly affected by beaming.
The beaming pattern may be quite complex
in view of the velocity field produced by the terminal oblique shock
(see Sect. 5.4).
.
This aspect of jet physics lead Perley et al.
to suggest that the Mach number may be as high as 40.
In terms of a realtivistic jet,
this is equivalent to a Lorentz factor of 24.
However, the inferred parameters of the hot-spot
(especially the pressure)
could be significantly affected by beaming.
The beaming pattern may be quite complex
in view of the velocity field produced by the terminal oblique shock
(see Sect. 5.4).
Ray-traced images from the simulations with parameters
![]() (see Fig. 10)
give bar and hot-spot features that are typically
only
(see Fig. 10)
give bar and hot-spot features that are typically
only ![]() 10 times brighter than the background cocoon.
The brightness contrast is greater
in simulations with
10 times brighter than the background cocoon.
The brightness contrast is greater
in simulations with
![]() (see Fig. 11).
In this case the contrast varies
bewteen 101.3 and 101.7.
Simulations of very fast jets,
(e.g. case C2L, with parameters
(see Fig. 11).
In this case the contrast varies
bewteen 101.3 and 101.7.
Simulations of very fast jets,
(e.g. case C2L, with parameters
![]() )
can yield brightness contrasts in the range, i.e
)
can yield brightness contrasts in the range, i.e ![]() 102-2.5 -
consistent with the radio images of Perley et al.
The tendency towards increasing contrast in the hot-spot and bar
can be seen in the example contour maps of surface brightness
for
102-2.5 -
consistent with the radio images of Perley et al.
The tendency towards increasing contrast in the hot-spot and bar
can be seen in the example contour maps of surface brightness
for
![]() and for the lower-M cases of
and for the lower-M cases of
![]() in Fig. 17.
in Fig. 17.
However this trend breaks
in the case C4L where
![]() ;
the brightness contrast is exceptionally low
- typically
;
the brightness contrast is exceptionally low
- typically ![]() 30 -
compared to the more sharply defined features
in the
30 -
compared to the more sharply defined features
in the
![]() and
and
![]() simulations.
This is an extreme manifestation of the surging behaviour
that we have already noted.
In this case the backflow turbulence is particularly vigorous
and remains so at locations well behind the front of the bow shock.
Strong eddies pinch off
the extremely light jet at numerous locations along its length,
and the jet's penetration into the cocoon
varies dramatically within a dynamical timescale.
Consequently, jet energy is deposited widely throughout the cocoon,
rather than being concentrated at a quasi-stable head;
moderately bright but transient rings and hot-spots
occur throughout a large volume.
This aspect may well be a feature of the
restriction to axisymmetry causing the two-dimensional turbulence
within the cocoon to be focussed on the jet.
simulations.
This is an extreme manifestation of the surging behaviour
that we have already noted.
In this case the backflow turbulence is particularly vigorous
and remains so at locations well behind the front of the bow shock.
Strong eddies pinch off
the extremely light jet at numerous locations along its length,
and the jet's penetration into the cocoon
varies dramatically within a dynamical timescale.
Consequently, jet energy is deposited widely throughout the cocoon,
rather than being concentrated at a quasi-stable head;
moderately bright but transient rings and hot-spots
occur throughout a large volume.
This aspect may well be a feature of the
restriction to axisymmetry causing the two-dimensional turbulence
within the cocoon to be focussed on the jet.
![\begin{figure}
\leavevmode
$\begin{array}{lcc}
&\eta=10^{-2}&\eta=10^{-4}
\\
M...
...m,clip]{MS1285f17_c_jet-4ml_cont0211.eps}\end{array}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg116.gif) |
Figure 17:
Ray-traced surface brightness contour maps of the hot-spot vicinity,
selected from the simulations with a closed left boundary.
Contour levels are at consecutive multiples of
|
| Open with DEXTER | |
Physical configurations producing the desired morphology of surface brightness are ephemeral products of the jet's pulsating head and turbulent motions within the cocoon. It is therefore interesting to consider how these transient features vary in time. These considerations are also motivated by the potential of using hot-spot brightness ratios as a measure of relativistic beaming. Although these calculations are not relativistic we can examine the intrinsic distribution of hot-spot intensities. If it were to be the case, for example, that order of magnitude fluctuations in the ratio of hot-spot luminosities were to be likely, then the use of luminosity ratios as a measure of relativistic speeds within hot-spots would be limited. We address this point below following consideration of the structure function of individual hot-spots.
The dynamical timescale of structures in the jet material,
such as the hot-spot and shocks in the jet and backflow,
characteristically depends upon the jet's diameter and internal sound speed,
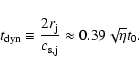 |
(5) |
On time scales longer than ![]()
![]() the behaviour of most structure functions is effectively white noise
(power index
the behaviour of most structure functions is effectively white noise
(power index ![]() );
whereas the behaviour is like "red noise'' on shorter time-scales.
The transition timescale between these behaviours is of order
);
whereas the behaviour is like "red noise'' on shorter time-scales.
The transition timescale between these behaviours is of order
![]() and depends little on M.
However jets with greater M generally show
greater relative variability.
and depends little on M.
However jets with greater M generally show
greater relative variability.
The one exceptional case is the
![]() simulation with the
closed boundary.
In this simulation there is long term evolution
(evident in the upturned curve at long time-scales in
the upper left panel of
Fig. 18)
related to the highly turbulent cocoon
upon which we have already commented in
Sect. 5.2.
simulation with the
closed boundary.
In this simulation there is long term evolution
(evident in the upturned curve at long time-scales in
the upper left panel of
Fig. 18)
related to the highly turbulent cocoon
upon which we have already commented in
Sect. 5.2.
In all cases bar the exceptional case, the left boundary condition has negligible effect on the variation of peak surface brightness (compare left and right columns of Fig. 18). This is the result of the proximity of the brightest structures to the terminal jet shock, rather than parts of the flow directly affected by the left boundary.
In physical units,
with
![]() ,
the dynamical timescale is
,
the dynamical timescale is
![]() for a jet with
for a jet with
![]() .
These time-scales are much shorter than the time taken for
light or jet plasma to traverse
the
.
These time-scales are much shorter than the time taken for
light or jet plasma to traverse
the
![]() projected distance
between the nucleus and either hot-spot.
Therefore the intrinsic flickering of two opposite hot-spots
are causally independent.
Figure 19
shows the cumulative distribution function of the ratio
of the peak brightness of one spot with respect to the other,
R = I1 / I2,
calculated from simulation output according to the derivation
in Appendix A.
The ratio has a more extended distribution
in cases with larger Mach number,
consistent with the larger amplitude of the structure function.
For a given choice of jet parameters
projected distance
between the nucleus and either hot-spot.
Therefore the intrinsic flickering of two opposite hot-spots
are causally independent.
Figure 19
shows the cumulative distribution function of the ratio
of the peak brightness of one spot with respect to the other,
R = I1 / I2,
calculated from simulation output according to the derivation
in Appendix A.
The ratio has a more extended distribution
in cases with larger Mach number,
consistent with the larger amplitude of the structure function.
For a given choice of jet parameters ![]() ,
an open boundary condition gives rise to substantially greater variability.
For instance, the probability that R>4 or
,
an open boundary condition gives rise to substantially greater variability.
For instance, the probability that R>4 or
![]() (see Table 3)
is approximately
(see Table 3)
is approximately ![]() for cases with M=50 and an open boundary
but only ranges from
for cases with M=50 and an open boundary
but only ranges from ![]()
![]() in the cases we studied with a closed boundary.
Likewise for small Mach number cases,
for example with
in the cases we studied with a closed boundary.
Likewise for small Mach number cases,
for example with
![]() the probability that R>4 or
the probability that R>4 or
![]() ranges from
ranges from ![]() with an open boundary
but only
with an open boundary
but only
![]() with a closed boundary.
Thus in cases where the jet has a low Mach number,
the relative brightnesses of hot-spots on different
sides of a source is a reasonable measure of non-intrinsic effects,
including relativistic beaming,
however intrinsic variability may be significant
if the Mach number is large (
with a closed boundary.
Thus in cases where the jet has a low Mach number,
the relative brightnesses of hot-spots on different
sides of a source is a reasonable measure of non-intrinsic effects,
including relativistic beaming,
however intrinsic variability may be significant
if the Mach number is large (![]() ).
In general terms these distributions provide a means
of quantifying the uncertainty in using hot-spot ratios in various
applications.
).
In general terms these distributions provide a means
of quantifying the uncertainty in using hot-spot ratios in various
applications.
 |
![\begin{figure}
\leavevmode
{
$\begin{array}{cc}
\mbox{closed boundary}&\mbox{op...
...th=7.5cm,clip]{MS1285f18_stru_op2.eps}\end{array}\\
\end{array}$ }
\end{figure}](/articles/aa/full/2002/39/aa1285/Timg136.gif) |
Figure 18: Normalised structure functions evaluated for flickering of the peak intensity of the emission regions. The left and right columns show different cases of the left boundary condition. For comparison of relative variability, the raw time series were normalised to the respective mean intensities. We excluded data points from during the early establishment of the cocoon and the eventual exit of the cocoon and jet through the right boundary. |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
{
$\begin{array}{cc}
\mbox{closed boundary}&\mbox{op...
...dth=7.5cm,clip]{MS1285f19_cdf_op2.eps}\end{array}\\
\end{array}$ }
\end{figure}](/articles/aa/full/2002/39/aa1285/Timg137.gif) |
Figure 19:
Cumulative probability distribution functions,
|
| Open with DEXTER | |
The reproduction of images resembling observations of
the western hot-spot of Pictor A requires
a strong shock on the jet axis,
and some other, wider shock structure
in high-![]() regions of the backflow.
However more than one kind of physical situation
can produce an appropriate image.
Here we consider the particular
instantaneous arrangements of shocks and jet plasma
that yield some of the example images selected and displayed in
Figs. 10-15.
Examples of the related dynamics are given in
Figs. 20-24,
in which the panels show simulated intensity maps
along with corresponding snapshots of
pressure,
regions of the backflow.
However more than one kind of physical situation
can produce an appropriate image.
Here we consider the particular
instantaneous arrangements of shocks and jet plasma
that yield some of the example images selected and displayed in
Figs. 10-15.
Examples of the related dynamics are given in
Figs. 20-24,
in which the panels show simulated intensity maps
along with corresponding snapshots of
pressure, ![]() and density with overlaid velocity vectors.
(In referring to these figures
we use L for left and R for right panels respectively.)
and density with overlaid velocity vectors.
(In referring to these figures
we use L for left and R for right panels respectively.)
In practice, a bar and hot-spot may arise from different underlying
structures at any stage of the jet's surging behaviour.
A hot-spot is commonly the termination shock
at the head of the jet.
However amongst our
![]() selections,
there are some cases
such as
Fig. 20L, 21L, 21R,
and the detailed case
Figs. 25-27
where the head of the jet is at the back of the leading cavity,
and not directly connected to the hot-spot.
In such cases the forward hot-spot consists of a high pressure region
of moderately mixed jet and thermal gas,
or is an isolated blob of high-
selections,
there are some cases
such as
Fig. 20L, 21L, 21R,
and the detailed case
Figs. 25-27
where the head of the jet is at the back of the leading cavity,
and not directly connected to the hot-spot.
In such cases the forward hot-spot consists of a high pressure region
of moderately mixed jet and thermal gas,
or is an isolated blob of high-![]() matter
previously separated from the jet.
matter
previously separated from the jet.
A bar may result from a variety of different kinds of annular or disk-like structures. In some cases (Figs. 20L, 20R, 24L) the bar is a broad shock at the head of the jet, or a body of jet plasma near the head. In some cases, it is the shocked rim of a funnel-shaped or disk-shaped volume of plasma that has split off the head of the jet but yet remains largely unmixed with the thermal gas in the cocoon (see Figs. 21R, 22R, 23R, 25-27). In other instances, the bar is a wide annular region in a part of the backflow well separated from the head of the jet, when such a region either preserves a moderate or high concentration of jet plasma, or experiences a strong shock locally (see Figs. 22R, 21L).
There are cases in which an ideal bar and hot-spot are formed,
but additional features spoil the resemblance to Pictor A.
For example,
in one selection at
t=0.4085t0(Fig. 23L;
or upper right panel of Fig. 11)
the bar and hot-spot are high-![]() shocks
in the vicinity of the jet's head,
but an additional strong reverse shock in the jet
appears as another bright feature to the left of the bar.
Such reverse shocks are an occasional by-product of the activity
that produces a hot-spot as a forward shock
and annular shocks propagating into the backflow.
Milder versions of the reverse shock may give the appearance
of the "knot'' or "pedestal'' observed on the jet axis.
shocks
in the vicinity of the jet's head,
but an additional strong reverse shock in the jet
appears as another bright feature to the left of the bar.
Such reverse shocks are an occasional by-product of the activity
that produces a hot-spot as a forward shock
and annular shocks propagating into the backflow.
Milder versions of the reverse shock may give the appearance
of the "knot'' or "pedestal'' observed on the jet axis.
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\includegraphics[width=7.5cm,clip...
...aphics[width=7.5cm]{MS1285f20_fine-4m5_flow1714.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg138.gif) |
Figure 20:
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\includegraphics[width=6.8cm,clip...
...cs[width=6.8cm,clip]{MS1285f21_jet-4m5_flow0265.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg139.gif) |
Figure 21:
Further examples of ray-traced frames resembling Pictor A,
with jet parameters
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\includegraphics[width=7.3cm,clip...
...s[width=7.3cm,clip]{MS1285f22_fine-4m5_flow0307.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg140.gif) |
Figure 22:
Further examples of ray-traced frames resembling Pictor A,
with jet parameters
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\includegraphics[width=7cm]{MS128...
...graphics[width=7cm]{MS1285f23_fine-4mx_flow2417.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg141.gif) |
Figure 23:
Further examples of ray-traced frames resembling Pictor A,
with jet parameters
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{cc}
\includegraphics[width=7cm]{MS128...
...egraphics[width=7cm]{MS1285f24_jet-2m5_flow0226.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg142.gif) |
Figure 24:
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...s[width=5cm,clip]{MS1285f25_s_fine-4m5_pres0992.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg143.gif) |
Figure 25: Sequence of pressure snapshots during the emergence and disappearance of a particular configuration of bar and hot-spot. Jet parameters are (10-4,5)and the left boundary is closed. |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...s[width=5cm,clip]{MS1285f26_s_fine-4m5_scal0992.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg144.gif) |
Figure 26: Sequence of scalar tracer images, showing local relative concentration of jet plasma, corresponding to the snapshots in Fig. 25. |
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5.4cm,cli...
...width=5.4cm,clip]{MS1285f27_s_fine-4m5_000f0992.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg145.gif) |
Figure 27:
Sequence of surface brightness images rendered at
|
| Open with DEXTER | |
![\begin{figure}
\leavevmode
$\begin{array}{ccc}
\includegraphics[width=5cm,clip]...
...s[width=5cm,clip]{MS1285f28_s_fine-4m5_flow0992.eps}\\
\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg146.gif) |
Figure 28:
Sequence of snapshots of the flow vectors
superimposed on |
| Open with DEXTER | |
It is not possible within the space of one paper to demonstrate the
physical details underlying the evolution
of all the physical configurations that
give the appearance of a bar and hot-spot.
In order to describe
one particular process for the formation of a bright hot-spot and bar,
we show in
Fig. 25,
a time sequence of linearly scaled pressure images
from the closed-boundary,
![]() simulation
with fine time resolution (simulation c4V).
The first frame is at
t=0.9952t0 and subsequent frames
are at intervals of 0.0006t0 numerical time units.
Figure 26
shows corresponding frames of the distribution of
simulation
with fine time resolution (simulation c4V).
The first frame is at
t=0.9952t0 and subsequent frames
are at intervals of 0.0006t0 numerical time units.
Figure 26
shows corresponding frames of the distribution of ![]() .
Figure 27
shows rendered images of the surface brightness at
.
Figure 27
shows rendered images of the surface brightness at
![]() .
Figure 28 shows corresponding flow velocity fields
superimposed upon
.
Figure 28 shows corresponding flow velocity fields
superimposed upon ![]() greyscale images.
greyscale images.
At the beginning of the sequence (frame 1),
we see the usual haze of emission from weak shocks
in the
![]() cavity at the head of the cocoon.
A bright hot-spot appears at the front of the cavity and this
is a high-pressure, shocked region with
cavity at the head of the cocoon.
A bright hot-spot appears at the front of the cavity and this
is a high-pressure, shocked region with
![]() ,
left behind by the head of the jet
when it was previously at the foremost extremity of its surging motion.
In this frame, the head of the jet is towards the rear of the cavity.
The jet splits at a terminal shock,
dividing into a funnel-shaped structure
consisting of unmixed jet plasma moving
in a radially outwards, positive-z direction,
at speeds comparable to
,
left behind by the head of the jet
when it was previously at the foremost extremity of its surging motion.
In this frame, the head of the jet is towards the rear of the cavity.
The jet splits at a terminal shock,
dividing into a funnel-shaped structure
consisting of unmixed jet plasma moving
in a radially outwards, positive-z direction,
at speeds comparable to ![]() .
The outermost edge of this structure is curled back upon itself,
and trails off into the backflow closest to the surface of the jet.
The region between this backflow and
the inner surface of the funnel is underpressured
compared to average conditions in the cocoon,
however the outer lip of the funnel is a high pressure surface.
.
The outermost edge of this structure is curled back upon itself,
and trails off into the backflow closest to the surface of the jet.
The region between this backflow and
the inner surface of the funnel is underpressured
compared to average conditions in the cocoon,
however the outer lip of the funnel is a high pressure surface.
In the second and third frames,
the edge of the funnel has advanced outwards.
In the third frame it collides with a flow of
![]() matter
moving in the negative-z direction near the outer surface of the cocoon.
The flow of gas around the funnel causes a strong annular shock which also
results in low presures at smaller r and z.
The shock produces significant emission,
and the result is a bright bar visible in images rendered at
matter
moving in the negative-z direction near the outer surface of the cocoon.
The flow of gas around the funnel causes a strong annular shock which also
results in low presures at smaller r and z.
The shock produces significant emission,
and the result is a bright bar visible in images rendered at
![]() .
.
During the activity that creates the bright ring, the diamond and transverse
shocks moving in both directions within the jet
produce several brighter knots of emission.
The knots move and fluctuate in brightness,
but they maintain an approximately constant separation.
Frames 3 to 5 also show a hazy skirt of emission surrounding the jet
to the left of the brightest knot;
it is a backflowing, high-![]() body of fluid
that previously came off the edge of the funnel.
body of fluid
that previously came off the edge of the funnel.
In frames 5 and 6
the front hot-spot fades,
as it spreads laterally, loses pressure
and undergoes a reduction in ![]() as a result of mixing.
Meanwhile,
the bright bar that persisted from frames 3 to 4 has also faded.
The interaction between the funnel's edge
and the well-mixed, outer-front backflow
has progressed.
The shocks of the initial interaction
have separated and spread into
a wider and complicated shock structure.
The outer edge of the high-
as a result of mixing.
Meanwhile,
the bright bar that persisted from frames 3 to 4 has also faded.
The interaction between the funnel's edge
and the well-mixed, outer-front backflow
has progressed.
The shocks of the initial interaction
have separated and spread into
a wider and complicated shock structure.
The outer edge of the high-![]() funnel is swept
in the negative-z, radially outwards direction
by the well-mixed backflow from the head of the cocoon.
In later frames (not shown), the funnel structure is greatly disrupted.
funnel is swept
in the negative-z, radially outwards direction
by the well-mixed backflow from the head of the cocoon.
In later frames (not shown), the funnel structure is greatly disrupted.
In this paper, we have presented a detailed analysis of simulations of light jets with a wide choice of parameters with the main aim of determining the cause of the filament upstream of the western hot-spot in Pictor A. The dominant physical principle underlying this analysis is that complex terminal shock structure is manifest in simulations of light supersonic jets and that, in projection, such a shock complex may resemble the Pictor A radio and optical observations of the region near the western hot-spot. Similar complexity has been realised in three dimensional simulations of light supersonic jets by Tregillis et al. (2001). One of the advantges of restriction to a two dimensional simulation, at this stage, is the ability to map out a larger region of parameter space and to utilise higher spatial resolution. In particular, we have carried out simulations with a density ratio of 10-4; these would be quite expensive in three dimensions.
One of the most important constraints on the simulations is that the bar is a thin structure and if it is three dimensional, it would appear to be almost edge-on. Our rendering of synthetic radio images at different orientations bears this out. Adequate morphologies are not reproduced at low inclinations. Another decisive requirement that implies an almost edge-on structure, is reproduction of a filament with low curvature.
At inclinations
![]() ,
geometric effects cannot convincingly produce
a long, straight bar frequently enough.
The projection of an annular structure with a ribbon-like cross-section
makes one side brighter than the other,
but the image is still significantly curved.
The accidental coincidence of the near and far sides of separate rings
in projection may give
the appearance of a straight feature,
but these tend to be narrower than the observed filament.
A structure with a very large radius of curvature
might appear straight,
but luminous structures of this type occur in our simulations
in regions where the coocon is no more than
,
geometric effects cannot convincingly produce
a long, straight bar frequently enough.
The projection of an annular structure with a ribbon-like cross-section
makes one side brighter than the other,
but the image is still significantly curved.
The accidental coincidence of the near and far sides of separate rings
in projection may give
the appearance of a straight feature,
but these tend to be narrower than the observed filament.
A structure with a very large radius of curvature
might appear straight,
but luminous structures of this type occur in our simulations
in regions where the coocon is no more than ![]()
![]() in radius.
Three dimensional hydrodynamical effects
may admit more complicated explanations for bar-like morphology.
However extreme departures from axial symmetry in the backflow seem unlikely,
given the strightness of the jet as indicated by the X-ray observations.
On the basis of non-relativistic hydrodynamics, we therefore think it likely
that the inclination angle,
in radius.
Three dimensional hydrodynamical effects
may admit more complicated explanations for bar-like morphology.
However extreme departures from axial symmetry in the backflow seem unlikely,
given the strightness of the jet as indicated by the X-ray observations.
On the basis of non-relativistic hydrodynamics, we therefore think it likely
that the inclination angle,
![]() .
.
If there is any easy way to produce the appearance of a bar
in a basically axisymmetric backflow
viewed at
![]() ,
it probably requires relativistic effects.
A ring or disk moving relativistically
appears more edge-on
than if it were at rest
(see Bicknell & Begelman 1996).
This would require the filament to be transient structure
moving with a pattern speed larger than the
expected hot-spot speed
,
it probably requires relativistic effects.
A ring or disk moving relativistically
appears more edge-on
than if it were at rest
(see Bicknell & Begelman 1996).
This would require the filament to be transient structure
moving with a pattern speed larger than the
expected hot-spot speed ![]() 0.1-0.2 c.
Relativistic beaming could also affect the brightness distribution
if the matter passing through the filament
and hot-spot shocks moves relativistically, brightening an annular structure
on whichever side has a post-shock flow directed towards our line of sight.
However the significance of these relativistic effects,
for hot-spots in general and for Pictor A in particular,
remains to be demonstrated,
and is beyond the scope of our present study.
0.1-0.2 c.
Relativistic beaming could also affect the brightness distribution
if the matter passing through the filament
and hot-spot shocks moves relativistically, brightening an annular structure
on whichever side has a post-shock flow directed towards our line of sight.
However the significance of these relativistic effects,
for hot-spots in general and for Pictor A in particular,
remains to be demonstrated,
and is beyond the scope of our present study.
Although all choices of the jet parameters, jet density ratio, ![]() ,
and
Mach number, M, yield instants with appropriate morphology,
the brightness characteristics of the resulting images
may distinguish the most plausible values of the Mach number.
Jets with larger Mach number typically produce terminal shock features
with higher peak intensity.
Perley et al. (1997) had deduced a high Mach number (
,
and
Mach number, M, yield instants with appropriate morphology,
the brightness characteristics of the resulting images
may distinguish the most plausible values of the Mach number.
Jets with larger Mach number typically produce terminal shock features
with higher peak intensity.
Perley et al. (1997) had deduced a high Mach number (
![]() )
for the jet in Pictor A based on the large ratio of the minimum pressures
in the hot-spot and lobes.
We have confirmed this in our simulations that show, for example,
a brightness contrast
)
for the jet in Pictor A based on the large ratio of the minimum pressures
in the hot-spot and lobes.
We have confirmed this in our simulations that show, for example,
a brightness contrast ![]() 100 for
100 for
![]() (see Sect. 5.2).
Nevertheless, the unusual
(see Sect. 5.2).
Nevertheless, the unusual
![]() simulation
produces a lower contrast and widely distributed rings in the backflow,
and these features are clearly ruled out by observation.
This may mean that the real jet parameters are less extreme,
or else the powerfully turbulent backflow that occurs in this case
may be less disruptive in three dimensions.
simulation
produces a lower contrast and widely distributed rings in the backflow,
and these features are clearly ruled out by observation.
This may mean that the real jet parameters are less extreme,
or else the powerfully turbulent backflow that occurs in this case
may be less disruptive in three dimensions.
We do not find such a clear diagnostic of the density contrast of the jet.
Cases with lower ![]() tend to produce broader cocoons,
especially the rounded cavity in
tend to produce broader cocoons,
especially the rounded cavity in
![]() simulations.
For jets with larger
simulations.
For jets with larger ![]() ,
the jet plasma and shocked thermal gas mix more rapidly in the cocoon.
However all of the parameter sets we investigated permit
the appearance of ephemeral bar-like sructures with
a range of widths,
including some with
,
the jet plasma and shocked thermal gas mix more rapidly in the cocoon.
However all of the parameter sets we investigated permit
the appearance of ephemeral bar-like sructures with
a range of widths,
including some with ![]()
![]() radius as required by the
observations.
radius as required by the
observations.
Many of our simulations
imply relativistic bulk flow,
![]() (see Table 2).
One aspect of the observations where relativistic effects may be relevant
concerns the large contrast between the
hot-spot and radio lobe empshasised by Perley et al. (1997).
On the basis of hydrodyamics alone,
this would indicate a Mach number of approximately 40-50,
or equivalently a Lorentz factor of approximately 25.
This has motivated the M=50 simulations described above.
Nevertheless, relativistic beaming may substantially contribute to the observed
hot-spot brightness.
This aspect may need to be taken into account with future
simulations with a fully relativistic code.
(see Table 2).
One aspect of the observations where relativistic effects may be relevant
concerns the large contrast between the
hot-spot and radio lobe empshasised by Perley et al. (1997).
On the basis of hydrodyamics alone,
this would indicate a Mach number of approximately 40-50,
or equivalently a Lorentz factor of approximately 25.
This has motivated the M=50 simulations described above.
Nevertheless, relativistic beaming may substantially contribute to the observed
hot-spot brightness.
This aspect may need to be taken into account with future
simulations with a fully relativistic code.
In their analysis of the Chandra X-ray Observatory data on Pictor A,
Wilson et al. (2001) have suggested that
an inclination
![]() is viable.
Larger angles are possible if jet magentic fields considerably less
than equipartition are allowed.
An inclination angle as small as
is viable.
Larger angles are possible if jet magentic fields considerably less
than equipartition are allowed.
An inclination angle as small as
![]() would be in direct contradiction to
our conclusion that the Pictor A radio structure is viewed at an angle of
would be in direct contradiction to
our conclusion that the Pictor A radio structure is viewed at an angle of
![]() .
It is therefore worthwhile to examine the question of orientation in
some detail.
.
It is therefore worthwhile to examine the question of orientation in
some detail.
The first part of the Wilson et al. (2001) argument relates to the arm-length
ratio of the radio source.
Assuming a velocity of advance for the hot-spot,
![]() (Arshakian & Longair 2000) and the measured
arm-length ratio of the source,
Wilson et al. (2001)
derive
(Arshakian & Longair 2000) and the measured
arm-length ratio of the source,
Wilson et al. (2001)
derive
![]() but caution that this estimate
by itself should not be taken too seriously for
an individual source.
The main limitation is probably the following:
The statistical result for hot-spot advance includes sources in which
the momentum of the jet is spread
over a wide area as a result of the "Dentist Drill'' effect
(Scheuer 1982), thereby slowing its average advance.
However, as we have remarked in justifying an axisymmetric
simulation, the western jet in Pictor
A appears to be very straight.
That is, it does not appear to be
substantially deflected and therefore
the advance of the hot-spot may be faster than the average
Arshakian & Longair (2000) value.
Moreover, in contrast to the western lobe,
the eastern lobe contains two hot-spots
indicating some spreading of the
jet force over a larger area than each hot-spot and a consequent
slower expansion rate and larger
arm-length ratio.
but caution that this estimate
by itself should not be taken too seriously for
an individual source.
The main limitation is probably the following:
The statistical result for hot-spot advance includes sources in which
the momentum of the jet is spread
over a wide area as a result of the "Dentist Drill'' effect
(Scheuer 1982), thereby slowing its average advance.
However, as we have remarked in justifying an axisymmetric
simulation, the western jet in Pictor
A appears to be very straight.
That is, it does not appear to be
substantially deflected and therefore
the advance of the hot-spot may be faster than the average
Arshakian & Longair (2000) value.
Moreover, in contrast to the western lobe,
the eastern lobe contains two hot-spots
indicating some spreading of the
jet force over a larger area than each hot-spot and a consequent
slower expansion rate and larger
arm-length ratio.
Now consider the effect of orientation on the X-ray emission and jet
brightness ratio.
As Wilson et al. (2001) remark, the X-ray emission resulting from scattering of
the cosmic microwave background radiation by the electrons in the jet is
proportional to
![]() where
where ![]() is the Doppler factor and
is the Doppler factor and
![]() is the
spectral index (Begelman & Sikora 1987; Dermer 1995).
The ratio of jet to counterjet X-ray brightnesses,
is the
spectral index (Begelman & Sikora 1987; Dermer 1995).
The ratio of jet to counterjet X-ray brightnesses, ![]() implies that
implies that
![]() for
for
![]() .
The radio estimate of
.
The radio estimate of ![]() does not provide as stringent a limit -
does not provide as stringent a limit -
![]() .
.
The main constraint on the angle
![]() is that it should not be so close to
is that it should not be so close to
![]() that the western jet is Doppler dimmed, in absolute terms,
irrespective of the ratio of jet to counterjet fluxes.
That is,
that the western jet is Doppler dimmed, in absolute terms,
irrespective of the ratio of jet to counterjet fluxes.
That is, ![]() should not be less than approximately 0.7 for an order of
magnitude decrease in the X-ray flux.
should not be less than approximately 0.7 for an order of
magnitude decrease in the X-ray flux.
For a given ratio, R, of jet to counterjet X-ray fluxes, we have
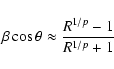 |
(6) |
A jet velocity of
![]() has other interesting
ramifications since gas would then emerge from oblique
shocks in the hot-spots with this velocity.
Some of this gas would be moving directly towards us with
has other interesting
ramifications since gas would then emerge from oblique
shocks in the hot-spots with this velocity.
Some of this gas would be moving directly towards us with
![]() (for
(for
![]() ).
The flux from that region of the hot-spot would be enhanced by a factor
of 60 and this may be another explanation for the large
ratio of hot-spot surface brightness to lobe surface brightness
(Perley et al. 1997).
).
The flux from that region of the hot-spot would be enhanced by a factor
of 60 and this may be another explanation for the large
ratio of hot-spot surface brightness to lobe surface brightness
(Perley et al. 1997).
If an almost side-on orientation proves to be untenable, then an alternative is that the limitations of an axisymmetric solution do not allow for a partial ring. That is, the ring could be brighter in one part than another as a result of three dimensional hydrodynamic effects. This may be consistent with the faint structures north of the filament seen in the greyscale image of the Perley et al. (1997) radio data, the Roeser (1989) optical image (see Fig. 3 of Wilson et al. 2001) and the VLT optical image (Fig. 2). These features may indicate a non-uniformly bright ring viewed at a more acute angle. We do not favour this explanation because of the straightness of the observed filament.
Another point in favour of
![]() is that the
western hot-spot appears, in projection, at the edge of a wide lobe.
If the source were to viewed at, say
is that the
western hot-spot appears, in projection, at the edge of a wide lobe.
If the source were to viewed at, say
![]() ,
then the hot-spot would most likely appear closer to the middle of the lobe.
In addition such a small viewing angle makes the total extent of the source
quite large (
,
then the hot-spot would most likely appear closer to the middle of the lobe.
In addition such a small viewing angle makes the total extent of the source
quite large (![]() 1.3 Mpc).
Radio galaxies this large are not unknown, but are fairly exceptional.
1.3 Mpc).
Radio galaxies this large are not unknown, but are fairly exceptional.
The construction of cumulative distribution functions for hot-spot ratios has been incidental to the main purpose of this paper. However, it is of general interest and quantifies the role of intrinsic variability in using such ratios for the estimation of say, relativistic effects.
The calculation of structure functions in jet simulations could have wide applicability. For example, the structure function of internal shocks could be applied to blazars.
![\begin{figure}
\leavevmode
$\begin{array}{c}
\includegraphics[width=8.8cm,clip]{MS1285f29_doppler.eps}\end{array}$\end{figure}](/articles/aa/full/2002/39/aa1285/Timg179.gif) |
Figure 29: The Doppler factor of the jet for a given ratio of jet to counter-jet surface brightness. The cases R=10, 20, 50are shown by solid, dotted and dashed lines respectively. Wilson et al. (2001) find R>10 for Pictor A. |
| Open with DEXTER | |
Acknowledgements
This work was supported by an Australian Research Council Large Grant, A69905341 and grants of computing time from the ANU Supercomputer Facility.
In each simulation the bright features in the vicinity of the hot-spot
are unsteady, dynamic structures.
The intrinsic variability of the peak intensity, I, of the hot-spot
is easily quantified as a cumulative probability distribution function,
G(I). This function is numerically approximated
by sorting the instantaneous I values
from a representative period
![]() of the simulation,
in which
of the simulation,
in which
![]() .
The sample must be representative in the sense that
it begins and ends during the time in which the cocoon is well
established and both the head of the jet and the bow shock
are not close to any of the boundaries of the computational grid.
If the intensity samples
.
The sample must be representative in the sense that
it begins and ends during the time in which the cocoon is well
established and both the head of the jet and the bow shock
are not close to any of the boundaries of the computational grid.
If the intensity samples ![]() are ranked in ascending order,
are ranked in ascending order,
![]() ,
for
,
for
![]() ,
then the cumulative distribution function of
the peak intensity is
,
then the cumulative distribution function of
the peak intensity is
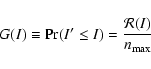 |
(A.1) |
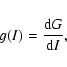 |
(A.2) |
If the two jet and counter-jet have the same physical parameters
and the respective hot-spots are separated by a distance
exceeding
![]() then the hot-spots are causally independent.
The probability distribution, f(R), of the ratio, R, of hot-spot peak intensities
can be derived from the intrinsic distributions of one hot-spot.
then the hot-spots are causally independent.
The probability distribution, f(R), of the ratio, R, of hot-spot peak intensities
can be derived from the intrinsic distributions of one hot-spot.
| f(R) | |||
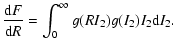 |
(A.3) |
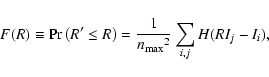 |
(A.4) |