A&A 393, 733-748 (2002)
DOI: 10.1051/0004-6361:20021067

Drifting sub-pulse analysis using the two-dimensional Fourier transform

R. T. Edwards1 - B. W. Stappers1,2


1 - Astronomical Institute ``Anton Pannekoek'', University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 - Stichting ASTRON, Postbus 2, 7990 AA Dwingeloo, The Netherlands

Received 27 November 2001 / Accepted 19 July 2002

Abstract
The basic form of drifting sub-pulses is that of a periodicity whose phase depends (approximately linearly) on both pulse longitude and pulse number. As such, we argue that the two-dimensional Fourier transform of the longitude-time data (called the Two-Dimensional Fluctuation Spectrum; 2DFS) presents an ideal basis for studies of this phenomenon. We examine the 2DFS of a pulsar signal synthesized using the parameters of an empirical model for sub-pulse behaviour. We show that the transform concentrates the modulation power to a relatively small area of phase space in the region corresponding to the characteristic frequency of sub-pulses in longitude and pulse number. This property enables the detection of the presence and parameters of drifting sub-pulses with great sensitivity even in data where the noise level far exceeds the instantaneous flux density of individual pulses. The amplitude of drifting sub-pulses is modulated in time by scintillation and pulse nulling and in longitude by the rotating viewing geometry (with an envelope similar to that of the mean pulse profile). In addition, sub-pulse phase as a function of longitude and pulse number can differ from that of a sinusoid due to variations in the drift rate (often associated with nulling) and through the varying rate of traverse of magnetic azimuth afforded by the sight line. These deviations from uniform sub-pulse drift manifest in the 2DFS as broadening of the otherwise delta-function response of a uniform sinusoid. We show how these phase and amplitude variations can be extracted from the complex spectrum.

Key words: methods: analytical - pulsars: general


1 Introduction

Very soon after the discovery of pulsars, it was noticed that the intensity data sometimes showed "second periodicities'' within each pulse, and that the relative phase of this periodic signal drifted in an organised manner from pulse to pulse (Drake & Craft 1968). The striking patterns made by drifting sub-pulses in two-dimensional pulse longitude-time diagrams seemed to be saying something about the fundamentals of radio pulsar emission, but the question was, and still is, "what?'' Numerous studies of the phenomenon were conducted in the first few years of pulsar science (e.g. Taylor et al. 1969; Sutton et al. 1970; Cole 1970; Backer 1970a,b; Taylor & Huguenin 1971; Backer 1973; Page 1973), their frequency steadily decreasing as the limitations of existing online (recording) and offline (analysis) equipment were reached. Along with attempts at fitting the data with sub-pulses and tracking their drift, the Fourier technique developed by Backer in the references above (now known as the longitude-resolved fluctuation spectrum, or LRFS) came to be perhaps the most widely used means of examining the average properties of sub-pulse drift.

With the availability of modern digital back-ends and convenient offline computing power, we believe that there is now potential for renewed progress in the field of drifting sub-pulses. We describe in this paper a means of analysis of drifting sub-pulse data using what may be considered an extension of the Fourier work of Backer. The technique was first conceived as a means of detecting and characterising drifting sub-pulses in the large population of moderately weak pulsars that have been discovered since the 1970s when most studies took place. It is also useful, when sufficient signal-to-noise ratio is available, for the investigation of what might be considered the fine details of the phenomenon: deviations from constant amplitude sub-pulses with purely uniform phase evolution. We begin with a mathematical description of a drifting sub-pulse signal as a function of pulse longitude and pulse number (Sect. 2) and examine its two-dimensional Fourier response (Sect. 3). We then describe a technique for measuring the deviations of a given signal from a uniform pure sinusoid (Sect. 4.1), examine what is expected under the usual model of drifting sub-pulses (Sect. 4.2), and use this model as a basis for simulations testing the applicability of the methods of analysis described here (Sect. 4.3).

   
2 Mathematical model of drifting sub-pulse signals

2.1 The form of drifting sub-pulses

The characteristic form of drifting sub-pulses is difficult to miss in a suitable plot of high-quality data. Plotted as intensity as a function of pulse longitude and pulse number, a distinctive "tire tread'' pattern is made as the sub pulses drift monotonically in longitude with each successive pulse. The form is essentially that of a windowed two-dimensional sinusoid. The characteristic period of the sub-pulses in pulse longitude (P2) and pulse number ($\hat{P_3}$when expressed as a time interval[*]) may be measured by a variety of techniques and is usually the first step in any analysis of pulsars exhibiting drifting sub-pulses.

Naturally the actual signal is not a uniform, pure two-dimensional sinusoid. The intensity at a given instant depends on the pulse longitude (the overall emission is, after all pulsed at the spin period P1) and also has a time variability that may be intrinsic to the pulsar or induced by interstellar scintillation. The spacing of the sub-pulses may also vary in a systematic manner with time and/or pulse longitude. We shall show later (Sect. 4.2) that under the most popular model for the origin of drifting sub-pulses, we may to a very good approximation model these variations in sub-pulse spacing as a dependence of P2 on pulse longitude and/or a time-variability of P3. Observational results showing that (in specific pulsars) P2 does not vary with time (Page 1973; Unwin et al. 1978; Lyne & Ashworth 1983) and that P3 is independent of pulse longitude (Backer 1970a,b; Krishnamohan 1980; Wright 1981; Davies et al. 1984; Biggs et al. 1987) serve to confirm this assertion. The only reported exception, to our knowledge, is the sub-pulse modulation reported in the putative pulsar remnant of Supernova 1987A (Middleditch et al. 2000), which, unlike other pulsars with drifting sub-pulses, is probably caused by precession. We therefore proceed to describe the signal mathematically on this basis.

2.2 Longitudinal modulation

The most obvious difference between a true sub-pulse signal and a purely periodic signal its longitude-dependent amplitude windowing. It is expected that the sub-pulses will be scaled in amplitude as a function of pulse phase with a shape similar to the average pulse profile. We denote this function $a_{\rm l}(\phi)$, where $\phi $ is the pulse longitude.

We may also expect some dependence of longitudinal sub-pulse spacing on pulse longitude. Expressed another way, the sub-pulses of a given pulse are periodic in a non-linear function of longitude. The phase must be at least monontonic and most likely almost linear, or we would not consider the sub-pulses to be (almost) periodic. We may therefore treat "sub-pulse phase'' ($\theta $) in a given pulse as the sum of a linear term and a longitude-dependent "phase envelope'' ( $p_{\rm l}(\phi)$).

The sub-pulse signal for a given pulse can then be represented as

$\displaystyle s(\phi) = a_{\rm l}A'(\phi) \sum_{k=1}^{N_h}A_k \sin [k(\phi P_1/ P_2 + p_{\rm l}(\phi) + \theta')+\theta_k],$     (1)

where P2 is an "average'' or "nominal'' spacing and A'and $\theta'$ are an amplitude scaling and phase shift specific to this pulse. The model periodic signal (with a period of P2) is composed of a series of Nh harmonics with amplitude and phase Ak and $\theta_k$ for each harmonic k. In most instances the sub-pulses will appear almost sinusoidal and the power of harmonics with k>1 will be small. We therefore neglect the higher harmonics in further analysis, keeping in mind however that in a real signal they may be present, with values of P2 and P3 factors of k smaller than those of fundamental (k=1). Through our choice of A' and $\theta'$ we may define A1=1 and $\theta_1=0$ so that they may be neglected in the case of the fundamental.

Since the deviation from pure periodicity is represented by a longitude-dependent amplitude scaling and phase shift, we may simply define a complex modulation envelope $m_{\rm l}(\phi) \equiv a_{\rm l}(\phi)\exp(ip_{\rm l}(\phi))$, writing the varying sub-pulse component of a given pulse as

\begin{displaymath}s(\phi) = {\rm Re}[m_{\rm l}(\phi)A'{\rm e}^{i \phi P_1 /P_2 + \theta'}], \end{displaymath} (2)

where ${\rm Re}(x)$ denotes the real part of x. However, it is never the case that sub-pulses subtract from the overall emission; if the sub-pulses are to be modelled with sinusoids, we must add a unity bias which itself is amplitude-modulated by $a_{\rm l}(\phi)$. In addition there may be some emission not associated with sub-pulses (the "non-drifting'' component, $u(\phi)$), which we include here under the simplifying assumption that it does not vary from pulse to pulse. Together these terms are referred to as the "steady'' part of the emission[*]. The full signal in a given pulse can be written:

 \begin{displaymath}i(\phi) = {\rm Re}\left[m_{\rm l}(\phi)A'{\rm e}^{i \phi P_1/... ...+ \theta'}\right] + A'\left[a_{\rm l}(\phi)+u(\phi)\right] . \end{displaymath} (3)

2.3 Time modulation

In addition to the longitude dependence covered in the previous section, drifting sub-pulse signals vary on time-scales longer than one pulse period (P1). We define a time-dependent amplitude scaling $a_{\rm t}(t)$ which gives rise to the pulse-specific A' factor used earlier. To describe the time-dependence of the spacing of sub-pulses in time, we may take a similar approach and define $p_{\rm t}(t)$ as the difference in phase between the true signal and a uniform sinusoid of period $\hat{P_3}$. This function is the source of the pulse-specific $\theta'$ terms of the previous section. Again we can define a complex envelope $m_{\rm t}(t) \equiv a_{\rm t}(t) \exp(ip_{\rm t}(t))$.

   
2.4 Full model of intensity signal

From the preceding two sections we are able to assemble a model for the observed intensity of pulsar signals as a function of time and pulse longitude. Under the assumption that the time-dependent and longitude-dependent modulations are independent, we may model the overall modulation as the product of the derived longitude and time windowing: $m(\phi, t) = m_{\rm l}(\phi)m_{\rm t}(t)$. Hence the model of the sub-pulse component is

 \begin{displaymath}s(\phi, t) = {\rm Re}\left[m(\phi,t){\rm e}^{i \phi P_1 /P_2 + 2\pi t/\hat{P_3}}\right], \end{displaymath} (4)

where t is taken as constant within a given pulse period. We note that in this formulation, if P2 and $\hat{P_3}$ have the same sign, the sub-pulses appear to arrive earlier with each successive pulse. We adopt this convention and choose to denote the opposite sense of drift with a negative value for $\hat{P_3}$. The full signal including steady components is:
 
$\displaystyle i(\phi, t) = a_{\rm t}(t)[u(\phi)+a_{\rm l}(\phi)] % + {\rm Re}\left[m(\phi, t) {\rm e}^{i (\phi P_1/ P_2 + 2\pi t/\hat{P_3})}\right].$     (5)

   
3 The two-dimensional fluctuation spectrum

3.1 Definition and properties

The two-dimensional Fourier transform of a function f(x, y) is defined as follows:

 
                 F(u, v) = $\displaystyle {\mathcal F}[f(x, y)]$  
  = $\displaystyle \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(x, y){\rm e}^{-2\pi i (ux + vy)} {\rm d}x{\rm d}y,$ (6)

where ${\mathcal F}$ denotes the Fourier transform operator. Its inverse differs only in the sign of the exponent:
 
                f(x, y) = $\displaystyle {\mathcal F}^{-1}[F(u, v)]$  
  = $\displaystyle \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} F(u, v){\rm e}^{2\pi i (ux + vy)} {\rm d}u{\rm d}v.$ (7)

It is usual that the x and y quantities are spatial or temporal, whilst u and v are spatial or temporal frequencies. The effect of the two-dimensional Fourier transform is to decompose the input function into a sum of complex exponentials, or in the case of a real-valued input function, sinusoids of specific frequency, phase and amplitude. The basic unit of this decomposition can be seen from the inverse response to a shifted delta function ( $\delta(u-u_0, v-v_0)$):

\begin{displaymath}{\mathcal F}^{-1}[\delta(u-u_0, v-v_0)](x,y) = {\rm e}^{2\pi i (u_0x + v_0y)}. \end{displaymath} (8)

The form of the real component of this is simply a sinusoid in a linear combination of x and y, that is a periodic function with maxima and minima lying on lines of constant u0x + v0y.

For a discretely, uniformly sampled function with $N_x\times N_y$ samples, the two-dimensional Discrete Fourier Transform (DFT) may be written as

                        F(u, v) = 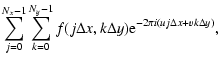$\displaystyle \sum_{j=0}^{N_x-1}\sum_{k=0}^{N_y-1} f(j\Delta x, k\Delta y){\rm e}^{-2\pi i (uj\Delta x + vk\Delta y)},$ (9)

and is computed over a grid of $N_x\times N_y$ values in the range $-1/2\Delta_x < u < 1/2\Delta_x$, $-1/2\Delta_y < v < 1/2\Delta_y$where $\Delta_x$ and $\Delta_y$ are the sampling intervals in x and yrespectively. As with the one-dimensional DFT, most of the important theorems concerning the continuous transform also apply to the discrete case.

When the signal of a pulsar with drifting sub-pulses is displayed as a function of pulse number and longitude, the patterns made by the sub-pulses and their drifting are very similar to those of the inverse Fourier transform of a delta function. This fact alone suggests that computing the (discrete) Fourier transform of the two dimensional signal $(i(\phi, t))$ may be an interesting exercise.

Since the signal is real-valued, the result of the Fourier transform ( $I(\nu_l, \nu_t)$) will obey the symmetry $I(\nu_l, \nu_t) = I(-\nu_l, -\nu_t)^*$, where the superscript * denotes the complex conjugate. From Eqs. (4), (5) and (6) the result of this operation (which we call the Two-Dimensional Fluctuation Spectrum or 2DFS) is

                 $\displaystyle I(\nu_l, \nu_t)$ = $\displaystyle {\mathcal F}[i(\phi, t)]$  
  = $\displaystyle A_{\rm t}(\nu_t)[U(\nu_l)+A_{\rm l}(\nu_l)] + S(\nu_l, \nu_t) + S(-\nu_l, -\nu_t)^*,$ (10)

where functions in upper case denote the (one- or two-dimensional) Fourier transform of their lower-case counterparts. Expanding just one of the two terms arising from the sub-pulse modulation $s(\phi, t)$, from the convolution theorem we find
                 $\displaystyle S(\nu_l, \nu_t)$ = $\displaystyle {\mathcal F}[m_{\rm l}(\phi)m_{\rm t}(t)]% * \delta[\nu_l-P_1/(2\pi P_2), \nu_t-1/\hat{P_3}]$ (11)
  = $\displaystyle M(\nu_l, \nu_t) * \delta[\nu_l-P_1/(2\pi P_2), \nu_t-1/\hat{P_3}],$ (12)

where * denotes the convolution operator. It is also worth noting that $M(\nu_l, \nu_t)$ is simply equal to $M_{\rm l}(\nu_l)M_{\rm t}(\nu_t)$ since the non-zero regions of two responses lie on orthogonal lines in the two-dimensional spectrum and the convolution reduces to multiplication.

So we see that the 2DFS consists of three main components: one for the response of the steady part of the pulsar emission, and two mirror-image components for the sub-pulse modulation. The steady component is centered at DC ( $\nu_l = \nu_t = 0$), whilst the sub-pulse components are centered approximately at $\nu_l = kP_1/(2\pi P_2)$ (cycles per radian of pulse longitude), $\nu_t = k/\hat{P_3}$ (cycles per time unit) where $k=\pm1$[*]. Since the modulation envelopes are not purely real-valued, their Fourier transforms are not expected to be entirely symmetrical, and there is no unique "center'' of the components, however in most cases the phase rotation of the envelope will be quite minor and a peak around the position specified will be seen.

The overall width and shape of the components depends on the nature of the modulation envelopes. For a pulsar with no nulling or scintillation, the steady component will have zero width in the $\nu_t$ direction[*], and a one-dimensional inverse Fourier transform of $I(\nu_l, 0)$ in the $\nu_l$ dimension yields the average pulse profile. If nulling and/or scintillation are significant, there may be some broadening in the $\nu_t$ direction however very frequent nulling or scintillation on very short time scales would be required to produce a strong, significantly extended component. In addition to the effects of nulling and scintillation, the sub-pulse components are broadened due to phase (or P3) variation over the course of the observation.

Broadening of the components in the $\nu_l$ axis derives from the finite width of the amplitude envelopes ( $a_{\rm l}(\phi)$and $u(\phi)$) and, in the case of the sub-pulse components, due to phase (or P2) variation across the pulse. The width of this component is generally quite large due to the small duty cycle of pulsars, and will tend to make the spectrum significantly non-zero at $\nu_l = 0$, $\nu_t = k/\hat{P_3}$ if the number of sub-pulses observable in each pulse is less than two.

As noted earlier, the frequency extent of the DFT is limited by the inverse of the sampling interval(s). Co-efficients for frequencies outside the range may be computed but will always be identical to those at some (calculable) point in the range due to aliasing. In the case of the 2DFS, the longitude sampling may be chosen arbitrarily (within the limits of the hardware and the bandwidth of the received radiation), but the "time'' or "pulse number'' sampling is naturally set at a value of P1. For this reason, drifting sub-pulse components outside the range -0.5 < P1/P3 < 0.5 are indistinguishable from those within it.

3.2 Relationship to the longitude-resolved fluctuation spectrum

It is readily apparent from Eq. (6) that the discrete two-dimensional Fourier transform can be computed by first computing a one-dimensional DFT along each column of the input data, and then computing the one-dimensional DFT along each row of the result (or alternatively, along rows first and columns second). The result of the first half of this operation when performed on the pulsar signal $i(\phi, t)$ is known as the longitude-resolved fluctuation spectrum (LRFS; Backer 1970a,b).

The expected form of this spectrum is easy to understand in the light of the preceding discussion. Each column (i.e. line of constant $\phi $) in the spectrum will have three components, as in the 2DFS. The steady component simply appears as a DC term equal to $u(\phi)+a(\phi)$, whilst the two components for the sub-pulse modulation appear at $\pm 1/\hat{P_3}$. Calculating the spectrum of both components (denoted I1 and I2), we find:

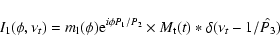\begin{displaymath}I_1(\phi, \nu_t) = m_{\rm l}(\phi){\rm e}^{i\phi P_1/P_2} \times M_{\rm t}(t)*\delta(\nu_t-1/\hat{P_3}) \end{displaymath} (13)

and

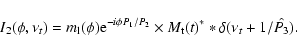\begin{displaymath}I_2(\phi, \nu_t) = m_{\rm l}(\phi){\rm e}^{-i\phi P_1/P_2} \times M_{\rm t}(t)^* *\delta(\nu_t+1/\hat{P_3}) . \end{displaymath} (14)

That is, the amplitude (or power) spectrum in each phase bin is identical excluding the scaling factor $a_{\rm l}(\phi)$, whilst the complex co-efficients are rotated from bin to bin by an amount $\phi P_1/P_2 +~\! p_{\rm l}(\phi)$.

Due to the presence of a component in both the positive and negative half of the spectrum, it is impossible to determine the sign of $\hat{P_3}$ from the LRF power spectrum. Signals are effectively aliased to the range $P_1/\hat{P_3} \in [0,0.5]$. Only by examining the sense of phase rotation of the complex co-efficients as a function of longitude and comparing this to the sign in $\nu_t$ of the component being considered can the sense of the drift be determined.

Since the phase relation between longitude bins is expected to be quasi-periodic, it makes sense to perform a Fourier transform across each row of the complex spectrum in order to determine the sense of the drift and its period (i.e. P2/P1), and to concentrate the sub-pulse power in a smaller region of phase space for greater signal-to-noise ratio in P3. The result of this operation is the two-dimensional DFT of the signal, in other words the 2DFS.

3.3 Relationship to the harmonic-resolved fluctuation spectrum

Recently a new technique for sub-pulse analysis has been devised by Deshpande & Rankin (2001). It involves the computation of the so-called Harmonic-Resolved Fluctuation Spectrum (HRFS). Working from the original time-series i(t), they compute the one-dimensional spectrum and "stack'' it about the $\nu=k/P_1$ harmonics of the signal. Thus,

\begin{displaymath}{\mathcal H}[i](x, y) = {\mathcal F}[i]([x+y]/P_1), \end{displaymath} (15)

where ${\mathcal H}$ denotes the HRFS and x and y are the fractional and integer components of the corresponding spectral frequency multiplied by P1. The HRF power spectrum is usually plotted with the x parameter as the abscissa (with a domain of 0 to 1) and the y parameter as the ordinate (with integer-valued bins up to the extent allowed by the sampling interval).

We note that the 2DFS is in fact intimately related (after scaling and rotation) to the HRFS. The former is formed by stacking the time-domain data about the pulse period P1 and then Fourier transforming, whilst the latter is formed by Fourier transforming and stacking the result about 1/P1. That the two should be essentially identical is not immediately obvious but is easy to show (see Appendix A). In fact, the decomposition of the one-dimensional DFT into a two-dimensional DFT is the basis of parallel FFT codes (Cooley & Tukey 1965).

We note that values of $\nu$ giving rise to $0.5 < \nu_t < 1$ are aliased to $\nu_t-1$ in the 2DFS (i.e. the opposite drift sense), however this is simply a matter of convention: by the same notion, signals which truly show the opposite drift sense (that is, negative P3P2) are aliased in the HRFS into the region $0.5 < \nu_t < 1$. In our view, given that there is no reason to prefer one sense of intrinsic sub-pulse drift over another, specification of $\hat{P_3}$ in the interval [-0.5,0.5] makes more sense than taking a preferred drift direction and mapping all drift to this interval (e.g. [0:1]).

Whilst the two spectra are equivalent, a knowledge of their basis in the two-dimensional Fourier transform of the longitude-time data is of value in further analysis, as we shall see below.

   
4 Sub-pulse analysis with the two-dimensional fluctuation spectrum

With an awareness of the mathematical basis of the 2DFS in relation to the form of the drifting sub-pulse signal described in the preceding sections, a range of analysis strategies can be developed for the investigation of particular aspects of the sub-pulses.

The technique was originally conceived with the aim of detecting the presence and basic parameters (P2 and P3) of sub-pulse drift in pulsars with limited instantaneous signal-to-noise ratio. The sensitivity of this method depends only on the coherence of the drift and the ratio of its amplitude to that of any non-drifting signal. The significance of a detection can by improved arbitrarily (for stable drifters) by simply integrating more pulses, unlike in traditional single-pulse studies where each individual sub-pulse must be detectable above the noise. This makes it well-suited to studying the sub-pulse properties of a large sample of weaker pulsars.

The complex 2DFS is also of use in studying the details of sub-pulse emission in bright pulsars. In this section we show how the complex modulation envelopes can be extracted from the spectrum, giving full information about the deviation from purely periodic sub-pulses.

   
4.1 Extraction of the modulation envelopes

In Sect. 3 we saw that the components arising in the 2DFS due to the sub-pulse drifting take the form of the Fourier transform of the combined modulation envelope $m(\phi, t)$, shifted to $\nu_l=P_2^{-1}P_1/2\pi$, $\nu_t=P_3^{-1}$. To obtain the envelope from the spectrum, we begin by masking out the steady component[*] and the mirror-image component. The inverse transform of this spectrum contains a complex version of the sub-pulse component of the data which, in the limit of perfect masking of other components, is its analytic signal. Its amplitude is only half of that present in the original data due to the loss of the mirror-image component, so to circumvent the effect of this in further analysis we multiply the complex co-efficients of the spectrum by two after performing the masking. Before performing the inverse transform we shift the spectrum by the appropriate amount horizontally and vertically to place the nominal centroid of the sub-pulse response at DC. The inverse Fourier transform of this shifted spectrum gives the two-dimensional modulation envelope $\hat{m}(\phi,t)$, as used in Sect. 2.4.

In performing the described procedure, is vital that the mirror image sub-pulse component and the steady component are both carefully removed from the spectrum. In the case where the conjugate mirror image components are not separated by regions of nearly zero power, it is likely that the Fourier transform of the "true'' complex signal had power in opposite quadrants, which as a result of the real sampling is added to that of its conjugated mirror image in the computed spectrum. Under such circumstances, it is not possible to reconstruct the true complex signal of the sub-pulse component, and the derived envelope will differ from that which we had hoped for to a degree dependent on how significant the overlap is. The same caveat applies if the drifting component is not clearly separated from the steady component.

The two dimensional envelope produced using the above procedure can be decomposed into longitude- and time-dependent parts under the assumptions made earlier about the form of drifting sub-pulses, as such:

 \begin{displaymath}\hat{m}(\phi,t) = \hat{m_{\rm l}}(\phi)\hat{m_{\rm t}}(t) + {\rm noise}. \end{displaymath} (16)

We use an iterative scheme to perform this decomposition. By assuming a form for $m_{\rm l}(\phi)$, one can compute $m_{\rm t}(t)$ through rearrangement of Eq. (16). Using the resultant $m_{\rm t}(t)$ a new $m_{\rm l}(\phi)$ is computed, and so on. The process is repeated until convergence, constraining the system to a stable solution by normalising $m_{\rm t}(t)$ to a mean amplitude of unity[*]. Use of simple inversion leads to domination of the inferred phases by noise, so we use instead the zero-lag of the normalised cross-correlation function,

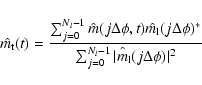\begin{displaymath}\hat{m_{\rm t}}(t) = \frac {\sum_{j=0}^{N_l-1}\hat{m}(j\Delt... ... {\sum_{j=0}^{N_l-1}\hat{\vert m_{\rm l}}(j\Delta\phi)\vert^2} \end{displaymath} (17)

(or the equivalent for $\hat{m_{\rm l}}(\phi)$), which is simply a weighted version of the longitude-averaged inversion of Eq. (16).

With noiseless data and adequate removal of unwanted spectral components, a convergent result of this algorithm clearly gives the correct answer. Under the presence of noise, however, care must be taken in the interpretation of derived amplitude values. Denoting the rms noise in the real and imaginary parts of the two-dimensional complex envelope by $\sigma_{\rm n}$ (which may be calculated from the variance of the off-pulse samples in the original data), the variance of the noise in the real and imaginary parts of $\hat{m_{\rm l}}$ is

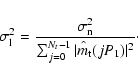\begin{displaymath}\sigma^2_{\rm l} = \frac {\sigma^2_{\rm n}} {\sum_{j=0}^{N_t-1}\hat{\vert m_{\rm t}}(jP_1)\vert^2} \cdot \end{displaymath} (18)

(A similar relation applies for $\sigma^2_{\rm m}$: both are reduced from $\sigma^2_{\rm n}$ by the integrated power of the complementary envelope.)

Taking the amplitude envelope incurs some bias due to the presence of this noise. The derived power values are over-estimated by, on average, $2\sigma^2_{\rm l}$, leading to significant bias in parts of the envelope with low (or zero) signal-to-noise ratio. This bias is intrinsic to the amplitude-phase representation of noisy data, and so is also familiar from the estimation of the longitude-dependent envelope from LRF spectra (Backer 1973) and of modulation indices (e.g. Taylor & Huguenin 1971). A second-order effect arises from the fact that the iterative algorithm described above includes the noise bias in its unity normalization of the time-dependent envelope, leading to less correlation and hence an unintended attenuation in the next estimate of the longitude envelope. The latter effect is easily accounted for by correction of the normalization to exclude the noise contribution. Compensating for the former effect requires a more careful approach.

At the cost of increasing the variance of the noise, the actual (noisy) values of an envelope may used to determine the bias to subtract from each element. Alternatively one may take $m^2-2\sigma^2$as an unbiased estimator of the power envelope, however a problem remains when amplitudes are to be calculated from negative power values (such as occurs when the signal-to-noise ratio is low). Nevertheless, this is the approach that is usually employed in the calculation of modulation indices. A final option that may be of practical use is to make a model longitude-dependent phase envelope $p_m(\phi)$ (since in most cases the measured phase envelope will be more smoothly varying than the amplitude envelope). Neglecting errors in the model envelope, the real part of the product $m_{\rm l}(\phi) \exp(-ip_m(\phi))$ (corresponding in the complex plane to the projection of the measured envelope on an axis aligned with the model phase for that longitude) should be free of bias[*].

Once the decomposition is performed, four major classes of questions can be asked:

1.
How does sub-pulse phase (or equivalently, P3) vary with time? Are there any systematic variations and if so what causes them?
2.
How does sub-pulse amplitude vary with time?
3.
How does sub-pulse phase (or equivalently, P2) vary with pulse longitude?
4.
How does the sub-pulse amplitude window compare to the mean profile? Is there a non-drifting component[*]?
All of the questions listed above can be (and in some cases have been) answered to a degree using LRFS, TRFS[*] or HRFS by taking one-dimensional "stacked'' power spectra (for amplitude windowing phenomena) or one-dimensional "slices'' (for examining phase relations). However both these techniques lose sensitivity, in the first case by summing incoherently and in the second case by using less than the full available modulation power. We believe that the technique presented here is likely to result in measurements of equal or (usually) better quality since (as long as the assumptions made are valid for the pulsar) the two envelopes form a complete representation of the drifting component of the signal.

   
4.2 The carousel model

   
4.2.1 Expected modulation envelopes

The most popular conceptual framework for understanding drifting sub-pulses is that of a carousel-like system of "sparks'' uniformly spaced about a ring of constant magnetic elevation and altitude from the star surface, with the system as a whole slowly rotating about the magnetic axis (Ruderman 1972). As the pulsar rotates and its beam periodically intersects the observer, a series of pulses, each composed of a series of sub-pulses is seen.

By treating the problem as if all radiation originates on the surface of a "polar cap'', and is beamed in a direction directly opposite to that of the center of the star (as shown in Fig. 1), we may consider the rotational geometry to effect, over the course of each successive pulse, a sampling of the polar cap emissivity along a locus defined by the intersection of the sight line and the cap. This simplification gives a means for good conceptual understanding of the origin of the observed pulse morphologies and is widely used for this purpose (e.g. Lyne & Manchester 1988; Mitra & Deshpande 1999; Deshpande & Rankin 2001), but it must be borne in mind that in reality the radiation is expected to be beamed along a tangent to the magnetic field line at the emission location. Therefore the observed emission at a given instant relates to a plasma flux tube with its foot at some point on an arc on the polar cap connecting the depicted "line of sight'' and the magnetic pole (labelled $\rho $ in Fig. 1c). However, since the field line tangent angle at a given altitude (where the emission originates) is approximately proportional to its magnetic colatitude angle, the derived sight-line locus differs from the true polar cap sampling by a simple scaling of the magnetic colatitude co-ordinate (see also Lyne & Manchester 1988)[*]. In any case, the true sampling effected in magnetic azimuth is the same as that derived assuming radial beaming, and if the polar cap emission pattern is a ring of sparks (or radial "spokes''), it is this co-ordinate alone that determines the pulse longitude of the observed sub-pulses.

In systems where the sight-line makes a tangential pass of the ring, the emission from the sparks is seen as a sequence of one to a few almost equally-spaced sub-pulses, the phase of which "drifts'' in time with respect to a fiducial point in pulse longitude due to the rotation of the carousel. The number of sparks present, the viewing geometry and the angle between the spin and magnetic axes determine the longitudinal spacing of the sub-pulses (P2), whilst the time spacing (P3) depends on the rotation rate of the carousel and the number of sparks it contains.

There are two main effects predicted under the carousel model that are of importance here.

Firstly, the carousel rotates continuously (with some period P4 = NP3, where there are N sparks), meaning that any variations in spark intensity, shape or spacing about the ring should manifest as a periodic feature in the drifting sub-pulse signal. This periodicity would appear as a periodicity in the time-dependent amplitude and phase envelopes, giving rise in the 2DFS to a pair of "sidebands'' at frequencies 1/P4 higher and lower than the primary feature at $\nu_{\rm t}=1/\hat{P_3}$. This was the startling finding of Deshpande & Rankin (2001) who applied the HRFS for the first time, to observations of PSR B0943+10. The detectability of this effect using 2DFS techniques is discussed further in Sect. 4.3.3.

The second effect predicted under the carousel model is that the longitudinal spacing of the sub-pulses depends on pulse longitude. The sparks are presumed to be spaced uniformly in magnetic azimuth ($\psi $) and their separation in spin longitude is known, but the mapping from pulse longitude to magnetic azimuth for the sight line is dependent on the degree of spin-magnetic pole misalignment ($\alpha $) and the viewing geometry (where $\zeta $ is the angle made between the line of sight and the positive spin pole). The relation is:

 \begin{displaymath}\tan{\psi} = \frac{\sin\phi\sin\zeta} {\cos\zeta\sin\alpha - \cos\phi\sin\zeta\cos\alpha} , \end{displaymath} (19)

where the signs of the numerator and denominator determine the quadrant for $\psi $ in the usual way (see Appendix B for derivation), and $\phi $ is measured relative to the pulse longitude at which the sight-line makes its nearest traverse of the sight-line.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f1.ps}\end{figure} Figure 1: Diagram of sub-pulse emission geometry. In part  a) the angular momentum, magnetic moment, and line-of-sight vectors are shown with symbols L, $\mu $, and d respectively. The pulsar rotates about the spin axis with an angular velocity $\omega _1 = 2\pi /P_1$, whilst the ring of sparks that gives rise to the sub-pulses rotates about the magnetic axis with an angular velocity $\omega _p=-2\pi /NP_3$, where N=10 is the number of sparks. The sight-line rotates relative to the pulsar spin frame and is shown here during the "on-pulse''. Its intersection with the star surface or the emitting surface is shown in bold. The co-rotation of the magnetic field (and the emission associated with the pulse) and the star causes the sparks to appear as sub-pulses that are amplitude-modulated at the main pulse (i.e. spin) period. Within this modulation window the longitudes of sub-pulses drift from one pulse to the next due to their physical motion about the magnetic pole. Part  b) shows the main vectors as they appear in the plane they share when the sight-line makes its closest approach to the magnetic pole. The angles $\zeta $(between the sight-line and the spin axis), $\alpha $ (between the magnetic and spin axes) and $\beta \equiv \zeta -\alpha $ (between the sight-line and the magnetic axis at their closest approach) are shown. In part  a) a second line of sight ($\vec{d'}$) is drawn, along with the meridian it shares with with the magnetic pole. The spherical triangle formed by $\vec{L}$, $\vec{\mu}$ and $\vec{d'}$ is duplicated in part  c). In addition to $\alpha $ and $\zeta $ this diagram illustrates the meaning of pulse longitude ($\phi $), polarization position angle ($\chi $, measured relative to the position angle of the spin axis) and magnetic azimuth ($\psi $) and co-latitude ($\rho $).
Open with DEXTER

The mapping of pulse longitude to magnetic azimuth is monotonic in the region in which emission is seen, with a gradient of the opposite sign to $\ensuremath {{\rm sgn}~}\beta \equiv \beta/\vert\beta\vert$ (where $\beta \equiv \zeta -\alpha $). In our analysis, P2 and hence the rate of change of sub-pulse phase ( ${\rm d}\theta/{\rm d}\phi$) are always positive, so a factor of $-\ensuremath {{\rm sgn}~}\beta$ will appear in the expression relating $\theta(\phi)$ to magnetic azimuth ( $\psi(\phi)$).

The fact that the carousel itself rotates with respect to a fixed point of magnetic azimuth must also be taken into account. The rotation period of the carousel is $2\pi/\omega_{\rm p}$ (see Fig. 1) where positive $\omega_{\rm p}$ indicates counter-clockwise rotation viewed from above the active magnetic pole. The direction of drift seen in the sub-pulses depends also on $\ensuremath {{\rm sgn}~}\beta$: if their signs are opposite (as is the case in Fig. 1) the sub-pulses will drift toward the trailing edge of the profile. We label this with a negative value for P3, via $P_3 = 2\pi(\ensuremath {{\rm sgn}~}\beta)/(N\omega_{\rm p})$.

Since the sub-pulse phase at a given longitude is only sampled once per rotation period (P1), we will always observe some periodicity $-0.5 < P_1/\hat{P_3} < 0.5$. Under the carousel model it is possible that each spark drifts in longitude by more than half of P2 from one pulse to the next. In this case we may say that the observed $\hat{P_3}$ is an "aliased'' version of the true time taken for the carousel to drift by 1/N turns, P3. The ambiguity in the "true'' P3 can be expressed in terms of the (signed, nearest whole) number of sparks (n) that drift by undetected from one pulse to the next: $P_1/P_3 = n + P_1/\hat{P_3}$. As shown by Deshpande & Rankin (2001), this aliasing can potentially be constrained with a measurement of P4 by observing that P4/P1 = |N/(n+P1/P3)| and solving for integer pairs of n and N (in their case $37.35\pm 0.52 = N/(n-0.4645\pm0.0003)$ implying n=1 and N=20)[*].

The expression for $\theta(\phi)$ is the sum of three terms, the first a sign-corrected and scaled version of $\psi(\phi)$(Eq. (19)), the second a term which accounts for carousel rotation over the course of the pulse, and the third an offset representing the carousel position at $\phi =0$.

 
$\displaystyle \theta(\phi) = - N \ensuremath {{\rm sgn}~}\beta \tan^{-1} \left[... ...eta\cos\alpha} \right] + \phi \left(n + \frac{P_1}{\hat{P_3}}\right) + \theta'.$     (20)

Near the point of zero longitude, the rate of traverse of magnetic azimuth is at its maximum:

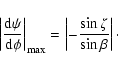\begin{displaymath}\left\vert\frac{{\rm d}\psi}{{\rm d}\phi}\right\vert _{\rm max} = \left\vert-\frac{\sin \zeta}{\sin \beta}\right\vert\cdot \end{displaymath} (21)

The apparent rate of traverse of sub-pulse phase is therefore given by

 \begin{displaymath}\left(\frac{{\rm d}\theta}{{\rm d}\phi}\right)_{\rm max} = N\... ...in \zeta}{\sin \beta}\right\vert + n + \frac{P_1}{\hat{P_3}}, \end{displaymath} (22)

and will generally be close to the "nominal'' frequency used in 2DFS analysis (via ${\rm d}\theta/{\rm d}\psi = P_1/P_2$). The difference between the predicted phase evolution and a constant slope of this gradient gives the predicted longitude-dependent phase envelope. An example is shown in Fig. 2. We note that the longitude-dependent phase envelope arising from a rotating carousel will always have a similar form (given sufficient signal to noise ratio). The gradient of $\theta(\phi)$ is at a maximum at $\phi =0$, and declines symmetrically on either side. The spectral shift, if the correct value of P2 is chosen (and this may be fine-tuned by examining the resultant envelope), will result in an envelope with zero gradient at $\phi =0$, and negative gradients at all other longitudes, with the steepness increasing towards the leading and trailing edges of the profile.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f2.ps}\end{figure} Figure 2: Illustration of the variation in sub-pulse phase ($\theta $) as a function of pulse longitude ($\phi $). We used $\alpha =10\hbox {$^\circ $ }$, $\beta =2\hbox {$^\circ $ }$ and N=10 in this example. The dashed line shows the value expected through the spherical geometry (Eq. (20)), the dotted line shows that of a pure periodicity with equal phase slope at $\phi =0$ to the dashed line (Eq. (22)), and the solid line shows their difference. This latter quantity can be considered to be a longitude-dependent phase-modulation envelope to be applied to the constant periodicity to produce the real signal.
Open with DEXTER

The techniques used in this work decompose the sub-pulse signal into the product of two complex envelopes which depend only on time and longitude respectively. As such, it is important that the longitudinal spacing of the sub-pulses does not vary with time, and that the time-spacing of sub-pulses does not vary with longitude. The longitude-independence of P3 is trivially true in the carousel model, since the carousel rotates as a whole and the angular speed is constant around the ring. This is seen in LRF spectra of virtually all pulsars with drifting sub-pulses, see e.g. Backer (1973). The time-independence of P2 is technically not satisfied under the carousel model, since the longitudinal spacing depends on P3 (see Eq. (20)), which in turn depends on the circulation rate, which may vary with time. However, for this effect to be significant Eq. (22) must be dominated by the carousel rotation, i.e. $\vert n\vert \gg 1$. In this case, even minor variations in the rotation rate could cause the observed (highly aliased) $\hat{P_3}$ to vary wildly in sign and magnitude. To our knowledge, the only pulsar to clearly show sense reversals in its drift is PSR B0826-34, and the longitudinal spacing is (within errors) independent of the instantaneous P3 (Biggs et al. 1985). Other pulsars that show major changes (but not sign reversals) in the drift rate are PSR B2016+28 (Taylor et al. 1975) and PSR B0809+74 (after nulls; Page 1973; Lyne & Ashworth 1983), both of which also show constant longitudinal spacing. It therefore appears safe to assume that most systems are not highly aliased and the longitudinal spacing can be assumed constant with time.

   
4.2.2 Comparison with polarization behaviour

The longitudinal dependence of the observed position angle of linearly polarized radiation is expected to be intimately related to carousel rotation sub-pulse behaviour, and comparisons between polarimetric and drifting-sub pulse analyses have the potential to provide more information than either alone. Under the "magnetic pole'' or "rotating vector model'' (RVM; Radhakrishnan & Cooke 1969), the position angle is that of the sky projection of the magnetic field line on which the emission region at a given instant lies. Analogous spherical geometry to that used in the derivation of the magnetic azimuth of the sight line leads to a similar relation:

 \begin{displaymath}\tan{-\chi} = \frac{\sin\phi\sin\alpha} {\cos\alpha\sin\zeta - \cos\phi\sin\alpha\cos\zeta}\cdot \end{displaymath} (23)

(See Appendix B, Eq. (23) differs from the formula of Komesaroff (1970) and virtually all later works on pulsar RVM fitting in that it assumes the standard astronomical convention of position angle increasing counter-clockwise.)

In principle, $\alpha $ and $\zeta $ can be determined directly by fitting the observed position angle swing. These values could then be used with a measurement of the longitude-dependent sub-pulse phase envelope and Eq. (20) to determine N and check the validity of the carousel model (both through its ability to fit the data and by unambiguous consistency of the fitted value of N with an integer). In practice there may often be little measurable curvature in either function, in which case it makes more sense to work with the (fitted and presumed constant) gradients of the curves.

The first thing to notice is that the position angle swing may have either positive or negative slope, depending on the sign of $\beta$. The maximum rate of position angle swing occurs at the closest point to the magnetic pole, where ${\rm d}\chi/{\rm d}\phi = -\sin\alpha/\sin\beta$. If the degree of sub-pulse aliasing is known (or presumed zero) we can determine the physical direction of carousel circulation via $\omega_{\rm p} = 2\pi (\ensuremath {{\rm sgn}~}\beta)/(NP_3)$.

Secondly, the difference in the absolute value of the slopes can provide useful information. Since $\sin\zeta/\sin\beta - \sin\alpha/\sin\beta \simeq \cos (\alpha+\beta/2)$ (for small $\beta$), one may take

 
$\displaystyle \frac{1}{N}\frac{{\rm d}\theta}{{\rm d}\phi} - \left\vert\frac{{\rm d}\chi}{{\rm d}\phi}\right\vert$ = $\displaystyle \left\vert\frac{\sin \zeta}{\sin \beta}\right\vert - \left\vert\f... ...lpha}{\sin\beta}\right\vert + \frac{1}{N}\left(n + \frac{P_1}{\hat{P_3}}\right)$ (24)
  $\textstyle \simeq$ $\displaystyle \ensuremath {{\rm sgn}~}\beta\cos(\alpha+\beta/2) + \frac{1}{N}\left(n + \frac{P_1}{\hat{P_3}}\right)\cdot$ (25)

Unless the degree of aliasing is very high (with of the order of one complete carousel rotation for every star rotation), the second term may be neglected since it is much smaller in magnitude than the likely uncertainty in $\cos(\alpha+\beta/2)$. The first term may be estimated for example from the pulse width (and position angle slope; Lyne & Manchester 1988; Rankin 1990), or taken as unknown to yield $N\simeq ({\rm d}\theta/{\rm d}\phi) / (\vert{\rm d}\chi/{\rm d}\phi\vert \pm 1)$. In certain fortuitous circumstances use of this expression may determine N to better than $\pm 1$, and we could use the nearest integer to calculate $\alpha $ and $\beta$ using the known position angle and sub-pulse phase slopes.

We note that the work of Deshpande & Rankin (2001) arrived at ${\rm d}\psi/{\rm d}\phi-{\rm d}\chi/{\rm d}\phi=-\ensuremath {{\rm sgn}~}\beta$[*], seemingly under the assumption of $\alpha\simeq 180\hbox{$^\circ$ }$. Their result of N=20 for PSR B0943+10 remains valid under the analysis of the preceding paragraph. Taking their value of 34 for the maximum sub-pulse phase slope, using the position angle slope of -2.5 from Suleymanova et al. (1988) and neglecting the (probably significant) uncertainty in this measurement, we find $N=14 \pm 6$. The marginal consistency may indicate that $\cos(\alpha+\beta/2)$ is close to -1, implying that $\alpha $ is close to $180\hbox{$^\circ$ }$ and the neutron star rotates clockwise as viewed by the observer, in agreement with Deshpande & Rankin (2001). If measurements of the position angle and sub-pulse phase slopes with quoted uncertainties were available, it would be possible to use the N=20 result to constrain $\alpha $ and $\beta$ without the usual recourse to the use of pulse width-period relations.

   
4.3 Tests on simulated data

Whilst the techniques outlined in Sect. 4.1 are simple and quite direct, we feel that it is important to demonstrate that they perform as expected. To this end, we used the carousel model to produce several simulated time series which we subjected to 2DFS modulation window estimation.

4.3.1 Form of the model

For each sample, we computed the pulse longitude ($\phi $), and the corresponding magnetic azimuth ($\psi $) that is sampled by the sight-line at that longitude using Eq. (19) and a geometry specified by $\alpha $ and $\beta$. This was converted to a "sub-pulse phase'' ($\theta $) through multiplication by $-\ensuremath {{\rm sgn}~}\beta N$, and addition of an offset $\theta_d(t+\phi P_1/2\pi)$ (recalling that tis taken as constant in any given pulse), advancing at a rate of one turn per interval P3(t), which produces the drifting as a function of time. To investigate the detectability of variations in P3, we simulated the effect of a pulse null as a period of no drifting ( $P_3\rightarrow \infty$) during the null, followed by an exponential recovery to the asymptotic rate P3'. The full form of P3(t) is given by the following equation:

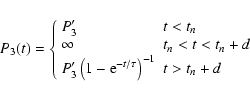\begin{displaymath}P_3(t) = \left\{ \begin{array}{ll} P_3'& t < t_n\\ \inft... ...\rm e}^{-t/\tau}\right)^{-1} & t > t_n+d \end{array} \right. \end{displaymath} (26)

where tn is the time at which the null begins, d is its duration, and $\tau$ is the time constant for drift rate recovery.

For each sample the flux contribution from each spark was computed as a Gaussian in magnetic azimuth (of width $\sigma_s$ and a peak value of unity) and the contributions added. The result was scaled by a factor of $1+c\sin\psi$ ( $0 \leq c \leq 1$) to simulate an asymmetry in the azimuthal flux distribution of the spark carousel, to test for detectability of the carousel circulation time.

Longitudinal amplitude windowing was applied through multiplication by a Gaussian in $\phi $ (of width $\sigma_m$, centered at $\phi =0$ with unity peak), and the resulting intensity was in turn scaled by a factor

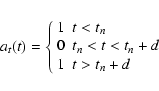\begin{displaymath}a_t(t) = \left\{ \begin{array}{ll} 1 & t < t_n\\ 0 & t_n < t < t_n+d\\ 1 & t > t_n+d \end{array} \right. \end{displaymath} (27)

to simulate the switching-off of the emission during the null. To this was added a random noise value (drawn from a Gaussian distribution of zero mean and standard deviation $\sigma_n$), giving the value $i(\phi, t)$ to use in later analysis.

This model leads to a sequence of pulses, each composed of sub-pulses whose amplitudes vary (in the specific simulations below) from $\sim $10% to $\sim $$100\%$ of the unity-peaked overall longitude envelope. The modulation envelopes measured from the simulated results are compared with a predicted envelope with amplitudes given by half the peak-to-peak sub-pulse variation produced by the noiseless model at a given longitude, after normalizing for a unity-mean time-dependent amplitude envelope. The predicted longitude envelope peaks at an amplitude of $\sim $0.45, compared to $\sim $0.50 for the average profile: that is, a small non-drifting component is present, since the model carousel has some emission at all points on the ring.

   
4.3.2 PSR B0809+74-like model

We chose a set of model parameters that give a pulse sequence similar to those observed from PSR B0809+74 at frequencies around 400 MHz. Specifically, we used a geometry of $\alpha=9\hbox{$^\circ$ }$, $\beta=4.5\hbox{$^\circ$ }$ (Rankin 1993a,b), requiring (from Eq. (22)) N=16 to reproduce the reported P2/P1 of 40 ms/1.29 s $\simeq 32$. A value of 11.0 P1 was used for P3'. The main pulse window had a full width at half-maximum (FWHM) of $w_{50}=12\hbox{$^\circ$ }$ (from $\sigma_m=0.014$ turns), with each sub-pulse having a FWHM of $5.0\hbox{$^\circ$ }$ (from $\sigma_s=0.2/N$). With the exception of $\alpha $ and $\beta$, all parameters above derive from Taylor et al. (1975). We included a null at tn = 100 P1, of duration d=8 P1 and recovery time constant $\tau=12 P_1$. No spark-to-spark intensity variation was included in this model (i.e. c=0) since a time-varying drift-rate complicates the analysis of this behaviour[*]. We produced two data sets, one with no noise ( $\sigma_n=0$) and one with moderate noise levels ( $\sigma_n=0.5$), each with 512 pulses in 4096 longitude bins, of which only the central 512 were used.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f3.ps}\end{figure} Figure 3: Simulated PSR B0809+74-like data. A sequence of 100 pulses from the noiseless data are shown, with the interval chosen to show the null.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f4.ps}\end{figure} Figure 4: Two-dimensional fluctuation power spectrum of simulated PSR B0809+74-like data. To enhance low-level structure, grey-levels have been over-saturated such that pure black corresponds to 10-3 times the peak power. The resolution used here is higher than that of the direct DFT and is achieved by zero-padding the input data.
Open with DEXTER

The noise-free data and the resultant 2DF power spectrum are shown in Figs. 3 and 4 respectively. The form of each is as expected from the considerations of the preceding sections. In particular, the spectrum consists of a DC component, and the first and second harmonics of the drifting response, with all components significantly extended in the horizontal axis (due to the longitudinal windowing) and also at a low level in the vertical axis (due to the nulling-induced time windowing). For clearer presentation, the spectrum in Fig. 4 was produced with enhanced resolution by padding the input data with zeroes before performing the DFT. In practice this would usually not be done, as it is unnecessary for the determination of a nominal $\hat{P_2}$ and $\hat{P_3}$, and complicates evaluation of the significance of concentrations of power. We therefore take the position of the coordinates of the peak bin of the 2DFS computed at the raw (non-padded) resolution as our nominal periodicity, giving $\hat{P_2}=P_1/32$ and $\hat{P_3}=P_1/0.092$. This is in agreement with the parameters used to generate the data, given the bin size of $8\times 0.002$ in $P_1/P_2\times P_1/P_3$.

After forming the full (symmetrical) complex spectrum and shifting it by the nominal values for $1/\hat{P_2}$ and $1/\hat{P_3}$, the responses of the average profile and the mirror-image of the fundamental were removed with a notch filter. To reduce the degree of "ringing'' in the impulse response of the resultant spectrum, the filters incorporated a gradual transition of the form

 \begin{displaymath}f(\nu_t) = \left\{ \begin{array}{ll} 0 & \vert\nu_t-\nu_{t... ...\\ 1 & \vert\nu_t-\nu_{tc}\vert/w > 1 \end{array} \right. , \end{displaymath} (28)

where $f(\nu_t)$ is the filter transmission as a function of frequency in the $\nu_t$ axis, $\nu_{tc}$ is the centre frequency of the component to be removed and w is half the total width of the filter, in this case w=0.01/P1. Since the components to be removed were broad in the $\nu_l$ axis (and certainly overlapping in this parameter with the desired component, now shifted to DC), the filter transmission was independent of frequency in this axis.

The resultant spectrum was then scaled by a factor of two to account for the use of only one of the two (conjugate-pair) components over which the modulation power is spread, and the inverse Fourier transform was taken. Using the scheme described in Sect. 4.1, we then decomposed the resultant two-dimensional complex modulation envelope into the product of longitude and time envelopes. The results are shown in Figs. 5 and 6.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f5.ps}\end{figure} Figure 5: Complex time-dependent modulation envelope and residuals for PSR B0809+74-like simulated data. The central panels  c) and  d) show the amplitude and phase response expected from the simulation parameters and the chosen nominal $\hat{P_2}$ and $\hat{P_3}$. Panels  b) and  e) show the difference between the measured and expected amplitude and phase envelopes for noiseless simulated data, whilst panels  a) and  f) show the equivalent quantities for the noisy data. The dotted vertical lines mark the start and end of the simulated null.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f6.ps}\end{figure} Figure 6: Complex longitude-dependent modulation envelope and residuals for PSR B0809+74-like simulated data. See caption for Fig. 5 for descriptions of the data shown in each panel.
Open with DEXTER

It is evident from the figures that some systematics are present in the residuals of envelopes of both axes. Beginning with the time-dependent envelope of the noiseless data, we see that there is some low-level periodic variation in both the amplitude and phase terms (panels b and e), with a period equal to P3. We believe that this is due to a combination of two effects. The first is the presence of the second harmonic of the sub-pulse modulation, which is shifted in the analysis to the former position of the fundamental. The second is the impulse response of the notch filters used to removed the DC component. This has a similar form to a sinc function (with a somewhat shorter time response due to the choice of transfer function), producing the enhanced oscillations around the null and the boundaries of the data set. The effect of the latter can be reduced by making a smoother transition in the filter, however this necessitates the loss of a greater range of the spectrum, which has the effect of corrupting both the amplitude and phase response to the post-null frequency recovery. In our view the phase evolution is more likely to be of interest than highly accurate amplitude evolution information, so a narrow filter was chosen.

As can be seen in panel (e), there is very little error in the estimated phase, beyond the low-level zero-mean P3 periodicity. The residuals of the noisy data appear, as expected, consistent with the addition of uncorrelated zero-mean noise to the values estimated from the noiseless data. The degree of scatter seen here indicates that estimation noise is likely to dominate over the systematic effects described above for data of all but the highest of signal-to-noise ratios. An exception is the time during the null itself, where the phase is of course not measurable, and the estimated amplitude is affected by the filter response. This error is trivial to correct by examining the pulse-to-pulse mean flux density to identify nulls.

The longitude-dependent modulation window (Fig. 6) also shows some systematic error in the estimates made from noiseless data. We believe this is largely due to errors in the estimated time-dependent phase envelope discussed earlier. This is a second-order effect, and its magnitude is very small, in the amplitude window appearing at the one percent level. The systematic trend in the amplitude window estimated from the noisy data is a simple artifact of the representation of noisy complex data as amplitude and phase values, as discussed in Sect. 4.1. Since the variance of the noise in the synthesized data was 0.25, and given the doubling of spectral coefficients to compensate for filtering out the mirror image component, the mean power of the noise in the 2D envelope is expected to be 1.0 per complex coefficient, giving $\sigma^2_{\rm n}=0.5$. This leads to a variance of $\sim 1.0\times10^{-3}$ in the real and imaginary parts of the longitude-dependent envelope (since $\sum_{j=0}^{N_t-1}\vert m_{\rm t}(jP_1)\vert^2 = N_t = 512$), and hence a bias of up to $\sim 0.045$ at the edges of the envelope. Techniques for removing this bias are discussed in Sect. 4.1. The second-order effect of underestimation by a normalization error (Sect. 4.1) is expected to amount to only $\sim $1%, making it insignificant and not visible in the plots.

   
4.3.3 PSR B0943+10-like model

As an alternative that illustrates the applicability of these techniques to other observed phenomena, we produced simulated data from a model with similar parameters to PSR B0943+10.

We assumed a geometry of $\alpha=11.5\hbox{$^\circ$ }$, $\beta=5.4\hbox{$^\circ$ }$(Rankin 1993a,b) with N=20 sparks (Deshpande & Rankin 2001). A profile width of $20.5\hbox{$^\circ$ }$ FWHM (Gould & Lyne 1998) (giving $\sigma_m=0.023$ turns) was used, with sparks evenly spaced with widths given by $\sigma_s=0.2/N$, as in Sect. 4.3.2. A value of P1/0.5355 was used for P3' (Deshpande & Rankin 2001), with a moderately strong dependence on spark number (c=0.2) applied to give rise to a measurable signal of carousel circulation. No nulls were included in the simulation, but the instantaneous P3 values were made to have some variation in order to model the observed (large but probably finite) Q( $=\nu/\Delta\nu$). To this end we produced samples from an uncorrelated Gaussian noise process and filtered them in the frequency domain with the function $g(\nu)=\exp[-\nu/{0.01 \rm Hz}]$, to produce a slowly varying function which was scaled to have a range of $\pm0.05/P_3'$. This was added to to the nominal 1/P3' to give an instantaneous 1/P3(t). As in Sect. 4.3.2, one noiseless and one noisy ( $\sigma_n=0.5$) data set was produced. Each data set contained 512 pulses in 2048 longitude bins, of which only the central 512 were used.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f7.ps}\end{figure} Figure 7: Simulated PSR B0943+10-like data. The first 100 pulses from the noiseless data are shown. The near odd-even modulation is visible, as is the amplitude modulation due to the simulated carousel rotation.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f8.ps}\end{figure} Figure 8: Two-dimensional fluctuation power spectrum of simulated PSR B0943+10-like data. See caption of Fig. 4.
Open with DEXTER

The noiseless data and the resulting 2DF power spectrum are shown in Figs. 7 and 8. Notice that the 1/P3 feature of the fundamental (at 0.5355 P1) is aliased to a frequency of -0.4645 P1. This reflects the fact that if each sub-pulse is associated with its closest neighbour in pulse longitude from the following pulse, its drift appears to progress from earlier to later longitudes. This approach treats all measured $P_1/\hat{P_3}$as coming from the range $\pm0.5$. The conclusion from the work of Deshpande & Rankin (2001) is that each sub-pulse actually drifts 0.5355 times the sub-pulse spacing towards earlier longitudes with each successive pulse. Hence, the "nearest sub-pulse'' ( $\vert P_1/\hat{P_3}\vert < 0.5$) convention makes a sub-pulse counting error of n=+1 (see Sect. 4.2.1). It is important to note that this is simply a choice of convention. The two cases are indistinguishable without additional clues as employed by Deshpande & Rankin (2001).

The 2DFS was filtered with a function of the form shown in Eq. (28), with w=0.03/P1, and shifted to place the observed peak of the fundamental ( $P_1/\hat{P_3}=-0.465$, $P_1/\hat{P_2}=40$) at DC. This was scaled by a factor of two and inverse transformed and the result decomposed into time- and longitude-dependent modulation envelopes as in Sects. 4.1 and 4.3.2. The results are shown in Figs. 9 and 10.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f9.ps}\end{figure} Figure 9: Complex time-dependent modulation envelope and residuals for PSR B0943+10-like simulated data. See caption for Fig. 5.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f10.ps}\end{figure} Figure 10: Complex longitude-dependent modulation envelope and residuals for PSR B0943+10-like simulated data. See caption for Fig. 5.
Open with DEXTER

As with the 0809+74-like data, some systematics are present in the results from the noiseless data. In this case they are less severe due to the good separation between the fundamental of the drifting component and the DC component. In any real (noisy) data the errors are likely to be dominated by noise. In this model, due to the broader simulated main pulse, the phase rate (i.e. $2\pi P_2$) variation across the profile is noticeable even in the noisy data. As expected, the bias in the wings of the longitude-dependent amplitude envelope is of the same magnitude as that in the 0809+74-like data.

The amplitude variations due to the simulated carousel circulation are clearly visible in the modulation envelope estimated from the noisy data, as are the phase variations due to the simulated frequency noise. Since the phase variations are quite small, the amplitude modulation appears highly periodic and can be detected in the power spectrum of the inferred amplitude envelope (Fig. 11). The modulation also appears as a pair of "sidebands'' around the steady and drifting components in the 2DFS (Fig. 8). After previous authors (e.g. Deshpande & Rankin 2001), we have "stacked'' the columns of the power spectrum corresponding to 1/P2 < 64 to produce an "average'' fluctuation power spectrum. Figure 12 shows the stacked power spectrum around the -0.4645 P1-1 drifting component. The sidebands associated with the carousel rotation are clearly present, offset by $0.5355 P_1^{-1}/20\simeq 0.0268 P_1^{-1}$ from their respective parent features.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f11.ps}\end{figure} Figure 11: Power spectrum of the time-dependent amplitude envelope estimated from the noisy data. Values are normalised by the mean of noise-floor bins.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3330f12.ps}\end{figure} Figure 12: Portion of "stacked'' 2DFS around the drifting component. Values are normalised by the mean of noise-floor bins. The central feature peaks at a value of $\sim $487.
Open with DEXTER

The significance of detections of the carousel circulation measured via the power spectrum of the inferred amplitude envelope versus the stacked 2DF power spectrum must be evaluated carefully. Since the former is estimated from a single Fourier transform, the baseline noise power (suitably scaled) is $\chi^2$ distributed with two degrees of freedom. In contrast, the stacked spectrum is formed by adding 16 columns of the two-dimensional spectrum, so the (suitably scaled) spectral values follow a $\chi^2$ distribution with 32 degrees of freedom. For a detection of 97.8% confidence (corresponding to the 2-sigma point if the noise was Gaussian), the threshold normalised spectral power values are $\sim $3.8 for the power spectrum of the inferred amplitude envelope, versus $\sim $1.6for the normalized stacked spectrum. The corresponding "4-sigma'' points are $\sim $10.4 and $\sim $2.3. Neglecting effects due to phase noise, each responds to a modulation of amplitude c with a spectral power value proportional to c2, plus the "noise floor'' value of (on average) unity. From the values of peaks observed in these simulated data we can infer a proportionality constant of $\sim $20between the (noise-subtracted) responses of the two types of spectra. Hence, values of c giving rise to "2-'' or "4-sigma'' detections in the stacked spectrum (with power levels of 1.6 and 2.3) would produce far more significant detections (with power levels of $\sim $13 and $\sim $27) in the power spectrum of the inferred amplitude envelope. This enhancement in sensitivity (amounting to a factor of $\sim $2 in the minimum detectable amplitude of carousel circulation modulation) can be understood as a result of exploiting the inherent phase relations of the complex spectrum, rather than (incoherently) summing spectral power values.

As noted earlier, the model assumed here also produces sidebands around the DC component of the spectrum. Such sidebands were not observed in the studies of Deshpande & Rankin (2001), a fact that needs to be understood if carousel circulation is to explain the other sidebands. One possible explanation is that the total (integrated) luminosity of each spark of the carousel is approximately equal (leading to no sidebands around DC) but that the width of sparks differs as a function of position in the carousel.

5 Conclusions

We have shown that the two-dimensional Fourier spectrum of pulsar longitude-time data is of value in the analysis of drifting sub-pulses. We consider the drifting component of the signal as the convolution of a complex "modulation envelope'' with a pure two-dimensional periodicity. The modulation envelope describes the variations in average sub-pulse amplitude and phase as a function of longitude and time, and can be decomposed into the product of two one-dimensional envelopes which are functions of time and longitude respectively. This makes the technique well-suited to studying a variety of phenomena associated with drifting sub-pulses, including longitudinal variations in sub-pulse spacing (induced due to viewing geometry or other factors), variations in the drift rate as a function of time (due to the recovery from a null, random phase noise, etc.), comparison of the longitudinal amplitude dependence of the drifting and steady components of the pulsar emission, and variations in the average sub-pulse amplitude as a function of time (due to nulling, carousel rotation, etc.).

Acknowledgements
We thank R. Ramachandran and M. van der Klis for helpful comments on the text, A. Deshpande for useful discussion, and the referee (J. Middleditch) for drawing our attention to the sub-pulse modulation of "PSR1987A''. RTE is supported by a NOVA fellowship. BWS is supported by NWO Spinoza grant 08-0 to E. P. J. van den Heuvel.

   
Appendix A: Equivalence of the 2DFS and HRFS

As noted earlier, the 2DFS and HRFS are in fact equivalent. In this section we briefly show how this fact arises.

Consider the response to a single sinusoid, $i(t) = \sin 2\pi\nu t$. This will appear as a delta function in the HRFS at $x={\rm Frac}[\nu P_1]$, $y = {\rm Int}[{\nu P_1}]$ (both in units of cycles per P1-interval), where ${\rm Frac}$ and ${\rm Int}$ denote the fractional and integer parts of their arguments. For the 2DFS, when the data are stacked the signal will appear in each pulse period (of length P1) as a sinusoid with frequency $\nu P_1/2\pi$ (cycles per radian of pulse longitude) and phase $2\pi t/P_1 \times {\rm Frac}[\nu P_1]$ where t/P1 is the integer pulse number. Transforming first across rows results in a delta function at $\nu_l=\nu P_1/2\pi$ with a phase angle of $2\pi t/P_1 \times {\rm Frac}[\nu P_1]$ (and a corresponding component at $-\nu P_1/2\pi$ which can be ignored for now as it is simply the source of the symmetry of the 2DFS). Considering the column corresponding to $\nu_l=\nu P_1/2\pi$, the response is a pure complex exponential with a frequency of ${\rm Frac}[\nu P_1]/P_1$ (cycles per time unit). Therefore the result of the two-dimensional DFT is a delta function at $\nu_l=\nu P_1/2\pi$, $\nu_t={\rm Frac}[\nu P_1]/P_1$. A 1:1 mapping of $\nu_t=xP_1$, $\nu_l = y/2\pi$ thus applies in this case, when the fact that the $\nu_l$ bin size in the discrete 2DFS is $1/2\pi$ is considered. Since both transformations are linear and 1:1 invertible, we therefore conclude that they are identical in all cases, given appropriate mapping between parameters.

   
Appendix B: Derivation of magnetic Azimuth

The derivation of Eq. (19) follows a straightforward coordinate frame transformation, from the spin frame (in which the sight line parameters $-\phi$ and $\zeta $ represent longitude and co-latitude), to the magnetic frame. In each frame longitude is defined such that the positive spin pole of the complementary frame is at longitude zero. We definine basis vectors $[\begin{array}{ccc}\vec{x}&\vec{y}&\vec{z}\end{array}]$ and $[\begin{array}{ccc}\vec{x'}&\vec{y'}&\vec{z'}\end{array}]$ for the spin and magnetic frames respectively, aligning $\vec{z}$ (and $\vec{z'}$) with the positive poles and placing $\vec{x}$ and $\vec{x'}$ at longitude zero in their respective frames. In what follows all vectors (including $\vec{d}$ and $\vec{\mu}$) are taken as being of unit length. The expression for $\vec{d}$ in the spin frame is:

\begin{displaymath}\vec{d} = \left[\begin{array}{c} \cos\phi\sin\zeta \\ -\sin\... ...y}{c} \vec{x} \\ \vec{y} \\ \vec{z} \end{array}\right] \cdot \end{displaymath} (B.1)

The transformation between frames may be accomplished by rotating about $\vec{y}$ by the angle $-\alpha$ (to align the pole with the magnetic pole), then rotating in longitude (i.e. about $\vec{z'}$) by $\pi$ radians (to place the spin pole at longitude zero). The transformation is expressed as follows:
                               $\displaystyle \vec{d}$ = $\displaystyle \left[\begin{array}{c} \cos\phi\sin\zeta \\ -\sin\phi\sin\zeta \... ...t] \left[\begin{array}{c} \vec{x'} \\ \vec{y'} \\ \vec{z'} \end{array}\right]$  
  = $\displaystyle \left[\begin{array}{c} \cos\zeta\sin\alpha - \cos\phi\sin\zeta\co... ...ft[\begin{array}{c} \vec{x'} \\ \vec{y'} \\ \vec{z'} \end{array}\right] \cdot$ (B.2)

Deriving the longitude of $\vec{d}$ in this frame (i.e. the magnetic azimuth) via $\tan\psi = d_{y'}/d_{x'}$ yields Eq. (19). This result, after differentiation and correction for a difference in the sign convention for $\psi $, agrees with that of Ashworth (1988).

The derivation of the polarization position angle follows a similar path. It is based in a third frame which is fixed to local rest frame the observer, has its origin at the star center, positive pole pointing to the viewer (i.e. $\vec{z''} = \vec{d}$) and places the positive spin pole at longitude zero. All meridians in this frame project as lines on the sky with position angles offset from the position angle of the spin axis by their longitude ($\chi $). Under the RVM, the position angle of linear polarization is given by the projection of the local magnetic field line on the sky, which is given by the projection of the great circle co-planar with the $\vec{\mu}$ and $\vec{d}$. Hence the (counter-clockwise) polarization position angle (minus the position angle of the projected spin axis) is given by the longitude of the magnetic pole in this frame. The transformation from the spin frame is a rotation of $\phi $ in longitude, followed by a rotation about $\vec{y}$ by $\alpha $ (versus $\zeta $ in the above) and a rotation of $\pi$ radians about $\vec{y''}$ as above, whilst the input vector has spherical coordinates $(0,\alpha)$ (versus $(-\phi,\zeta)$ in the above). From this it follows that Eqs. (19) and (23) differ only through switching of $\alpha $ and $\zeta $ and a sign reversal (in $\phi $or equivalently, in the final longitude value).

References

 

Copyright ESO 2002