A&A 393, 523-542 (2002)
DOI: 10.1051/0004-6361:20021053
Relativistic simulations of rotational core collapse
II. Collapse dynamics and gravitational radiation
H. Dimmelmeier 1 - J. A. Font 1,2 - E. Müller 1
1 - Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
2 -
Departamento de Astronomía y Astrofísica,
Universidad de Valencia, 46100 Burjassot (Valencia), Spain
Received 12 April 2002 / Accepted 4 July 2002
Abstract
We have performed hydrodynamic simulations of relativistic
rotational supernova core collapse in axisymmetry and have computed
the gravitational radiation emitted by such an event. The Einstein
equations are formulated using the conformally flat metric
approximation, and the corresponding hydrodynamic equations are
written as a first-order flux-conservative hyperbolic
system. Details of the methodology and of the numerical code have
been given in an accompanying paper. We have simulated the evolution
of 26 models in both Newtonian and relativistic gravity. The
initial configurations are differentially rotating relativistic
4 / 3-polytropes in equilibrium which have a central density of
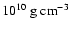 .
Collapse is initiated by decreasing
the adiabatic index to some prescribed fixed value. The equation of
state consists of a polytropic and a thermal part for a more
realistic treatment of shock waves. Any microphysics like
electron capture and neutrino transport is neglected.
Our simulations show that the three different types of rotational
supernova core collapse and gravitational waveforms identified in
previous Newtonian simulations (regular collapse, multiple bounce
collapse, and rapid collapse) are also present in relativistic
gravity. However, rotational core collapse with multiple bounces is
only possible in a much narrower parameter range in relativistic
gravity. The relativistic models cover almost the same range of
gravitational wave amplitudes
(
.
Collapse is initiated by decreasing
the adiabatic index to some prescribed fixed value. The equation of
state consists of a polytropic and a thermal part for a more
realistic treatment of shock waves. Any microphysics like
electron capture and neutrino transport is neglected.
Our simulations show that the three different types of rotational
supernova core collapse and gravitational waveforms identified in
previous Newtonian simulations (regular collapse, multiple bounce
collapse, and rapid collapse) are also present in relativistic
gravity. However, rotational core collapse with multiple bounces is
only possible in a much narrower parameter range in relativistic
gravity. The relativistic models cover almost the same range of
gravitational wave amplitudes
(
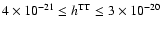 for a
source at a distance of 10 kpc) and
frequencies (
for a
source at a distance of 10 kpc) and
frequencies (
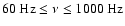 )
as the
corresponding Newtonian ones. Averaged over all models, the total
energy radiated in the form of gravitational waves is
)
as the
corresponding Newtonian ones. Averaged over all models, the total
energy radiated in the form of gravitational waves is
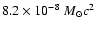 in the relativistic case, and
in the relativistic case, and
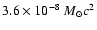 in the Newtonian case. For all collapse models that are of the
same type in both Newtonian and relativistic gravity, the
gravitational wave signal is of lower amplitude. If the collapse
type changes, either weaker or stronger signals are found in the
relativistic case. For a given model, relativistic gravity can
cause a large increase of the characteristic signal frequency of up
to a factor of five, which may have important consequences for the signal
detection. Our study implies that the prospects for
detection of gravitational wave signals from axisymmetric supernova
rotational core collapse do not improve when taking into account
relativistic gravity. The gravitational wave signals obtained in our
study are within the sensitivity range of the first generation laser
interferometer detectors if the source is located within the Local
Group. An online catalogue containing the gravitational wave signal
amplitudes and spectra of all our models is available at the URL
http://www.mpa-garching.mpg.de/Hydro/hydro.html.
in the Newtonian case. For all collapse models that are of the
same type in both Newtonian and relativistic gravity, the
gravitational wave signal is of lower amplitude. If the collapse
type changes, either weaker or stronger signals are found in the
relativistic case. For a given model, relativistic gravity can
cause a large increase of the characteristic signal frequency of up
to a factor of five, which may have important consequences for the signal
detection. Our study implies that the prospects for
detection of gravitational wave signals from axisymmetric supernova
rotational core collapse do not improve when taking into account
relativistic gravity. The gravitational wave signals obtained in our
study are within the sensitivity range of the first generation laser
interferometer detectors if the source is located within the Local
Group. An online catalogue containing the gravitational wave signal
amplitudes and spectra of all our models is available at the URL
http://www.mpa-garching.mpg.de/Hydro/hydro.html.
Key words: gravitation - gravitational waves - hydrodynamics -
stars: neutron - stars: rotation - stars: supernovae: general
1 Introduction
At the end of their thermonuclear evolution, massive stars develop a
core composed of iron group nuclei (hence iron core) which becomes
dynamically unstable against gravitational collapse. The iron core
collapses to a neutron star or a black hole, releasing gravitational
binding energy of the order 
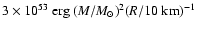 ,
which is sufficient to power a supernova explosion. If the core
collapse and/or the supernova explosion are nonspherical, part of the
liberated gravitational binding energy will be emitted in the form of
gravitational waves. Nonsphericity can be caused by the effects of
rotation, convection and anisotropic neutrino emission leading either
to a large-scale deviation from spherical symmetry or to small-scale
statistical mass-energy fluctuations (for a review, see e.g.,
Müller 1998).
,
which is sufficient to power a supernova explosion. If the core
collapse and/or the supernova explosion are nonspherical, part of the
liberated gravitational binding energy will be emitted in the form of
gravitational waves. Nonsphericity can be caused by the effects of
rotation, convection and anisotropic neutrino emission leading either
to a large-scale deviation from spherical symmetry or to small-scale
statistical mass-energy fluctuations (for a review, see e.g.,
Müller 1998).
According to present knowledge the energy radiated away in form of
gravitational waves does not exceed
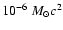 in rotational
core collapse (Müller 1982; Finn & Evans 1990; Mönchmeyer et al. 1991;
Bonazzola & Marck 1993; Yamada & Sato 1994a; Zwerger & Müller 1997; Rampp et al. 1998; Fryer et al. 2002) and
from convection or anisotropic neutrino emission in neutrino-driven
supernovae (Müller & Janka 1997). The frequency of the emitted
radiation ranges from about a few Hz to a few kHz, and the
(dimensionless) signal amplitudes for a source located at a distance
of 10 Mpc (within the Virgo cluster) do not exceed
in rotational
core collapse (Müller 1982; Finn & Evans 1990; Mönchmeyer et al. 1991;
Bonazzola & Marck 1993; Yamada & Sato 1994a; Zwerger & Müller 1997; Rampp et al. 1998; Fryer et al. 2002) and
from convection or anisotropic neutrino emission in neutrino-driven
supernovae (Müller & Janka 1997). The frequency of the emitted
radiation ranges from about a few Hz to a few kHz, and the
(dimensionless) signal amplitudes for a source located at a distance
of 10 Mpc (within the Virgo cluster) do not exceed 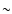 10-22.
The smallness of the signals calls for accurate waveform templates to
alleviate the technical difficulties in extracting the signal from
noisy data (Pradier et al. 2001). For the current generation of laser
interferometric detectors (GEO 600, LIGO, VIRGO, TAMA) such small
amplitudes imply that the prospects for detection of gravitational
waves from core collapse supernovae are limited to those events
occurring within the Local Group. However, if measured, a
gravitational wave signal does provide (as observations of neutrinos)
a direct diagnosis of the dynamics of the events.
10-22.
The smallness of the signals calls for accurate waveform templates to
alleviate the technical difficulties in extracting the signal from
noisy data (Pradier et al. 2001). For the current generation of laser
interferometric detectors (GEO 600, LIGO, VIRGO, TAMA) such small
amplitudes imply that the prospects for detection of gravitational
waves from core collapse supernovae are limited to those events
occurring within the Local Group. However, if measured, a
gravitational wave signal does provide (as observations of neutrinos)
a direct diagnosis of the dynamics of the events.
Investigations of rotational core collapse are also important in the
context of the supernova explosion mechanism (Müller & Hillebrandt 1981;
Bodenheimer & Woosley 1983; Symbalisty 1984; Mönchmeyer & Müller 1989; Janka & Mönchmeyer 1989;
Imshennik & Nadezhin 1992; Yamada & Sato 1994b; Fryer & Heger 2000) and for the collapsar
scenario of gamma-ray bursts, where the collapse of a rotating
massive star leads to the formation of a Kerr black hole and a
relativistic jet (MacFadyen et al. 2001; Aloy et al. 2000; Wheeler et al. 2000).
Numerous studies have addressed quite different aspects of rotational
core collapse at different levels of sophistication. Ideally, such
studies should incorporate a relativistic treatment of gravity and
hydrodynamics without symmetry restrictions, a detailed description of
the complex microphysics and of the neutrino transport, and should use
consistent initial models from evolutionary calculations of rotating
stars. The latter point is still a nagging problem (for a major step
forward in this context see Heger et al. 2000), as up to now all
studies, except that of Fryer et al. (2002), have relied on
parameterized initial models.
As the general relativistic corrections of the gravitational potential
during supernova core collapse, and for a neutron star, do not exceed
30%, it is often argued that they can be neglected or only taken into
account approximately. While this approach may be justified to some
degree in the case of non-rotational core collapse, it becomes very
questionable when the core possesses a significant amount of angular
momentum. In the latter case, a relativistic treatment of gravity is
much more important, because the stabilizing effect of rotation is
counteracted by the destabilizing effect of the deeper relativistic
potential. This is reflected in the expression for the critical
adiabatic index
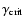 ,
below which a rigidly rotating
relativistic configuration is dynamically unstable against
pseudo-radial (linear) isentropic perturbations (see, e.g., Chap. 14
of Tassoul 1978):
,
below which a rigidly rotating
relativistic configuration is dynamically unstable against
pseudo-radial (linear) isentropic perturbations (see, e.g., Chap. 14
of Tassoul 1978):
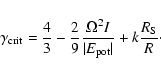 |
(1) |
Here 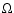 ,
I,
,
I,
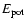 ,
,
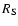 ,
and R are
the (constant) angular velocity, the moment of inertia about the
center of mass, the gravitational potential energy, the Schwarzschild
radius, and the radius of the star, respectively. The positive
constant k depends on the density distribution of the star.
,
and R are
the (constant) angular velocity, the moment of inertia about the
center of mass, the gravitational potential energy, the Schwarzschild
radius, and the radius of the star, respectively. The positive
constant k depends on the density distribution of the star.
Axisymmetric Newtonian hydrodynamic collapse and explosion simulations
using a realistic equation of state (EoS) and some treatment of weak
interaction processes have been performed by Müller (1982),
Bodenheimer & Woosley (1983), Symbalisty (1984) and
Bonazzola & Marck (1993) neglecting neutrino transport, and by
Mönchmeyer & Müller (1989), Janka & Mönchmeyer (1989),
Mönchmeyer et al. (1991), Imshennik & Nadezhin (1992), Fryer & Heger (2000)
and Fryer et al. (2002) employing some approximative description of
neutrino transport. In addition, Finn & Evans (1990),
Yamada & Sato (1994b) and Zwerger & Müller (1997) have performed Newtonian
parameter studies of the axisymmetric collapse of rotating
polytropes. Rampp et al. (1998) and Brown (2001) have extended
the work of Zwerger & Müller (1997) by relaxing the assumption of
axisymmetry.
Wilson (1979), Evans (1986), Nakamura (1981,
1983) and Stark & Piran (1985) pioneered investigations of
axisymmetric collapse of rotating configurations in full general
relativity (GR). Wilson (1979) computed neutron star bounces of
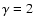 polytropes, while Nakamura (1981)
(see also
Nakamura et al. 1987) simulated the formation of rotating black holes
resulting from the collapse of a
polytropes, while Nakamura (1981)
(see also
Nakamura et al. 1987) simulated the formation of rotating black holes
resulting from the collapse of a
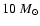 "core'' of a massive star
with different amounts of rotational energy and an initial central
density of
"core'' of a massive star
with different amounts of rotational energy and an initial central
density of
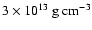 .
Nakamura (1983) (see also Nakamura et al. 1987) considered a
configuration consisting of a neutron star (
.
Nakamura (1983) (see also Nakamura et al. 1987) considered a
configuration consisting of a neutron star (
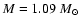 ,
,
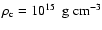 )
with an
accreted envelope of
)
with an
accreted envelope of
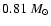 ,
which was thought to mimic mass
fall-back in a supernova explosion. To this configuration he added
rotation and infall velocity, and simulated the evolution depending on
the prescribed rotation rates and rotation laws. In both scenarios the
EoS consisted of a relativistic degenerate lepton gas
(
,
which was thought to mimic mass
fall-back in a supernova explosion. To this configuration he added
rotation and infall velocity, and simulated the evolution depending on
the prescribed rotation rates and rotation laws. In both scenarios the
EoS consisted of a relativistic degenerate lepton gas
(
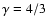 )
at low densities
(
)
at low densities
(
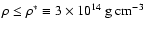 ,
and
of a stiff (
,
and
of a stiff (
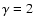 )
component at large densities
(
)
component at large densities
(
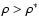 ). Stark & Piran (1985) were the first to compute the
gravitational radiation from the relativistic collapse of a rotating
polytropic (
). Stark & Piran (1985) were the first to compute the
gravitational radiation from the relativistic collapse of a rotating
polytropic (
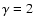 )
star to a black hole. The initial model was
a spherically symmetric relativistic polytrope in equilibrium of mass
M, central density
)
star to a black hole. The initial model was
a spherically symmetric relativistic polytrope in equilibrium of mass
M, central density
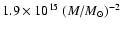 ,
and radius
,
and radius
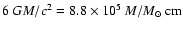 .
Rotational
collapse was induced by lowering the pressure in the initial model by
a prescribed fraction, and by simultaneously adding an angular
momentum distribution approximating rigid-body
rotation. Stark & Piran (1985) found a low efficiency of gravitational
wave emission (
.
Rotational
collapse was induced by lowering the pressure in the initial model by
a prescribed fraction, and by simultaneously adding an angular
momentum distribution approximating rigid-body
rotation. Stark & Piran (1985) found a low efficiency of gravitational
wave emission (
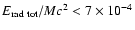 ,
where
,
where
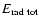 is the total energy radiated by graviational
waves), and that for sufficient rotation the star bounces and no black
hole forms.
is the total energy radiated by graviational
waves), and that for sufficient rotation the star bounces and no black
hole forms.
After the work of Stark & Piran (1985) it took about 15 years before the
next simulations of GR rotational core collapse were published. This
was mainly caused by persistent numerical problems occurring in
axisymmetric GR simulations due to coordinate singularities at the
symmetry (= rotation) axis. These coordinate singularities hamper the
development of methods which guarantee accuracy and stability in long
term (covering many dynamical time scales) simulations.
Alcubierre et al. (2001) proposed a method which does not suffer from
stability problems and where, in essence, Cartesian coordinates are
used even for axisymmetric systems. Using this method
Shibata (2000) investigated the effects of rotation on the
criterion for prompt adiabatic collapse of rigidly and differentially
rotating (
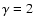 )
polytropes to a black hole. Collapse of the
initial approximate (computed by assuming a conformally flat spatial
metric) equilibrium models was induced by a pressure
reduction. Shibata (2000) found that the criterion for black
hole formation depends strongly on the amount of angular momentum, but
only weakly on its (initial) distribution. He also studied the
effects of shock heating using a gamma-law EoS, and found that shock
heating is important in preventing prompt collapse to black holes in
case of large rotation rates.
)
polytropes to a black hole. Collapse of the
initial approximate (computed by assuming a conformally flat spatial
metric) equilibrium models was induced by a pressure
reduction. Shibata (2000) found that the criterion for black
hole formation depends strongly on the amount of angular momentum, but
only weakly on its (initial) distribution. He also studied the
effects of shock heating using a gamma-law EoS, and found that shock
heating is important in preventing prompt collapse to black holes in
case of large rotation rates.
Hayashi et al. (1999) investigated the possibility of secular, i.e. quasi-static, core contraction from white dwarf to neutron star
densities using equilibrium sequences of rapidly rotating, general
relativistic compact stars with phenomenological equations of state.
They demonstrated that there is a possibility for the existence of
"fizzlers'' in the framework of GR, at least for the simplified equations
of state used in their study.
The above discussion shows that previous investigations in GR
rotational core collapse were mainly concerned with the question of
black hole formation under idealized conditions, but none of these
studies has really addressed the problem of supernova core collapse
which proceeds from white dwarf densities to neutron star densities,
involves core bounce, shock formation, and shock propagation. Exactly
this is the motivation for the present work. To this end, we apply the
numerical methodology presented in an accompanying paper
(Dimmelmeier et al. 2002, hereafter Paper I) and study the dynamics of
axisymmetric, relativistic rotational supernova core collapse and the
associated emission of gravitational radiation. In particular, we have
simulated the collapse of a comprehensive set of rotating relativistic
stellar models parameterized by the initial degree of differential
rotation, the initial rotation rate and the adiabatic indices at
subnuclear (supranuclear) matter densities. Thus, our study is a GR extension of the previous work of Zwerger (1995) and
Zwerger & Müller (1997), who computed the gravitational radiation from
rotational core collapse supernovae using Newtonian gravity. First
results from our study have already been published in a short
communication (Dimmelmeier et al. 2001)![[*]](/icons/foot_motif.gif) .
.
The organization of the paper is as follows:
Sect. 2 contains a brief repetition of
the assumptions made in our study (for more details see Paper I). In
Sect. 3 we analyze in detail the collapse
dynamics and introduce the three different types of collapse and
gravitational waveforms we have identified.
Section 4 is devoted to the gravitational wave
emission of the models, and to the prospects of detectability of
gravitational waves from core collapse supernovae. We conclude with a
summary in Sect. 5. Additional information is
given in Appendix A where we discuss the
issue of gravitational wave extraction.
2 Model assumptions
The matter model obeys an ideal gas EoS with the pressure Pconsisting of a polytropic and a thermal part for a more realistic
treatment of the effects of shock waves (Janka et al. 1993;
Zwerger & Müller 1997). Since we are mostly interested in the gravitational
radiation emission, which is controlled by the bulk motion of the
fluid, we neglect microphysics like electron capture and neutrino
transport. The initial configurations are differentially rotating
relativistic 4 / 3-polytropes in equilibrium (Komatsu et al. 1989a,b;
Stergioulas & Friedman 1995) which are marginally stable, and
which have a central density
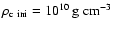 .
Collapse is
initiated by decreasing the adiabatic index (initially 4 / 3 in
all models) to some prescribed fixed value
.
Collapse is
initiated by decreasing the adiabatic index (initially 4 / 3 in
all models) to some prescribed fixed value 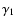 (for more
details see Paper I).
(for more
details see Paper I).
The initial models are determined by three parameters, which are also
used to name the models. The first parameter A is a length scale,
which specifies the degree of differential rotation (see Eq. (33) of
Paper I). The smaller the value of A the more differentially
rotating the model is. Model parameters A1, A2, A3 and A4 correspond
to
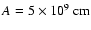 ,
,
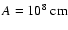 ,
,
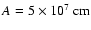 ,
and
,
and
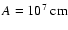 ,
respectively. The second parameter is the initial rotation rate
,
respectively. The second parameter is the initial rotation rate
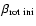 ,
which is given by the ratio of rotational
energy and the absolute value of the gravitational binding
energy. Model parameters B1, B2, B3, B4 and B5 correspond to
,
which is given by the ratio of rotational
energy and the absolute value of the gravitational binding
energy. Model parameters B1, B2, B3, B4 and B5 correspond to
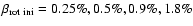 and
and 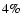 ,
respectively. The third parameter
,
respectively. The third parameter 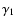 is the adiabatic index
at subnuclear densities (
is the adiabatic index
at subnuclear densities (
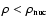 ),
with model parameters G1, G2, G3, G4 and G5
corresponding to
),
with model parameters G1, G2, G3, G4 and G5
corresponding to
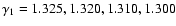 and 1.280, respectively. The name of a simulated model is then given
by a combination of parameters from the three sets (e.g., A3B4G5).
We define the nuclear matter density
and 1.280, respectively. The name of a simulated model is then given
by a combination of parameters from the three sets (e.g., A3B4G5).
We define the nuclear matter density
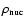 as
as
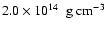 .
.
The adiabatic index at supranuclear densities
(
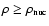 )
is fixed to
)
is fixed to
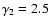 ,
except
in one model which has also been run with
,
except
in one model which has also been run with
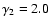 in order to
test the influence of a softer supranuclear EoS on the collapse dynamics.
in order to
test the influence of a softer supranuclear EoS on the collapse dynamics.
In total, we have simulated the evolution of 26 models (see
Table 1). In order to identify the relativistic
effects on the collapse dynamics, we have simulated these models also
in Newtonian gravity. Note that the Newtonian simulations are a subset
of those performed by Zwerger (1995) and Zwerger & Müller (1997).
The Einstein equations are formulated using the so-called conformally
flat (CF) metric approximation (Wilson et al. 1996, conformal flatness condition - CFC) and the corresponding hydrodynamic equations are
formulated as a first-order flux-conservative hyperbolic system
(Banyuls et al. 1997), well-adapted to numerical schemes based on
Riemann solvers. The applicability and quality of the CFC for
rotational core collapse has been discussed in detail in Paper I,
where we demonstrated that its usage is appropriate.
3 Collapse dynamics
3.1 Collapse and waveform types
Zwerger (1995) first identified three distinct classes of core
collapse types. This classification is based on the form of the
gravitational wave signal. However, as the gravitational radiation
waveform is closely linked to the collapse dynamics, it also mirrors
the collapse behavior. Thus, the signal types can generally be used to
classify the collapse type, too.
In our relativistic simulations, each of the examined models belongs
to one of Zwerger's three collapse types, which he called type I, II
and III. In the following we describe a representative model from each
class, discuss its characteristic properties and explain the physical
effects which lead to its collapse classification.
In general, the evolution of any supernova core collapse can be
divided into three phases (see, e.g., Müller 1998):
Infall phase: this phase covers the initial collapse of the core
from the onset of the gravitational instability triggered by the
sudden softening of the EoS due to the reduction of the subnuclear
adiabatic index. The inner part of the core, which collapses
homologously (
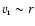 ), constitues the "inner core'', while
the "outer core'' is falling supersonically. Depending on the model
parameters the infall phase lasts between 30 ms and 100 ms.
), constitues the "inner core'', while
the "outer core'' is falling supersonically. Depending on the model
parameters the infall phase lasts between 30 ms and 100 ms.
Bounce phase: when the EoS stiffens because repulsive nuclear
forces become important at densities above nuclear density
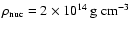 ,
or when
centrifugal forces begin to dominante over gravitational attraction
due to angular momentum conservation and rotational spin-up, the inner
core decelerates on a timescale of about 1 ms. Because of its large
inertia and infall kinetic energy, the inner core does not come to
rest immediately. The core overshoots the equilibrium configuration it
will eventually approach, and bounces back, which results in the
formation of a shock wave at the outer edge of the inner core. During
core bounce the amplitude of the gravitational wave signal is largest.
,
or when
centrifugal forces begin to dominante over gravitational attraction
due to angular momentum conservation and rotational spin-up, the inner
core decelerates on a timescale of about 1 ms. Because of its large
inertia and infall kinetic energy, the inner core does not come to
rest immediately. The core overshoots the equilibrium configuration it
will eventually approach, and bounces back, which results in the
formation of a shock wave at the outer edge of the inner core. During
core bounce the amplitude of the gravitational wave signal is largest.
Ring-down phase, or re-expansion phase: if centrifugal forces
remain sufficiently small until nuclear density is reached in the
center of the core, the bounce occurs at central densities slightly in
excess of nuclear density due to the stiffening of the EoS. In this
case the inner core rapidly settles down into a new equilibrium state,
which we will call the "compact remnant''![[*]](/icons/foot_motif.gif) in the following. While the shock wave propagates
outwards, the inner core oscillates for about 10 ms with a
superposition of several damped eigenmodes with frequencies of about
in the following. While the shock wave propagates
outwards, the inner core oscillates for about 10 ms with a
superposition of several damped eigenmodes with frequencies of about
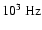 (ring-down). If the infall is moderately fast
(collapse timescale longer than about 50 ms), we will talk of a
regular collapse model giving rise to a type I gravitational wave
signal according to the nomenclature of Zwerger & Müller (1997). In case
of a very rapid infall (collapse timescale of about 30 ms), the core
plunges unimpeded by centrifugal forces deeply into the gravitational
potential well, with its central density significantly exceeding
nuclear density. In such rapid collapse models, the gravitational
waveform (type III according to the nomenclature of
Zwerger & Müller 1997) is qualitatively different from that of a
regular (type I) collapse model (see below).
(ring-down). If the infall is moderately fast
(collapse timescale longer than about 50 ms), we will talk of a
regular collapse model giving rise to a type I gravitational wave
signal according to the nomenclature of Zwerger & Müller (1997). In case
of a very rapid infall (collapse timescale of about 30 ms), the core
plunges unimpeded by centrifugal forces deeply into the gravitational
potential well, with its central density significantly exceeding
nuclear density. In such rapid collapse models, the gravitational
waveform (type III according to the nomenclature of
Zwerger & Müller 1997) is qualitatively different from that of a
regular (type I) collapse model (see below).
On the other hand, if core collapse is only or predominantly stopped
by centrifugal forces, the inner core experiences several distinct
sequences of infall, bounce, and re-expansion separated by up to
50 ms before it eventually settles down into an equilibrium state.
During each bounce an outward shock is generated. The multiple large
scale bounces occur because the deceleration by centrifugal forces is
less abrupt than that due to the stiffness of the supranuclear
EoS. The latter is characterized by an adiabatic index
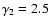 (see Sect. 2), while
rotation acts like a
(see Sect. 2), while
rotation acts like a
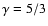 gas according to the virial
theorem (see, e.g., Tassoul 1978, Chap. 14). Multiple bounce
models produce type II gravitational wave signals (Zwerger & Müller 1997)
which consist of a distinct large amplitude peak for every bounce.
gas according to the virial
theorem (see, e.g., Tassoul 1978, Chap. 14). Multiple bounce
models produce type II gravitational wave signals (Zwerger & Müller 1997)
which consist of a distinct large amplitude peak for every bounce.
If the peak central density at bounce is close to (or exceeds)
nuclear matter density, and if the core rotates differentially and
rapidly, a mixture of a regular and multiple collapse type model can
occur. In these transition models of type I/II the core re-expands
less than in a genuine multiple bounce model, but it still exhibits
distinct bounces and coherent large scale oscillations.
3.1.1 Regular collapse - type I
As in the work of Zwerger & Müller (1997) we choose model A1B3G3 as a
representative model for a regular collapse.
Figure 1 shows the time evolution of the
central density
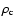 and the gravitational wave signal
amplitude
and the gravitational wave signal
amplitude
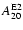 ;
the definition of the wave amplitude
;
the definition of the wave amplitude
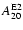 and the description of the numerical wave
extraction technique are given in
Appendix A. The three phases of the collapse
are clearly identifiable in both panels. During the infall phase
and the description of the numerical wave
extraction technique are given in
Appendix A. The three phases of the collapse
are clearly identifiable in both panels. During the infall phase
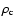 increases and exceeds nuclear matter density at 48.26 ms. The peak value of the density is reached at the time of
bounce at
increases and exceeds nuclear matter density at 48.26 ms. The peak value of the density is reached at the time of
bounce at
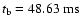 with
with
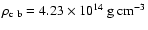 ,
which is
about twice nuclear matter density. Subsequently, the core slightly
re-expands and rings down to an equilibrium state with a central
density of
,
which is
about twice nuclear matter density. Subsequently, the core slightly
re-expands and rings down to an equilibrium state with a central
density of
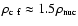 .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f1.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg85.gif) |
Figure 1:
Time evolution of the central density
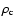 (upper panel) and the gravitational wave signal amplitude
(upper panel) and the gravitational wave signal amplitude
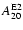 (lower panel) for the regular collapse
model A1B3G3. The horizontal dotted line in the upper panel marks
nuclear matter density
(lower panel) for the regular collapse
model A1B3G3. The horizontal dotted line in the upper panel marks
nuclear matter density
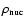 ,
and the vertical dotted
line indicates the time of peak central density ,
and the vertical dotted
line indicates the time of peak central density 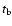 . . |
| Open with DEXTER |
The gravitational wave amplitude (lower panel of
Fig. 1) increases during the infall phase,
but has a negative peak value with
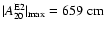 at
at
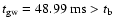 .
In all regular collapse
models the maximum signal amplitude is negative. For some models (not
in model A1B3G3) the signal amplitude exhibits a small local minimum
around the time of bounce, a feature which was identified and
discussed by Zwerger & Müller (1997). The ring-down phase of the
pulsating inner core is directly reflected in the wave signal which
oscillates accordingly. As in the Newtonian runs of
Zwerger & Müller (1997), we find that during the ring-down phase the
maxima of
.
In all regular collapse
models the maximum signal amplitude is negative. For some models (not
in model A1B3G3) the signal amplitude exhibits a small local minimum
around the time of bounce, a feature which was identified and
discussed by Zwerger & Müller (1997). The ring-down phase of the
pulsating inner core is directly reflected in the wave signal which
oscillates accordingly. As in the Newtonian runs of
Zwerger & Müller (1997), we find that during the ring-down phase the
maxima of
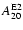 are less damped than the minima, because
larger accelerations are encountered at the high density extrema of
the core.
are less damped than the minima, because
larger accelerations are encountered at the high density extrema of
the core.
3.1.2 Multiple bounce collapse - type II
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms2576f2.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg88.gif) |
Figure 2:
Time evolution of the central density
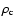 (upper panel) and the gravitational wave signal amplitude
(upper panel) and the gravitational wave signal amplitude
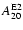 (lower panel) for the multiple bounce
collapse model A2B4G1. The vertical dotted lines mark the times
of peak central density for each bounce.
(lower panel) for the multiple bounce
collapse model A2B4G1. The vertical dotted lines mark the times
of peak central density for each bounce. |
| Open with DEXTER |
For an adiabatic index 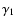 close to the initial value
close to the initial value
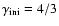 (see Sect. 2),
and for rapid and highly differential rotation, centrifugal forces can
halt the collapse at densities below nuclear matter density. Such
subnuclear bounces can indeed be observed in some of our collapse
models, e.g. model A2B4G1, for which the time evolution of the
central density
(see Sect. 2),
and for rapid and highly differential rotation, centrifugal forces can
halt the collapse at densities below nuclear matter density. Such
subnuclear bounces can indeed be observed in some of our collapse
models, e.g. model A2B4G1, for which the time evolution of the
central density
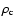 and the gravitational wave signal
amplitude
and the gravitational wave signal
amplitude
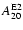 are shown in
Fig. 2.
are shown in
Fig. 2.
In both the central density evolution and the signal waveform distinct
extrema are discernable. The (negative) maximum of the signal
amplitude
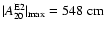 is reached
at a time
is reached
at a time
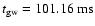 ,
which is shortly after
the time
,
which is shortly after
the time
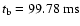 when the central density
reaches its first peak
when the central density
reaches its first peak
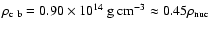 .
During the subsequent bounces the peaks of the central density are
significantly smaller than the peak value at first bounce. The
prominent peaks in the gravitational wave signal are clearly
associated with the distinct bounces visible in the density evolution.
.
During the subsequent bounces the peaks of the central density are
significantly smaller than the peak value at first bounce. The
prominent peaks in the gravitational wave signal are clearly
associated with the distinct bounces visible in the density evolution.
We point out that model A1B3G1, which shows multiple bounces in
Newtonian gravity (Zwerger & Müller 1997), does not exhibit such a
behavior in the relativistic simulations. This change of collapse type
due to relativistic effects is discussed in
Sect. 3.3.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f3.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg94.gif) |
Figure 3:
Time evolution of the central density
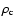 (upper panel) and the gravitational wave signal amplitude
(upper panel) and the gravitational wave signal amplitude
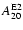 (lower panel) for the rapid collapse
model A1B3G5. The horizontal dotted line in the upper panel marks
nuclear matter density
(lower panel) for the rapid collapse
model A1B3G5. The horizontal dotted line in the upper panel marks
nuclear matter density
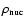 ,
and the vertical dotted
line indicates the time of peak central density ,
and the vertical dotted
line indicates the time of peak central density 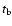 .
Note the qualitative difference in the waveform
compared to the regular collapse (type I) model shown in
Fig. 1. .
Note the qualitative difference in the waveform
compared to the regular collapse (type I) model shown in
Fig. 1. |
| Open with DEXTER |
3.1.3 Rapid collapse - type III
If the core collapses very rapidly due to values of 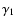 which
are much smaller than 4/3, the qualitative behavior of the density
evolution is very similar to that of the regular (type I) collapse
model, except that the bounce and equilibrium densities are slightly
higher, and the post-bounce pulsations of the inner core are even more
strongly suppressed. For example, in model A1B3G5
(Fig. 3), which is a typical rapid collapse
model, the values of the peak and the final central density are
which
are much smaller than 4/3, the qualitative behavior of the density
evolution is very similar to that of the regular (type I) collapse
model, except that the bounce and equilibrium densities are slightly
higher, and the post-bounce pulsations of the inner core are even more
strongly suppressed. For example, in model A1B3G5
(Fig. 3), which is a typical rapid collapse
model, the values of the peak and the final central density are
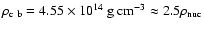 (reached at
(reached at
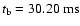 ), and
), and
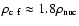 .
.
On the other hand, the shape of the gravitational wave signal
amplitude is qualitatively different compared to type I models. This
is shown in the lower panel of Fig. 3, where
the time evolution of
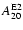 is plotted. The maximum signal
amplitude
is plotted. The maximum signal
amplitude
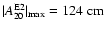 at
at
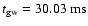 is now assigned to the first positive
peak of the waveform contrary to the signal waveform of the regular
collapse models. In the case of rapid collapse, the negative peak is almost
entirely suppressed and the overall amplitude of the signal is
significantly smaller. There is no clear feature in the waveform
allowing one to identify the time of bounce
is now assigned to the first positive
peak of the waveform contrary to the signal waveform of the regular
collapse models. In the case of rapid collapse, the negative peak is almost
entirely suppressed and the overall amplitude of the signal is
significantly smaller. There is no clear feature in the waveform
allowing one to identify the time of bounce  .
.
For a given initial model, the transition between type I and
type III collapse models occurs gradually with decreasing values of 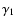 .
In the gravitational wave signal this is reflected by a
decrease of the negative main peak and an increase of the first
positive peak (Zwerger & Müller 1997).
.
In the gravitational wave signal this is reflected by a
decrease of the negative main peak and an increase of the first
positive peak (Zwerger & Müller 1997).
3.1.4 Additional remarks
In the above models the central density
 coincides
with
coincides
with
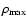 ,
the maximum density of the model at any
time. However, very rapidly and differentially rotating models, like
all "A4'' models, either already possess a toroidal density distribution
initially, or develop one during their evolution. In such models the
maximum density is attained at some off-center location, and
,
the maximum density of the model at any
time. However, very rapidly and differentially rotating models, like
all "A4'' models, either already possess a toroidal density distribution
initially, or develop one during their evolution. In such models the
maximum density is attained at some off-center location, and
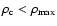 holds. Nevertheless, the time
evolution of
holds. Nevertheless, the time
evolution of
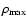 can be used to classify the collapse
type according to the criteria discussed above.
can be used to classify the collapse
type according to the criteria discussed above.
Our results show that relativistic simulations of rotational core
collapse exhibit the same qualitative collapse dynamics and allow for
the same classification as Newtonian simulations (Zwerger 1995,
1997). However, there exist important differences in other
aspects of the collapse arising from relativistic effects. These are
discussed in the subsequent sections.
3.2 Compactness of the core remnant
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{ms2576f4.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg106.gif) |
Figure 4:
Time evolution of the central density
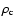 (upper panel) and the gravitational wave signal amplitude
(upper panel) and the gravitational wave signal amplitude
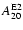 (lower panel) in the relativistic (solid
lines) and Newtonian (dashed lines) simulation of the regular
collapse model A3B2G4
(lower panel) in the relativistic (solid
lines) and Newtonian (dashed lines) simulation of the regular
collapse model A3B2G4
 .
The horizontal dotted line
in the upper panel marks nuclear matter density .
The horizontal dotted line
in the upper panel marks nuclear matter density
 .
The vertical dotted line indicates the time of
peak central density .
The vertical dotted line indicates the time of
peak central density  . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ms2576f5.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg107.gif) |
Figure 5:
Same as Fig. 4, but
for the multiple bounce collapse model A2B4G1. The vertical dotted
lines mark the times of peak central density 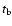 for
each bounce.
for
each bounce. |
| Open with DEXTER |
For all models the central density at bounce
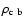 (for
all A4 models and model A3B5G4 the off-center maximum density
(for
all A4 models and model A3B5G4 the off-center maximum density
 )
is larger in the relativistic simulation than in
the corresponding Newtonian one, the relative increase reaching
)
is larger in the relativistic simulation than in
the corresponding Newtonian one, the relative increase reaching 
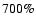 in special cases (see
Table 1). This also holds for the maximum
density of the compact remnant after ring-down in case of instant
formation of a stable equilibrium state (types I and III). This
generic property is illustrated in the upper panel of
Figs. 4 and 5 for the type I
model A3B2G4
in special cases (see
Table 1). This also holds for the maximum
density of the compact remnant after ring-down in case of instant
formation of a stable equilibrium state (types I and III). This
generic property is illustrated in the upper panel of
Figs. 4 and 5 for the type I
model A3B2G4
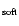 (where relativistic effects are
particularly large due to its soft EoS and thus high central density)
and the type II model A2B4G1, respectively.
(where relativistic effects are
particularly large due to its soft EoS and thus high central density)
and the type II model A2B4G1, respectively.
When comparing models of the same collapse type in Newtonian and
relativistic gravity, we find that although all relativistic models
reach higher central and/or maximum densities and, on average, larger
infall and rotation velocities, only six models (see
Table 1) have also larger maximum signal
amplitudes than their Newtonian counterparts. The maximum
signal amplitudes of all other relativistic models
are (up to 57%) smaller than those of the corresponding Newtonian ones
(Table 1). As already discussed in
Dimmelmeier et al. (2001), the reduced maximum signal strength can be
explained by the fact that the amplitude, which is calculated
using the quadrupole formula (see Appendix A),
is determined by the bulk motion of the core rather than just by
the motion of the densest mass shells, strictly speaking by the second
time derivative of the quadrupole moment. Therefore, a core which is
more condensed in the center can give rise to a smaller
gravitational wave signal than a core which is less centrally
condensed, but which is denser and moves faster in its outer
regions. This is reflected by the weight factor r2 in the
integrand of the quadrupole formula
(A.4). Due to this factor matter at
moderately large r contributes significantly to the gravitational
wave signal amplitude, while at very large radii (outside the inner
core) the decrease in density more than compensates the increase of
the weight factor.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{ms2576f6.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg110.gif) |
Figure 6:
Radial density profiles
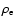 along the equator
near bounce time for model A3B2G4
along the equator
near bounce time for model A3B2G4
 (upper panel) and
model A2B4G1 (lower panel). In both models, the density of the
relativistic simulation (solid line) is larger than that of the
Newtonian simulation (dashed line) in the central region. At
(upper panel) and
model A2B4G1 (lower panel). In both models, the density of the
relativistic simulation (solid line) is larger than that of the
Newtonian simulation (dashed line) in the central region. At
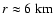 (upper panel) and
(upper panel) and
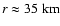 (lower panel) the density of the relativistic model drops below
that of the Newtonian one. The radii of the density crossing are
indicated by the vertical dotted lines, and the horizontal dotted
lines mark nuclear matter density
(lower panel) the density of the relativistic model drops below
that of the Newtonian one. The radii of the density crossing are
indicated by the vertical dotted lines, and the horizontal dotted
lines mark nuclear matter density
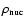 . . |
| Open with DEXTER |
The upper panel of Fig. 6 shows
the equatorial density profiles in the inner core of model
A3B2G4
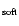 for both the relativistic (solid line) and the
Newtonian (dashed line) simulation at bounce. As already seen in the
central density evolution
(Fig. 4), the simulation in
relativistic gravity yields up to 36% larger densities in the central
regions. However, at radii
for both the relativistic (solid line) and the
Newtonian (dashed line) simulation at bounce. As already seen in the
central density evolution
(Fig. 4), the simulation in
relativistic gravity yields up to 36% larger densities in the central
regions. However, at radii
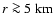 the density in the
Newtonian model exceeds that of the relativistic one. This "density
crossing'', which takes place at different radii for different polar
angles
the density in the
Newtonian model exceeds that of the relativistic one. This "density
crossing'', which takes place at different radii for different polar
angles 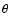 ,
can be observed in all the models we have
investigated, at all times
,
can be observed in all the models we have
investigated, at all times
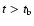 and at all polar
angles. The surface of density crossing is located inside the
compact remnant for type I and type III models, and in the case of
type II multiple bounce models in the coherently re-expanding and
contracting inner core, which has not yet settled into a compact
remnant at the end of the simulation. The effect is persistent in time
as demonstrated in
Fig. 7, which
shows the time evolution of the density for model
A3B2G4
and at all polar
angles. The surface of density crossing is located inside the
compact remnant for type I and type III models, and in the case of
type II multiple bounce models in the coherently re-expanding and
contracting inner core, which has not yet settled into a compact
remnant at the end of the simulation. The effect is persistent in time
as demonstrated in
Fig. 7, which
shows the time evolution of the density for model
A3B2G4
 at two different radial locations in the
equatorial plane. After bounce, the central density
at two different radial locations in the
equatorial plane. After bounce, the central density
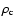 of the relativistic configuration is always larger than the
corresponding Newtonian one (upper panel). However, at larger radii,
but still inside the compact remnant (lower panel), the density of
the relativistic model is smaller by up to 50%.
of the relativistic configuration is always larger than the
corresponding Newtonian one (upper panel). However, at larger radii,
but still inside the compact remnant (lower panel), the density of
the relativistic model is smaller by up to 50%.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f7.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg114.gif) |
Figure 7:
Time evolution of the density at different radii in the
relativistic (solid lines) and Newtonian (dashed lines) simulation
of model A3B2G4
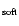 .
Whereas the central density (upper
panel) is larger in relativistic gravity, the (equatorial) density
of the Newtonian model exceeds that of the relativistic model at a
radius of .
Whereas the central density (upper
panel) is larger in relativistic gravity, the (equatorial) density
of the Newtonian model exceeds that of the relativistic model at a
radius of
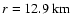 (lower panel). The vertical
dotted lines indicate the time of bounce
(lower panel). The vertical
dotted lines indicate the time of bounce  ,
and the
horizontal dotted line in the upper plot indicates nuclear matter
density ,
and the
horizontal dotted line in the upper plot indicates nuclear matter
density
 .
Note the different vertical scale of
the two plots. .
Note the different vertical scale of
the two plots. |
| Open with DEXTER |
The analysis of the multiple bounce model A2B4G1, which yields a
smaller signal amplitude in relativistic gravity (see lower panel of
Fig. 5), leads to a similar
result as the regular bounce model A3B2G4
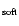 .
In the
relativistic case, the central density at bounce is more than 8 times
larger than in the Newtonian one. As in model A3B2G4
.
In the
relativistic case, the central density at bounce is more than 8 times
larger than in the Newtonian one. As in model A3B2G4
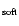 ,
the equatorial density profiles cross (lower panel of
Fig. 6), but now the crossing
occurs at a much larger radius
,
the equatorial density profiles cross (lower panel of
Fig. 6), but now the crossing
occurs at a much larger radius
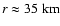 .
Hence, the
region where the relativistic model is denser is considerably more
extended. Inside the crossing radius, the cores of both the
relativistic and the Newtonian model oscillate coherently. The density
of the relativistic model is considerably higher in this region, and
the matter experiences stronger accelerations, which causes narrower
density peaks and shorter time intervals between two consecutive
bounces (Fig. 5).
.
Hence, the
region where the relativistic model is denser is considerably more
extended. Inside the crossing radius, the cores of both the
relativistic and the Newtonian model oscillate coherently. The density
of the relativistic model is considerably higher in this region, and
the matter experiences stronger accelerations, which causes narrower
density peaks and shorter time intervals between two consecutive
bounces (Fig. 5).
The effects of the reduced density in the outer regions of the inner
core in relativistic gravity on the gravitational wave signal can be
inferred from Fig. 8, which shows the
equatorial density profile weighted by a factor r2. Inside the
crossing radius
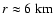 ,
the profiles of the
weighted density
,
the profiles of the
weighted density 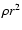 of model A3B2G4
of model A3B2G4
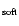 (upper
panel) coincide closely in both relativistic and Newtonian gravity. On
the other hand, for
(upper
panel) coincide closely in both relativistic and Newtonian gravity. On
the other hand, for
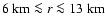 the
weighted density
the
weighted density 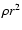 of the Newtonian model is significantly
larger than that of the relativistic model. Consequently, as the
density crossing occurs at all polar angles, the resulting quadrupole
moment (Eq. (A.4)) is larger, too. In
order to see whether the enhanced quadrupole moment also gives rise to
a stronger gravitational wave signal, one has to consider the second
time derivative of the quadrupole moment (see
Eq. (A.4)), which results from the
acceleration of the matter distribution in the core. We find that
despite the somewhat lower average acceleration in Newtonian gravity
which is reflected in the 18% lower frequency of the gravitational
wave signal, the large quadrupole moment of the more extended density
distribution results in a maximum signal amplitude
of the Newtonian model is significantly
larger than that of the relativistic model. Consequently, as the
density crossing occurs at all polar angles, the resulting quadrupole
moment (Eq. (A.4)) is larger, too. In
order to see whether the enhanced quadrupole moment also gives rise to
a stronger gravitational wave signal, one has to consider the second
time derivative of the quadrupole moment (see
Eq. (A.4)), which results from the
acceleration of the matter distribution in the core. We find that
despite the somewhat lower average acceleration in Newtonian gravity
which is reflected in the 18% lower frequency of the gravitational
wave signal, the large quadrupole moment of the more extended density
distribution results in a maximum signal amplitude
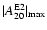 ,
which is 26% larger than that of the
centrally denser compact remnant in relativistic gravity (see
lower panel of Fig. 4 and
Table 1).
,
which is 26% larger than that of the
centrally denser compact remnant in relativistic gravity (see
lower panel of Fig. 4 and
Table 1).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f8.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg117.gif) |
Figure 8:
Weighted radial density profile
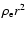 along
the equator (solid lines denote relativistic models; dashed lines denote Newtonian models) close to the time of core bounce for model A3B2G4
along
the equator (solid lines denote relativistic models; dashed lines denote Newtonian models) close to the time of core bounce for model A3B2G4
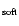 (upper panel;
(upper panel;
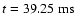 )
and
model A2B4G1 (lower panel; )
and
model A2B4G1 (lower panel;
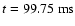 ),
respectively. The crossing radii are indicated by the vertical
dotted lines. ),
respectively. The crossing radii are indicated by the vertical
dotted lines. |
| Open with DEXTER |
For the multiple bounce model A2B4G1, the situation is similar (lower
panel). In relativistic gravity the weighted density 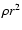 is
enhanced in the central parts of the inner core, and reduced in the
outer parts compared to the Newtonian profile. Contrary to model
A3B2G4
is
enhanced in the central parts of the inner core, and reduced in the
outer parts compared to the Newtonian profile. Contrary to model
A3B2G4
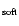 ,
the relativistic density increase close to the
center has a strong effect on the weighted density profile inside the
crossing radius
,
the relativistic density increase close to the
center has a strong effect on the weighted density profile inside the
crossing radius
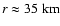 .
Nevertheless, and despite
the higher accelerations (i.e., larger second time derivatives) of the
coherently oscillating inner core in relativistic gravity, the smaller
densities at larger radii again yield a smaller gravitational wave
signal (see lower panel of
Fig. 5). However, in
relativistic gravity the increase of both the central density (718%
vs. 36%) and the frequency (41% vs. 23%) are larger in model
A3B2G4
.
Nevertheless, and despite
the higher accelerations (i.e., larger second time derivatives) of the
coherently oscillating inner core in relativistic gravity, the smaller
densities at larger radii again yield a smaller gravitational wave
signal (see lower panel of
Fig. 5). However, in
relativistic gravity the increase of both the central density (718%
vs. 36%) and the frequency (41% vs. 23%) are larger in model
A3B2G4
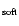 compared to model A2B4G1. Thus, the maximum
signal amplitude
compared to model A2B4G1. Thus, the maximum
signal amplitude
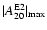 of the former model
is only reduced by 16% instead of 21% in model A2B4G1 when changing
from Newtonian to relativistic gravity (see
Table 1).
of the former model
is only reduced by 16% instead of 21% in model A2B4G1 when changing
from Newtonian to relativistic gravity (see
Table 1).
The above considerations also explain the much weaker gravitational
wave signal of model A1B1G1 in case of relativistic gravity
(see upper panel in Fig. 9). In
general relativity the central parts of the inner core collapse to
almost
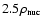 ,
and rapidly settle down to an
equilibrium state with constant density after a single bounce (middle
panel). Since the matter is more concentrated towards the center, the
density is relatively small in the outer parts of the core (lower
panel). The fluid motion in the outer regions of the core near
,
and rapidly settle down to an
equilibrium state with constant density after a single bounce (middle
panel). Since the matter is more concentrated towards the center, the
density is relatively small in the outer parts of the core (lower
panel). The fluid motion in the outer regions of the core near
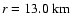 ,
where the shock forms, is not in phase with the
fluid motion in the inner regions (see two lower panels in
Fig. 9). In Newtonian gravity the
inner core is much less compact. It has a lower central density
(middle panel), but a much higher density at
,
where the shock forms, is not in phase with the
fluid motion in the inner regions (see two lower panels in
Fig. 9). In Newtonian gravity the
inner core is much less compact. It has a lower central density
(middle panel), but a much higher density at
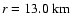 (lower panel). In this case the entire inner core oscillates
coherently with large amplitude motions, which give rise to a large
time variation of the quadrupole moment and thus a large gravitational
wave signal, the maximum amplitude being almost twice as large as the
corresponding one in relativistic gravity (see
Table 1).
(lower panel). In this case the entire inner core oscillates
coherently with large amplitude motions, which give rise to a large
time variation of the quadrupole moment and thus a large gravitational
wave signal, the maximum amplitude being almost twice as large as the
corresponding one in relativistic gravity (see
Table 1).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ms2576f9.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg120.gif) |
Figure 9:
Effects of a coherent motion of the inner core on the
gravitational wave signal in the relativistic (solid lines) and
Newtonian (dashed lines) simulation of model A1B1G1. In the upper
panel the evolution of the gravitational wave amplitude
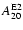 is plotted. The middle and lower panels show
the evolution of the central density
is plotted. The middle and lower panels show
the evolution of the central density
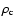 and of the
equatorial density
and of the
equatorial density
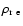 evaluated at a radius
evaluated at a radius
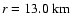 ,
respectively. Contrary to the relativistic
simulation, the inner core shows large amplitude oscillations in
Newtonian gravity, which causes a much larger gravitational wave
signal. The vertical dotted lines indicate the time of bounce ,
respectively. Contrary to the relativistic
simulation, the inner core shows large amplitude oscillations in
Newtonian gravity, which causes a much larger gravitational wave
signal. The vertical dotted lines indicate the time of bounce 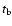 ,
and the horizontal dotted line in the middle panel
marks nuclear matter density ,
and the horizontal dotted line in the middle panel
marks nuclear matter density
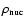 . . |
| Open with DEXTER |
3.3 Change of the collapse dynamics
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms2576f10.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg121.gif) |
Figure 10:
Evolution of the central density
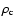 (upper
panel) and the gravitational wave signal amplitude
(upper
panel) and the gravitational wave signal amplitude
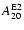 (lower panel) in the relativistic (solid
lines) and Newtonian (dashed lines) simulation of model A1B3G1. The vertical dotted lines mark the times of peak central
density for each bounce, and the horizontal dotted line in the
density plot marks nuclear matter density
(lower panel) in the relativistic (solid
lines) and Newtonian (dashed lines) simulation of model A1B3G1. The vertical dotted lines mark the times of peak central
density for each bounce, and the horizontal dotted line in the
density plot marks nuclear matter density
 . . |
| Open with DEXTER |
In the comprehensive study of Newtonian rotational core collapse
carried out by Zwerger & Müller (1997), models with multiple bounces were
observed quite often. Relativistic gravity can have a qualitative
impact on the dynamics of these models. If the density increase due to
the deeper relativistic potential is sufficiently large, a collapse
which is stopped by centrifugal forces at subnuclear densities (and
thus undergoes multiple bounces) in a Newtonian simulation, becomes a
regular, single bounce collapse in relativistic gravity.
Only two of the 26 models of our sample, A2B4G1 and A3B4G2,
show unambiguous multiple bounces in relativistic gravity. These two
models share some common features. In the relativistic simulations
their peak central densities associated with the individual bounces
are much larger (up to a factor 7) compared to those of the Newtonian
runs (Table 1). Consequently, the time elapsed
between subsequent bounces decreases by a factor of up to 4. These
type II models also show the effect of density crossing (see
Sect. 3.2). As a result, despite the
increase of the central density and the decrease of the oscillation
timescale (giving rise to a larger average acceleration of the inner
parts of the core), the maximum gravitational wave amplitude is lower
for the relativistic models.
When the central densities become very large, relativistic gravity can
even change the collapse dynamics qualitatively, i.e. the collapse
type is altered with respect to the Newtonian case (see
Table 1). We have observed mostly
transitions from a Newtonian type II (multiple bounce collapse) to a
relativistic type I (regular collapse) case, and less frequently
transitions from or to type I/II. A typical example is model A1B3G1
(Fig. 10). The change of type is clearly
visible both in the evolution of the central density (upper panel) and
of the gravitational wave signal (lower panel).
Centrifugal forces cause most of the type II multiple bounce models of
Zwerger & Müller (1997) to bounce at densities below
 .
Only a few models collapse to nuclear matter
density, the largest maximum density at bounce being
.
Only a few models collapse to nuclear matter
density, the largest maximum density at bounce being
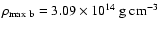 in the
case of model A4B1G2. Accordingly, in the two relativistic type II
models the maximum bounce density does not exceed this
threshold. Whenever the deeper relativistic gravitational potential
drives the maximum density in the core beyond the threshold of
in the
case of model A4B1G2. Accordingly, in the two relativistic type II
models the maximum bounce density does not exceed this
threshold. Whenever the deeper relativistic gravitational potential
drives the maximum density in the core beyond the threshold of
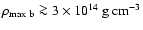 ,
a type
transition occurs (see Table 1).
,
a type
transition occurs (see Table 1).
A collapse type transition does not only alter the signal waveform
qualitatively, but also has important consequences for the maximum
gravitational wave signal amplitude, as e.g. in the case of model A1B1G1 (Fig. 9). In this Newtonian
type I/II model the concurrence of both high densities and a
coherent motion of the inner core yields a large gravitational wave
amplitude of 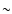
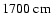 .
As the stronger relativistic
gravitational potential leads to the almost immediate formation of a
new equilibrium state, efficiently suppressing coherent large
amplitude motions of the inner core, the maximum signal amplitude is
only
.
As the stronger relativistic
gravitational potential leads to the almost immediate formation of a
new equilibrium state, efficiently suppressing coherent large
amplitude motions of the inner core, the maximum signal amplitude is
only
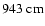 ,
which is 44% less than in the Newtonian case.
,
which is 44% less than in the Newtonian case.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms2576f11.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg126.gif) |
Figure 11:
Parameter space spanned by the rotation law parameter A and the rotation rate
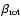 for multiple bounce
collapse models in relativistic and Newtonian simulations. Filled
circles mark models which are of multiple bounce type both in
relativistic and Newtonian gravity, and empty circles mark those
models which show multiple bounces in Newtonian gravity only.
for multiple bounce
collapse models in relativistic and Newtonian simulations. Filled
circles mark models which are of multiple bounce type both in
relativistic and Newtonian gravity, and empty circles mark those
models which show multiple bounces in Newtonian gravity only. |
| Open with DEXTER |
In Newtonian gravity and for an adiabatic index
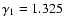 or
or
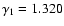 (i.e. close to the initial value
(i.e. close to the initial value
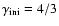 )
even models with rather small rotation
rates
)
even models with rather small rotation
rates
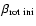 and moderately differential rotation
(i.e. larger values of A) show multiple bounces. Our simulations
demonstrate that relativistic gravity drastically narrows the region
in the parameter space of
and moderately differential rotation
(i.e. larger values of A) show multiple bounces. Our simulations
demonstrate that relativistic gravity drastically narrows the region
in the parameter space of
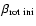 and A where
multiple bounce models are
possible. Figure 11 shows that only
models with high rotation rates and moderate differential rotation
undergo an unambiguous type II multiple bounce collapse.
and A where
multiple bounce models are
possible. Figure 11 shows that only
models with high rotation rates and moderate differential rotation
undergo an unambiguous type II multiple bounce collapse.
3.4 Rapidly and highly differentially rotating core collapse
When rapidly (large
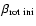 )
and strongly
differentially (small A) rotating initial models collapse on a
short timescale due to a low adiabatic exponent
)
and strongly
differentially (small A) rotating initial models collapse on a
short timescale due to a low adiabatic exponent 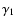 ,
angular
momentum conservation results in a considerable spin-up of the
core. Consequently, the increasing centrifugal forces stop the
collapse before or slightly above nuclear matter density, as in
type II multiple bounce models. However, the maximum density is
reached off-center, the topology of the density distribution in the
core being torus-like. Some initial models (e.g. A4B4 and A4B5)
already exhibit a toroidal structure. During collapse the toroidal
character of such a model is significantly enhanced, and the maximum
density
,
angular
momentum conservation results in a considerable spin-up of the
core. Consequently, the increasing centrifugal forces stop the
collapse before or slightly above nuclear matter density, as in
type II multiple bounce models. However, the maximum density is
reached off-center, the topology of the density distribution in the
core being torus-like. Some initial models (e.g. A4B4 and A4B5)
already exhibit a toroidal structure. During collapse the toroidal
character of such a model is significantly enhanced, and the maximum
density
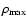 can exceed the central density
can exceed the central density
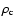 by up to two orders of magnitude. Other rapidly and
highly differentially rotating initial models, like A3B5, A4B1 and A4B2, in general do not change their initial oblate density
stratification during the evolution. However, for particular values of
the parameter
by up to two orders of magnitude. Other rapidly and
highly differentially rotating initial models, like A3B5, A4B1 and A4B2, in general do not change their initial oblate density
stratification during the evolution. However, for particular values of
the parameter 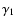 ,
they also develop a toroidal topology
during the infall phase.
,
they also develop a toroidal topology
during the infall phase.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f12.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg129.gif) |
Figure 12:
Equatorial density profiles of the moderately rapidly
rotating model A3B3G5 in case of relativistic (solid line) and
Newtonian (dashed line) gravity, depicted after ring-down. In
relativistic gravity the core has an oblate density structure. The
less deep Newtonian gravitational potential leads to the
development of a toroidal density configuration. The horizontal
dotted line marks nuclear matter density
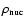 . . |
| Open with DEXTER |
Due to their deeper gravitational potential, relativistic
configurations tend to be more compact compared to the corresponding
Newtonian ones (see Sect. 3.2). This also
holds for relativistic models with a toroidal density stratification,
i.e. for models rotating rapidly and strongly differentially. These
models have off-center density maxima which exceed those of their
Newtonian counterparts (see Table 1).
In some borderline models which rotate moderately fast and not too
differentially, the core develops a toroidal density stratification
only in Newtonian gravity and possesses an oblate spheroidal density
stratification in relativistic gravity. A prototype of such a case is
model A3B3G5 (see Fig. 12).
In both relativistic and Newtonian simulations of rapidly and highly
differentially rotating cores, the gravitational wave amplitudes are
generally large, because of the large quadrupole moments of toroidal
configurations (see Table 1). If the rotation
rate is modest (models A4B1 and A4B2), the density in the torus at
bounce can reach high supranuclear densities in relativistic gravity.
The characteristic frequencies of the gravitational wave signal of
these toroidal models become particularly high, as they change to
regular collapse type models in relativistic gravity. The combination
of a high density torus and large accelerations (reflected by the
higher frequencies) yields very large wave amplitudes up to almost
3400 cm, which is significantly larger than in Newtonian
gravity. However, in the case of the extremely rapidly rotating models A4B4 and A4B5, centrifugal forces surmount relativistic gravity. The
collapse type does not change, and the bounce is partially due to
centrifugal forces (type I/II collapse). Consequently, the densities
at bounce are less extreme and the average accelerations are smaller
than in less rapidly rotating toroidal models. Therefore, the maximum
signal amplitudes
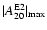 of models A4B4 and A4B5 are smaller than in the corresponding Newtonian models.
of models A4B4 and A4B5 are smaller than in the corresponding Newtonian models.
![\begin{figure}
\includegraphics[width=17cm,clip]{ms2576f13.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg131.gif) |
Figure 13:
Formation of a torus and shock-propagation in the very
rapidly and highly differentially rotating model A4B5G5. The three
snapshots show color coded contour plots of the logarithm of the
density, 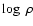 (scaled to nuclear matter density),
together with the meridional
flow field during the infall phase at
(scaled to nuclear matter density),
together with the meridional
flow field during the infall phase at
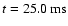 (left
panel), shortly before the centrifugal bounce at
(left
panel), shortly before the centrifugal bounce at
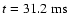 (middle panel), and at
(middle panel), and at
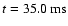 (right panel) when the torus is surrounded
by large scale flow vortices. The length of the velocity vectors
is scaled to the maximum value in the plotted region. Note that
the size of the displayed region and the color coding (which is
given above each panel) vary from plot to plot.
(right panel) when the torus is surrounded
by large scale flow vortices. The length of the velocity vectors
is scaled to the maximum value in the plotted region. Note that
the size of the displayed region and the color coding (which is
given above each panel) vary from plot to plot. |
| Open with DEXTER |
Compared to models with a moderate amount of rotation, the propagation
of the shock wave is drastically different in a rapidly and
differentially rotating model, as e.g. in model A4B5G5
(Fig. 13). In this model the density
maximum is located off-center already during collapse (left panel).
After core bounce the inner core settles down to an approximate
equilibrium state with a distinctive toroidal density stratification
surrounded by an equatorial disk from which matter is accreted onto
the torus (middle panel). In this accretion disk the shock encounters
relatively dense matter with large infall velocities between 0.1 cand 0.15 c, and thus it propagates outward comparatively slowly
along this direction. On the other hand, the region close to the
rotation axis has been emptied of matter during the collapse, the
average density being orders of magnitude lower than close to the
equatorial plane. Therefore, here the shock propagates out very
rapidly (right panel). As a result, the flow velocity in the
meridional plane exhibits a jet-like structure, with matter being
ejected from the inner core predominantly along the rotation axis.
3.5 Evolution of the rotation rate
The influence of relativistic gravity on the evolution of the rotation
rate during core collapse is demonstrated in Fig. 14,
which shows the radial profiles of
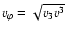 at the
time of core bounce for several representative models. Both the
maximum and average rotation velocities are higher in the relativistic
models, and the maximum of
at the
time of core bounce for several representative models. Both the
maximum and average rotation velocities are higher in the relativistic
models, and the maximum of  is shifted to smaller
radii. Note that this maximum is located near the edge of the
compact remnant. The differences are most pronounced for model A1B3G1 (lower panel), which changes from multiple bounce collapse to
regular collapse due to relativistic effects (see
Sect. 3.3). Model A1B3G1 also shows the
largest rotation velocities of all our models,
is shifted to smaller
radii. Note that this maximum is located near the edge of the
compact remnant. The differences are most pronounced for model A1B3G1 (lower panel), which changes from multiple bounce collapse to
regular collapse due to relativistic effects (see
Sect. 3.3). Model A1B3G1 also shows the
largest rotation velocities of all our models,  approaching 0.2 c at
approaching 0.2 c at
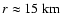 during core bounce. This
corresponds to a rotation period of
during core bounce. This
corresponds to a rotation period of
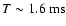 at the
edge of the inner core. When collapsing from the same initial model (A1B3), but imposing a larger initial reduction of the adiabatic index
to
at the
edge of the inner core. When collapsing from the same initial model (A1B3), but imposing a larger initial reduction of the adiabatic index
to
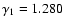 (i.e. model A1B3G5; upper panel in
Fig. 14), the spin-up is less and
(i.e. model A1B3G5; upper panel in
Fig. 14), the spin-up is less and
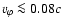 .
This result can be explained as follows: in model A1B3G1 the reduced
adiabatic index
.
This result can be explained as follows: in model A1B3G1 the reduced
adiabatic index
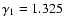 is very close to 4 / 3, i.e. a large fraction of the core collapses nearly homologously
(Goldreich & Weber 1980). However, this does not hold for model A1B3G5,
where the outer parts of the core fall much slower than in model A1B3G1, and hence also fall less far in radius until the time of
bounce. Consequently, the spin-up of mass zones located initially at
the same radial position in both models is less in model A1B3G5 than
in model A1B3G1 except for the very center of the core.
is very close to 4 / 3, i.e. a large fraction of the core collapses nearly homologously
(Goldreich & Weber 1980). However, this does not hold for model A1B3G5,
where the outer parts of the core fall much slower than in model A1B3G1, and hence also fall less far in radius until the time of
bounce. Consequently, the spin-up of mass zones located initially at
the same radial position in both models is less in model A1B3G5 than
in model A1B3G1 except for the very center of the core.
![\begin{figure}
\includegraphics[width=8cm,clip]{ms2576f14.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg137.gif) |
Figure 14:
Radial profiles of the rotation velocity 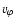 in the
equatorial plane plotted shortly after core bounce obtained in the
relativistic (solid lines) and Newtonian (dashed lines) simulation
of models A1B3G5 (upper panel), A2B4G1 (middle panel) and A1B3G1
(lower panel). The vertical dotted lines mark the radius of
maximum rotation velocity.
in the
equatorial plane plotted shortly after core bounce obtained in the
relativistic (solid lines) and Newtonian (dashed lines) simulation
of models A1B3G5 (upper panel), A2B4G1 (middle panel) and A1B3G1
(lower panel). The vertical dotted lines mark the radius of
maximum rotation velocity. |
| Open with DEXTER |
Assuming angular momentum conservation for the core, the rotation rate
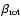 scales like the inverse of the radius of the core
(see, e.g., Shapiro & Teukolsky 1983),
scales like the inverse of the radius of the core
(see, e.g., Shapiro & Teukolsky 1983),
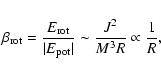 |
(2) |
where
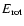 ,
,
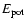 ,
M, R and J are the
rotational energy, potential energy, mass, radius and angular momentum
of the core, respectively.
,
M, R and J are the
rotational energy, potential energy, mass, radius and angular momentum
of the core, respectively.
Knowing the behavior of the evolution of
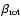 during
core collapse is important for several reasons. Firstly, the rotation
state of the inner core after bounce determines the rotation rate and
profile of the compact remnant provided no significant fall-back of
matter occurs later in the evolution. Pulsar observations show that
neutron stars can spin with very high rotation periods of the order of
milliseconds (see Lorimer 2001 and references therein).
However, such millisecond pulsars are believed to be born not as fast
rotators, but are thought to be old objects which are spun up via mass
transfer from a companion star much later in their evolution.
Observations of pulsars in young supernova remnants (see, e.g.
Kaspi 2000) provide only upper limits on the rotational state
of newborn neutron stars, because significant angular momentum losses
may have occurred since their formation. Presently, the fastest known
young pulsar is the 16 ms X-ray pulsar in the Crab-like supernova
remnant N157B (Marshall et al. 1998). Secondly, at sufficiently high
rotation rates the core will become unstable against triaxial
perturbations due to various mechanisms (see Stergioulas 1998
and references therein). Such nonaxisymmetric rotating configurations
are an additional source of gravitational radiation.
during
core collapse is important for several reasons. Firstly, the rotation
state of the inner core after bounce determines the rotation rate and
profile of the compact remnant provided no significant fall-back of
matter occurs later in the evolution. Pulsar observations show that
neutron stars can spin with very high rotation periods of the order of
milliseconds (see Lorimer 2001 and references therein).
However, such millisecond pulsars are believed to be born not as fast
rotators, but are thought to be old objects which are spun up via mass
transfer from a companion star much later in their evolution.
Observations of pulsars in young supernova remnants (see, e.g.
Kaspi 2000) provide only upper limits on the rotational state
of newborn neutron stars, because significant angular momentum losses
may have occurred since their formation. Presently, the fastest known
young pulsar is the 16 ms X-ray pulsar in the Crab-like supernova
remnant N157B (Marshall et al. 1998). Secondly, at sufficiently high
rotation rates the core will become unstable against triaxial
perturbations due to various mechanisms (see Stergioulas 1998
and references therein). Such nonaxisymmetric rotating configurations
are an additional source of gravitational radiation.
![\begin{figure}
\includegraphics[width=8.4cm,clip]{ms2576f15.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg140.gif) |
Figure 15:
Evolution of the rotation rate
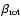 in the
relativistic (solid lines) and Newtonian (dashed lines)
simulations of models A2B4G1 (upper panel), A4B4G4 (middle panel)
and A4B5G4 (lower panel). The horizontal lines mark the critical
rotation rates above which MacLaurin spheroids are secularly
(
in the
relativistic (solid lines) and Newtonian (dashed lines)
simulations of models A2B4G1 (upper panel), A4B4G4 (middle panel)
and A4B5G4 (lower panel). The horizontal lines mark the critical
rotation rates above which MacLaurin spheroids are secularly
(
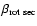 )
and dynamically
( )
and dynamically
(
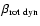 )
unstable against triaxial perturbations
in Newtonian gravity. )
unstable against triaxial perturbations
in Newtonian gravity. |
| Open with DEXTER |
For uniformly rotating, constant density MacLaurin spheroids in
Newtonian gravity, the threshold values for the development of
triaxial instabilities on secular and dynamic timescales are
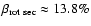 and
and
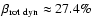 ,
respectively (see, e.g.,
Tassoul 1978).
,
respectively (see, e.g.,
Tassoul 1978).
The secular instability, which is driven for example by gravitational
radiation or viscosity, has been analyzed in compressible stars, both
uniformly and differentially rotating, within linear perturbation
theory in full general relativity by Bonazzola et al. (1996,
1998), Stergioulas & Friedman (1998), and
Yoshida & Eriguchi (1999). The analysis shows that
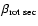 depends on the compactness of the star, on the rotation law, and on
the dissipative mechanism. Whereas
depends on the compactness of the star, on the rotation law, and on
the dissipative mechanism. Whereas
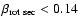 for
the gravitational radiation-driven instability (for extremely compact
or strongly differentially rotating stars
for
the gravitational radiation-driven instability (for extremely compact
or strongly differentially rotating stars
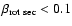 ), secular instabilities driven by viscosity occur for larger
rotation rates, i.e. for values
), secular instabilities driven by viscosity occur for larger
rotation rates, i.e. for values
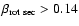 ,
when
the configurations become more compact.
,
when
the configurations become more compact.
The dynamic instability, on the other hand, is driven by hydrodynamics
and gravity. The onset of the dynamic bar-mode instability has been
investigated in full general relativity only recently
(Shibata et al. 2000; Saijo et al. 2001), because it requires fully nonlinear
multidimensional simulations (for Newtonian investigations see, e.g.,
New et al. (2000), and references therein). The simulations show that
in relativistic gravity the critical rotation rates for the onset of
the dynamic bar-mode instability are only slightly smaller
(
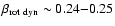 )
than in the Newtonian
case, and depend only very weakly on the degree of differential
rotation (within the moderate range surveyed by the investigations).
)
than in the Newtonian
case, and depend only very weakly on the degree of differential
rotation (within the moderate range surveyed by the investigations).
What do these general considerations concerning triaxial instabilities
imply for our models? Since the rotation rates are larger in
relativistic gravity than in the Newtonian case for the same initial
conditions, we expect that the criteria for the development of dynamic
and secular triaxial instabilities are fulfilled in more models and
for longer time intervals in relativistic gravity. To see whether this
statement is correct we consider the evolution of the rotation rate
 for models A2B4G1, A4B4G4 and A4B5G4 (see
Fig. 15). In all these models
for models A2B4G1, A4B4G4 and A4B5G4 (see
Fig. 15). In all these models
 reaches its maximum value at the time of
bounce. If the core experiences multiple bounces, this is reflected in
multiple peaks of
reaches its maximum value at the time of
bounce. If the core experiences multiple bounces, this is reflected in
multiple peaks of
 (see upper panel). As expected,
the rotation rate in the relativistic models exceeds that of the
corresponding Newtonian ones. This holds both for the maximum value
and the average value of the rotation rate.
(see upper panel). As expected,
the rotation rate in the relativistic models exceeds that of the
corresponding Newtonian ones. This holds both for the maximum value
and the average value of the rotation rate.
Using the Newtonian thresholds
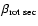 and
and
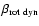 (see discussion above) to judge whether a
model is prone to developing triaxial instabilities, we see that
relativistic effects do not cause an important change in the case of
model A2B4G1 (upper panel of Fig. 15), because
(see discussion above) to judge whether a
model is prone to developing triaxial instabilities, we see that
relativistic effects do not cause an important change in the case of
model A2B4G1 (upper panel of Fig. 15), because
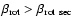 for less than 10 ms. On the
other hand, the behaviour of the rapidly rotating model A4B4G4 (middle
panel) is quite different. Its rotation rate exceeds
for less than 10 ms. On the
other hand, the behaviour of the rapidly rotating model A4B4G4 (middle
panel) is quite different. Its rotation rate exceeds
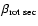 near bounce time and remains above that value
after core bounce in relativistic gravity (even exceeding
near bounce time and remains above that value
after core bounce in relativistic gravity (even exceeding
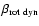 for a short time), while in Newtonian gravity
it falls below
for a short time), while in Newtonian gravity
it falls below
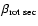 again after ring-down. Since
relativistic effects tend to lower the threshold value
again after ring-down. Since
relativistic effects tend to lower the threshold value
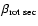 in case of the gravitational radiation-driven
instability (see discussion above), this model demonstrates that
Newtonian simulations can yield incorrect predictions about the
development of secular instabilities. On the other hand, in the
extremely rapidly and differentially rotating model A4B5G4 (lower
panel), secular instabilities are likely to develop in both Newtonian
and relativistic gravity. However, instabilities on a dynamic
timescale should only appear in the latter case, where
in case of the gravitational radiation-driven
instability (see discussion above), this model demonstrates that
Newtonian simulations can yield incorrect predictions about the
development of secular instabilities. On the other hand, in the
extremely rapidly and differentially rotating model A4B5G4 (lower
panel), secular instabilities are likely to develop in both Newtonian
and relativistic gravity. However, instabilities on a dynamic
timescale should only appear in the latter case, where
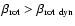 for almost 4 ms. We note
that for a neutron star with an average density of
for almost 4 ms. We note
that for a neutron star with an average density of 
 and a radius of
and a radius of 
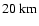 ,
the
dynamical timescale (= sound crossing timescale) is roughly 1 ms.
,
the
dynamical timescale (= sound crossing timescale) is roughly 1 ms.
Note that in this discussion
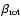 is the ratio of
rotational energy to potential energy of the entire core. Strictly
speaking, the criteria for triaxial instabilities should only be
evaluated for the rotation rate
is the ratio of
rotational energy to potential energy of the entire core. Strictly
speaking, the criteria for triaxial instabilities should only be
evaluated for the rotation rate
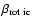 of the inner
core (which eventually becomes the compact remnant), because the
outer core is a separate entity as far as the dynamics is concerned.
However, due to the rapid drop of density and rotation velocity
observed in all models at the outer boundary of the inner core, the
outer core contributes only little to the total rotation rate. Thus,
we can safely assume that
of the inner
core (which eventually becomes the compact remnant), because the
outer core is a separate entity as far as the dynamics is concerned.
However, due to the rapid drop of density and rotation velocity
observed in all models at the outer boundary of the inner core, the
outer core contributes only little to the total rotation rate. Thus,
we can safely assume that
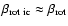 .
This behavior has
also been observed in the Newtonian core collapse simulations of
Zwerger (1995).
.
This behavior has
also been observed in the Newtonian core collapse simulations of
Zwerger (1995).
Despite the knowledge of the evolution of
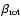 during
core collapse, predictions about the actual development of triaxial
instabilities are difficult. The thresholds originate from a linear
stability analysis and involve restrictions (e.g. homogeneous
density, uniform rotation, etc.). Unfortunately, we cannot simulate
the actual nonlinear growth of triaxial instabilities, because our
code is restricted to axisymmetric flows. Therefore, we have begun to
extend our code to three spatial dimensions. The results of the 3D simulations planned to be performed with the extended code will be
presented in a future publication. Still, at present our results may
help to predict the behavior and consequences of
during
core collapse, predictions about the actual development of triaxial
instabilities are difficult. The thresholds originate from a linear
stability analysis and involve restrictions (e.g. homogeneous
density, uniform rotation, etc.). Unfortunately, we cannot simulate
the actual nonlinear growth of triaxial instabilities, because our
code is restricted to axisymmetric flows. Therefore, we have begun to
extend our code to three spatial dimensions. The results of the 3D simulations planned to be performed with the extended code will be
presented in a future publication. Still, at present our results may
help to predict the behavior and consequences of
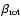 of fully three-dimensional models (Houser et al. 1994; Smith et al. 1996;
Rampp et al. 1998).
of fully three-dimensional models (Houser et al. 1994; Smith et al. 1996;
Rampp et al. 1998).
For large values of
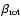 the neutron star is highly
nonspherical. In this regime we expect deviations of the CF metric
from the exact metric in the range of a few percent (see Sect. 5.5
in Paper I). Additionally, in the equation for
the neutron star is highly
nonspherical. In this regime we expect deviations of the CF metric
from the exact metric in the range of a few percent (see Sect. 5.5
in Paper I). Additionally, in the equation for
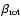 (see Sects. 1 and 5.4 in Paper I), the potential energy
(see Sects. 1 and 5.4 in Paper I), the potential energy
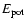 is determined by the (small) difference between the
gravitational mass
is determined by the (small) difference between the
gravitational mass
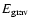 and proper mass
and proper mass
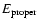 .
Even for strongly gravitating systems like neutron
stars, this difference is only about 10% of the individual
terms. Thus, if the values for
.
Even for strongly gravitating systems like neutron
stars, this difference is only about 10% of the individual
terms. Thus, if the values for
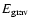 and
and
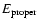 are subject to an error of a few percent in the CFC approximation, we
expect
are subject to an error of a few percent in the CFC approximation, we
expect
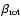 to deviate by several 10% relative to its
value in an exact spacetime. In simulations of rapidly rotating
neutron stars in equilibrium we could observe relative deviations
between
to deviate by several 10% relative to its
value in an exact spacetime. In simulations of rapidly rotating
neutron stars in equilibrium we could observe relative deviations
between
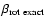 and
and
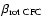 of
about 15%. Owing to the uncertainties with the stability thresholds
and the calculation of the rotation rate in the CFC approximation, the
above predictions from the evolution of
of
about 15%. Owing to the uncertainties with the stability thresholds
and the calculation of the rotation rate in the CFC approximation, the
above predictions from the evolution of
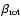 for the
actual development of triaxial instabilities should be regarded as an
estimate.
for the
actual development of triaxial instabilities should be regarded as an
estimate.
4 Gravitational wave emission
4.1 Gravitational wave energy spectrum and emission
A detailed discussion of the spectra of gravitational waves emitted
during Newtonian rotational core collapse, and their dependence on the
collapse type and dynamics can be found in the work of
Zwerger & Müller (1997). In the quadrupole approximation and in
axisymmetry, the gravitational radiation field is solely determined by
the amplitude
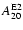 (see
Appendix A). The total energy radiated away by
gravitational waves is then given by
(see
Appendix A). The total energy radiated away by
gravitational waves is then given by
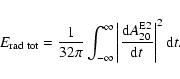 |
(3) |
By replacing the gravitational wave amplitude in the time domain
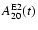 by its Fourier transform in the frequency
domain
by its Fourier transform in the frequency
domain
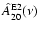 ,
the total radiated energy
,
the total radiated energy
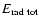 can be expressed as a frequency integral:
can be expressed as a frequency integral:
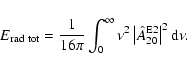 |
(4) |
The spectral energy distribution is then
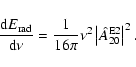 |
(5) |
As a characteristic spectral measure of the gravitational wave signal
we define the frequency
 at which the energy spectrum
at which the energy spectrum
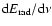 has its maximum (see also
Zwerger & Müller 1997).
has its maximum (see also
Zwerger & Müller 1997).
![\begin{figure}
\includegraphics[width=8.2cm,clip]{ms2576f16.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg163.gif) |
Figure 16:
Spectral energy distribution
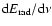 of the gravitational wave
signal in the relativistic (solid lines) and Newtonian (dashed
lines) simulations of models A1B3G3 (upper panel), A3B3G1 (middle
panel) and A1B3G1 (lower panel). The energy spectrum of model A1B3G3, with a strong low frequency part and a weaker high
frequency part, is typical for the signal of a regular
collapse. Model A3B3G1 is a multiple bounce collapse model in both
Newtonian and relativistic gravity. In its energy spectrum a broad
low frequency peak dominates. In model A1B3G1 relativistic effects
change the collapse type from multiple bounce collapse to regular
collapse. The energy spectrum reflects this change. The left
(right) vertical dotted lines mark the maxima of the energy
spectrum in Newtonian (relativistic) gravity. Due to higher
average central densities in the relativistic simulations, the
maximum of the energy spectrum is shifted to higher frequencies.
of the gravitational wave
signal in the relativistic (solid lines) and Newtonian (dashed
lines) simulations of models A1B3G3 (upper panel), A3B3G1 (middle
panel) and A1B3G1 (lower panel). The energy spectrum of model A1B3G3, with a strong low frequency part and a weaker high
frequency part, is typical for the signal of a regular
collapse. Model A3B3G1 is a multiple bounce collapse model in both
Newtonian and relativistic gravity. In its energy spectrum a broad
low frequency peak dominates. In model A1B3G1 relativistic effects
change the collapse type from multiple bounce collapse to regular
collapse. The energy spectrum reflects this change. The left
(right) vertical dotted lines mark the maxima of the energy
spectrum in Newtonian (relativistic) gravity. Due to higher
average central densities in the relativistic simulations, the
maximum of the energy spectrum is shifted to higher frequencies. |
| Open with DEXTER |
As discussed in Sect. 3.2, the average and
peak central densities of our relativistic models are larger than
those of the Newtonian ones. This leads to an increase of the
oscillation frequencies of the inner core during the ring-down phase
in a regular collapse situation, and to a decrease of the time
interval between consecutive bounces in multiple bounce models.
Therefore, the gravitational wave spectrum is shifted towards higher
frequencies in the relativistic models. This shift can be as large as
a factor 5 in frequency (see Table 1 and lower
panel of Fig. 16). The models with the largest
frequency shift are those where the deeper relativistic gravitational
potential changes a multiple bounce collapse into a regular collapse
(see Sect. 3.3). We find that in
Newtonian gravity only three models have a higher characteristic
frequency
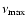 than the corresponding relativistic ones.
However, the energy spectra of these models show many local maxima
near
than the corresponding relativistic ones.
However, the energy spectra of these models show many local maxima
near
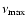 having almost the same spectral energy
density. Fitting the energy spectra of the three models by a smooth
function yields again a higher value of
having almost the same spectral energy
density. Fitting the energy spectra of the three models by a smooth
function yields again a higher value of
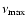 in case of
relativistic gravity.
in case of
relativistic gravity.
The energy spectra of three models are plotted in
Fig. 16. They are obtained by Fourier
transforming the gravitational signal. A Welch filter is applied in
the Fourier transformation to reduce the noise caused by the finite
length of the wave signal (Press et al. 1992). To compensate for the
power loss due to filtering, the spectrum is rescaled by the
requirement that the total energy in the time domain,
Eq. (3) equals that of the frequency
domain, Eq. (4). The energy
spectra are similar for both relativistic and Newtonian simulations in
cases where the collapse type does not change (see upper and middle
panel in Fig. 16). On the other hand, when a
Newtonian model exhibiting multiple bounces changes to a regular
collapse model in relativistic gravity, like e.g. model A3B3G1, the
shape of its energy spectrum is shifted significantly (see lower panel
in Fig. 16).
By integrating the spectral energy distribution,
Eq. (5), over all frequencies, one obtains the
total energy radiated away by the system in gravitational waves, as
given in Eq. (4). However, when
analyzing numerical data this method is inappropriate, because high
frequency noise contributes significantly to
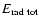 .
For
most models it is impossible to unambiguously define a cutoff
frequency beyond which there exists only noise, as
.
For
most models it is impossible to unambiguously define a cutoff
frequency beyond which there exists only noise, as
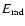 does not drop sharply at some specific frequency. On the other hand,
applying a filter (like the Welch filter used in
Fig. 16) causes a leakage of spectral energy
density, and thus leads to a underestimate of
does not drop sharply at some specific frequency. On the other hand,
applying a filter (like the Welch filter used in
Fig. 16) causes a leakage of spectral energy
density, and thus leads to a underestimate of
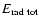 .
Therefore, we use Eq. (3) to
calculate
.
Therefore, we use Eq. (3) to
calculate
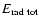 .
.
We find that the total energy (measured in units of
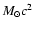 )
radiated in form of gravitational waves lies in the
range
)
radiated in form of gravitational waves lies in the
range
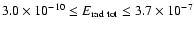 for the relativistic models, and in the range
for the relativistic models, and in the range
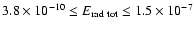 for the Newtonian ones. Averaged over all models,
for the Newtonian ones. Averaged over all models,
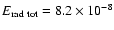 in the relativistic case,
and
in the relativistic case,
and
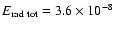 in the Newtonian one,
which corresponds to an increase of 128% due to relativistic effects.
in the Newtonian one,
which corresponds to an increase of 128% due to relativistic effects.
4.2 Gravitational wave amplitudes and frequencies
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{ms2576f17.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg170.gif) |
Figure 17:
Prospects of detection of the gravitational wave signal
from axisymmetric rotational supernova core collapse in relativistic
(black filled circles) and Newtonian (red unfilled circles)
gravity. The figure gives the (dimensionless) gravitational wave
amplitude
 and the frequency range for all 26 models. For a source at a distance of 10 kpc the signals of all
models are above the burst sensitivity of the LIGO I detector
(except for some low amplitude, high frequency models), and well
above that of the LIGO II interferometer. The burst sensitivity
gives the rms noise amplitude
and the frequency range for all 26 models. For a source at a distance of 10 kpc the signals of all
models are above the burst sensitivity of the LIGO I detector
(except for some low amplitude, high frequency models), and well
above that of the LIGO II interferometer. The burst sensitivity
gives the rms noise amplitude
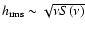 over a bandwith of width
over a bandwith of width 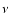 at a frequency
at a frequency 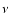 for the instrument noise power
spectral density
for the instrument noise power
spectral density 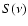 .
The error bars mark the frequency
range inside which the spectral energy density is within 50% of
its peak value. .
The error bars mark the frequency
range inside which the spectral energy density is within 50% of
its peak value. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{ms2576f18.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg171.gif) |
Figure 18:
Impact of the frequency and wave amplitude shift on the
signal detectability for relativistic models which experience
multiple bounces in Newtonian gravity. In the
"best case'', both amplitude and frequency increase in relativistic
gravity (a). However, on average only the frequency increases (b). In neither case the shift is as steep as the high frequency
sensitivity curve of an interferometer detector, and thus a
relativistic model may fall out of the sensitivity window of the
detector, if the Newtonian model is just within detection
range. Note that the vertical scale is arbitrary. Symbols and
error bars as in Fig. 17. |
| Open with DEXTER |
The distribution of the dimensionless signal amplitude seen by an
observer located in the equatorial plane of the source, i.e. the
gravitational wave strain (see Eq. (A.3) with
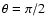 )1.75pt
)1.75pt
is shown in Fig. 17 for all 26 models,
scaled to a distance of
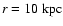 from the source. The
corresponding wave amplitudes
from the source. The
corresponding wave amplitudes
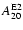 are listed in
Table 1.
are listed in
Table 1.
A comparison of Fig. 17 with Fig. 8 in
Zwerger & Müller (1997) proves that our sample, encompassing 25 of the 78 models considered in the parameter study of Zwerger & Müller (1997) - we
have simulated the additional model A3B2G4
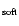 - covers
almost the same range of wave amplitudes
(
- covers
almost the same range of wave amplitudes
(
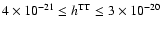 )
and
frequencies (
)
and
frequencies (
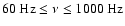 ). Thus,
relativistic effects have no significant impact on the gross
distribution of expected signals in the amplitude-frequency
diagram. Only in the high frequency, low amplitude region of the
diagram, i.e. for models which collapse rapidly and have type I or
III waveforms, the weaker signal amplitudes cause a discernible change
in the model distribution. The bulk of the models falls into the range
of detectability of the LIGO I interferometer (Gustafson et al. 1999)
provided the source is located at a distance of less than
). Thus,
relativistic effects have no significant impact on the gross
distribution of expected signals in the amplitude-frequency
diagram. Only in the high frequency, low amplitude region of the
diagram, i.e. for models which collapse rapidly and have type I or
III waveforms, the weaker signal amplitudes cause a discernible change
in the model distribution. The bulk of the models falls into the range
of detectability of the LIGO I interferometer (Gustafson et al. 1999)
provided the source is located at a distance of less than
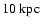 (see Fig. 17).
(see Fig. 17).
For all models which are of the same type in both Newtonian and
relativistic gravity, the gravitational wave signal has a lower
amplitude. When selecting those 13 models which are of type II in
Newtonian gravity (see Sect. 3.1.2),
the influence of relativistic effects on the signal amplitude is not
as clearcut. The two relativistic models which remain of type II (see
Table 1) yield smaller maximum amplitudes
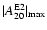 .
If the collapse type changes due to the
higher central densities reached in relativistic gravity, some models
exhibit significantly higher signal amplitudes than in Newtonian
gravity (e.g.
.
If the collapse type changes due to the
higher central densities reached in relativistic gravity, some models
exhibit significantly higher signal amplitudes than in Newtonian
gravity (e.g. 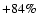 for model A1B3G1), whereas others possess
smaller signal amplitudes (e.g.
for model A1B3G1), whereas others possess
smaller signal amplitudes (e.g. 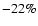 for model A3B1G1). In
models which change their collapse type, the increase or decrease of
the signal strength, and thus the change of location in the
amplitude-frequency diagram, depends very strongly on the rotational
state of the initial model and on the value of
for model A3B1G1). In
models which change their collapse type, the increase or decrease of
the signal strength, and thus the change of location in the
amplitude-frequency diagram, depends very strongly on the rotational
state of the initial model and on the value of 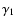 .
However,
as in all other models, relativistic gravity always causes a rise of
the characteristic signal frequencies.
.
However,
as in all other models, relativistic gravity always causes a rise of
the characteristic signal frequencies.
The overall behaviour of the 13 models which are of type II in
Newtonian gravity, can be summarized by considering the arithmetic
mean of their peak amplitudes and peak frequencies:
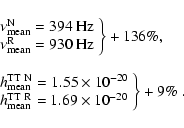 |
(7) |
Our simulations show that while the average gravitational wave signal
amplitude
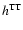 does not change significantly, the frequency
more than doubles.
does not change significantly, the frequency
more than doubles.
This large frequency shift can have important consequences for the
prospects of detection of gravitational waves. If the signal of a
particular model is close to the detection threshold of a detector, as
shown in Fig. 18 for the 13
models which experience multiple bounces in Newtonian gravity, the
influence of relativity can be twofold. In the "best case scenario''
the signal is shifted to both higher frequencies and amplitudes
(case a). However, more frequently the location of the model will only
shift towards higher frequencies in the amplitude-frequency diagram
(case b - see Eq. (7)), and
therefore in a borderline case the signal may actually leave the
sensitivity window of the detector.
5 Summary and conclusions
We have presented hydrodynamic simulations of relativistic rotational
supernova core collapse in axisymmetry and have analyzed the
gravitational radiation emitted by such an event. We have simulated
the evolution of 26 models in both Newtonian and relativistic
gravity. Collapse of the initial configurations, which are
differentially rotating relativistic 4 / 3-polytropes in
equilibrium, is induced by decreasing the adiabatic index to some
prescribed fixed value 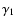 with
with
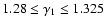 .
The stiffening of the equation of
state at nuclear matter density and the thermal pressure in the matter
heated by the prompt shock are simulated by means of a simplified
equation of state consisting of a polytropic and a thermal
part. Microphysics like electron captures and neutrino transport is
neglected.
.
The stiffening of the equation of
state at nuclear matter density and the thermal pressure in the matter
heated by the prompt shock are simulated by means of a simplified
equation of state consisting of a polytropic and a thermal
part. Microphysics like electron captures and neutrino transport is
neglected.
Our simulations show that the three different types of rotational
supernova core collapse and gravitational waveforms identified in
previous Newtonian simulations (regular collapse, multiple bounce
collapse, and rapid collapse) are also present in relativistic
gravity. We find, however, that rotational core collapse with multiple
bounces, which occurs when the collapse is only or predominantly stopped
by centrifugal forces, is possible only in a much narrower parameter
range in relativistic simulations. Only two of the 26 models of our
sample show unambiguous multiple bounces in relativistic gravity.
The peak central densities associated with the individual bounces in
such models are much larger (up to a factor of 8) in the relativistic
models compared to the corresponding Newtonian ones. Consequently, the
time elapsed between subsequent bounces decreases by a factor of up to 4.
We further find that relativistic gravity can have a qualitative
impact on the dynamics. If the density increase due to the deeper
relativistic potential is sufficiently large, a collapse which is
stopped by centrifugal forces at subnuclear densities (and thus
undergoes multiple bounces) in a Newtonian simulation, becomes a
regular, single bounce collapse in relativistic gravity. A collapse
type transition also has important consequences for the maximum
gravitational wave signal amplitude.
For all relativistic models the peak density at bounce is larger than
in the corresponding Newtonian models, the relative increase reaching 
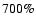 in some cases. This also holds for the maximum density
of the compact remnant after ring-down in case of instant formation
of a stable equilibrium state (types I and III). Nevertheless, we
find that only six models have also larger maximum signal amplitudes
than their Newtonian counterparts. The maximum signal amplitudes of
all other relativistic models are (up to 57%) smaller than those of
the corresponding Newtonian ones. The reduced maximum signal strength
can be explained by the fact that the quadrupole amplitude is
determined by the bulk motion of the core rather than just by
the motion of the densest mass shells. Therefore, a core which is
more condensed in the center can give rise to a smaller
gravitational wave signal than a core which is less centrally
condensed, but which is denser and moves faster in its outer regions.
However, the fact that all relativistic models show an increased
central and reduced peripheral density of the collapsed core
relative to their Newtonian counterparts does not necessarily imply a
weaker gravitational wave signal, as in 6 of 26 relativistic models
the maximum gravitational wave amplitudes are larger than in the
corresponding Newtonian models. In all these six cases the collapse
changes from type II (or type I/II) to type I when changing from
Newtonian to relativistic gravity.
in some cases. This also holds for the maximum density
of the compact remnant after ring-down in case of instant formation
of a stable equilibrium state (types I and III). Nevertheless, we
find that only six models have also larger maximum signal amplitudes
than their Newtonian counterparts. The maximum signal amplitudes of
all other relativistic models are (up to 57%) smaller than those of
the corresponding Newtonian ones. The reduced maximum signal strength
can be explained by the fact that the quadrupole amplitude is
determined by the bulk motion of the core rather than just by
the motion of the densest mass shells. Therefore, a core which is
more condensed in the center can give rise to a smaller
gravitational wave signal than a core which is less centrally
condensed, but which is denser and moves faster in its outer regions.
However, the fact that all relativistic models show an increased
central and reduced peripheral density of the collapsed core
relative to their Newtonian counterparts does not necessarily imply a
weaker gravitational wave signal, as in 6 of 26 relativistic models
the maximum gravitational wave amplitudes are larger than in the
corresponding Newtonian models. In all these six cases the collapse
changes from type II (or type I/II) to type I when changing from
Newtonian to relativistic gravity.
Overall, the relativistic models cover almost the same range of
gravitational wave amplitudes
(
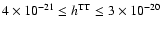 )
and
frequencies (
)
and
frequencies (
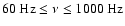 )
as the
corresponding Newtonian ones. For all models which are of the same
collapse type in both Newtonian and relativistic gravity, the
gravitational wave signal is of lower amplitude. If the collapse type
changes, either weaker or stronger signals are found in the
relativistic case. Averaged over all models, the total energy radiated
in form of gravitational waves is
)
as the
corresponding Newtonian ones. For all models which are of the same
collapse type in both Newtonian and relativistic gravity, the
gravitational wave signal is of lower amplitude. If the collapse type
changes, either weaker or stronger signals are found in the
relativistic case. Averaged over all models, the total energy radiated
in form of gravitational waves is
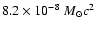 in the relativistic case, and
in the relativistic case, and
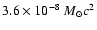 in the Newtonian one.
in the Newtonian one.
For a given model, relativistic gravity can cause a large increase of
the characteristic signal frequency of up to a factor of five. This
frequency shift is an effect common to all models, and can have
important consequences for the prospects of detection of gravitational
waves. If the signal of a particular model is close to the
high-frequency detection threshold of a detector, the influence of
relativity can be twofold. In the "best case scenario'' both the
signal frequency and amplitude increase; however, more often only the
signal frequency increases. In either case, in a borderline situation the
signal may actually leave the sensitivity window of the detector, as
the high-frequency detection threshold of a laser interferometer rises
steeply with increasing frequency. Hence, within the limits of our
physical model of rotational core collapse, relativistic effects on
average tend to decrease the prospects of detectability of
gravitational radiation by interferometric detectors. Nevertheless,
the gravitational wave signals obtained in our study are within the
sensitivity range of the first generation laser interferometer
detectors if the source is located within the Local Group.
In our study we have restricted ourselves to simplified supernova core
models. The complicated microphysics (electron captures and other
weak interactions, equation of state) and neutrino transport processes
have all been absorbed in one model parameter (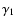 ). Although
this is an extreme simplification, we nevertheless think that it does
not change the qualitative nature of our results. In particular,
we do not expect that more realistic (axisymmetric) core collapse
models will produce significantly stronger gravitational wave signals.
Larger initial rotation rates and lower values of the (effective)
adiabatic index
). Although
this is an extreme simplification, we nevertheless think that it does
not change the qualitative nature of our results. In particular,
we do not expect that more realistic (axisymmetric) core collapse
models will produce significantly stronger gravitational wave signals.
Larger initial rotation rates and lower values of the (effective)
adiabatic index 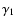 ,
which could lead to stronger gravitational
wave signals, are most likely excluded. This is also supported by the
fact that the signal strengths of the microscopically more realistic,
but Newtonian models of Mönchmeyer et al. (1991) agree well with those
of our simplified models. To check whether these expectations are
indeed correct we plan to incorporate a realistic equation of state
and a simplified treatment of neutrino transport into our relativistic
code in the near future.
,
which could lead to stronger gravitational
wave signals, are most likely excluded. This is also supported by the
fact that the signal strengths of the microscopically more realistic,
but Newtonian models of Mönchmeyer et al. (1991) agree well with those
of our simplified models. To check whether these expectations are
indeed correct we plan to incorporate a realistic equation of state
and a simplified treatment of neutrino transport into our relativistic
code in the near future.
In several models the rotation rate of the compact remnant exceeds
the critical value where MacLaurin spheroids become secularly, and in
some cases even dynamically unstable against triaxial perturbations
(
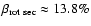 and
and
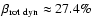 ). It has been have pointed out
that if such instabilities indeed occur, a much stronger gravitational
wave signal might be produced than by cores which remain axisymmetric
(for a review, see e.g. Thorne 1995). According to this idea,
the core will be transformed into a bar-like configuration that spins
end-over-end like an American football. One has further speculated,
whether the core might even break up into two or more massive pieces,
if
). It has been have pointed out
that if such instabilities indeed occur, a much stronger gravitational
wave signal might be produced than by cores which remain axisymmetric
(for a review, see e.g. Thorne 1995). According to this idea,
the core will be transformed into a bar-like configuration that spins
end-over-end like an American football. One has further speculated,
whether the core might even break up into two or more massive pieces,
if
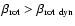 .
In that case the
resulting gravitational radiation could be almost as strong as
that from coalescing neutron star binaries (Thorne 1995). The
strength of the gravitational signal sensitively depends on what
fraction of the angular momentum of the non-axisymmetric core goes
into gravitational waves, and what fraction into hydrodynamic
waves. These sound and shock waves are produced as the bar or lumps,
acting like a twirling-stick, plow through the surrounding matter. In
order to investigate these effects, three-dimensional relativistic
simulations of rotational core collapse have to be performed, which
can follow the growth of non-axisymmetric instabilities (bar modes and
gravitational wave driven unstable inertial modes). To this end
we are currently extending our code to three spatial dimensions.
.
In that case the
resulting gravitational radiation could be almost as strong as
that from coalescing neutron star binaries (Thorne 1995). The
strength of the gravitational signal sensitively depends on what
fraction of the angular momentum of the non-axisymmetric core goes
into gravitational waves, and what fraction into hydrodynamic
waves. These sound and shock waves are produced as the bar or lumps,
acting like a twirling-stick, plow through the surrounding matter. In
order to investigate these effects, three-dimensional relativistic
simulations of rotational core collapse have to be performed, which
can follow the growth of non-axisymmetric instabilities (bar modes and
gravitational wave driven unstable inertial modes). To this end
we are currently extending our code to three spatial dimensions.
Acknowledgements
This work was finished during a visit of H.D. at the Universidad de
Valencia, Spain. He would like to thank for the hospitality at the
Departamento de Astronomía y Astrofísica. J.A.F. acknowledges support from a Marie Curie fellowship by the European
Union (MCFI-2001-00032). All computations were performed on the NEC
SX-5/3C supercomputer at the Rechenzentrum Garching.
Appendix A: Gravitational wave extraction
In the appendix we summarize the technical aspects related to the
gravitational wave extraction and the different methods we have
used. As stated in Paper I, the use of a CF metric implies the
removal of the gravitational radiation degrees of freedom. Therefore,
in order to compute the waveforms we apply the Newtonian quadrupole
formula.
In that approximation and for an axisymmetric source in spherical
coordinates, it can be shown (Thorne 1980) that the transverse
traceless gravitational field has one independent component
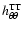 ,
which depends only on the quadrupole
signal amplitude
,
which depends only on the quadrupole
signal amplitude
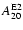 ,
,
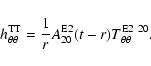 |
(A.1) |
As the l = 2, m = 0 spherical tensor harmonic
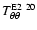 is defined according to
is defined according to
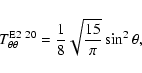 |
(A.2) |
the quadrupole radiation field
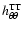 is given by
is given by
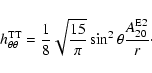 |
(A.3) |
A.1 Different formulations of the quadrupole formula
The amplitude
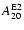 in Eq. (A.3) is the second
time derivative of the mass quadrupole moment of the source,
in Eq. (A.3) is the second
time derivative of the mass quadrupole moment of the source,
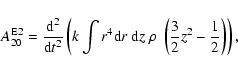 |
(A.4) |
where
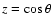 ,
and
,
and
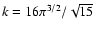 .
This
formulation of the radiation field is known as the standard
quadrupole formula.
.
This
formulation of the radiation field is known as the standard
quadrupole formula.
A direct numerical implementation of this formula is problematic, as
the discretization of the second time derivative causes high frequency
noise in the gravitational wave signal. The amplitude of this noise
can be larger than the total amplitude of the signal. The problem is
worsened by the fact that the density distribution in the integrand of
Eq. (A.4) is weighted by r4,
i.e. mass elements in the outer parts of the star - where the grid
resolution is coarser - contribute strongly to the signal.
To overcome this problem a standard practice is to replace the time
derivatives by spatial derivatives (Finn 1989; Blanchet et al. 1990).
This procedure leads to the stress formula for the gravitational
wave amplitude:
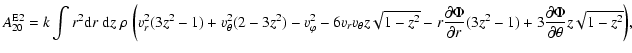 |
|
|
(A.5) |
where 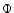 is the Newtonian gravitational potential. This modified
formulation of the quadrupole formula was used in our analysis.
is the Newtonian gravitational potential. This modified
formulation of the quadrupole formula was used in our analysis.
A.2 Ambiguity of the stress formula in the CFC approximation
In a mathematically strict sense the quadrupole approximation of the
radiation field, Eq. (A.1), is only
defined for a flat Minkowski spacetime where the gravitational waves
propagate as a linear perturbation. However, the multipole amplitudes
and the tensor harmonics, although defined in flat spacetime, contain
information about the wave source, which is situated in a strong field
and high velocity region. In our simulations the quadrupole moment
 is computed as a spatial integral over the
relativistic matter configuration in a curved spacetime, as the metric
is computed as a spatial integral over the
relativistic matter configuration in a curved spacetime, as the metric
 is not Minkowskian. Therefore, our methods to compute
the radiation field are hampered by several ambiguities in the
quadrupole formula.
is not Minkowskian. Therefore, our methods to compute
the radiation field are hampered by several ambiguities in the
quadrupole formula.
Whereas in the Newtonian formulation, which is based on Euclidean
geometry, the definition of the radius coordinate r is no source
of ambiguity, in the Riemannian geometry of a curved spacetime the
circumferential radius and the coordinate radius do not necessarily
coincide. In our simulations we use the isotropic radial coordinate r in the computation of the quadrupole moment. Tests where we
replaced r by the circumferential radius in the wave extraction
produced almost identical waveforms.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2576f19.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg193.gif) |
Figure 19:
Reduction of the offset in the gravitational wave amplitude
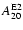 for model A3B2G4 with the weighting method
applied to the stress formula. If the Newtonian potential
for model A3B2G4 with the weighting method
applied to the stress formula. If the Newtonian potential 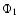 is used, the wave signal shows a large positive offset
(dashed-dotted line). If the combination of metric components
is used, the wave signal shows a large positive offset
(dashed-dotted line). If the combination of metric components 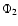 is used, a large negative offset occurs (dashed
line). The weighted sum
is used, a large negative offset occurs (dashed
line). The weighted sum
 of these two
signals yields a waveform with practically zero offset (solid
line). This combined signal exhibits no high frequency noise, as
its constituents have been obtained using the stress formula.
of these two
signals yields a waveform with practically zero offset (solid
line). This combined signal exhibits no high frequency noise, as
its constituents have been obtained using the stress formula. |
| Open with DEXTER |
The spatial derivatives of the Newtonian potential present in
Eq. (A.5) need particular attention. When simply
using Poisson's equation,
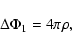 |
(A.6) |
which we solve by an expansion into Legendre polynomials
(Zwerger 1995), the waveform shows an offset, particularly after
core bounce (see the dashed-dotted line in
Fig. A.1). For strong gravity,
the Newtonian potential 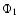 is therefore inappropriate for
describing the radiation field. Another manifestation of this problem
is a large constant offset in
is therefore inappropriate for
describing the radiation field. Another manifestation of this problem
is a large constant offset in
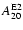 for rapidly rotating
neutron stars in equilibrium, where the gravitational radiation should
vanish.
for rapidly rotating
neutron stars in equilibrium, where the gravitational radiation should
vanish.
The Newtonian potential can also be computed accurately up to the
first post-Newtonian order by setting
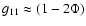 equal to the conformal factor
equal to the conformal factor 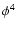 .
This leads to
.
This leads to
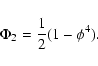 |
(A.7) |
The waveforms obtained from this expression also show an offset, but
this time a negative one (see the dashed line in
Fig. A.1). However, combining
both expressions for  ,
Eqs. (A.6) and (A.7), into
,
Eqs. (A.6) and (A.7), into
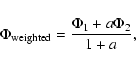 |
(A.8) |
where
 is a parameter with an appropriate value,
one is able to reduce the offset almost to zero in all core collapse
models (see the solid line in
Fig. A.1).
is a parameter with an appropriate value,
one is able to reduce the offset almost to zero in all core collapse
models (see the solid line in
Fig. A.1).
-
Alcubierre, M., Brandt, S., Brügmann, B., et al. 2001,
Int. J. Mod. Phys. D, 10, 273
In the text
NASA ADS
-
Aloy, M. A., Müller, E., Ibáñez, J. M., Martí, J. M., & MacFadyen,
A. 2000, ApJ, 531, L119
In the text
NASA ADS
-
Banyuls, F., Font, J. A., Ibáñez, J. M., Martí, J. M., & Miralles,
J. A. 1997, ApJ, 476, 221
In the text
NASA ADS
-
Blanchet, L., Damour, T., & Schäfer, G. 1990,
MNRAS, 242, 289
In the text
NASA ADS
-
Bodenheimer, P., & Woosley, S. E. 1983,
ApJ, 269, 281
In the text
NASA ADS
-
Bonazzola, S., Frieben, J., & Gourgoulhon, E. 1996,
ApJ, 460, 379
In the text
NASA ADS
-
Bonazzola, S., Frieben, J., & Gourgoulhon, E. 1998,
A&A, 331, 280
In the text
NASA ADS
-
Bonazzola, S., & Marck, J. A. 1993,
A&A, 267, 623
In the text
NASA ADS
-
Brown, J. D. 2001,
Astrophysical sources for ground-based gravitational wave detectors,
ed. J. M. Centrella, AIP Conf. Proc., 575, pp. 234-245
(American Institute of Physics, Melville, New York, USA)
In the text
-
Dimmelmeier, H., Font, J. A., & Müller, E. 2001,
ApJ, 560, L163
In the text
NASA ADS
-
Dimmelmeier, H., Font, J. A., & Müller, E. 2002,
A&A, 388, 917 (Paper I)
In the text
NASA ADS
-
Evans, C. R. 1986,
in Dynamical spacetimes and numerical
relativity, ed. J. M. Centrella (Cambridge University Press, Cambridge, UK), pp. 3-39
In the text
-
Finn, L. S. 1989,
in Frontiers in
numerical relativity, ed. C. R. Evans, S. L. Finn, & D. W. Hobill (Cambridge University Press, Cambridge,
UK), pp. 126-145
In the text
-
Finn, L. S., & Evans, C. R. 1990,
ApJ, 351, 588
In the text
NASA ADS
-
Fryer, C., & Heger, A. 2000,
ApJ, 541, 1033
In the text
NASA ADS
-
Fryer, C., Holz, D. E., & Hughes, S. A. 2002,
ApJ, 565, 430
In the text
NASA ADS
-
Goldreich, P., & Weber, S. V. 1980,
ApJ, 238, 991
In the text
NASA ADS
-
Gustafson, E., Shoemaker, D., Strain, K., & Weiss, R. 1999,
LSC white paper on detector research and development,
Technical Report LIGO T990080-00-D
In the text
-
Hayashi, A., Eriguchi, Y., & Hashimoto, M. 1999,
ApJ, 521, 376
In the text
NASA ADS
-
Heger, A., Langer, N., & Woosley, S. E. 2000,
ApJ, 528, 368
In the text
NASA ADS
-
Houser, J. L., Centrella, J. M., & Smith, S. C. 1994,
Phys. Rev. Lett., 72, 1314
In the text
NASA ADS
-
Imshennik, V. S., & Nadezhin, D. K. 1992,
Sov. Astron. Lett., 18, 79
In the text
NASA ADS
-
Janka, H.-T., & Mönchmeyer, R. 1989,
A&A, 226, 69
In the text
NASA ADS
-
Janka, H.-T., Zwerger, T., & Mönchmeyer, R. 1993,
A&A, 268, 360
In the text
NASA ADS
-
Kaspi, V. M. 2000,
in Pulsar Astronomy -
2000 and Beyond,
M. ed. Kramer, N. Wex, & N. Wielebinski
(Astronomical Society of the Pacific, San Franciso, CA, USA), ASP Conf. Ser., 202, 485-490
In the text
-
Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989a,
MNRAS, 237, 355
In the text
NASA ADS
-
Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989b,
MNRAS, 239, 153
NASA ADS
-
Lorimer, D. R. 2001,
Living Rev. Relativity 4,
cited on 10 Dec 2001, In the text
http://www.livingreviews.org/Articles/Volume4/2001-5lorimer/
-
MacFadyen, A. I., Woosley, S. E., & Heger, A. 2001,
ApJ, 550, 410
In the text
NASA ADS
-
Marshall, F., Gotthelf, E., Zhang, W., Middleditch, J., & Wang, Q. 1998,
ApJ, 499, L179
In the text
NASA ADS
-
Mönchmeyer, R., & Müller, E. 1989,
in NATO ASI
Timing neutron stars, ed. H. Ögelman, & E. P. J. van den Heuvel
(Kluwer, Dordrecht, Netherlands), pp. 549-572
In the text
-
Mönchmeyer, R., Schäfer, G., Müller, E., & Kates, R. E. 1991,
A&A, 246, 417
In the text
NASA ADS
-
Müller, E, 1982,
A&A, 114, 53
In the text
NASA ADS
-
Müller, E. 1998, in
Computational methods for
astrophysical fluid flow, Saas-Fee Advanced Course 27,
ed. O. Steiner, & A. Gautschy (Springer, Berlin, Germany), pp. 343-494
In the text
-
Müller, E., & Hillebrandt, W. 1981,
A&A, 103, 358
In the text
NASA ADS
-
Müller, E., & Janka, H.-T. 1997,
A&A, 317, 140
In the text
NASA ADS
-
Nakamura, T. 1981,
Prog. Theor. Phys., 65, 1876
In the text
-
Nakamura, T. 1983,
Prog. Theor. Phys., 70, 1144
In the text
-
Nakamura, T., Oohara, K., & Kojima, Y. 1987,
Prog. Theor. Phys., 90, 1
In the text
-
New, K. C. B., Centrella, J. M., & Tohline, J. E. 2000,
Phys. Rev. D, 62, 064019
In the text
-
Pradier, T., Arnaud, N., Bizouard, M.-A., et al. 2001,
Phys. Rev. D, 63, 042002
In the text
-
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992,
Numerical recipes in C: The art of scientific programming
(Cambridge University Press, Cambridge, UK)
In the text
-
Rampp, M., Müller, E., & Ruffert, M. 1998,
A&A, 332, 969
In the text
NASA ADS
-
Saijo, M., Shibata, M., Baumgarte, T. W., & Shapiro, S. L. 2001,
ApJ, 548, 919
In the text
NASA ADS
-
Shapiro, S. L., & Teukolsky, S. A. 1983,
Black holes, white dwarfs, and neutron stars
(Wiley, New York, USA)
In the text
-
Shibata, M. 2000,
Prog. Theor. Phys., 104
In the text
-
Shibata, M., Baumgarte, T. W., & Shapiro, S. L. 2000,
ApJ, 542, 453
In the text
NASA ADS
-
Smith, S. C., Houser, J. L., & Centrella, J. M. 1996,
ApJ, 458, 236
In the text
NASA ADS
-
Stark, R. F., & Piran, T. 1985,
Phys. Rev. Lett., 55, 891
In the text
NASA ADS
-
Stergioulas, N. 1998,
Living Rev. Relativity 1,
cited on 10 Dec. 2001, In the text
http://www.livingreviews.org/Articles/Volume1/1998-8stergio/
-
Stergioulas, N., & Friedman, J. L. 1995,
ApJ, 444, 306
In the text
NASA ADS
-
Stergioulas, N., & Friedman, J. L. 1998,
ApJ, 492, 301
In the text
NASA ADS
-
Symbalisty, E. M. D. 1984,
ApJ, 285, 729
In the text
NASA ADS
-
Tassoul, J.-L. 1978,
Theory of rotating stars
(Princeton University Press, Princeton, USA)
In the text
-
Thorne, K. S. 1980,
Rev. Mod. Phys., 52, 299
In the text
NASA ADS
-
Thorne, K. S. 1995,
in Snowmass 1994 Summer Study on
Particle and Nuclear Astrophysics and Cosmology in the next millennium,
ed. E. W. Kolb, & R. C. Peccei (World Scientific, Singapore),
pp. 160-184
In the text
-
Wheeler, J. C., Yi, I., Höflich, P., & Wang, L. 2000,
ApJ, 537, 810
In the text
NASA ADS
-
Wilson, J. R., 1979,
in Sources of gravitational radiation,
ed. L. L. Smarr (Cambridge University Press, Cambridge, UK), pp. 423-445
In the text
-
Wilson, J. R., Mathews, G. J., & Marronetti, P. 1996,
Phys. Rev. D, 54, 1317
In the text
NASA ADS
-
Yamada, S., & Sato, K. 1994a,
ApJ, 450, 245
In the text
NASA ADS
-
Yamada, S., & Sato, K. 1994b,
ApJ, 434, 268
In the text
NASA ADS
-
Yoshida, S., & Eriguchi, Y. 1999,
ApJ, 515, 414
In the text
NASA ADS
-
Zwerger, T. 1995,
Ph.D. Thesis, Technische Universität München, München,
Germany
In the text
-
Zwerger, T., & Müller, E. 1997,
A&A, 320, 209
In the text
NASA ADS
Copyright ESO 2002
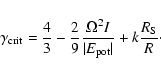
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f1.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms2576f2.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f3.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg94.gif)
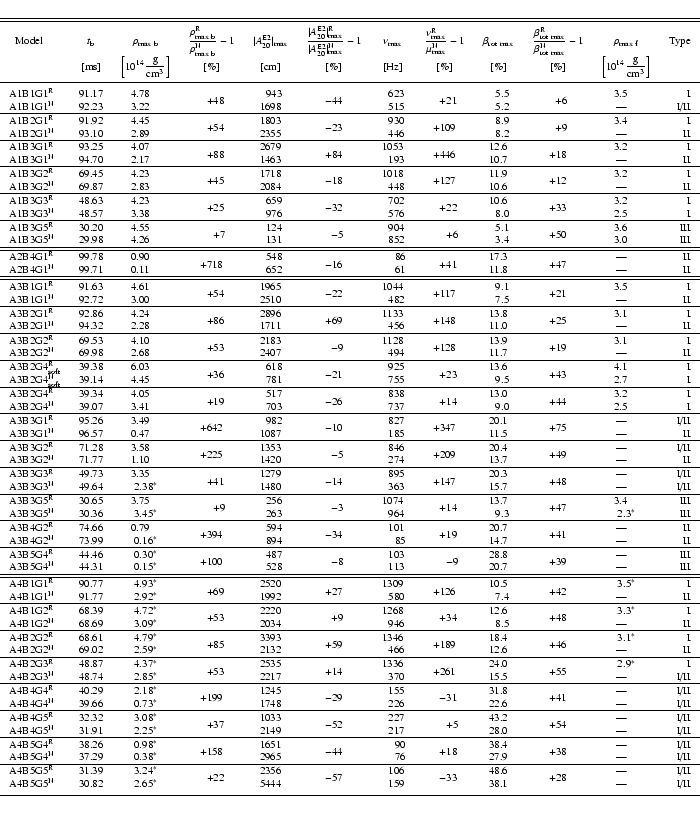
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{ms2576f4.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ms2576f5.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{ms2576f6.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg110.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f7.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f8.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ms2576f9.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg120.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms2576f10.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms2576f11.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms2576f12.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg129.gif)
![\begin{figure}
\includegraphics[width=17cm,clip]{ms2576f13.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg131.gif)
![\begin{figure}
\includegraphics[width=8cm,clip]{ms2576f14.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg137.gif)
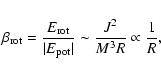
![\begin{figure}
\includegraphics[width=8.4cm,clip]{ms2576f15.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg140.gif)
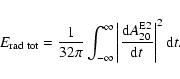
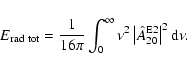
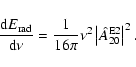
![\begin{figure}
\includegraphics[width=8.2cm,clip]{ms2576f16.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg163.gif)
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{ms2576f17.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg170.gif)
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{ms2576f18.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg171.gif)
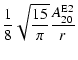
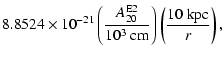
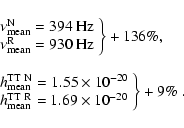
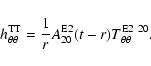
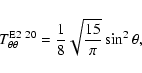
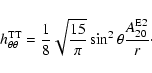
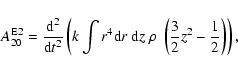
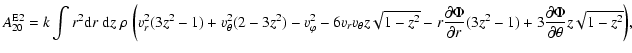
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2576f19.eps}
\end{figure}](/articles/aa/full/2002/38/aa2576/Timg193.gif)