A&A 393, 57-68 (2002)
DOI: 10.1051/0004-6361:20021018

Local velocity field from sosie galaxies[*]

I. The Peebles' model

J. N. Terry1 - G. Paturel1 - T. Ekholm 1

CRAL-Observatoire de Lyon, UMR 5574, 69230 Saint-Genis Laval, France

Received 24 May 2000 / Accepted 20 June 2002

Abstract
Pratton et al. (1997) showed that the velocity field around clusters could generate an apparent distortion that appears as tangential structures or radial filaments. In the present paper we determine the parameters of the Peebles' model (1976) describing infall of galaxies onto clusters with the aim of testing quantitatively the amplitude of this distortion.

The distances are determined from the concept of sosie galaxies (Paturel 1984) using 21 calibrators for which the distances were recently calculated from two independent Cepheid calibrations. We use both B and I-band magnitudes.

The Spaenhauer diagram method is used to correct for the Malmquist bias. We give the equations for the construction of this diagram. We analyze the apparent Hubble constant in different regions around Virgo and obtain simultaneously the Local Group infall and the unperturbed Hubble constant. We found:

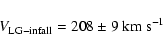
\begin{displaymath}\hspace*{1cm}V_{\rm LG-infall} = 208 \pm 9~\rm km~s^{-1}\end{displaymath}


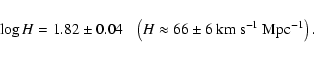
\begin{displaymath}\hspace*{1cm}\log H = 1.82 \pm 0.04 \ \ \ \left(H \approx 66 \pm 6~\rm km~s^{-1}~Mpc^{-1}\right).\end{displaymath}

The front side and backside infalls can be seen around Virgo and Fornax. In the direction of Virgo the comparison is made with the Peebles' model. We obtain:

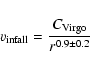
\begin{displaymath}\hspace*{1cm}v_{\rm infall} = \frac{C_{\rm Virgo}}{r^{0.9 \pm 0.2}}\end{displaymath}

with $C_{\rm Virgo}=2800$ for Virgo and $C_{\rm Fornax}=1350$ for Fornax, with the adopted units (km s-1 and Mpc).

We obtain the following mean distance moduli:

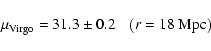
\begin{displaymath}\hspace*{1.05cm}\mu _{\rm Virgo}=31.3 \pm 0.2 \ \ \ \left(r=18 \rm ~Mpc\right)\end{displaymath}


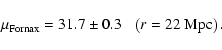
\begin{displaymath}\hspace*{1.05cm}\mu _{\rm Fornax}=31.7 \pm 0.3 \ \ \ \left(r=22\rm ~Mpc\right).\end{displaymath}

All these quantities form an accurate and coherent system.

Key words: galaxies: general - galaxies: distances and redshifts - cosmology: distance scale - methods: statistical


1 Introduction

The distribution of galaxies in the universe is seen as a foam with bubbles and voids. This picture was predicted by Zel'dovich (1970) and seen by Joeveer et al. (1978). In the near universe these structures appear as large 2D filaments or large 3D walls (de Lapparent et al. 1986; Haynes & Giovanelli 1986). Indeed, the 3D distribution of galaxies built from their position and their radial velocity clearly shows these kinds of structures. In Fig. 1 we plotted galaxies with known radial velocities in a slice of $\pm 10$ Mpc around the plane defined by the closest superclusters (Paturel et al. 1988). The polar direction, perpendicular to this plane is about $l=52^{\circ}$ and $b=16^{\circ}$ in galactic coordinates according to Di Nella & Paturel (1994).


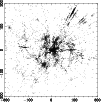  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms9954f1.eps}}\end{figure} Figure 1: Distribution of galaxies seen from their positions and radial velocities within a slice of $\pm 10$ Mpc around the plane defined by near superclusters. The distances are in Mpc assuming a Hubble constant of 70 km s-1 Mpc-1.
Open with DEXTER

Pratton et al. (1997) showed that the velocity field around clusters could generate an apparent distortion which appears as tangential structures or radial filaments ("Finger of God''), similar to observed ones. A remarkable result shown by Rauzy et al. (1992) is that infall velocity does not affect the observed cosmological radial velocity for galaxies located on a sphere (hereafter the Rauzy sphere) having a diameter with ends at the position of the observer and at the center of the attractive galaxy cluster (on the Rauzy sphere, the infall direction is perpendicular to the line of sight). When plotting the distribution of galaxies with distances calculated from their observed radial velocities and a given Hubble constant (d=v/H), an artificial density enhancement on the Rauzy sphere is produced. This is illustrated in Fig. 2.


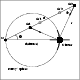  \begin{figure} \par\resizebox{7cm}{!}{\includegraphics{ms9954f2.eps}}\end{figure} Figure 2: Illustration of the apparent density enhancement around a cluster. A galaxy in position G1will be placed at position G'1 (because its radial velocity is augmented by the projection $\Delta V$ of its infall velocity. So the displacement $G_1G'_1=\Delta V / H$), while a galaxy in position G2 will be placed at position G'2. The galaxies are placed closer to the Rauzy sphere. On the contrary, in the direction of the cluster center the galaxies are placed far from the Rauzy's sphere because their infall velocities are very high.
Open with DEXTER

This description, applied to near clusters, could lead to the scheme given in Fig. 3. This resembles the observed distribution of galaxies (Fig. 1).


  \begin{figure} \par\resizebox{7cm}{!}{\includegraphics{ms9954f3.eps}}\end{figure} Figure 3: Illustration of the density enhancement around near clusters. The apparent density enhancement is shown for each cluster placed as in Fig. 1. Beyond the doted circle, the selection function on apparent magnitudes contributes to give the circular aspect (doted circle). The approximate mean radial velocity of each cluster is given in parenthesis under the name.
Open with DEXTER

A kinematical model is needed to give a more quantitative description. The linearized model made by Peebles (1976) is a simple way to get the infall velocities from a limited set of parameters. It leads to the following equation of the infall velocity:

 \begin{displaymath}v_{\rm infall} = \frac{C}{r^{\gamma - 1}}\cdot \end{displaymath} (1)

In the present paper we want to get realistic values for parameters C and $\gamma $. The determination of accurate extragalactic distances is the fundamental step for achieving this goal. Let us explain the process to go from extragalactic distances to the parameters of the Peebles' model. From an extragalactic distance and the Hubble constant one can predict the cosmological radial velocity at this distance ( $V_{\rm predicted}=H.d$). The comparison with the observed radial velocity directly gives the line of sight component of the infall velocity for this galaxy. On the other hand, if the distances of the cluster and of the considered galaxy are known, all the geometrical elements are also known to calculate both $v_{\rm infall}$ and r entering Eq. (1).

The spiral galaxies are good tracers of the velocity field because they are located, on average, in the outskirts of clusters. On the other hand, the relation between the absolute magnitude of a spiral galaxy and the rotation velocity of its disk (Tully & Fisher 1977) is the best known distance indicator. The method of sosie galaxies (look-alike galaxies) is a particular application of the Tully-Fisher method which bypasses some practical problems (Paturel 1984). However, the method does not correct for the Malmquist bias (Malmquist 1922; Sandage & Tammann 1975; Teerikorpi 1975) which has to be taken into account. The Spaenhauer diagram (Spaenhauer 1978; Sandage 1994) can be used to find galaxies not affected by this bias. In a recent paper (Paturel et al. 1998), the method of sosie galaxies and Spaenhauer diagram were presented for two calibrators (M 31 and M 81). The limited number of sosie galaxies didn't allow the present study. Here, we extend the method to 21 calibrators for which the distance has been recently calculated from the Cepheid Period-Luminosity relation using two independent zero-point calibrations. We use both B- and I-band magnitudes. The sample is deep enough to check directly Peebles' model.

In Sect. 2, we will select the calibrating galaxies and in Sect. 3 we will search for sosie galaxies of these selected calibrators. Then, in Sect. 4 we apply the Spaenhauer diagram method in order to select unbiased galaxies from which we analyze (Sect. 5) the Hubble constant in different regions around Virgo. In the direction of Virgo the comparison is made with predictions by Peebles' model.

2 Selection of primary calibrators

The distance moduli of calibrators come from two independent calibrations of Cepheid Period-luminosity relations (Paturel et al. 2002a,b) based on the sample by Gieren et al. (1998) and on the HIPPARCOS Cepheid sample (Lanoix et al. 1999). The apparent magnitudes come from the LEDA database (http://www-obs.univ-lyon1.fr). They are corrected for galactic extinction and inclination effects following the precepts of Schlegel et al. (1998) and Bottinelli et al. (1995), respectively.

The Malmquist bias introduces a major difficulty in estimating distances of astronomical objects. It is caused to the fact that faint galaxies are missing in the sample because of the limiting apparent magnitude (see the review paper by Teerikorpi 1997). To reach large distances with limited bias, we have to consider only intrinsically bright galaxies. Then, because the method of sosie galaxies selects galaxies having almost the same absolute magnitude as calibrators, we have to consider the brightest calibrators. On the other hand, we need a large sample and should not reject too many calibrators. The best compromise was judged from histograms of B- and I-absolute magnitudes. We kept only calibrators satisfying either MB < -19 or MI < -21. One calibrator (NGC 4603) was rejected because of the large uncertainty on its distance modulus (0.86 mag). The 21 remaining calibrators are presented in Table 1 as follows:
Column 1: PGC number from LEDA.
Column 2: NGC number.
Column 3: Distance modulus and its mean error (Paturel et al. 2002a,b).
Column 4: Morphological type from LEDA.
Column 5: Adopted inclination from LEDA following Fouqué et al. (1990).
Column 6: Internal extinction in B following Bottinelli et al. (1995).
Column 7: Galactic Extinction from Schlegel et al. (1998).
Column 8: $B_{\rm o}$, corrected B-magnitude from LEDA with its actual uncertainty (Paturel et al. 1997).
Column 9: Same as Col. 8 for I-band magnitudes. The corrections are 0.44 times the B-band ones (Cols. 6 and 7). This 0.44 factor should be slightly larger for the internal extinction (Han 1992) but for the method of sosie this correction vanishes because the inclination is the same for the calibrator and its sosies.
Column 10: log of maximum rotation velocity and its actual uncertainty taken from LEDA. It is calculated as a weighted mean of $\log V_M$ from both the 21-cm line width and $H_{\alpha}$ rotation curve.


 

 
Table 1: List of calibrating galaxies. The distance moduli come from the Cepheid Period-Luminosity relation calibrated with two independent samples. The rest of the data is extracted from LEDA2002.
PGC NGC $\mu$ Type i Ai Ag $B_{\rm o}$ $I_{\rm o}$ $\log ~V_{\rm M}$
0002557 NGC 224 $24.47\pm0.23$ Sb 78.0 0.67 0.46 $ 3.18\pm0.30$ $ 1.47\pm0.10$ $2.39\pm0.01$
0005818 NGC 598 $24.77\pm0.39$ Sc 55.0 0.38 0.18 $ 5.73\pm0.12$   $2.02\pm0.02$
0013179 NGC 1365 $31.31\pm0.15$ SBb 57.7 0.32 0.09 $ 9.90\pm0.18$ $ 8.18\pm0.04$ $2.34\pm0.03$
0013602 NGC 1425 $31.68\pm0.17$ Sb 69.5 0.54 0.06 $10.83\pm0.24$ $ 9.56\pm0.02$ $2.25\pm0.01$
0017819 NGC 2090 $30.36\pm0.15$ Sc 68.3 0.54 0.17 $10.94\pm0.39$ $ 9.35\pm0.11$ $2.17\pm0.02$
0028630 NGC 3031 $27.70\pm0.16$ Sab 59.0 0.38 0.35 $ 7.12\pm0.10$ $ 5.41\pm0.10$ $2.36\pm0.01$
0030197 NGC 3198 $31.11\pm0.23$ SBc 70.0 0.80 0.05 $10.22\pm0.32$ $ 9.22\pm0.06$ $2.19\pm0.01$
0031671 NGC 3319 $30.83\pm0.18$ SBc 59.1 0.48 0.06 $11.33\pm0.64$ $10.39\pm0.06$ $2.03\pm0.03$
0032007 NGC 3351 $29.85\pm0.16$ SBb 41.5 0.33 0.12 $10.05\pm0.12$ $ 8.32\pm0.06$ $2.27\pm0.03$
0032192 NGC 3368 $30.08\pm0.17$ SBab 54.7 0.21 0.11 $ 9.75\pm0.13$ $ 7.99\pm0.05$ $2.30\pm0.04$
0034554 NGC 3621 $29.14\pm0.15$ SBcd 65.6 0.64 0.35 $ 9.11\pm0.22$ $ 8.01\pm0.06$ $2.13\pm0.01$
0034695 NGC 3627 $29.79\pm0.15$ SBb 57.3 0.48 0.14 $ 8.97\pm0.19$ $ 7.54\pm0.06$ $2.30\pm0.02$
0039600 NGC 4258 $29.48\pm0.16$ SBbc 72.0 0.65 0.07 $ 8.37\pm0.12$ $ 7.04\pm0.08$ $2.34\pm0.01$
0040692 NGC 4414 $31.35\pm0.26$ Sc 54.0 0.41 0.08 $10.65\pm0.55$ $ 8.87\pm0.10$ $2.35\pm0.02$
0041471 NGC 4496A $30.89\pm0.18$ SBd 48.1 0.23 0.11 $11.78\pm0.20$   $1.97\pm0.06$
0041812 NGC 4535 $30.98\pm0.20$ SBc 44.0 0.20 0.08 $10.35\pm0.15$ $ 8.89\pm0.06$ $2.29\pm0.06$
0041823 NGC 4536 $30.93\pm0.19$ SBbc 58.9 0.62 0.08 $10.43\pm0.26$ $ 9.15\pm0.08$ $2.25\pm0.01$
0041934 NGC 4548 $30.94\pm0.17$ SBb 37.0 0.12 0.16 $10.66\pm0.10$ $ 8.89\pm0.06$ $2.27\pm0.08$
0042741 NGC 4639 $31.71\pm0.21$ SBbc 52.0 0.30 0.11 $11.81\pm0.07$ $10.27\pm0.06$ $2.25\pm0.05$
0043451 NGC 4725 $30.46\pm0.18$ SBab 54.4 0.23 0.05 $ 9.74\pm0.15$ $ 8.04\pm0.06$ $2.36\pm0.04$
0069327 NGC 7331 $30.86\pm0.22$ Sbc 75.0 0.62 0.39 $ 9.24\pm0.17$ $ 7.70\pm0.05$ $2.40\pm0.01$


The use of some calibrators (e.g., NGC 598 and NGC 4496A) is debatable because they are faint with poor photometry. This point is discussed in Sect. 5.

3 Selection of sosie galaxies

The sosie galaxies of a given calibrator are defined with a given range around relevant parameters for the application of the Tully-Fisher relationship (morphological type code T, log of axis ratio $\log R_{25}$and log of maximum rotation velocity $\log V_{\rm M}$). The range of a given parameter is related to the typical error attached to this parameter. In order to choose the best range for each parameter we plot histograms of actual uncertainties (Fig. 4) as they are extracted from LEDA, for galaxies having known T, $\log R_{25}$ and $\log V_{\rm M}$.


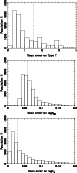  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms9954f5a.eps}}\par\res... ...54f5b.eps}}\par\resizebox{8.8cm}{!}{\includegraphics{ms9954f5c.eps}}\end{figure} Figure 4: Histogram of actual uncertainties on morphological type code T, log of axis ratio $\log R_{25}$ and log of maximum rotation velocity $\log V_M$. For each parameter, we show the limit (vertical doted lines) beyond which the parameter is considered as different from the one of the calibrator.
Open with DEXTER

Thus, we define a sosie of a calibrator with the following conditions (the parameters of the calibrator are noted with the upperscript "calib''):

\begin{displaymath}T = T^{\rm calib} \pm 1.5 \end{displaymath} (2)


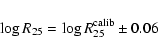\begin{displaymath}\log R_{25} =\log R_{25}^{\rm calib} \pm 0.06 \end{displaymath} (3)


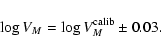\begin{displaymath}\log V_M =\log V_M^{\rm calib} \pm 0.03. \end{displaymath} (4)

A galaxy obeying these criteria does not have parameters significantly different from those of the considered calibrator, and thus, following the TF precepts, it has the same absolute magnitude. The distance modulus is then simply deduced from the relation:

 \begin{displaymath}\mu = \mu^{\rm calib} + m_{\rm o} -m_{\rm o}^{\rm calib} \end{displaymath} (5)

where $m_{\rm o}$ are corrected apparent magnitudes (in B or I).

The application of the previous criteria to galaxies of the LEDA2002 gives a sample of 2732 galaxies which are sosie of one of the 21 calibrators of Table 1. 495 galaxies are sosie of two or three calibrators[*]. For these galaxies we compared the distance moduli obtained from different calibrators. The mean standard deviation of their distance moduli is 0.29.

4 Correction for the Malmquist bias

The method of sosie galaxies (Eq. (5)) does not correct for statistical bias due to magnitude incompleteness (Malmquist bias). Two methods exist to detect unbiased galaxies: the method of normalized distances (Bottinelli et al. 1986) and the Spaenhauer diagram (Spaenhauer 1978) used by Sandage (1994). A detailed discussion about these methods is given by Teerikorpi (1997). In the case of galaxies which are sosie of a same calibrator, both diagrams are equivalent. In order to correct for the Malmquist bias we have first to determine the actual completeness limit of the apparent magnitudes.

4.1 Completeness limit in B and I apparent magnitudes

The knowledge of the limiting apparent magnitude informs us about galaxies missing at a given distance for a given absolute magnitude. The construction of the curve $\log N$ vs. apparent magnitude (N is the number of galaxies brighter than the considered apparent magnitude) is a classical way to estimate this limit. If the distribution of galaxies is homogeneous, the slope expected is 0.6. In Fig. 5 we show the completeness curves for our sample, in B- and I-band respectively. The limiting apparent magnitude is given where the curve begins to bend down.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms9954f6a.eps}}\par\resizebox{8.8cm}{!}{\includegraphics{ms9954f6b.eps}}\end{figure} Figure 5: Completeness curve for the B and I-band apparent magnitudes. The curve begins to bend down at $\approx $14 mag and $\approx $12.5 mag, respectively.
Open with DEXTER

The limiting apparent magnitude is $m_{\rm lim}=14 $ mag in B and $m_{\rm lim}=12.5$ mag in I. The slopes are $0.39\pm0.01$ and $0.37 \pm 0.01$, for B and I respectively. The result that the slope is smaller than the theoretical one has already been discussed (Paturel et al. 1994; Teerikorpi et al. 1998). In the following sections we will use the observed slope (0.4) and the limits 14 and 12.5 for B and I magnitudes.

4.2 Theoretical aspects of the Spaenhauer diagram

The Spaenhauer diagram for galaxies which are sosie of a given calibrator is a diagram of absolute magnitude against distance. From a practical point of view, we are drawing the absolute magnitude versus the radial velocity which is an estimate of the distance through the Hubble law, after correction for the infall of our Local Group (hereafter LG) towards Virgo. For this correction a preliminary infall velocity has been adopted (200 km s-1). Eventually, it will be revised in forthcoming sections.

The construction of the Spaenhauer diagram requires three curves:

1.
The curve showing the cut due to the limiting apparent magnitude. We recall the equation of this curve:

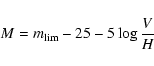\begin{displaymath}M = m_{\rm lim} - 25 - 5 \log \frac{V}{H} \end{displaymath} (6)

where H is the adopted Hubble constant and $m_{\rm lim}$ the limiting apparent magnitude, as defined in the previous section.

2.
The bias curve for a galaxy with a Gaussian absolute magnitude distribution $\mathcal{G}(M_{\rm o} \sigma)$ is given by the equation (Teerikorpi 1975):

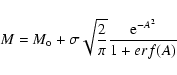\begin{displaymath}M= M_{\rm o} + \sigma {\sqrt{\frac{2}{\pi}} \frac {{\rm e}^{-A^2}}{1+erf(A)}} \end{displaymath} (7)

with

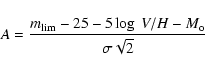\begin{displaymath}A= \frac {m_{\rm lim} -25 -5\log~V/H - M_{\rm o}} {\sigma \sqrt{2}} \end{displaymath} (8)

and

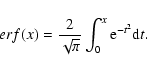\begin{displaymath}erf(x) = \frac{2}{\sqrt{\pi}} \int_0^x {\rm e}^{-t^2} {\rm d}t. \end{displaymath} (9)

3.
The envelope of the distribution is given by the following equations demonstrated in the Appendix A:

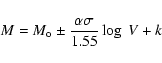\begin{displaymath}M = M_{\rm o} \pm \frac{\alpha \sigma}{1.55}\log~V + k \end{displaymath} (10)

where $\alpha$ is the slope of the completeness curve divided by 0.2 (e.g., for the theoretical slope of 0.6 we expect $\alpha= 3$). We assume that $\sigma $does not depend on the distance, but its value will be calculated at each step of the iterative process. k depends on the adopted Hubble constant and on the mean density of the considered galaxies. Its expression is:

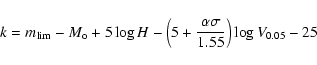\begin{displaymath}k= m_{\rm lim} - M_{\rm o} + 5 \log H - \left(5+ \frac {\alpha \sigma}{1.55}\right) \log V_{0.05} - 25 \end{displaymath} (11)

where V0.05 is the velocity at which the biased absolute magnitude is changed by 5 percent. This level is arbitrarily chosen as the beginning of the observable bias.

4.3 Application to our sample

We construct the Spaenhauer diagram for each calibrator using our sample of sosie galaxies. Let us recall that the adopted parameters are the following: $m_{\rm lim}=14 $ in B-band and 12.5 in I-band (Sect. 4.1). From Fig. 5, we use the observed values $\alpha= 0.4 / 0.2 = 2$ for both B and I magnitudes. We adopt provisionally a Local Group infall velocity of 200 km s-1 In a first step we start with a preliminary value of H and $\sigma $. We adopted a starting dispersion $\sigma =0.7$ in B and $\sigma =0.6$ in I and a Hubble constant of 70 km s-1 Mpc-1 These values have no incidence on the final result. They only affect the number of iterations. We calculate the new H and $\sigma $ values from the unbiased galaxies of the "plateau'' (i.e. galaxies with a velocity less than V0.05)[*] The new estimates are re-injected in a new iteration, and so on. The calculation is stopped when H becomes stable. Figures 6 and 7 give the Spaenhauer diagrams in B and Ifor the 21 calibrators (two calibrators have no I-band magnitude). It is interesting to compare NGC 224 = M 31 and NGC 598 = M 33, the first two galaxies in Fig. 6, because they represent two opposite cases: one luminous galaxy (M 31) and one low luminosity one (M 33). The effect of the bias is clearly visible.


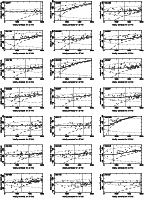  \begin{figure} \par\resizebox{16.5cm}{!}{\includegraphics{ms9954f7.eps}}\end{figure} Figure 6: Spaenhauer diagrams in B magnitudes. For each calibrator we plot its sosie galaxies, with the predicted envelope (doted curve). The bias curve is show as a solid curve. The region of completeness is above the dashed curve. Finally, the unbiased region ("plateau'') is defined on the left of the vertical line. The name of the calibrating galaxy is indicated in the upperleft corner of each frame.
Open with DEXTER


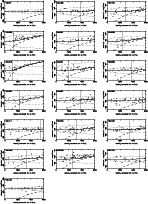  \begin{figure} \par\resizebox{17cm}{!}{\includegraphics{ms9954f8.eps}}\end{figure} Figure 7: Spaenhauer diagrams in I magnitudes (same as Fig. 6).
Open with DEXTER

4.4 The unbiased sample

From the Spaenhauer diagram we extract the galaxies with a velocity below V0.05. This is done for B and I separately. A mean distance modulus is derived in B and I for each galaxy using Eq. (5): The weighted mean distance modulus is then:

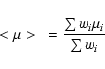\begin{displaymath}<\mu>~=\frac{\sum{w_i \mu_i}}{\sum{w_i}} \end{displaymath} (12)

where the weight ( $w_i = 1/\sigma_{i}^{2}$) of each individual distance modulus ($\mu_i$) is calculated from the mean error on B or I magnitudes using the relations:

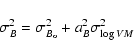\begin{displaymath}\sigma_{B}^2 = \sigma_{B_{\rm o}}^{2} + a_{B}^{2} \sigma_{\log VM}^{2} \end{displaymath} (13)


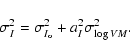\begin{displaymath}\sigma_{I}^2 = \sigma_{I_{\rm o}}^{2} + a_{I}^{2} \sigma_{\log VM}^{2}. \end{displaymath} (14)

Here aB=5.9 and aI=7.7 are the adopted slopes of the Tully-Fisher relations in B and I, respectively. The mean errors $\sigma_{B_{\rm o}}$, $\sigma_{I_{\rm o}}$ and $\sigma_{\log VM}$ are taken from LEDA.

The mean error on the mean distance modulus is then:

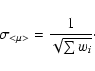\begin{displaymath}\sigma_{<\mu>} = \frac{1}{\sqrt{\sum{w_i}}}\cdot \end{displaymath} (15)

The list of 283 unbiased galaxies is given in Table 2 with the following parameters:
Column 1: PGC number from LEDA.
Column 2: Alternate name from LEDA.
Column 3: Right Ascension and declination for equinox 2000 in hours, minutes, seconds and tenth and degrees, arcminute and arcseconds.
Column 4: Radial velocity corrected for a preliminary infall velocity of the LG towards Virgo ( $V_{\rm infall}= 200$ km s-1).
Column 5: Weighted mean distance modulus and its mean error. The merging of B and I bands is given in Fig. 8.
Column 6: Angular distance from the Virgo center. The center of Virgo is placed on M 87 at equatorial coordinates of J123049.2+122329.


 

 
Table 2: The sample of 283 unbiased galaxies. The full table is available in electronic form at CDS.
PGC Alternate name RA.DEC.2000 $V_{\rm vir}$ $<\mu>$ $\Theta $
    $\rm h,mn,s\ \ \deg \ '\ ''$ km s-1   $\deg$

0004596

 NGC 452 J011614.8+310201 5078 $ 34.24\pm 0.14$ 135.2
0005035 NGC 494 J012255.4+331025 5582 $ 34.17\pm 0.06$ 132.8
0005268 NGC 523 J012520.8+340130 4881 $ 33.70\pm 0.11$ 131.8
0010048 NGC 1024 J023911.8+105049 3522 $ 33.34\pm 0.08$ 140.6
0014906 NGC 1558 J042016.1-450154 4278 $ 33.99\pm 0.07$ 121.6
0016359 UGC 3207 J045609.8+020926 4494 $ 34.26\pm 0.12$ 112.6
0018739 UGC 3420 J061601.8+755611 5353 $ 34.52\pm 0.42$ 78.9
0021336 NGC 2410 J073502.5+324921 4769 $ 34.05\pm 0.40$ 69.9
0026101 IC530 J091517.0+115309 4981 $ 34.64\pm 0.43$ 47.7
...          


We can now start the study of the local velocity field around Virgo from this unbiased sample.

5 Influence of Virgo on log H

The histograms of $\log H$ derived from B and I are presented in Fig. 8. The visible result is that both photometric bands give the same mean.

The means $\log H (B{-}\rm band)= 1.8263 \pm 0.0085$ and $\log H (I {-}\rm band)= 1.8264 \pm 0.0075$ are obviously not significantly different from each other. This justifies that the distance moduli in B and I are combined as explained in the previous section. Similarly, the $\log H$ will be now the weighted mean of $\log H$ in B and I. In order to see the influence of Virgo, we plot now $\log H$ vs. $\Theta $. Three regions are defined (Fig. 9):

1.
Region I: This is the region in the direction of Virgo. It is defined by $\Theta < 60^{\circ}$. For $\Theta < 20^{\circ}$, the diagram divides in two branches. This is the trace of the frontside and backside infalls onto Virgo. For $20^{\circ} \leq \Theta < 60^{\circ}$ (hereafter region Ib) the velocity field appears quieter ($\log H$ does not differ from the unperturbed region III).

2.
Region II: This region is perpendicular to the direction of Virgo. It is defined by $60 \deg \leq \Theta < 140 \deg$. The mean $\log H$ does not differ from values of unperturbed regions (region III and region around $\Theta \approx 50 \deg$).

3.
Region III: Region opposite to the direction of Virgo. It is defined by $140 \deg \leq \Theta$.

Let us study in detail these regions with the target of fitting Peebles' model.

In region III the influence of Virgo is small on individual galaxies because they are far from the Virgo center but the infall of our Local Group may be not negligible. If the adopted LG-infall is too large the $\log H$ for this region will be too high (and vice versa). On the contrary, in region Ib (i.e., region I without the central region Ia of the Virgo center) one expects $\log H$ to diminish when the adopted LG-infall increases. This is confirmed by Fig. 10 where we calculated the mean $\log H$ in regions Ib and III for different LG-infall velocities. The error bar on each point is used to define internal uncertainties on $V_{\rm LG-infall}$ and $\log H$.

The intersection of the two curves of Fig. 10 gives accurately both the infall velocity of the LG and $\log H$. We obtain:

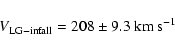\begin{displaymath}V_{\rm LG-infall} = 208 \pm 9.3 \rm ~km~s^{-1} \end{displaymath} (16)


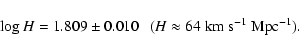\begin{displaymath}\log H = 1.809 \pm 0.010 \ \ \ (H \approx 64\rm ~km~s^{-1}~Mpc^{-1}). \end{displaymath} (17)

The uncertainty on $\log H$ is the internal uncertainty. The total uncertainty is discussed in the conclusion. The present infall velocity $V_{\rm LG-infall}$ is comparable with the mean value, $ 222 \pm 15~\rm km~s^{-1}$, found in the recent literature (Mould et al. 2000; Theureau et al. 1997; Bureau et al. 1996; Hamuy et al. 1996). Although our present target is the derivation of the parameters of Peebles' model it is not possible to disentangle it from the calculation of the Hubble constant and of the LG-infall velocity.


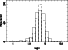  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms9954f9.eps}}\end{figure} Figure 8: Histograms of $\log H$ derived from B and I. The dashed line shows the B-band histogram and the solid line the I-band one. Both photometric bands give the same mean.
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms9954f10.eps}}\end{figure} Figure 9: Mean $\log H$ derived from B and I against the angular distance to the Virgo center. This figure allows us to define three regions: region I in the direction of Virgo (also separated in Ia and Ib), region II perpendicular to the direction of Virgo and region III opposite to Virgo.
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms9954f11.eps}}\end{figure} Figure 10: Determination of the LG infall velocity onto Virgo and of the corrected Hubble constant. The full curve represents how $\log H$changes in region III when LG infall velocity is changed. The dashed curve gives the same result for the region Ib. The LG infall velocity and the corrected $\log H$ are accurately determined at the intersection of both curves (vertical doted line).
Open with DEXTER

In order to search for possible residual bias, we plotted the mean $\log H$ of each calibrator class versus the absolute magnitude of its calibrator, in Band I-band, (Fig. 11). A tendency to have large $\log H$ when the calibrator is faint might be present for the less luminous calibrator. The slope of this relation is $0.015 \pm 0.006$. This is barely significant at the 0.01 probability level (to be significant, the Student's t test requires t0.01>2.57, while we observe t=0.015/0.006=2.5). If one removes the six less luminous calibrators (NGC 598, NGC 4496A, NGC 2090, NGC 3319, NGC 3351 and NGC 4639), the tendency disappears (t=0.4). In this case, the mean log of the Hubble constant becomes $\log H=1.815 \pm 0.007$ (instead of $1.826\pm 0.006$). Thus, the mean Hubble constant is not severely affected, but small $\log H$ is probably better.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms9954f12.eps}}\end{figure} Figure 11: Relation between the mean $\log H$ of each calibrator class versus the B- or I-absolute magnitude. There is no significant increase of H with the absolute magnitude. The small tendency is well within the error.
Open with DEXTER

5.1 Peebles' model

Let us consider now the galaxies in the direction of Virgo (region Ia). The infall of each individual galaxy ( $V_{\rm g-infall}$) can be calculated from their distance (d), from their observed radial velocity ( $V_{\rm vir}$) corrected for the LG infall and from the angle ($\Phi$) between Virgo and the LG seen from this considered galaxy (see Fig. 2 for the definitions of r, d and $\Phi$):

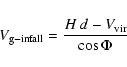\begin{displaymath}V_{\rm g-infall}= \frac{H \ d - V_{\rm vir}}{\cos \Phi} \end{displaymath} (18)

with,

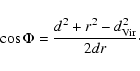\begin{displaymath}\cos \Phi=\frac{d^2 + r^2 - d_{\rm Vir}^{2}}{2dr}\cdot \end{displaymath} (19)

The adopted distance to Virgo is $d_{\rm Vir}=18~\rm Mpc$.

Now, we can plot $V_{\rm g-infall}$ vs. r (Fig. 12) to check directly Peebles' model (Eq. (1)). From the previous relation it can be seen that the errors on x- and y-axis are strongly correlated. The dominant error comes from d. The asymptotic velocity infall is zero at large r distances. The location of the LG is represented by a large open square. We calculated $\gamma $ by minimizing the dispersion on $V_{\rm g-infall}$. For this calculation we limited r between 3 Mpc and 30 Mpc in order to avoid the Virgo center, where there is a very large uncertainty on $V_{\rm g-infall}$ due to the small value of r. The best result is obtained for $\gamma =1.9$. This result is quite comparable with the value adopted by Peeblees ($\gamma =2$) but the uncertainty, estimated visually, is large (about 0.2). The application to the Local Group infall leads to $C_{\rm Virgo}=2800$. In order to highlight the tendency, we plot the mean x and y values of individual points in four x-boxes: (3 to 7) Mpc, (7 to 13) Mpc, (13 to 21) Mpc and (21 to 31) Mpc. These mean points (open circles) are represented with their observed scatter divided by the square root of the number of points in each box.


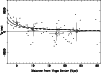  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms9954f13.eps}}\end{figure} Figure 12: Direct determination of the parameters of Peebles' model. The adopted model is represented with the solid curve. Dashed curves correspond to a change of $\gamma $ by $\pm 0.2$. Without infall the points should be distributed around the horizontal line. The position of the Local Group is represented with a large open square. Mean points are represented with their uncertainty (open circles) in order to show better the expected tendency.
Open with DEXTER

It is interesting to see in detail which galaxies are exactly in the direction of the Virgo center. If we consider galaxies with $\Theta<15 \ \deg$ and $\mu \leq 32.50$only 9 galaxies remain. They are presented in Table 3 following increasing radial velocities. For each galaxy we give the observed Hubble constant H. In this table two parameters are independent: the radial velocity and the distance modulus.


 

 
Table 3: Detail of the central region of Virgo. Galaxies with NGC name have their distance from the Cepheid PL relation.
PGC NGC $V_{\rm vir}$ $\mu$ $\Theta $ H
0041934 NGC 4548 587 $30.94 \pm0.37$ 2.4 38
0042833   917 $31.86 \pm0.17$ 5.1 39
0043798   1089 $32.26 \pm0.25$ 11.7 38
0042741 NGC 4639 1097 $31.70 \pm0.18$ 3.1 50
0043451 NGC 4725 1360 $30.81 \pm0.15$ 13.9 94
0041823 NGC 4536 1846 $30.93 \pm0.11$ 10.2 120
0041812 NGC 4535 2029 $30.98 \pm0.31$ 4.3 129
0041024   2069 $31.29 \pm0.23$ 4.7 114
0042069   2342 $31.47 \pm0.11$ 1.8 119
Mean     $31.36 \pm0.17$    
Adopted     $31.3 \pm0.17$    


The main feature from this table is that the apparent Hubble constants are sorted according to velocities. This means that the distance does not intervene very much. The natural interpretation is that all these galaxies are almost at the same distance (distance of Virgo). The Hubble constant reflects only the infall velocity. Large velocities correspond to galaxies in front of Virgo and falling onto Virgo, away from us. On the contrary, galaxies with small velocities are beyond Virgo and falling onto it in our direction. Indeed, the four galaxies with small velocities have a mean distance modulus of $\mu=31.69\pm0.27$ while the four galaxies with high velocities have a larger mean distance modulus of $\mu=31.17\pm0.13$. The difference is significant at about $3 \sigma$. This confirms clearly the interpretation. From the table one can conclude that the distance modulus of Virgo is $\mu=31.4\pm0.2$. However, it is difficult to give a mean radial velocity because of the strong perturbation of the velocity field. Amazingly, it is better to measure radial velocities out of the center to obtain a good mean velocity of a cluster. If one adopts the velocity of 980 km s-1 (see the discussion in Teerikorpi et al. 1992), and both the LG-infall velocity and the Hubble constant found in this paper, the distance modulus of the Virgo cluster is $\mu=31.3$. This gives a coherent system of parameters.

We can also discuss the region perpendicular to the direction of Virgo (region II). The weighted mean Hubble constant in this region is nearly the same as the one found in region III (i.e., $\log H=1.827\pm0.007$). In the direction of the Fornax cluster one can repeat what we have done in the direction of Virgo, but the number of galaxies is smaller. The center of Fornax is assumed to be $\rm RA(2000)=03h42m$ and $\rm DEC(2000)=-36 \ \deg$. In Table 4 we summarize the results. It appear that galaxies PGC 12390 and PGC 10330 can be considered as backside galaxies falling onto Fornax towards us (small radial velocity, large distance, small apparent Hubble constant). Galaxies PGC 13255 and PGC 13602 are roughly at the position of Fornax, while PGC13179 and PGC 13059 are in front of Fornax (large radial velocity, small distance and large apparent Hubble constant). From the table one can conclude that the distance modulus of Fornax is $\mu=31.7\pm0.3$. It is not possible to measure how the infall velocity changes with the distance to the center of Fornax. Nevertheless, if one still adopt $\gamma =1.9$one can determine the parameter C for Fornax. Indeed, the observed infall velocity is roughly 270 km s-1 at a distance of 6 Mpc of the center. This leads to $C_{\rm Fornax}=1350$.


 

 
Table 4: Detail of the central region of Fornax. Note that the angular separation $\Theta $ is counted with respect to the direction of the Fornax center.
PGC $V_{\rm vir}$ $\mu$ $\Theta $ H
0012390 767 $31.98 \pm0.19$ 14.5 31
0010330 1249 $32.73 \pm0.33$ 14.4 36
0013255 1279 $31.92 \pm0.17$ 11.1 53
0013602 1299 $31.51 \pm0.05$ 6.0 65
0013179 1423 $30.96 \pm0.13$ 2.1 91
0013059 1670 $31.31 \pm0.11$ 3.4 91
Mean   $31.74 \pm0.25$    


6 Conclusion

The main conclusions are the following:

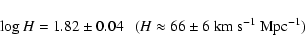
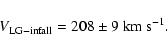
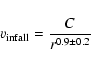
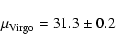
The next step will be an application of this model to nearby clusters. The purpose is to test quantitatively the amplitude of the distortion on the apparent galaxy distribution induced by infalls.

Acknowledgements
We thank the anonymous referee and P. Fouqué for their remarks. T.E. acknowledges the support by the Academy of Finland (the projects "Galaxy Streams and Structures in the nearby Universe'' and "Cosmology in the local to the deep galaxy universe'').

Appendix A: Calculation of the envelope of the Spaenhauer diagram

We consider the population of sosie galaxies for a calibrator of absolute magnitude M0. The distribution function of its population Nis assumed to be Gaussian $\mathcal{G}(M_{\rm o},\sigma)$; The probability for a galaxy of this population, to have an absolute magnitude Mi, with Mi<M' is given by:
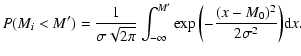$\displaystyle P(M_{i}<M')=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{M'}\exp{\left(-\frac{(x-M_{0})^2}{2{\sigma}^2}\right)} {\rm d}x.$      


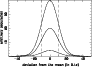  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms9954fA1.eps}}\end{figure} Figure A.1: Several Gaussian functions with the same standard deviation $\sigma $and different populations N. The actual range n x around the mean depends on the population.

The difficulty is illustrated in Fig. A.1. With the same standard deviation, the number of points beyond a given limit $r\sigma$ increases with the population N. Our goal is to take into account this fact to calculate the equation of the curve enveloping the points of the Spaenhauer diagram.

Let us write the probability of having a galaxy with $M_{i}>M_{0}+r\sigma$. We will consider only this case but obviously, there is a similar case on the other side of the Gaussian distribution.

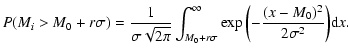$\displaystyle P(M_{i}>M_{0}+r\sigma)=\frac{1}{\sigma\sqrt{2\pi}}\int_{M_{0}+r\sigma}^{\infty}\exp{\left(-\frac{(x-M_{0})^2}{2{\sigma}^2}\right)}{\rm d}x.$      

It is useful to take the centered variable u=x-M0:
 
$\displaystyle P(M_{i}-M_{0}> r\sigma)=\frac{1}{\sigma\sqrt{2\pi}}\int_{r\sigma}^{\infty}\exp{\left(-\frac{u^2}{2{\sigma}^2}\right)}{\rm d}u$     (A.1)

For a population of N observed galaxies, the probability for one of them to be at $r\sigma$ from M0 is:
 
$\displaystyle P\left(\bigcup_{i=1}^N{[M_{i}-M_{0} > r\sigma]}\right)$ = $\displaystyle N.P(M_{i}-M_{0} > r\sigma)$ (A.2)

because events are independent and have the same probability.

The criterion defining the upper limit of the points in the Spaenhauer diagram is simply:

$\displaystyle P\left(\bigcup_{i=1}^N{[M_{i}-M_{0} > r\sigma]}\right) < \epsilon$      

where $\epsilon$ is an arbitrary probability level.

Then, using Eqs. (A.1) and (A.2), we obtain:

 \begin{displaymath}\frac{N}{\sigma\sqrt{2\pi}}\int_{r\sigma}^{\infty}\exp{\left(-\frac{u^2}{2{\sigma}^2}\right)}{\rm d}u < \epsilon. \end{displaymath} (A.3)

With $v=u / \sigma\sqrt{2}$, the envelope equation becomes:
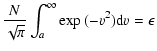$\displaystyle \frac{N}{\sqrt{\pi}}\int_{a}^{\infty}\exp{(-v^2)}{\rm d}v = \epsilon$      

where $a={r}/{\sqrt{2}}$. After integration, we obtain:

 \begin{displaymath}\frac{N}{2}\left[1-erf\left(\frac{r}{\sqrt{2}}\right)\right] = \epsilon \end{displaymath} (A.4)

i.e.,

 \begin{displaymath}\log~N = -\log ({\rm erfc}(\frac{r}{\sqrt{2}}) + \log (2\epsilon). \end{displaymath} (A.5)


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms9954fA2.eps}}\end{figure} Figure A.2: Representation of Eq. (A.5) for an arbitrary probability level $\epsilon = 0.05$. The curve (solid line) is the true equation. The dashed line represents our linear representation for a population between about 10 and 3000 galaxies.

Figure A.2 shows the shape of the curve and the linear representation we adopted over the population range 10 to 3000. With $\epsilon = 0.05$, this linear representation is:

$\displaystyle \log~N=1.55r-3.08.$      

In fact, with a normalization procedure, we need only the slope which does not depend on $\epsilon$. The number of galaxies observed up to a distance d is:
$\displaystyle N= \frac{4}{3}\pi \rho d^{\alpha}$      

where $\rho$ is the space density of the considered galaxies and $\alpha$ is the fractal dimension describing the distribution of galaxies ($\alpha= 3$ in the case of homogeneous distribution). Using the Hubble law (d=V/H), we obtain:
$\displaystyle \log~N ={\alpha }\log V + {\rm constant}(H,\rho).$      

Hence, the points of the envelop must fulfil simultaneously:
$\displaystyle \vert M-M_{0}\vert = r\sigma$      


$\displaystyle \log~N=1.55r+b(\epsilon)$      


$\displaystyle \log~N={\alpha} \log v+b'(H,\rho)$      

where b depends on $\epsilon$ only and b' depends on $\rho$, H.

The equation of the envelop obtained is then:

 \begin{displaymath}\vert M-M_{0}\vert = \frac{\alpha\sigma}{1.55} \log V + k. \end{displaymath} (A.6)

The constant k depends on the values of $\rho$, H. We can find k (normalization) if we know a point of the curve. This is done (see the main text) by imposing that the intersection of the completeness curve with the envelope has an abscissa V0.05.

References

 
Copyright ESO 2002