In the present paper a statistical analysis of the intensity distribution and the vertical flow structure of quiet solar granulation has been carried out. The results show a good agreement between the broad band intensity structure and the vertical flow velocities. The latter show almost no variation within the probed photospheric height range. The intensity fluctuations depend much more on the photospheric height than the velocities. Only the very largest granules produce a positive intensity excess at a height of 320 km whereas smaller structures dissolve at much lower photospheric heights which is - partially - in good agreement with former results of e.g. Komm et al. (1991). In this latter study it has also been found that small scale velocity fluctuations dissolve at much lower photospheric heights than larger ones. These findings are not supported by the results obtained from the present data.
An image segmentation algorithm has been applied to separate granular and intergranular regions. The fractional granular area is about 47.7% which is much larger than that found by Roudier & Muller (1987) but much smaller than the fractional granular area found in Bovelet & Wiehr (2001). In the analyzed data the fractional area brighter than the mean photospheric brightness is 47% (broad band images) and the fractional area belonging to upward directed granular velocities (at i=50%) amounts to 49% of the total area which is in good agreement with the segmented granular area.
The segmented granular structures have quite complex shapes containing a rich internal structure. In small granules the maximum intensities and the maximum upward velocities are located close to the granular barycenters whereas in large granules the brightest parts and the maximum upward velocities are shifted towards the granular boundaries. This is in good agreement with findings of Nesis et al. (1992) and with numerical models of Rast (1995). However, Nesis et al. (1993) have found high intensities but zero or even downward directed velocities at the granular boundaries. They surmise that enhanced turbulence appears at the granular boundaries which produces the low correlation values, found by them, between intensities and velocities at the granular boundaries.
The maximum horizontal intensity and velocity gradients coincide - as expected - well with the granular boundaries. Moreover, the data exhibit a clear and nearly linear dependence of the maximum gradients on the maximum intensities and velocities, respectively. It can be concluded from this result that the widths of the transition zones between granules and intergranular lanes are independent of the intensity and the size of the granules. This conclusion can also be drawn when studying the gradient images (e.g. the one in Fig. 1) and the same conclusion holds for granular velocities.
According to numerical simulations of Rast (1995, 1999a) the
intergranular lanes are formed by the development of localized
downflowing plumes due to Rayleigh-Taylor instabilities. These
plumes cause a displacement of matter away from the downflow
channels which produce intensity and velocity maxima just at
the boundaries of solar granules. The amplitude of the intensity
and velocity excesses at the granular boundaries are, therefore,
"...locally in response to buoyancy and pressure gradient
forces induced by the downflowing fluid...'' (Rast 1995). Hence,
a close connection between both brightness and velocities of granules
and intensity and velocity gradients has to be expected. The constant
width of the transition zone between granules and intergranular lanes
- which is in the range of about
![]() - needs also an
explanation. One possibility is that it is produced by lateral heat
exchange due to radiative effects. Another possibility is the
generation of a turbulent layer due to shear forces in the region
where the sign of the vertical flow velocity is changing (see Stein
& Nordlund 1998).
- needs also an
explanation. One possibility is that it is produced by lateral heat
exchange due to radiative effects. Another possibility is the
generation of a turbulent layer due to shear forces in the region
where the sign of the vertical flow velocity is changing (see Stein
& Nordlund 1998).
The temporal coherence analysis shows that the dependence of the
lifetime of granules on structural size obeys a power law with an
exponent of
![]() with high significance. Many attempts
for estimating granular lifetimes can be found in the literature
(see e.g. Mehltretter 1978; Kawaguchi 1980; Dialetis et al. 1986;
Title et al. 1989; Müller et al. 2001). The published mean values
are in the range from t=5 min up to t=16 min although the
lifetimes of individual features spread between t<1 min (see e.g.
Hirzberger et al. 1999) for the smallest structures up to t>40 min
(cf. e.g. Müller et al. 2001). The e-folding times estimated from
the present data fit into these values although the maximum of
with high significance. Many attempts
for estimating granular lifetimes can be found in the literature
(see e.g. Mehltretter 1978; Kawaguchi 1980; Dialetis et al. 1986;
Title et al. 1989; Müller et al. 2001). The published mean values
are in the range from t=5 min up to t=16 min although the
lifetimes of individual features spread between t<1 min (see e.g.
Hirzberger et al. 1999) for the smallest structures up to t>40 min
(cf. e.g. Müller et al. 2001). The e-folding times estimated from
the present data fit into these values although the maximum of
![]() min lies in the lower range of the published values. However,
lifetimes estimated using cross-correlation methods are generally
lower than those estimated from a tracking of individual granules
(cf. Muller 1999; Alissandrakis et al. 1987).
min lies in the lower range of the published values. However,
lifetimes estimated using cross-correlation methods are generally
lower than those estimated from a tracking of individual granules
(cf. Muller 1999; Alissandrakis et al. 1987).
Hirzberger et al. (1999) have measured granular lifetimes by
tracking individual granules and have found a linear relation
between granular areas and lifetimes (for granules with
![]() ). Kawaguchi (1980) has found a linear
relation between size and lifetimes only for granules which
end their "lives'' dissolving into the background.
The discrepancy with the present results might come from the effect
that the coherence drops to very low values when the size of granules
is significantly changing in time whereas a tracking algorithm - at
least the one applied by Hirzberger et al. (1999) - is robust
against temporal variations of granular sizes.
). Kawaguchi (1980) has found a linear
relation between size and lifetimes only for granules which
end their "lives'' dissolving into the background.
The discrepancy with the present results might come from the effect
that the coherence drops to very low values when the size of granules
is significantly changing in time whereas a tracking algorithm - at
least the one applied by Hirzberger et al. (1999) - is robust
against temporal variations of granular sizes.
If one assumes that solar granulation is a manifestation of
turbulent gas motions in the solar atmosphere the lifetimes
of granules should obey the Kolmogorov-Oboukhov theory for
isotropic turbulence (Kolmogorov 1941; Oboukhov 1941).
According to this theory a characteristic local time scale,
![]() ,
of the energy cascade can be written as
,
of the energy cascade can be written as
![]() where E(k) denotes
the turbulent energy spectrum depending on the wavenumber k.
If it is assumed that
where E(k) denotes
the turbulent energy spectrum depending on the wavenumber k.
If it is assumed that
![]() it follows that
it follows that
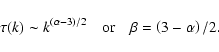 |
(10) |
Another possibility solving the contradictions between the different scaling laws might be that solar granulation is not an ergodic regime. The ergodic theorem is not yet proven for the Navier-Stokes equations (see Lesieur 1997). Therefore, the scaling laws of power spectra (spatial statistics) and that of the coherence spectra (temporal statistics) might be intrinsically incommensurable.
Acknowledgements
The author is grateful to Prof. F. Kneer and to an anonymous referee for fruitful comments on the manuscript. The Vacuum Tower Telescope is operated by the Kiepenheuer-Institut für Sonnenphysik in Freiburg (Germany) in the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias in Tenerife. Financial support by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (Erwin-Schrödinger-Rückkehrprogramm No. R11) is gratefully acknowledged. The author thanks the Universitäts-Sternwarte Göttingen for the hospitality and the financial support.
Copyright ESO 2002