A&A 392, 791-793 (2002)
DOI: 10.1051/0004-6361:20020808

A further study of the BATSE Gamma-Ray Burst duration distribution

I. Horváth[*]

Dept. of Physics, Bolyai Military University, Budapest, POB 12, 1456, Hungary

Received 21 March 2002 / Accepted 27 May 2002

Abstract
Two classes of gamma-ray bursts have been identified so far, characterized by durations shorter and longer than about 2 s. In 1998 two independent papers indicated the existence of the third class of the bursts with duration between approximately 2 and 10 s. In this paper, using the full BATSE Catalog, the maximum likelihood estimation is presented, which gives a 0.5% probability for having only two subclasses. A Monte-Carlo simulation also confirms this probability.

Key words: gamma rays: bursts, theory, observations - methods: data analysis, observational, statistical


1 Introduction

In the BATSE Current Catalog (Meegan et al. 2001) there are 2702 Gamma-Ray Bursts (GRBs), of which 2041 have duration information. Kouveliotou et al. (1993) have identified two groups of GRBs based on durations, for which the value of T90 (the time during which 90% of the fluence is accumulated) is smaller or larger than 2 s. Each group exhibits an acceptable bimodal log-normal ("two-Gaussian'') fit. This bimodal distribution has been further quantified in another paper (Kouveliotou et al. 1995), where a two-Gaussian fit was made, however the best parameters of the fit were published in McBreen et al. (1994) and Koshut et al. (1996).

Previously we have published an article (Horváth 1998), where both two- and three-Gaussian fits were made using the $\chi^2$ method. The results indicated that the third Gaussian is needed at a 99.98% significance level. This is in agreement with the result of Mukherjee et al. (1998), who used a multivariate analysis and found that the probability of existence of two groups, rather than three, is less than 10-4. Hakkila et al. (2000c) also confirmed this result by statistical clustering analysis. However, they suggested that the third group was caused by instrumental biases (Hakkila et al. 2000a; Hakkila et al. 2000b).

Recently Balastegui et al. (2001) have applied automatic classifier algorithms and obtain three different classes of GRBs. Further, the intermediate subgroup shows a remarkable angular distribution on the sky (Balázs et al. 1998; Balázs et al. 1999; Mészáros et al. 2000; Litvin et al. 2001).

Although the high probabilities for the presence of the third (intermediate in duration) subgroup are suggestive, the existence of this subgroup is a matter of debate. Hence additional studies concerning this subclass are highly desireable. In order to make further progress in quantifying this classification, one of the issues which needs to be addressed is an evaluation of the probabilities associated with the bimodal, or - in general - with the multimodal distribution.

In this paper we again examine the trimodal log-normal distribution of T90, finding a new small probability that the third subclass is a chance occurrence.


 \begin{figure} \par\resizebox{\hsize}{!} {\includegraphics[angle=-90,width=8.8cm]{h3563f1.ps}} \end{figure} Figure 1: Duration distribution of the observed BATSE bursts.
Open with DEXTER

In Sect. 2 bi and a tri-modal log-normal fits made using the maximum likelihood method are discussed. In Sect. 3 one hundred Monte-Carlo simulations are shown to confirm the low probability. In Sect. 4 a systematic triggering effect is discussed. The conclusions are given in Sect. 5.

2 Fits in log $T_\mathsf{90}$

For this investigation we have used a smaller set of 1929 burst durations from the Current Catalog, because only they have peak flux information as well. We use the T90 measures provided in the catalog. Figure 1 shows the distribution of $\log T_{90}$.


  
Table 1: Two Gaussian fit of the GRB duration distribution.
\begin{table} \begin{displaymath} \begin{array}{cccc} \hline\hline \noalign{\... ...$ ) standard deviation ($\sigma$ ) and weight ($w$ ) of the groups. \end{table}

A fit to the duration distribution was made using a maximum likelihood method with the superposition of two log-normal distributions. This can be done by a standard search for 5 parameters with N=1929 measured points (cf. Press et al. 1992; Chapt. 15). Both log-normal distributions have two parameters; the fifth parameter defines the weight (w1) of the first log-normal distribution. The second weight is w2=(1-w1) due to the normalization. Therefore we obtain the best fit to the 5 parameters through a maximum likelihood estimation (e.g., Kendall & Stuart 1976).

We search for the maximum of the formula

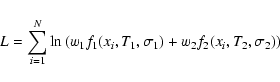\begin{displaymath}L = \sum_{i=1}^{N} \ln \left( w_1 f_1(x_i,T_{1},\sigma_{1}) + w_2 f_2(x_i,T_{2},\sigma_{2} ) \right) \end{displaymath} (1)

where

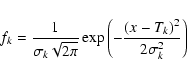\begin{displaymath}f_k = \frac{1}{ \sigma_k \sqrt{2 \pi }} \exp\left( - \frac{(x-T_k)^2}{2\sigma_k^2} \right) \end{displaymath} (2)

where Tk is the mean in log T90 and $\sigma $ is the standard deviation. This fit gives us the best parameters of the two-Gaussian fit (Table 1), which are very similar to previously published values (Horváth 1998).

Secondly, a three-Gaussian fit was made combining three fk functions with eight parameters (three means, three standard deviations and two weights). For the best fitted parameters see Table 2. The best logarithm of the likelihood (L3) is 12 326.25 (Kendall & Stuart 1976). For two Gaussians the maximum of the likelihood was L2=12 320.11. According to the mathematical theory, twice the difference of these numbers follows the $\chi^2$ distribution with three degrees of freedom because the new fit has three more parameters

 \begin{displaymath}2 ( L_{3} - L_{2}) \simeq \chi^2_{3}, \end{displaymath} (3)

The difference is 6.14 which gives us a 0.5% probability. Therefore the three-Gaussian fit is better and there is a 0.005 probability that it is caused by statistical fluctuation.


  
Table 2: Three Gaussian fit of the GRB duration distribution.
\begin{table} \begin{displaymath} \begin{array}{cccc} \hline\hline \noalign{\... ...$ ) standard deviation ($\sigma$ ) and weight ($w$ ) of the groups. \end{table}

3 Monte-Carlo simulation

One can check this 0.005 probability using a Monte-Carlo (MC) simulation and adopting the following procedure. Take the two-Gaussian distribution with the best fitted parameters of the observed data, and generate 1929 numbers for T90whose distribution follows the two-Gaussian distribution. Then find the best likelihood with five free parameters (two means, two dispersions and two weights; but the sum of the last two must be 1929). Secondly make a fit with the three-Gaussian distribution (eight free parameters, three means, dispersions and weights). Finally, take a difference between the two logarithms of the maximum likelihood, which gives one number.

After this procedure is repeated 99 more times, we have a hundred MC simulated numbers. Only one of these numbers is bigger than the value obtained from the BATSE data (6.14). The distribution of these differences are given in Fig. 2. Therefore the MC simulations confirm the likelihood result and gives us a similar probability (1%) that the third group is a statistical fluctuation.


 \begin{figure} \par\resizebox{\hsize}{!} {\includegraphics[angle=-90,width=8.8cm]{h3563f2.ps}} \end{figure} Figure 2: Distribution of the MC simulated L3-L2. L3 is a likelihood with the three-Gaussian function and L2 is a likelihood with the two-Gaussian function.
Open with DEXTER

Also the population of the third group generated by MC simulations is far from the GRB third group population which is 6% (see Table 2). The average of the fluctuation population is 2.5% and only one of the hundred numbers is bigger than 6%.

4 Systematics

In this section the possibility that the third intermediate subgroup is an instrumental effect is discussed. The BATSE on-board software tests for the existence of bursts by comparing the count rates to the threshold levels for three separate time intervals: 64 ms, 256 ms, and 1024 ms. The efficiency changes for shorter bursts because the 1024 ms trigger is becoming less sensitive as burst durations fall below about one second. This means that at the "intermediate" timescale a large systematic deviation is possible. To reduce the systematic effects of the trigger in this region we truncated the dataset to include only GRBs that would have triggered BATSE on the 64 ms timescale.

Using the Current BATSE catalog CmaxCmin table (Meegan et al. 2001) we choose the GRBs, with numbers larger than one in the second column (64 ms scale maximum counts divided by the threshold count rate). This process reduced the burst numbers very much, and unfortunately just 958 bursts satisfied the above condition.

We repeated the maximum likelihood test with these burst durations. The computed probability is still below 1%. Therefore after eliminating some systematic effects, the third group is still statistically significant.

5 Conclusions

1.
It is possible that the fit using three log-normal functions is accidental, and that there are only two types of GRBs. However, if the T90 distribution of these two types of GRBs is log-normal, then the probability that the third group of GRBs is an accidental fluctuation is less than 0.5%.

2.
Therefore, the statistics indicate that the third component is present. However, the physical existence of the third group is still argueable. The sky distribution of the third component is anisotropic as proven by Balázs et al. (1998), Balázs et al. (1999), Mészáros et al. (2000), Litvin et al. (2001). The $\log N{-}\log S$ distribution may also differ from the other group's distributions (Horváth 1998). Alternatively Hakkila et al. (2000c) believe the third statistically proved subgroup is only a deviation caused by a complicated instrumental effect, which can reduce some faint long burst durations. This paper does not deal with this particular effect, however systematic triggering effects were examined and after that the third group was still statistically significant.

3.
Therefore, this theme should be discussed in future papers to further elucidate the reality and properties of the third class.

Acknowledgements
This research was supported in part through NATO advanced research fellowship 1037/NATO/01, OTKA F029461, OTKA T034549. Useful discussions with L. G. Balázs, J. T. Bonnell, E. Fenimore, J. Hakkila, A. Mészáros, P. Mészáros, are appreciated. The author also thanks B. McBreen, the referee, for useful comments that improved the paper.

References

 

Copyright ESO 2002