A&A 392, 1119-1127 (2002)
DOI: 10.1051/0004-6361:20020993
S. Régnier1,3 - T. Amari2 - E. Kersalé2
1 - Institut d'Astrophysique Spatiale, Unité Mixte
CNRS-Université Paris XI, Bât. 121, 91405 Orsay, France
2 -
Centre de Physique Théorique, École Polytechnique, 91128
Palaiseau, France
3 -
Montana State University, Department of Physics,
Bozeman, MT 59717, USA
Received 16 May 2002 / Accepted 3 July 2002
Abstract
The Active Region 8151 (AR 8151) observed in February 1998 is the site of
an eruptive event associated with a filament and a S-shaped structure,
and producing a slow Coronal Mass Ejection (CME). In order to determine
how the CME occurs, we compute the 3D coronal magnetic field and we
derive some relevant parameters such as the free magnetic energy and the
relative magnetic helicity. The 3D magnetic configuration is
reconstructed from photospheric magnetic magnetograms (IVM, Mees Solar
Observatory) in the case of a non-constant-![]() force-free ( nlff) field model. The reconstruction method is divided into three main
steps: the analysis of vector magnetograms (transverse fields, vertical
density of electric current, ambiguity of 180
force-free ( nlff) field model. The reconstruction method is divided into three main
steps: the analysis of vector magnetograms (transverse fields, vertical
density of electric current, ambiguity of 180![]() ), the numerical
scheme for the nlff magnetic field, the
interpretation of the computed magnetic field with respect to the
observations. For AR 8151, the nlff field matches the coronal
observations from EIT/SOHO and from SXT/Yohkoh. In particular, three
characteristic flux tubes are shown: a highly twisted flux tube, a long
twisted flux tube and a quasi-potential flux tube. The maximum energy
budget is estimated to
), the numerical
scheme for the nlff magnetic field, the
interpretation of the computed magnetic field with respect to the
observations. For AR 8151, the nlff field matches the coronal
observations from EIT/SOHO and from SXT/Yohkoh. In particular, three
characteristic flux tubes are shown: a highly twisted flux tube, a long
twisted flux tube and a quasi-potential flux tube. The maximum energy
budget is estimated to
![]() erg and the relative magnetic
helicity to
erg and the relative magnetic
helicity to
![]() G2 cm4. From the simple photospheric
magnetic distribution and the evidence of highly twisted flux tubes, we
argue that the flux rope model is the most likely to describe the
initiation mechanism of the eruptive event associated with AR 8151.
G2 cm4. From the simple photospheric
magnetic distribution and the evidence of highly twisted flux tubes, we
argue that the flux rope model is the most likely to describe the
initiation mechanism of the eruptive event associated with AR 8151.
Key words: Sun: corona - Sun: magnetic fields - Sun: coronal mass ejections (CMEs)
In the solar atmosphere, eruptive events as flares, coronal mass ejections
(CMEs) and filament eruptions are frequently observed. To understand the
origin of these phenomena, it is important to know what are the structures
involved in those events (e.g. filaments, sigmoids) and what is the
evolution in time before the eruption (e.g. energy storage, emergence of
flux). As the solar corona is dominated by the magnetic field (i.e., a low
![]() plasma), the knowledge of the coronal magnetic field configuration
will be able to answer these questions. Unfortunately measurements of
the magnetic field in the corona are not yet easily performed in spite of
the recent works using the Hanle effect (Raouafi 2000), EUV and radio
measurements (e.g. Brosius et al. 1992) or Zeeman splitting from infrared lines
(Lin et al. 2000). Therefore methods to determine the topology and the geometry of the
coronal magnetic field have been developed: the determination of the geometry of
active region loops (height, inclination, radius, width) applying a dynamical
stereoscopy method to coronal EUV observations (Aschwanden et al. 1999a, 1999b,
2000), the reconstruction of the coronal magnetic field using
photospheric measurements as boundary condition (see reviews by Sakurai 1989;
Amari & Démoulin 1992).
plasma), the knowledge of the coronal magnetic field configuration
will be able to answer these questions. Unfortunately measurements of
the magnetic field in the corona are not yet easily performed in spite of
the recent works using the Hanle effect (Raouafi 2000), EUV and radio
measurements (e.g. Brosius et al. 1992) or Zeeman splitting from infrared lines
(Lin et al. 2000). Therefore methods to determine the topology and the geometry of the
coronal magnetic field have been developed: the determination of the geometry of
active region loops (height, inclination, radius, width) applying a dynamical
stereoscopy method to coronal EUV observations (Aschwanden et al. 1999a, 1999b,
2000), the reconstruction of the coronal magnetic field using
photospheric measurements as boundary condition (see reviews by Sakurai 1989;
Amari & Démoulin 1992).
The latter method, the so-called reconstruction problem (Amari et al. 1997;
McClymont et al. 1997 and reference therein),
consists of solving the magnetohydrostatic equations with appropriated boundary
conditions. As the solar corona is considered as a low ![]() plasma (e.g. Priest 1984), the magnetohydrostatic equilibria can be reduced to three
different equilibium states (Sakurai 1989): the current-free field, the
constant-
plasma (e.g. Priest 1984), the magnetohydrostatic equilibria can be reduced to three
different equilibium states (Sakurai 1989): the current-free field, the
constant-![]() force-free (lff) field and the non-constant-
force-free (lff) field and the non-constant-![]() force-free (nlff)
field. The potential field (no electric current within the magnetic
configurations) and the lff field (the
electric current proportional to the magnetic field) have been well studied (see review by Sakurai 1989). Using either the longitudinal or the vertical component
of the photospheric magnetic field as boundary condition, these
methods have been compared to chromospheric and coronal observations (e.g. Mandrini et al. 1997) for active regions with a slow evolution and a relatively simple
topology. To determine the 3D magnetic configuration of active regions with a
complex topology, the nlff field which
takes into account the existence of localized electric currents is more
suitable (Démoulin et al. 1997). Due to the intrinsic nonlinearity of the nlff
field equations, the reconstruction methods are essentially computational
methods. A variety of computational methods has been developed for which the
main differences are the numerical schemes (Amari et al. 1997) and the boundary
conditions imposed at the photospheric level (Amari & Démoulin 1992; Démoulin et al. 1997). In the present paper, we apply the vector potential Grad-Rubin-like method
(Amari et al. 1997; Amari et al. 1999)
using the vertical component of the magnetic field, Bz, and the vertical
component of the electric current density, Jz, for a given magnetic polarity
(Bz> 0 or Bz< 0) as the boundary condition at the photospheric level
(Sakurai 1981). These
two vertical components are provided by vector magnetograms.
force-free (nlff)
field. The potential field (no electric current within the magnetic
configurations) and the lff field (the
electric current proportional to the magnetic field) have been well studied (see review by Sakurai 1989). Using either the longitudinal or the vertical component
of the photospheric magnetic field as boundary condition, these
methods have been compared to chromospheric and coronal observations (e.g. Mandrini et al. 1997) for active regions with a slow evolution and a relatively simple
topology. To determine the 3D magnetic configuration of active regions with a
complex topology, the nlff field which
takes into account the existence of localized electric currents is more
suitable (Démoulin et al. 1997). Due to the intrinsic nonlinearity of the nlff
field equations, the reconstruction methods are essentially computational
methods. A variety of computational methods has been developed for which the
main differences are the numerical schemes (Amari et al. 1997) and the boundary
conditions imposed at the photospheric level (Amari & Démoulin 1992; Démoulin et al. 1997). In the present paper, we apply the vector potential Grad-Rubin-like method
(Amari et al. 1997; Amari et al. 1999)
using the vertical component of the magnetic field, Bz, and the vertical
component of the electric current density, Jz, for a given magnetic polarity
(Bz> 0 or Bz< 0) as the boundary condition at the photospheric level
(Sakurai 1981). These
two vertical components are provided by vector magnetograms.
The paper is organized as follows. In Sect. 2, we describe the characteristic
features of the Active Region 8151 (AR 8151) which have motivated its choice
for this study. In Sect. 3, we detail the vector magnetic field
observations from IVM (Imaging Vector Magnetogram, Mees Solar Observatory,
Hawaii). In particular, we analyse the vertical current density Jz and the
distribution of ![]() on the photosphere. The vector potential
Grad-Rubin-like method is described in Sect. 4. The photospheric boundary
condition
determined in Sect. 3 is used to compute the 3D nlff magnetic
field (Sect. 5). We focus on three characteristic flux tubes which are
compared to coronal EUV and soft X-ray observations. In Sect. 6, we discuss
the implications of the computed nlff magnetic configuration in the CME mechanisms.
on the photosphere. The vector potential
Grad-Rubin-like method is described in Sect. 4. The photospheric boundary
condition
determined in Sect. 3 is used to compute the 3D nlff magnetic
field (Sect. 5). We focus on three characteristic flux tubes which are
compared to coronal EUV and soft X-ray observations. In Sect. 6, we discuss
the implications of the computed nlff magnetic configuration in the CME mechanisms.
In most eruptive events (flares, filament eruptions or CMEs), the observed active regions have characteristic magnetic features which take an active or inactive part in the phenomena. Two features are commonly associated with eruptive events: filaments-prominences and/or sigmoids. Using LASCO/SOHO and EIT/SOHO data, Subramanian and Dere (2001) have shown that 44% of the 32 studied CMEs are related to filament eruptions occuring in active regions. From X-ray images (SXT/Yohkoh), Canfield et al. (2000) have deduced that the existence of a sigmoid (S-shaped or reverse S-shaped structure) in active regions is a precursor of eruptive events. These two structures are observed in AR 8151. In addition AR 8151 has a relatively simple distribution of the photospheric magnetic field as we show in the following description.
AR 8151 was observed on February 5-14, 1998 during Carrington Rotation 1932.
AR 8151 is located in the South hemisphere with an average latitude of
24![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_1.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg15.gif) |
Figure 1:
Photospheric distribution of the line-of-sight magnetic field obtained
by MDI/SOHO on February 11, 1998 at 17:36 UT. Black (white) pixels are negative
(positive) values of the magnetic flux. The spatial resolution is 2
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_2.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg16.gif) |
Figure 2:
H |
| Open with DEXTER | |
The line-of-sight photospheric magnetic field is provided by MDI/SOHO
(Michelson Doppler Imager, Scherrer et al. 1995). As magnetograph, MDI measures the
Zeeman splitting of the NiI line at 6767.8 Å. Figure 1 shows the
distribution of the photospheric field of AR 8151 observed on February 11, 1998
at 17:36 UT with a
![]() field-of-view (extracted
from the 96 min full-disk image). The spatial resolution is 2
field-of-view (extracted
from the 96 min full-disk image). The spatial resolution is 2
![]() .
AR 8151
has a near-bipolar magnetic distribution with a leading negative sunspot
(black) and a diffuse positive polarity (white). The length between the two
opposite polarities is estimated to
.
AR 8151
has a near-bipolar magnetic distribution with a leading negative sunspot
(black) and a diffuse positive polarity (white). The length between the two
opposite polarities is estimated to
![]() .
Here it is important to note
that most reconstructed active regions had a more compact and intense
magnetic field (e.g. McClymont & Mikic 1994). This feature will be developed in Sect. 3.
.
Here it is important to note
that most reconstructed active regions had a more compact and intense
magnetic field (e.g. McClymont & Mikic 1994). This feature will be developed in Sect. 3.
At the chromospheric and the low corona level, the structure of AR 8151 can be
described by the H![]() image from the Paris-Meudon Observatory on
February 11, 1998 at 08:58 UT (see Fig. 2). The spatial resolution
is
image from the Paris-Meudon Observatory on
February 11, 1998 at 08:58 UT (see Fig. 2). The spatial resolution
is
![]() .
A filament (dark feature) is clearly observed in AR 8151. This
elongated structure (core length of 90
.
A filament (dark feature) is clearly observed in AR 8151. This
elongated structure (core length of 90
![]() )
is aligned with the inversion
line of the line-of-sight magnetic field (Fig. 1). The width of the
filament is estimated to be 10
)
is aligned with the inversion
line of the line-of-sight magnetic field (Fig. 1). The width of the
filament is estimated to be 10
![]() .
.
A system of coronal loops (Fig. 3) is observed in the corona by
EIT/SOHO (EUV Imaging Telescope, Delaboudinière et al. 1995) in the 195 Å FeXII line on
February 11, 1998 at 08:51 UT. The system connects the two opposite main
polarities (Fig. 1). The spatial resolution is 5.2
![]() with the
same
with the
same
![]() field-of-view.
field-of-view.
The soft X-ray image of AR 8151 (Fig. 4) is provided by SXT/Yohkoh
(Soft X-ray Telescope, Tsuneta et al. 1991). The spatial resolution is 2.5
![]() .
Again, the field-of-view is
.
Again, the field-of-view is
![]() .
One observes a sigmoid
connecting the two polarities of AR 8151. The core of the sigmoid is aligned
with the inversion line of the line-of-sight magnetic field (see Fig. 1). The forward S-shaped structure is in agreement with the chirality
rules defined by Canfield & Pevtsov (1999): in the South (resp. North) hemisphere, sigmoids
have preferencially (
.
One observes a sigmoid
connecting the two polarities of AR 8151. The core of the sigmoid is aligned
with the inversion line of the line-of-sight magnetic field (see Fig. 1). The forward S-shaped structure is in agreement with the chirality
rules defined by Canfield & Pevtsov (1999): in the South (resp. North) hemisphere, sigmoids
have preferencially (![]() 2/3) S-shaped (resp. inverse S-shaped)
configurations.
2/3) S-shaped (resp. inverse S-shaped)
configurations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_3.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg20.gif) |
Figure 3:
EUV coronal observation from EIT/SOHO in the FeXII line at 195 Å on
February 11, 1998 at 08:51 UT. A system of coronal loops is observed connecting
the opposite polarities of AR 8151. The spatial resolution is 2.8
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_4.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg21.gif) |
Figure 4:
Soft X-ray image from SXT/Yohkoh on February 11, 1998 at 09:19 UT
(negative image). A sigmoid is observed as dark feature. The central part of
the sigmoid is aligned with the inversion line of the line-of-sight magnetic
field (see Fig. 1). The spatial resolution is 2.5
|
| Open with DEXTER | |
A slow CME was both observed by EIT/SOHO and LASCO/SOHO
(Régnier et al. 1999a,b). The CME was observed on February 12, 1998 at 13:51 UT with a velocity in the plane of sky estimated to 280 km s-1(![]() 20 km s-1). If we assume that the development of the CME is radial,
the estimated velocity of the CME is less than 540 km s-1. A time series of
EIT images at 195 Å was recorded during the eruptive event with a temporal
spacing of 15 min. No EIT flare is observed before or after the CME. The
magnetic evolution of AR 8151 does not reveal magnetic changes such as flux
emergence.
20 km s-1). If we assume that the development of the CME is radial,
the estimated velocity of the CME is less than 540 km s-1. A time series of
EIT images at 195 Å was recorded during the eruptive event with a temporal
spacing of 15 min. No EIT flare is observed before or after the CME. The
magnetic evolution of AR 8151 does not reveal magnetic changes such as flux
emergence.
For all those features, AR 8151 is a good candidate for our study of the existing relation between magnetic structures (filaments, sigmoids) and eruptive events (CMEs, prominence eruptions, flares).
In this section, we describe the vector magnetic field of AR 8151 and
we especially focus on the measurements of transverse magnetic fields and on
calculations of the current density and
![]() on the
photosphere.
on the
photosphere.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{regnier2700_5a.eps}\hspace...
...space*{0.5cm}
\includegraphics[width=5.5cm,clip]{regnier2700_5c.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg24.gif) |
Figure 5: The three components of the magnetic field deduced from the IVM data in heliographic coordinates: Bx (left), By (center), Bz (right). The black box on the Bz image is the area selected for the calculations. |
| Open with DEXTER | |
IVM (Imaging Vector Magnetograph, Mees solar Observatory, Hawaii, Mickey et al. 1996)
measures the four Stokes parameters (I, U, Q, V) for the 6302.5 Å FeI line on
February 11, 1998 at 17:36 UT.
To obtain the vector magnetic field from the Stokes parameters, the raw data
are first corrected for the instrumental and the Earth's atmosphere systematic
effects (see Labonte et al. 1999). The magnetic field parameters (strength, polar and
azimuthal angles) are inferred from Stokes profiles using the "weak-field''
approximation (Jefferies et al. 1989; Jefferies & Mickey 1991). This approximation is valid up to a magnetic splitting of 1.5 times the Doppler width of the observed line
(Jefferies & Mickey 1991). For the 6302.5 Å FeI line, the maximum magnetic splitting
corresponds to a magnetic field strength of about 1500 G (Mickey et al. 1996).
The three magnetic components are
![]() the line-of-sight component,
the line-of-sight component,
![]() and
and
![]() the two transverse components in the plane
perpendicular to the line-of-sight. The
equations allowing the inversion of Stokes parameters introduce a
180
the two transverse components in the plane
perpendicular to the line-of-sight. The
equations allowing the inversion of Stokes parameters introduce a
180![]() -ambiguity on the azimuthal component
-ambiguity on the azimuthal component
![]() which can be resolved
using the method detailed in Canfield et al. (1993):
which can be resolved
using the method detailed in Canfield et al. (1993):
| min. value | max. value | mean value | |
|
|
-755 | 885 | 18 |
|
|
-545 | 820 | 28 |
|
|
-1470 | 420 | 28 |
|
|
-30 | 50 | 3 |
|
|
-1 | 1 | see Sect. 3.2 |
If we compare the vertical component of the magnetic field observed by IVM (Fig. 5 right) and MDI (Fig. 1) magnetographs, we note that the IVM field-of-view does not contain some polarities surrounding the main positive and negative polarities. Therefore, we create a composite map (Fig. 6). We extend the IVM field-of-view with MDI data: the line-of-sight magnetic field from MDI is transformed into a vertical component assuming no transverse fields.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_6.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg37.gif) |
Figure 6:
Composite IVM-MDI image for the vertical component of the magnetic
field
|
| Open with DEXTER | |
For the composite image, the magnetic flux through the photospheric surface is
balanced: if we consider a threshold of 50 G on the
![]() component,
the magnetic fluxes for the positive (
component,
the magnetic fluxes for the positive (![]() )
and negative (
)
and negative (![]() )
values are
)
values are
![]() Mx (the magnetic flux
Mx (the magnetic flux
![]() is given by
is given by
![]() where dS is the pixel
surface).
where dS is the pixel
surface).
Knowing the three components of the magnetic field, we deduce the vertical
current density since
![]()
![]() and the distribution of the force-free function since,
and the distribution of the force-free function since,
![]() .
In order to obtain
consistent values for
.
In order to obtain
consistent values for
![]() and for
and for
![]() ,
we must fix
thresholds (see Leka & Skumanich 1999) on the vertical magnetic field component
(
,
we must fix
thresholds (see Leka & Skumanich 1999) on the vertical magnetic field component
(
![]() 50 G) and on the transverse magnetic field
components (
50 G) and on the transverse magnetic field
components (
![]() 200 G).
200 G).
The distribution of the vertical current density (see Fig. 7)
exhibits strong positive and negative values in the negative magnetic polarity
region (
![]() 30 mA m-2, see Table 1). The
distribution of Jz is quite different from usual concentrated magnetic
field (and electric current density) used to reconstruct the coronal magnetic
field. In Sect. 5, we will see that this kind of real data can give the 3D
coronal magnetic configuration. The values of
30 mA m-2, see Table 1). The
distribution of Jz is quite different from usual concentrated magnetic
field (and electric current density) used to reconstruct the coronal magnetic
field. In Sect. 5, we will see that this kind of real data can give the 3D
coronal magnetic configuration. The values of
![]() range between -1 Mm-1 and 1 Mm-1. The mean value of
range between -1 Mm-1 and 1 Mm-1. The mean value of
![]() for the whole active region is
for the whole active region is ![]() 0.12 Mm-1. This
positive mean value and the South location of AR 8151 are in agreement with the
statistical study on the sign of
0.12 Mm-1. This
positive mean value and the South location of AR 8151 are in agreement with the
statistical study on the sign of
![]() performed by Pevtsov et al. (1995) which
demonstrated that
performed by Pevtsov et al. (1995) which
demonstrated that ![]() 70% of active regions observed in the South have a positive
value of
70% of active regions observed in the South have a positive
value of
![]() (see also Longcope et al. 1998). The mean values of each polarity are 0.18 Mm-1 for
the diffuse positive polarity and 2.18
(see also Longcope et al. 1998). The mean values of each polarity are 0.18 Mm-1 for
the diffuse positive polarity and 2.18 ![]() 10-3 Mm-1 for the negative
polarity. The small mean value of
10-3 Mm-1 for the negative
polarity. The small mean value of
![]() in the negative spot hides
strong positive and negative values.
in the negative spot hides
strong positive and negative values.
The positive and negative values for the distribution of the vertical current density
and of
![]() characterize the existence of return currents
(since
characterize the existence of return currents
(since
![]() )
which would create in almost physical MHD process
(Régnier & Amari 2001).
)
which would create in almost physical MHD process
(Régnier & Amari 2001).
Let us recall the equations governing the nlff magnetic field in the
half-space ![]() above the photosphere
above the photosphere
![]() :
:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_7.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg69.gif) |
Figure 7:
Distribution of the vertical current density
|
| Open with DEXTER | |
A method has been developed by Amari et al. (1997) (see also Amari et al. 1999) using the vector potential representation in order to guarantee Eq. (3):
| (7) |
| (8) |
| (9) |
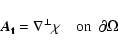 |
(10) |
| (11) |
| (12) |
As mentioned in the preceding Section, the method to reconstruct the 3D
coronal magnetic field uses the vertical component of the magnetic field
Bz (i.e. g in Eq. (6)) and the distribution of
![]() (i.e. h in Eq. (5)) for one polarity on the photosphere as
boundary condition:
(i.e. h in Eq. (5)) for one polarity on the photosphere as
boundary condition:
![]() on
on
![]() (Fig. 6),
(Fig. 6),
![]() on
on
![]() (Fig. 8).
(Fig. 8). ![]() is transported from
is transported from
![]() which corresponds to the sunspot magnetic field. The continuous non-uniform grid takes into account the
photospheric variation of the magnetic flux: the grip steps are shorter where the
magnetic flux is higher.
which corresponds to the sunspot magnetic field. The continuous non-uniform grid takes into account the
photospheric variation of the magnetic flux: the grip steps are shorter where the
magnetic flux is higher.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{regnier2700_8.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg87.gif) |
Figure 8:
Distribution of the force-free function |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{regnier2700_9a.eps}\hspace*{1cm}
\includegraphics[width=7.75cm]{regnier2700_9b.eps}\end{figure}](/articles/aa/full/2002/36/aa2700/Timg88.gif) |
Figure 9: Three characteristic magnetic flux tubes seen from top view (left) and from side view (right). The photospheric positive (resp. negative) polarity is drawn as solid (resp. dashed) contours. Black arrows (left) indicate the direction of the electric current density on each flux tube. The estimated height of flux tubes is indicated on the right image. |
| Open with DEXTER | |
The three components of the magnetic field (Bx, By, Bz) are
computed in a box of
![]() grid steps. These components
satisfy the equations mentioned in the preceding section. To visualize the
magnetic configuration of AR 8151, we plot the magnetic field lines defined as
follows:
grid steps. These components
satisfy the equations mentioned in the preceding section. To visualize the
magnetic configuration of AR 8151, we plot the magnetic field lines defined as
follows:
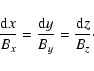 |
(15) |
Note the existence of twisted flux tubes on the magnetic configuration.
Hood & Priest (1981) have demonstrated that a twisted flux tube (assuming cylindrical
geometry and considering the line-tying effect) is stable
when the twist ![]() is less than one turn whatever geometrical parameter
such as length, width and height (see also Baty 2001 for a review of recent
studies of twisted
flux tube kink instability and Amari & Luciani 1999 for 3D MHD disruption of a twisted flux tube). The value of
is less than one turn whatever geometrical parameter
such as length, width and height (see also Baty 2001 for a review of recent
studies of twisted
flux tube kink instability and Amari & Luciani 1999 for 3D MHD disruption of a twisted flux tube). The value of
![]() at which the twisted flux
tube becomes unstable mainly depends on the height and on the width of the flux
tube. For flux tube (1), we estimate
at which the twisted flux
tube becomes unstable mainly depends on the height and on the width of the flux
tube. For flux tube (1), we estimate
![]() or 1.5 turns. For
the nlff configuration of AR 8151, the twisted flux (2) is stable and the
twist of flux tube (1) is close to
or 1.5 turns. For
the nlff configuration of AR 8151, the twisted flux (2) is stable and the
twist of flux tube (1) is close to
![]() (but less than
(but less than
![]() ).
This important point for CME mechanisms is also a main point for the validity
of the computed configuration: the reconstruction method is based on the finding
of an equilibrium state, therefore for twisted flux tubes we
should always satisfy the condition
).
This important point for CME mechanisms is also a main point for the validity
of the computed configuration: the reconstruction method is based on the finding
of an equilibrium state, therefore for twisted flux tubes we
should always satisfy the condition
![]() .
.
We now compare the nlff magnetic field lines to the coronal observations. The three characteristic flux tubes (see Fig. 9) are in good agreement with the coronal observations:
The magnetic energy
![]() is defined by:
is defined by:
For a given photospheric magnetic field, the minimum magnetic energy is
obtained for the potential field (e.g. Aly 1989). The free magnetic energy
of the nlff force-free field has a maximum value
![]() :
:
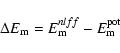 |
(17) |
For AR 8151, the magnetic energy of the potential field (initial state of the
configuration) is:
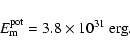 |
(18) |
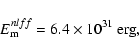 |
(19) |
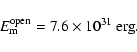 |
(20) |
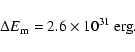 |
(21) |
The magnetic helicity
![]() takes into account the complexity of the magnetic
field topology such as twist or writhe (see review by Berger 1999):
takes into account the complexity of the magnetic
field topology such as twist or writhe (see review by Berger 1999):
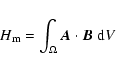 |
(22) |
| (23) |
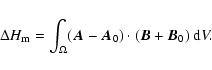 |
(24) |
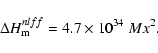 |
(25) |
We have detailed a method to obtain the 3D coronal magnetic field of an active region using photospheric vector magnetograms as boundary conditions. This method comprises into three main steps:
Determining the 3D magnetic configuration at a given time before the eruption affords us the ability to evaluate the validity of the different mechanisms of CME. Most CME mechanisms involve magnetic reconnection in the corona. Three main classes of CMEs are often discussed: the "breakout'' model (Antiochos et al. 1999), the twisted flux rope model (Amari et al. 2000) and the tether-cutting model (Sturrock 1989). For the breakout model, the reconnection of arcades occurs above an active region with a complex topology. The instability of the twisted flux rope creates a current sheet implying reconnection in the corona. The tether-cutting model assumes that a flux rope overlaid by arcades rises in the corona and current sheets are formed below the flux rope. The latter two models do not required complex topology on the photophere. For AR 8151, the distribution of the vertical magnetic field on the photosphere is dipolar (see Fig. 1). The reconstructed 3D magnetic field evidences twisted magnetic flux tubes close to the instability condition (see Sect. 5). Hence, the breakout model seems not to be the scenario of AR 8151's CME. Most probably the destabilization of twisted flux tubes and/or the formation of current sheets under the rising twisted flux tubes can explain the existence of the CME.
As the snapshot of the 3D magnetic configuration is given ![]() 20 hours before
the eruption, we cannot expect that the twisted flux rope model is the unique
mechanism to trigger the CME. To clarify the CME mechanism, we propose to
use a time series of vector magnetic fields in order to follow the evolution of
the nlff field topology before and after eruptive events. This time
evolution will also give information on the storage of magnetic energy and
on the conservation of relative magnetic helicity. As the filament cannot be
directly reconstructed, we extend our method to the finding of magnetic dips
which support filament material (see Régnier 2001). Thermodynamic aspects
of isolated field lines
are currently being investigated. In a further paper, we compare the topological and
geometrical configurations of the current-free, the lff and the nlff
magnetic field configurations and we investigate support and modeling of
prominences in such configurations.
20 hours before
the eruption, we cannot expect that the twisted flux rope model is the unique
mechanism to trigger the CME. To clarify the CME mechanism, we propose to
use a time series of vector magnetic fields in order to follow the evolution of
the nlff field topology before and after eruptive events. This time
evolution will also give information on the storage of magnetic energy and
on the conservation of relative magnetic helicity. As the filament cannot be
directly reconstructed, we extend our method to the finding of magnetic dips
which support filament material (see Régnier 2001). Thermodynamic aspects
of isolated field lines
are currently being investigated. In a further paper, we compare the topological and
geometrical configurations of the current-free, the lff and the nlff
magnetic field configurations and we investigate support and modeling of
prominences in such configurations.
Acknowledgements
We thank D. L. Mickey and B. J. LaBonte for providing IVM data. We are grateful to R. C. Canfield and R. J. Leamon for comments on a previous version of this article. We wish to thank the Centre National d'Études Spatiales (CNES) for its financial support. Data used here from Mees Solar Observatory, University of Hawaii, are produced with the support of NASA grant NAG 5-4941 and NASA contract NAS8-40801. Data processing of SOHO and Yohkoh images was performed using the facilities of the MEDOC archive center (Institut d'Astrophysique Spatiale, Orsay, France).