A&A 392, 1081-1088 (2002)
DOI: 10.1051/0004-6361:20020981
M. Röllig 1 - M. Hegmann - W. H. Kegel
Institut für Theoretische Physik/Astrophysik, Johann Wolfgang Goethe-Universität, Robert-Mayer-Str. 8-10, 60325 Frankfurt a.M., Germany
Received 22 April 2002 / Accepted 27 June 2002
Abstract
We study the formation of CO molecules at the edge of dense molecular clouds. As shown by van Dishoeck & Black 1988 the CO photodissociation process is dominated by line rather than continuous absorption. Hence, a turbulent velocity field, modifying the line shape, strongly affects the CO density distribution. We investigate these effects in detail. To describe the turbulent velocity field we use the statistical approach by G. Traving and collaborators (cf. Gail et al. 1974) which accounts for a finite correlation length for the velocity field. We solve the radiative transfer equation selfconsistently with the rate equations describing the chemical reactions.
One main goal of the investigation is an improvement of molecular cloud models used to analyze observational data. To bring the observational data into agreement with the model of an isothermal spherical cloud being stabilized by turbulent and thermal pressure it turned out to be neccessary to implement a cut off radius for the CO density distribution in order to define a cloud edge (Piehler & Kegel 1995). This radius depends heavily on the intensity and density distribution in the outer parts of the cloud. Our calculations show that turbulence has substantial influence on the penetration of UV radiation into a molecular cloud. Even turbulent velocities in the order of a few thermal velocities are sufficient to allow the radiation to penetrate significantly deeper into the cloud than in a nonturbulent medium. On the other hand correlation length effects may lead to a decrease in photodissociation efficiency. By accounting for a finite correlation length of the stochastic velocity field the self-shielding of CO absorption bands is considerably enhanced and CO molecules can effectively form in depths that have a much stronger UV intensity in standard radiative transfer models.
Key words: radiative transfer - turbulence - ISM: clouds - ISM: molecules - ultraviolet: ISM - line: formation
Shielded from far ultraviolet (FUV) radiation, the gas inside dense interstellar clouds occurs mainly in molecular form. On the surface of these clouds, FUV photons heavily effect the physical and chemical structure of the interstellar medium (ISM) by means of photoionization and photodissociation processes. One of the keys to understanding these photon-dominated regions (PDRs) lies in understanding the attenuation of the FUV flux through the PDR. Hence, various authors have studied the penetration of FUV radiation into molecular clouds. However, most of the early work was done for homogeneous clouds only (e.g. Roberge et al. 1991). In recent years, it has become increasingly clear that interstellar clouds are inhomogeneous down to the smallest accessible scales (see e.g. Falgarone & Phillips 1996). Authors, which studied the profound influence of this clumpy structure of interstellar clouds on the radiative transfer, are for example Boissé (1990), Hobson & Scheuer (1993), Spaans (1996), and Hegmann & Kegel (1996).
Most of these studies were done for the transport of radiation in the continuum. Hence, the influence of a turbulent velocity field on the radiative transfer was neglected in general. However, a turbulent velocity field becomes important, if, as in the case of CO, photodissociation takes place by line absorption into predissociated bound states rather than by continuous absorption (van Dishoeck & Black 1988). Since, in addition, line absorption by CO dominates over absorption and scattering by dust, the formation rate of CO is strongly subject to velocity fluctuations within the cloud.
The present paper is aimed at studying the effects of a turbulent velocity field on the formation of CO. The spatial variation of the turbulent velocity field is described in a statistical sense only. Following Gail et al. (1974), the variation of the turbulent velocity field along each line of sight is assumed to correspond to a Markov process. This approach accounts for a finite correlation length of the turbulent velocity field.
Our calculations show, that both, the mean square turbulent velocity and the
correlation length, strongly affect the shape and the strength of the CO
absorption lines (see e.g.: Levshakov & Kegel 1994). As a consequence, the CO abundance is modified, too. In
particular it has turned out, that self-shielding of CO is considerably
enhanced by accounting for a finite correlation length ![]() of the turbulent
velocity field. CO can be effectively formed in depths that would have a much
stronger FUV intensity in conventional microturbulent models
of the turbulent
velocity field. CO can be effectively formed in depths that would have a much
stronger FUV intensity in conventional microturbulent models
![]() .
.
We accounted for a small chemical network consisting of 38 different species interacting in 434 reactions. As cloud geometry we assumed a plane parallel semi infinite slab. In this work we present calculations done for a uniform density distribution with constant gas temperature.
Here we give a short summary of our statistical approach only. For a detailed description of the model see Hegmann & Kegel (2000) and Gail et al. (1974) and references therein.
The turbulent velocity field is described in a statistical sense only. We assume the one-point distribution function of the component of the hydrodynamical velocity along the line of sight to be given by a Gaussian
If the density and velocity distribution is known, the propagation of radiation inside a medium along a line of sight s can be calculated by means of the ordinary radiative transfer equation:
| (7) |
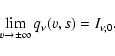 |
(8) |
The photodissociation of CO molecules is known to be dominated by line rather than continuous absorption. In the wavelength range 912 Å ![]()
![]() Å no absorption continuum can be found (Letzelter et al. 1987). Instead, a great number of discrete absorption bands can be seen. It has been shown (Letzelter et al. 1987; Eidelsberg et al. 1991) that the photodissociation of CO occurs through absorption of photons in discrete rotational lines from the ground vibrational state towards excited predissociated Rydberg electronic states. Predissociated means, that these excited states overlap with the dissociative continuum of a lower state. Thus there is a finite probability of a radiationless transition to the lower unbound state. Together with the continuous absorption by dust the overall absorption coefficient can be written as:
Å no absorption continuum can be found (Letzelter et al. 1987). Instead, a great number of discrete absorption bands can be seen. It has been shown (Letzelter et al. 1987; Eidelsberg et al. 1991) that the photodissociation of CO occurs through absorption of photons in discrete rotational lines from the ground vibrational state towards excited predissociated Rydberg electronic states. Predissociated means, that these excited states overlap with the dissociative continuum of a lower state. Thus there is a finite probability of a radiationless transition to the lower unbound state. Together with the continuous absorption by dust the overall absorption coefficient can be written as:
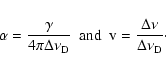 |
(14) |
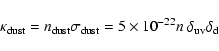 |
(15) |
We assume chemical equilibrium and determine the relative abundances from a chemical network consisting of 38 different species formed and destroyed in 434 reactions (Millar et al. 1995; Le Teuff et al. 2000). All processes forming and destroying a specific species i are described in the rate equations:
Hydrogen plays a key role in both parts of our model:
Firstly, ![]() is a very strong absorber for UV photons penetrating the cloud and due to its broad absorption lines is very effective in shielding deeper parts from photodestruction. This affects the CO absorption spectrum as well. There is a significant number of CO absorption bands that are at least partially overlapped by broad hydrogen absorption lines. In order to save computing time, we considered all CO absorption bands overlapping with hydrogen lines to be completely shielded. This is the case for the bands: 7D, 9A, 13, 14, 15A, 15B, 19, 24, 31, 33, 38 (we applied the identification scheme and spectroscopic parameters from Warin et al. 1996).
is a very strong absorber for UV photons penetrating the cloud and due to its broad absorption lines is very effective in shielding deeper parts from photodestruction. This affects the CO absorption spectrum as well. There is a significant number of CO absorption bands that are at least partially overlapped by broad hydrogen absorption lines. In order to save computing time, we considered all CO absorption bands overlapping with hydrogen lines to be completely shielded. This is the case for the bands: 7D, 9A, 13, 14, 15A, 15B, 19, 24, 31, 33, 38 (we applied the identification scheme and spectroscopic parameters from Warin et al. 1996).
Secondly, it is an important part for the chemical evolution of the cloud. The formation of ![]() takes place on the surface of interstellar dust grains:
takes place on the surface of interstellar dust grains:
| (17) |
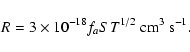 |
(18) |
![\begin{displaymath}S=[1+0.04(T+T_{\rm dust})^{1/2}+2\times 10^{-3}T+8\times 10^{-6}T^2]^{-1},
\end{displaymath}](/articles/aa/full/2002/36/aa2607/img85.gif) |
(19) |
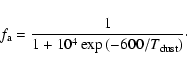 |
(20) |
To account for the photodissociation properties of ![]() we took the hydrogen shielding factors
we took the hydrogen shielding factors
![]() given by Lee et al. (1996):
given by Lee et al. (1996):
| (21) |
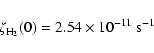 |
(22) |
In the present context we are mainly interested in the photodissociation of CO which we treat in considerable detail. In contrast to this, we model the photodissociation of ![]() only crudely using shielding factors (Lee et al. 1996). This appears justifiable since photodissociation of
only crudely using shielding factors (Lee et al. 1996). This appears justifiable since photodissociation of ![]() is important only in a rather shallow layer (
is important only in a rather shallow layer (
![]() cm-2). This implies that in most of the volume we are considering, hydrogen is found almost completely in the form of
cm-2). This implies that in most of the volume we are considering, hydrogen is found almost completely in the form of ![]() .
Furthermore, in greater depths the
.
Furthermore, in greater depths the ![]() lines are dominated by their damping wings and therefore are almost independent of the details of the velocity field.
lines are dominated by their damping wings and therefore are almost independent of the details of the velocity field.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2607f1.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg92.gif) |
Figure 1:
Depth dependence of |
| Open with DEXTER | |
The photodissociation is subject to different shielding effects (van Dishoeck & Black 1988):
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2607f2.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg96.gif) |
Figure 2:
Photodissociation rate coefficients of the broad bands
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{MS2607f3.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg97.gif) |
Figure 3:
Expectation values of the photodissociation rate coefficients |
| Open with DEXTER | |
The non-local coupling of the radiation field and the molecular abundances over the whole cloud is one of the main characteristics of our model. It is neccessary to simultaneously solve the radiative transfer Eq. (6) with the rate equation for all points in physical space and velocity space. We use the finite differences method of Cranck-Nicolson to solve the generalized radiative transfer equation together with numerical routines using a modified Powell Hybrid method to solve the system of rate equations. This is done in an iterative way: starting with a density distribution for all species the resulting radiation field is computed. Using the new radiation field we recalculated the densities. Then the next iteration step starts. In order to save computing time not all absorption bands are calculated by means of the generalized radiative transfer equation. Absorption bands with small radiative lifetimes are showing the strongest overlap of individual absorption lines. Radiative lifetimes in the order of
![]() s correspond to natural line widths of 2-20 km s-1 compared to turbulent velocities of a few km s-1. These broad absorption bands would hardly respond to turbulent variations of their individual components. It is therefore a reasonable simplification to compute these bands in the microturbulent approximation. We divided the set of CO absorption bands in two groups:
s correspond to natural line widths of 2-20 km s-1 compared to turbulent velocities of a few km s-1. These broad absorption bands would hardly respond to turbulent variations of their individual components. It is therefore a reasonable simplification to compute these bands in the microturbulent approximation. We divided the set of CO absorption bands in two groups:
We assume a simple plane-parallel geometry with uniform density
![]() cm-3 and temperature T=15, 50, 75 Kelvin. For the elemental abundances we adopted the values H:He:C:O = 1:0.1:3.
cm-3 and temperature T=15, 50, 75 Kelvin. For the elemental abundances we adopted the values H:He:C:O = 1:0.1:3.
![]() :8.
:8.
![]() .
The parameters of turbulence are varied between
.
The parameters of turbulence are varied between
![]() and
and
![]() cm. The incident UV field is taken from Mezger et al. (1982) and is approximated by
cm. The incident UV field is taken from Mezger et al. (1982) and is approximated by
![]() erg cm-2 s-2
erg cm-2 s-2 ![]() m-1 with
m-1 with
![]() Å.
Å.
In order to study the principal physical effects, and in order to save computing time we first investigated the influence of turbulence by modeling the absorption spectrum by one single line (compare with one line approximation by Spaans 1996). The resulting photodissociation rate coefficient was scaled to a rate coefficient at the cloud edge of ![]()
![]() s-1 in order to receive reasonable results from the chemical density calculations. Afterwards we accounted for the full absorption spectrum as described before and did calculations for a variety of different model parameters.
s-1 in order to receive reasonable results from the chemical density calculations. Afterwards we accounted for the full absorption spectrum as described before and did calculations for a variety of different model parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2607f4.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg115.gif) |
Figure 4:
Curves of growth for the single line approximation for different correlation legths and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{MS2607f5.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg116.gif) |
Figure 5:
Expectation values of photodissociation rate coefficients |
| Open with DEXTER | |
In Fig. 4, curves of growth for different correlation lengths and a turbulent velocity of
![]() for n=1000 cm-3 and T=15 K are shown. At high correlation lengths the line center becomes optically thick at much smaller CO column densities than is the case for smaller correlation length (compare e.g. Albrecht & Kegel). In Figs. 3c and d the corresponding expectation values of the photodissociation rate coefficients
for n=1000 cm-3 and T=15 K are shown. At high correlation lengths the line center becomes optically thick at much smaller CO column densities than is the case for smaller correlation length (compare e.g. Albrecht & Kegel). In Figs. 3c and d the corresponding expectation values of the photodissociation rate coefficients ![]() (top) and the corresponding relative CO abundance
(top) and the corresponding relative CO abundance
![]() (bottom) for the same models are shown. The penetration depth for photons decreases with increasing correlation length. The sharp bend in the curves for higher correlation lengths corresponds to the turning points in the curves of growth. In Figs. 3a and b,
(bottom) for the same models are shown. The penetration depth for photons decreases with increasing correlation length. The sharp bend in the curves for higher correlation lengths corresponds to the turning points in the curves of growth. In Figs. 3a and b, ![]() and
and
![]() are plotted for a fixed (rather low) value of the correlation length and a set of different
are plotted for a fixed (rather low) value of the correlation length and a set of different ![]() .
Higher
.
Higher ![]() increase the photodissociation probability at a given cloud depth due to the stronger Doppler shift in different volume elements along the line of sight. Both effects, the influence of the correlation length
increase the photodissociation probability at a given cloud depth due to the stronger Doppler shift in different volume elements along the line of sight. Both effects, the influence of the correlation length ![]() and of the mean turbulent velocity
and of the mean turbulent velocity ![]() ,
are well understood in principle but the quantitative influence is surprising, even in our crude model.
,
are well understood in principle but the quantitative influence is surprising, even in our crude model.
In the next step we accounted for a full absorption spectrum and did calculations for different model parameters. We determined the unshielded total photodissociation probability at the edge of the cloud. In contrast to earlier values of around
![]() s-1 (e.g. van Dishoeck & Black 1988) we find a value of
s-1 (e.g. van Dishoeck & Black 1988) we find a value of
![]() s-1 which is comparable to results from Lee et al. (1996).
s-1 which is comparable to results from Lee et al. (1996).
Figure 5 shows the depth dependent expectation values for the photodissociation probability and the relative CO density for calculations with the full line spectrum. We adopted a temperature of 15 K, n=2000 cm-3, and
![]() .
As expected, the influence of a finite correlation length on the depth dependency is smaller than in the case of a single line absorption spectrum. The photodissociation now depends on a wide range of absorption bands that differently contribute to the total photodissociation probability at different cloud depths. Hence, the depth dependency is less strong than for a single absorption line. Nevertheless the influence is far from being negligible. Figure 6 shows the influence of mesoturbulence on the expectation value of the relative CO density for two different values of
.
As expected, the influence of a finite correlation length on the depth dependency is smaller than in the case of a single line absorption spectrum. The photodissociation now depends on a wide range of absorption bands that differently contribute to the total photodissociation probability at different cloud depths. Hence, the depth dependency is less strong than for a single absorption line. Nevertheless the influence is far from being negligible. Figure 6 shows the influence of mesoturbulence on the expectation value of the relative CO density for two different values of ![]() .
The depth at which the CO density saturates is strongly dependent on the turbulence. For different correlations lengths and turbulent velocities the depth at which the CO density is no more influenced by the incident UV field differs by a factor of two. In the interpretation of observational data this difference may lead to an error in the estimation of the spatial cloud radius of up to 100%.
.
The depth at which the CO density saturates is strongly dependent on the turbulence. For different correlations lengths and turbulent velocities the depth at which the CO density is no more influenced by the incident UV field differs by a factor of two. In the interpretation of observational data this difference may lead to an error in the estimation of the spatial cloud radius of up to 100%.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2607f6.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg118.gif) |
Figure 6: Maximum model variations for the expected relative CO density due to mesoturbulent photodissociation of CO. The density is n=2000 cm-3, T=15 K. |
| Open with DEXTER | |
In order to compare the results of our calculations with commonly used methods, we plotted the expectation value of the photodissociation probability as well as the results from standard parametrized shielding factors as given by van Dishoeck & Black (1988) or Lee et al. (1996). Figure 7 shows this comparison for two different cloud models. The strong lines are results of our calculations and the thin lines are calculated from shielding factors. The difference in our results for different densities are due to the nonlinear coupling of the chemical rate equations with the radiative transfer and the varying ratio of correlation length to the mean free path of photons.
We discussed the formation of CO molecules in interstellar molecular clouds under the influence of a UV radiation field. In particular we investigated the influence of a stochastic velocity distribution with finite correlation lengths on the photodissociation properties of CO molecules forming in interstellar clouds. At first the principle effects were studied by modeling the absorption spectrum by only one single line. The results show a strong dependency of the CO stratification on the turbulent velocity field in the cloud. In a second approach we accounted for the full UV absorption spectrum of CO. It turned out that the depth dependent properties of CO photodissociation and forming are affected. The results can be summarized as follows: a higher mean turbulent velocity of the stochastic velocity distribution along the line of sight leads to an increasing penetration depth of UV photons and therefore to a stronger photodissociation on CO molecules. On the other hand correlation length effects can lead to a decreasing photodissociation rate coefficient. By accounting for a finite correlation length of the mesoturbulent velocity field, the shielding of CO absorption bands is considerably enhanced and CO molecules can effectively form in depths that have a much stronger UV intensity in standard radiative transfer models. The depth dependent behavior of the photodissociation rate coefficient obtained from standard CO shielding factors show a large deviation from our results. This leads to significant differences in the interpretation of observational data. Therefore it may be neccessary to correct physical parameters of interstellar clouds derived by standard non-turbulent analysis.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2607f7.eps}\end{figure}](/articles/aa/full/2002/36/aa2607/Timg119.gif) |
Figure 7:
Comparison of mesoturbulent calculations with standard shielding factors for two different cloud models. The unshielded photodissociation probability at the cloud edge is the same for both models (
|
| Open with DEXTER | |
Acknowledgements
This work was supported in part by the FAZIT Stiftung, Frankfurt a.M., Germany.