The X-ray observing logs for both clusters are given in
Table 7. For both ROSAT/HRI images we have used
![]() /pixel binning of the event list in order to reduce the noise
as much as possible without losing information on the cluster
extension. The raw photon images were then filtered using wavelet
analysis with Poisson noise modeling (Starck & Pierre 1998) at
10-4 (
/pixel binning of the event list in order to reduce the noise
as much as possible without losing information on the cluster
extension. The raw photon images were then filtered using wavelet
analysis with Poisson noise modeling (Starck & Pierre 1998) at
10-4 (![]()
![]() )
significance level for the wavelet
coefficients.
)
significance level for the wavelet
coefficients.
| Date | Object | RA Dec | Airmass | MOS | Exposure |
| (J2000) | masks/slits | (s) | |||
| 1993 Mar. 29 | Abell 1451 | 12:03:15 -21:31:36 | 1.2 | 1/15 | 900 |
| 1993 Mar. 29 | RXJ1314-25 | 13:14:29 -25:16:25 | 1.1 | 1/15 | 2 |
| 1999 Apr. 19/20 | Abell 1451E | 12:03:12 -21:33:25 | 1.34 | 2/20+21 | 3 |
| 1999 Apr. 19/20 | Abell 1451W | 12:03:23 -21:33:25 | 1.40 | 2/21+19 | 2 |
| 1999 Apr. 19/20 | RXJ1314-25N | 13:14:22 -25:14:55 | 1.06 | 2/17+18 | 2 |
| 1999 Apr. 19/20 | RXJ1314-25S | 13:14:22 -25:17:55 | 1.04 | 2/17+18 | 4 |
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{MS2550f3.eps} \end{figure}](/articles/aa/full/2002/36/aa2550/Timg41.gif) |
Figure 3: RXJ1314-25: I-band image from the Danish 1.5-m telescope showing the objects in the spectroscopic study. Numbers correspond to the object identifications in Table 4; those marked with diamonds denote either stars or non-cluster members. Note that we have not plotted galaxy #20 because it is not resolved spatially from galaxy #19. |
The X-ray contours are shown overlaid on optical images and radio observations (see Sect. 4) in Fig. 7 for Abell 1451 and in Fig. 8 for RXJ1314-25.
| Characteristic | Value |
| N = 57 | |
| Bi-weighted location:
|
|
| Bi-weighted scale:
|
1330+130-90 km s-1 |
| Maximum gap | 564 km s-1 |
The X-ray image in Fig. 7 shows a very strong point source
![]()
![]() south of the cluster centre which coincides
with a QSO at z=1.17 (object #32 in Table 3). The cluster
emission is regular, with the inner contours slightly twisted but no
sign of substructure. The X-ray emission peaks at RA =
south of the cluster centre which coincides
with a QSO at z=1.17 (object #32 in Table 3). The cluster
emission is regular, with the inner contours slightly twisted but no
sign of substructure. The X-ray emission peaks at RA =
![]() and Dec =
and Dec =
![]() ,
which is
,
which is
![]() (150 kpc) north of the brightest cluster galaxy (#34 in
Table 3) and
(150 kpc) north of the brightest cluster galaxy (#34 in
Table 3) and
![]() west of the second brightest galaxy
(#39), and
west of the second brightest galaxy
(#39), and ![]()
![]() from the catalogued cluster
position (Abell et al. 1989).
from the catalogued cluster
position (Abell et al. 1989).
The cluster X-ray emission is quite irregular, showing two central
peaks and a SE-NW elongation. Unfortunately, there is an X-ray
emitting star projected in front of the cluster (object #29 in
Table 4) only ![]()
![]() from the adopted X-ray centre.
The strong point source SE of the cluster centre is a Sy1 galaxy
(object #47 in Table 4) and a cluster member. There is no
indication of substructure in the X-ray emission associated with the
eastern group or the brightest cluster galaxy (see Fig. 6).
from the adopted X-ray centre.
The strong point source SE of the cluster centre is a Sy1 galaxy
(object #47 in Table 4) and a cluster member. There is no
indication of substructure in the X-ray emission associated with the
eastern group or the brightest cluster galaxy (see Fig. 6).
To estimate the basic physical cluster parameters we model the X-ray
surface brightness using the isothermal ![]() -model (King
1962; Cavaliere & Fusco-Femiano 1976)
-model (King
1962; Cavaliere & Fusco-Femiano 1976)
To derive the count-rate in the [0.1-2.4] keV ROSAT/HRI band we
integrate the fitted surface brightness profile analytically,
excluding the background. The integration is usually carried out to a
given radius
![]() ,
where the surface brightness profile
reaches the detection limit; for both clusters we put
,
where the surface brightness profile
reaches the detection limit; for both clusters we put
![]() .
For the overall count rate C we have
.
For the overall count rate C we have
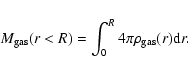 |
(4) |
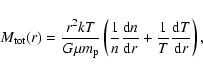 |
(5) |
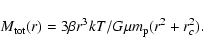 |
(6) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{MS2550f4.eps} \end{figure}](/articles/aa/full/2002/36/aa2550/Timg66.gif) |
Figure 4:
Abell 1451: redshift histogram for cluster members; the bin size is 0.0019.
The bi-weighted location (
|
| Characteristic | Value |
| Total, N = 37 | |
|
|
|
|
|
1100+140-90 km s-1 |
| Maximum gap | 523 km s-1 |
| Group 1 (East), N = 15 | |
|
|
|
|
|
590+110-150 km s-1 |
| Maximum gap | 516 km s-1 |
| Group 2 (West), N = 22 | |
|
|
|
|
|
560+120-70 km s-1 |
| Maximum gap | 523 km s-1 |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{MS2550f5.eps} \end{figure}](/articles/aa/full/2002/36/aa2550/Timg70.gif) |
Figure 5:
RXJ1314-25: redshift histogram for cluster members; the bin size is 0.0015.
The
|
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{MS2550f6.eps} \end{figure}](/articles/aa/full/2002/36/aa2550/Timg71.gif) |
Figure 6: RXJ1314-25: sky distribution for cluster members. Open circles denote the members of the eastern group, while the filled circles are those belonging to the western group as assigned by KMM (see Table 6). The contours are the adaptive kernel density estimate (Silverman 1986; Pisani 1996) of the SuperCOSMOS galaxy distribution. The asterisk and filled triangle mark the positions of the first- and second-ranked BCGs respectively (#48 and #19 in Table 4). Note that galaxy #20 is too close to galaxy #19 to be plotted separately. |
| Cluster | Date | Exposure (s) |
| Abell 1451 | 1997 Jul. 14-16 | 25 603 |
| RXJ1314-25 | 1996 Jan. 27-31 | 29 294 |
Derived cluster masses should be considered with caution, as the combined X-ray/optical analysis tends to indicate that neither cluster has reached equilibrium.
Although the X-ray emission in both clusters is not centrally peaked,
we have tried to estimate the cooling flow radius - the zone where
the time for isobaric cooling is less than the age of the universe
(Sarazin 1986; Fabian 1994). For any reasonable choice of
the Hubble constant and gas parameters (
![]() )
there is no
such zone.
)
there is no
such zone.
Copyright ESO 2002