

Up: Physical parameters of the 4U1700-37
Subsections
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2500f7.ps}\end{figure}](/articles/aa/full/2002/36/aa2500/Timg107.gif) |
Figure 7:
Mass distribution for neutron stars and black holes (after
Charles 1998). Neutron star masses are from Ash et al. (1999),
Barziv et al. (2001), van Kerkwijk et al. (1995) and Thorsett &
Chakrabarty (1999). Black hole masses provided by Charles
(priv. comm.). Error bars for systems other than 4U1700-37
are 1 sigma errors; see Sect. 3 for a discussion of the errors
associated with the mass of 4U1700-37 but note that the
probability of
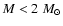 is less than 3.5 per cent, and no
trials results in
is less than 3.5 per cent, and no
trials results in
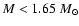 . . |
At present mass determinations exist for 36 compact objects, of which
21 are neutron stars and the remainder black hole candidates (Fig. 7).
Thorsett & Chakrabarthy (1999) found that the masses of
neutron stars are clustered in a remarkably narrow range (mean of
1.35 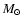 and a standard deviation of
0.04
and a standard deviation of
0.04 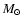 ). However, recent analysis of Vela X-1 by
Barziv et al. (2001) suggests that the pulsar has a mass of
1.87
+0.23-0.17
). However, recent analysis of Vela X-1 by
Barziv et al. (2001) suggests that the pulsar has a mass of
1.87
+0.23-0.17 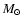
![[*]](/icons/foot_motif.gif) ,
while Orosz & Kuulkers (1999) find a mass of
,
while Orosz & Kuulkers (1999) find a mass of
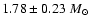 for Cygnus X-2 (however Titarchuk
& Shaposhnikov 2002 have recently proposed
for Cygnus X-2 (however Titarchuk
& Shaposhnikov 2002 have recently proposed
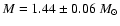 on the basis of Type-I X-ray bursts).
on the basis of Type-I X-ray bursts).
Based on assumptions about the origin of kilohertz quasi-periodic oscillations
Zhang et al. (1997) suggest that several LMXBs may also
contain massive (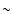 2
2 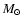 )
neutron stars, resulting from the
accretion of substantial amounts of material over long (108 yrs)
periods of time. However their putative descendants, radio pulsar+white
dwarf binaries, provide no evidence for massive neutron stars (Barziv et al. 2001). The same is true for the Be/X-ray binaries, which
have evolved from lower mass systems than the OB-supergiant HMXBs.
Only in the latter systems evidence has been found for massive neutron
stars and black hole candidates.
)
neutron stars, resulting from the
accretion of substantial amounts of material over long (108 yrs)
periods of time. However their putative descendants, radio pulsar+white
dwarf binaries, provide no evidence for massive neutron stars (Barziv et al. 2001). The same is true for the Be/X-ray binaries, which
have evolved from lower mass systems than the OB-supergiant HMXBs.
Only in the latter systems evidence has been found for massive neutron
stars and black hole candidates.
Masses for a number of black hole candidates have also been
determined; lower limits to their masses comfortably exceed
3 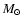 .
Indeed several objects appear to have masses
.
Indeed several objects appear to have masses
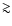 10
10 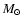 (e.g.
(e.g.
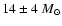 for
GRS 1915+105; Greiner et al. 2001),
with most typically
for
GRS 1915+105; Greiner et al. 2001),
with most typically 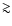 6
6 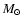 .
At present the binary system
with the lowest mass candidate black hole is Nova Vel
(
.
At present the binary system
with the lowest mass candidate black hole is Nova Vel
(
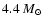 ;
Fillipenko et al. 1999).
;
Fillipenko et al. 1999).
Given that the mass of the compact object in 4U1700-37 lies
outside the present observational range for both neutron stars and
candidate black holes, is it possible to increase/decrease the mass of
the compact object such that it is consistent with either type of
object? For the case of a circular orbit we find no solutions
consistent with
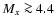
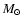 .
Very eccentric orbital
solutions do allow values of Mx in this range although we note
there is no physical motivation for them. Such solutions imply values
of
.
Very eccentric orbital
solutions do allow values of Mx in this range although we note
there is no physical motivation for them. Such solutions imply values
of 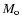 greatly in excess of 100
greatly in excess of 100 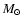 ,
well above current
evolutionary predictions for the mass of an O6.5 Iaf+ star. Stars
with masses in excess of 100
,
well above current
evolutionary predictions for the mass of an O6.5 Iaf+ star. Stars
with masses in excess of 100 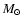 are instead expected to
evolve to H depleted WR stars via a H rich pseudo-WNL phase
where their powerful stellar winds mimic the spectra of more
(chemically) evolved stars of lower masses.
are instead expected to
evolve to H depleted WR stars via a H rich pseudo-WNL phase
where their powerful stellar winds mimic the spectra of more
(chemically) evolved stars of lower masses.
Such a large mass would also be inconsistent with the constraints
imposed by the surface gravity (Sect. 2.2) and the relationship
between stellar mass and the terminal wind velocity. Finally the
result would imply that even very massive stars (given that the
initial mass of the SN progenitor had to be significantly in excess of
the present mass of HD 153919) leave relatively low mass
remnants post supernova, presenting significant problems for the
origin of heavy (>10 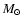 )
black holes such as
e.g. Cyg X-1. Therefore we conclude that Mx appears to be
inconsistent with the range of masses of known black hole
candidates.
)
black holes such as
e.g. Cyg X-1. Therefore we conclude that Mx appears to be
inconsistent with the range of masses of known black hole
candidates.
Given the stringent lower limits derived in Sect. 3 it also appears
difficult to bring the mass of the compact object into line with the
range of masses found by Thorsett & Chakrabarthy (1999).
Inspection of the evolutionary tracks in Fig. 6 suggest that stars
with initial masses of the order of 60 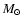 initially evolve
redwards before returning bluewards after undergoing significant mass
loss, most likely during an LBV phase. While we note that the
behaviour of stars in this short lived phase is very uncertain it is
unlikely that we could be observing HD 153919 after such an
excursion, since we would expect significant chemical enrichment - the
H rich mantle having been lost - which is not observed. Likewise, the
mass constraint imposed by the determination of the surface gravity
also appears to exclude this scenario.
initially evolve
redwards before returning bluewards after undergoing significant mass
loss, most likely during an LBV phase. While we note that the
behaviour of stars in this short lived phase is very uncertain it is
unlikely that we could be observing HD 153919 after such an
excursion, since we would expect significant chemical enrichment - the
H rich mantle having been lost - which is not observed. Likewise, the
mass constraint imposed by the determination of the surface gravity
also appears to exclude this scenario.
Furthermore, such a low value for 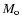 and Mx would reintroduce
the problem of HD 153919 being undermassive for its spectral
type by a factor
and Mx would reintroduce
the problem of HD 153919 being undermassive for its spectral
type by a factor 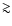 2. While the primaries in some HMXB systems are
found to be undermassive (e.g. Cen X-3 and LMC X-4;
Kaper 2001) this is attributed to mass loss via RLOF - wind
fed systems do not show this effect (Kaper 2001). Given that
4U1700-37 is currently a wind fed system and is yet to evolve
into a RLOF system this could not explain such a mass discrepancy.
Indeed, given the evolutionary constraints imposed by the present
orbital period it is likely that no significant mass transfer has
occured onto HD 153919 during its lifetime, and it will have
evolved as if it were an isolated star.
2. While the primaries in some HMXB systems are
found to be undermassive (e.g. Cen X-3 and LMC X-4;
Kaper 2001) this is attributed to mass loss via RLOF - wind
fed systems do not show this effect (Kaper 2001). Given that
4U1700-37 is currently a wind fed system and is yet to evolve
into a RLOF system this could not explain such a mass discrepancy.
Indeed, given the evolutionary constraints imposed by the present
orbital period it is likely that no significant mass transfer has
occured onto HD 153919 during its lifetime, and it will have
evolved as if it were an isolated star.
If we accept
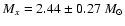 - as implied by the
simulations - the nature of the compact companion remains
uncertain. Conflicting claims as to the nature of the object have been
made on the basis of the X-ray spectrum of 4U1700-37
(Sect. 1). While we cannot discriminate between the twin possibilities
of massive neutron star or low mass black hole from our present
measurements we note that consideration of the masses of both
components of the binary appear to exclude the possibility that stars
with masses of
- as implied by the
simulations - the nature of the compact companion remains
uncertain. Conflicting claims as to the nature of the object have been
made on the basis of the X-ray spectrum of 4U1700-37
(Sect. 1). While we cannot discriminate between the twin possibilities
of massive neutron star or low mass black hole from our present
measurements we note that consideration of the masses of both
components of the binary appear to exclude the possibility that stars
with masses of 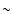 60
60 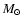 can produce 5-10
can produce 5-10 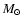 black
holes via case A or B evolution.
black
holes via case A or B evolution.
If the compact object in 4U1700-37 is a black hole it
confirms Brown et al.'s prediction of the existence of "low mass black
holes'' (based on their "soft'' equation of state, Brown et al. 1996), while if the object is a neutron star the high mass
would severely constrain the equation of state of matter at
supra-nuclear densities.
The relationship between the mass of a neutron star and its central
density is calculated by integration of the Tolman-Oppenheimer-Volkoff
(TOV) equation (Oppenheimer & Volkoff 1939) which is
the relativistic expression for hydrostatic equilibrium. In order to
perform the integration it is neccesary to understand the equation of
state of the degenerate nuclear matter in the star.
Because of their non-perturbative nature, strong interactions between
nuclei are extremely difficult to calculate even under normal conditions.
However, there are several models of the internuclear potential in the
literature which have achieved much success in modelling nuclei e.g.
Stoks et al. (1994), Wiringa et al. (1995) and
Machleidt et al. (1996). One of the most successful
and up to date of these models has been applied to the neutron star
equation of state by Akmal et al. (1998) yielding a maximum
mass of between 2.2 and 2.4 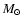 for a neutron star made completely
of normal nuclear matter.
for a neutron star made completely
of normal nuclear matter.
There is also the possibility of a QCD phase transition occuring in
the centre of the neutron star. The large chemical potential has a
similar effect to a large temperature on the QCD coupling constant.
Consequently the interquark coupling can be reduced to the point where
deconfinement occurs and nuclei dissolve into quark matter. The
presence of quark matter has the effect of softening the equation of
state which leads to a lower possible maximum mass for the neutron
star. The energy scale at which deconfinement occurs can be
parameterised by the QCD bag constant B, a phenomenological
parameter representing the difference in energy density between the
vacua of hadronic and quark matter (
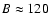 -200 MeV fm-3).
Inclusion of a phase transition to such a mixed state reduces the
maximum mass of the neutron star to
-200 MeV fm-3).
Inclusion of a phase transition to such a mixed state reduces the
maximum mass of the neutron star to 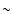 2
2 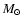 for B=200MeV fm-3 and
for B=200MeV fm-3 and 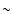 1.9
1.9 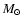 for B=122 MeV fm-3(Akmal et al. 1998)
for B=122 MeV fm-3(Akmal et al. 1998)![[*]](/icons/foot_motif.gif) .
.
If the neutron is rotating rapidly, the TOV equation ceases to be a
valid approximation and one must drop the assumption of spherical
symmetry in the metric. The effect of the rotation will increase the
allowed mass of the neutron star as one might expect, but it is shown
(Heiselberg & Hjorth-Jensen 1999) that even with
rotation one cannot obtain a neutron star with a mass much higher than
those listed above without using an equation of state so stiff that
the sound speed in the neutron-star interior becomes superluminal.
To summarize this subsection, state of the art models for nuclear
equations of state which include the effects of three nucleon
interactions marginally allow the existence of a 2.4 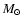 neutron star. However, the existence of such a star would place
severe constraints upon the onset of new physics at high hadronic
densities.
For instance, in the model where a quark matter core is
expected to develop, the bag constant B would have to be
considerably larger than 200 MeV fm-3 in order for such a star
to be viable.
neutron star. However, the existence of such a star would place
severe constraints upon the onset of new physics at high hadronic
densities.
For instance, in the model where a quark matter core is
expected to develop, the bag constant B would have to be
considerably larger than 200 MeV fm-3 in order for such a star
to be viable.


Up: Physical parameters of the 4U1700-37
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2500f7.ps}\end{figure}](/articles/aa/full/2002/36/aa2500/Timg107.gif)