

Up: Asteroid (216) Kleopatra
Subsections
3.1 Occultations
Two successful occultations of Kleopatra have been reported by a few observers
(Dunham 1981,1992). In Fig. 1 the predicted shape of Kleopatra
based on the radar model is plotted against the chords of the 1980 and 1991
occultations. The plots in Fig. 1 are given in the plane of the occultation,
i.e. the plane perpendicular to the direction of the occulted star as seen from the
asteroid. If no error were present in the predicted position of the star and the
asteroid, the images would be centered in the graph origin. Thus the error of the
predicted occultation path is of the order of 100 km in 1991. Error bars on the
occultation chords, as derived from a timing error of 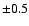 s for visual
observations, are of the order of 15 km; for photoelectric observations they
reduce to
s for visual
observations, are of the order of 15 km; for photoelectric observations they
reduce to 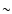 3 km.
One isolated point, not constraining a chord length and in clear disagreement with
nearby chords has been omitted in the 1980 occultation plot. Also one chord of the
1991 event, probably affected by a strong dating error of the emersion point, has
been removed from the plot. Negative observations (i.e. observations for which no
occultation was detected) are indicated by dashed lines. They put some limits in
Kleopatra's size and shape during the 1991 event.
The superposition of the model's profile to the observed occultation chords in
Fig. 1, is obtained by a translation of the physical model, along the
abscissa and ordinate axes (X and Y), such that the predicted contour fits most
of the immersion and emersion points. The sub-Earth point longitude was
3 km.
One isolated point, not constraining a chord length and in clear disagreement with
nearby chords has been omitted in the 1980 occultation plot. Also one chord of the
1991 event, probably affected by a strong dating error of the emersion point, has
been removed from the plot. Negative observations (i.e. observations for which no
occultation was detected) are indicated by dashed lines. They put some limits in
Kleopatra's size and shape during the 1991 event.
The superposition of the model's profile to the observed occultation chords in
Fig. 1, is obtained by a translation of the physical model, along the
abscissa and ordinate axes (X and Y), such that the predicted contour fits most
of the immersion and emersion points. The sub-Earth point longitude was
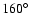 and
and
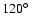 ,
during the 1980 and 1991 occultation, respectively.
Longitudes of
,
during the 1980 and 1991 occultation, respectively.
Longitudes of
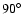 and
and
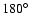 correspond roughly to lightcurve maximum
and minimum, respectively.
correspond roughly to lightcurve maximum
and minimum, respectively.
The topographic model was originally scaled in size to the occultations chords. From
Fig. 1 we infer that Kleopatra's shape model is in general good agreement
with the observed chords. The largest discrepancies are of the order of 30 km, well
within the error bars of the model. Despite the inherent difficulty of obtaining robust
occultation data, it must be noted that the overall size of the contour on its most
elongated direction is well constrained in the 1991 event by a photoelectric chord or
by two independent and consistent chords. Hence, based mainly on the 1991 data, it
cannot be excluded that a more elongated topographic model could provide a better fit
to the measured chords, without drastic change to the 1980 plot.
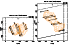 |
Figure 1:
Comparison between the observed occultation data and the radar model.
Left panel: occultation of Oct. 10, 1980 at 7.00 h UTC.
Right panel: occultation of Jan. 1, 1991 at 5.28 h UTC.
The dashed lines correspond to negative observations. Error bars are
given by crosses and are negligible for the photoelectric observations. |
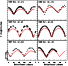 |
Figure 2:
Observed and computed lightcurves for (216) Kleopatra at nearly equatorial
views (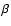 is the SEP latitude).
The curves for the computed values correspond to the radar model
with a Minnaert law (k=0.6, see text).
is the SEP latitude).
The curves for the computed values correspond to the radar model
with a Minnaert law (k=0.6, see text). |
3.2 Lightcurves
Many lightcurves of Kleopatra at different geometries were obtained during the last
decades. Since the rotation period is known with good accuracy, no shift in the position
of the extrema is observed. Figure 2 shows the comparison of the nominal radar
model to the photometric observations acquired at large aspect angle (i.e. close to an
equatorial view), assuming a homogeneous albedo distribution (Hammergren et al. 2000).
Calculation of the global flux depends on the resolution of the topographic
model. The radar model is provided with a resolution in spherical coordinates better
than
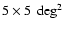 ,
which provides enough internal accuracy for comparison to
typical lightcurves. Synthetic lightcurves are constructed by considering the
size and orientation - with respect to the Earth and the Sun - of the illuminated
and visible elementary surface (the facets for a topographic model). For non-convex
shapes like Kleopatra, one also needs to take into account shadows cast by facets
and hidden facets.
Moreover the computed lightcurves in Fig. 2 were obtained by considering
the moderate limb-darkening effect (Minnaert law with k=0.6) mentioned in
Sect. 2.
,
which provides enough internal accuracy for comparison to
typical lightcurves. Synthetic lightcurves are constructed by considering the
size and orientation - with respect to the Earth and the Sun - of the illuminated
and visible elementary surface (the facets for a topographic model). For non-convex
shapes like Kleopatra, one also needs to take into account shadows cast by facets
and hidden facets.
Moreover the computed lightcurves in Fig. 2 were obtained by considering
the moderate limb-darkening effect (Minnaert law with k=0.6) mentioned in
Sect. 2.
It appears in Fig. 2 that the computed lightcurves do not reproduce the large
amplitude of the observed ones. This could be due to the choice of the limb-darkening
parameter, since the higher the limb-darkening, the larger the amplitude of the curve.
However, we have verified that even using the largest possible Lambertian center-to-limb
darkening - which is typical of icy satellites and shall not be realistic for a M-type
asteroid - the amplitude would still be underestimated in some cases by about 20%.
This suggests that, assuming a moderate limb-darkening parameter, either important
albedo variations are present on both ends of Kleopatra's surface, or its actual
shape is likely to be more elongated with dimensions ratio of the order of
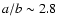 ,
hence consistent with the error-bars of the model (
,
hence consistent with the error-bars of the model (
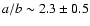 ).
).
The calculation of a synthetic HST/FGS interferogram (or S-curve) is performed
by the convolution of an observed point-like source transfer function TF along one of
the FGS axis (obtained from the HST calibration data-base)
with the body's image 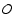 (Hestroffer et al. 2002, and reference therein):
(Hestroffer et al. 2002, and reference therein):
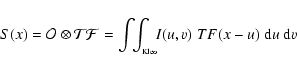 |
(1) |
where I(u,v) is the brightness distribution, and the integral limits are given by the
target's shape as obtained from the physical ephemerides (see Sect. 2).
These interferograms can be computed in a straightforward manner by numerical integration
for any shape modeled by polygons and vertices given in topographic coordinates.
Kleopatra was observed with the HST/FGS astrometer on January 13, 2000,
providing data with a moderate to good signal-to-noise ratio (Tanga et al. 2001). Due to
the limitation in time allocation, the observing run covers only 15% of Kleopatra's
5.385 hour rotation period (see Table 1).
Deriving shape models from the inversion of these data is limited by such short
time-span, but on the other hand, the high resolution HST/FGS data can provide
valuable information and constraints on existing 3-dimensional topographic models.
The HST observing run is divided into 17 visits of about 2.5 min duration
each, producing a number of S-curves given by Eq. (1) along the two
perpendicular FGS-X and -Y axes. The orientation of Kleopatra
with respect to the FGS axes is given in Fig. 3 for the last
visit. The sub-Earth point longitude was increasing from
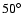 at the first
visit, to
at the first
visit, to
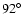 at the last visit.
at the last visit.
Figure 4 shows the comparison of the radar model to the HST/FGS
observations for five arbitrarily selected visits. The modeled S-curve in
Eq. (1) needs to be translated both along the abscissa and ordinate
directions to check the agreement with the observations. This is done by
minimizing the residuals over the interval
![$x\in[-0.4;~0.4]$](/articles/aa/full/2002/35/aah3771/img26.gif) .
This procedure is of
little consequence, but useful to mention in order to understand the meaning of the
superposition of the observed and computed curves in case of lower goodness of fit.
It appears that the discrepancies between the observed and calculated data are, on
the average, within the uncertainties of the nominal shape model of Kleopatra.
However the residuals between the observed and calculated interferograms are larger
- and statistically significant - in the second half of the observing run. These
systematic features on the residuals, approximately two to three times larger than
the typical rms of the FGS observational data noise, shows that the
HST/FGS data available for Kleopatra can valuably constrain the shape
determination of this object.
.
This procedure is of
little consequence, but useful to mention in order to understand the meaning of the
superposition of the observed and computed curves in case of lower goodness of fit.
It appears that the discrepancies between the observed and calculated data are, on
the average, within the uncertainties of the nominal shape model of Kleopatra.
However the residuals between the observed and calculated interferograms are larger
- and statistically significant - in the second half of the observing run. These
systematic features on the residuals, approximately two to three times larger than
the typical rms of the FGS observational data noise, shows that the
HST/FGS data available for Kleopatra can valuably constrain the shape
determination of this object.
Table 1:
HST/FGS observations log from January 2000, 13.
|
Visit # |
UTC mid [hr] |
Visit # |
UTC mid [hr] |
|
1 |
13.57 |
a |
13.93 |
| 2 |
13.62 |
b |
13.97 |
| 3 |
13.66 |
c |
14.01 |
| 4 |
13.70 |
d |
14.05 |
| 5 |
13.74 |
e |
14.09 |
| 6 |
13.78 |
f |
14.13 |
| 7 |
13.82 |
g |
14.17 |
| 8 |
13.86 |
h |
14.21 |
| 9 |
13.89 |
|
|
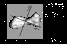 |
Figure 3:
Physical ephemeris of the shape model for Kelopatra on the last visit. |


Up: Asteroid (216) Kleopatra
Copyright ESO 2002
![]() ,
hence consistent with the error-bars of the model (
,
hence consistent with the error-bars of the model (
![]() ).
).
![]() at the first
visit, to
at the first
visit, to
![]() at the last visit.
at the last visit.
![]() .
This procedure is of
little consequence, but useful to mention in order to understand the meaning of the
superposition of the observed and computed curves in case of lower goodness of fit.
It appears that the discrepancies between the observed and calculated data are, on
the average, within the uncertainties of the nominal shape model of Kleopatra.
However the residuals between the observed and calculated interferograms are larger
- and statistically significant - in the second half of the observing run. These
systematic features on the residuals, approximately two to three times larger than
the typical rms of the FGS observational data noise, shows that the
HST/FGS data available for Kleopatra can valuably constrain the shape
determination of this object.
.
This procedure is of
little consequence, but useful to mention in order to understand the meaning of the
superposition of the observed and computed curves in case of lower goodness of fit.
It appears that the discrepancies between the observed and calculated data are, on
the average, within the uncertainties of the nominal shape model of Kleopatra.
However the residuals between the observed and calculated interferograms are larger
- and statistically significant - in the second half of the observing run. These
systematic features on the residuals, approximately two to three times larger than
the typical rms of the FGS observational data noise, shows that the
HST/FGS data available for Kleopatra can valuably constrain the shape
determination of this object.