A&A 392, 729-733 (2002)
DOI: 10.1051/0004-6361:20021006

Research Note

Asteroid (216) Kleopatra

Tests of the radar-derived shape model

D. Hestroffer1 - J. Berthier1 - P. Descamps1 - P. Tanga2,[*] - A. Cellino2 - M. Lattanzi2 - M. Di Martino2 - V. Zappalà2


1 - IMCCE, UMR CNRS 8028, Observatoire de Paris, 77 Av. Denfert Rochereau, 75014 Paris, France
2 - Osservatorio Astronomico di Torino (OATo), Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy

Received 10 April 2002 / Accepted 5 July 2002

Abstract
The shape model of Ostro et al. (2000) for (216) Kleopatra - obtained from inversion of the radar data (Hudson & Ostro 1994) - is compared to the high resolution interferometric observations of the HST/FGS astrometer, and additionally to observed lightcurves and stellar occultations data. It appears that the radar nominal-model, while being in global agreement with these data, doesn't adequately reproduce all of them. In particular the flattening seems to be underestimated by $\sim$20%. The HST/FGS observations should provide valuable constraints for determining a more refined shape model, since the model obtained from the radar data alone is subject to some uncertainty. Such a refined model of Kleopatra should provide valuable insights for explaining the formation of this interesting object, and the formation and evolution of binary asteroids in general.

Key words: techniques: high angular resolution - occultations - minor planets, asteroids


1 Introduction

The main-belt asteroid (216) Kleopatra has been extensively observed during the last years by adaptive optics, speckle, radar, and interferometric techniques (e.g. Marchis et al. 1999; Hammergren et al. 2000; Merline et al. 2000; Ostro et al. 2000; Tanga et al. 2001). Such observations, with higher resolution than those previously obtained by Storrs et al. (1999) or Mitchell et al. (1995), show that this large M-type asteroid has a particular non-convex, dumbbell or bi-lobated shape. Radar delay-Doppler imaging technique has shown to be very powerful to determine the shape of near-Earth asteroids (e.g. Ostro et al. 1999; Benner et al. 1999; Hudson & Ostro 1999), and to put into evidence possible bifurcated or binary structures (e.g. Hudson & Ostro 1994; Benner et al. 2001; Margot et al. 2002). The Arecibo radar has been used to provide a 3-dimensional modelling of Kleopatra with the highest resolution presently possible from ground-based instruments. These data however do not directly provide spatially-resolved images and - since Kleopatra is in the main-belt - have limited signal-to-noise ratio yielding to an uncertainty in the model's shape of $\pm15~$km and, additionally, $\pm25$% in absolute size. The radar nominal-model has been shown to be consistent with ground-based adaptive optics observations (Hammergren et al. 2000; Merline et al. 2000), which confirm the bi-lobated shape of Kleopatra. Moreover, no significant albedo variations were detected on Kleopatra's surface (Hammergren et al. 2000).

Knowledge of the shapes of large asteroids in the main-belt is important because they are the result of a complex collisional history. Apart from "giant'' asteroids like Ceres and few others, most asteroids are the outcomes of catastrophic collisions, yielding to "rubble pile'' structures whose overall shapes may correspond to equilibrium figures (Farinella et al. 1981,1982). Collisions characterized by large angular momentum transfer may even produce binary systems that may eventually evolve into a single body having a bifurcated shape. An alternative could be the result of a gentle collision, in cases in which the shape of a "rubble pile'' could follow internal stress contours in a compressible material (Washabaugh & Scheeres 2001). It is therefore important to test the validity and limits of Kleopatra's shape models using data from independent observational techniques. This analysis can be done taking profit of a large set of available data, including photometric lightcurves, stellar occultation data, and high resolution interferometric observations recently obtained using the HST/FGS astrometer (Tanga et al. 2001).

   
2 Construction of the physical ephemeris

Radar observations provide the spin-axis direction $(72^\circ; 27^\circ)$ in ecliptic B1950 coordinates, and the topographic model of Kleopatra. The zero rotational phase is calculated in this work in order to match the positions of observed lightcurve extrema. The resulting orientation of the body agrees within a few degrees with the November 1999 radar observations (Fig. 2 of Ostro et al. 2000). From this, the body's physical ephemeris, or apparent shape and size in the plane-of-sky-view, can easily be obtained for any given epoch of observation.

Predicted lightcurves can then be computed from the physical ephemeris. However, radar images do not carry information about the photometric properties in the optical domain of a body's surface. These light-scattering properties can, on the other hand, be constrained from observed lightcurves[*] (Lagerkvist et al. 1996). We have introduced different scattering laws, i.e. normalized brightness distributions: uniform brightness I=1, Lambert $I=\mu_0$, Lommel-Seeliger $I=\mu_0/(\mu+\mu_0)$, Minnaert $I=\mu_0^k~\mu^{k-1}$, where $\mu_0$ and $\mu$ are cosines of the angles of emission and incidence, respectively. Among these scattering laws the parameterized Minnaert law (Minnaert 1941) with $k=0.6\pm0.1$ better reproduces the lightcurves of Kleopatra observed at moderate aspect and solar-phase angles. This means that Kleopatra appears with a moderate center-to-limb darkening, in agreement with Hestroffer & Mignard (1997), Hestroffer (1998) or Ragazzoni et al. (2000). Once the physical ephemeris, albedo variation, and light-scattering are set, it is possible to model the image and brightness distribution at visible wavelengths at any epoch.

3 Comparisons

   
3.1 Occultations

Two successful occultations of Kleopatra have been reported by a few observers (Dunham 1981,1992). In Fig. 1 the predicted shape of Kleopatra based on the radar model is plotted against the chords of the 1980 and 1991 occultations. The plots in Fig. 1 are given in the plane of the occultation, i.e. the plane perpendicular to the direction of the occulted star as seen from the asteroid. If no error were present in the predicted position of the star and the asteroid, the images would be centered in the graph origin. Thus the error of the predicted occultation path is of the order of 100 km in 1991. Error bars on the occultation chords, as derived from a timing error of $\pm0.5$ s for visual observations, are of the order of 15 km; for photoelectric observations they reduce to $\sim$3 km. One isolated point, not constraining a chord length and in clear disagreement with nearby chords has been omitted in the 1980 occultation plot. Also one chord of the 1991 event, probably affected by a strong dating error of the emersion point, has been removed from the plot. Negative observations (i.e. observations for which no occultation was detected) are indicated by dashed lines. They put some limits in Kleopatra's size and shape during the 1991 event. The superposition of the model's profile to the observed occultation chords in Fig. 1, is obtained by a translation of the physical model, along the abscissa and ordinate axes (X and Y), such that the predicted contour fits most of the immersion and emersion points. The sub-Earth point longitude was $160\hbox{$^\circ$ }$ and $120\hbox{$^\circ$ }$, during the 1980 and 1991 occultation, respectively. Longitudes of $90\hbox{$^\circ$ }$ and $180\hbox{$^\circ$ }$ correspond roughly to lightcurve maximum and minimum, respectively.

The topographic model was originally scaled in size to the occultations chords. From Fig. 1 we infer that Kleopatra's shape model is in general good agreement with the observed chords. The largest discrepancies are of the order of 30 km, well within the error bars of the model. Despite the inherent difficulty of obtaining robust occultation data, it must be noted that the overall size of the contour on its most elongated direction is well constrained in the 1991 event by a photoelectric chord or by two independent and consistent chords. Hence, based mainly on the 1991 data, it cannot be excluded that a more elongated topographic model could provide a better fit to the measured chords, without drastic change to the 1980 plot.


  \begin{figure} \par\resizebox{\hsize}{!}{ \includegraphics{H3771F1.PS} \includegraphics{H3771F2.PS} }\end{figure} Figure 1: Comparison between the observed occultation data and the radar model. Left panel: occultation of Oct. 10, 1980 at 7.00 h UTC. Right panel: occultation of Jan. 1, 1991 at 5.28 h UTC. The dashed lines correspond to negative observations. Error bars are given by crosses and are negligible for the photoelectric observations.
Open with DEXTER


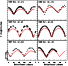  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{H3771F3.PS}}\end{figure} Figure 2: Observed and computed lightcurves for (216) Kleopatra at nearly equatorial views ($\beta $ is the SEP latitude). The curves for the computed values correspond to the radar model with a Minnaert law (k=0.6, see text).
Open with DEXTER

   
3.2 Lightcurves

Many lightcurves of Kleopatra at different geometries were obtained during the last decades. Since the rotation period is known with good accuracy, no shift in the position of the extrema is observed. Figure 2 shows the comparison of the nominal radar model to the photometric observations acquired at large aspect angle (i.e. close to an equatorial view), assuming a homogeneous albedo distribution (Hammergren et al. 2000). Calculation of the global flux depends on the resolution of the topographic model. The radar model is provided with a resolution in spherical coordinates better than $5\times5~\deg^2$, which provides enough internal accuracy for comparison to typical lightcurves. Synthetic lightcurves are constructed by considering the size and orientation - with respect to the Earth and the Sun - of the illuminated and visible elementary surface (the facets for a topographic model). For non-convex shapes like Kleopatra, one also needs to take into account shadows cast by facets and hidden facets. Moreover the computed lightcurves in Fig. 2 were obtained by considering the moderate limb-darkening effect (Minnaert law with k=0.6) mentioned in Sect. 2.

It appears in Fig. 2 that the computed lightcurves do not reproduce the large amplitude of the observed ones. This could be due to the choice of the limb-darkening parameter, since the higher the limb-darkening, the larger the amplitude of the curve. However, we have verified that even using the largest possible Lambertian center-to-limb darkening - which is typical of icy satellites and shall not be realistic for a M-type asteroid - the amplitude would still be underestimated in some cases by about 20%. This suggests that, assuming a moderate limb-darkening parameter, either important albedo variations are present on both ends of Kleopatra's surface, or its actual shape is likely to be more elongated with dimensions ratio of the order of $a/b \sim 2.8$, hence consistent with the error-bars of the model ( $a/b \sim 2.3\pm0.5$).

3.3 Interferometric data from the HST/FGS

The calculation of a synthetic HST/FGS interferogram (or S-curve) is performed by the convolution of an observed point-like source transfer function TF along one of the FGS axis (obtained from the HST calibration data-base) with the body's image ${\cal O}$ (Hestroffer et al. 2002, and reference therein):

 \begin{displaymath}S(x) = {\cal O} \otimes {\cal TF} = \int\!\!\int_{_{\rm Kleo}} \!\! I(u,v)\;TF(x-u)\;{\rm d}u~{\rm d}v \end{displaymath} (1)

where I(u,v) is the brightness distribution, and the integral limits are given by the target's shape as obtained from the physical ephemerides (see Sect. 2). These interferograms can be computed in a straightforward manner by numerical integration for any shape modeled by polygons and vertices given in topographic coordinates.

Kleopatra was observed with the HST/FGS astrometer on January 13, 2000, providing data with a moderate to good signal-to-noise ratio (Tanga et al. 2001). Due to the limitation in time allocation, the observing run covers only 15% of Kleopatra's 5.385 hour rotation period (see Table 1). Deriving shape models from the inversion of these data is limited by such short time-span, but on the other hand, the high resolution HST/FGS data can provide valuable information and constraints on existing 3-dimensional topographic models. The HST observing run is divided into 17 visits of about 2.5 min duration each, producing a number of S-curves given by Eq. (1) along the two perpendicular FGS-X and -Y axes. The orientation of Kleopatra with respect to the FGS axes is given in Fig. 3 for the last visit. The sub-Earth point longitude was increasing from  $50\hbox{$^\circ$ }$ at the first visit, to $92\hbox{$^\circ$ }$ at the last visit.

Figure 4 shows the comparison of the radar model to the HST/FGS observations for five arbitrarily selected visits. The modeled S-curve in Eq. (1) needs to be translated both along the abscissa and ordinate directions to check the agreement with the observations. This is done by minimizing the residuals over the interval $x\in[-0.4;~0.4]$. This procedure is of little consequence, but useful to mention in order to understand the meaning of the superposition of the observed and computed curves in case of lower goodness of fit. It appears that the discrepancies between the observed and calculated data are, on the average, within the uncertainties of the nominal shape model of Kleopatra. However the residuals between the observed and calculated interferograms are larger - and statistically significant - in the second half of the observing run. These systematic features on the residuals, approximately two to three times larger than the typical rms of the FGS observational data noise, shows that the HST/FGS data available for Kleopatra can valuably constrain the shape determination of this object.


 

 
Table 1: HST/FGS observations log from January 2000, 13.

Visit # 		UTC mid [hr] Visit # UTC mid [hr]

1		 13.57 a 13.93
2 13.62 b 13.97
3 13.66 c 14.01
4 13.70 d 14.05
5 13.74 e 14.09
6 13.78 f 14.13
7 13.82 g 14.17
8 13.86 h 14.21
9 13.89    



  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3771F4.PS}}\end{figure} Figure 3: Physical ephemeris of the shape model for Kelopatra on the last visit.
Open with DEXTER

4 Discussion

The epochs at which the HST/FGS and radar data were taken differ by about two months from each other, hence the aspect angle did not significantly change between the two observing runs. The overall sizes of the radar nominal model are coherent with the HST/FGS data, but significant departures from the observations are also present in Fig. 4. It is a known characteristic of the FGS interferogram that the largest the object, the largest the flattening of the S-curve. Thus changing the scaling of the radar-derived model in one direction will change the shape of the computed interferogram. We hence have derived computed interferograms for increased sizes of the nominal 3-dimensional model along its principal axes. It appears that the goodness of fit, for both FGS axes, is somewhat increased, particularly in the last visits, when increasing the flattening of the nominal model by about 20%. This corresponds to an increase of the largest dimension parallel to the principal axis of 43 km, compatible with the uncertainty of the radar model. It would moreover result in a more elongated body in agreement with the result obtained in previous Sect. 3.2, and coherent with the stellar occultation data of Sect. 3.1.

The FGS data are limited to a single epoch and cover approximately 45 min, thus they do not test the whole structure of the radar-derived model. In addition to the nominal 3-dimensional topographic model, some parameters such as those describing the scattering of light at the surface, possible albedo variations, and the rotational phase angle have to be introduced in this analysis. However, we have verified that changing the light-scattering law or variations in its associated parameter, as well as variations in the zero rotational phase-angle of a few degrees have little effect on the interferogram shape, while albedo features must be large and important to significantly change the overall shape of the computed S-curves. Hence, reasonable errors in the above approximations should produce only second order effects on the modeled lightcurves and S-curve shapes, and cannot exclusively explain the discrepancy between the radar-derived model and these independent observations. Nevertheless, a larger and more elongated body-model could be more consistent with the occultations, the photometric and the interferometric HST/FGS results. This suggests that Kleopatra's modeled overall size and shape flattening are likely underestimated to be fully compatible with the whole set of observations available for this object. Also the accuracy in size and shape of the present model could be improved by combining all these observations and in particular the radar and FGS data.


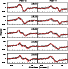  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3771F5.PS}}\end{figure} Figure 4: Comparison between the observed HST/FGS data and the radar model. The computed interferogram (see text) is plotted (line) against the observed one for five selected visits and for both FGS axes (X on the left side, and Y on the right). The UTC (hours and decimals) of the observations are given in the small box.
Open with DEXTER

Interestingly, the radar data (Ostro et al. 2000) and the adaptive optics data (Marchis et al. 1999) might be consistent with the presence of an empty gap in the middle of the asteroid, hence closer to a separated binary model. On an other hand, a simple model of a non-convex single-object consisting of two "overlapping ellipsoids'' (i.e. the shape is modeled by the union two ellipsoids whose center-to-center separation is less than the sum of the semi-major axes) provides a better fit to the HST/FGS data (Tanga et al. 2001). The latter model also better reproduces the large amplitude of the lightcurves given in Fig. 2. However, it does not completely match neither the observed stellar occultation chords, nor the detailed features of the observed lightcurves of this body. In particular the size of the medium and shortest axes of the Tanga et al. (2001) model are underestimated, while the longest axis fits inside the limits of the 1991 occultation. Other observations with the HST/FGS astrometer at different aspect angle would be needed to better constrain the shape in those directions.

5 Conclusion

Ephemerides for the physical observations of (216) Kleopatra have been constructed. They provide, at any given epoch of observation, the aspect and orientation in the plane-of-sky view of this object as well as its brightness distribution. The present paper shows that the radar-derived nominal-model of Kleopatra could be improved to be fully compatible with the whole set of available data for this object, including photometric lightcurves, stellar occultation data, and high resolution interferometric data from the HST/FGS. It results from this analysis that the available data coming from different observational techniques suggest that the actual shape of Kleopatra is more elongated than the radar nominal-solution. On the other hand, models with an empty gap and/or "overlapping ellipsoids'' cannot be totally ruled out on the basis of current observational evidence. A more detailed assessment of this possibility deserves some further scrutiny, due to potential implications for our understanding on the formation and evolution of this object in particular, and of binary asteroids in general. A combined analysis of existing and future high-resolution observations from the HST/FGS interferometer, or from the ESO/VLT in the optical domain and/or radar data that will be hopefully obtained in the future, should lead to a more conclusive evidence about the real shape and overall structure of this interesting object. This should be a necessary starting point for a more detailed modelling of the internal structure of Kleopatra, and its overall collisional history.

References

 
Copyright ESO 2002