Massey & Conti (1977) inferred the relative brightness of the components of HDE 228766 from the ratio of the intensities of their H8 and H9 lines. In this way, they derived a roughly equal brightness ( $\Delta m_{V} \leq 0.5$ mag). We used the EWs of the He I $\lambda$ 4471 and He II $\lambda$ 4542 lines as measured on the spectra of maximum RV-separation and compared them with the EWs of single O-stars quoted by Conti & Alschuler (1971). The results depend of course on the (rather uncertain) spectral types adopted for each star, but they essentially confirm the results of MC77: the line ratios suggest in fact that both stars have more or less the same brightness with the secondary being somewhat brighter ( $m_{{V, {\rm p}}} - m_{{V, {\rm s}}} \sim 0.3$ ).

Unfortunately, the distance of HDE 228766 is extremely uncertain. Popova & Kraicheva (1984) associated the system with the open cluster Dolidze 3. Zakirov (1999) determined a distance of 1.9 kpc for the eclipsing binary KV Cyg near the center of Dolidze 3. However, the membership of HDE 228766 in Dolidze 3 seems questionable since the system lies at $\sim$ 38 $^\prime$ from the cluster center (according to Ruprecht et al. 1983). On the other hand, HDE 228766 lies in the region of the sky spanned by the Cyg OB1 association for which Humphreys (1978) quoted a mean distance of 1.82 kpc. Let us start by assuming that HDE 228766 lies indeed at a distance of 1.9 kpc. Adopting the V = 9.14 magnitude and B-V = 0.65 colour ( $E_{B-V} \simeq 0.95$ ) quoted by Hiltner (1956) and assuming a ratio of total-to-selective extinction R = 3.2, we find that the absolute magnitude of HDE 228766 should be -5.29. Note that the magnitude (9.15) and colour (0.60) found by Demers & Fernie (1964) yield an absolute magnitude of -5.12. These absolute magnitudes are at odds with the idea that HDE 228766 consists of two O-type giants or supergiants which should rather have a combined absolute magnitude of $\sim$ -6.6 to $\sim$ -7.2 (Schmidt-Kaler 1982). It appears rather unlikely that a peculiar extinction law could account for the entire discrepancy. Therefore, it seems more plausible that the actual distance of the system is larger than 1.9 kpc. For instance, if we assume an absolute magnitude of $M_{V, {\rm s}} = -6.0$ for the secondary and $M_{V, {\rm p}} = -5.7$ for the primary, we obtain a distance of 3.5 kpc for HDE 228766.

To determine the stellar properties of HDE 228766 we have modelled the combined spectrum of HDE 228766 by means of model atmosphere codes. For the primary's photospheric spectrum we have adopted a TLUSTY non-LTE model (Hubeny & Lanz 1995) corresponding to the O8 III star $\lambda$ Ori. The relevant model parameters are $T_{\rm eff, p} = 36~000$ K, $R_{*, \rm p} = 16~R_{\odot}$ ( $L_{\rm bol, p} = 380~000~L_{\odot}$ ), $\log{g} = 3.5$ and $v~\sin{i} = 200$ km s^-1. At this stage, it is worth emphasizing that the value of the projected rotational velocity of the primary has to be significantly larger than 100 km s^-1 (the value that matches the secondary, see below) to achieve a good fit of the primary's lines.

For the secondary, we have utilised the non-LTE code of Hillier & Miller (1998) which solves the radiative transfer equation subject to the constraints of statistical and radiative equilibrium, in a spherical, extended atmosphere. Line blanketing is incorporated directly through the use of a super-level approach. We use a similar atomic model to that employed by Crowther et al. (2002) in their study of early-type O supergiants, including H I, He I-II, C III-IV, N III-V, O III-VI, Si IV, P IV-V, S IV-VI and Fe IV-VII (see Crowther et al. for further details). The velocity in the supersonic part of the wind is described by a standard ${\beta }$ -law:

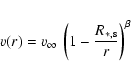
The synthetic photospheric spectrum of the primary and the synthetic photospheric + wind spectrum of the secondary are combined allowing for the visual brightness ratio ( $m_{{V, {\rm p}}} - m_{{V, {\rm s}}} = 0.3$ ) and the parameters of the secondary model are fine-tuned to match the observed line profiles. We adjust the stellar temperature and mass-loss rate of an individual model until the "photospheric'' He II $\lambda$ 4542 and He I $\lambda$ 4471 lines are reproduced. Simultaneously, we vary the mass-loss rate until H ${\alpha }$ is also matched. The exponent of the ${\beta }$ -law is adjusted until the shape of H ${\alpha }$ is well reproduced - for HDE 228766 we find $\beta \sim 1.5$ . Since HDE 228766 is very heavily reddened and no UV spectra are available, we adopt a representative terminal wind velocity of $v_{\infty} = 1800$ km s^-1. Our calculations assume a microturbulence $v_{\rm turb} = 10$ km s^-1 and, due to the severe blending of the lines, we nominally adopt $v~\sin{i} = 100$ km s^-1 for the secondary.

As discussed by Hillier et al. (2002), it is extremely difficult to determine accurate He/H abundances in O supergiants. Consequently, we adopt He/H = 0.2 by number, whilst C and N abundances are varied until diagnostic optical line profiles are reproduced. In Fig. 9, we present selected optical line profile fits. Overall, agreement for $T_{\rm eff, s} = 38~000$ K is good. He I $\lambda$ 4471 provides our main temperature constraint since other blue optical He I lines are weak or absent. Alternatively, we considered using He I $\lambda$ 5876 (or He I $\lambda$ 10830) together with the He II $\lambda$ 4686 line. However, this method (followed by Crowther & Bohannan 1997) yields significantly ( $\sim$ 4000 K) lower stellar temperatures, and suffers from inconsistencies involving the ionization balance of UV/optical metal lines. Therefore, we have greater confidence in our adopted diagnostics, which do not suffer from such problems.

$\begin{figure} \par\includegraphics[width=11.8cm,clip]{MS2665fig9.ps} \end{figure}$

Figure 9: Fit of the spectrum of HDE 228766 as observed in September 2000 (except for the N IV $\lambda \lambda$ 7103-29 lines observed in August 1990) with a non-LTE model atmosphere code. The combined synthetic model is shown by the dotted line, whilst the observations are displayed by the continuous line. The individual normalized synthetic spectra are shown by the dashed lines offset by -0.1 and +0.1 for the primary and the secondary respectively. The synthetic spectra have been shifted in velocity to match the radial velocities of the two components at the orbital phases of the observations.

A reasonable fit of the combined spectrum is achieved for $R_{*, {\rm s}} = 17$ $R_{\odot}$ ( $L_{\rm bol, s} = 550~000~L_{\odot}$ ). Assuming the secondary to solely contribute to the H ${\alpha }$ and He II $\lambda$ 4686 emission, its mass-loss rate is $10^{-5}~M_{\odot}$ yr^-1. We note that our value of the mass loss rate is in perfect agreement with the estimate of MC77 who used the strength of the H ${\alpha }$ line to infer $\dot{M} = 10^{-5}~M_{\odot}$ yr^-1. Moderate clumping would reduce this value by a factor of $\sim$ 2. Our primary nitrogen abundance diagnostics is N III $\lambda \lambda$ 4634-41 which implies $\epsilon_{\rm N} = 6~\epsilon_{{\rm N},\odot}$ . Carbon is somewhat more difficult to constrain, with an upper limit to the strength of C III $\lambda \lambda$ 4647-51 of $\epsilon_{\rm C} = 0.08~\epsilon_{{\rm C},\odot}$ . As discussed elsewhere (e.g. Hillier et al. 2002), oxygen is exceedingly difficult to constrain in mid-O supergiants due to the lack of suitable optical diagnostics.

Table 5: Summary of the main parameters of our non-LTE analysis of the spectrum of HDE 228766.
Primary Secondary

$T_{\rm eff}$ (K) 36 000 38 000

$\log{(L_{{\rm bol}}/L_{\odot})}$ 5.58 5.74

R_* ( $R_{\odot}$ ) 16 17

$\log{g}$ 3.5

$\dot{M}$ ( $M_{\odot}$ yr^-1) 10^-5

$v~\sin{i}$ (km s^-1) 200 100

**Table 5:** Summary of the main parameters of our non-LTE analysis of the spectrum of HDE 228766.
	Primary	Secondary
$T_{\rm eff}$ (K)	36 000	38 000
$\log{(L_{{\rm bol}}/L_{\odot})}$	5.58	5.74
R_* ( $R_{\odot}$ )	16	17
$\log{g}$	3.5
$\dot{M}$ ( $M_{\odot}$ yr^-1)		10^-5
$v~\sin{i}$ (km s^-1)	200	100

While the synthetic model fits the H I Balmer, He II (including He II $\lambda$ 10124), N III and N IV lines pretty well, the fit of the He I $\lambda$ 4471 profile is less good and the model fails to reproduce the observed He I $\lambda \lambda$ 5876, 10830 emission profiles as well as the N V $\lambda \lambda$ 4604, 4620 lines. To match the He I profiles, the temperature of the model would have to be much lower and would therefore be in disagreement with the value derived from the optical nitrogen lines. While a significant fraction of the He I emission could be associated with the primary wind (He I $\lambda$ 10830 emission is common among O supergiants, e.g. Andrillat & Vreux 1979) or with an interaction region, our S-wave analysis clearly indicates that the N V lines belong to the same star (i.e. the secondary) as the N III and N IV lines. The effective temperature of the secondary indicates an O6-7 spectral type, in agreement with the results derived from the EW ratio of the He I $\lambda$ 4471 and He II $\lambda$ 4542 lines. However, the puzzling presence of the N V $\lambda \lambda$ 4604, 4620 lines cannot be explained by this temperature. A higher temperature of approximately 40 000-42 000 K would be needed to fit the N V lines. However, the temperature cannot be much larger than 38 000 K because otherwise the N IV line gets too strong.

The spectrum of HDE 228766 is remarkably similar to that of the O4If⁺ star HDE 269698 in the LMC. HDE 269698 also displays N III, N IV and N V lines in its spectrum and Crowther et al. (2002) derive $T_{\rm eff}$ = 40 000 K for this star, which also provides a good match to He I/He II, UV, and far-UV lines.

The structure of the secondary's atmosphere in HDE 228766 could be intermediate between the winds of HDE 269698 and of the WN7ha star in WR 22. The latter star also displays N III, N IV and N V emission lines in its spectrum (Rauw et al. 1996). Note that an analysis of the H I, He I and He II spectrum of WR 22 with a non-LTE code yielded a rather low stellar temperature ( T_* = 31 900 K, Crowther et al. 1995), whereas the He II, N III and N IV lines profiles were reasonably well reproduced using a higher stellar temperature ( T_* = 36 500 K, Crowther et al. 1995). Combining the results of our tomographic analysis, the mean EW of the He II $\lambda$ 4686 line in the observed spectrum of HDE 228766 and the optical brightness ratio we infer that the EW of the intrinsic He II $\lambda$ 4686 emission in the secondary's spectrum is of order $\sim$ 10 Å. This puts the secondary's intrinsic emission strength beyond the nominal Of range, but below that of regular WNL stars. However a WNLha classification (see Smith et al. 1996) could account for the observed line strength. In fact, comparing with the observed spectra of the presumably single WNLha stars WR 25 (WN7ha) and WR 108 (WN9ha), we find the secondary in HDE 228766 to be intermediate in excitation between these two objects, but similar in wind strength. These results suggest that a WN8ha classification might be appropriate.

6.2 Evolutionary status

Although the parameters derived hereabove depend on the unknown distance of HDE 228766 and the poorly constrained optical brightness ratio, our analysis clearly reveals an evolved secondary star as witnessed by the large mass loss rate and the peculiar abundances. The secondary star in HDE 228766 appears therefore most likely as a kind of transition object at the beginning of the WR stage.

Adopting the parameters inferred hereabove, we can compare the properties of the stars in HDE 228766 with the evolutionary tracks of Schaller et al. (1992). The most stricking feature is that the secondary appears to be the most evolved component and is clearly overluminuous for its present-day mass. Hence, the secondary must have been the initially more massive component of the system. The only way to account for this situation in the framework of single star evolutionary models would be if the secondary were moving bluewards after an excursion towards the lower temperature regime. Note that in this case, the evolutionary model suggests that the secondary would be a fully developed WN Wolf-Rayet star.

Alternatively, the evolution of the whole system could have been influenced by mass exchange. Evolutionary tracks from Vanbeveren & de Loore (1994) and de Loore & Vanbeveren (1994) could indeed account for the overluminosity of the secondary. The initially more massive component could have undergone mass loss through Roche lobe overflow (RLOF) and would now be the less massive star. We note also that the primary has broader lines and seems to be rotating faster than the secondary. If the stars were in synchronous rotation, they should roughly have the same $v~\sin{i}$ . In the framework of a binary evolution model, the larger $v~\sin{i}$ of the present-day primary could be due to spinning up through accretion (Vanbeveren & de Loore 1994). It seems therefore plausible that HDE 228766 is in a post RLOF stage. The evolutionary tracks of Vanbeveren & de Loore (1994) indicate that the secondary should be in the WNL stage.

6.3 A wind interaction in HDE 228766?

Our data reveal a weak H ${\alpha }$ emission feature that could be an indication of a wind interaction in the optical spectrum of HDE 228766. A colliding wind phenomenon could also produce a signature in the X-ray domain through a phase-dependent excess X-ray emission (e.g. Stevens et al. 1992). We have therefore searched the ROSAT archive for observations of HDE 228766. Unfortunately there is only a single pointed observation (rp500248a01) where the star happened to lie within the field of view of the ROSAT-PSPC (though it was outside the inner ring of the PSPC detector). Using our new ephemeris we find that the orbital phase of HDE 228766 at the time of the PSPC observation was $\phi = 0.64$ . We extracted a background corrected spectrum using the XSELECT software. We have fitted this spectrum with an absorbed single-temperature optically thin plasma model (Raymond & Smith 1977) within the XSPEC software. Fixing the neutral hydrogen column density at the interstellar value of $N_{\rm H}^{\rm ISM} = 0.53 \times 10^{22}$ cm^-2, we obtain a best fitting temperature kT = 0.88^+.25_-.16 keV. The corresponding dereddened X-ray flux in the energy band 0.1-2.0 keV is $1.6 \times 10^{-12}$ erg cm^-2 s^-1 yielding an unabsorbed X-ray luminosity of $L_{\rm X} = 2.34 \times 10^{33}$ erg s^-1 for a distance of 3.5 kpc. If the total bolometric luminosity of the binary amounts to $L_{\rm bol} = 9.3 \times 10^5~L_{\odot}$ (see above), we obtain $\log{{L}_{\rm X}/{L}_{\rm bol}} = -6.18$ . The ${L}_{\rm X}/{L}_{\rm bol}$ ratio appears a factor $\sim$ 3.6 larger than expected from the empirical relation for single O-stars given by Berghöfer et al. (1997). Although the snapshot ROSAT observation does not provide any information about the variability of the X-ray flux, it seems tempting to associate the X-ray "overluminosity'' with a binary interaction.

Adopting the mass ratio q = 1.67 derived in Sect. 4, we can estimate the minimum radii of the Roche lobes of the components using the formula of Eggleton (1983). In this way we find $R_{\rm RL}~\sin{i} = 32.2$ and 25.5 $R_{\odot}$ for the primary and secondary respectively. From our non-LTE model hereabove, we infer a radius of 17 $R_{\odot}$ for the secondary. Therefore it appears rather unlikely that any of the components currently fills up its critical volume. The interaction in HDE 228766 is therefore more likely associated with a wind collision rather than an ongoing Roche lobe overflow.

Since the secondary wind is by far more energetic than that of the primary, it is likely that the former crashes onto the surface of the primary star. Such a shock could in turn compress the primary wind resulting in a high density region near the point of head-on wind collision, where the weak H ${\alpha }$ emission would be formed through recombination. Figure 10 illustrates a possible model for the location of the H ${\alpha }$ emitting material in HDE 228766. While the bulk of the emission is produced in the stellar wind of the secondary, the weaker emission component could arise in a plasma volume which is passing by the primary's surface. This geometry could at least qualitatively account for the double-peaked line shape observed near the quadrature phases.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2665fig10.ps} \end{figure}$

Figure 10: Schematic view of the H ${\alpha }$ emission region in the HDE 228766 binary system. The projection of the line of sight onto the plane of the orbit is indicated at four orbital phases. The bulk of the emission arises in the wind of the secondary star. An additional contribution comes from the small shaded area close to the primary's surface. The arrows indicate the direction of the orbital motion of the stars and of the velocity of the material in the small emitting region.

6.4 Final remarks and conclusions

Our analysis of HDE 228766 suggests that the secondary star is the most evolved component of the system and accounts for almost all the emission features seen in the spectrum. The only exception to this rule comes from a weak H ${\alpha }$ emission component that moves in anti-phase with the secondary and arises most probably in a wind interaction region near the surface of the primary. HDE 228766 offers the unique opportunity to study the fundamental properties of a massive star which is just in the transition between an Of⁺ and a WNL Wolf-Rayet star. However, a couple of crucial ingredients are missing that prevent us from deriving absolute values for some parameters. The most obvious parameter that needs to be determined is the distance. Future astrometric observations (e.g. with ESA's planned GAIA satellite) will hopefully allow to solve this problem. Moreover, a photometric monitoring of the binary over an entire orbital cycle is badly needed to clarify whether or not the system displays photometric eclipses. Our orbital solutions suggest that the orbital inclination i might be large enough for such eclipses to occur. If this is the case, then an analysis of the light curve should allow to constrain not only the inclination, but also the radii of the stars and their relative brightness. This would make HDE 228766 a cornerstone for our understanding of massive star evolution.

6 Discussion

6.1 The fundamental parameters of HDE 228766

6.2 Evolutionary status

6.3 A wind interaction in HDE 228766?

6.4 Final remarks and conclusions