A&A 392, 515-528 (2002)
DOI: 10.1051/0004-6361:20020854

On the Period-Luminosity-Colour-Metallicity relation and the pulsational characteristics of $\lambda $ Bootistype stars[*]

E. Paunzen1,2 - G. Handler3 - W. W. Weiss1 - N. Nesvacil1 - A. Hempel4,5 - E. Romero-Colmenero3 - F. F. Vuthela3,6 - P. Reegen1 - R. R. Shobbrook7 - D. Kilkenny3


1 - Institut für Astronomie der Universität Wien, Türkenschanzstr. 17, 1180 Wien, Austria
2 - Zentraler Informatikdienst der Universität Wien, Universitätsstr. 7, 1010 Wien, Austria
3 - South African Astronomical Observatory, PO Box 9, Observatory 7935, South Africa
4 - Department of Physics, University of Cape Town, Private Bag, Rondebosch 7701, South Africa
5 - Max-Planck-Institut für Astronomie, Königsstuhl 17, 69117 Heidelberg, Germany
6 - Department of Physics, University of the North-West, Private Bag X2046, Mmabatho 2735, South Africa
7 - Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 0200, Australia

Received 12 April 2002 / Accepted 6 June 2002

Abstract
Generally, chemical peculiarity found for stars on the upper main sequence excludes $\delta $ Scuti type pulsation (e.g. Ap and Am stars), but for the group of $\lambda $ Bootisstars it is just the opposite. This makes them very interesting for asteroseismological investigations. The group of $\lambda $ Bootistype stars comprises late B- to early F-type, Population I objects which are basically metal weak, in particular the Fe group elements, but with the clear exception of C, N, O and S. The present work is a continuation of the studies by Paunzen et al. (1997, 1998), who presented first results on the pulsational characteristics of the $\lambda $ Bootisstars. Since then, we have observed 22 additional objects; we found eight new pulsators and confirmed another one. Furthermore, new spectroscopic data (Paunzen 2001) allowed us to sort out misidentified candidates and to add true members to the group. From 67 members of this group, only two are not photometrically investigated yet which makes our analysis highly representative. We have compared our results on the pulsational behaviour of the $\lambda $ Bootisstars with those of a sample of $\delta $ Scuti type objects. We find that at least 70% of all $\lambda $ Bootistype stars inside the classical instability strip pulsate, and they do so with high overtone modes (Q < 0.020 d). Only a few stars, if any, pulsate in the fundamental mode. Our photometric results are in excellent agreement with the spectroscopic work on high-degree nonradial pulsations by Bohlender et al. (1999). Compared to the $\delta $ Scuti stars, the cool and hot borders of the instability strip of the $\lambda $ Bootisstars are shifted by about 25 mmag, towards smaller (b-y)0. Using published abundances and the metallicity sensitive indices of the Geneva 7-colour and Strömgren $uvby\beta$ systems, we have derived [Z] values which describe the surface abundance of the heavier elements for the group members. We find that the Period-Luminosity-Colour relation for the group of $\lambda $ Bootisstars is within the errors identical with that of the normal $\delta $ Scuti stars. No clear evidence for a statistically significant metallicity term was detected.

Key words: stars - $\lambda $ Bootis; stars - chemically peculiar; stars - early type


1 Introduction

In this paper we present an extensive survey to analyse the pulsational characteristics of the $\lambda $ Bootisstars. This small group comprises late B- to early F-type, Population I stars which are metal weak (particularly the Fe group elements), but with the clear exception of C, N, O and S. Only a maximum of about 2% of all objects in the relevant spectral domain are believed to be $\lambda $ Bootistype stars.

Several theories were developed to explain the peculiar abundance pattern for members of this group. The most acknowledged models include diffusion as main mechanism together either with mass-loss (Michaud & Charland 1986; Charbonneau 1993) or with accretion of circumstellar material (Venn & Lambert 1990; Turcotte & Charbonneau 1993). Another two theories deal with the influence of binarity on this phenomenon (Andrievsky 1997; Faraggiana & Bonifacio 1999). Heiter (2002) and Heiter et al. (2002) also tried to explain the abundance pattern in the context of the proposed theories.

In general, chemical peculiarity inhibits $\delta $ Scuti type pulsation (e.g. for Ap and Am stars, see Kurtz 2000 for a recent discussion) but for the group of $\lambda $ Bootisstars it is just the opposite. In two previous studies (Paunzen et al. 1997, 1998), we presented non-variable as well as pulsating $\lambda $ Bootis stars. Since then, we have observed 22 additional objects and found eight new pulsators and confirmed another. Furthermore, new spectroscopic data (Paunzen 2001) has allowed us to sort out misidentified candidates and to add true members of the group.

Turcotte et al. (2000) investigated the effect of diffusion (probably the main cause of the $\lambda $ Bootisphenomenon) on the pulsation of stars at the upper main sequence. Although these authors mainly investigated the theoretical behaviour of apparently metal-rich objects, their conclusions also have an impact for the $\lambda $ Bootisgroup: little direct pulsational excitation from Fe-peak elements was found, but effects due to settling of helium along with the enhancement of hydrogen are important. Turcotte et al. (2000) find that, as their models of peculiar stars evolve, they become generally pulsationally unstable near the red edge of the instability strip, whereas the behaviour at the blue edge is mainly sensitive to the surface metal abundance. Although the proposed models are still simplified (e.g. treatment of convection) these preliminary results already point towards the most important effects on the theoretical pulsational instability and behaviour of chemically peculiar stars.

The aim of the present paper is to analyse the pulsational characteristics of the group of $\lambda $ Bootisstars and to test for the presence of a possible Period-Luminosity-Colour-Metallicity relation. The latter is especially interesting in the light of the models by Turcotte et al. (2000). The pulsational characteristics of the $\lambda $ Bootisgroup (e.g. ratio of variable to non-variable objects and distribution of pulsational constants) may help to put tighter constraints on these models.

2 Program stars, observations and reductions

Since our previous works (Paunzen et al. 1997, 1998) several then-selected group members were investigated with classification resolution spectroscopy and found to be misclassified. These are: HD 66920, HD 79025, HD 82573, HD 141851, HD 143148, HD 145782, HD 149303, HD 179791, HD 188164 and HD 192424 (Paunzen 2001). In total, 65 members were selected from the lists of Gray & Corbally (1993) and Paunzen (2001) which contain well established as well as good candidate $\lambda $ Bootis type objects. Together with the two newly discovered objects (HD 42503 and HD 213669; Sect. 2.3.1), we have a sample of 67 $\lambda $ Bootistype stars.


 

 
Table 1: Sites, dates and telescopes used for our survey.
Site Date Telescope Stars Ref.
APT (Fairborn) 05.2001 0.75 3 1
SAAO 04.2001 0.50 8 2
  07.2001      
  08.2001      
  09.2001      
  10.2001      
SAAO 12.2000 0.75 9 3
  01.2001      
SAAO 08.2001 1.00 1 4
Siding Spring 01.2002 0.60 1 5



 

 
Table 2: Observing log of eight newly discovered and one confirmed (HD 75654) pulsating $\lambda $ Bootisstars. Some information on the comparison stars is also given. The differential light curves are shown in Fig. 1.
HD JD hrs mV Spec. Freq. Amp. Ref.
      [mag]   [d-1] [mag]  
13755 2 451 899 3.2 7.84 $\lambda $ Boo 12.50 0.015 3
  2 451 903 2.5     16.85 0.007  
  2 451 905 3.1          
  2 451 909 3.1          
13602     8.52 F6      
13710     8.32 K5      
35242 2 451 900 2.1 6.35 $\lambda $ Boo 38.61 0.005 3
  2 451 902 5.4     34.16 0.003  
  2 451 908 3.3     41.33 0.003  
35134     6.74 A0      
34888     6.78 A5      
42503 2 452 291 4.2 7.45 $\lambda $ Boo 7.00 0.015 5
  2 452 292 1.9          
42058     6.99 A0      
43452     7.71 F5      
75654 2 451 898 3.0 6.38 $\lambda $ Boo 14.80 0.005 3
  2 451 902 1.8     15.99 0.002  
  2 451 905 3.1          
  2 451 906 1.2          
  2 451 907 3.8          
  2 451 909 3.6          
74978     6.87 A1      
75272     6.98 B9.5      
111604 2 452 061 4.1 5.89 $\lambda $ Boo 8.77 0.020 1
112412     5.61 F1      
110375     8.33 F5      
120896 2 452 097 3.9 8.50 $\lambda $ Boo 17.79 0.010 2
121372     8.67 G5      
148638 2 452 097 4.6 7.90 $\lambda $ Boo 16.32 0.016 2
  2 452 123 5.0          
148596     8.60 F2      
148573     8.63 B9      
213669 2 451 823 6.5 7.42 $\lambda $ Boo 15.01 0.023 2
  2 451 826 1.6          
  2 451 827 1.1          
211878     7.70 F5      
214390     7.90 F3      
290799 2 451 904 3.0 10.63 $\lambda $ Boo 23.53 0.006 3
  2 451 906 4.8          
37652     7.35 F5      
290798     10.40 A2      


The photometric observations were performed as described by Paunzen et al. (1998) using photoelectric detectors (except for Ref. "4'', Table 1, for which a CCD was used) and (if possible) two comparison stars. A standard reduction method for dealing with dead-time, dark counts and tube drifts was applied. The sky measurements (typically one per half hour) were subtracted and differential light curves were generated. For the reduction of the CCD frames for HD 290492 the standard SAAO reduction package as well as the program MOMF (Kjeldsen & Frandsen 1992) were used. Figure 1 shows light curves of some of our variable program stars.

Frequencies and amplitudes for the variable program stars (listed in Table 2) were derived using a standard Fourier algorithm (Deeming 1975). An analysis with the Phase-Dispersion-Minimization (Stellingwerf 1978) gave essentially the same results. A star is considered to be constant, if the Fourier spectrum of the differential light curve does not contain a statistically significant peak (Paunzen et al. 1997). These objects are listed in Table 3.


  \begin{figure} \par\includegraphics[width=16cm,clip]{ms2573f1.eps}\end{figure} Figure 1: Differential light curves of eight newly discovered and one confirmed (HD 75654) pulsating $\lambda $ Bootisstars in Strömgren b and Johnson B; the dates of the corresponding nights are given as JD 2 450 000+ (Table 2).
Open with DEXTER

2.1 Previously known pulsating $\lambda $ Bootisstars

The following nine stars were already known as variable. With the only exception of HD 75654 (see below), they have not been re-observed by us:

We have used the published frequencies and amplitudes of these objects from the above-mentioned references in our analysis. If more than one frequency has been published, we have weighted the individual periods with the squared amplitude to obtain a mean period.


 

 
Table 3: Observing log of thirteen $\lambda $ Bootisstars not found to pulsate as well as some comparison star information.
HD/BD JD hrs mV Spec. Limit Ref
      [mag]   [mmag]  
7908 2 451 898 2.0 7.29 $\lambda $ Boo 0.3 3
  2 451 907 2.3        
7629     7.13 A9    
7896     7.95 G6    
24472 2 451 900 2.9 7.09 $\lambda $ Boo 0.8 3
24616     6.70 G8    
25385     7.40 F0    
54272 2 451 908 2.6 8.80 $\lambda $ Boo 1.4 3
54692     8.51 A0    
+19 622     8.90 A2    
74873 2 451 904 3.5 5.89 $\lambda $ Boo 1.6 3
74228     5.65 A3    
75108     8.38 G5    
83277 2 451 901 3.5 8.30 $\lambda $ Boo 1.4 3
83547     8.62 A0    
82709     8.04 A9    
90821 2 452 039 2.0 9.47 $\lambda $ Boo 2.2 1
90878     7.82 F8    
90748     8.67 F8    
107223 2 452 003 5.2 7.35 $\lambda $ Boo 1.9 2
107143     7.87 A1    
107265     8.76 A0    
111005 2 452 004 1.9 7.96 $\lambda $ Boo 2.1 2
110705     8.36 F0    
110989     8.41 F8    
130767 2 452 039 5.5 6.91 $\lambda $ Boo 1.2 1
130556     7.84 F1    
130396     7.41 F8    
149130 2 452 127 5.6 8.50 $\lambda $ Boo 2.4 2
148597     8.25 B9    
149471     8.94 F6    
216847 2 452 190 2.9 7.06 $\lambda $ Boo 1.7 2
  2 452 191 3.2        
216349     7.84 K1    
217686     7.56 F7    
290492 2 451 901 3.0 9.27 $\lambda $ Boo 1.8 2
  2 452 190 2.2        
  2 452 192 4.0        
290575     9.85 F5    
-00 984     8.37 HgMn    
261904 2 452 190 2.1 10.20 $\lambda $ Boo 3.5 4
  2 452 191 2.2        
261941     10.94 A2    


2.2 Group members not observed by us

Five well established members of the $\lambda $ Bootisgroup were not photometrically investigated: HD 110411, HD 125889, HD 170680, HD 184779 and HD 198160. For three of them (HD 110411, HD 170680 and HD 198160) photometric measurements in the HIPPARCOS and TYCHO catalogues (ESA 1997) were found. Since these observations are not optimal to find $\delta $ Scuti type pulsation, only a rough estimate for variability can be made. We find a level of non-variability based on the HIPPARCOS photometry of 3 mmag for HD 110411 and HD 170680, and 4 mmag for HD 198160. In fact, HD 110411 was suspected as variable by Bartolini et al. (1980a), but Antonello & Mantegazza (1982) concluded that there is no evidence for periodic terms in the light curve: different oscillation modes may be excited occasionally and then be damped again. We therefore treat this star as being constant within a limit of 3 mmag. Consequently, the other two objects (HD 125889 and HD 184779) were not considered in the following analysis.

2.3 Notes on individual stars

In the following sections we describe special properties of some individual stars in more detail.

   
2.3.1 HD 42503 and HD 213669

These two objects were suspected $\delta $ Scuti type pulsators based on HIPPARCOS photometry (Handler 2002). Handler (1999) presented Strömgren $uvby\beta$ photometry which puts these stars well within the typical area of the $\lambda $ Bootisobjects in a $m_{\rm 1}$ versus (b-y) diagram (Paunzen et al. 1998). Our photometric measurements confirmed the pulsation.

We have performed additional spectroscopic observations to establish the nature of these stars. These observations were done on the 1.9 m telescope at SAAO in the night of 03./04.10.2000. The Grating Spectrograph with the SITe CCD together with the 600 lines mm-1 grating resulted in a useful wavelength range of 1600 Å, a resolution of 2 Å and a signal-to-noise ratio of about 200. The wavelength calibration was done with the help of a CuAr lamp within standard IRAF routines. The classification was done within the system described by Paunzen (2001). Both objects are very good $\lambda $ Bootiscandidates, with derived spectral types of A2 V ($\lambda $ Boo) and kA1hF0mA1 V $\lambda $Boo for HD 42503 and HD 213669, respectively. The notation of the spectral classification is according to Gray (1988) where k stands for the classification of the Caii K line, h for the hydrogen lines and m for the appearance of the metallic-line spectrum compared to MK standards. We therefore included them in our sample. Figure 2 shows their spectra together with those of two well established $\lambda $ Bootisstars (HD 107233 and HD 198160; taken from Paunzen 2001) which exhibit similar spectral characteristics. However, we note that a final decision on their group membership has to be made after a detailed determination of their chemical abundances (especially of C, N, O and S) which was not done so far.

2.3.2 HD 64491 and HD 111786

Both stars are $\delta $ Scuti type pulsators and were reported as well established members of the group by Gray (1988) and Paunzen & Gray (1997). However, both objects are spectroscopic binary systems (Faraggiana & Bonifacio 1999; Iliev et al. 2001). The published information on these stars does not allow us to decide whether they are true $\lambda $ Bootistype objects, thus we have not included either of them in our sample.

2.3.3 HD 74873

We have re-observed this object because the upper limit for non-variability given by Paunzen et al. (1997) was very high (9.4 mmag). Our new observations showed no variability within a limit of 1.6 mmag.

2.3.4 HD 175445

This object exhibits a peculiar behaviour which we have, so far, been unable to understand. During our first short observing run (on 06/07 July 2001), its magnitude and colour were consistent with their standard values from the literature (b = 7.85, v-b = 0.222), and marginal evidence for pulsational variability was found. However, when we attempted to re-observe the star on 05/06 August 2001, it appeared much fainter and redder than in the previous month.


 

 
Table 4: Pulsating $\lambda $ Bootisstars; an asterisk denotes stars without an accurate HIPPARCOS parallax; $\sigma $(b-y) = $\pm $0.005 mag. In parenthesis are the errors in the final digits of the corresponding quantity.
HD (b-y)0 log  $T_{\rm eff}~$ log g v sin i [Z] MV MB log  $L_{\ast }/L_{\odot }$ log P Q
  [mag] [dex] [dex] [km s-1] [dex] [mag] [mag] [dex]   [d]
6870 0.164 3.865(6) 3.84(11) 165 -1.03(20) +2.29(42) +2.20 1.02(17) -1.19 0.023
11413 0.104 3.899(7) 3.91(21) 125 -1.17(10) +1.49(10) +1.36 1.35(4) -1.38 0.014
13755 0.181 3.850(10) 3.26(10) - -0.75(30) +0.93(10) +0.83 1.57(4) -1.12 0.010
15165 0.189 3.846(12) 3.23(10) 90 -1.15(17) +1.12(16) +1.01 1.50(6) -0.87 0.017
30422 0.098 3.896(6) 4.00(20) 135 -1.50(20) +2.35(2) +2.23 1.01(1) -1.68 0.010
35242 0.058 3.916(5) 3.90(14) 90 -1.40(20) +1.75(22) +1.60 1.26(9) -1.58 0.010
42503 0.110 3.885(16) 3.10(10) - -0.83(20) -0.03(4) -0.14 1.96(2) -0.85 0.013
75654 0.158 3.866(6) 3.77(11) 45 -0.91(11) +1.83(12) +1.74 1.20(5) -1.18 0.019
83041 0.185 3.852(13) 3.76(20) 95 -1.03(8) +1.70(30) +1.60 1.26(12) -1.18 0.018
84948B$^{\ast}$ 0.196 3.833(13) 3.70(15) 55 -0.82(19) +1.63(30) +1.75 1.20(12) -1.11 0.020
87271 0.149 3.876(13) 3.43(10) - -1.11(30) +1.02(8) +0.92 1.53(3) -1.27 0.009
102541 0.141 3.885(10) 4.22(16) - -0.95(20) +2.34(21) +2.23 1.01(9) -1.30 0.029
105058 0.127 3.889(10) 3.77(30) 140 -0.82(7) +0.86(30) +0.75 1.60(12) -1.40 0.010
105759 0.142 3.874(6) 3.65(10) 120 -0.92(30) +1.35(21) +1.25 1.40(8) -1.20 0.015
109738$^{\ast}$ 0.144 3.881(8) 3.90(13) - -1.02(20) +1.85(30) +1.75 1.20(12) -1.49 0.012
110377 0.120 3.888(5) 3.97(14) 170 -0.83(20) +1.96(11) +1.85 1.16(5) -1.45 0.014
111604 0.112 3.890(8) 3.61(25) 180 -1.04(3) +0.48(7) +0.37 1.75(3) -0.94 0.022
120500 0.064 3.915(4) 3.86(10) 125 -0.73(14) +0.85(34) +0.70 1.62(13) -1.32 0.014
120896$^{\ast}$ 0.166 3.861(5) 3.76(10) - -0.82(30) +1.90(30) +1.81 1.18(12) -1.25 0.016
125162 0.042 3.941(8) 4.07(9) 115 -1.61(24) +1.71(23) +1.54 1.28(9) -1.64 0.011
142703 0.177 3.861(9) 3.93(12) 100 -1.32(5) +2.41(12) +2.32 0.97(5) -1.43 0.015
142944$^{\ast}$ 0.198 3.845(8) 3.19(4) 180 -0.91(38) +0.80(30) +0.69 1.62(12) -0.85 0.016
148638$^{\ast}$ 0.106 3.882(13) 3.39(10) - -0.80(30) +0.33(30) +0.23 1.81(12) -1.21 0.009
153747 0.068 3.914(5) 3.70(24) - -0.86(20) +1.24(30) +1.09 1.46(12) -1.31 0.013
168740 0.128 3.883(5) 3.88(14) 145 -0.91(8) +1.82(2) +1.72 1.21(1) -1.44 0.013
168947$^{\ast}$ 0.145 3.878(11) 3.67(10) - -0.74(20) +1.28(30) +1.18 1.43(12) -1.23 0.014
183324 0.032 3.952(10) 4.13(4) 90 -1.47(6) +1.64(42) +1.44 1.32(17) -1.68 0.011
191850$^{\ast}$ 0.163 3.869(9) 3.61(10) - -0.96(30) +1.50(30) +1.41 1.34(12) -1.13 0.017
192640 0.095 3.900(5) 3.95(18) 80 -1.46(8) +1.84(2) +1.71 1.22(1) -1.55 0.011
210111 0.136 3.878(7) 3.84(15) 55 -1.04(20) +1.76(15) +1.66 1.23(6) -1.36 0.014
213669 0.155 3.872(8) 3.82(17) - -0.93(20) +1.79(21) +1.69 1.22(8) -1.18 0.021
221756 0.046 3.930(10) 3.90(3) 105 -0.71(3) +1.16(16) +1.00 1.50(6) -1.36 0.015
290799$^{\ast}$ 0.114 3.889(5) 4.18(10) 70 -0.82(26) +2.62(30) +2.51 0.90(12) -1.37 0.025



 

 
Table 5: $\delta $ Scuti stars selected from the list by Rodriguez et al. (2000); $\sigma $(b-y) = $\pm $0.005 mag; $\sigma $[Z] = $\pm $0.15 dex. In parenthesis are the errors in the final digits of the corresponding quantity.
HD (b-y)0 log  $T_{\rm eff}$ log g v sin i [Z] MV MB log  $L_{\ast }/L_{\odot }$ log P Q
  [mag] [dex] [dex] [km s-1] [dex] [mag] [mag] [dex]   [d]
432 0.211 3.841(4) 3.44(7) 70 +0.45 1.19(29) 1.08 1.47(11) -1.00 0.017
3112 0.127 3.883(5) 3.59(9) 80 +0.28 0.54(84) 0.44 1.73(34) -1.31 0.009
4490 0.156 3.867(3) 3.55(9) 180 +0.22 0.92(15) 0.83 1.57(6) -0.98 0.019
4849 0.168 3.862(2) 3.78(8) - +0.52 1.65(30) 1.56 1.27(12) -1.26 0.016
7312 0.169 3.861(3) 3.79(6) - +0.24 1.71(28) 1.62 1.25(11) -1.38 0.012
8511 0.134 3.880(4) 3.96(6) 190 -0.06 2.04(1) 1.94 1.12(1) -1.16 0.027
8781 0.213 3.838(6) 3.46(6) - -0.03 1.57(18) 1.46 1.32(7) -0.95 0.020
9065 0.200 3.844(6) 3.46(6) - -0.14 1.72(21) 1.61 1.26(8) -1.02 0.018
9100 0.087 3.899(8) 3.53(22) 120 -0.34 0.43(28) 0.30 1.78(11) -0.87 0.024
11522 0.162 3.861(5) 3.41(6) 120 -0.04 0.76(13) 0.67 1.63(5) -1.04 0.014
15550 0.152 3.871(3) 3.84(6) 170 +0.13 1.89(1) 1.80 1.18(1) -1.17 0.022
15634 0.179 3.858(2) 3.81(7) 140 +0.28 1.57(50) 1.48 1.31(20) -1.01 0.028
17093 0.133 3.883(8) 4.04(11) 75 -0.10 2.22(4) 2.12 1.05(2) -1.45 0.016
19279 0.063 3.913(8) 3.76(17) 285 -0.16 1.69(61) 1.54 1.28(25) -1.16 0.022
23728 0.178 3.859(5) 3.70(16) 105 -0.21 1.62(15) 1.53 1.29(6) -1.00 0.025
24809 0.119 3.890(10) 4.26(20) 130 -0.36 2.51(7) 2.40 0.94(3) -1.26 0.035
24832 0.158 3.865(4) 3.69(13) 140 +0.12 1.12(30) 1.03 1.49(12) -0.81 0.035
26574 0.196 3.847(4) 3.49(12) 100 +0.62 1.22(38) 1.11 1.46(15) -1.13 0.013
27397 0.166 3.864(3) 3.96(5) 100 +0.22 2.30(5) 2.21 1.02(2) -1.26 0.022
27459 0.123 3.884(5) 3.96(13) 75 +0.25 1.92(21) 1.82 1.17(9) -1.44 0.014
28024 0.159 3.865(7) 3.40(18) 210 +0.22 0.77(24) 0.68 1.63(9) -0.83 0.022
28319 0.093 3.901(9) 3.70(12) 80 +0.16 0.32(78) 0.19 1.82(31) -1.12 0.016
28910 0.139 3.877(4) 3.97(5) 125 +0.19 1.58(75) 1.48 1.31(30) -1.17 0.024
30780 0.114 3.887(3) 3.87(11) 150 +0.23 1.41(50) 1.30 1.38(20) -1.38 0.013
32846 0.189 3.845(9) 3.37(10) - -0.19 1.16(5) 1.05 1.48(2) -0.87 0.021
50018 0.217 3.836(6) 3.35(10) 135 +0.78 0.49(1.03) 0.37 1.75(41) -0.81 0.019
57167 0.214 3.844(2) 3.97(3) 100 +0.18 2.49(15) 2.38 0.95(6) -1.33 0.019
71496 0.133 3.878(4) 3.61(8) 130 +0.41 1.18(10) 1.08 1.47(4) -1.02 0.021
71935 0.140 3.872(4) 3.67(9) 160 +0.32 1.14(20) 1.04 1.49(8) -1.15 0.016
73575 0.137 3.874(5) 3.41(12) 150 +0.32 0.38(21) 0.28 1.79(8) -0.99 0.015
74050 0.106 3.892(7) 3.85(16) 145 +0.25 1.71(44) 1.59 1.26(18) -1.24 0.019
84999 0.192 3.851(4) 3.41(8) 110 +0.13 1.09(27) 0.99 1.50(11) -0.88 0.021
88824 0.153 3.870(2) 3.83(10) 235 +0.08 1.76(2) 1.67 1.23(1) -0.90 0.039
94985 0.088 3.903(9) 3.62(5) - -0.11 0.82(16) 0.69 1.62(6) -0.82 0.032
103313 0.110 3.889(4) 3.67(8) 70 +0.24 0.79(36) 0.68 1.63(14) -1.10 0.017
104036 0.086 3.899(7) 4.09(14) - +0.01 1.67(40) 1.54 1.28(16) -1.52 0.013
107131 0.097 3.897(5) 4.03(20) 185 -0.08 1.91(25) 1.78 1.19(10) -1.18 0.029
107904 0.224 3.837(6) 3.20(12) 115 +0.68 0.83(15) 0.72 1.61(6) -0.93 0.013
109585 0.208 3.841(4) 3.59(10) 80 +0.16 1.80(18) 1.69 1.22(7) -1.09 0.018
115308 0.199 3.846(6) 3.36(8) 75 +0.06 1.16(2) 1.05 1.48(1) -0.93 0.017
117661 0.095 3.900(4) 3.95(11) 55 +0.14 1.70(12) 1.57 1.27(5) -1.37 0.016
124675 0.111 3.884(6) 3.67(17) 120 -0.11 1.02(29) 0.91 1.54(12) -1.19 0.015
125161 0.128 3.885(8) 4.10(19) 135 +0.08 2.40(14) 2.29 0.98(5) -1.58 0.013
127762 0.112 3.890(3) 3.69(12) 130 +0.02 0.94(2) 0.83 1.57(1) -1.14 0.017
127929 0.143 3.876(3) 3.65(11) 70 +0.00 0.80(29) 0.70 1.62(12) -1.06 0.018
138918 0.146 3.870(5) 3.77(23) 85 +0.16 0.19(1.13) 0.10 1.86(45) -0.81 0.032
143466 0.177 3.863(5) 3.92(15) 145 +0.24 2.29(8) 2.20 1.02(3) -1.12 0.029
152569 0.160 3.864(3) 3.81(13) 195 +0.16 1.83(4) 1.74 1.21(2) -1.12 0.023
155514 0.119 3.886(6) 3.90(16) 175 +0.08 1.49(17) 1.38 1.35(7) -1.05 0.029
171369 0.159 3.863(3) 3.79(8) 80 +0.05 1.64(20) 1.55 1.28(8) -1.04 0.026
176723 0.200 3.848(3) 3.62(9) 265 +0.10 1.66(19) 1.56 1.27(8) -0.87 0.031
177392 0.168 3.861(6) 3.54(16) 140 +0.15 0.96(10) 0.87 1.55(4) -0.96 0.020
177482 0.161 3.862(5) 3.45(8) 145 +0.26 0.86(14) 0.77 1.59(6) -1.01 0.016
181333 0.138 3.877(4) 3.53(6) 55 +0.38 0.47(47) 0.37 1.75(19) -0.82 0.025
182475 0.194 3.850(3) 3.63(14) 130 +0.32 1.61(47) 1.51 1.30(19) -1.11 0.018



 
Table 5: continued.
HD (b-y)0 log  $T_{\rm eff}~$ log g v sin i [Z] MV MB log  $L_{\ast }/L_{\odot }$ log P Q
  [mag] [dex] [dex] [km s-1] [dex] [mag] [mag] [dex]   [d]
185139 0.157 3.869(2) 3.80(7) - +0.29 1.38(51) 1.29 1.39(20) -1.19 0.018
186786 0.181 3.856(2) 3.86(8) - +0.19 2.09(3) 2.00 1.10(1) -1.10 0.027
188520 0.123 3.885(7) 4.05(15) - +0.03 2.19(19) 2.08 1.07(8) -1.26 0.025
199124 0.167 3.859(3) 3.74(8) 150 -0.12 1.89(13) 1.80 1.18(5) -1.00 0.028
199908 0.192 3.848(4) 3.42(7) 60 +0.27 1.23(21) 1.13 1.45(8) -1.10 0.013
206553 0.171 3.859(4) 3.70(15) - +0.20 1.46(2) 1.37 1.35(1) -1.20 0.016
208435 0.198 3.844(5) 3.26(8) - +0.36 0.67(43) 0.56 1.68(17) -0.83 0.017
211336 0.170 3.862(3) 3.90(7) 90 +0.17 2.12(2) 2.03 1.09(1) -1.39 0.015
214441 0.205 3.847(4) 3.55(11) - +0.45 1.28(59) 1.18 1.43(23) -0.90 0.024
215874 0.163 3.863(4) 3.48(5) 100 +0.23 0.88(20) 0.79 1.58(8) -1.06 0.015
217236 0.152 3.868(4) 3.52(8) 100 +0.22 0.51(59) 0.42 1.73(24) -0.90 0.020
219891 0.076 3.902(8) 3.77(15) 165 -0.02 0.80(6) 0.67 1.63(3) -1.00 0.025
220061 0.100 3.882(17) 3.51(2) 140 +0.04 0.95(14) 0.85 1.56(6) -1.27 0.010
223781 0.098 3.897(4) 3.92(12) 165 -0.20 1.47(8) 1.34 1.37(3) -1.22 0.021



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms2573f2.eps}\end{figure} Figure 2: Classification resolution spectra of the two newly discovered $\lambda $ Bootiscandidates HD 42503 (A2 V $\lambda $ Boo; upper panel) and HD 213669 (kA1hF0mA1 V $\lambda $ Boo; lower panel) together with the two well established objects HD 107233 (kA1hF0mA1 V $\lambda $ Boo) and HD 198160 (A2 Vann $\lambda $ Boo) for comparison.
Open with DEXTER

Consequently, we double-checked its correct identification and re-examined the literature. We found no evidence for a misidentification or previous peculiar behaviour. We obtained a 3 hr light curve on the night of 06/07 August 2001, where the object appeared as a star of b = 10.67 and v-b = 1.17. These observations are consistent with an eclipse by a late K subgiant companion. However, the evolutionary history of such a system would require the binary to be close, and no other possible eclipses have yet been reported.

2.3.5 HD 290799

Paunzen et al. (1998) reported this star as constant with an upper limit of 10 mmag in Geneva V1. Our new observations show the star to be pulsating with a frequency of 23.53 d-1 and an amplitude of 6 mmag in Strömgren b.

   
3 Basic stellar parameters

In this section we describe the calibration procedures within various photometric systems and derivation of the basic stellar parameters required to analyse the pulsational characteristics of these stars, such as the effective temperature, surface gravity and the luminosity.

The required standard photometric colours were taken from the General Catalogue of Photometric Data (GCPD; http://obswww.unige.ch/gcpd/) as well as the HIPPARCOS and TYCHO databases (ESA 1997). If available, averaged and weighted mean values were used.

The following calibrations for the individual photometric systems were used to derive effective temperatures and surface gravities:

The calibrations for the Johnson UBV and Geneva 7-colour system need an a-priori knowledge of the reddening, which is, in general, not easy to estimate.

Normally, the reddening for objects within the solar neighborhood is estimated using photometric calibrations in the Strömgren $uvby\beta$ system (Strömgren 1966; Crawford 1979; Hilditch et al. 1983). These calibrations are not very reliable for stars with spectral types from A0 to A3 (Gerbaldi et al. 1999), mainly because for these stars, the reddening free parameter $\beta$is no longer a temperature indicator alone but is also sensitive to the luminosity. From the photometry we find that two of our pulsating (HD 125162 and HD 183324) and nine constant (HD 23392, HD 31295, HD 36726, HD 74873, HD 110411, HD 130767, HD 170680, HD 261904 and HD 294253) program stars fall into A0 to A3 spectral region.

An independent way to derive the interstellar reddening is to use galactic reddening maps, which are derived from open clusters as well as from galactic field stars. Several different models have been published in the literature (Arenou et al. 1992; Hakkila et al. 1997). Chen et al. (1998) compared the results from Arenou et al. (1992) and those derived from the HIPPARCOS measurements and found an overestimation of previously published results from Arenou et al. (1992) for distances less than 500 pc. They consequently proposed a new model for galactic latitudes of $\pm $10 $\hbox{$^\circ$ }$, but otherwise find excellent agreement with the model by Sandage (1972). We have used the proposed model by Chen et al. (1998) to derive the interstellar reddening for all program stars. The values from the calibration of the Strömgren $uvby\beta$ and the model by Chen et al. (1998) are in very good agreement. To minimize possible inconsistencies we have averaged the values from both approaches.

In Table 7, we compare our photometrically derived effective temperatures and surface gravities of 29 program stars from this work (TW) with those of Table 1 from Heiter et al. (2002), which contains averaged values from the literature based on spectroscopic analyses. The average difference for the effective temperature is $\Delta T_{\rm eff}$ = $T_{\rm eff}$(Lit.) -  $T_{\rm eff}$(TW) = +72(210) K, and for the average surface gravity $\Delta \log g$ = $\log g$(Lit.) - $\log g$(TW) = +0.07(24) dex. We note that there are some stars for which the spectroscopically derived values are significantly different from the photometrically derived ones (e.g. HD 106223 and HD 107233). These cases were already extensively discussed by Heiter et al. (2002). Although such deviating cases obviously exist, we believe that our calibration method is consistent and therefore suitable for a statistical analysis.

For all program stars photometrically calibrated absolute magnitudes (assuming that all objects are single) were estimated with an error of $\pm $0.3 mag. As an independent source we have taken the HIPPARCOS parallaxes (if available) to derive absolute magnitudes using the visual magnitude and reddening. Since we also corrected for the Lutz-Kelker effect (Koen 1992) which is only possible for parallax measurements with an absolute error of [ $\sigma(\pi)/\pi$] < 0.175 it seriously limits the useful data. Oudmaijer et al. (1998) showed that this effect has to be taken into account if individual absolute magnitudes are calculated using HIPPARCOS parallaxes. Stars without measurements satisfying [ $\sigma(\pi)/\pi$] < 0.175 are marked with an asterisk in Tables 4 and 6 (20 stars in total). For the other 45 objects we are able to derive weighted means (taking the errors as weights, i.e. a larger error is a lower weight) for the absolute magnitude using the values from the photometric calibration procedure and the conversion of the HIPPARCOS parallax measurements. For the remaining 20 stars only photometrically calibrated absolute magnitudes are available. We then calculated luminosities (log $L_{\ast}$/$L_{\odot}$) using the absolute bolometric magnitude of the Sun $M_{\rm Bol}(\odot)$ = 4.75 mag (Cayrel de Strobel 1996) and bolometric corrections taken from Drilling & Landolt (2000).

For HD 84948B we have used the astrophysical parameters listed by Iliev et al. (2002; Table 1). This is an evolved spectroscopic binary system which contains two similar $\lambda $ Bootiscomponents; Iliev et al. (2002) have taken the binary nature into account.

Individual abundances and projected rotational velocities for members of the $\lambda $ Bootisgroup were published by Uesugi & Fukuda (1982), Venn & Lambert (1990), Stürenburg (1993), Abt & Morrell (1995), Holweger & Rentzsch-Holm (1995), Chernyshova et al. (1998), Heiter et al. (1998), Paunzen et al. (1999a,b), Kamp et al. (2001), Solano et al. (2001), Heiter (2002) and Andrievsky et al. (2002). The individual values were weighted (if possible) with the errors listed in the references and averaged.

The published abundances do not allow an investigation of the correlation of individual abundances of different elements (which have different diffusion properties) with the pulsational period. It is well known that the typical abundance pattern of $\lambda $ Bootisstars is characterized by moderate to strong underabundances of elements heavier than C, N, O and S. To get an overall estimate of the (surface) abundance we have applied the following method:

The third step is only valid for effective temperatures cooler than 8500 K; otherwise the metallicity indices are no longer sensitive. This method was applied to nine pulsating $\lambda $ Bootistype objects: HD 6870, HD 30422, HD 42503, HD 102541, HD 109738, HD 110377, HD 153747, HD 168947 and HD 213669.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{ms2573f3.eps}\end{figure} Figure 3: The histogram of our upper levels for non-variability. See text for details.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.92cm,clip]{ms2573f4.eps}\end{figure} Figure 4: The log  $L_{\ast }/L_{\odot }$ versus log  $T_{\rm eff}$ (upper panel) and MV versus (b-y)0 (lower panel) diagrams for the non-variable (open circles) and pulsating (filled circles) $\lambda $ Bootisstars. The Zero Age Main Sequences are taken from Crawford (1979) and Claret (1995). The borders of the classical instability strip (dotted lines) are taken from Breger (1995). The observed borders from our sample are indicated as filled lines in the lower panel.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.92cm,clip]{ms2573f5.eps}\end{figure} Figure 5: The log  $L_{\ast }/L_{\odot }$ versus log  $T_{\rm eff}$ (upper panel) and MV versus (b-y)0 (lower panel) diagrams for pulsating $\lambda $ Bootis(filled circles) and selected $\delta $ Scuti (open triangles) stars. The location of both samples are comparable justifying our selection criteria of the $\delta $ Scuti type stars. The lines are the same as in Fig. 4.
Open with DEXTER

4 Results

Besides two objects (HD 125889 and HD 184779), all members of the $\lambda $ Bootisgroup were photometrically investigated. All previously published results were taken from Paunzen et al. (1997, 1998) as well as from the references quoted in Sect. 3. Of these 65 stars, 32 are presumed to be constant whereas 33 are pulsating. The upper limits for non-variability, which are below 5 mmag for all but three stars (HD 31925, HD 91130 and HD 294253), are shown in Fig. 3.

In order to investigate the pulsational characteristics of the $\lambda $ Bootisstars as a group, we compare them with those of "normal'' $\delta $ Scuti variables. The next subsection describes the compilation of the latter sample.

4.1 A sample of $\delta $ Scuti stars

As a basis we have used the catalogue of Rodriguez et al. (2000). From this sample, stars have been rejected following these criteria:

Such a choice is based on the characteristics of our $\lambda $ Bootistype sample and is hoped to guarantee a comparable sample of $\delta $ Scuti type stars. In total, 69 objects remain in the sample. The basic parameters, etc. were derived in exactly the same way as for the $\lambda $ Bootistype objects, as described in Sect. 3. Table 5 lists all calibrated parameters together with the periods given by Rodriguez et al. (2000).

4.2 Hertzsprung-Russell-diagram and the pulsational characteristics

First of all, we have investigated the location of all $\lambda $ Bootisstars within the log  $L_{\ast }/L_{\odot }$ versus log  $T_{\rm eff}$and MV versus (b-y)0 diagrams (Fig. 4). The borders of the classical instability strip are taken from Breger (1995). There are several conclusions from this figure:

Figure 5 shows the same diagrams for this sample (filled circles) together with those of the selected $\delta $ Scuti stars (open triangles). Besides one object (HD 57167), the cool borders are in excellent agreement with the observations. However, there are four hot $\lambda $ Bootistype pulsators: HD 120500, HD 125162, HD 183324 and HD 221756. The reason for these shifts is not yet clear. We are able to exclude measurements errors (mean values from several references were used) and the effects of rotation (all stars have moderate v sin i values). In addition, taking the unreddened colours, all four stars are still outside the hot border. Therefore it is somewhat surprising that only one object (HD 183324) lies significantly outside the borders within the log  $L_{\ast }/L_{\odot }$ versus log  $T_{\rm eff}$ diagram.


  \begin{figure} \par\includegraphics[width=7cm,clip]{ms2573f6.eps}\end{figure} Figure 6: The histograms of the pulsational constant Q for the selected $\delta $ Scuti (upper panel) and $\lambda $ Bootis(lower panel) stars.
Open with DEXTER

As a next step towards analyzing the pulsational characteristics we have calculated the pulsation constants given by

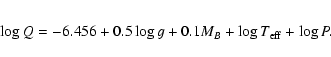
\begin{eqnarray*}\log Q = -6.456 +0.5 \log g + 0.1 M_{B} + \log T_{\rm eff} + \log P. \end{eqnarray*}


The resulting Q-values are listed in Table 4 and in Table 5 for our program $\lambda $ Bootisstars and for the comparison sample of $\delta $ Scuti stars, respectively. For the $\lambda $ Bootisgroup, the Q-values range from 0.038 to 0.033 for the fundamental radial modes and decrease to about 0.012 for the fifth radial overtone (Stellingwerf 1979; Fitch 1981). Figure 6 (lower panel) shows a histogram of the Q-values for the pulsating program stars. It seems that only a few stars, if any, pulsate in the fundamental mode, but there is a high percentage with Q < 0.020 d (high overtone modes).


  \begin{figure} \par\includegraphics[width=7cm,clip]{ms2573f7.eps}\end{figure} Figure 7: Correlation of (b-y)0, the absolute magnitude and metallicity with log P for all $\lambda $ Bootistype stars.
Open with DEXTER


 

 
Table 6: Nonvariable $\lambda $ Bootisstars, an asterisk denotes stars without an accurate HIPPARCOS parallax; $\sigma $(b-y) = $\pm $0.005 mag. In parenthesis are the errors in the final digits of the corresponding quantity.
HD (b-y)0 log  $T_{\rm eff}~$ MV log  $L_{\ast }/L_{\odot }$
  [mag]   [mag]  
319 +0.078 3.904(7) 1.27(19) 1.45(8)
7908 +0.192 3.854(5) 2.60(18) 0.90(7)
23392$^{\ast}$ -0.008 3.991(12) 1.43(30) 1.45(12)
24472 +0.213 3.842(8) 2.14(11) 1.09(5)
31295 +0.029 3.950(9) 1.66(22) 1.32(9)
36726$^{\ast}$ -0.004 3.978(10) 1.74(30) 1.32(12)
54272$^{\ast}$ +0.214 3.846(13) 2.33(30) 1.01(12)
74873 +0.046 3.940(12) 1.82(1) 1.24(1)
81290$^{\ast}$ +0.225 3.839(13) 1.85(30) 1.20(12)
83277 +0.196 3.845(12) 1.49(29) 1.35(12)
84123 +0.226 3.847(11) 1.58(15) 1.31(6)
90821$^{\ast}$ +0.065 3.913(4) 0.74(30) 1.66(12)
91130 +0.073 3.910(5) 1.36(26) 1.42(11)
101108$^{\ast}$ +0.113 3.893(4) 1.33(30) 1.42(12)
106223 +0.225 3.836(16) 1.83(45) 1.22(18)
107233 +0.181 3.861(9) 2.64(13) 0.88(5)
110411 +0.029 3.951(10) 1.90(28) 1.22(11)
111005 +0.222 3.836(4) 1.76(53) 1.24(21)
130767 +0.002 3.964(10) 1.27(2) 1.48(1)
149130$^{\ast}$ +0.208 3.842(6) 1.51(30) 1.34(12)
154153 +0.194 3.848(7) 1.86(29) 1.19(11)
156954 +0.188 3.853(6) 2.81(33) 0.82(13)
170680 -0.013 3.993(11) 0.83(23) 1.70(9)
175445 +0.030 3.930(10) 1.08(27) 1.53(11)
193256$^{\ast}$ +0.101 3.889(5) 1.08(30) 1.51(12)
193281$^{\ast}$ +0.072 3.905(6) 0.41(30) 1.79(12)
198160 +0.103 3.896(7) 1.47(41) 1.36(16)
204041 +0.086 3.902(5) 1.75(18) 1.25(7)
216847 +0.155 3.867(5) 0.93(24) 1.56(10)
261904$^{\ast}$ +0.005 3.974(9) 1.33(30) 1.48(12)
290492$^{\ast}$ +0.084 3.908(8) 2.04(30) 1.14(12)
294253$^{\ast}$ -0.038 4.027(6) 1.32(30) 1.58(12)



 

 
Table 7: Comparison of effective temperatures and surface gravities for $\lambda $ Bootis stars from Heiter et al. (2002; Table 1; columns "Literature'') and this work; $\Delta T_{\rm eff}$ = $T_{\rm eff}$(Lit.) -  $T_{\rm eff}$(TW) = +72(210) K; $\Delta \log g$ = $\log g$(Lit.) - $\log g$(TW) = +0.07(24) dex.
  Literature This work
HD $T_{\rm eff}$ log g $T_{\rm eff}$ log g
  $\pm $200 K $\pm $0.3 dex    
319 8100 3.8 8020(135) 3.74(8)
11413 7900 3.8 7925(124) 3.91(21)
15165 7200 3.7 7010(167) 3.23(10)
31295 8800 4.2 8920(177) 4.20(1)
74873 8900 4.6 8700(245) 4.21(11)
75654 7250 3.8 7350(104) 3.77(11)
81290 6780 3.5 6895(214) 3.82(28)
84123 6800 3.5 7025(145) 3.73(17)
101108 7900 4.1 7810(90) 3.90(18)
105759 8000 4.0 7485(102) 3.65(10)
106223 7000 4.3 6855(247) 3.49(18)
107233 7000 3.8 7265(143) 4.03(10)
109738 7575 3.9 7610(145) 3.90(13)
110411 9100 4.5 8930(206) 4.14(14)
111005 7410 3.8 6860(66) 3.72(10)
125162 8650 4.0 8720(156) 4.07(9)
142703 7100 3.9 7265(150) 3.93(12)
156954 6990 4.1 7130(93) 4.04(13)
168740 7700 3.7 7630(81) 3.88(14)
170680 10000 4.1 9840(248) 4.15(6)
183324 9300 4.3 8950(204) 4.13(4)
192640 7960 4.0 7940(96) 3.95(18)
193256 7800 3.7 7740(94) 3.69(17)
193281 8070 3.6 8035(115) 3.54(4)
198160 7900 4.0 7870(129) 3.99(9)
204041 8100 4.1 7980(97) 3.97(8)
210111 7530 3.8 7550(123) 3.84(15)
221756 9010 4.0 8510(188) 3.90(3)


The distribution of the Q-values for the $\lambda $ Bootistype stars is different from that of the $\delta $ Scuti type sample (Fig. 6, upper panel) at a 99.9% level (derived from a t-test).

We also noticed four pulsators (HD 15165, HD 42503, HD 111604 and HD 142994) that have considerably longer periods (log P > -0.94 corresponding to P < 8.7 d-1) than the rest of our sample. They do, however, show a similar behaviour to the remaining group members.

4.3 The Period-Luminosity-Colour-Metallicity (PLCZ) relation

A Period-Luminosity-Metallicity relation was found for Population II type variables such as RR Lyrae and SX Phoenicis stars as well as Cepheids (Nemec et al. 1994). These objects pulsate in the radial fundamental, first and second overtone modes. The dependence of the pulsational period on the metallicity is purely evolutionary, i.e. older objects exhibit a lower overall abundance and a different pulsational period. The Period-Luminosity-Metallicity relation serves as a distance indicator widely used for extragalactic objects.

The situation for $\lambda $ Bootisstars is very different. All evidence indicates that we find only peculiar surface abundances whereas the overall abundance of the stars is solar, i.e. these stars are true Population I objects. The conclusion that $\lambda $ Bootisstars are true Population I objects is based on their galactic space motions (Faraggiana & Bonifacio 1999) combined with their location in the Hertzsprung-Russell-diagram (Fig. 4). With the exception of the SX Phe stars, Population II type objects are located at much higher absolute magnitudes and thus luminosities than found for the $\lambda $ Bootisgroup. However, the space motions of SX Phe stars are inconsistent with Population I, which facilitates an easy separation from $\lambda $ Bootisstars.

To examine the presence of a PLCZ relation, the following basic approach was chosen:

\begin{eqnarray*}\log P = a + b(b-y)_{0} +c(M_{B}) + d[Z]. \end{eqnarray*}


The [Z]-values range from -0.71 dex to -1.61 dex for the $\lambda $ Bootistype sample whereas the $\delta $Scuti type stars have values from -0.36 dex to +0.78 dex compared to the Sun. The coefficients for the PLCZ relation were determined simultaneously, applying a multiregression analysis (Christensen 1996). This takes into account the individual errors of the bolometric absolute magnitude and metallicity as weights, whereas the errors for the period and colour were assumed to be constant for all stars. The solution was determined using a least-squares fit and a maximum-likelihood method. Both give consistent results, as summarized in Table 8. Figure 7 shows the individual correlations. The correlations of the bolometric magnitude and color with the pulsational period are compatible with those found for the $\delta $ Scuti stars.


 

 
Table 8: Estimates for log  P=a+b(b-y)0+c(MB)+d[Z]for all pulsating program stars (left upper column), for stars with [Z] > -1.3 excluding HD 30422, HD 35242, HD 125162, HD 142703, HD 183324 and HD 192640 (right upper column) as well as for the selected $\delta $ Scuti stars (lower column); F denotes the significance level of the test for a zero hypothesis; in brackets are the standard errors of the estimates.
coeff. value F value F
    [%]   [%]
$\lambda $ Bootis        
a -1.25(9) <0.01 -1.41(9) <0.01
b(b-y)0 +3.01(41) <0.01 +2.71(46) <0.01
c(MB) -0.20(3) <0.01 -0.19(3) <0.01
d[Z] +0.14(6) 13.20 -0.06(17) 74.49
$\delta $ Scuti        
a -1.17(6) <0.01    
b(b-y)0 +2.71(43) <0.01    
c(MB) -0.23(3) <0.01    
d[Z] -0.28(7) <0.01    


To investigate whether the [Z] term is indeed significant, a plot [log P -  2.86(b-y)0 + 0.195(MB)] versus [Z] was drawn (Fig. 8). The coefficients for (b-y)0 and MB are the mean values from Table 8 and are consistent within the errors for both the $\delta $ Scuti and $\lambda $ Bootissamples. Figure 8 shows that both samples exhibit a trend with [Z] (with an offset of about 1 dex). Whereas the [Z] term is statistically significant for the selected sample of $\delta $ Scuti stars, it is caused by only six $\lambda $ Bootis stars with strong underabundances (HD 30422, HD 35242, HD 125162, HD 142703, HD 183324 and HD 192640) and vanishes after excluding them. We have also tested the sample for possible correlations of the [Z] term by excluding other data points. We find no other selection criteria of objects by means of a physical explanation, only "suitable'' discarding would yield a clear correlation. This implies that the peculiar abundances do not affect the pulsational period for the group of $\lambda $ Bootistype stars. However, we find within the errors no difference of the PLC relation for the $\lambda $ Bootisand $\delta $ Scuti type stars.

5 Conclusions

We have investigated the pulsational characteristics of a group of $\lambda $ Bootis stars and compared it to a sample of $\delta $ Scuti pulsators. The latter was chosen such that it matches our program stars within the global astrophysical parameters. The following properties of the $\lambda $ Bootisstars are different from those of the $\delta $ Scuti pulsators:

We find no clear evidence for a significant term for a [Z] correlation with the period, luminosity and colour but the PLC relation is within the errors identical with that of the $\delta $ Scuti type stars. We note that for all but one of the investigated pulsators, high-degree nonradial modes were detected spectroscopically (Bohlender et al. 1999), which represents excellent agreement with our work. The spectral variability of the $\lambda $ Bootisstars is very similar to that seen in rapidly rotating $\delta $ Scuti stars (Kennelly et al. 1992).


  \begin{figure} \par\includegraphics[width=6.4cm,clip]{ms2573f8.eps}\end{figure} Figure 8: Correlation of [Z] for the $\lambda $ Bootis(filled circles) and selected $\delta $ Scuti type (open triangles) stars.
Open with DEXTER

Acknowledgements
This work benefitted from the Fonds zur Förderung der wissenschaftlichen Forschung, project P14984. ERC would like to thank D. Romero, E. Colmenero and S. Potter for their support. Use was made of the SIMBAD database, operated at CDS, Strasbourg, France and the GCPD database, operated at the Institute of Astronomy of the University of Lausanne. We are also indebted to the committees of the SAAO, Siding Spring and Fairborn Observatory who granted observing time.

References

 
Copyright ESO 2002