A&A 392, 605-611 (2002)
DOI: 10.1051/0004-6361:20020956
G. Rüdiger1 - D. Elstner1 - A. F. Lanza2 - Th. Granzer1
1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam,
Germany
2 - Osservatorio Astrofisico di Catania dell'Istituto
Nazionale di Astrofisica, Via Santa Sofia 78, 95125 Catania, Italy
Received 10 April 2002 / Accepted 21 June 2002
Abstract
The question is answered whether dynamo-generated magnetic fields are
able to produce such quadrupole terms in the gravity potential which can
explain the observed cyclic orbital variation of RS CVn stars. We start with spherical
dynamo models with outer convection zones but without any differential
rotation, i.e. with ![]() 2-dynamos which are known as nonoscillating. With
the known anisotropic
2-dynamos which are known as nonoscillating. With
the known anisotropic ![]() -tensor of rapidly rotating stars the magnetic modes
with the lowest dynamo numbers are nonaxisymmetric with a slow azimuthal
drift. We also find, however, stable (i.e. with the lowest dynamo number)
axisymmetric oscillating modes but only for a very special, highly inhomogeneous
-tensor of rapidly rotating stars the magnetic modes
with the lowest dynamo numbers are nonaxisymmetric with a slow azimuthal
drift. We also find, however, stable (i.e. with the lowest dynamo number)
axisymmetric oscillating modes but only for a very special, highly inhomogeneous ![]() -tensor.
The dynamo model is a
linear one with an arbitrary field amplitude which can be scaled in order
to reproduce the observations. The star proves to be as prolate during
the maximum of the toroidal field energy and it proves to be as oblate
during the maximum of the poloidal field energy. In the time average the
influence of the toroidal field dominates and the star is slightly prolate.
From the
computed temporal variations of the gravitation quadrupole moment a magnetic
field of more than 105
G is found in order to produce the period modulation of
order 10-5 which has been observed.
-tensor.
The dynamo model is a
linear one with an arbitrary field amplitude which can be scaled in order
to reproduce the observations. The star proves to be as prolate during
the maximum of the toroidal field energy and it proves to be as oblate
during the maximum of the poloidal field energy. In the time average the
influence of the toroidal field dominates and the star is slightly prolate.
From the
computed temporal variations of the gravitation quadrupole moment a magnetic
field of more than 105
G is found in order to produce the period modulation of
order 10-5 which has been observed.
Key words: magnetic fields - MHD - stars: individual: RS CVn
The RS CVn systems defined by Hall (1976) are characterized by solar-like activity, the signatures of which have been observed in X-rays, UV, optical and radio spectral domains (see Linsky 1988; Rodonò 1992; Guinan & Gimenez 1993; Strassmeier et al. 1993).
On the other hand, the eclipse times of the close binary systems of (say)
4... 5 days varies by about 10 s with the time scale of the activity cycle
(Fig. 1).
The modulation time scale for RS CVn binaries goes from a few to several decades with
a median value of around 40-50 yrs. The amplitude of the modulation is usually of the
order of
![]() (Hall 1989, 1990).
(Hall 1989, 1990).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2560f1.eps}\end{figure}](/articles/aa/full/2002/35/aa2560/Timg16.gif) |
Figure 1: The observed data for some considered close binary systems: period modulation, orbital period and magnetic cycle times (Lanza & Rodonò 1999). |
| Open with DEXTER | |
The presence of a third body in the system, inducing a motion of the binary
around a common centre of mass, with the related orbital period change,
has been proposed as an
explanation. However, in RS CVn systems, the mass derived for
the third body is usually 1... 5 ![]() and it is therefore very difficult
to explain why such remarkable masses have not yet been detected.
and it is therefore very difficult
to explain why such remarkable masses have not yet been detected.
Other possible causes of period modulation have therefore been suggested. Hall (1989) has shown that orbital period changes of alternate sign, in a sample of 101 Algols, are observed only in systems having a secondary of spectral type F5 or later, i.e., those systems with components possessing deep outer convection zones. Systems with an early secondary typically exhibit monotone period changes. Such a result has recently been confirmed by Simon (1999) and Zavala et al. (2002).
The possibility that a time-variable angular momentum loss, due to magnetic activity, be responsible for alternate orbital period changes was investigated by DeCampli & Baliunas (1979). They concluded that this explanation was implausible because of the large mass loss required (about 3-4 orders of magnitude larger than allowed by observations) and also because of the long time scale needed to couple the variation of the stellar rotation to the orbital motion through tidal effects. The characteristic time scale for spin-orbit coupling in RS CVn binaries turns out to be of the order of 103 years, i.e., about two orders of magnitude longer than the periods of the observed short-term modulations (Zahn 1989).
In view of such difficulties, Matese & Whitmire (1983) proposed a new
mechanism,
based on a direct effect related to a cyclic change of the gravitational
quadrupole
moment of active stars. In this paper, we shall discuss the orbital
period
modulation under the hypothesis that a change of the gravitational
quadrupole
moment of active stars is responsible for the phenomenon based on an
oscillating ![]() -dynamo (cf. Lanza et al. 1998).
-dynamo (cf. Lanza et al. 1998).
After Lanza & Rodonò (1999) the orbital modulation of close
binaries is due to a modulation of the quadrupole moment J2 of the
gravitation potential of the active component, i.e.
The modulated quadrupole moment, in the present paper, may be assumed as to be
due to the action of an oscillatory ![]() -dynamo. The typical value
-dynamo. The typical value
![]() holds for RS CVn stars. If the potential series after Legendre
polynomials,
holds for RS CVn stars. If the potential series after Legendre
polynomials,
Consider the equation system
The resulting value for K is
According to the above considerations we are in particular interested in the
coefficients of P2 in the series expansion (2), so that the equation system which we have to solve reads
The equations must be integrated from x=0 where
![]() up to the surface of the unperturbed model at x=1 where we also have used
up to the surface of the unperturbed model at x=1 where we also have used
![]() (see Appendix).
(see Appendix).
The Poisson equation (15)2 must also be integrated from x=0
(where
![]() )
to x=1
where d
)
to x=1
where d
![]() d
d
![]() .
.
The mass and age of the stellar model considered is chosen to represent a
typical RS CVn primary. In Table 1 the main properties of the
model are listed. It was calculated from a fully convective, polytropic (
![]() )
start-model at a temperature of
T0 = 4570 K, luminosity
)
start-model at a temperature of
T0 = 4570 K, luminosity
![]() ,
a helium abundance of Y=0.277 and a metallicity of
Z=0.02.
Its quasi-static evolution to the main sequence and up to the sub-giant phase has been
calculated with an updated version of the Kippenhahn et al. (1967) stellar evolution code.
Rotation was not taken into account.
For the low-temperature regime, opacities of
Alexander & Ferguson (1994) were used to complement the OPAL96
opacities (Iglesias & Rogers 1996).
The OPAL equation-of-state (Rogers et al. 1996) was used whenever
applicable, otherwise the MHD equation of state
(Mihalas et al. 1990) was
adopted. Local mixing-length theory was used for modeling the convection zone.
The
,
a helium abundance of Y=0.277 and a metallicity of
Z=0.02.
Its quasi-static evolution to the main sequence and up to the sub-giant phase has been
calculated with an updated version of the Kippenhahn et al. (1967) stellar evolution code.
Rotation was not taken into account.
For the low-temperature regime, opacities of
Alexander & Ferguson (1994) were used to complement the OPAL96
opacities (Iglesias & Rogers 1996).
The OPAL equation-of-state (Rogers et al. 1996) was used whenever
applicable, otherwise the MHD equation of state
(Mihalas et al. 1990) was
adopted. Local mixing-length theory was used for modeling the convection zone.
The
![]() parameter required by mixing-length theory was set to
parameter required by mixing-length theory was set to
![]() .
The nuclear reactions considered include the entire pp-chain
and the CNO-cycle. The nuclear reaction rates and the energy generation rates
are taken from Caughlan & Fowler (1988).
The inclusion of He-reactions is unnecessary due to the evolutionary stage of
the star.
.
The nuclear reactions considered include the entire pp-chain
and the CNO-cycle. The nuclear reaction rates and the energy generation rates
are taken from Caughlan & Fowler (1988).
The inclusion of He-reactions is unnecessary due to the evolutionary stage of
the star.
| t | M | L | R |
|
|
|
|
| 934 | 2.0 | 35.4 | 8.77 | 4760 | 0.103 | 89.4 |
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2560f2.eps}\end{figure}](/articles/aa/full/2002/35/aa2560/Timg58.gif) |
Figure 2:
The stellar model of a subgiant with
|
| Open with DEXTER | |
The induction equation is
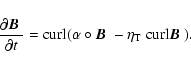 |
(16) |
Rädler & Bräuer (1987) suggested the possible existence of oscillating spherical
![]() -dynamos for outer convection zones of thickness smaller than 31%
for
-dynamos for outer convection zones of thickness smaller than 31%
for ![]() uniform throughout the whole convection domain. The real
situation is much more complicated. The
uniform throughout the whole convection domain. The real
situation is much more complicated. The ![]() -effect is antisymmetric with
respect to the equator and it is strongly anisotropic insofar as the
-effect is antisymmetric with
respect to the equator and it is strongly anisotropic insofar as the
![]() -component differs even by sign from the
-component differs even by sign from the
![]() -component
(
-component
(
![]() ,
Brandenburg et al. 1990; Ferrière 1992;
Rüdiger &
Kitchatinov 1993). The immediate consequence of this situation is the existence
of nonaxisymmetric modes (Rüdiger & Elstner 1994; Moss & Brandenburg 1995).
Always, the nonaxisymmetric modes are drifting rather than oscillating. In the
present paper the idea is followed whether more complicated
,
Brandenburg et al. 1990; Ferrière 1992;
Rüdiger &
Kitchatinov 1993). The immediate consequence of this situation is the existence
of nonaxisymmetric modes (Rüdiger & Elstner 1994; Moss & Brandenburg 1995).
Always, the nonaxisymmetric modes are drifting rather than oscillating. In the
present paper the idea is followed whether more complicated ![]() -profiles exist (for the
components of the anisotropic
-profiles exist (for the
components of the anisotropic ![]() -tensor) for which the
-tensor) for which the
![]() -dynamo indeed
yields oscillating magnetic fields. The tendency of the latitudinal
profiles which we use for the
-dynamo indeed
yields oscillating magnetic fields. The tendency of the latitudinal
profiles which we use for the ![]() -effect is to concentrate it more and more towards the equator,
i.e.
-effect is to concentrate it more and more towards the equator,
i.e.
| A0 | S0 | A1 | S1 | |
| 0 | 8.87 | 8.85 | 9.43 | 9.28 |
| 1 | 28.6 (osc) | 28.5 (osc) | 26.7 | 26.1 |
| 2 | 41.9 (osc) | 41.5 (osc) | 38.5 | 38.6 |
| 3 | 52.8 (osc) | 52.4 (osc) | 49.9 | 50.2 |
| A0 | S0 | A1 | S1 | |
| 0 | 21.9 (osc) | 21.8 (osc) | 14.3 | 14.2 |
| 1 | 41.9 (osc) | 40.5 (osc) | 39.4 | 38.9 |
| 2 | 59.7 (osc) | 57.1 (osc) | 58.8 | 58.3 |
| 3 | 77.3 (osc) | 74.3 (osc) | 76.8 | 76.2 |
| 0 | 1 | 2 | 3 | |
| mode | S0 | S1 | A1 | A1 |
Obviously, there are axisymmetric modes (for ![]() in Eq. (17)) and nonaxisymmetric modes
(for
in Eq. (17)) and nonaxisymmetric modes
(for ![]() in Eq. (17)) - but oscillations do never
occur.
in Eq. (17)) - but oscillations do never
occur.
For anisotropic ![]() -effect (
-effect (
![]() )
there
are, however,
important differences (see Table 3). The excited modes are now:
)
there
are, however,
important differences (see Table 3). The excited modes are now:
| 0 | 1 | 2 | 3 | |
| mode | S1 | S1 | S0(osc) | S0(osc) |
We find nonaxisymmetric field
geometry for latitudinally spread ![]() -effect but for
-effect but for ![]() -effect concentrated in the equatorial region
oscillatory and axisymmetric solutions occur.
This situation remains unchanged for shallow convection zones but for
deep convection zones the oscillatory modes disappear and are again replaced by
drifting nonaxisymmetric modes (Rüdiger et al. 2002).
-effect concentrated in the equatorial region
oscillatory and axisymmetric solutions occur.
This situation remains unchanged for shallow convection zones but for
deep convection zones the oscillatory modes disappear and are again replaced by
drifting nonaxisymmetric modes (Rüdiger et al. 2002).
One always has to check the existence of all possible modes. The mode with the lowest dynamo number is the stable one. All our computations do not confirm the results by Weisshaar (1982) and Schubert & Zhang (2000) who present oscillatory modes for much simpler models. They are probably not presenting the modes with the lowest eigenvalues, i.e. their solutions are unstable in the nonlinear regime (Krause & Meinel 1988).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2560f3.eps}
\medskip\end{figure}](/articles/aa/full/2002/35/aa2560/Timg68.gif) |
Figure 3:
Left: magnetic field configuration for the standard dynamo model
with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2560f4.eps}\medskip
\end{figure}](/articles/aa/full/2002/35/aa2560/Timg69.gif) |
Figure 4: The same as in Fig. 3 but for the timestep 0.2 diffusion time. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2560f5.eps}\end{figure}](/articles/aa/full/2002/35/aa2560/Timg70.gif) |
Figure 5: The same as in Fig. 3 but for the timestep 0.4 diffusion time. Cycle time is 0.4 diffusion times. |
| Open with DEXTER | |
The standard dynamo model with
![]() and with anisotropic
and with anisotropic ![]() -effect
(
-effect
(
![]() )
for
)
for ![]() is used in the
following for the astrophysical applications. In units of
the magnetic diffusivity in the convection zone the inner diffusivity
(
is used in the
following for the astrophysical applications. In units of
the magnetic diffusivity in the convection zone the inner diffusivity
(
![]() )
is 0.01 (high temperature plasma) and the outer diffusivity
(x>1) is 10 (pseudovacuum).
)
is 0.01 (high temperature plasma) and the outer diffusivity
(x>1) is 10 (pseudovacuum).
The cycle time from minimum to minimum proves to be 0.4 diffusion times. The
Figs. 3-5 exhibit the magnetic fields at ![]() ,
,
![]() and
and ![]() covering a complete half-cycle. On the right-hand
sides of the plots the Lorentz force divergence q2* is given. It is
similar in Figs. 3 and 5, but it differs in Fig. 4
by sign. The amplitude is always maximal below the convection zone. The magnetic
pressure there has a source or a sink which yields magnetic-induced
deformation of the star, if - as we do - any magnetic-induced internal flows
are neglected. The resulting magnetic-induced deformation, therefore, can only
be considered as a maximum and, on the other hand, the derived magnetic
amplitudes must be considered as lower limits.
covering a complete half-cycle. On the right-hand
sides of the plots the Lorentz force divergence q2* is given. It is
similar in Figs. 3 and 5, but it differs in Fig. 4
by sign. The amplitude is always maximal below the convection zone. The magnetic
pressure there has a source or a sink which yields magnetic-induced
deformation of the star, if - as we do - any magnetic-induced internal flows
are neglected. The resulting magnetic-induced deformation, therefore, can only
be considered as a maximum and, on the other hand, the derived magnetic
amplitudes must be considered as lower limits.
In Fig. 6 the time series for the magnetic parameters are given, i.e.
the magnetic energy which defines the cycle and the maximal field amplitudes.
The latter are varying with amplitudes of order 0.5. The variation is also reflected by
the maximum of the Lorentz force (not shown) which finally, after the solution
of the Eq. (15), yields the results plotted in Fig. 7. The ![]() at the stellar surface is positive and negative, i.e. the shape of the star varies between
prolate and oblate. Figures 6 and 7 lead thus to the final result
of our computations, i.e.
at the stellar surface is positive and negative, i.e. the shape of the star varies between
prolate and oblate. Figures 6 and 7 lead thus to the final result
of our computations, i.e.
It is interesting to note that Eq. (18) can be compared with that obtained from consideration of the tensor virial theorem (cf. Lanza & Rodonò 1999). Our detailed dynamo model basically confirms the connection between the quadrupole moment variation and the magnetic energy as indicated by that model.
We have shown that a star with a deep convection zone can exhibit cyclic
magnetic activity which may result in an axisymmetric deformation of the stellar
sphere. No differential rotation was taken into account, the dynamo is a simple
![]() -dynamo. However, the cyclic solution only exists for highly
anisotropic and inhomogeneous
-dynamo. However, the cyclic solution only exists for highly
anisotropic and inhomogeneous ![]() -effect. While the used anisotropy is
well-established in theory and simulation, the high concentration of the
-effect. While the used anisotropy is
well-established in theory and simulation, the high concentration of the
![]() -effect towards the equator (which was necessary for the oscillatory
solution) is a speculation.
-effect towards the equator (which was necessary for the oscillatory
solution) is a speculation.
In order to compute the deformation of the star we have neglected the whole system of magnetic-induced internal flows. As this is certainly not completely correct, the resulting quadrupole moment must be considered as a maximal value.
The question arises for the stability against buoyancy of such strong
magnetic fields. Although there is, of course, no final answer to this
question we want to stress that the result is fully consistent with the
advection-computations within the frame of the second order correlation
approximation. It is shown by Kitchatinov & Rüdiger (1992) that for
very strong magnetic fields one of the both advection phenomina
(the "diamagnetism'') disappears while the other one
(the "turbulent buoyancy'') survives and it goes downwards. In nonlinear
dynamo models this effect must also be involved in the simulations but
here, considering kinematic dynamos, this argument only suggests
selfconsistency. Note that the turbulent buoyancy only exists in the
mean-field concept but this is also true for the ![]() -effect
-effect![]() .
.
Our model, of course, only forms an example in order to simulate the real
situation. We started the presented new application of stellar dynamo
theory with three serious approximations. The first one concerns the stellar
model because of its high values of mass and radius. It is not easy to
discuss the consequences of variations of mass and radius. What we present
here is one of the possible examples. Probably more serious is the neglect
of any differential rotation and/or the ignorance of the off-diagonal
elements in the ![]() -tensor. Diamagnetism, turbulent buoyancy and
longitudinal pumping have strong implications for the temporal character of
the dynamo. The presented highly simplified dynamo model is only an
example. Again it is not easy to estimate the influences of the neglected
turbulence-induced phenomena. In particular, all the
-tensor. Diamagnetism, turbulent buoyancy and
longitudinal pumping have strong implications for the temporal character of
the dynamo. The presented highly simplified dynamo model is only an
example. Again it is not easy to estimate the influences of the neglected
turbulence-induced phenomena. In particular, all the ![]()
![]() -dynamos
differ from
-dynamos
differ from ![]() -dynamos by the highly different amplitudes of
toroidal and poloidal fields. There should, of course, result
modifications for the
magnetic-induced gravity quadrupole moment and the resulting minimum magnetic
field necessary for the observation of orbital modulations.
-dynamos by the highly different amplitudes of
toroidal and poloidal fields. There should, of course, result
modifications for the
magnetic-induced gravity quadrupole moment and the resulting minimum magnetic
field necessary for the observation of orbital modulations.
Also the last of our simplifications seems to be a serious one and this is the complete ignorance of internal flows in our model. As known, a dynamo can saturate by inducing large-scale poloidal flow patterns (Malkus & Proctor 1975) as well cyclic variations of the rotation law (Schüssler 1981; Yoshimura 1981). One can thus also argue with Applegate (1992) that the centrifugal force must be included into Eq. (5) in order to remain self-consistent. As known from the theory of the solar torsional oscillations then one has to solve the time-dependent equation for the angular momentum. With the present paper we have only done here a first step to bring together dynamo theory computations with observations in close binary systems.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2560f6.eps}\par\end{figure}](/articles/aa/full/2002/35/aa2560/Timg79.gif) |
Figure 6: Time series for important magnetic parameters. Top: total magnetic energy, Middle: radial magnetic field component at x=0.25 and in the equatorial plane, Bottom: toroidal magnetic field component at x=0.25 and in the equatorial plane. The cycle time is 0.4. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa2560f7.eps}\end{figure}](/articles/aa/full/2002/35/aa2560/Timg80.gif) |
Figure 7:
Time series for |
| Open with DEXTER | |
Acknowledgements
The numerical assistance of Y. Zhang during his stay in Potsdam is acknowledged by the authors.
If the Lorentz force can be neglected near the outer boundary the
momentum equation is
| (A.1) |
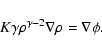 |
(A.2) |
![\begin{displaymath}\frac{{\rm d}\rho}{{\rm d}\phi} = \frac{[\rho(\phi)]^{2-\gamma}}{K \gamma}\cdot
\end{displaymath}](/articles/aa/full/2002/35/aa2560/img84.gif) |
(A.3) |
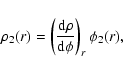 |
(A.6) |
![\begin{displaymath}\rho_{2} (r) = \frac{[\rho(\phi)]^{2-\gamma}}{K \gamma} \phi_{2}(r).
\end{displaymath}](/articles/aa/full/2002/35/aa2560/img90.gif) |
(A.7) |
| (A.8) |
| (A.9) |