A&A 392, 529-533 (2002)
DOI: 10.1051/0004-6361:20020962
A calibration of the 85 Peg binary system
J. Fernandes1 - P. Morel2 - Y. Lebreton3
1 - Observatório Astronómico da Universidade de Coimbra, Santa Clara, 3040 Coimbra,
Portugal and Departamento de Matemática da Faculdade de Ciências e
Tecnologia da Universidade de Coimbra, Portugal
2 - Département Cassini, UMR CNRS 6529, Observatoire de la Côte
d'Azur, BP 4229, 06304 Nice Cedex 4, France
3 -
GEPI, Observatoire de Paris Meudon, 92195 Meudon, France
Received 28 September 2001 / Accepted 11 June 2002
Abstract
We have calibrated the
initial abundances, age and mixing-length parameters
of the visual binary system 85 Pegasi. We obtain an age
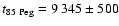 Myr, masses
Myr, masses
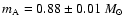 and
and
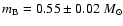 ,
an initial helium mass fraction
,
an initial helium mass fraction
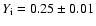 ,
an initial metallicity
,
an initial metallicity
![$\rm [\frac{Fe}H]_i=-0.185\pm0.054$](/articles/aa/full/2002/35/aa1948/img14.gif) and mixing-length parameters
and mixing-length parameters
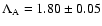 and
and
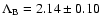 .
We find that, as already proposed, 85 Peg B is itself
a binary.
The mass of the unseen companion is
.
We find that, as already proposed, 85 Peg B is itself
a binary.
The mass of the unseen companion is
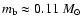 .
.
Key words: stars: binaries: visual - stars: evolution -
stars: fundamental parameters - stars: individual: 85 Peg
1 Introduction
The calibration of a binary system is based on the
adjustment of stellar modeling parameters
![$(t_\star, Y_{\rm i}, {\rm [\frac{Fe}H]_i}, \Lambda_{\rm A}, \Lambda_{\rm B})$](/articles/aa/full/2002/35/aa1948/img18.gif) to the observational data at the age
to the observational data at the age 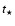 of the system, with the reasonable hypothesis of a common origin
for both components (same initial chemical composition and age).
of the system, with the reasonable hypothesis of a common origin
for both components (same initial chemical composition and age).
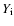 and
and
![${\rm [\frac{Fe}H]_i}$](/articles/aa/full/2002/35/aa1948/img20.gif) are, respectively, the initial
helium mass fraction and metallicity,
are, respectively, the initial
helium mass fraction and metallicity,
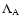 and
and
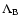 are
respectively the mixing-length parameters of the primary A and secondary B.
For each component one also infers a mass value
consistent with theoretical stellar modeling.
are
respectively the mixing-length parameters of the primary A and secondary B.
For each component one also infers a mass value
consistent with theoretical stellar modeling.
Taking into account the most recent theoretical and observational astrometric,
spectroscopic and photometric results we undertake the calibration of
85 Pegasi (HD 224930, HIP 171, BD+26 4734 4, HR 9088, 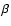 733
ADS 17175, IDS 23569 +2633;
733
ADS 17175, IDS 23569 +2633;
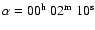 ,
,
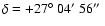 (2000)). It is a well-known visual
and single-lined spectroscopic binary system.
The components, 85Peg A and B, are main sequence low mass
stars of spectral types G5 and K7 respectively (ten
Brummelaar et al. 2000). The shortness of the period (
(2000)). It is a well-known visual
and single-lined spectroscopic binary system.
The components, 85Peg A and B, are main sequence low mass
stars of spectral types G5 and K7 respectively (ten
Brummelaar et al. 2000). The shortness of the period (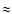 27 years) and the proximity to the Sun (
27 years) and the proximity to the Sun (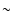 12pc) give it an
interesting place among the binary stars. The visual orbit is very well
known (Hall 1948). Nevertheless, some studies of the orbit have
been recently published. The latest (Söderhjelm 1999) has yielded improvements to the Hipparcos trigonometric parallax and orbit,
combining data from the satellite with ground-based observations.
85Peg is one of the rare cases for which the mass ratio can be
obtained by both astrometric and spectroscopic observations. For many years investigators have claimed that 85 Peg B, the fainter component,
is more massive than 85 Peg A the brighter one (e.g. Slocum 1915;
Hall 1948; Underhill 1963). This was found again by
Martin & Mignard (1998) on the basis of Hipparcos
observations. This abnormal situation could be explained by the fact that
85PegB is an undetected binary. 85
PegA is known as a metal-poor star and found to be much older
than the Sun (Perrin et al. 1977). Because of its small mass, 85 Peg
A sits close to the ZAMS which gives a constraint on its initial helium
abundance, a value traditionally associated with
primordial helium (Perrin et al. 1977; Catchpole et al. 1967;
Smak 1960).
12pc) give it an
interesting place among the binary stars. The visual orbit is very well
known (Hall 1948). Nevertheless, some studies of the orbit have
been recently published. The latest (Söderhjelm 1999) has yielded improvements to the Hipparcos trigonometric parallax and orbit,
combining data from the satellite with ground-based observations.
85Peg is one of the rare cases for which the mass ratio can be
obtained by both astrometric and spectroscopic observations. For many years investigators have claimed that 85 Peg B, the fainter component,
is more massive than 85 Peg A the brighter one (e.g. Slocum 1915;
Hall 1948; Underhill 1963). This was found again by
Martin & Mignard (1998) on the basis of Hipparcos
observations. This abnormal situation could be explained by the fact that
85PegB is an undetected binary. 85
PegA is known as a metal-poor star and found to be much older
than the Sun (Perrin et al. 1977). Because of its small mass, 85 Peg
A sits close to the ZAMS which gives a constraint on its initial helium
abundance, a value traditionally associated with
primordial helium (Perrin et al. 1977; Catchpole et al. 1967;
Smak 1960).
The photometry and the atmospheric parameters of 85Peg
A have been determined many times. The first spectroscopic determination of the
metallicity is from Wallerstein & Helfer (1959), while the most
recent metallicity and effective temperature determinations are due to
van't Veer (2000) and Fulbright (2000). While
85PegA is a well known star, the secondary
component is less well known. The greatest limitations to studying 85 PegB in detail were the lack of individual
photometric and spectroscopic measurements due to its proximity to 85PegA (
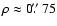 ). Recently,
ten Brummelaar et al. (2000), performed differential photometry
in the Johnson VRI system for both stars using adaptative optics, which allows us to determine the
effective temperatures and bolometric magnitudes of both components.
). Recently,
ten Brummelaar et al. (2000), performed differential photometry
in the Johnson VRI system for both stars using adaptative optics, which allows us to determine the
effective temperatures and bolometric magnitudes of both components.
In their pioneering work Fernandes et al. (1998) tried to calibrate
the helium abundance and age of both 85PegA and B by
means of stellar models. No solution was possible when fitting both components
for the same helium and age values. The models appeared to be
hotter than the observations. The discrepancy appears to be removed if the
microscopic diffusion of helium and heavy elements, the enrichment of
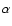 -elements and the non- LTE effects in the iron abundances
determinations are taken into account in models of low mass
stars (Lebreton et al. 1999). Nevertheless, Lebreton et al. did not perform a full calibration of 85Peg
A and did not examine the secondary component.
-elements and the non- LTE effects in the iron abundances
determinations are taken into account in models of low mass
stars (Lebreton et al. 1999). Nevertheless, Lebreton et al. did not perform a full calibration of 85Peg
A and did not examine the secondary component.
Our purpose here is (1) to provide a complete modeling of the system
based on more appropriate stellar models (i.e. including microscopic
diffusion) and (2) to propose a calibration of the unknown parameters
(age, helium, individual masses) that fulfills the recent
observational constraints.
The paper is divided as follows. In
Sect. 2, we collect and discuss the observational constraints.
Section 3 is devoted to the description of physics and
modeling.
We summarize and
conclude in Sect. 4.
For 85Peg we are in the fortunate position of having two precise,
self consistent and independent determinations of the trigonometrical
parallax and improved orbital elements; from these data individual masses
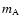 and
and 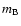 can be derived independently.
Table 1 shows the excellent agreement of the relevant elements
of the astrometric orbits of Hall (1948) and
Söderhjelm (1999).
The first determination of the parallax is the
standard photographic parallax (Wyller 1956; Heintz 1993)
based on improved orbit and several decades of photographic long focus
observations: the absolute photographic parallax amounts to
can be derived independently.
Table 1 shows the excellent agreement of the relevant elements
of the astrometric orbits of Hall (1948) and
Söderhjelm (1999).
The first determination of the parallax is the
standard photographic parallax (Wyller 1956; Heintz 1993)
based on improved orbit and several decades of photographic long focus
observations: the absolute photographic parallax amounts to
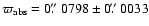 (Heintz 1993).
The second determination is the recently improved adjustment of parallax
and orbital elements by Söderhjelm (1999) based on the
Hipparcos 3.25 yr data and old ground-based observations yielding
(Heintz 1993).
The second determination is the recently improved adjustment of parallax
and orbital elements by Söderhjelm (1999) based on the
Hipparcos 3.25 yr data and old ground-based observations yielding
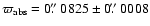 .
With the orbit of Hall (1948) and the parallax of Heintz (1993)
we derive the sum of masses
.
With the orbit of Hall (1948) and the parallax of Heintz (1993)
we derive the sum of masses
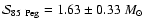 .
Using the data from Söderhjelm (1999) we obtain
.
Using the data from Söderhjelm (1999) we obtain
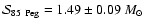 .
For the sum of
masses we adopt the weighted average value:
.
For the sum of
masses we adopt the weighted average value:
An estimate of the mass fraction
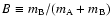 is provided by long-focus astrometry (Heintz 1993):
is provided by long-focus astrometry (Heintz 1993):
Another estimate of Bis provided by the spectroscopic orbit (e.g. Underhill 1963).
Combined spectroscopic observations covering about
four decades and astrometric measurements give
the velocity semi-amplitude of the primary
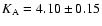 kms-1 (Duquennoy & Mayor 1991). With the
adopted orbital elements and parallax, we derive the "spectroscopic'' mass
fraction:
kms-1 (Duquennoy & Mayor 1991). With the
adopted orbital elements and parallax, we derive the "spectroscopic'' mass
fraction:
Note the remarkable agreement between spectroscopic and photographic
determinations of the mass fraction. A weighted average of the photographic and
spectroscopic values leads to:
With the sum of masses and mass fraction derived above, the masses of the
components are respectively:
showing 85PegA definitively to be the more massive
star.
Stellar parameters were determined from spectroscopic and
photometric analysis. Table 2 lists recently published data
for the photometry, effective temperature and metallicity of 85
Peg.
For 85 Peg A we chose to retain the recent
determinations
![$\rm {[\frac{Fe}{H}]}_A=-0.69~dex$](/articles/aa/full/2002/35/aa1948/img49.gif) and
and
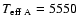 K
of van't Veer (2000). This
K
of van't Veer (2000). This
 determination
relies on the careful fit of Balmer line profiles with Kurucz's (1991)
ATLAS model atmospheres with the constraint that the model reproduces
both the
determination
relies on the careful fit of Balmer line profiles with Kurucz's (1991)
ATLAS model atmospheres with the constraint that the model reproduces
both the
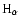 and
and
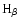 profiles.
Furthermore we point out that, according to
Thévenin & Idiart (1999), the metallicity of metal-poor
stars, computed using model atmospheres in the LTE approximation
is underestimated by about 0.12 dex at the metallicity of 85 Peg.
This is particularly important for the stellar position on the HR
diagram (Lebreton et al. 1999).
We take into account
this correction and adopt the value
profiles.
Furthermore we point out that, according to
Thévenin & Idiart (1999), the metallicity of metal-poor
stars, computed using model atmospheres in the LTE approximation
is underestimated by about 0.12 dex at the metallicity of 85 Peg.
This is particularly important for the stellar position on the HR
diagram (Lebreton et al. 1999).
We take into account
this correction and adopt the value
![$\rm {[\frac{Fe}{H}]}_A=-0.57\pm 0.11$](/articles/aa/full/2002/35/aa1948/img53.gif) (Thévenin 2001).
The
(Thévenin 2001).
The 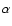 -elements (Mg, Ca, Si, Na, Al, Ti) have been found to be enriched
with respect to the Sun in 85 Peg A (Fuhrmann 1998;
van't Veer 2000; Fulbright 2000).
In our calculations we take account of an
-elements (Mg, Ca, Si, Na, Al, Ti) have been found to be enriched
with respect to the Sun in 85 Peg A (Fuhrmann 1998;
van't Veer 2000; Fulbright 2000).
In our calculations we take account of an 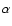 -elements enrichment,
-elements enrichment,
![$\rm [\alpha/Fe]=+0.40\ dex$](/articles/aa/full/2002/35/aa1948/img54.gif) ,
through appropriate opacities and input
mixture.
We computed the effective temperature of 85 Peg B using the calibrations
,
through appropriate opacities and input
mixture.
We computed the effective temperature of 85 Peg B using the calibrations
![$T_{%
\rm {eff}}=T_{\rm {eff~}}\rm {\{color,\rm {[\frac{Fe}{H}]}\}}$](/articles/aa/full/2002/35/aa1948/img55.gif) from Lejeune et al. (1998) and Bessell et al. (1998).
We use both the
color index (R-I) and (V-I) from ten Brummelaar et al. (2000).
These indices are not very sensitive to the metallicity (Alonso et al. 1996). We obtain
from Lejeune et al. (1998) and Bessell et al. (1998).
We use both the
color index (R-I) and (V-I) from ten Brummelaar et al. (2000).
These indices are not very sensitive to the metallicity (Alonso et al. 1996). We obtain
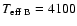 K using (R-I) and
K using (R-I) and
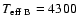 K using (V-I). We choose
K using (V-I). We choose
 K as a representative value of the effective
temperature for the secondary.
K as a representative value of the effective
temperature for the secondary.
The luminosities are computed using the photometry of
ten Brummelaar et al. (2000), the corrected
Hipparcos parallax from Söderhjelm (1999) and the bolometric
correction either from Bessell et al. (1998) or from Flower (1996).
Using Bessell et al.'s (1998) results we obtain
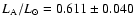 and
and
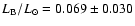 and with Flower's (1996)
results we get
and with Flower's (1996)
results we get
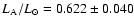 and
and
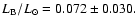 The agreement is satisfactory
and we take the average values.
The agreement is satisfactory
and we take the average values.
Table 3 lists the sum of masses, mass fraction, effective
temperatures, luminosities and metallicities we selected to constrain the
models.
3 Modeling
Stellar
models have been computed using the CESAM code (Morel 1997).
The physics of the models and the calibration method
employed here are described in Morel et al. (2000); element diffusion
and pre-main sequence evolution are taken into account. We
search a solution with the 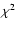 -minimization described by Lastennet et
al. (1999) and Morel et al. (2000).
The confidence limits of each modeling parameter, the other being fixed,
correspond to the maximum/minimum values it can reach, in order that the
generated models fit the observable targets within their error bars.
Table 4 lists the set of modeling parameters
we derive for 85 Peg A & B. Figure 1
shows the corresponding
evolutionary tracks in the HR diagram.
-minimization described by Lastennet et
al. (1999) and Morel et al. (2000).
The confidence limits of each modeling parameter, the other being fixed,
correspond to the maximum/minimum values it can reach, in order that the
generated models fit the observable targets within their error bars.
Table 4 lists the set of modeling parameters
we derive for 85 Peg A & B. Figure 1
shows the corresponding
evolutionary tracks in the HR diagram.
Table 4:
Calibration parameters and global parameters of 85 Peg A and B
models lying within the uncertainty boxes.
The four first rows show the modeling parameters
 is the age of the binary in Myr,
is the age of the binary in Myr,
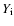 ,
,
![${\rm [\frac{Fe}H]_i}$](/articles/aa/full/2002/35/aa1948/img20.gif) are the initial values of respectively the
helium mass fraction and the metallicity,
are the initial values of respectively the
helium mass fraction and the metallicity,  is the mixing-length
parameter.
The next six rows shows the theoretical values obtained
for the observational constraints of
Table 3 recalled in parenthesis,
is the mixing-length
parameter.
The next six rows shows the theoretical values obtained
for the observational constraints of
Table 3 recalled in parenthesis,
 is the sum of masses in solar unit, B is the mass fraction,
is the sum of masses in solar unit, B is the mass fraction,
 in K and L in solar unit are respectively the effective
temperature and the luminosity,
in K and L in solar unit are respectively the effective
temperature and the luminosity,
![$\rm [\frac{Fe}H]_s$](/articles/aa/full/2002/35/aa1948/img98.gif) is the surface metallicity.
In next rows
m is the mass in solar unit, R the radius in solar unit and
is the surface metallicity.
In next rows
m is the mass in solar unit, R the radius in solar unit and  the helium mass fraction at the surface.
the helium mass fraction at the surface.
| |
 |
 |
 |
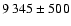 |
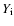 |
 |
![${\rm [\frac{Fe}H]_i}$](/articles/aa/full/2002/35/aa1948/img20.gif) |
 |
 |
 |
 |
 |
 |
| B |
 |
 |
 |
 |
| L |
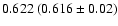 |
 |
![$\rm [\frac{Fe}H]_s$](/articles/aa/full/2002/35/aa1948/img98.gif) |
 |
-0.49 |
| m |
 |
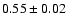 |
| R |
0.846 |
0.500 |
 |
0.216 |
0.237 |
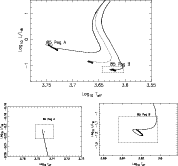 |
Figure 1:
Evolutionary tracks in the H-R diagram (see text). Dashed rectangles delimit
the observed uncertainty domains. Top panel: full tracks from PMS, the dotted
evolutionary track is for of a
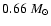 model computed with the
calibration parameters of 85 Peg B (see text). The stellar evolution
sequences are initialized on the pre-main sequence soon after the deuteron
ignition. The "+'' denote 1 Gyr time intervals along the evolutionary
tracks. Bottom left and right panels: enlargements around the observed
85 Peg A, & B loci.
model computed with the
calibration parameters of 85 Peg B (see text). The stellar evolution
sequences are initialized on the pre-main sequence soon after the deuteron
ignition. The "+'' denote 1 Gyr time intervals along the evolutionary
tracks. Bottom left and right panels: enlargements around the observed
85 Peg A, & B loci. |
| Open with DEXTER |
4 Discussion and conclusion
According to the 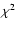 minimization we achieved the first
calibration of the visual binary system
85 Peg, i.e. we found a set of calibration parameters
minimization we achieved the first
calibration of the visual binary system
85 Peg, i.e. we found a set of calibration parameters
![$(t_\star, Y_{\rm i}, {\rm [\frac{Fe}H]_i}, \Lambda_{\rm A}, \Lambda_{\rm B})$](/articles/aa/full/2002/35/aa1948/img18.gif) and theoretical masses
and theoretical masses 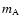 and
and 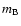 which
give models that fit the observables within their error bars.
Table 4 and Fig. 1 show the calibration
parameters and the evolutionary tracks in the HR diagram.
The most amazing result concerns the masses in the
system. Table 4 shows that the models predict
the sum of masses with satisfactory
agreement (error of 4.6% between models and observations).
This is also true for the mass of 85 Peg A (error of 4.5%). The fact
that the observational mass of the main component is in agreement with the
"astrophysical'' one was already pointed out by Lebreton et
al. (1999). On
the other hand, the mass ratio is poorly reproduced. This has a direct
influence on the prediction of the mass of 85 Peg B:
which
give models that fit the observables within their error bars.
Table 4 and Fig. 1 show the calibration
parameters and the evolutionary tracks in the HR diagram.
The most amazing result concerns the masses in the
system. Table 4 shows that the models predict
the sum of masses with satisfactory
agreement (error of 4.6% between models and observations).
This is also true for the mass of 85 Peg A (error of 4.5%). The fact
that the observational mass of the main component is in agreement with the
"astrophysical'' one was already pointed out by Lebreton et
al. (1999). On
the other hand, the mass ratio is poorly reproduced. This has a direct
influence on the prediction of the mass of 85 Peg B:
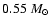 from the models against
from the models against  0.66
0.66  from the observations.
Our fit strongly suggests that 85 Peg B is itself a binary B-b, with a
from the observations.
Our fit strongly suggests that 85 Peg B is itself a binary B-b, with a
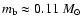 third component.
The theoretical mass we derive for the fainter component significantly
differs from the astrometric result by more than
third component.
The theoretical mass we derive for the fainter component significantly
differs from the astrometric result by more than 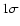 .
Such disagreement between the mass determinations from astrometric and from
stellar modeling reveals either erroneous data (observational or theoretical)
or a too large astrometrical mass determination due to an unseen component.
On the other hand, one reasonably expects a
mass difference between the two main sequence stars 85Peg A & B
fulfilling the mass luminosity relationship ( MLR).
Using the MLR in the V filter of Henry &
Mc Carthy (1993, formula 3a) one derives a mass difference
of
.
Such disagreement between the mass determinations from astrometric and from
stellar modeling reveals either erroneous data (observational or theoretical)
or a too large astrometrical mass determination due to an unseen component.
On the other hand, one reasonably expects a
mass difference between the two main sequence stars 85Peg A & B
fulfilling the mass luminosity relationship ( MLR).
Using the MLR in the V filter of Henry &
Mc Carthy (1993, formula 3a) one derives a mass difference
of 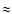
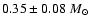 between the components,
while the astrometric data predict
between the components,
while the astrometric data predict 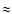
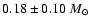 .
This difference is
consistent with the possibility of an unseen
companion around the secondary.
We emphasize that a star of
.
This difference is
consistent with the possibility of an unseen
companion around the secondary.
We emphasize that a star of
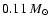 is 35 times fainter than a
is 35 times fainter than a
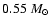 star (Baraffe et
al. 1998) and does not contribute to the luminosity of 85 Peg B+b,
while it affects the astrometric mass determination.
Figure 1 shows the evolutionary tracks for the models of
star (Baraffe et
al. 1998) and does not contribute to the luminosity of 85 Peg B+b,
while it affects the astrometric mass determination.
Figure 1 shows the evolutionary tracks for the models of
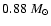 and
and
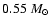 corresponding to our best solution.
We also plot the evolutionary track of a
corresponding to our best solution.
We also plot the evolutionary track of a
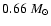 model computed
with the same initial chemical composition and age.
Our results give a mixing-length parameter for 85 Peg A
slightly lower than the solar one (
model computed
with the same initial chemical composition and age.
Our results give a mixing-length parameter for 85 Peg A
slightly lower than the solar one (
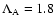 against
against
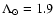 ). This could support the suggestion that the mixing-length parameter decreases with
decreasing mass made by Lebreton et al. (2001) in the case of
the Hyades cluster. This is however in disagreement
with results from the 2D simulations where the
mixing-length parameter appears to decrease
with increasing effective temperature (Ludwig et al. 1999).
According to our calibration 85 Peg is older than the
Sun and is under-abundant in helium with respect to the Sun, which is
consistent with what is expected for an old star in the Galaxy (Perrin
et al. 1977). We point out that, due to element diffusion during evolution, our results show an observed metallicity at the surface of 85 Peg A and B considerably lower than the initial value, giving a 0.3 dex depletion in 9 Gyr.
). This could support the suggestion that the mixing-length parameter decreases with
decreasing mass made by Lebreton et al. (2001) in the case of
the Hyades cluster. This is however in disagreement
with results from the 2D simulations where the
mixing-length parameter appears to decrease
with increasing effective temperature (Ludwig et al. 1999).
According to our calibration 85 Peg is older than the
Sun and is under-abundant in helium with respect to the Sun, which is
consistent with what is expected for an old star in the Galaxy (Perrin
et al. 1977). We point out that, due to element diffusion during evolution, our results show an observed metallicity at the surface of 85 Peg A and B considerably lower than the initial value, giving a 0.3 dex depletion in 9 Gyr.
Acknowledgements
We would like to express our thanks to the anonymous referee,
for helpful comments.
We would like to express our thanks to C. van't Veer, R. Cayrel,
F. Thévenin and E. Lastennet for illuminating discussions
and helpful advices.
This research has made use of the Simbad data base, operated at
CDS, Strasbourg, France.
This work has been performed using the computing facilities
provided by the OCA program
"Simulations Interactives et Visualisation en Astronomie et Mécanique
(SIVAM)''.
This work was partially supported by the "Convénio ICCTI-Embaixada
de França'' (B0-60)
and by the project "PESO/P/PRO/15128/1999''
from "Fundação para a Ciência e Tecnologia''.
-
Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 291, 895
In the text
NASA ADS
-
Axer, M., Fuhrmann, & Gehren, T. 1994, A&A, 291, 896
In the text
-
Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403
In the text
NASA ADS
-
Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231
In the text
NASA ADS
-
Catchpole, R., Pagel, B., & Powell, A. 1967, MNRAS, 136,
403
In the text
NASA ADS
-
Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485
In the text
NASA ADS
-
Fernandes, J., Lebreton, Y., Baglin, A., & Morel, P.
1998, A&A, 338, 455
In the text
NASA ADS
-
Flower, P. J. 1996, ApJ, 469, 355
In the text
NASA ADS
-
Fulbright, J. P. 2000, AJ, 120, 1841
In the text
NASA ADS
-
Fuhrmann, K. 1998, A&A, 338, 161
In the text
NASA ADS
-
Hall, R. J. Jr 1948, AJ, 54, 102
In the text
NASA ADS
-
Heintz, W. D. 1993, AJ, 105, 1188
In the text
NASA ADS
-
Henry, T. J., & Mc Carthy, D. W. 1993, AJ, 106, 773
In the text
NASA ADS
-
Kurucz, R. L. 1991, in Stellar Atmospheres: Beyond
Classical Models, ed. L. Crivallery, I. Hibeny, & D. G. Hammer, NATO
ASI Series (Kluwer, Dordrecht)
In the text
-
Lastennet, E., Valls-Gabaud, D., Lejeune, Th., & Oblak,
E. 1999, A&A, 349, 485
In the text
NASA ADS
-
Lejeune, Th., Cusenier, F., & Buser, R. 1998, A&A, 130, 65
In the text
-
Lebreton, Y., Perrin, M.-N., Cayrel, R., Baglin, A.,
& Fernandes, J. 1999, A&A, 350, 587
In the text
NASA ADS
-
Lebreton, Y., Fernandes, J., & Lejeune, T. 2001, A&A, 374, 540
In the text
NASA ADS
-
Ludwig, H. G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111
In the text
NASA ADS
-
Martin, C., & Mignard, F. 1998, A&A, 330, 585
In the text
NASA ADS
-
Morel, P. 1997, A&AS, 124, 597
In the text
NASA ADS
-
Morel, P., Provost, J., Lebreton, Y., Thévenin,
F., & Berthomieu, G. 2000, A&A, 363, 675
In the text
NASA ADS
-
Perrin, M.-N., Hejleson, P. M., Cayrel de Strobel, G., et al. 1977, A&A, 54, 779
In the text
NASA ADS
-
Slocum, F. 1915, ApJ, 41, 273
In the text
-
Smak, J. 1960, Acta Astron., 10, 153
In the text
-
Söderhjelm, S. 1999, A&A, 341, 121
In the text
NASA ADS
-
tenBrummelaar, T., Mason, B., McAlister,
H., et al. 2000, AJ, 119, 2403
In the text
NASA ADS
-
Thévenin, F., & Idiart, T. 1999, ApJ, 521, 753
In the text
NASA ADS
-
Thévenin, F. 2001, private communication
In the text
-
van't Veer, C. 2000, private communication
In the text
-
Underhill, A. B. 1963, Pub. Dominion Astrophys. Obs.,
12, 159
In the text
NASA ADS
-
Wallerstein, G., & Helfer, H. L. 1959, ApJ, 129, 720
In the text
NASA ADS
-
Wyller, A. A. 1956, AJ, 61, 76
In the text
NASA ADS
Copyright ESO 2002
![]() Myr, masses
Myr, masses
![]() and
and
![]() ,
an initial helium mass fraction
,
an initial helium mass fraction
![]() ,
an initial metallicity
,
an initial metallicity
![]() and mixing-length parameters
and mixing-length parameters
![]() and
and
![]() .
We find that, as already proposed, 85 Peg B is itself
a binary.
The mass of the unseen companion is
.
We find that, as already proposed, 85 Peg B is itself
a binary.
The mass of the unseen companion is
![]() .
.
![]() to the observational data at the age
to the observational data at the age ![]() of the system, with the reasonable hypothesis of a common origin
for both components (same initial chemical composition and age).
of the system, with the reasonable hypothesis of a common origin
for both components (same initial chemical composition and age).
![]() and
and
![]() are, respectively, the initial
helium mass fraction and metallicity,
are, respectively, the initial
helium mass fraction and metallicity,
![]() and
and
![]() are
respectively the mixing-length parameters of the primary A and secondary B.
For each component one also infers a mass value
consistent with theoretical stellar modeling.
are
respectively the mixing-length parameters of the primary A and secondary B.
For each component one also infers a mass value
consistent with theoretical stellar modeling.
![]() 733
ADS 17175, IDS 23569 +2633;
733
ADS 17175, IDS 23569 +2633;
![]() ,
,
![]() (2000)). It is a well-known visual
and single-lined spectroscopic binary system.
The components, 85Peg A and B, are main sequence low mass
stars of spectral types G5 and K7 respectively (ten
Brummelaar et al. 2000). The shortness of the period (
(2000)). It is a well-known visual
and single-lined spectroscopic binary system.
The components, 85Peg A and B, are main sequence low mass
stars of spectral types G5 and K7 respectively (ten
Brummelaar et al. 2000). The shortness of the period (![]() 27 years) and the proximity to the Sun (
27 years) and the proximity to the Sun (![]() 12pc) give it an
interesting place among the binary stars. The visual orbit is very well
known (Hall 1948). Nevertheless, some studies of the orbit have
been recently published. The latest (Söderhjelm 1999) has yielded improvements to the Hipparcos trigonometric parallax and orbit,
combining data from the satellite with ground-based observations.
85Peg is one of the rare cases for which the mass ratio can be
obtained by both astrometric and spectroscopic observations. For many years investigators have claimed that 85 Peg B, the fainter component,
is more massive than 85 Peg A the brighter one (e.g. Slocum 1915;
Hall 1948; Underhill 1963). This was found again by
Martin & Mignard (1998) on the basis of Hipparcos
observations. This abnormal situation could be explained by the fact that
85PegB is an undetected binary. 85
PegA is known as a metal-poor star and found to be much older
than the Sun (Perrin et al. 1977). Because of its small mass, 85 Peg
A sits close to the ZAMS which gives a constraint on its initial helium
abundance, a value traditionally associated with
primordial helium (Perrin et al. 1977; Catchpole et al. 1967;
Smak 1960).
12pc) give it an
interesting place among the binary stars. The visual orbit is very well
known (Hall 1948). Nevertheless, some studies of the orbit have
been recently published. The latest (Söderhjelm 1999) has yielded improvements to the Hipparcos trigonometric parallax and orbit,
combining data from the satellite with ground-based observations.
85Peg is one of the rare cases for which the mass ratio can be
obtained by both astrometric and spectroscopic observations. For many years investigators have claimed that 85 Peg B, the fainter component,
is more massive than 85 Peg A the brighter one (e.g. Slocum 1915;
Hall 1948; Underhill 1963). This was found again by
Martin & Mignard (1998) on the basis of Hipparcos
observations. This abnormal situation could be explained by the fact that
85PegB is an undetected binary. 85
PegA is known as a metal-poor star and found to be much older
than the Sun (Perrin et al. 1977). Because of its small mass, 85 Peg
A sits close to the ZAMS which gives a constraint on its initial helium
abundance, a value traditionally associated with
primordial helium (Perrin et al. 1977; Catchpole et al. 1967;
Smak 1960).
![]() ). Recently,
ten Brummelaar et al. (2000), performed differential photometry
in the Johnson VRI system for both stars using adaptative optics, which allows us to determine the
effective temperatures and bolometric magnitudes of both components.
). Recently,
ten Brummelaar et al. (2000), performed differential photometry
in the Johnson VRI system for both stars using adaptative optics, which allows us to determine the
effective temperatures and bolometric magnitudes of both components.
![]() -elements and the non- LTE effects in the iron abundances
determinations are taken into account in models of low mass
stars (Lebreton et al. 1999). Nevertheless, Lebreton et al. did not perform a full calibration of 85Peg
A and did not examine the secondary component.
-elements and the non- LTE effects in the iron abundances
determinations are taken into account in models of low mass
stars (Lebreton et al. 1999). Nevertheless, Lebreton et al. did not perform a full calibration of 85Peg
A and did not examine the secondary component.
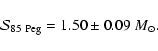
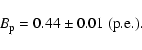
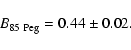
![]() and
and
![]() K
of van't Veer (2000). This
K
of van't Veer (2000). This
![]() determination
relies on the careful fit of Balmer line profiles with Kurucz's (1991)
ATLAS model atmospheres with the constraint that the model reproduces
both the
determination
relies on the careful fit of Balmer line profiles with Kurucz's (1991)
ATLAS model atmospheres with the constraint that the model reproduces
both the
![]() and
and
![]() profiles.
Furthermore we point out that, according to
Thévenin & Idiart (1999), the metallicity of metal-poor
stars, computed using model atmospheres in the LTE approximation
is underestimated by about 0.12 dex at the metallicity of 85 Peg.
This is particularly important for the stellar position on the HR
diagram (Lebreton et al. 1999).
We take into account
this correction and adopt the value
profiles.
Furthermore we point out that, according to
Thévenin & Idiart (1999), the metallicity of metal-poor
stars, computed using model atmospheres in the LTE approximation
is underestimated by about 0.12 dex at the metallicity of 85 Peg.
This is particularly important for the stellar position on the HR
diagram (Lebreton et al. 1999).
We take into account
this correction and adopt the value
![]() (Thévenin 2001).
The
(Thévenin 2001).
The ![]() -elements (Mg, Ca, Si, Na, Al, Ti) have been found to be enriched
with respect to the Sun in 85 Peg A (Fuhrmann 1998;
van't Veer 2000; Fulbright 2000).
In our calculations we take account of an
-elements (Mg, Ca, Si, Na, Al, Ti) have been found to be enriched
with respect to the Sun in 85 Peg A (Fuhrmann 1998;
van't Veer 2000; Fulbright 2000).
In our calculations we take account of an ![]() -elements enrichment,
-elements enrichment,
![]() ,
through appropriate opacities and input
mixture.
We computed the effective temperature of 85 Peg B using the calibrations
,
through appropriate opacities and input
mixture.
We computed the effective temperature of 85 Peg B using the calibrations
![]() from Lejeune et al. (1998) and Bessell et al. (1998).
We use both the
color index (R-I) and (V-I) from ten Brummelaar et al. (2000).
These indices are not very sensitive to the metallicity (Alonso et al. 1996). We obtain
from Lejeune et al. (1998) and Bessell et al. (1998).
We use both the
color index (R-I) and (V-I) from ten Brummelaar et al. (2000).
These indices are not very sensitive to the metallicity (Alonso et al. 1996). We obtain
![]() K using (R-I) and
K using (R-I) and
![]() K using (V-I). We choose
K using (V-I). We choose
![]() K as a representative value of the effective
temperature for the secondary.
K as a representative value of the effective
temperature for the secondary.
![]() and
and
![]() and with Flower's (1996)
results we get
and with Flower's (1996)
results we get
![]() and
and
![]() The agreement is satisfactory
and we take the average values.
The agreement is satisfactory
and we take the average values.
