

Up: Bispectrum speckle interferometry of
Subsections
3 Discussion
3.1 Dust and winds
On larger scales, most AGB stars are surrounded by dust shells of
spherical symmetry. This holds also for the dust shell of
IRC +10216 (Mauron & Huggins 1999,2000).
However, on sub-arcsecond scales this symmetry appears to break down for
giants in very advanced stages of their AGB evolution, with
IRC +10216 being their most prominent representative.
The 2D radiative transfer modelling
presented in Paper III strongly suggested that
the central star of IRC +10216 is surrounded by an optically
thick dust shell with bipolar cavities of a full opening angle of
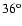 tilted with the southern lobe towards the observer (although
there may exist different interpretations, see
Sect. 1). The bright compact component A is not the direct light
from the central star but is the southern cavity of this bipolar structure
dominated by scattered light. According to this model, the carbon star is at
the position of the fainter northern component B.
tilted with the southern lobe towards the observer (although
there may exist different interpretations, see
Sect. 1). The bright compact component A is not the direct light
from the central star but is the southern cavity of this bipolar structure
dominated by scattered light. According to this model, the carbon star is at
the position of the fainter northern component B.
This dust-shell model and the
possible existence of acceleration within the cavities may
be understood in terms of the beginning operation of interacting winds
which later lead to the shaping
of planetary nebulae (Kwok 1982; Balick 1987).
Within this scenario a fast stellar wind interacts with the
fossil, slow AGB wind. The AGB mass-loss is thought to be aspherical
and to take preferentially place in the equatorial plane.
Accordingly, the polar regions show lower densities than the equatorial
regions. Later,
after a fast wind has developed, the less dense
polar material is carved out leading to the formation of outflow cavities.
This fast wind can be expected to turn on slowly at the very end of the
AGB evolution resulting into the formation of
biconical dust-shell structures on sub-arcsecond scales
as observed for IRC +10216.
The high spatial and temporal resolution of the present observations reveals
details of the mass-loss process even
in the immediate vicinity of the dust condensation zone.
The monitoring, covering more than 3 pulsation
periods, shows that the structural variations are not related to the
stellar pulsation cycle in a simple way.
This is consistent with the predictions of
hydrodynamical models that enhanced dust formation takes place on a timescale
of several pulsation periods (Fleischer et al. 1995).
In Sect. 3.3 simplified dust formation
models are compared with the observations.
![\begin{figure}
\includegraphics[width=14cm,clip]{h3683f5.ps}\end{figure}](/articles/aa/full/2002/34/aah3683/Timg29.gif) |
Figure 5:
J-K (left) and H-K (right)
color images (greyscale images)
of the central region of IRC +10216
in March 2001,
confined to regions which are brighter than
2% of the peak intensity in the J and K images
(J-K color image)
and 3% of the peak intensity in the H and K images
(H-K color image), resp.
The resolution is 115 mas.
Contour lines refer to the K-band image and are shown from 0.2 mag to 3 mag
relative to the peak brightness
in steps of 0.7 mag.
To construct the respective
color images, the J, H, and K reconstructions were centered at the
positions of maximum intensity.
White regions refer to magnitude differences of
7.4 mag (J-K) and 3.9 mag (H-K);
the regions shown in the darkest grey correspond to magnitude differences of
5.0 mag (J-K) and 2.7 mag (H-K).
North is up and east is to the left.
Dashed lines indicate the biconical geometry of the cavities
according to the 2D radiative transfer model of Paper III. |
3.2 Observed changes interpreted by 2D modeling
The large number of epochs available now seems to make the interpretation of
the sub-arcsecond structures and their evolution even more difficult and
puzzling than before. Here we suggest a physical picture of what presently is
going on in this object based on the results of our previous 2D radiative
transfer modeling (Paper III). The model was designed to derive the structure
and physical properties of the star and its dusty envelope at a single moment,
corresponding to the third epoch (January 23, 1997) of our images. Our
simplified attempt to handle the difficult problem of self-consistent time-dependent multidimensional radiative transfer modeling will be presented
elsewhere (Men'shchikov et al. 2002, submitted).
Key point to the understanding of the structure and evolution of the
sub-arcsecond environment of IRC +10216 is the knowledge of the
position of the central star in the images. As we have suggested in the
previous modeling (Paper III), the brightest compact peak A seen in all images
is not the direct light from the central star. The star is most likely
located at the position of the fainter peak B, whereas component A is the
radiation emitted and scattered in the optically thinner conical cavity of the
optically thick bipolar dust shell. The even fainter components C and D in the
H and K images were identified with smaller-scale deviations of the density
distribution of the circumstellar environment from axial symmetry
(Figs. 1 and 2 in Paper III). These inhomogeneities are less opaque
than other, more regular regions of the compact dense shell.
An alternative interpretation of the morphology of our images of
IRC +10216 would be that components A and B are the lobes of a
bipolar nebula and that the star is located in the dark region between
them. However, this interpretation disagrees with our radiative transfer
modeling presented in Paper III. A reason for this is that the optically
thick dust which would form the bipolar lobes cannot exist so close to the
star, at half the distance between the components. Thus, the star is
probably located either at A or B. The fan-shaped morphology of component A in
the J- and H-band images, as well as other evidence presented in Papers II
and III, strongly suggest that the star is located at the position of B.
Having defined the stellar position at component B, we can now interpret the
evolving appearance of IRC +10216 in terms of an increased
mass-loss rate during the last  30 years. One of the main features of the
entire 8-epoch sequence of imaging is the relative fading of the stellar
component B (Figs. 1 and 2). Other changes seen in the
images are the increasing distances of components A, C, D from the star
(Fig. 4) and their greatly varying shapes. Our radiative transfer
modeling (Paper III) has shown that the observed components are cavities
in the dense opaque shell; therefore, the observed motion requires an
additional discussion (Sect. 3.2.4).
30 years. One of the main features of the
entire 8-epoch sequence of imaging is the relative fading of the stellar
component B (Figs. 1 and 2). Other changes seen in the
images are the increasing distances of components A, C, D from the star
(Fig. 4) and their greatly varying shapes. Our radiative transfer
modeling (Paper III) has shown that the observed components are cavities
in the dense opaque shell; therefore, the observed motion requires an
additional discussion (Sect. 3.2.4).
In order to better visualize the relative location of the components, we have
shown the structure (conical cavities) of our model (Paper III) in the observed
images by dashed lines in Figs. 3 and 5. The lines
intersecting at the position of the central star and making an angle of
46
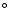 between them, outline the biconical geometry of the cavities.
between them, outline the biconical geometry of the cavities.
The April 1996 J-band image in Fig. 3 best exhibits the bipolar
geometry of IRC +10216. Clearly visible at this wavelength are the
fan shape of the brightest component A and even the scattered light from the
opposite (northern) cavity on the far side of the dense shell. Faint
direct stellar light is visible near the origin of the conical cavities.
The star (component B) appears much brighter in the January 1997 H-band
image (Fig. 3), whereas the fan shape of the cavity
(component A) is less prominent but still well visible at this
wavelength. The H and K images in 1997 agree very well with our model
presented in Paper III. The March 2001 H and K images are qualitatively
similar to the older images obtained in 1997, but distorted by the appearance
of several fainter structures close to component D and by merging of the bright
component A with component C. The faint direct stellar light has become more
difficult to identify in H and it has been buried in the enhanced dust
emission from all the other components in the March 2001 K-band image.
The most recent J image of IRC +10216 with a 3 times higher
resolution (50 mas, Fig. 2) shows in much greater detail the fine
structure of the envelope. The image reveals a rather isolated, faint peak at
the position of the central star (marked in Fig. 2). The following
evidence suggests that this peak is indeed the direct light from the star,
not just a clump that happened to be there: (1) its position angle relative to
A (PA
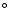 ) is the same as in all the images where the star
(component B) is clearly visible, (2) the H image at the same epoch shows a
(less isolated) peak at the same position, (3) the distance of approximately
347 mas between the peak and the component A is consistent with the fit of
Fig. 4.
) is the same as in all the images where the star
(component B) is clearly visible, (2) the H image at the same epoch shows a
(less isolated) peak at the same position, (3) the distance of approximately
347 mas between the peak and the component A is consistent with the fit of
Fig. 4.
One might think that the faint stellar peak should be much better visible in
K band (Fig. 2), where optical depths are significantly lower
compared to J. However, the greatly enhanced hot dust emission in K band
may well make it completely invisible. In fact, from the continuum of the model
stellar atmosphere used in Paper III, we estimate that the stellar brightness
in J and K bands is approximately the same. The dust model of Paper III
would predict that the star is a factor of 
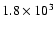 brighter in
K than in J band, whereas our new model of IRC+10216 (Men'shchikov
et al., submitted), computed specifically for the latest epoch of March 2001,
predicts a larger factor of
brighter in
K than in J band, whereas our new model of IRC+10216 (Men'shchikov
et al., submitted), computed specifically for the latest epoch of March 2001,
predicts a larger factor of 
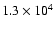 .
On the other hand, from the
calibrated color images of Fig. 5 we know that the nebula becomes
much brighter between J and K (and thus redder), by a factor of
.
On the other hand, from the
calibrated color images of Fig. 5 we know that the nebula becomes
much brighter between J and K (and thus redder), by a factor of 
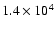 .
Therefore, it is unlikely that in K the stellar peak is
visible better than in J band.
.
Therefore, it is unlikely that in K the stellar peak is
visible better than in J band.
The high-resolution J-H, J-K, and H-K color images in Fig. 5
observed in March 2001 confirm our interpretation that the bright components
A, C, and D are, respectively, the cavity and smaller-scale
inhomogeneities in the dense shell, not dense clumps of dust as it might
appear from the images alone (Figs. 1-3). In fact, all
the bright components coincide with the blue areas in the color images, the
cavity A corresponding to the bluest spot. This is a natural
consequence of lower optical depths along those directions from the star, with
the "hot'' stellar photons being scattered into the direction of the observer.
This is illustrated in Fig. 5 by the dashed lines showing the
geometry of our model (Paper III). The bluest, optically thinnest spot is
located precisely inside the conical cavity. The star, obscured by  40 mag of visual circumstellar extinction, is situated in the red
area of the color images, as it was also in the previous epochs (Fig. 16 in
Paper III).
40 mag of visual circumstellar extinction, is situated in the red
area of the color images, as it was also in the previous epochs (Fig. 16 in
Paper III).
3.2.4 Moving dense layer or dust evaporation?
The apparent motion of the components A, C, and D (Fig. 1) could be
attributed either to the real radial expansion of the opaque dense layer with
several "holes'' in the dense dust formation zone or to a displacement of the
dust formation radius due to evaporation of recently formed dust by a hotter
environment. Here, we analyze both processes and argue that the
temperature-induced displacement of the dust formation zone is acting in
IRC +10216. For simplicity, we consider a single dust formation
radius corresponding to the formation of carbon dust (cf. Paper III).
One can explain the observed decreasing brightness of the star by assuming a
monotonically increasing mass-loss rate and, hence, higher densities and
optical depths of the wind in the dust formation zone. Higher mass loss and
continuing condensation of new dust in the wind out of the gas phase increase
the temperatures of the outflowing gas and dust due to backwarming. Increasing
temperatures affect the location of the inner dust boundary of the envelope via
dust sublimation, causing its displacement with a velocity that has nothing to
do with the outflow motion of the envelope.
Crucial to distinguishing between the real motion of a dense
layer and the temperature-induced shift of the dust formation zone are
estimates of the apparent velocities of the components A, C, and D relative to
the star. For the assumed distance of 130 pc, the linear fit in
Fig. 4 gives for the brightest component A a velocity
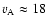 km s-1 in the plane of sky. On the basis of our model
(Paper III), one can derive for the component a deprojected radial velocity
km s-1 in the plane of sky. On the basis of our model
(Paper III), one can derive for the component a deprojected radial velocity
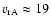 km s-1.
km s-1.
Since the deprojected radial velocity is higher than the observed (terminal)
wind outflow speed in IRC +10216 of
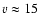 km s-1,
it is unlikely that the observed changes reflect just an expansion of a
dense layer in which grains are forming. In fact, the standard picture of a
stationary stellar wind predicts an acceleration of dust and gas within
distances by a factor of
km s-1,
it is unlikely that the observed changes reflect just an expansion of a
dense layer in which grains are forming. In fact, the standard picture of a
stationary stellar wind predicts an acceleration of dust and gas within
distances by a factor of 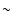 2-5 larger than the dust formation radius
(Steffen et al. 1997). Due to
the radiation pressure on dust grains, the wind velocity increases in this
transition zone, approaching asymptotically the terminal velocity at larger
distances. As our model (Paper III) associates the observed components of
IRC +10216 with the dust formation zone, we expect that dust and
gas are not yet fully accelerated there, i.e. that the radial outflow velocity
2-5 larger than the dust formation radius
(Steffen et al. 1997). Due to
the radiation pressure on dust grains, the wind velocity increases in this
transition zone, approaching asymptotically the terminal velocity at larger
distances. As our model (Paper III) associates the observed components of
IRC +10216 with the dust formation zone, we expect that dust and
gas are not yet fully accelerated there, i.e. that the radial outflow velocity
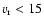 km s-1.
km s-1.
However, the deprojected velocity
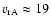 km s-1 is
significantly larger than the expected wind velocity in the dust formation
zone. Only if we assume an unlikely lower limit of 100 pc (Becklin et al.
1969), does the deprojected velocity
km s-1 is
significantly larger than the expected wind velocity in the dust formation
zone. Only if we assume an unlikely lower limit of 100 pc (Becklin et al.
1969), does the deprojected velocity
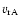 approach
(from above)
approach
(from above)
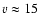 km s-1, which is still too high for the dust
formation zone. If, however, the actual distance to IRC +10216 is
larger than 130 pc, one would obtain
km s-1, which is still too high for the dust
formation zone. If, however, the actual distance to IRC +10216 is
larger than 130 pc, one would obtain
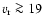 km s-1 and an even
larger discrepancy.
km s-1 and an even
larger discrepancy.
Moreover, there are reasons to believe that the acceleration depicted by the
parabolic fit in Fig. 4 is real and that the actual apparent
motion of A is now as fast as
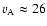 km s-1. The
corresponding deprojected velocity is then
km s-1. The
corresponding deprojected velocity is then
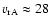 km s-1, much higher than the expected wind speed, for any realistic
distance to IRC +10216. Taken in context with increasing optical
depths in the shell, this suggests that the observed motions are caused
by the rapid dust evaporation due to backwarming and higher temperatures in the
dense environment formed by the increased mass loss.
km s-1, much higher than the expected wind speed, for any realistic
distance to IRC +10216. Taken in context with increasing optical
depths in the shell, this suggests that the observed motions are caused
by the rapid dust evaporation due to backwarming and higher temperatures in the
dense environment formed by the increased mass loss.
We believe that a reasonable interpretation of the observed changes in
IRC +10216 would be the following picture. During the recent
period of increasing mass-loss which started 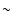 20-30 years ago, a compact
dense shell has formed around the star. The mass-loss rate was recently as
high as
20-30 years ago, a compact
dense shell has formed around the star. The mass-loss rate was recently as
high as
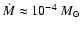 yr-1 (Paper III) and the
innermost regions of the dust shell are expanding outward at a local wind
velocity
yr-1 (Paper III) and the
innermost regions of the dust shell are expanding outward at a local wind
velocity 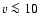 km s-1. Dust formation continues in the expanding
material, thus increasing its optical depth and obscuring the central star.
The optical depths in the polar regions remain significantly smaller than in the
other regions of the dense shell, making the cavity (A) and the other
components relatively brighter than at previous epochs. As the dense,
increasingly optically thick dusty shell expands, steeply rising temperatures
inside it (due to the backwarming from the steepening density front) inhibit
further dust condensation and evaporate outflowing grains. In effect, these
processes have been shifting recently the dust formation radius outward with
an average velocity
km s-1. Dust formation continues in the expanding
material, thus increasing its optical depth and obscuring the central star.
The optical depths in the polar regions remain significantly smaller than in the
other regions of the dense shell, making the cavity (A) and the other
components relatively brighter than at previous epochs. As the dense,
increasingly optically thick dusty shell expands, steeply rising temperatures
inside it (due to the backwarming from the steepening density front) inhibit
further dust condensation and evaporate outflowing grains. In effect, these
processes have been shifting recently the dust formation radius outward with
an average velocity
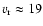 km s-1 (or as high as
km s-1 (or as high as 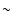 30
km s-1 in 2001, if the apparent acceleration measured in this work is
real). One can predict that the star will remain obscured until
30
km s-1 in 2001, if the apparent acceleration measured in this work is
real). One can predict that the star will remain obscured until 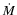 starts to drop back to lower values. In a few years from that moment, we could
probably be witnessing the star (B) reappearing whereas the cavities becoming
relatively fainter.
starts to drop back to lower values. In a few years from that moment, we could
probably be witnessing the star (B) reappearing whereas the cavities becoming
relatively fainter.
3.3 Dust formation models and the fading of B
If the star is located at the position of component B, as is suggested by
the two-dimensional radiative transfer model (see Sect. 3.2 and
Paper III),
the fading of B might be caused by the formation of new
dust along the line of sight towards the star.
To investigate, whether such a scenario would be
capable of explaining the observed time scale of the fading of B, we
constructed a very simple gas box model. The idea is to follow the
process of carbon grain formation in a gas element moving away from
the star at a constant velocity. To characterize the changing
thermodynamic conditions experienced by the gas element, we assume a
power-law gas temperature stratification
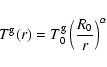 |
(1) |
and evaluate the gas density structure from mass conservation in a stationary,
spherically symmetric configuration
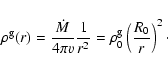 |
(2) |
For the co-moving gas element, the time coordinate is given by
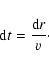 |
(3) |
In this gas element, we consider heteromolecular formation and
growth of carbon grains which we compute according to the moment method
derived by Gail & Sedlmayr (1988).
The growth process includes reactions with the molecular species C, C2, C2H, and C2H2.
In order to calculate the concentrations of the
relevant carbon-bearing molecules, chemical equilibrium in the gas phase is
assumed. We consider a carbon-rich element mixture with otherwise solar
abundances.
In Fig. 6 the resulting temporal evolution of the gas box
is depicted for the following parameters:
T0 = 3000 K at a radius
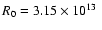 cm
(corresponding to
the Stefan-Boltzmann radius for T0 and a stellar luminosity
of
cm
(corresponding to
the Stefan-Boltzmann radius for T0 and a stellar luminosity
of
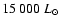 ),
),
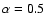 (i.e. an optically thin temperature
distribution),
(i.e. an optically thin temperature
distribution),
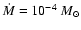 yr-1 (reflecting a presently
increased mass-loss rate of IRC +10216), a constant outflow velocity
of v = 15 km s-1, and a carbon abundance (by number)
of
yr-1 (reflecting a presently
increased mass-loss rate of IRC +10216), a constant outflow velocity
of v = 15 km s-1, and a carbon abundance (by number)
of
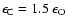 .
.
In the upper panel of Fig. 6 the prescribed
time evolution of gas temperature (Eq. (1))
and density (Eq. (2)) in the gas box are shown.
The second panel depicts the nucleation rate J*, i.e. the number of
seed particles formed per second and hydrogen
nucleus (solid line) and the number of dust grains per
hydrogen nucleus (dash-dotted line). In the third panel,
the degree of condensation, i.e. the fraction of condensible material that
is actually condensed is shown (solid line).
The dash-dotted line indicates the optical depth
at 2.2 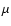 m (measured from the star), that would build up in a stationary
situation. To calculate the dust extinction coefficient, we assume the small
particle limit of Mie theory. This is justified, since the mean particle
radius
m (measured from the star), that would build up in a stationary
situation. To calculate the dust extinction coefficient, we assume the small
particle limit of Mie theory. This is justified, since the mean particle
radius
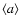 reached
after 15 P is
reached
after 15 P is
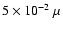 m, giving a maximum size
parameter
m, giving a maximum size
parameter
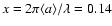 at the
considered wavelength of
at the
considered wavelength of
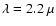 m. The optical properties of the
grains are described by the complex refractive index of amorphous carbon
tabulated in Preibisch et al. (1993). In the lower panel we plot
the normalized intensity at 2.2
m. The optical properties of the
grains are described by the complex refractive index of amorphous carbon
tabulated in Preibisch et al. (1993). In the lower panel we plot
the normalized intensity at 2.2 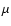 m that would emerge along the line of
sight from the increasingly obscured radiation source (solid line).
This intensity is calculated from the formal solution of the radiative
transfer equation:
m that would emerge along the line of
sight from the increasingly obscured radiation source (solid line).
This intensity is calculated from the formal solution of the radiative
transfer equation:
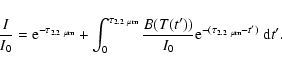 |
(4) |
Here we assume thermal emission of the dust grains
(B is the Kirchhoff-Planck
function) and normalize the intensity to
I0 = B(T0).
For comparison, we also plotted in the lower panel of
Fig. 6 the observed intensity of component B,
normalized to its
intensity in our 1997 speckle image (crosses). The intensity of component B
fades from its maximum value to 17% of this value within about 1400 d,
corresponding to 2.2 pulsation periods of IRC +10216. This time
interval is indicated in the lower panel of Fig. 6
by the vertical dashed
lines. The comparison shows that dust condensation in front of the
star in fact can reproduce the observed time scale of the fading of
component B for realistic values of the parameters characterizing our
simple toy model.
In Table 2 the timescale 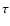 of the intensity drop to 17% of
the initial value is summarized for
various parameter combinations. We note a steep dependence of
of the intensity drop to 17% of
the initial value is summarized for
various parameter combinations. We note a steep dependence of 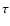 on the C/O ratio, i.e. on the amount of material available for dust
formation. Consistent model calculations for dust driven outflows
(e.g., Winters et al. 2000b; Arndt et al. 1997; Dominik et al. 1990)
show, that the outflow velocity of a
carbon-rich dust-driven wind also depends strongly on the C/O
ratio. For the observed outflow velocity of IRC +10216 of
on the C/O ratio, i.e. on the amount of material available for dust
formation. Consistent model calculations for dust driven outflows
(e.g., Winters et al. 2000b; Arndt et al. 1997; Dominik et al. 1990)
show, that the outflow velocity of a
carbon-rich dust-driven wind also depends strongly on the C/O
ratio. For the observed outflow velocity of IRC +10216 of  15 km s-1, C/O ratios in the range
15 km s-1, C/O ratios in the range
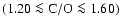 are required. Therefore, Table 2 implies, that the
present day mass-loss rate of IRC +10216 in fact should have increased
considerably above the "canonical'' value of (a few)
are required. Therefore, Table 2 implies, that the
present day mass-loss rate of IRC +10216 in fact should have increased
considerably above the "canonical'' value of (a few)
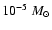 /yr
derived from CO rotational line observations
probing the outer and therefore, older parts of the circumstellar shell
(e.g., Schöier & Olofsson 2001) or from CO infrared line
profiles observed about one decade ago (e.g., Winters et al. 2000a).
/yr
derived from CO rotational line observations
probing the outer and therefore, older parts of the circumstellar shell
(e.g., Schöier & Olofsson 2001) or from CO infrared line
profiles observed about one decade ago (e.g., Winters et al. 2000a).
Once dust has formed in the circumstellar shell, its opacity would lead
to a pronounced backwarming and therefore, to a steeper temperature gradient
in the dust formation zone.
Accordingly, in our simple gas box model, lower temperatures would be
reached at the same density.
As a result, dust growth becomes more
efficient in this region and a reduced C/O ratio is sufficient to recover the
observed fading time scale (see Table 2; compare the corresponding
entries for
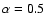 with
with
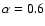 and 0.7).
and 0.7).
A more realistic treatment of the dust formation and mass-loss process in
IRC +10216 would require the simultaneous
solution of the time dependent hydrodynamic equations, taking into
account the pulsation of the star, together with the equations
describing the dust formation process and the radiative transfer
problem. Such a consistent investigation will be presented in a forthcoming
paper.
An alternative interpretation of the fading of component B, together
with its increasing separation from A, could be based on a scenario,
where the star is located in the direction of component A, as argued
in previous studies by Weigelt et al. (1998), Haniff & Buscher
(1998), and Tuthill et al. (2000). In this
case, component B would indicate thermal emission from a dust
cloud, ejected from the star in a direction almost perpendicular to
the line of sight. The temporal evolution of the
brightness of B would then be the result of a competition between the
initially increasing thermal emission due to ongoing dust formation in
the cloud and decreasing temperature of the cloud as it is moving away
from the star. Preliminary results for this scenario, which are based on
a consistent model calculation, are presented in
Winters et al. (2002).
Although the time scale of the fading of component B is
reproduced quite well in this model, the calculated intensity ratio
between the expanding cloud and the star is smaller than the observed
intensity ratio between components B and A by about a factor of 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3683f21.eps}\end{figure}](/articles/aa/full/2002/34/aah3683/Timg63.gif) |
Figure 6:
Temporal evolution of the gas box.
The time coordinate is given in units
of P=649 d, the pulsation period
of IRC +10216.
Upper panel: gas temperature (Eq. (1), solid line,
l.h.s. ordinate)
and density (Eq. (2), dash-dotted line, r.h.s. ordinate);
second panel: dust nucleation rate J* (solid line, l.h.s. ordinate)
and number of dust grains per hydrogen nucleus
(dash-dotted line, r.h.s. ordinate);
third panel: degree of condensation
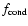 (solid line, l.h.s. ordinate) and optical depth
at 2.2 (solid line, l.h.s. ordinate) and optical depth
at 2.2 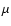 m (dash-dotted line, r.h.s. ordinate);
lower panel: normalized emergent intensity at 2.2 m (dash-dotted line, r.h.s. ordinate);
lower panel: normalized emergent intensity at 2.2 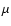 m (solid line) and
observed intensity of component B, normalized to its
maximum value (crosses). See text for more details. m (solid line) and
observed intensity of component B, normalized to its
maximum value (crosses). See text for more details. |


Up: Bispectrum speckle interferometry of
Copyright ESO 2002
![\begin{figure}
\includegraphics[width=14cm,clip]{h3683f5.ps}\end{figure}](/articles/aa/full/2002/34/aah3683/Timg29.gif)
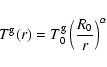
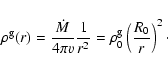
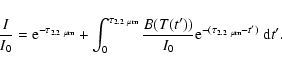
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3683f21.eps}\end{figure}](/articles/aa/full/2002/34/aah3683/Timg63.gif)