A&A 392, 353-368 (2002)
DOI: 10.1051/0004-6361:20020912
Non-radial instabilities of isothermal Bondi accretion
with a
shock: Vortical-acoustic cycle vs. post-shock acceleration
T. Foglizzo
Service d'Astrophysique, CEA/DSM/DAPNIA, CEA-Saclay, 91191
Gif-sur-Yvette, France
Received 17 May 2002 / Accepted 12 June 2002
Abstract
The linear stability of isothermal Bondi accretion with a shock is
studied analytically in the asymptotic limit of high incident Mach number
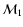 .
The flow is unstable with respect to radial perturbations as
expected by Nakayama (1993), due to post-shock acceleration.
Its growth-time scales like the advection time from the shock
.
The flow is unstable with respect to radial perturbations as
expected by Nakayama (1993), due to post-shock acceleration.
Its growth-time scales like the advection time from the shock
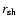 to the sonic point
to the sonic point
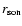 .
The growth rate of non-radial perturbations
l=1 is higher by a factor
.
The growth rate of non-radial perturbations
l=1 is higher by a factor
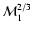 ,
and is therefore intermediate
between the advection and acoustic frequencies.
Besides these instabilities based on post-shock acceleration, our
study revealed another generic mechanism based on the cycle of acoustic and
vortical perturbations between the shock and the sonic radius,
independently of the sign of post-shock acceleration.
The vortical-acoustic instability is fundamentally non-radial. It
is fed by the efficient excitation of vorticity waves by the isothermal
shock perturbed by acoustic waves. The growth rate exceeds the advection
frequency by a factor
,
and is therefore intermediate
between the advection and acoustic frequencies.
Besides these instabilities based on post-shock acceleration, our
study revealed another generic mechanism based on the cycle of acoustic and
vortical perturbations between the shock and the sonic radius,
independently of the sign of post-shock acceleration.
The vortical-acoustic instability is fundamentally non-radial. It
is fed by the efficient excitation of vorticity waves by the isothermal
shock perturbed by acoustic waves. The growth rate exceeds the advection
frequency by a factor
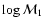 .
Unstable modes cover a wide range of frequencies from the
fundamental acoustic frequency
.
Unstable modes cover a wide range of frequencies from the
fundamental acoustic frequency 
 up to a cut-off
up to a cut-off 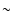
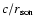 associated with the sonic radius. The highest growth rate is reached
for l=1 modes near the cut-off. The additional cycle of acoustic waves
between the shock and the sonic radius is responsible for variations of the
growth rate by a factor up to 3 depending on its phase relative to the
vortical-acoustic cycle.
The instability also exists, with a similar growth rate, below the fundamental
acoustic frequency down to the advection frequency, as vorticity waves are
efficiently coupled to the region of pseudosound.
These results open new perspectives to address the stability of
shocked accretion flows.
associated with the sonic radius. The highest growth rate is reached
for l=1 modes near the cut-off. The additional cycle of acoustic waves
between the shock and the sonic radius is responsible for variations of the
growth rate by a factor up to 3 depending on its phase relative to the
vortical-acoustic cycle.
The instability also exists, with a similar growth rate, below the fundamental
acoustic frequency down to the advection frequency, as vorticity waves are
efficiently coupled to the region of pseudosound.
These results open new perspectives to address the stability of
shocked accretion flows.
Key words: accretion, accretion disks - hydrodynamics -
instabilities - shock waves - stars binaries: close - X-rays: stars
Hydrodynamic instabilities in accretion flows can help our understanding of
the variability observed in the luminosity of X-ray binaries.
Numerical simulations have revealed the existence of such a
hydrodynamical instability in the accretion flow of a gas on a compact
accretor moving at supersonic velocity (Bondi-Hoyle-Lyttleton
accretion). A first step towards understanding
the physical mechanism underlying this instability was made by Foglizzo
& Tagger (2000, hereafter FT00) who recognized the unstable cycle of
entropic and acoustic perturbations between the shock and the sonic surface.
This cycle is unstable if there is a large enough temperature difference
between the shock and the sonic surface. The academic case of shocked
Bondi accretion was studied by Foglizzo (2001, hereafter F01) who revealed the
importance of non radial perturbations, and vorticity in particular.
Both vorticity and entropy perturbations are advected from the shock
to the accretor, and both are coupled to the acoustic perturbations.
This coupling was formulated in a compact way by Howe (1975).
If the adiabatic index is in the range
 ,
entropy and
vorticity perturbations are intimately related in the shocked Bondi
flow (Foglizzo 2002, in preparation), so that it is difficult to identify their
respective roles in the instability mechanism. By contrast, their roles
are well separated in the isothermal limit (
,
entropy and
vorticity perturbations are intimately related in the shocked Bondi
flow (Foglizzo 2002, in preparation), so that it is difficult to identify their
respective roles in the instability mechanism. By contrast, their roles
are well separated in the isothermal limit ( ), where entropy
perturbations are absent from the problem. The present paper is
therefore dedicated to the study of the linear stability of shocked
accretion in the isothermal Bondi flow, where the incident Mach number is the
only parameter. The stability of shocked isothermal flows was studied
by Nakayama (1992, 1993) in the more general context of flows with
small angular momentum. The study of Nakayama was restricted to
axisymmetric perturbations, thus precluding any possible vortical
acoustic cycle. In this approximation, Nakayama analytically obtained
the result that the flow is unstable if the flow accelerates immediately
after the shock surface. In this respect the shocked Bondi flow should
be unstable. We are therefore interested here in an
extension of Nakayama's results to the case of non radial
perturbations, in order to include the effect of vorticity.
It should be noted that isothermal flows are very particular as far as
Bondi-Hoyle-Lyttleton (hereafter BHL) accretion is concerned, with unsettled
issues concerning the influence of the numerical resolution.
The instability observed in numerical simulations seems very weak in 3-D
according to Ruffert (1996), whereas it is violent in 2-D (Ishii et al.1993;
Shima et al.1998). Pogorelov et al.(2000) discussed the possible responsability
of the numerical procedure in producing the instability. With a
different approach, the instability of the shocked Bondi flow described in
this paper could contribute to guide our physical understanding of more
complex flows involving isothermal shocks.
), where entropy
perturbations are absent from the problem. The present paper is
therefore dedicated to the study of the linear stability of shocked
accretion in the isothermal Bondi flow, where the incident Mach number is the
only parameter. The stability of shocked isothermal flows was studied
by Nakayama (1992, 1993) in the more general context of flows with
small angular momentum. The study of Nakayama was restricted to
axisymmetric perturbations, thus precluding any possible vortical
acoustic cycle. In this approximation, Nakayama analytically obtained
the result that the flow is unstable if the flow accelerates immediately
after the shock surface. In this respect the shocked Bondi flow should
be unstable. We are therefore interested here in an
extension of Nakayama's results to the case of non radial
perturbations, in order to include the effect of vorticity.
It should be noted that isothermal flows are very particular as far as
Bondi-Hoyle-Lyttleton (hereafter BHL) accretion is concerned, with unsettled
issues concerning the influence of the numerical resolution.
The instability observed in numerical simulations seems very weak in 3-D
according to Ruffert (1996), whereas it is violent in 2-D (Ishii et al.1993;
Shima et al.1998). Pogorelov et al.(2000) discussed the possible responsability
of the numerical procedure in producing the instability. With a
different approach, the instability of the shocked Bondi flow described in
this paper could contribute to guide our physical understanding of more
complex flows involving isothermal shocks.
The paper is organized as follows. Perturbed equations are described in
Sect. 2 and eigenfrequencies are determined numerically in
Sect. 3.
Analytical methods are used to disentangle the effect of advection from the
effect of the boundary. In the spirit of F01, the
coupling between the vorticity and acoustic perturbations in the classical
isothermal Bondi flow, without a shock, is described in
Sect. 4. Boundary conditions are
taken into account to build a vortical acoustic-cycle in
Sects. 5 and 6. The instability due to post-shock
acceleration is analysed in Sect. 7.
The relationship between the vortical-acoustic instability and existing
numerical simulations of BHL accretion and shocked discs is discussed in
Sect. 8.
2 Linearized equations of the shocked Bondi flow
2.1 Properties of the unperturbed shocked flow
 |
Figure 1:
Radial profile of the Mach number in the unperturbed
shocked flow, for M1=5 (full line). The subsonic cavity stands between
the sonic point and the shock radius. The dashed lines show the analytical
continuation of the solutions beyond the shock radius. |
| Open with DEXTER |
The Mach number in the unperturbed transonic flow satisfies the following
equation deduced from the conservation of the mass flux and Bernoulli
constant B and the regularity at the sonic radius:
 |
(1) |
The sonic radius is half of the Bondi radius GM/c2. The
Bernoulli constant,
 |
(2) |
is conserved along the flow lines. By contrast with the
adiabatic case  ,
this quantity is not conserved through a shock.
The shock radius
,
this quantity is not conserved through a shock.
The shock radius
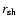 corresponding to an incident Mach number
corresponding to an incident Mach number
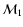 is determined from Eq. (1) together
with the Rankine Hugoniot jump condition
is determined from Eq. (1) together
with the Rankine Hugoniot jump condition
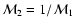 .
The Mach number profile is shown in Fig. 1. It should be
noted that the presence of a radial shock is not guaranteed a priori,
since the supersonic preshock flow (
.
The Mach number profile is shown in Fig. 1. It should be
noted that the presence of a radial shock is not guaranteed a priori,
since the supersonic preshock flow (
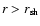 )
could be continued without a
shock down to the accretor (dashed line in Fig. 1).
Several physical mechanisms could trigger the formation of a shock, such as the
heating of protons to temperatures at which the fluid becomes collisionless
(Mezaros & Ostriker 1983), the trapping of relativistic particules
(Protheroe & Kazanas 1983) or the dissipation of magnetic fields
(McCrea 1956; Scharlemann 1981).
In the context of Bondi-Hoyle-Lyttleton accretion, the existence of a
stagnation point behind the accretor implies that a fraction of the supersonic
flow decelerates to subsonic velocities, and therefore naturally produces
a shock. The shock radius deduced from Eq. (1)
increases with
)
could be continued without a
shock down to the accretor (dashed line in Fig. 1).
Several physical mechanisms could trigger the formation of a shock, such as the
heating of protons to temperatures at which the fluid becomes collisionless
(Mezaros & Ostriker 1983), the trapping of relativistic particules
(Protheroe & Kazanas 1983) or the dissipation of magnetic fields
(McCrea 1956; Scharlemann 1981).
In the context of Bondi-Hoyle-Lyttleton accretion, the existence of a
stagnation point behind the accretor implies that a fraction of the supersonic
flow decelerates to subsonic velocities, and therefore naturally produces
a shock. The shock radius deduced from Eq. (1)
increases with
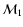 for spherical accretion:
for spherical accretion:
 |
(3) |
Compared to BHL accretion, the presence of an accretion shock at a distance
exceeding the accretion radius
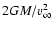 is rather artificial and
due simply to the assumption of purely radial velocity. In the highly
supersonic limit
is rather artificial and
due simply to the assumption of purely radial velocity. In the highly
supersonic limit
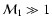 initially considered by Hoyle & Lyttleton (1939),
any trajectory with an angular momentum larger than
initially considered by Hoyle & Lyttleton (1939),
any trajectory with an angular momentum larger than 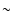 2
2
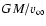 would
of course miss the accretor. Bearing this feature in mind, the case of strong
shocks studied in this paper is still very useful in order to understand the
mechanisms involved, because of the separation of timescales it enables.
would
of course miss the accretor. Bearing this feature in mind, the case of strong
shocks studied in this paper is still very useful in order to understand the
mechanisms involved, because of the separation of timescales it enables.
2.2 Scaling of timescales in the shocked Bondi
flow
If the shock is strong, the timescale
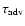 associated with
advection is much longer than the sound crossing time
associated with
advection is much longer than the sound crossing time
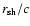 :
:
 |
(4) |
The third fundamental timescale of the flow is related to the presence
of the sonic radius 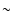
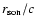 .
Together with Eq. (3), the scaling of the three special
timescales of the problem is thus the following for strong shocks:
.
Together with Eq. (3), the scaling of the three special
timescales of the problem is thus the following for strong shocks:
 |
(5) |
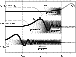 |
Figure 2:
Schematic structure of the perturbed acoustic (full line) and
vorticity (dotted line) fields, depending on the frequency of the perturbation.
The curve beyond the shock radius shows the acousticperturbation in the Bondi
flow without a shock. The turning point 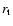 separates the
region of pseudosound from the region of propagation of acoustic
pertrbations. The vortical-acoustic coupling is most efficient in the
region between
separates the
region of pseudosound from the region of propagation of acoustic
pertrbations. The vortical-acoustic coupling is most efficient in the
region between
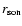 and
and
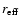 . . |
| Open with DEXTER |
As in the case 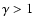 studied by F01, the
vorticity equation can be directly integrated, so that the three quantities
(
studied by F01, the
vorticity equation can be directly integrated, so that the three quantities
(
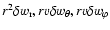 )
are
conserved when advected.
The perturbations of the radial velocity
)
are
conserved when advected.
The perturbations of the radial velocity
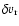 and density
and density
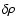 in the isothermal Bondi flow are conveniently described by
the functions f, g defined by:
in the isothermal Bondi flow are conveniently described by
the functions f, g defined by:
They satisfy the same differential equations as the functions f, g in
the Appendix B of F01, by suppressing the entropy terms:
where the function
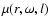 is defined by:
is defined by:
The constant 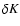 is related to vorticity as follows
is related to vorticity as follows
 |
(12) |
By contrast with the case of adiabatic flows (F01), 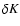 is the unique
source term for the excitation of acoustic waves.
For radial perturbations (
is the unique
source term for the excitation of acoustic waves.
For radial perturbations (
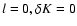 ), the equations
analysed by Nakayama (1992, 1993), with
), the equations
analysed by Nakayama (1992, 1993), with
 ,
are
recovered.
,
are
recovered.
The position of the turning point  of non-radial acoustic
waves is defined by
of non-radial acoustic
waves is defined by  in Eq. (10). This turning point
lies inside the subsonic cavity if
in Eq. (10). This turning point
lies inside the subsonic cavity if
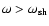 ,
with
,
with
 |
(13) |
Below
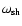 (or inside the turning point
(or inside the turning point 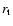 if it
exists), the acoustic perturbation is not propagating. It was named
"pseudosound'' by Ffowcs Williams (1969).
if it
exists), the acoustic perturbation is not propagating. It was named
"pseudosound'' by Ffowcs Williams (1969).
The threshold between absorbed and trapped sound was introduced in F01
through the cut-off frequency
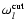 ,
which is independent of the
shock strength:
,
which is independent of the
shock strength:
 |
(14) |
This cut-off frequency used to be
refered to as a "refraction'' cut-off in F01 for 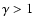 ,
due to the
non-homogeneity of the sound speed which bends trajectories outwards.
By contrast, in the isothermal flow
considered here, acoustic trajectories are only bent inwards, due to the
sole effect of flow acceleration. The existence of a cut-off for
non-radial acoustic waves can be
understood by considering the frequency dependence of the direction
,
due to the
non-homogeneity of the sound speed which bends trajectories outwards.
By contrast, in the isothermal flow
considered here, acoustic trajectories are only bent inwards, due to the
sole effect of flow acceleration. The existence of a cut-off for
non-radial acoustic waves can be
understood by considering the frequency dependence of the direction
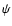 of propagation of the incoming acoustic flux relative to the radial
direction. This angle is approximated in Appendix E in the WKB approximation
(Eq. (E.11)). The higher the frequency, the smaller
of propagation of the incoming acoustic flux relative to the radial
direction. This angle is approximated in Appendix E in the WKB approximation
(Eq. (E.11)). The higher the frequency, the smaller 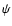 ,
so that
high frequency waves with a given order l are pointing towards the
accretor and are absorbed inside the sonic sphere.
,
so that
high frequency waves with a given order l are pointing towards the
accretor and are absorbed inside the sonic sphere.
The scaling of frequencies stressed in Eq. (5) for strong shocks
consequently separates three ranges of eigenmodes schematized
in Fig. 2:
(i) absorbed sound
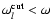 ,
,
(ii) trapped sound
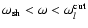 ,
,
(iii) pseudosound
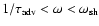 .
The corresponding structure of the vorticity wave is also displayed in
Fig. 2, in each range of frequencies.
.
The corresponding structure of the vorticity wave is also displayed in
Fig. 2, in each range of frequencies.
The boundary conditions at the shock associated with the variables
f,g can be computed with the same method as Nakayama (1992), extended to
the case of non radial perturbations.
Let us denote by
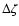 the radial displacement of the shock produced
by a sound wave propagating against the stream in the subsonic region, and
the radial displacement of the shock produced
by a sound wave propagating against the stream in the subsonic region, and
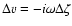 its velocity. The incident Mach number
its velocity. The incident Mach number
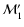 in the frame of the shock is altered by the perturbations
of velocity and displacement as folllows:
in the frame of the shock is altered by the perturbations
of velocity and displacement as folllows:
where the parameter 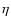 measures the strength of the local
gradient of the Mach number immediately after the shock:
measures the strength of the local
gradient of the Mach number immediately after the shock:
 |
(17) |
The boundary conditions
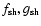 ,
written as functions of
,
written as functions of
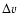 ,
are deduced from the conservation of the mass flux and impulsion
across the shock:
,
are deduced from the conservation of the mass flux and impulsion
across the shock:
The non radial perturbation of the velocity, and the perturbed
vorticity computed in Appendix A enable us to relate
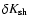 to
to 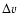 :
:
 |
(20) |
Equation (20) can be used together with
Eqs. (18)-(19) in order to express
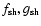 as functions of
as functions of
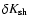 for
non-radial perturbations.
In Appendix C the boundary value problem is reduced to a single
equation incorporating the boundary conditions both at the shock and
at the sonic point. The eigenfrequencies satisfy the following
equation, where f0 is the unique homogeneous solution which is
regular at the sonic point:
for
non-radial perturbations.
In Appendix C the boundary value problem is reduced to a single
equation incorporating the boundary conditions both at the shock and
at the sonic point. The eigenfrequencies satisfy the following
equation, where f0 is the unique homogeneous solution which is
regular at the sonic point:
 |
|
|
(21) |
Equation (22) is independent of the normalization of f0.
It should be noted that the integral on the right hand side is
well defined despite the singularity of the phase near the sonic radius.
This equation describes the perturbation of the shock by the interplay of the
acoustic and vortical perturbations. The same calculation in any other
potential (e.g.the Paczynski-Wiita potential) would lead to the same
system of Eqs. (21)-(22), only the shape of 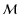 (and its derivative
(and its derivative 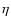 )
described by Eq. (1) would be affected.
The left hand side of Eq. (22) involves only the acoustic
perturbation f0, and is independent of the vortical perturbation.
By contrast, the integral on the right hand side describes the acoustic feed back of the vortical
perturbation coupled to the acoustic field.
)
described by Eq. (1) would be affected.
The left hand side of Eq. (22) involves only the acoustic
perturbation f0, and is independent of the vortical perturbation.
By contrast, the integral on the right hand side describes the acoustic feed back of the vortical
perturbation coupled to the acoustic field.
3 Spectrum of eigenfrequencies
The regularity of the solution at the sonic radius has already been discussed
in F01: the sonic point is a regular singularity if
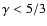 .
For a given incident Mach number
.
For a given incident Mach number
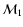 ,
numerical intergration
is performed from
the sonic point towards the shock in order to determine the eigenfrequencies
of perturbations with a latitudinal number l. For a
given value of
,
numerical intergration
is performed from
the sonic point towards the shock in order to determine the eigenfrequencies
of perturbations with a latitudinal number l. For a
given value of 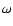 ,
the unique solution which is regular at the
sonic point is expanded in a Frobenius series in order to start the
numerical integration away from the singularity. A Runge-Kutta
algorithm is then used to simultaneously integrate four functions,
namely
,
the unique solution which is regular at the
sonic point is expanded in a Frobenius series in order to start the
numerical integration away from the singularity. A Runge-Kutta
algorithm is then used to simultaneously integrate four functions,
namely
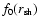 ,
,
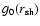 ,
the integral on the right hand side of
Eq. (22) and the integral phase inside it.
,
the integral on the right hand side of
Eq. (22) and the integral phase inside it. 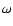 is
varied and shooting is repeated until Eq. (22) is satisfied.
is
varied and shooting is repeated until Eq. (22) is satisfied.
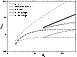 |
Figure 3:
Growth rate of the purely growing radial instability,
multiplied by the advection time (thick dashed line). The thin dashed lines
correspond to the lower and upper bounds determined by Nakayama (1993).
Anticipating on the calculations of the rest of the paper,
the four other curves are analytical estimates of the growth rate of
l=1 perturbations at high Mach number. The growth rate of the
entropic-acoustic instability increases along the dotted line at low
frequency(Eq. (74)), and is bounded by the two thin lines
at high frequency (Eqs. (67)-(68)). The thick full line describes the
most unstable branch (Eq. (85)). |
| Open with DEXTER |
The radial instability found numerically in Fig. 3 is consistent
with the result of Nakayama (1992, 1993), who found that the local acceleration
of the flow immediately after the shock is a source of non-oscillating radial
instability.
The growth rate is shown as a function of the incident Mach number,
in units of the advection time
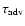 .
The lower and upper bounds found analytically by Nakayama (1993, Eq. (27))
are also displayed in Fig. 3:
.
The lower and upper bounds found analytically by Nakayama (1993, Eq. (27))
are also displayed in Fig. 3:
 |
(23) |
where the parameter 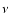 describes the acceleration of the flow and is
proportionnal to
describes the acceleration of the flow and is
proportionnal to 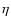 :
:
Note that Eq. (24) is corrected for a factor of 2 for spherical flows,
as noticed by Nakayama (1993). The lower and upper bounds of
Eq. (23) cover a wide range of frequencies from the advection
frequency 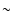
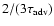 up to the acoustic frequency
up to the acoustic frequency 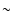
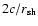 .
In the present case of isothermal radial accretion, the growth rate computed
numerically converges precisely towards the value
.
In the present case of isothermal radial accretion, the growth rate computed
numerically converges precisely towards the value
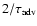 .
.
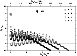 |
Figure 4:
Real and imaginary parts of the eigenfrequencies of the modes
l=0,1,2,3 in the isothermal flow, for
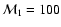 (
(
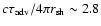 ). The real part is measured in units of
the cut-off frequency ). The real part is measured in units of
the cut-off frequency
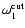 (lower axis) and advection frequency
(upper axis). The imaginary part is normalized to the advection time.
Analytical estimates of the growth rates of the modes l=0,1,2 at
low freqency are indicated using big symbols (Eqs. (78), (83) and (85) in Sects. 6 and 7).
(lower axis) and advection frequency
(upper axis). The imaginary part is normalized to the advection time.
Analytical estimates of the growth rates of the modes l=0,1,2 at
low freqency are indicated using big symbols (Eqs. (78), (83) and (85) in Sects. 6 and 7). |
| Open with DEXTER |
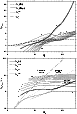 |
Figure 5:
Real and imaginary parts of the eigenfrequencies of the
modes l=1 in the isothermal flow, for different Mach numbers.
Frequencies are multplied by the advection time. The strong l=1
instability due to postshock acceleration corresponds to the thick
line in both plots. In the upper plot, the growth
rate of the fastest of the mode l=0 is also displayed (thick dashed line).
The analytical approximation of the fastest growth rates
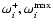 of the l=1instabilities due to the entropic-acoustic cycle and to
post-shock acceleration are shown as the thin dashed line (Eqs. (68))
and the thin dotted line Eq. (85).
In the bottom plot, the cut-off
frequency
of the l=1instabilities due to the entropic-acoustic cycle and to
post-shock acceleration are shown as the thin dashed line (Eqs. (68))
and the thin dotted line Eq. (85).
In the bottom plot, the cut-off
frequency
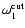 ,
the minimum acoustic frequency ,
the minimum acoustic frequency
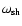 ,
and the frequency ,
and the frequency
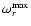 of the most unstable mode
(Eq. (84)) are indicated as references.
of the most unstable mode
(Eq. (84)) are indicated as references. |
| Open with DEXTER |
The effect of non radial perturbations (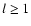 )
involves an integral on the right hand side of Eq. (22), which
reflects the cumulative excitation of acoustic waves by the vorticity
perturbations advected from the shock to the sonic radius.
Figure 4 shows the eigenspectrum of the isothermal Bondi flow for
M1=100, l=0,1,2,3. This spectrum is characterized as follows:
)
involves an integral on the right hand side of Eq. (22), which
reflects the cumulative excitation of acoustic waves by the vorticity
perturbations advected from the shock to the sonic radius.
Figure 4 shows the eigenspectrum of the isothermal Bondi flow for
M1=100, l=0,1,2,3. This spectrum is characterized as follows:
(i) The most unstable mode is asymmetric (l=1)
and well separated from the other eigenmodes. The growth rate of this low
frequency mode is significantly larger than the advection time, nearly four times
faster than the unstable radial mode. The analytical estimates of the growth
rates at low frequency correspond to Eqs. (77)-(78),
(81)-(83) and (84)-(85)
in Sects. 6 and 7.
(ii) Non radial unstable modes are very numerous and cover a wide range of
frequencies, from the advection frequency (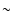
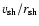 ), up to the
cut-off frequency (
), up to the
cut-off frequency (
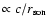 ).
).
(iii) A striking feature of the eigenspectrum in Fig. 4 is
the apparent
oscillation of the imaginary part as a function of the real part of the frequency.
This behaviour is explained in Sect. 5 on the basis of the
vortical-acoustic cycle.
The variation of the growth rate with the incident
Mach number is shown in Fig. 5. The higher the Mach number,
the more unstable the non radial modes, while the radial instability
saturates. The growth rate of the most unstable l=1 mode increases
with the incident Mach number much faster than in the other modes.
The real part of its complex frequency is intermediate
between the advection and acoustic frequencies. It is
computed analytically in Sect. 7.
The rest of the paper is dedicated to understanding this
apparently complicated spectrum, and to questioning the role of post-shock
acceleration.
4 The sound of vorticity
 |
Figure 6:
Efficiency
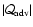 of the excitation of
acoustic waves propagating against the stream by the advection of a vortex in an
isothermal flow, for l=1,2,3. The frequency is in units of the
cut-off frequency
of the excitation of
acoustic waves propagating against the stream by the advection of a vortex in an
isothermal flow, for l=1,2,3. The frequency is in units of the
cut-off frequency
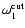 .
The dotted lines correspond to the
asymptotic behaviour .
The dotted lines correspond to the
asymptotic behaviour
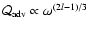 at
low frequency determined analytically in Eq. (30).
at
low frequency determined analytically in Eq. (30). |
| Open with DEXTER |
Let us assume that a vorticity wave is
advected from infinity towards the accretor: what is the sound
produced by the advection of this vorticity? This question is solved
in Appendix D by computing the coupling coefficient
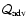 measuring the outgoing acoustic flux F-
associated with a vorticity perturbation
measuring the outgoing acoustic flux F-
associated with a vorticity perturbation 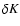 :
:
 |
(26) |
The relationship between the acoustic flux 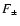 and the acoustic
perturbation
and the acoustic
perturbation 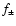 is deduced from the WKB approximation in Appendix B:
is deduced from the WKB approximation in Appendix B:
 |
(27) |
Thus the complex efficiency
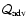 is defined at a
radius
is defined at a
radius
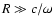 ,
in the region of propagation of acoustic waves,
as follows:
,
in the region of propagation of acoustic waves,
as follows:
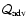 is approximately independent of R in the WKB region
of propagation of acoustic waves, i.e.away from their turning point.
This coefficient is approximated in Appendix D in the low frequency limit
is approximately independent of R in the WKB region
of propagation of acoustic waves, i.e.away from their turning point.
This coefficient is approximated in Appendix D in the low frequency limit
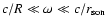 ,
i.e.below the cut-off frequency, using the
function
,
i.e.below the cut-off frequency, using the
function
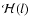 defined from an integral of the Spherical Bessel
function jl (Eq. (D.7)):
defined from an integral of the Spherical Bessel
function jl (Eq. (D.7)):
 |
(30) |
with
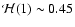 ,
,
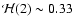 and
and
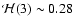 .
The direct integration of Eq. (29) is compared to the
approximation obtained in Eq. (30) for l=1,2,3 in
Fig. 6. The asymptotic behaviour
.
The direct integration of Eq. (29) is compared to the
approximation obtained in Eq. (30) for l=1,2,3 in
Fig. 6. The asymptotic behaviour
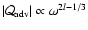 is correctly reproduced. The scaling factor of this power law
obtained analytically is too low by a factor 2 for l=1 perturbations,
which can be attributed to the roughness of the approximation.
This calculation clearly indicates that the vortical-acoustic coupling is
most efficient near the cut-off frequency. The same conclusion
was reached in F01 concerning the efficiency of the entropic-acoustic
coupling.
is correctly reproduced. The scaling factor of this power law
obtained analytically is too low by a factor 2 for l=1 perturbations,
which can be attributed to the roughness of the approximation.
This calculation clearly indicates that the vortical-acoustic coupling is
most efficient near the cut-off frequency. The same conclusion
was reached in F01 concerning the efficiency of the entropic-acoustic
coupling.
4.2 Region of coupling
This approximation enables us to determine the region where the coupling
between the vorticity and the acoustic perturbations is most efficient.
It occurs mainly in the
subsonic region
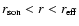 where the wavelength of the vorticity
perturbation is largest (see Fig. 2):
where the wavelength of the vorticity
perturbation is largest (see Fig. 2):
 |
(31) |
A similar result was obtained in F01 concerning entropy perturbations for
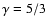 .
Due to the differences in velocity profiles in
Eq. (31),
.
Due to the differences in velocity profiles in
Eq. (31),
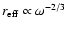 for
for
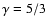 at high frequency
(Eqs. (E.6), (E.11) and (E.12) of F01), whereas
at high frequency
(Eqs. (E.6), (E.11) and (E.12) of F01), whereas
 |
(32) |
in the isothermal flow at low frequency. It is therefore important to note
that the most efficient coupling at low frequency lies in the region of
pseudosound well within the turning point (
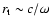 )
of
acoustic waves:
)
of
acoustic waves:
 |
(33) |
According to Eq. (31), the upper bound
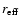 of the
coupling region for perturbations near the advection frequency coincides with
the shock radius.
of the
coupling region for perturbations near the advection frequency coincides with
the shock radius.
5 Vortical-acoustic instability at high frequency
The formalism developed in FT00 for the entropic-acoustic cycle within the
WKB approximation can be transposed to the case of the
vortical-acoustic cycle. This formalism requires the frequency to be high
enough so that acoustic waves can be identified and their propagation time
measured. An initial perturbation of vorticity
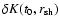 at the
shock, advected towards the accretor, triggers the excitation of an
acoustic flux F- propagating outwards. As it reaches the shock
surface, this acoustic flux induces new vorticity perturbations
at the
shock, advected towards the accretor, triggers the excitation of an
acoustic flux F- propagating outwards. As it reaches the shock
surface, this acoustic flux induces new vorticity perturbations
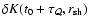 ,
where
,
where
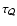 is the duration of
this cycle. The global efficiency
is the duration of
this cycle. The global efficiency 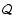 of the cycle is naturally
of the cycle is naturally
 |
(34) |
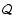 and
and
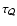 depend a priori on the frequency
depend a priori on the frequency
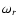 and spatial structure l of the perturbation considered.
The growth (or damping) rate of the cycle is identified with the imaginary
part of the eigenfrequency, given by:
and spatial structure l of the perturbation considered.
The growth (or damping) rate of the cycle is identified with the imaginary
part of the eigenfrequency, given by:
 |
(35) |
The timescale
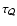 is dominated by the
advection timescale
is dominated by the
advection timescale
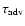 if the shock is strong
(
if the shock is strong
(
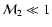 ,
,
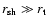 ):
):
 |
(36) |
The global efficiency 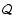 can be decomposed
in terms of the efficiencies of the coupling between
F- and
can be decomposed
in terms of the efficiencies of the coupling between
F- and 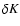 during advection (
during advection (
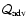 )
and at the shock (
)
and at the shock (
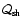 ), defined immediately after
the shock according to Eq. (28) and:
), defined immediately after
the shock according to Eq. (28) and:
 | (37) |
 | (38) |
The modulus of
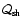 is directly interpreted as a coupling efficiency
between F- and
is directly interpreted as a coupling efficiency
between F- and
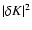 :
:
 |
(39) |
The efficiency
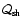 is computed in Appendix E,
following a method introduced by D'Iakov (1958) and Kontorovich (1958, 1959).
is computed in Appendix E,
following a method introduced by D'Iakov (1958) and Kontorovich (1958, 1959).
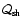 can be approximated
by a WKB analysis when the wavelength of the perturbation is small
compared to the lengthscale of the local gradients of the flow, by
keeping only the first order terms in
can be approximated
by a WKB analysis when the wavelength of the perturbation is small
compared to the lengthscale of the local gradients of the flow, by
keeping only the first order terms in
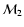 and
and
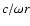 ,
at high frequency and for strong shocks:
,
at high frequency and for strong shocks:
 |
(40) |
This calculation proves that the flow reacceleration does not affect
the vortical-acoustic coupling at the shock for
 |
(41) |
and that
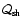 is approximately independent of
frequency in the range
is approximately independent of
frequency in the range
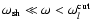 .
As a consequence of Eqs. (37) and (40), the
vorticity is produced at the shock with an efficiency proportional to
the shock strength:
.
As a consequence of Eqs. (37) and (40), the
vorticity is produced at the shock with an efficiency proportional to
the shock strength:
 |
(42) |
The global efficiency 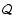 should consequently peak near the
cut-off frequency, and drop abruptly above it. The frequency dependence
of
should consequently peak near the
cut-off frequency, and drop abruptly above it. The frequency dependence
of 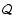 appears in Fig. 8 (top picture, full line),
as deduced from Fig. 6 and Eq. (40) in the WKB
approximation. Thus the instability should be strongest near the
cut-off frequency with the following scaling, obtained from
Eqs. (14), (30) and (40) for
appears in Fig. 8 (top picture, full line),
as deduced from Fig. 6 and Eq. (40) in the WKB
approximation. Thus the instability should be strongest near the
cut-off frequency with the following scaling, obtained from
Eqs. (14), (30) and (40) for
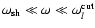 :
:
 |
(43) |
where the scaling factor
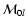 depends on l through both
depends on l through both
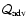 and
and
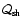 :
:
 |
(44) |
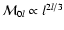 diverges for
diverges for 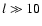 ,
thus favouring the instability
of low degree modes. According to Fig. 6, the
extrapolation of Eq. (43) to
,
thus favouring the instability
of low degree modes. According to Fig. 6, the
extrapolation of Eq. (43) to
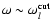 gives a very
rough upper bound of
gives a very
rough upper bound of
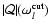 ,
particularly
overestimlating it for high degree perturbations. Although
,
particularly
overestimlating it for high degree perturbations. Although
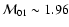 exceeds
exceeds
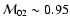 and
and
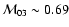 ,
the actual
efficiency
,
the actual
efficiency
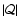 is maximal for the mode l=1, as checked in
Fig. 8 by multiplying the curve
is maximal for the mode l=1, as checked in
Fig. 8 by multiplying the curve
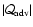 (Fig. 6) by
(Fig. 6) by
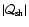 (Eq. (40)).
Using Eqs. (35) and (36), the growth rate
(Eq. (40)).
Using Eqs. (35) and (36), the growth rate
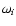 at high frequency is deduced from Eq. (43):
at high frequency is deduced from Eq. (43):
 |
|
|
(45) |
Equation (47) indicates that the range of unstable frequencies
below the cut-off frequency gets narrower for 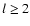 .
This is also confirmed by the eigenspectrum obtained numerically for
l=1,2,3 in Fig. 4. Note that the efficiency
.
This is also confirmed by the eigenspectrum obtained numerically for
l=1,2,3 in Fig. 4. Note that the efficiency
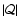 was estimated using
was estimated using
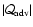 which was computed for
perturbations with a purely real frequency. Thus the estimate of the
growth rate in Eq. (46) implicitly assumes that the imaginary
part is small compared to the real part. This is true since
which was computed for
perturbations with a purely real frequency. Thus the estimate of the
growth rate in Eq. (46) implicitly assumes that the imaginary
part is small compared to the real part. This is true since
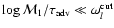 .
This calculation proves that the vortical-acoustic cycle is unstable
for strong shocks, with a growth rate exceeding the growth rate of
the radial mode, and a mechanism which is independent of the
sign of the local flow acceleration immediately after the shock.
A more refined description of the entropic-acoustic cycle is
developped in the next section
in order to understand the apparent oscillations in the
spectrum obtained numerically in Figs. 4 and 5.
.
This calculation proves that the vortical-acoustic cycle is unstable
for strong shocks, with a growth rate exceeding the growth rate of
the radial mode, and a mechanism which is independent of the
sign of the local flow acceleration immediately after the shock.
A more refined description of the entropic-acoustic cycle is
developped in the next section
in order to understand the apparent oscillations in the
spectrum obtained numerically in Figs. 4 and 5.
5.2.1 Dispersion relation for the double cycle
The role of the purely acoustic cycle had been anticipated in FT00.
It is characterized by a time scale
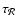 and a global efficiency
and a global efficiency
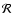 .
Let us show how the simultaneous existence
of the two cycles can explain the apparent oscillation in the
eigenspectrum of Fig. 4. The following extension of the analysis
of FT00 is valid for both entropic-acoustic and vortical-acoustic cycles,
by replacing "vortical'' by "entropic''.
.
Let us show how the simultaneous existence
of the two cycles can explain the apparent oscillation in the
eigenspectrum of Fig. 4. The following extension of the analysis
of FT00 is valid for both entropic-acoustic and vortical-acoustic cycles,
by replacing "vortical'' by "entropic''.
A perturbation f is influenced by the two cycles as follows:
 |
(48) |
A solution of the form
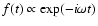 satisfies
Eq. (48) if the complex eigenfrequency (
satisfies
Eq. (48) if the complex eigenfrequency (
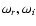 )
is a solution of the following dispersion equation (Eq. (25) of FT00):
)
is a solution of the following dispersion equation (Eq. (25) of FT00):
 |
(49) |
This dispersion relation is recovered in Appendix F as a WKB
approximation of the exact dispersion relation (22).
The analysis of the dispersion relation (49) in Appendix G
enables us to extract physical information from the complicated
eigenspectrum in Fig. 4, such as the ratio of timescales
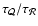 ,
and the dimensionless efficiencies
,
and the dimensionless efficiencies
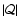 and
and
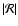 .
.
 |
Figure 7:
Number of eigenmodes in each oscillation of the
eigenspectrum in Fig. 4, identified as the ratio of the
timescales of the two cycles. For strong shocks,
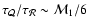 . . |
| Open with DEXTER |
The timescale
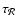 of the acoustic cycle for strong shocks
can be written approximately:
of the acoustic cycle for strong shocks
can be written approximately:
 |
(50) |
According to Eqs. (36) and (50), the ratio
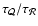 for a strong shock is simply:
for a strong shock is simply:
 |
(51) |
As shown in Appendix G, this ratio is the average
number of eigenmodes in each oscillation of the eigenspectrum.
As an illustration, this number is reported in Fig. 7 for
the modes l=1,2,3 in the case
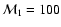 corresponding to Fig. 4,
in good agreement with Eq. (51).
corresponding to Fig. 4,
in good agreement with Eq. (51).
 |
Figure 8:
Global efficiencies
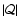 , ,
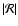 asociated to non radial
perturbations l=1,2,3 deduced from the eigenspectrum in Fig. 4
in the framework of the double cycle model (dotted line), compared
with the efficiencies deduced from the calculation of
asociated to non radial
perturbations l=1,2,3 deduced from the eigenspectrum in Fig. 4
in the framework of the double cycle model (dotted line), compared
with the efficiencies deduced from the calculation of
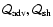 and
and
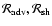 . . |
| Open with DEXTER |
As noticed in FT00, the acoustic cycle can be neglected (
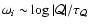 )
if the efficiencies and timescales
of the two cycles are such that
)
if the efficiencies and timescales
of the two cycles are such that
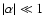 ,
with
,
with
 |
(52) |
If 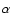 is not negligible, the acoustic cycle can contribute to either
stabilize or destabilize the vortical-acoustic cycle. The most stabilizing effect of the acoustic cycle
is the effective reduction of
is not negligible, the acoustic cycle can contribute to either
stabilize or destabilize the vortical-acoustic cycle. The most stabilizing effect of the acoustic cycle
is the effective reduction of 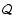 by a factor 2 (see Appendix G).
By contrast, its destabilizing contribution can be much larger
comparatively, if the acoustic time is short compared to the advection time.
This is the case for strong shocks. Depending on the
relative phases of the two cycles, the growth rate can then cover the following
range:
by a factor 2 (see Appendix G).
By contrast, its destabilizing contribution can be much larger
comparatively, if the acoustic time is short compared to the advection time.
This is the case for strong shocks. Depending on the
relative phases of the two cycles, the growth rate can then cover the following
range:
 |
(53) |
Conversely, the values of the dimensionless physical parameters
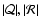 can be extracted from the eigenspectrum,
as in Fig. 4, by measuring
can be extracted from the eigenspectrum,
as in Fig. 4, by measuring
(i) the extremal values
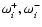 ,
,
(ii) the period
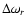 of the oscillations
of the oscillations
(iii) the average number n of modes per period.
As demonstrated in Appendix G, the timescale of
the acoustic cycle is simply
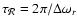 .
Thus the oscillations are well resolved in the eigenspectrum only if the
advection time is significantly longer than the acoustic time
(i.e.
.
Thus the oscillations are well resolved in the eigenspectrum only if the
advection time is significantly longer than the acoustic time
(i.e.
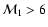 ).
).
The values of
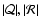 are determined using the following
relations:
are determined using the following
relations:
where
 | (56) |
 | (57) |
As an illustration, Fig. 8 is obtained
from the eigenspectrum of Fig. 4 using Eqs. (54)
and (55). The accuracy of the measurements of
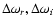 and
and
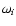 is of course of the order 1/n.
As a check of consistency, the value of
is of course of the order 1/n.
As a check of consistency, the value of
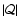 obtained
from the product of
obtained
from the product of
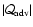 (Fig. 6) and
(Fig. 6) and
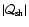 (Eq. (40)) is also displayed,
showing an excellent agreement except for the lowest frequency modes
where WKB approximation breaks down. It is remarkable that
(Eq. (40)) is also displayed,
showing an excellent agreement except for the lowest frequency modes
where WKB approximation breaks down. It is remarkable that
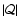 seems
to be maximized at low frequency for l=1 whereas it is maximized near the
cut-off frequency
seems
to be maximized at low frequency for l=1 whereas it is maximized near the
cut-off frequency
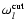 for
for 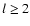 .
The efficiency
.
The efficiency
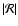 of the acoustic cycle is bounded by
one and decreases to zero above the cut-off frequency, as could be expected
from FT00 and F01.
of the acoustic cycle is bounded by
one and decreases to zero above the cut-off frequency, as could be expected
from FT00 and F01.
The global efficiency 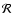 can be decomposed
in terms of the efficiencies
can be decomposed
in terms of the efficiencies
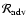 and
and
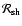 of the coupling between the acoustic
fluxes
of the coupling between the acoustic
fluxes 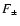 ,
such that the
global efficiency
,
such that the
global efficiency 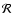 is
is
 |
(58) |
The efficiency
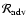 measures the outgoing acoustic flux F- produced by the
deviation of an ingoing acoustic flux F+:
measures the outgoing acoustic flux F- produced by the
deviation of an ingoing acoustic flux F+:
 |
|
|
(61) |
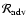 is simply the limit when
is simply the limit when
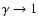 of the
efficiency
computed in F01: it is close to unity below the cut-off frequency
of the
efficiency
computed in F01: it is close to unity below the cut-off frequency
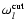 ,
and decreases exponentially above this cut-off.
Conversely, an acoustic flux F- reaching a shock
produces a reflected ingoing acoustic flux F+ with the efficiency
,
and decreases exponentially above this cut-off.
Conversely, an acoustic flux F- reaching a shock
produces a reflected ingoing acoustic flux F+ with the efficiency
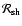 :
:
 |
|
|
(62) |
 |
|
|
(63) |
Keeping only the first order terms in
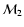 and
and
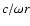 ,
the complex
efficiency is computed in Appendix E:
,
the complex
efficiency is computed in Appendix E:
 |
(64) |
Thus the global efficiency
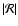 should be close to unity below
the cut-off frequency. The product
should be close to unity below
the cut-off frequency. The product
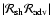 is displayed in Fig. 8 (bottom picture), in good agreement
with the value of
is displayed in Fig. 8 (bottom picture), in good agreement
with the value of
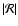 deduced from Fig. 4 and Eq. (55).
deduced from Fig. 4 and Eq. (55).
The extremal values
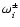 of the growth rate of the
vortical-acoustic cycle are computed
in Appendix G (Eq. (G.7)) for strong shocks:
of the growth rate of the
vortical-acoustic cycle are computed
in Appendix G (Eq. (G.7)) for strong shocks:
 |
(65) |
The asymptotic scaling of 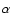 is deduced from
Eqs. (43), (51) and (64) :
is deduced from
Eqs. (43), (51) and (64) :
 |
(66) |
Together with Eq. (36), and despite the roughness of the
approximation in Eq. (30) near the cut-off frequency, the leading
order of the asymptotic values of
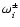 is
comparable to:
is
comparable to:
The values of
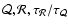 are thus responsible for a dispersion of the growth rate by a factor 3in Eqs. (67)-(68) near the cut-off frequency, depending on
the relative phases of the two cycles. This factor 3 is consistent
with both Figs. 4 and 5.
are thus responsible for a dispersion of the growth rate by a factor 3in Eqs. (67)-(68) near the cut-off frequency, depending on
the relative phases of the two cycles. This factor 3 is consistent
with both Figs. 4 and 5.
6 Vortical-acoustic instability at low frequency
The region of efficient coupling between the vorticity and acoustic
perturbations lies in the region of pseudosound according to
Eq. (33). Thus it seems natural to expect an instability at
low frequency as long as the coupling region determined from
Eq. (32) lies inside the shock radius, i.e.down to the
advection frequency.
This case is similar to the hole tone instability (e.g.whistling kettle)
studied by Chanaud & Powell (1965), or in the oscillations of impinging
shear layers (see a review by Rockwell 1983).
In some of these cycles, the vorticity perturbations are coupled to the
acoustic field in the region of pseudosound. As stressed by Chanaud
& Powell (1965), this does not preclude the use of the term "acoustic feedback''
so that we may talk of a vortical-acoustic cycle even in this range of
frequencies.
Although the problem cannot be treated in the WKB
limit, the homogeneous solution can be approximated by a Spherical Bessel
function of the first kind in the region of pseudosound far from the sonic
point. The calculation in Appendix H shows that the case l=1 and
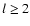 must be treated separately.
In the domain of pseudosound
must be treated separately.
In the domain of pseudosound
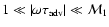 ,
Eq. (22) is reduced to:
,
Eq. (22) is reduced to:
The l=1 acoustic perturbation is approximated in Appendix H
as
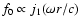 ,
and Eq. (69) is
transformed into
,
and Eq. (69) is
transformed into
 |
(70) |
A branch of solutions with
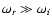 corresponds to a vortical-acoustic cycle between the shock and the sonic point:
corresponds to a vortical-acoustic cycle between the shock and the sonic point:
 |
|
|
|
 |
|
|
(71) |
 |
|
|
|
 |
|
|
(72) |
The maximum growth rate of this branch of solution is reached for a
real frequency similar to the frequency of the local instability.
 |
|
|
(75) |
This growth rate is compared to the results of numerical calculations
in Fig. 5. This growth rate exceeds the growth rate of
the vortical-acoustic instability at high frequency (Eq. (46)), but
is asymptotically smaller than the maximum growth rate
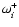 reached when the purely acoustic and vortical acoustic cycles are in phase
(Eq. (68)).
reached when the purely acoustic and vortical acoustic cycles are in phase
(Eq. (68)).
If 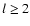 ,
the acoustic feedback due to an isolated vortical perturbation near
the shock is negligible compared to the integral effect for strong shocks.
Eq. (69) is reduced to:
,
the acoustic feedback due to an isolated vortical perturbation near
the shock is negligible compared to the integral effect for strong shocks.
Eq. (69) is reduced to:
 |
|
|
(76) |
The most unstable modes are therefore the modes l=2, with
These approximations are in excellent agreement with the numerical
result of Fig. 4.
By contrast with the case of high frequency perturbations,
it seems difficult to separate completely the effect of postshock
acceleration from the global vortical-acoustic cycle in this range of
frequencies.
7 Effects of post-shock acceleration: A global instability
with a local criterion
The boundary condition (18) can be rewritten
for strong shocks as follows:
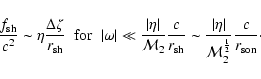 |
(79) |
This equation is similar to the argument of Nobuta & Hanawa (1994)
concerning the balance total pressures (thermal and dynamical)
on both sides of the shock. Rather than treating the shock surface
as a material surface pushed by the local pressures on both sides of it,
Eq. (79) is interpreted as follows: an excess of Bernoulli perturbation
f (which we may call "energy'') on the subsonic side of the shock is
associated with a displacement of the shock in the direction of increase of
the local Mach number. If 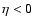 (Eq. (17)), an excess of
f produces an outward displacement of the shock. This statement alone is not
conclusive: instability occurs only if the flow is not able to evacuate this
excess of energy. Although the displacement of the shock indeed liberates
some potential energy locally, the instability depends
on the leakage of energy through the sonic radius (Nakayama 1993).
(Eq. (17)), an excess of
f produces an outward displacement of the shock. This statement alone is not
conclusive: instability occurs only if the flow is not able to evacuate this
excess of energy. Although the displacement of the shock indeed liberates
some potential energy locally, the instability depends
on the leakage of energy through the sonic radius (Nakayama 1993).
For radial perturbations (l=0), the only way of evacuating the
excess of energy is through acoustic perturbations.
Acoustic energy, however, is trapped in the subsonic region if the real
frequency of the mode is low enough. Thus a low frequency instability
is expected. Although the criterion of the instability is indeed local,
its growth rate depends on the spatial structure of
the acoustic perturbation from the sonic radius to the shock, as illustrated
by Eq. (22) for strong shocks:
 |
(80) |
f0 is approximated as the acoustic perturbation of a uniform
medium in spherical coordinates (see Appendix B), using a Spherical Bessel
function
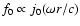 for
for
 .
The solution of the dispersion relation (80)
at low frequency is a purely imaginary eigenfrequency:
.
The solution of the dispersion relation (80)
at low frequency is a purely imaginary eigenfrequency:
The fact that the growth time scales like the advection time is not
obvious a priori.
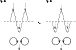 |
Figure 9:
Interaction of the vortex with the shock. The contribution of a
vorticity perturbation
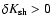 to the Bernoulli perturbation is
positive (
to the Bernoulli perturbation is
positive (
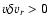 ), and induces an increase of the local accretion
rate (g>0).Depending on the sign of the postshock acceleration, a
vorticity perturbation contributes to a local expansion ( ), and induces an increase of the local accretion
rate (g>0).Depending on the sign of the postshock acceleration, a
vorticity perturbation contributes to a local expansion (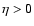 )
or
collapse ( )
or
collapse (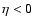 )
of the shock. )
of the shock. |
| Open with DEXTER |
Non radial perturbations generate vorticity, which contribute to the
energy balance in the subsonic part of the flow. Figure 9
illustrates the contribution of a vorticity perturbation to the
Bernoulli perturbation through the radial component of velocity
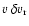 .
Thus the vorticity perturbation participates to
increase the local accretion rate (i.e.g>0) in the regions where the shock
moves inward (
.
Thus the vorticity perturbation participates to
increase the local accretion rate (i.e.g>0) in the regions where the shock
moves inward (
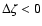 ). Comparing this statement with
). Comparing this statement with
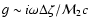 deduced from Eq. (19), we
conclude that the vorticity contributes to the instability if
deduced from Eq. (19), we
conclude that the vorticity contributes to the instability if 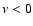 .
A quantitative calculation of the growth rate requires taking into
account the acoustic perturbation in the region from the shock to the sonic
point. The fastest instability of the flow, well isolated from all the other
modes of instability, is obtained by neglecting the last term on the right
hand side of Eq. (70):
.
A quantitative calculation of the growth rate requires taking into
account the acoustic perturbation in the region from the shock to the sonic
point. The fastest instability of the flow, well isolated from all the other
modes of instability, is obtained by neglecting the last term on the right
hand side of Eq. (70):
It is in excellent agreement with the numerical calculations in
Figs. 4 and 5.
This growth rate is intermediate between the advection and the
fundamental acoustic frequencies. The real and imaginary parts being
comparable, the growth rate is the time taken by the vorticity
perturbation to travel by one wavelength
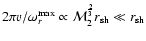 .
.
8 Discussion
Most shock instabilities identified and studied in astrophysics are
related to the acceleration or deceleration of the shock itself. The
most famous is of course the Rayleigh-Taylor instability of accelerated shocks,
analysed by Bernstein & Book (1978). Decelerated shocks are also
unstable to a rippling instability, studied by Vishniac (1983), Bertshinger
(1986) and Vishniac & Ryu (1989). By definition, stationary shocks are
stable with respect to these mechanisms, but can still be unstable.
Nakayama (1992, 1993) pointed out the radial instability of the shock if the
flow is immediately accelerated after the shock, in isothermal flows.
The validity of the postshock acceleration criterion for adiabatic flows
is still uncertain, even for radial perturbations (Nakayama 1994).
The vortical-acoustic cycle studied in the present paper resembles
by many aspects to the entropic-acoustic cycle studied by FT00 and F01
in adiabatic flows. Two distinct mechanisms, however, are at work:
(i) the vortical-acoustic cycle is fed by the vorticity production
by a perturbed shock, which is highest for isothermal flows with a
strong shock,
(ii) the entropic-acoustic cycle is fed by the temperature
increase from the shock to the sonic radius, which is highest if
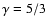 (FT00, F01).
(FT00, F01).
A calculation similar to Appendix E for adiabatic flows would show
that the vorticity production by a perturbed shock is large only in the
isothermal limit:
 |
(86) |
Although shocked adiabatic flows with
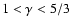 are subject to both
entropic-acoustic and vortical-acoustic cycles in principle, their stability
cannot be determined without a specific calculation.
are subject to both
entropic-acoustic and vortical-acoustic cycles in principle, their stability
cannot be determined without a specific calculation.
The stability of BHL accretion can be addressed with new tools, using
the present results and the entropic-acoustic cycle of FT00 and F01.
Although a detailed analysis of the existing numerical simulations of
BHL accretion is postponed to a forthcoming paper, let us outline the
possible consequences of the entropic-acoustic and vortical-acoustic
mechanisms on this specific flow.
Numerical simulations of BHL accretion in 3-D show a strong instability
for adiabatic flows with
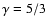 and small accretors
(Ruffert & Arnett 1994; Ruffert 1994): this coincides nicely with the
properties of the entropic-acoustic cycle,
which is most unstable if the temperature gradient in the subsonic part of
the flow is strongest (FT00, F01). By contrast, nearly isothermal flows are rather
stable in 3-D numerical simulations (Ruffert 1996). This could seem puzzling
given the strong vortical-acoustic instability described in the present
paper: why would the entropic-acoustic cycle be relevant for
the BHL instability with
and small accretors
(Ruffert & Arnett 1994; Ruffert 1994): this coincides nicely with the
properties of the entropic-acoustic cycle,
which is most unstable if the temperature gradient in the subsonic part of
the flow is strongest (FT00, F01). By contrast, nearly isothermal flows are rather
stable in 3-D numerical simulations (Ruffert 1996). This could seem puzzling
given the strong vortical-acoustic instability described in the present
paper: why would the entropic-acoustic cycle be relevant for
the BHL instability with
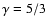 ,
and the
vortical-acoustic cycle be irrelevant to the BHL stability for
,
and the
vortical-acoustic cycle be irrelevant to the BHL stability for 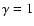 ?
This apparent contradiction can be partly solved by remembering the
difference of topology between the spherical Bondi flow and the BHL
flow, following the remark of Sect. 2.1.
All the numerical simulations of isothermal BHL
accretion seem to agree with the fact that the shock is attached to the accretor,
whereas it is detached in high resolution simulations of adiabatic flows
with
?
This apparent contradiction can be partly solved by remembering the
difference of topology between the spherical Bondi flow and the BHL
flow, following the remark of Sect. 2.1.
All the numerical simulations of isothermal BHL
accretion seem to agree with the fact that the shock is attached to the accretor,
whereas it is detached in high resolution simulations of adiabatic flows
with
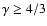 .
This can be understood qualitatively in terms of
the weakness of pressure forces in isothermal flows compared to
adiabatic flows (
.
This can be understood qualitatively in terms of
the weakness of pressure forces in isothermal flows compared to
adiabatic flows (
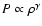 ). More quantitatively,
Foglizzo & Ruffert (1997) proved that the shock in the isothermal BHL
flow cannot be detached unless the sonic surface extends up to distances
comparable to the Bondi radius GM/c2, i.e.much larger than the
accretion radius. In view of this topological difference between
isothermal and adiabatic BHL flows, it seems easier to extend the
results obtained for shocked Bondi accretion to the subsonic region
ahead of the accretor, for detached shocks, than in the very
non-radial region of accretion behind the accretor for attached
shocks. Although true, however, this argument is not conclusive. Even in a non
radial isothermal flow, a small pressure perturbation of the shock is
able to generate vorticity perturbations very efficiently. The lack of
instability of isothermal BHL accretion in 3-D must be sought for in the
lack of acoustic feedback from the advected vorticity perturbation.
Unfortunately we do not have quantitative arguments to explain why
the acoustic feedback is so weak, apart from noticing that geometric
compression of the vorticity perturbation from the shock to the sonic
radius might be insufficient in the BHL flow. Any coherent explanation
should of course also account for the strong instability observed in 2-D
simulations of BHL accretion (Shima et al.1998).
). More quantitatively,
Foglizzo & Ruffert (1997) proved that the shock in the isothermal BHL
flow cannot be detached unless the sonic surface extends up to distances
comparable to the Bondi radius GM/c2, i.e.much larger than the
accretion radius. In view of this topological difference between
isothermal and adiabatic BHL flows, it seems easier to extend the
results obtained for shocked Bondi accretion to the subsonic region
ahead of the accretor, for detached shocks, than in the very
non-radial region of accretion behind the accretor for attached
shocks. Although true, however, this argument is not conclusive. Even in a non
radial isothermal flow, a small pressure perturbation of the shock is
able to generate vorticity perturbations very efficiently. The lack of
instability of isothermal BHL accretion in 3-D must be sought for in the
lack of acoustic feedback from the advected vorticity perturbation.
Unfortunately we do not have quantitative arguments to explain why
the acoustic feedback is so weak, apart from noticing that geometric
compression of the vorticity perturbation from the shock to the sonic
radius might be insufficient in the BHL flow. Any coherent explanation
should of course also account for the strong instability observed in 2-D
simulations of BHL accretion (Shima et al.1998).
Inviscid accretion flows with low angular momentum are much more
complex than the Bondi flow in the sense that the shock position is
not unique (Fukue 1987; Chakrabarti 1989).
The numerical simulations of Nobuta & Hanawa (1994) did not detect
the effects of vorticity perturbations since they were restricted
to axisymmetric motion. These simulations showed
the evolution of the radial instability due to postshock
acceleration: the unstable shock is either absorbed by the accretor
or inflates to reach the stable outer position.
Molteni et al. (1999) performed non axisymmetric numerical
simulations of shocked inviscid accretion flows with low angular momentum,
for
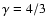 .
Unstable m=1 oscillations were observed, with no
physical explanation. The entropic-acoustic and vortical-acoustic
cycles might provide a physical basis to understand this instability.
.
Unstable m=1 oscillations were observed, with no
physical explanation. The entropic-acoustic and vortical-acoustic
cycles might provide a physical basis to understand this instability.
If the existence of the shock is postulated a priori, as in the
present study, the flow might simply converge towards another
solution, as illustrated by the dashed lines in Fig. 1. The shock
can either be absorbed by the accretor, leading to the fully supersonic
solution, or could expand towards infinity to establish the Bondi
solution if the outer boundary condition allows it.
In accretion flows stable with respect to the postshock acceleration
criterion, but unstable through the vortical-acoustic (or
entropic-acoustic) cycle, the instability might be saturated by the effect of
the geometric dilution of the acoustic energy in the
subsonic cavity. Let us assume that advected vorticity perturbations
generate an acoustic flux propagating outward
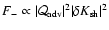 (Eq. (26)), and that the acoustic perturbation produces in turn a
vorticity perturbation
(Eq. (26)), and that the acoustic perturbation produces in turn a
vorticity perturbation
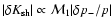 (Eq. (42)). The amplitude of the pressure perturbation
(Eq. (42)). The amplitude of the pressure perturbation
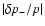 depends on the volume in which the acoustic flux F-
is diluted through Eq. (27):
depends on the volume in which the acoustic flux F-
is diluted through Eq. (27):
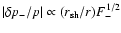 .
Thus the vortical-acoustic cycle is naturally
stabilized when the shock reaches a distance
.
Thus the vortical-acoustic cycle is naturally
stabilized when the shock reaches a distance
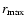 defined by
defined by
 |
(87) |
where
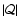 is the global efficiency of the vortical-acoustic
cycle in the linear regime. If the shock is not simply absorbed by
the accretor, the non linear evolution of the instability could
lead to quasi periodic oscillations of amplitude comparable to
is the global efficiency of the vortical-acoustic
cycle in the linear regime. If the shock is not simply absorbed by
the accretor, the non linear evolution of the instability could
lead to quasi periodic oscillations of amplitude comparable to
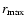 .
However, given the number of unstable modes in a spectrum like
Fig. 4, the vortical-acoustic instability might as well
saturate into turbulence rather than be dominated by a single QPO.
This issue can only be solved with numerical simulations.
.
However, given the number of unstable modes in a spectrum like
Fig. 4, the vortical-acoustic instability might as well
saturate into turbulence rather than be dominated by a single QPO.
This issue can only be solved with numerical simulations.
9 Conclusions
The linear stability of shocked isothermal Bondi accretion has been
studied by comparing the complex eigenfrequencies obtained through
a direct numerical integration (Sect. 3) to the analytical
results obtained for strong shocks by two different methods:
(i) an analytical estimate of the growth rate corresponding to
a cycle of perturbations with a purely real frequency, obtained
by separating the effects of advection from the boundary effects of
the shock. This WKB approximation, valid in the range
of acoustic waves (
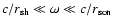 ), was used in
Sects. 4 and 5,
), was used in
Sects. 4 and 5,
(ii) an analytical estimate of the complex eigenfrequencies in the range
of pseudosound (
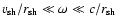 )
using Spherical Bessel
functions (Sects. 6 and 7).
)
using Spherical Bessel
functions (Sects. 6 and 7).
The results obtained by these methods are summarized as follows:
- As expected by the postshock acceleration of Nakayama (1993), the
isothermal Bondi accretion with a shock is unstable with respect to
radial perturbations. Its growth rate is comparable to the advection time
from the shock to the sonic point.
- The present analysis has revealed the existence of a new instability,
based on the cycle of vortical and acoustic perturbations in the subsonic
part of the flow.
The analytical study of this instability at high frequency
(
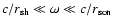 )
proves
that it is independent of the postshock acceleration criterion
established by Nakayama (1992, 1993). It is fed by the efficient
production of vorticity perturbations when the shock is perturbed non
radially (Eq. (42)), and by the
vortical-acoustic coupling in the region of the sonic radius which
enables the acoustic feedback. In this sense this non radial instability is
generic and can be expected in more complex situations such as
shocked flows with a weak angular momentum accreting into a black
hole, even if the flow is decelerated immediately after the
shock.
)
proves
that it is independent of the postshock acceleration criterion
established by Nakayama (1992, 1993). It is fed by the efficient
production of vorticity perturbations when the shock is perturbed non
radially (Eq. (42)), and by the
vortical-acoustic coupling in the region of the sonic radius which
enables the acoustic feedback. In this sense this non radial instability is
generic and can be expected in more complex situations such as
shocked flows with a weak angular momentum accreting into a black
hole, even if the flow is decelerated immediately after the
shock.
In the shocked Bondi flow the vortical-acoustic instability is faster than
the radial instability if the shock is strong, by a factor
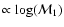 .
.
The vortical-acoustic instability occurs for low degree perturbations
on a wide range of frequencies below the cut-off frequency 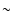
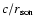 .
A branch of unstable l=1 eigenmodes corresponds to a
vortical-acoustic cycle in which the acoustic feedback is produced in the
pseudosound domain (
.
A branch of unstable l=1 eigenmodes corresponds to a
vortical-acoustic cycle in which the acoustic feedback is produced in the
pseudosound domain (
 ). The resulting growth
rate is comparable to the growth rate of the vortical-acoustic cycle at high
frequency.
). The resulting growth
rate is comparable to the growth rate of the vortical-acoustic cycle at high
frequency.
The role of the purely acoustic cycle was pointed out at high
frequency in order to explain the large variations of the growth rate from
one mode to another. More generally, the formalism developped in Appendix G
concerning the simultaneous acoustic and vortical-acoustic cycles applies to
any context where the efficiencies
 and timescales
and timescales
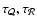 can be defined.
can be defined.
- A strong l=1 oscillatory instability was found in the pseudosound domain,
at a frequency which is intermediate between the acoustic and advection
frequencies (
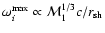 ).
With comparable real and imaginary parts of the eigenfrequency, vorticity
perturbations are advected over a very short distance during one growth time.
On the basis of the contribution of a vortex to the Bernoulli perturbation
sketched in Fig. 9, this strong instability is a non radial
consequence of post-shock acceleration.
).
With comparable real and imaginary parts of the eigenfrequency, vorticity
perturbations are advected over a very short distance during one growth time.
On the basis of the contribution of a vortex to the Bernoulli perturbation
sketched in Fig. 9, this strong instability is a non radial
consequence of post-shock acceleration.
- As outlined in Sect. 8, the vortical-acoustic
mechanism can be used as a tool in order to analyse the
instability observed in numerical simulations of more complicated accretion
flows. The specific application to BHL accretion or shocked flows with low
angular momentum will be developped in a forthcoming paper.
The non radial perturbation of velocity is deduced from the continuity
of the velocity parallel to the shock, as in Landau & Lifshitz (1987,
Chap. 90, p. 336):
The perturbed vorticity in the flow is deduced from the
Eqs. (A.1)-(A.2) and the Euler equation:
| wr=0, |
(A.3) |
 = = |
(A.4) |
 = = |
(A.5) |
The conserved quantity
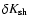 defined by Eq. (12)
is deduced from Eqs. (A.4)-(A.5), resulting in Eq. (20).
defined by Eq. (12)
is deduced from Eqs. (A.4)-(A.5), resulting in Eq. (20).
If the wavelength of the perturbation is shorter than the lengthscale
of the flow inhomogeneity (
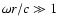 ), a WKB approximation enables
us to describe the propagation of acoustic waves in the direction of the
flow (f0+) or against it (f0+):
), a WKB approximation enables
us to describe the propagation of acoustic waves in the direction of the
flow (f0+) or against it (f0+):
 |
(B.1) |
where we have chosen the normalization of
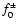 such that the
lower bound of the integral is the turning point
such that the
lower bound of the integral is the turning point 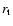 .
The condition that
.
The condition that
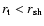 defines a minimum frequency
defines a minimum frequency
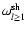 using Eq. (11) and
using Eq. (11) and
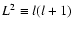 :
:
 |
(B.2) |
Far from the accretor, the flow velocity decreases like
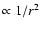 and the density of the gas is uniform. If the shock is strong
(
and the density of the gas is uniform. If the shock is strong
(
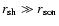 ), the homogeneous equation associated with
Eq. (C.1) is approximated for
), the homogeneous equation associated with
Eq. (C.1) is approximated for
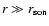 and
and
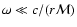 as follows:
as follows:
 |
(B.3) |
which is nothing more than the equation of acoustic waves in a uniform
steady medium, in spherical coordinates.
The solution f0 can therefore be approximated with a
spherical Bessel function of the first kind jl, which is normalized
here as in Eq. (B.1):
The differential system (8-9) is written as a single
differential equation of second order:
 |
|
|
|
 |
|
|
(C.1) |
Following the method used in F01, the general solution of Eq. (C.1)
can be written using the solutions
f0,f1 of the homogeneous equation,
where f0 is the unique solution which is regular at the sonic radius.
Let us normalize f0 using the following definition of
the WKB solutions
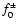 (Eq. (B.1)).
The complex coefficient
(Eq. (B.1)).
The complex coefficient
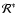 is defined by:
is defined by:
 |
(C.2) |
The wronskien of the couple of solutions
f0+,f0- is deduced
from Eqs. (B.1) and (C.1):
 |
(C.3) |
Let us normalize f1 such that the wronskien of the couple of solutions
f0,f1 is the same as in Eq. (C.3). The general
solution is then:
f= |
|
 |
(C.4) |
A Frobenius analysis of
f0,f1 near the sonic points leads to:
thus the integrals in Eq. (C.4) are converging when
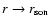 if
if
 .
The regularity at the sonic radius
therefore requires A1=0.
A combination of Eq. (C.4) and its derivative at the shock
radius leads to eliminate A0 as follows:
.
The regularity at the sonic radius
therefore requires A1=0.
A combination of Eq. (C.4) and its derivative at the shock
radius leads to eliminate A0 as follows:
 |
|
|
(C.7) |
Equations (18)-(20) provide the boundary
conditions at the shock in order to replace
 ,
,
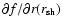 and
and
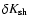 in Eq. (C.7), resulting in Eq. (22).
in Eq. (C.7), resulting in Eq. (22).
The analytical expression for
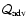 can be determined
by writting the solution corresponding to zero acoustic flux F+
at an outer boundary R, using the couple of homogeneous solutions (
f0+,f0-):
can be determined
by writting the solution corresponding to zero acoustic flux F+
at an outer boundary R, using the couple of homogeneous solutions (
f0+,f0-):
f= |
 |
(D.1) |
The regularity at the sonic radius requires
 |
(D.2) |
The condition of absence of an incoming acoustic flux at the outer
boundary is obtained by canceling the coefficient of f0+ at
r=R, in the WKB limit of high frequency (
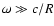 ):
):
 |
(D.3) |
Together with Eqs. (D.2) and (D.3), Eq. (D.1)
at the outer boundary becomes:
f(R)= |
 |
(D.4) |
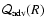 ,
defined by Eq. (28), is deduced
from the asymptotic behaviour of f0- in the WKB
approximation (Eq. (B.1)).
This calculation is formally similar to the calculation of
,
defined by Eq. (28), is deduced
from the asymptotic behaviour of f0- in the WKB
approximation (Eq. (B.1)).
This calculation is formally similar to the calculation of
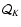 in F01,
corrected for a phase shift. The efficiency
in F01,
corrected for a phase shift. The efficiency
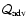 involved
in the vortical-acoustic cycle is deduced from
Eq. (29), with
involved
in the vortical-acoustic cycle is deduced from
Eq. (29), with
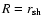 .
In the strong shock limit, below the cut-off frequency
(
.
In the strong shock limit, below the cut-off frequency
(
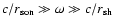 ), the acoustic efficiency
), the acoustic efficiency
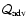 is
approximated using the Spherical Bessel function jl (B.5):
is
approximated using the Spherical Bessel function jl (B.5):
For
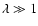 ,
a function
,
a function
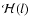 may be defined such that
may be defined such that
 |
(D.7) |
The main contribution to the integral in
Eq. (D.7) comes from the region
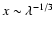 .
Equation (30) is obtained from Eqs. (D.5) and (D.7)
.
Equation (30) is obtained from Eqs. (D.5) and (D.7)
The perturbations f,g immediately after the shock, defined by
Eqs. (18) and (19) are decomposed as follows:
 |
= |
f-+f++fK, |
(E.1) |
 |
= |
g-+g++gK, |
(E.2) |
where
fK,gK correspond to the vorticity wave
associated with the vorticity perturbation 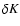 ,
and
,
and
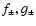 correspond to the purely acoustic waves propagating
in the direction of the flow (index +) or against the flow
(index -).
An exact calculation can be made in the case of the reflexion
of an acoustic wave
correspond to the purely acoustic waves propagating
in the direction of the flow (index +) or against the flow
(index -).
An exact calculation can be made in the case of the reflexion
of an acoustic wave
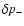 with wavevector
(
with wavevector
(
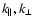 )
on a plane shock in Cartesian
coordinates, in the absence of a gradient of
)
on a plane shock in Cartesian
coordinates, in the absence of a gradient of 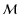 .
The vorticity wave fK,gK is advected at the velocity of the fluid:
.
The vorticity wave fK,gK is advected at the velocity of the fluid:
Replacing these derivatives in Eqs. (8), (9), we obtain:
fK= |
(E.5) |
gK= |
(E.6) |
 |
(E.7) |
Equations (E.5)-(E.7) are used with
Eqs. (18), (19) in order to obtain Eq. (20) and
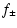 = = |
(E.8) |
where 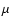 in Cartesian coordinates is also defined by
Eq. (10), but replacing
l(l+1)/r2 by the wavenumber
in Cartesian coordinates is also defined by
Eq. (10), but replacing
l(l+1)/r2 by the wavenumber
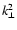 .
According to the definitions of
.
According to the definitions of
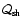 and
and
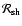 in Eqs. (37) and (62),
together with Eqs. (20) and (E.8):
in Eqs. (37) and (62),
together with Eqs. (20) and (E.8):
These equations show the decrease of the vortical-acoustic
coupling for weak shocks (
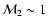 ), and the existence of maximal
efficiency at low frequency. Indeed, the maximum
), and the existence of maximal
efficiency at low frequency. Indeed, the maximum
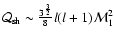 is reached for a frequency such that
is reached for a frequency such that
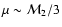 ,
with
,
with
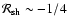 .
.
The angle 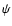 between
the direction of propagation of the wave and the vector orthogonal to the
shock surface is given by:
between
the direction of propagation of the wave and the vector orthogonal to the
shock surface is given by:
 |
(E.11) |
As remarked by Kontorovich (1958), the reflected sound wave propagates away
from the shock with the same angle as the incident wave
(
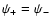 ), as in a classical reflexion.
The presence of a gradient of
), as in a classical reflexion.
The presence of a gradient of
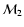 in the Bondi flow precludes
the use of these formulae at low frequency. In the following
calculation we assume
in the Bondi flow precludes
the use of these formulae at low frequency. In the following
calculation we assume
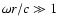 and
and
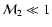 ,
and keep only
the first order terms in
,
and keep only
the first order terms in
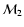 and
and
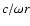 .
Thus
.
Thus 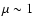 .
Neglecting the coupling between the vorticity and acoustic waves in
the vicinity of the shock, the vorticity wave fK,gK is still advected
at the velocity of the fluid. Eqs. (E.5) and (E.6) are now
approximated at high frequency by
.
Neglecting the coupling between the vorticity and acoustic waves in
the vicinity of the shock, the vorticity wave fK,gK is still advected
at the velocity of the fluid. Eqs. (E.5) and (E.6) are now
approximated at high frequency by
Acoustic waves are described by Eqs. (8), (9) in the
absence of vorticity perturbations, i.e.when
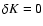 .
Using the WKB approximation of Eq. (B.1), the radial
derivative of
.
Using the WKB approximation of Eq. (B.1), the radial
derivative of 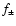 is approximated by:
is approximated by:
 |
(E.14) |
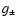 is deduced from Eqs. (8) and (E.14):
is deduced from Eqs. (8) and (E.14):
 |
(E.15) |
Equations (E.12), (E.13) and (E.15) are used with
Eqs. (18), (19) in order to obtain Eq. (20) and
Combining Eq. (20) with Eq. (E.16), we obtain the
expressions for
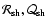 in
Eqs. (40) and (64).
The pressure perturbations
in
Eqs. (40) and (64).
The pressure perturbations
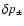 associated with the acoustic waves
associated with the acoustic waves 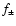 are deduced
from Eqs. (6)-(7) and Eq. (E.15):
are deduced
from Eqs. (6)-(7) and Eq. (E.15):
Using the integral expression of
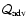 (Eq. (29)),
Eq. (22) can be approximated as follows
for strong shocks (
(Eq. (29)),
Eq. (22) can be approximated as follows
for strong shocks (
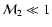 ):
):
 |
|
|
|
 |
|
|
(F.1) |
In the WKB limit
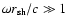 ,
Eq. (F.1) can be simplified
into
,
Eq. (F.1) can be simplified
into
 |
|
|
(F.2) |
Using the expressions for
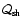 and
and
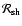 (Eqs. (40) and (64)), and the definition of
(Eqs. (40) and (64)), and the definition of 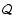 and
and 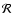 (Eqs. (38) and (58)), the global dispersion relation
(49) is recovered.
(Eqs. (38) and (58)), the global dispersion relation
(49) is recovered.
Let us introduce the new complex variable
 |
(G.1) |
The resolution of the dispersion relation (49) is then equivalent to
finding the complex number z satisfying:
 |
(G.2) |
where the dimensionless parameter
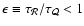 and
and
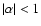 is defined by Eq. (52).
The minimum and maximum values
is defined by Eq. (52).
The minimum and maximum values  of |z| satisfy an equation
similar to Eq. (E3) of FT00:
of |z| satisfy an equation
similar to Eq. (E3) of FT00:
 |
(G.3) |
The minimum and maximum effect of the acoustic cycle on the growth
rate
 are directly related to
are directly related to 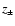 through Eq. (G.1):
through Eq. (G.1):
 |
(G.4) |
From Eq. (G.3),
we deduce that the maximum stabilizing effect of the acoustic
cycle is to divide the efficiency 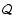 by a factor 2:
by a factor 2:
 |
(G.6) |
If the acoustic time is much shorter than the advection time
(
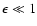 ), we deduce from Eq. (G.3) the values of
), we deduce from Eq. (G.3) the values of 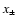 :
:
 |
|
|
(G.7) |
Thus the acoustic cycle may participate efficiently to the instability
if
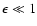 and
and
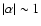 .
In the more general case where
.
In the more general case where
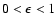 ,
the following bounds on
x are obtained from Eq. (G.2):
,
the following bounds on
x are obtained from Eq. (G.2):
 |
(G.8) |
The resolution of Eq. (G.2) can be decomposed into a
phase condition applied to the points of a continuous curve 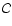 ,
defined by:
,
defined by:
 |
(G.9) |
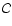 is a closed curve containing the point (1,0) in its
interior, and (0,0) in its exterior. It can be described in a univoque
way by the angle
is a closed curve containing the point (1,0) in its
interior, and (0,0) in its exterior. It can be described in a univoque
way by the angle
![$\varphi\equiv {\rm Arg}(z-1)\in[-\pi,\pi]$](/articles/aa/full/2002/34/aa2673/img394.gif) .
Let us define the angle
.
Let us define the angle
![$\theta\equiv {\rm Arg}(z)\in[-\pi,\pi]$](/articles/aa/full/2002/34/aa2673/img395.gif) .
The solutions of Eq. (G.2) are recovered by applying to the
solutions of Eq. (G.9) the following phase condition:
.
The solutions of Eq. (G.2) are recovered by applying to the
solutions of Eq. (G.9) the following phase condition:
 |
(G.10) |
where k,k' are two integers.
Since (0,0) is exterior to 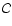 ,
the range of values covered
by
,
the range of values covered
by 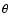 when
when 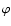 covers
covers
![$[-\pi,\pi]$](/articles/aa/full/2002/34/aa2673/img399.gif) is limited to
is limited to
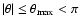 .
The discrete solutions of the phase Eq. (G.10) can be seen in a graphic way as the intersection of the
periodic curve
.
The discrete solutions of the phase Eq. (G.10) can be seen in a graphic way as the intersection of the
periodic curve
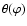 with the straight line
with the straight line
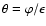 .
The number of solutions in each phase
.
The number of solutions in each phase
![$\varphi\in[0,2\pi]$](/articles/aa/full/2002/34/aa2673/img403.gif) is therefore equal to
is therefore equal to
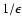 on average.
Comparing Eq. (G.1), Eq. (G.9) with the definitions
of
on average.
Comparing Eq. (G.1), Eq. (G.9) with the definitions
of
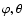 ,
one period of
,
one period of 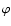 corresponds to a
variation of
corresponds to a
variation of
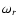 of
of
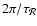 ,
and one period of
,
and one period of 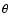 corresponds to
corresponds to
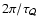 .
The values of
.
The values of
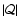 and
and
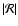 in Eqs. (54) and (55)
can be determined from the
measurement of
in Eqs. (54) and (55)
can be determined from the
measurement of
 ,
,
 and the average number
and the average number
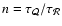 of eigenmodes per period
of eigenmodes per period
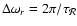 ,
by eliminating
,
by eliminating
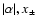 from the set of Eqs. (G.3), (G.4), and (52).
from the set of Eqs. (G.3), (G.4), and (52).
The integral involved in Eq. (22) can be approximated in the low
frequency limit by introducing the complex variable z:
 |
(H.1) |
The contour of integration is deformed in the complex plane
introducing a point on the real axis at 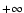 ,
and performing two
integrations by parts:
,
and performing two
integrations by parts:
The turning point in the Bondi flow would be at
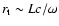 .
For
.
For
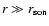 ,
the homogeneous solution f0 is
approximated by a Spherical Bessel function of the first kind
,
the homogeneous solution f0 is
approximated by a Spherical Bessel function of the first kind
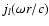 .
For
.
For
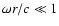 ,
it is approximated as
follows:
,
it is approximated as
follows:
 |
(H.3) |
The first integral on the right hand side of Eq. (H.2)
is approximated using a Gamma function:
The second integral on the right hand side of Eq. (H.2) is
negligible if
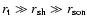 .
In view of the particular case l=1, the differential equation
satisfied by f0 is used to sum up terms of same order:
.
In view of the particular case l=1, the differential equation
satisfied by f0 is used to sum up terms of same order:
 |
|
|
|
 |
|
|
(H.7) |
Using Eqs. (H.2), (H.6) and (H.7), the
dispersion relation (22) is approximated in the
pseudosound domain as follows:
 |
|
|
(H.8) |
The left hand side of Eq. (H.8) is dominated
by the second derivative of f0 if 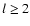 :
:
 |
|
|
(H.9) |
If l=1, the second derivative of f0 is approximated as follows:
 | (H.10) |
 | (H.11) |
Thus Eq. (H.8) becomes:
 |
|
|
(H.12) |
-
Bernstein, I. B., & Book, D. L. 1978, ApJ, 225, 633
In the text
NASA ADS
-
Bertschinger, E. 1986, ApJ, 304, 154
In the text
NASA ADS
-
Chakrabarti, S. K. 1989, MNRAS, 240, 7
In the text
NASA ADS
-
Chanaud, R. C., & Powell, A. 1965, J. Acoust. Soc. Am., 37, 902
In the text
-
D'Iakov, S. P. 1958, Sov. Phys. JETP, 6, 729, 739
-
Ffowcs Williams, J. E. 1969, Ann. Rev. Fluid. Mech., 1, 197
In the text
-
Foglizzo, T., & Ruffert, M. 1997, A&A, 320, 342
In the text
NASA ADS
-
Foglizzo, T., & Tagger, M. 2000, A&A, 363, 174 (FT00)
In the text
NASA ADS
-
Foglizzo, T. 2001, A&A, 368, 311 (F01)
In the text
NASA ADS
-
Fukue, J. 1987, PASJ, 39, 309
In the text
NASA ADS
-
Howe, M. S. 1975, J. Fluid Mech., 71, 625
In the text
NASA ADS
-
Hoyle, F., & Lyttleton, R. A. 1939, Proc. Cam. Phil. Soc., 35, 405
In the text
-
Ishii, T., Matsuda, T., Shima, E., et al.
1993, ApJ, 404, 706
In the text
NASA ADS
-
Kontorovich, V. M. 1958, Sov. Phys. JETP, 6, 729, 1180
In the text
-
Kontorovich, V. M. 1959, Sov. Phys. Acoust., 5, 320
In the text
-
Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics, 6 (Pergamon Press)
In the text
-
McCrea, W. H. 1956, ApJ, 124, 461
In the text
NASA ADS
-
Meszaros, P., & Ostriker, J. P. 1983, ApJ, 273, L59
In the text
NASA ADS
-
Molteni, D., Tóth, G., & Kuznetsov, O. A. 1999, ApJ, 516, 411
In the text
NASA ADS
-
Nakayama, K. 1992, MNRAS, 259, 259
In the text
NASA ADS
-
Nakayama, K. 1993, PASJ, 45, 167
In the text
NASA ADS
-
Nakayama, K. 1994, MNRAS, 270, 871
In the text
NASA ADS
-
Nobuta, K., & Hanawa, T. 1994, PASJ, 46, 257
In the text
NASA ADS
-
Pogorelov, N. V., Ohsugi, Y., & Matsuda, T. 2000, MNRAS, 313, 198
In the text
NASA ADS
-
Protheroe, R. J., & Kazanas, D. 1983, ApJ, 265, 620
In the text
NASA ADS
-
Rockwell, D. 1983, AIAA J., 21, 645
In the text
-
Ruffert, M. 1994, A&AS, 106, 505
In the text
NASA ADS
-
Ruffert, M. 1996, A&A, 311, 817
In the text
NASA ADS
-
Ruffert, M., & Arnett, D. 1994, ApJ, 427, 351
NASA ADS
-
Scharlemann, E. T. 1981, ApJ, 246, L15
In the text
NASA ADS
-
Shima, E., Matsuda, T., Anzer, U., Börner, G., & Boffin, H. M. J. 1998,
A&A, 337, 311
In the text
NASA ADS
-
Vishniac, E. T. 1983, ApJ, 274, 152
In the text
NASA ADS
-
Vishniac, E. T., & Ryu, D. 1989, ApJ, 337, 917
In the text
NASA ADS
Copyright ESO 2002
![]() .
The flow is unstable with respect to radial perturbations as
expected by Nakayama (1993), due to post-shock acceleration.
Its growth-time scales like the advection time from the shock
.
The flow is unstable with respect to radial perturbations as
expected by Nakayama (1993), due to post-shock acceleration.
Its growth-time scales like the advection time from the shock
![]() to the sonic point
to the sonic point
![]() .
The growth rate of non-radial perturbations
l=1 is higher by a factor
.
The growth rate of non-radial perturbations
l=1 is higher by a factor
![]() ,
and is therefore intermediate
between the advection and acoustic frequencies.
Besides these instabilities based on post-shock acceleration, our
study revealed another generic mechanism based on the cycle of acoustic and
vortical perturbations between the shock and the sonic radius,
independently of the sign of post-shock acceleration.
The vortical-acoustic instability is fundamentally non-radial. It
is fed by the efficient excitation of vorticity waves by the isothermal
shock perturbed by acoustic waves. The growth rate exceeds the advection
frequency by a factor
,
and is therefore intermediate
between the advection and acoustic frequencies.
Besides these instabilities based on post-shock acceleration, our
study revealed another generic mechanism based on the cycle of acoustic and
vortical perturbations between the shock and the sonic radius,
independently of the sign of post-shock acceleration.
The vortical-acoustic instability is fundamentally non-radial. It
is fed by the efficient excitation of vorticity waves by the isothermal
shock perturbed by acoustic waves. The growth rate exceeds the advection
frequency by a factor
![]() .
Unstable modes cover a wide range of frequencies from the
fundamental acoustic frequency
.
Unstable modes cover a wide range of frequencies from the
fundamental acoustic frequency ![]()
![]() up to a cut-off
up to a cut-off ![]()
![]() associated with the sonic radius. The highest growth rate is reached
for l=1 modes near the cut-off. The additional cycle of acoustic waves
between the shock and the sonic radius is responsible for variations of the
growth rate by a factor up to 3 depending on its phase relative to the
vortical-acoustic cycle.
The instability also exists, with a similar growth rate, below the fundamental
acoustic frequency down to the advection frequency, as vorticity waves are
efficiently coupled to the region of pseudosound.
These results open new perspectives to address the stability of
shocked accretion flows.
associated with the sonic radius. The highest growth rate is reached
for l=1 modes near the cut-off. The additional cycle of acoustic waves
between the shock and the sonic radius is responsible for variations of the
growth rate by a factor up to 3 depending on its phase relative to the
vortical-acoustic cycle.
The instability also exists, with a similar growth rate, below the fundamental
acoustic frequency down to the advection frequency, as vorticity waves are
efficiently coupled to the region of pseudosound.
These results open new perspectives to address the stability of
shocked accretion flows.
![]() ,
entropy and
vorticity perturbations are intimately related in the shocked Bondi
flow (Foglizzo 2002, in preparation), so that it is difficult to identify their
respective roles in the instability mechanism. By contrast, their roles
are well separated in the isothermal limit (
,
entropy and
vorticity perturbations are intimately related in the shocked Bondi
flow (Foglizzo 2002, in preparation), so that it is difficult to identify their
respective roles in the instability mechanism. By contrast, their roles
are well separated in the isothermal limit (![]() ), where entropy
perturbations are absent from the problem. The present paper is
therefore dedicated to the study of the linear stability of shocked
accretion in the isothermal Bondi flow, where the incident Mach number is the
only parameter. The stability of shocked isothermal flows was studied
by Nakayama (1992, 1993) in the more general context of flows with
small angular momentum. The study of Nakayama was restricted to
axisymmetric perturbations, thus precluding any possible vortical
acoustic cycle. In this approximation, Nakayama analytically obtained
the result that the flow is unstable if the flow accelerates immediately
after the shock surface. In this respect the shocked Bondi flow should
be unstable. We are therefore interested here in an
extension of Nakayama's results to the case of non radial
perturbations, in order to include the effect of vorticity.
It should be noted that isothermal flows are very particular as far as
Bondi-Hoyle-Lyttleton (hereafter BHL) accretion is concerned, with unsettled
issues concerning the influence of the numerical resolution.
The instability observed in numerical simulations seems very weak in 3-D
according to Ruffert (1996), whereas it is violent in 2-D (Ishii et al.1993;
Shima et al.1998). Pogorelov et al.(2000) discussed the possible responsability
of the numerical procedure in producing the instability. With a
different approach, the instability of the shocked Bondi flow described in
this paper could contribute to guide our physical understanding of more
complex flows involving isothermal shocks.
), where entropy
perturbations are absent from the problem. The present paper is
therefore dedicated to the study of the linear stability of shocked
accretion in the isothermal Bondi flow, where the incident Mach number is the
only parameter. The stability of shocked isothermal flows was studied
by Nakayama (1992, 1993) in the more general context of flows with
small angular momentum. The study of Nakayama was restricted to
axisymmetric perturbations, thus precluding any possible vortical
acoustic cycle. In this approximation, Nakayama analytically obtained
the result that the flow is unstable if the flow accelerates immediately
after the shock surface. In this respect the shocked Bondi flow should
be unstable. We are therefore interested here in an
extension of Nakayama's results to the case of non radial
perturbations, in order to include the effect of vorticity.
It should be noted that isothermal flows are very particular as far as
Bondi-Hoyle-Lyttleton (hereafter BHL) accretion is concerned, with unsettled
issues concerning the influence of the numerical resolution.
The instability observed in numerical simulations seems very weak in 3-D
according to Ruffert (1996), whereas it is violent in 2-D (Ishii et al.1993;
Shima et al.1998). Pogorelov et al.(2000) discussed the possible responsability
of the numerical procedure in producing the instability. With a
different approach, the instability of the shocked Bondi flow described in
this paper could contribute to guide our physical understanding of more
complex flows involving isothermal shocks.

![]() associated with
advection is much longer than the sound crossing time
associated with
advection is much longer than the sound crossing time
![]() :
:

![]() of non-radial acoustic
waves is defined by
of non-radial acoustic
waves is defined by ![]() in Eq. (10). This turning point
lies inside the subsonic cavity if
in Eq. (10). This turning point
lies inside the subsonic cavity if
![]() ,
with
,
with
![]() ,
which is independent of the
shock strength:
,
which is independent of the
shock strength:
![]() ,
,
![]() ,
,
![]() .
The corresponding structure of the vorticity wave is also displayed in
Fig. 2, in each range of frequencies.
.
The corresponding structure of the vorticity wave is also displayed in
Fig. 2, in each range of frequencies.
![]() the radial displacement of the shock produced
by a sound wave propagating against the stream in the subsonic region, and
the radial displacement of the shock produced
by a sound wave propagating against the stream in the subsonic region, and
![]() its velocity. The incident Mach number
its velocity. The incident Mach number
![]() in the frame of the shock is altered by the perturbations
of velocity and displacement as folllows:
in the frame of the shock is altered by the perturbations
of velocity and displacement as folllows:
![]() .
For a given incident Mach number
.
For a given incident Mach number
![]() ,
numerical intergration
is performed from
the sonic point towards the shock in order to determine the eigenfrequencies
of perturbations with a latitudinal number l. For a
given value of
,
numerical intergration
is performed from
the sonic point towards the shock in order to determine the eigenfrequencies
of perturbations with a latitudinal number l. For a
given value of ![]() ,
the unique solution which is regular at the
sonic point is expanded in a Frobenius series in order to start the
numerical integration away from the singularity. A Runge-Kutta
algorithm is then used to simultaneously integrate four functions,
namely
,
the unique solution which is regular at the
sonic point is expanded in a Frobenius series in order to start the
numerical integration away from the singularity. A Runge-Kutta
algorithm is then used to simultaneously integrate four functions,
namely
![]() ,
,
![]() ,
the integral on the right hand side of
Eq. (22) and the integral phase inside it.
,
the integral on the right hand side of
Eq. (22) and the integral phase inside it. ![]() is
varied and shooting is repeated until Eq. (22) is satisfied.
is
varied and shooting is repeated until Eq. (22) is satisfied.



![]()
![]() ), up to the
cut-off frequency (
), up to the
cut-off frequency (
![]() ).
).

![]() where the wavelength of the vorticity
perturbation is largest (see Fig. 2):
where the wavelength of the vorticity
perturbation is largest (see Fig. 2):
![]() at the
shock, advected towards the accretor, triggers the excitation of an
acoustic flux F- propagating outwards. As it reaches the shock
surface, this acoustic flux induces new vorticity perturbations
at the
shock, advected towards the accretor, triggers the excitation of an
acoustic flux F- propagating outwards. As it reaches the shock
surface, this acoustic flux induces new vorticity perturbations
![]() ,
where
,
where
![]() is the duration of
this cycle. The global efficiency
is the duration of
this cycle. The global efficiency ![]() of the cycle is naturally
of the cycle is naturally



![]() and a global efficiency
and a global efficiency
![]() .
Let us show how the simultaneous existence
of the two cycles can explain the apparent oscillation in the
eigenspectrum of Fig. 4. The following extension of the analysis
of FT00 is valid for both entropic-acoustic and vortical-acoustic cycles,
by replacing "vortical'' by "entropic''.
.
Let us show how the simultaneous existence
of the two cycles can explain the apparent oscillation in the
eigenspectrum of Fig. 4. The following extension of the analysis
of FT00 is valid for both entropic-acoustic and vortical-acoustic cycles,
by replacing "vortical'' by "entropic''.



![]() .
Thus the oscillations are well resolved in the eigenspectrum only if the
advection time is significantly longer than the acoustic time
(i.e.
.
Thus the oscillations are well resolved in the eigenspectrum only if the
advection time is significantly longer than the acoustic time
(i.e.
![]() ).
).
![]() are determined using the following
relations:
are determined using the following
relations:

![]() can be decomposed
in terms of the efficiencies
can be decomposed
in terms of the efficiencies
![]() and
and
![]() of the coupling between the acoustic
fluxes
of the coupling between the acoustic
fluxes ![]() ,
such that the
global efficiency
,
such that the
global efficiency ![]() is
is
![]() of the growth rate of the
vortical-acoustic cycle are computed
in Appendix G (Eq. (G.7)) for strong shocks:
of the growth rate of the
vortical-acoustic cycle are computed
in Appendix G (Eq. (G.7)) for strong shocks:

![]() must be treated separately.
In the domain of pseudosound
must be treated separately.
In the domain of pseudosound
![]() ,
Eq. (22) is reduced to:
,
Eq. (22) is reduced to:
![]() ,
and Eq. (69) is
transformed into
,
and Eq. (69) is
transformed into



![]() ,
the acoustic feedback due to an isolated vortical perturbation near
the shock is negligible compared to the integral effect for strong shocks.
Eq. (69) is reduced to:
,
the acoustic feedback due to an isolated vortical perturbation near
the shock is negligible compared to the integral effect for strong shocks.
Eq. (69) is reduced to:
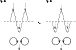
![]() (FT00, F01).
(FT00, F01).

![]() and small accretors
(Ruffert & Arnett 1994; Ruffert 1994): this coincides nicely with the
properties of the entropic-acoustic cycle,
which is most unstable if the temperature gradient in the subsonic part of
the flow is strongest (FT00, F01). By contrast, nearly isothermal flows are rather
stable in 3-D numerical simulations (Ruffert 1996). This could seem puzzling
given the strong vortical-acoustic instability described in the present
paper: why would the entropic-acoustic cycle be relevant for
the BHL instability with
and small accretors
(Ruffert & Arnett 1994; Ruffert 1994): this coincides nicely with the
properties of the entropic-acoustic cycle,
which is most unstable if the temperature gradient in the subsonic part of
the flow is strongest (FT00, F01). By contrast, nearly isothermal flows are rather
stable in 3-D numerical simulations (Ruffert 1996). This could seem puzzling
given the strong vortical-acoustic instability described in the present
paper: why would the entropic-acoustic cycle be relevant for
the BHL instability with
![]() ,
and the
vortical-acoustic cycle be irrelevant to the BHL stability for
,
and the
vortical-acoustic cycle be irrelevant to the BHL stability for ![]() ?
This apparent contradiction can be partly solved by remembering the
difference of topology between the spherical Bondi flow and the BHL
flow, following the remark of Sect. 2.1.
All the numerical simulations of isothermal BHL
accretion seem to agree with the fact that the shock is attached to the accretor,
whereas it is detached in high resolution simulations of adiabatic flows
with
?
This apparent contradiction can be partly solved by remembering the
difference of topology between the spherical Bondi flow and the BHL
flow, following the remark of Sect. 2.1.
All the numerical simulations of isothermal BHL
accretion seem to agree with the fact that the shock is attached to the accretor,
whereas it is detached in high resolution simulations of adiabatic flows
with
![]() .
This can be understood qualitatively in terms of
the weakness of pressure forces in isothermal flows compared to
adiabatic flows (
.
This can be understood qualitatively in terms of
the weakness of pressure forces in isothermal flows compared to
adiabatic flows (
![]() ). More quantitatively,
Foglizzo & Ruffert (1997) proved that the shock in the isothermal BHL
flow cannot be detached unless the sonic surface extends up to distances
comparable to the Bondi radius GM/c2, i.e.much larger than the
accretion radius. In view of this topological difference between
isothermal and adiabatic BHL flows, it seems easier to extend the
results obtained for shocked Bondi accretion to the subsonic region
ahead of the accretor, for detached shocks, than in the very
non-radial region of accretion behind the accretor for attached
shocks. Although true, however, this argument is not conclusive. Even in a non
radial isothermal flow, a small pressure perturbation of the shock is
able to generate vorticity perturbations very efficiently. The lack of
instability of isothermal BHL accretion in 3-D must be sought for in the
lack of acoustic feedback from the advected vorticity perturbation.
Unfortunately we do not have quantitative arguments to explain why
the acoustic feedback is so weak, apart from noticing that geometric
compression of the vorticity perturbation from the shock to the sonic
radius might be insufficient in the BHL flow. Any coherent explanation
should of course also account for the strong instability observed in 2-D
simulations of BHL accretion (Shima et al.1998).
). More quantitatively,
Foglizzo & Ruffert (1997) proved that the shock in the isothermal BHL
flow cannot be detached unless the sonic surface extends up to distances
comparable to the Bondi radius GM/c2, i.e.much larger than the
accretion radius. In view of this topological difference between
isothermal and adiabatic BHL flows, it seems easier to extend the
results obtained for shocked Bondi accretion to the subsonic region
ahead of the accretor, for detached shocks, than in the very
non-radial region of accretion behind the accretor for attached
shocks. Although true, however, this argument is not conclusive. Even in a non
radial isothermal flow, a small pressure perturbation of the shock is
able to generate vorticity perturbations very efficiently. The lack of
instability of isothermal BHL accretion in 3-D must be sought for in the
lack of acoustic feedback from the advected vorticity perturbation.
Unfortunately we do not have quantitative arguments to explain why
the acoustic feedback is so weak, apart from noticing that geometric
compression of the vorticity perturbation from the shock to the sonic
radius might be insufficient in the BHL flow. Any coherent explanation
should of course also account for the strong instability observed in 2-D
simulations of BHL accretion (Shima et al.1998).
![]() .
Unstable m=1 oscillations were observed, with no
physical explanation. The entropic-acoustic and vortical-acoustic
cycles might provide a physical basis to understand this instability.
.
Unstable m=1 oscillations were observed, with no
physical explanation. The entropic-acoustic and vortical-acoustic
cycles might provide a physical basis to understand this instability.
![]() (Eq. (26)), and that the acoustic perturbation produces in turn a
vorticity perturbation
(Eq. (26)), and that the acoustic perturbation produces in turn a
vorticity perturbation
![]() (Eq. (42)). The amplitude of the pressure perturbation
(Eq. (42)). The amplitude of the pressure perturbation
![]() depends on the volume in which the acoustic flux F-
is diluted through Eq. (27):
depends on the volume in which the acoustic flux F-
is diluted through Eq. (27):
![]() .
Thus the vortical-acoustic cycle is naturally
stabilized when the shock reaches a distance
.
Thus the vortical-acoustic cycle is naturally
stabilized when the shock reaches a distance
![]() defined by
defined by
![]() ), was used in
Sects. 4 and 5,
), was used in
Sects. 4 and 5,
![]() )
using Spherical Bessel
functions (Sects. 6 and 7).
)
using Spherical Bessel
functions (Sects. 6 and 7).
![]() )
proves
that it is independent of the postshock acceleration criterion
established by Nakayama (1992, 1993). It is fed by the efficient
production of vorticity perturbations when the shock is perturbed non
radially (Eq. (42)), and by the
vortical-acoustic coupling in the region of the sonic radius which
enables the acoustic feedback. In this sense this non radial instability is
generic and can be expected in more complex situations such as
shocked flows with a weak angular momentum accreting into a black
hole, even if the flow is decelerated immediately after the
shock.
)
proves
that it is independent of the postshock acceleration criterion
established by Nakayama (1992, 1993). It is fed by the efficient
production of vorticity perturbations when the shock is perturbed non
radially (Eq. (42)), and by the
vortical-acoustic coupling in the region of the sonic radius which
enables the acoustic feedback. In this sense this non radial instability is
generic and can be expected in more complex situations such as
shocked flows with a weak angular momentum accreting into a black
hole, even if the flow is decelerated immediately after the
shock.
![]() .
.
![]()
![]() .
A branch of unstable l=1 eigenmodes corresponds to a
vortical-acoustic cycle in which the acoustic feedback is produced in the
pseudosound domain (
.
A branch of unstable l=1 eigenmodes corresponds to a
vortical-acoustic cycle in which the acoustic feedback is produced in the
pseudosound domain (
![]() ). The resulting growth
rate is comparable to the growth rate of the vortical-acoustic cycle at high
frequency.
). The resulting growth
rate is comparable to the growth rate of the vortical-acoustic cycle at high
frequency.
![]() and timescales
and timescales
![]() can be defined.
can be defined.
![]() ).
With comparable real and imaginary parts of the eigenfrequency, vorticity
perturbations are advected over a very short distance during one growth time.
On the basis of the contribution of a vortex to the Bernoulli perturbation
sketched in Fig. 9, this strong instability is a non radial
consequence of post-shock acceleration.
).
With comparable real and imaginary parts of the eigenfrequency, vorticity
perturbations are advected over a very short distance during one growth time.
On the basis of the contribution of a vortex to the Bernoulli perturbation
sketched in Fig. 9, this strong instability is a non radial
consequence of post-shock acceleration.
![]() ), a WKB approximation enables
us to describe the propagation of acoustic waves in the direction of the
flow (f0+) or against it (f0+):
), a WKB approximation enables
us to describe the propagation of acoustic waves in the direction of the
flow (f0+) or against it (f0+):
![]() and the density of the gas is uniform. If the shock is strong
(
and the density of the gas is uniform. If the shock is strong
(
![]() ), the homogeneous equation associated with
Eq. (C.1) is approximated for
), the homogeneous equation associated with
Eq. (C.1) is approximated for
![]() and
and
![]() as follows:
as follows:


![]() can be determined
by writting the solution corresponding to zero acoustic flux F+
at an outer boundary R, using the couple of homogeneous solutions (
f0+,f0-):
can be determined
by writting the solution corresponding to zero acoustic flux F+
at an outer boundary R, using the couple of homogeneous solutions (
f0+,f0-):
![]() between
the direction of propagation of the wave and the vector orthogonal to the
shock surface is given by:
between
the direction of propagation of the wave and the vector orthogonal to the
shock surface is given by:
![]() (Eq. (29)),
Eq. (22) can be approximated as follows
for strong shocks (
(Eq. (29)),
Eq. (22) can be approximated as follows
for strong shocks (
![]() ):
):


