A&A 392, 19-31 (2002)
DOI: 10.1051/0004-6361:20020785
Evolutionary synthesis models of starbursts
IV. Soft X-ray emission
M. Cerviño1
- J. M. Mas-Hesse1 - D. Kunth2
1 - Laboratorio de Astrofísica Espacial y Física
Fundamental (LAEFF-INTA), PO Box 50727, 28080 Madrid, Spain
2 - Institut d'Astrophysique de Paris, 98 bis Bd. Arago, 75014
Paris, France
Received 9 January 2002 / Accepted 22 May 2002
Abstract
In this work we investigate the evolution of the X-ray emission
of a cluster of single young massive stars with different metallicities.
We have considered the X-ray contribution originated by the diffuse gas
heated by the mechanical energy released by stellar winds and SN
explosions as well as the X-ray contribution from SN remnants. The
resulting ionizing spectrum (i.e.
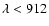 Å) has been used to
compute the expected intensity of the nebular He II
Å) has been used to
compute the expected intensity of the nebular He II 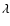 4686
Å. The observational ratio He II/H
4686
Å. The observational ratio He II/H could be reproduced by
the models assuming that a fraction of the mechanical energy produced by
the star-formation episode is reprocessed by interaction with the ISM as
soft X-ray radiation, contributing to the He ionization. However, the
discreteness of the stellar populations affects the ionizing flux and may
be responsible for the observed dispersion of the ratio. We have finally
used the synthesis models to estimate the contribution of circumnuclear
star-forming regions to the multiwavelength energy distribution in Active
Galactic Nuclei, finding that the UV to soft X-ray continuum in many
Seyfert 2 galaxies seems to be dominated by star-formation processes.
could be reproduced by
the models assuming that a fraction of the mechanical energy produced by
the star-formation episode is reprocessed by interaction with the ISM as
soft X-ray radiation, contributing to the He ionization. However, the
discreteness of the stellar populations affects the ionizing flux and may
be responsible for the observed dispersion of the ratio. We have finally
used the synthesis models to estimate the contribution of circumnuclear
star-forming regions to the multiwavelength energy distribution in Active
Galactic Nuclei, finding that the UV to soft X-ray continuum in many
Seyfert 2 galaxies seems to be dominated by star-formation processes.
Key words: galaxies: evolution - X-rays: galaxies
In the last years convincing observational evidences have been collected
about the presence of starburst regions in or around active Seyfert 2
nuclei (Heckman et al. 1997; González-Delgado et al. 1998, and references therein). It has been
found that most of their UV light originates in (circum-)nuclear
star-formation sites; the possible connection between the nuclear activity
and the properties of these starbursts is still a matter of debate.
According to the unified scheme of Seyfert galaxies, the active nucleus
should be hidden by an opaque torus in the case of Seyferts 2, explaining
why the collected UV light is dominated by young, massive stars. The low
degree of contamination by the active source in the UV provides detailed
information about the properties of the star-formation processes. Moreover,
extrapolating to the radio - X-ray ranges the emission associated with the
starbursts, it should be possible to disentangle the fractional
contribution of both sources (the starburst and the active nucleus) at
different energy ranges. Multiwavelength evolutionary synthesis models
normalized to the observed UV emission would be the ideal tool to perform
this analysis.
With these ideas in mind we started some years ago a program to extend our
evolutionary synthesis models (Arnault et al. 1989, Paper I; Mas-Hesse & Kunth 1991,
Paper II, hereafter MHK; Cerviño & Mas-Hesse 1994, Paper III, hereafter CMH) to
high-energy ranges (soft and hard X-rays, 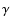 -rays). The predictions
of
-rays). The predictions
of 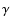 -ray emission were presented in Cerviño et al. (2000a), and this
paper is devoted to the X-ray emission. It became evident from the
beginning that to properly reproduce the X-ray emission, both the
contribution of evolved binary systems and the heating of the diffuse
interstellar gas by the release of mechanical energy (by stellar winds and
supernova explosions), had to be considered. Nevertheless, while High Mass
X-ray binaries contribute essentially to the hard X-ray range
(above few keV, Van Bever & Vanbeveren 1999; Van Bever et al. 2000), the soft X-ray emission is dominated by very
hot diffuse gas, heated by the release of mechanical energy from the
starburst
(Heckman et al. 1995, 1996; Dickow et al. 1996; Stevens & Strickland 1998a,b; Strickland & Stevens 1999; Summers et al. 2001). We will therefore discuss in this paper the predicted soft X-ray
emission, and its effects on other observables, like the relative intensity
of hydrogen and helium emission lines. The contribution of binary systems
and evolved sources to the hard X-ray emission will be discussed in a
forthcoming paper.
-ray emission were presented in Cerviño et al. (2000a), and this
paper is devoted to the X-ray emission. It became evident from the
beginning that to properly reproduce the X-ray emission, both the
contribution of evolved binary systems and the heating of the diffuse
interstellar gas by the release of mechanical energy (by stellar winds and
supernova explosions), had to be considered. Nevertheless, while High Mass
X-ray binaries contribute essentially to the hard X-ray range
(above few keV, Van Bever & Vanbeveren 1999; Van Bever et al. 2000), the soft X-ray emission is dominated by very
hot diffuse gas, heated by the release of mechanical energy from the
starburst
(Heckman et al. 1995, 1996; Dickow et al. 1996; Stevens & Strickland 1998a,b; Strickland & Stevens 1999; Summers et al. 2001). We will therefore discuss in this paper the predicted soft X-ray
emission, and its effects on other observables, like the relative intensity
of hydrogen and helium emission lines. The contribution of binary systems
and evolved sources to the hard X-ray emission will be discussed in a
forthcoming paper.
Additionally, the statistical dispersion due to the discreteness of actual
stellar populations as presented in Cerviño et al. (2000b, 2002, 2001) is
particularly important in the high energy domain, where the number of
effective sources is lower. This computed statistical dispersion allows to
perform a better comparison with real systems and to evaluate the
statistically relevant sources in each energy range.
We present in Sect. 2 our evolutionary synthesis model and
show how the X-ray emission and its associated statistical dispersion have
been computed. In Sect. 3 we show the predictions on soft
X-ray emission. In Sect. 4 we explore the effects of the soft
X-ray contribution on the He II nebular emission line. In
Sect. 5 we compare our predictions with observational data from
star-forming and Seyfert galaxies, aiming to disentangle the relative
contribution of starbursts to the global energy budget of Seyferts. We
finally summarize in Sect. 6 our conclusions.
2 The evolutionary synthesis model and the X-ray emission
We have updated and improved the synthesis model presented in
Arnault et al. (1989), Mas-Hesse & Kunth (1991), Cerviño & Mas-Hesse (1994) with the following modifications:
- 1.
- Inclusion of the full set of Geneva evolutionary tracks including
standard (Schaller et al. 1992) and enhanced mass-loss rates
(Meynet et al. 1994);
- 2.
- Inclusion of metallicity dependent atmosphere models for normal stars
from Kurucz (1991), CoStar (Schaerer & De Koter 1997) and the atmosphere models for WR
stars from Schmutz et al. (1992);
- 3.
- Inclusion of an analytical Initial Mass Function (IMF) formulation
using a dynamical mass-bin
![[*]](/icons/foot_motif.gif) (see Cerviño et al. 2001, and references therein for a full description). We have also
maintained the original Monte Carlo formulation;
(see Cerviño et al. 2001, and references therein for a full description). We have also
maintained the original Monte Carlo formulation;
- 4.
- Use of parabolic interpolations in time for the computation of the
isochrones (see Cerviño et al. 2001, for a full study and discussion);
- 5.
- Evaluation of the dispersion due to the discreteness of the stellar
populations in all the outputs (see Cerviño et al. 2002 and
Buzzoni 1989 for more details).
For this work, we will use only an analytical formulation of the IMF
without Monte Carlo simulations. The basic input parameters of the model
are: (i) instantaneous burst of star formation. (ii) Salpeter
IMF (
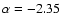 )
with a lower mass-limit equal to 2
)
with a lower mass-limit equal to 2 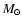 and upper
mass-limit equal to 120
and upper
mass-limit equal to 120 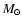 (iii) set of evolutionary tracks
with standard mass-loss rates from Schaller et al. (1992).
(iii) set of evolutionary tracks
with standard mass-loss rates from Schaller et al. (1992).
In the following sections we describe how the different contributions to
the soft X-ray emission have been included in the computations.
We will consider as soft X-rays all photons with energies between 0.07 and
2.4 keV (the ROSAT band), while hard X-ray photons will have energies
between 2.5 and 10 keV. We will also use the EINSTEIN band (range 0.1-3.4 keV) in Sect. 5 and the total X-ray luminosity (0.02-10 keV), 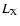 .
.
The main (persistent) contributors to the X-ray emission in a star-forming
region with only single-star populations will be essentially individual
stars, supernova remnants (SNR) and hot diffuse gas. In addition, other
sources like supernova explosions themselves, produce transient peaks of
X-ray emission. Since these peaks would be of very short duration, we have
not included them in our calculations, but we want to stress that they
could provide some degree of variability in the high-energy emission of
starbursts. Additionally, neither pulsars in young supernova remnants nor
X-ray binaries have been included in the computations, as explained below.
In the case of massive stars, strong mass losses produce first a cloud of
material surrounding the star. In a second stage, winds from the star
shocks this material generating X-ray emission (Chlebowski & Garmany 1991). The luminosity
in X-rays for stars hotter than B1 may be approximated by Chlebowski et al. (1989):
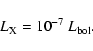 |
(1) |
The maximum contribution from the total population of individual stars is
about 1030 erg s-1
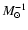 at 3 Myr after the onset of a
burst, assuming an instantaneous burst following a Salpeter IMF slope. As
we will see, this contribution is around 2 orders of magnitude lower than
the emission from other sources and has not been taken into account for
computing of the total X-ray spectral energy distribution. We have instead
included the amount of mechanical energy released by the stellar winds in
the total budget of energy injected into the interstellar medium, as
discussed later.
at 3 Myr after the onset of a
burst, assuming an instantaneous burst following a Salpeter IMF slope. As
we will see, this contribution is around 2 orders of magnitude lower than
the emission from other sources and has not been taken into account for
computing of the total X-ray spectral energy distribution. We have instead
included the amount of mechanical energy released by the stellar winds in
the total budget of energy injected into the interstellar medium, as
discussed later.
Supernova explosions (SN) will contribute strongly to the whole spectral
energy distribution, but only during a very short time (the light-curve of
a SN decays very quickly in few years). This contribution is furthermore
very variable in a short time scale and has not been taken into account in
the models.
On the other hand, after a SN explosion, there will be a remnant of
expanding hot gas that will contribute essentially to the X-ray and radio
domains during its free-fall and adiabatic phases. The time scale of the
free-fall phase is about 90 yr (Woltjer 1972), and has not been taken into
account in the models. The adiabatic phase has a time scale of
(Woltjer 1972):
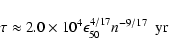 |
(2) |
where n is the density where the SNR expands and
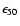 the mechanical energy released by the SN explosion in units
of 1050 erg. Assuming a mean value of
the mechanical energy released by the SN explosion in units
of 1050 erg. Assuming a mean value of
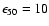 and n=1atoms cm-3, a SNR emits in X-rays during
and n=1atoms cm-3, a SNR emits in X-rays during
 yr.
Following MHK, the contribution to the spectral energy distribution from
SNRs can be approximated by:
yr.
Following MHK, the contribution to the spectral energy distribution from
SNRs can be approximated by:
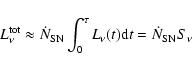 |
(3) |
where
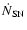 is the SN rate,
is the SN rate, 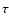 the time in which the
SNR shows X-ray (or radio) emission and
the time in which the
SNR shows X-ray (or radio) emission and 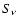 the emission associated to
one individual SNR. Equation (3) assumes that the supernova rate is
high enough to maintain a steady emission from SNRs during the burst.
the emission associated to
one individual SNR. Equation (3) assumes that the supernova rate is
high enough to maintain a steady emission from SNRs during the burst.
It is important to point out that in the case of the analytical-IMF
computations, we have used a mass bin such that there is, at least, one
star suffering a SN explosion in every step of 104 years starting 2 Myr
before the computed age. This assures that the computation of the X-ray
emission is correctly made and that there is no bias due to the choice of
the mass bin. The final output is the average value over the used time
step.
For the emission in radio and X-rays of SNR we have done the following
assumptions concerning 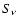 :
:
- X-rays: during the adiabatic phase of the SNR evolution, we have
assumed it will emit soft X-rays following a composite Raymond-Smith
hot-plasma law (Raymond & Smith 1977) at different temperatures and at a
metallicity consistent with the metal abundance of the region. In
accordance with the compilation of Dickel et al. (1990), we have assumed the
same average temperature for the hot gas in the cavity of all SNR, as
given by Eq. (4):
where 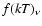 is a Raymond-Smith spectrum of temperature kT. We
have normalized the emission of each individual SNR within the
EINSTEIN band (0.1-3.4 keV) to an average value of 1036 erg
s-1, similar to the emissions given for the Cygnus Loop by
Cox (1972) and Chu & Mac Low (1990) for SNR in the Large Magellanic Cloud.
With these values, and assuming that the emissivity within the
EINSTEIN band is roughly constant in the range of temperatures of the
adiabatic phase, we obtain finally
is a Raymond-Smith spectrum of temperature kT. We
have normalized the emission of each individual SNR within the
EINSTEIN band (0.1-3.4 keV) to an average value of 1036 erg
s-1, similar to the emissions given for the Cygnus Loop by
Cox (1972) and Chu & Mac Low (1990) for SNR in the Large Magellanic Cloud.
With these values, and assuming that the emissivity within the
EINSTEIN band is roughly constant in the range of temperatures of the
adiabatic phase, we obtain finally
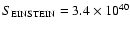 erg s-1 year, which is the value we have considered in our
calculations.
We have assumed in addition a harder component with kT = 6.4 keV
(Cox 1972) originated at the shock front of the SNR, accounting for
around 20% of the total emission;
erg s-1 year, which is the value we have considered in our
calculations.
We have assumed in addition a harder component with kT = 6.4 keV
(Cox 1972) originated at the shock front of the SNR, accounting for
around 20% of the total emission;
- Radio: following MHK, we have assumed that the radio emission
originated by a SNR follows a power law with index
 from
408 MHz to 4885 MHz (6 cm). We have updated the emission associated with
a single SNR considered in MHK to a value at 6 cm of
from
408 MHz to 4885 MHz (6 cm). We have updated the emission associated with
a single SNR considered in MHK to a value at 6 cm of
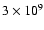 Jy
Kpc2 year, that takes into account the possible contribution from
cosmic rays and interaction with other remnants (see MHK and
Mas-Hesse 1992 for more details).
Jy
Kpc2 year, that takes into account the possible contribution from
cosmic rays and interaction with other remnants (see MHK and
Mas-Hesse 1992 for more details).
Individual point sources detected by ROSAT in nearby galaxies are
indeed generally associated with SNR (Aschenbach 1998).
The large amounts of mechanical energy released by the starburst process
are expected to heat the interstellar medium around the newly formed stars.
Observations with EINSTEIN already showed the presence of hot diffuse
gas within the H II shells of 30 Dor (Wang & Helfand 1991). Combining
ROSAT and ASCA data, Wang (1999) confirmed the thermal nature of
the emission, originated by diffuse gas at 2-9
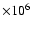 K, in the soft
X-ray band. Similar results have been obtained in many other
starburst-dominated galaxies: Stevens & Strickland (1998a,b) found that the soft X-ray
spectra of a sample of 7 Wolf-Rayet galaxies could typically be well fitted
by a thermal Raymond-Smith component with temperatures in the range
kT = 0.3-1.0 keV (corresponding to few times 106 K). These authors concluded
that a large fraction of the observed X-ray emission in these galaxies
originated in a hot superbubble formed by the combined action of stellar
winds from the massive, young stars in the central cluster. Strickland & Stevens (1999)
showed with hydrodynamical simulations that the observed soft X-ray
emission in NGC 5253 was consistent with the predictions for young
superbubbles blown by the starburst. Other starburst galaxies showing
thermal soft X-ray emission are: NGC 1569, with kT = 0.8 keV
(Heckman et al. 1995); Arp 220, kT = 0.61 keV (Heckman et al. 1996) or
Henize 2-10 with kT = 0.31 keV (Dickow et al. 1996) and Mrk 33 = Haro 2
(Summers et al. 2001), among others (see also Heckman et al. 1997).
K, in the soft
X-ray band. Similar results have been obtained in many other
starburst-dominated galaxies: Stevens & Strickland (1998a,b) found that the soft X-ray
spectra of a sample of 7 Wolf-Rayet galaxies could typically be well fitted
by a thermal Raymond-Smith component with temperatures in the range
kT = 0.3-1.0 keV (corresponding to few times 106 K). These authors concluded
that a large fraction of the observed X-ray emission in these galaxies
originated in a hot superbubble formed by the combined action of stellar
winds from the massive, young stars in the central cluster. Strickland & Stevens (1999)
showed with hydrodynamical simulations that the observed soft X-ray
emission in NGC 5253 was consistent with the predictions for young
superbubbles blown by the starburst. Other starburst galaxies showing
thermal soft X-ray emission are: NGC 1569, with kT = 0.8 keV
(Heckman et al. 1995); Arp 220, kT = 0.61 keV (Heckman et al. 1996) or
Henize 2-10 with kT = 0.31 keV (Dickow et al. 1996) and Mrk 33 = Haro 2
(Summers et al. 2001), among others (see also Heckman et al. 1997).
We have computed the total release of mechanical energy from stellar winds
following the prescriptions in Leitherer et al. (1992). The mechanical energy
released by SN explosions has been taken from the solar metallicity SN
simulations of Woosley & Weaver (1995) for SN II and from the simulations of helium
bare cores of Woosley et al. (1995) for WR stars. We have subtracted from the
energy of each SN explosion the total energy emitted in the 0.02-10 keV
band by the SNR during the adiabatic phase. It has a value in the
EINSTEIN band of
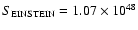 erg.
erg.
We have also assumed that a variable fraction
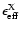 of the total mechanical energy released will end up interacting with and
heating the diffuse interstellar gas to an average temperature of 0.5 keV.
As a first approximation we have thus considered a contribution to the
X-ray emission from starbursts coming from a Raymond-Smith thermal plasma
at a fixed temperature kT = 0.5 keV.
of the total mechanical energy released will end up interacting with and
heating the diffuse interstellar gas to an average temperature of 0.5 keV.
As a first approximation we have thus considered a contribution to the
X-ray emission from starbursts coming from a Raymond-Smith thermal plasma
at a fixed temperature kT = 0.5 keV.
Different estimations of
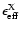 can be found in the
literature based on hydrodynamical models, but they are quite dependent on
the assumed input physic (see 1999, 2000, for an extensive review).
The standard bubble model of Castor et al. (1975), that assumes a constant energy
input into the bubble, shows that only 20% of the energy injected into the
ISM is used in the bubble expansion (i.e.
can be found in the
literature based on hydrodynamical models, but they are quite dependent on
the assumed input physic (see 1999, 2000, for an extensive review).
The standard bubble model of Castor et al. (1975), that assumes a constant energy
input into the bubble, shows that only 20% of the energy injected into the
ISM is used in the bubble expansion (i.e.
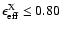 ). On the other hand Strickland & Stevens (1999) find
). On the other hand Strickland & Stevens (1999) find
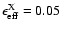 from their hydrodynamical simulations
(assuming also a constant energy input into the expanding bubble).
We have chosen an arbitrary value of
from their hydrodynamical simulations
(assuming also a constant energy input into the expanding bubble).
We have chosen an arbitrary value of
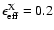 for
the presentation of this work. But we want to stress that the actual value
of
for
the presentation of this work. But we want to stress that the actual value
of
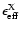 should be derived by fitting the
observational values on an object by object basis. It is interesting to
note that a high value of
should be derived by fitting the
observational values on an object by object basis. It is interesting to
note that a high value of
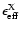 leads to a high X-ray
emission, but, since the total energy in the burst must be conserved, it
also leads to a small radius for the expanding bubbles. Therefore, the
comparison with observational data will only be consistent when both the
X-ray emission and the structure of expanding bubbles are taken into
account. The effect of changing the efficiency could be computed at any
time using the relative values given in Table 1.
leads to a high X-ray
emission, but, since the total energy in the burst must be conserved, it
also leads to a small radius for the expanding bubbles. Therefore, the
comparison with observational data will only be consistent when both the
X-ray emission and the structure of expanding bubbles are taken into
account. The effect of changing the efficiency could be computed at any
time using the relative values given in Table 1.
- High Mass X-ray Binaries (HMXRB): high Mass X-ray Binaries
become X-ray "active'' (permanent) after the primary star has collapsed
in a compact companion, and when the secondary star enters the giant or
supergiant phases, starting to accrete material onto the surface of the
compact companion. HMXRB will become therefore active only after the
first 4-5 Myr of evolution, depending on the upper mass limit of the IMF.
The X-ray emission properties will be dependent on the radius of the
compact companion. Assuming a radius of the compact companion of around
10 km, the bulk of the emission will be mainly in the hard X-ray band
(2.5-10 keV) with a tail that will also emit in soft X-rays. The hard
X-ray predictions of our models including binary systems and their
statistical relevance will be presented in a forthcoming paper;
- Pulsars in young SN remnants (YSNR): Van Bever & Vanbeveren (2000) show that
the loss of rotational energy of young pulsars in the form of
electromagnetic waves are another possible source of X-ray emission. This
emission can be fitted by a Raymond-Smith model with a temperature kT around 2 keV. According to these authors, the total X-ray luminosities
associated to these sources are around 1032 erg s-1
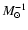 (for a starburst with a mass normalization given by an IMF
with a slope
(for a starburst with a mass normalization given by an IMF
with a slope
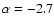 and mass range 10-100
and mass range 10-100 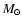 ). This
emission takes place only after the most massive stars have exploded as
supernovae, and is negligible when compared with the total emission
associated to both SNR and diffuse hot gas, even for rather low
efficiency values. Furthermore, only a very small number of such objects
is expected, so that their prediction is affected by very strong
statistical fluctuations. For these reasons we have not considered this
contribution in this work;
). This
emission takes place only after the most massive stars have exploded as
supernovae, and is negligible when compared with the total emission
associated to both SNR and diffuse hot gas, even for rather low
efficiency values. Furthermore, only a very small number of such objects
is expected, so that their prediction is affected by very strong
statistical fluctuations. For these reasons we have not considered this
contribution in this work;
- Low-mass X-ray (LMXRB) binaries and Compton scattering:
Persic & Rephaeli (2002) compute the steady-state X-ray emission of star forming
galaxies. In their work they include the emission produced by low-mass
X-ray binaries, compton scattering and the emission of the compact
nucleus in AGNs. They also include the contributions from the diffuse
emission and HMXRB. Since our work aims to establish the contribution to
the soft X-ray from star-forming regions, we have not included the
emission of compact nuclei. We are also restricted to young ages (t < 20 Myr) and single stellar evolution, hence the contribution of LMXRB
has not been considered. Finally, compton scattering is related to the
electron density and the presence of magnetic fields and will emit mainly
in the hard X-ray domain (see Persic & Rephaeli 2002, and references therein) and
has not been included in the current computations.
As pointed out before, we have not considered these contributions,
but we keep in mind that the emission from YSNR could be significant in
starbursts devoid of interstellar gas, where no contribution from hot gas
is present and that HMXRB may increase the emission in both soft and hard
X-rays.
As far as the X-ray predictions are dependent on the assumed band, we have
summarized in Table 1 the conversion factors for the two
components discussed in this work normalized to the total X-ray luminosity
(0.02-10 keV). Such conversion factors have been obtained by the
integration of the assumed X-ray spectrum over the given band. The results
for all the bands can be found in graphic and tabular form in our WWW
server at http://www.laeff.esa.es/users/mcs/SED, but we will show
here only the predictions for the X-ray luminosity in the ROSAT band,
for which most observational data are available. In the table we also give
the ROSAT bands needed for the computation of the ROSAT
hardness ratio.
Table 1:
Values of X-ray luminosities in different bands normalized to
the total X-ray luminosity (0.02-10 keV).
| Metallicity |
ROSAT |
EINSTEIN |
| |
(0.07-0.4 keV) |
(0.41-2.4 keV) |
(0.41-1.0 keV) |
(1.0-2.4
keV) |
(0.07-2.4 keV) |
(0.1-3.4 keV) |
| |
SNR |
| 0.001 |
0.290 |
0.441 |
0.251 |
0.190 |
0.731 |
0.745 |
| 0.004 |
0.263 |
0.490 |
0.301 |
0.189 |
0.753 |
0.759 |
| 0.008 |
0.243 |
0.526 |
0.337 |
0.188 |
0.769 |
0.770 |
| 0.020 |
0.220 |
0.568 |
0.380 |
0.188 |
0.788 |
0.783 |
| 0.040 |
0.207 |
0.591 |
0.403 |
0.188 |
0.798 |
0.789 |
| |
Diffuse hot gas |
| 0.001 |
0.408 |
0.457 |
0.360 |
0.097 |
0.865 |
0.813 |
| 0.004 |
0.284 |
0.606 |
0.494 |
0.112 |
0.891 |
0.859 |
| 0.008 |
0.221 |
0.683 |
0.563 |
0.120 |
0.904 |
0.883 |
| 0.020 |
0.160 |
0.756 |
0.629 |
0.127 |
0.917 |
0.905 |
| 0.004 |
0.134 |
0.788 |
0.658 |
0.130 |
0.922 |
0.915 |
We have also taken into account that X-ray emission will produce a
relatively small fraction of ionizing photons (compared with those
generated by massive stars). Nevertheless, such photons will be
predominantly more energetic than the ones of stellar origin,
and will affect the
ionization structure of the nebular gas, and thus the relative emission of
some lines, as we will discuss below. The number of ionizing photons
between the ionizing edges of H and He are given in Table 2 for
the two components considered, as obtained from the integration over the
assumed spectrum of each component. In this case, we have normalized the
values to the total luminosity emitted in the ROSAT band. Note that
the normalization is different to the one used in Table 1.
As an example for any further use of this table, let us assume a Z=0.001metallicity star forming region where the X-ray luminosity produced by SNR
is
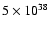 erg s-1 and the X-ray luminosity produced by the
diffuse hot gas is
erg s-1 and the X-ray luminosity produced by the
diffuse hot gas is
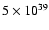 erg s-1, both in the ROSAT
band. There will be an additional component in Q(H+) of
erg s-1, both in the ROSAT
band. There will be an additional component in Q(H+) of
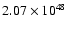 and
and
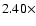 1049 photons s-1 due to the X-ray
spectrum from the SNR and the hot diffuse component respectively. Of
course, these additional Q(H+) values are dependent on the assumed X-ray
spectrum, but it gives us a first order approximation of how important the
contributions of the X-rays sources to the ionizing flux are.
1049 photons s-1 due to the X-ray
spectrum from the SNR and the hot diffuse component respectively. Of
course, these additional Q(H+) values are dependent on the assumed X-ray
spectrum, but it gives us a first order approximation of how important the
contributions of the X-rays sources to the ionizing flux are.
In the following paragraph we summarize how to calculate the dispersion due
to the discreteness of the stellar population. We refer to Buzzoni (1989)
and Cerviño et al. (2002, 2001) for further details.
The IMF gives the probability, wi, of finding a number of stars within a
given mass range. Each wi corresponds to the mass binning used in
analytical-IMF synthesis codes. If we assume that each wi follows a
Poissonian distribution (Cerviño et al. 2002), the variance,
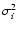 of
each wi is equal to the mean value of the distribution, wi. Let us
assume now that each star has a property ai whose contribution to the
integrated property A is given by wi ai with a variance
of
each wi is equal to the mean value of the distribution, wi. Let us
assume now that each star has a property ai whose contribution to the
integrated property A is given by wi ai with a variance
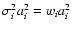 .
The total variance of the observable A is the sum of
all the variances. The relative dispersion is:
.
The total variance of the observable A is the sum of
all the variances. The relative dispersion is:
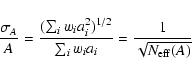 |
(5) |
where the last term gives us the definition of
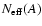 described by Buzzoni (1989). Note that
described by Buzzoni (1989). Note that
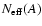 is normalized to the total mass.
is normalized to the total mass.
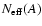 is not a real number of stars, but is gives us an
idea of how many effective sources contribute to any given
observable. Cerviño et al. (2002) show that
is not a real number of stars, but is gives us an
idea of how many effective sources contribute to any given
observable. Cerviño et al. (2002) show that
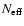 also defines the
mean value of a Poissonian distribution that can be used to obtain the
corresponding confidence levels of any observable in function of the amount
of mass transformed into stars.
also defines the
mean value of a Poissonian distribution that can be used to obtain the
corresponding confidence levels of any observable in function of the amount
of mass transformed into stars.
Let us stress that IMF fluctuations are present in Nature (the number of
stars are always discrete), so,
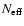 is not an evaluation
of the errors of the synthesis models. It is an evaluation of the
dispersion intrinsically present in real clusters, i.e. the dispersion
is also an observable. This intrinsic dispersion must be taken into
account when fitting observed quantities to model outputs before
establishing any conclusion.
is not an evaluation
of the errors of the synthesis models. It is an evaluation of the
dispersion intrinsically present in real clusters, i.e. the dispersion
is also an observable. This intrinsic dispersion must be taken into
account when fitting observed quantities to model outputs before
establishing any conclusion.
For differential quantities, like the SN rate or the mechanical
power, the obtained quantities are the mean value averaged over the
time step (0.1 Myr in our case). The corresponding dispersion
shows the variation over such average mean value (Cerviño et al. 2001).
3 Predictions on soft X-ray emission
As discussed in the previous section, both supernova remnants and diffuse
hot gas will be the main contributors to the soft X-ray emission if only
single-stars are considered. Depending on the evolutionary state of the
starburst, one or the other component will dominate the emission at a given
energy. We show in the top panels of Fig. 1 the predicted X-ray
emission in the ROSAT band as a function of metallicity for two
cases: (a) X-ray emission produced by SNR plus hot gas, with
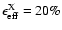 in the left panel, and (b) the X-ray
emission produced by SNR only (i.e., with
in the left panel, and (b) the X-ray
emission produced by SNR only (i.e., with
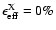 )
in the right panel.
)
in the right panel.
The X-ray emission depends on the star-forming region metallicity only
during the first few Myr, when the emission is dominated by the
reprocessing of mechanical energy, since stellar winds are strongly
metallicity dependent. On the other hand, after around 5 Myr the effect of
metallicity on the X-ray emission is small since the supernova rate is
essentially independent of metallicity.
It is clear that the total X-ray intensity is strongly dependent on the
associated
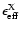 value, as shown in the top panel of
Fig. 3. It is remarkable that even a relatively low value
value, as shown in the top panel of
Fig. 3. It is remarkable that even a relatively low value
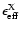 = 0.05 is enough to produce significant X-ray
emission, even during the first Myr of a starburst, when no other sources
are yet active. This is especially interesting considering that most
star-forming galaxies have been observed at ages between 3 and 7 Myr
(Mas-Hesse & Kunth 1999). In general, a change in the reprocessing
= 0.05 is enough to produce significant X-ray
emission, even during the first Myr of a starburst, when no other sources
are yet active. This is especially interesting considering that most
star-forming galaxies have been observed at ages between 3 and 7 Myr
(Mas-Hesse & Kunth 1999). In general, a change in the reprocessing
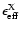 from 0.05 to 1 implies approximately one order
of magnitude in total X-ray emission.
from 0.05 to 1 implies approximately one order
of magnitude in total X-ray emission.
Since most starbursts seem to have formed massive stars according to an IMF
with a slope close to Salpeter's one (Mas-Hesse & Kunth 1999), and since their
metallicities can be derived from the analysis of optical emission lines,
it should be possible to derive a first order estimation of the average
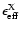 value by just comparing the predictions with
the observed soft X-ray luminosities.
value by just comparing the predictions with
the observed soft X-ray luminosities.
The effective mechanical energy and mechanical power remaining
available to drive gas flows away are smaller than the total amounts
generated by the starburst, since some fraction of the energy,
parameterized by
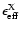 ,
is reprocessed into thermal
emission, and does not contribute to accelerate the gas. If such effect is
omitted, the age deduced from kinematical studies will result
systematically lower than the one obtained from the global analysis of the
starburst.
,
is reprocessed into thermal
emission, and does not contribute to accelerate the gas. If such effect is
omitted, the age deduced from kinematical studies will result
systematically lower than the one obtained from the global analysis of the
starburst.
In Fig. 2 we show the mechanical energy and mechanical power and
the corresponding effective mechanical energy and power when a value
of
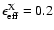 is used for the X-ray emission for a
solar metallicity burst. We also show these quantities when the correction
due to the X-ray emission of the SNR is not taken into account
(
is used for the X-ray emission for a
solar metallicity burst. We also show these quantities when the correction
due to the X-ray emission of the SNR is not taken into account
(
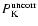 ).
).
Lower panels of Figs. 1, 2 show the
value of
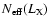 ,
,
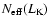 and
and
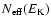 .
The right axis shows the amount of
gas transformed into stars for the given IMF and mass limits needed to
ensure a dispersion lower than 10%, denoted as
.
The right axis shows the amount of
gas transformed into stars for the given IMF and mass limits needed to
ensure a dispersion lower than 10%, denoted as 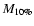 (
(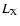 ),
),
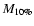 (
(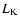 )
and
)
and 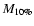 (
(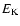 ). We will use this
notation for subsequent figures.
). We will use this
notation for subsequent figures.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{CMHKf1.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg58.gif) |
Figure 1:
Top panels: X-ray emission in the ROSAT band in
erg s-1
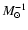 as a function of metallicity for an
instantaneous burst with Salpeter IMF slope in the mass range 2-120
as a function of metallicity for an
instantaneous burst with Salpeter IMF slope in the mass range 2-120 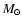 for two cases: a) SNR and
for two cases: a) SNR and
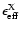 equal
20%. (Left) and b) only SNR (right). Low panels:
equal
20%. (Left) and b) only SNR (right). Low panels:
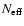 ( (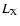 )
in units of )
in units of
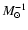 .
Right axis
show the amount of gas transformed into stars needed to obtain a
relative dispersion of 10%, .
Right axis
show the amount of gas transformed into stars needed to obtain a
relative dispersion of 10%, 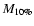 ( (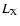 ). ). |
| Open with DEXTER |
In the case of the X-ray luminosities and the mechanical power two regimes
can be separated. At the beginning of the burst the dispersion is dominated
by the stellar wind component, i.e. there is a large number of effective
sources that are contributing to the luminosity. When the first SN
explodes, the value of
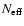 decreases abruptly: as far as the
remnant of a single SN produces more X-ray emission than the stellar winds
associated component, the effective number of sources decreases and the
dispersion due to the discreteness of the stellar population becomes
larger. It is also consistent with the fact that for evolved starburst the
possible dispersion will be dominated by the occurrence of SN events, and
so does the X-ray emission. In the case of the mechanical energy, the value
of
decreases abruptly: as far as the
remnant of a single SN produces more X-ray emission than the stellar winds
associated component, the effective number of sources decreases and the
dispersion due to the discreteness of the stellar population becomes
larger. It is also consistent with the fact that for evolved starburst the
possible dispersion will be dominated by the occurrence of SN events, and
so does the X-ray emission. In the case of the mechanical energy, the value
of
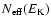 is larger (hence the dispersion lower)
because it is an integrated quantity
(see Cerviño et al. 2001, for more details).
is larger (hence the dispersion lower)
because it is an integrated quantity
(see Cerviño et al. 2001, for more details).
There are at least two other studies predicting the soft X-ray emission in
starburst galaxies: Silich et al. (2001) and (1999,2000). In both cases
the X-ray emission is obtained by simulations of superbubbles and
hydrodynamical models taking into account the time evolution of the kinetic
luminosity.
In Silich et al. (2001), the X-ray luminosity is obtained from two
components: the interior of the superbubble and the shell, with
an analytical dependence of the metallicity on the radiative cooling
function,
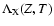 .
They show that the soft X-ray emission
depends on the enrichment of the hot ISM by stellar winds and SN
explosions. Nevertheless, their results are similar to the ones obtained in
Strickland & Stevens (1999).
.
They show that the soft X-ray emission
depends on the enrichment of the hot ISM by stellar winds and SN
explosions. Nevertheless, their results are similar to the ones obtained in
Strickland & Stevens (1999).
The study by Strickland & Stevens (1999) uses a superbubble model expanding in a vacuum
medium (i.e. an external pressure equal to zero) and obtains the X-ray
luminosity from the integration of the density structure and the radiative
cooling function over the volume of the bubble. They find a correlation
between the mechanical luminosity and the soft X-ray emission of
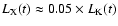 with a time delay
between both quantities (variations in
with a time delay
between both quantities (variations in
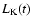 occurs earlier
than variations in
occurs earlier
than variations in
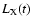 ). They also present an extensive
discussion of the factors affecting the computed X-ray emission, assuming
superbubbles (see Strickland & Stevens 2000). Their results (their Fig. 6) are quite
similar to the ones we have obtained (cf. Fig. 2 scaled to a 106
). They also present an extensive
discussion of the factors affecting the computed X-ray emission, assuming
superbubbles (see Strickland & Stevens 2000). Their results (their Fig. 6) are quite
similar to the ones we have obtained (cf. Fig. 2 scaled to a 106 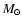 burst) with an efficiency of 5%, except for the time delay as we
have explained above.
burst) with an efficiency of 5%, except for the time delay as we
have explained above.
Additionally, 1-D hydrodynamical simulations computed by Plüschke (2001)
taking into account the environment where the bubble expands (an ambient
density of 40 atoms cm-3 is assumed in their models), show that the
dissipation of
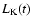 is around 80% (which includes not only
radiative cooling, but also the effects of mass-loading inside the
bubbles). Note that such effects may change the time delay between
is around 80% (which includes not only
radiative cooling, but also the effects of mass-loading inside the
bubbles). Note that such effects may change the time delay between
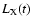 and
and
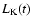 .
.
In summary, our approximation parameterized in terms of
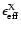 ,
although quite simplistic, provides a good first order
approximation to the more detailed superbubble simulations.
,
although quite simplistic, provides a good first order
approximation to the more detailed superbubble simulations.
As an example, we have applied our models to Mrk 33. It is not the scope
of this paper to perform a detailed analysis of the properties of this
galaxy and it has been used only as a first order consistency check. We
refer to Summers et al. (2001) for a more complete study using different
constraints and synthesis models.
The first step to apply the model is to obtain an estimation of the age of
the burst. For this we refer to the W(H )
value used by Mas-Hesse & Kunth (1999),
which was obtained through a large aperture and was corrected from the
contamination by the underlying stellar population. We show in
Fig. 4 the predictions of the models as a function of age,
with the corresponding 90% confidence limits for different amounts of gas
transformed into stars and a metallicity Z=0.008. The predicted W(H
)
value used by Mas-Hesse & Kunth (1999),
which was obtained through a large aperture and was corrected from the
contamination by the underlying stellar population. We show in
Fig. 4 the predictions of the models as a function of age,
with the corresponding 90% confidence limits for different amounts of gas
transformed into stars and a metallicity Z=0.008. The predicted W(H )
values have been computed assuming that a fraction of 0.3 of ionizing
photons are not absorbed by the gas and the other 0.7 is transformed in
H
)
values have been computed assuming that a fraction of 0.3 of ionizing
photons are not absorbed by the gas and the other 0.7 is transformed in
H luminosity following Case B recombination (see Mas-Hesse & Kunth 1999, for details).
luminosity following Case B recombination (see Mas-Hesse & Kunth 1999, for details).
As we can see in the figure, W(H )
alone constrains the age of the
starburst to around 4.2 Myr. By using a previous version of our set of
models, Mas-Hesse & Kunth (1999) derived an age around 4.8 Myr. For our case, it should
be enough to constrain the age of the starburst within the range 4 to 5
Myr, assuming an instantaneous burst.
)
alone constrains the age of the
starburst to around 4.2 Myr. By using a previous version of our set of
models, Mas-Hesse & Kunth (1999) derived an age around 4.8 Myr. For our case, it should
be enough to constrain the age of the starburst within the range 4 to 5
Myr, assuming an instantaneous burst.
The kinetic energy of the neutral expanding gas that is pushed out by the
shell in this galaxy is (see Lequeux et al. 1995; Legrand et al. 1997)
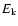 (H I) =
(H I) =
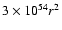 (kpc) erg, where r is the
size of the expanding shell. Some possible values of r have been proposed
in the literature: (i) Legrand et al. (1997) derived an r value of 1.23 kpc
from the expanding H
(kpc) erg, where r is the
size of the expanding shell. Some possible values of r have been proposed
in the literature: (i) Legrand et al. (1997) derived an r value of 1.23 kpc
from the expanding H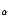 shell and using a distance of 19.5 Mpc (ii)
Summers et al. (2001) found a extended X-ray source with an ellipsoidal shape and
diameters of of 2.3 kpc and 1.9 kpc assuming a distance of 22 Mpc (i.e.
shell and using a distance of 19.5 Mpc (ii)
Summers et al. (2001) found a extended X-ray source with an ellipsoidal shape and
diameters of of 2.3 kpc and 1.9 kpc assuming a distance of 22 Mpc (i.e.
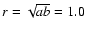 kpc) and (iii). Also Summers et al. (2001) obtain an average radius
1.1 kpc from B band images. From this last study, we assume the same
distance and a value of 1.1 kpc and so a
kpc) and (iii). Also Summers et al. (2001) obtain an average radius
1.1 kpc from B band images. From this last study, we assume the same
distance and a value of 1.1 kpc and so a 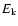 (H I) =
(H I) =
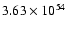 erg.
Finally, the observed soft X-ray luminosity in the ROSAT band ranges
from 0.2 to
erg.
Finally, the observed soft X-ray luminosity in the ROSAT band ranges
from 0.2 to
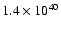 erg s-1. The first value corresponds
to the HRI observations of Summers et al. (2001), while the second one was derived
by Strickland & Stevens (1999) from PSPC data.
Our model predicts
erg s-1. The first value corresponds
to the HRI observations of Summers et al. (2001), while the second one was derived
by Strickland & Stevens (1999) from PSPC data.
Our model predicts 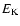 between
between
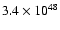 and
and
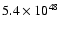 erg
erg
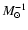 at 4 and 5 Myr respectively, and
at 4 and 5 Myr respectively, and
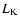 between
between
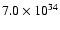 (at 4 Myr) and
(at 4 Myr) and
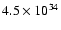 erg s-1
erg s-1
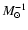 (at 5 Myr). The uncertainty in
(at 5 Myr). The uncertainty in
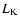 is lower than 5% in a 90% confidence level and lower than
2% (also in the 90% confidence level) for
is lower than 5% in a 90% confidence level and lower than
2% (also in the 90% confidence level) for 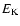 assuming a mass
transformed into stars,
assuming a mass
transformed into stars,
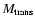 ,
larger than 106
,
larger than 106 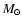 using a Salpeter IMF slope with mass limits from 2 to 120
using a Salpeter IMF slope with mass limits from 2 to 120 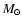
A first order estimation of
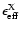 and the mass of the
cluster can be obtained using the following relations:
and the mass of the
cluster can be obtained using the following relations:
Note that, for a fixed value of
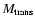 ,
larger values of
,
larger values of
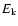 produce larger values in
produce larger values in
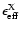 ,
and
lower values in
,
and
lower values in 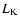 produce larger values in
produce larger values in
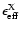 .
.
Assuming a constant
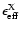 value along the evolution,
it is possible to obtain
value along the evolution,
it is possible to obtain
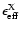 values between 0.02
(at 4 Myr with HRI data and
values between 0.02
(at 4 Myr with HRI data and
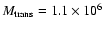
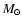 )
and 0.31 (at 5 Myr with PSPC data and
)
and 0.31 (at 5 Myr with PSPC data and
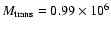
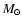 ).
On the other hand,
).
On the other hand,
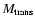 ranges from
ranges from
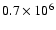
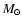 (at 5 Myr with HRI data and
(at 5 Myr with HRI data and
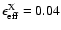 )
to
)
to
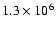
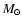 (at 4 Myr
with PSPC data and
(at 4 Myr
with PSPC data and
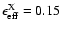 ).
).
So, the observed values can be explained with a 4-5 Myr old burst with a
mass transformed into stars of 0.7-
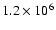
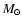 (following a
Salpeter IMF slope in the mass range 2-120
(following a
Salpeter IMF slope in the mass range 2-120 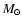 )
and a
)
and a
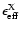 value from 0.02 to 0.31.
value from 0.02 to 0.31.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{CMHKf3a.eps}\includegraphics[width=8.4cm,clip]{CMHKf3b.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg86.gif) |
Figure 2:
Effective mechanical power and
energy for solar metallicity and several hypothesis about the X-ray
emission and its corresponding
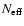 ( (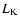 )
and )
and
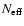 ( (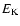 )
in units of )
in units of
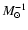 and
and
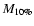 ( (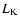 )
and )
and 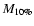 ( (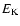 )
values. )
values. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{CMHKf2.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg87.gif) |
Figure 3:
X-ray emission in the ROSAT band as a function of
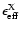 ,
for an instantaneous burst with Salpeter
IMF slope and solar metallicity and its corresponding ,
for an instantaneous burst with Salpeter
IMF slope and solar metallicity and its corresponding
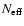 ( (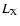 )
in units of )
in units of
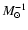 and
and
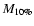 ( (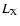 )
values. )
values. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{CMHKf4.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg88.gif) |
Figure 4:
90%
confidence limits of W(H )
for different amounts of gas
transformed into stars as a function of age, for a cluster with
Z=0.008. We have overplotted the observed W(H )
for different amounts of gas
transformed into stars as a function of age, for a cluster with
Z=0.008. We have overplotted the observed W(H )
value of Mrk 33,
as given by Mas-Hesse & Kunth (1999). )
value of Mrk 33,
as given by Mas-Hesse & Kunth (1999). |
| Open with DEXTER |
In this simple approximation we have not considered observational errors on
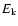 ,
neither different treatments of the mass-loss rates in the
evolutionary tracks nor different velocity laws in the computation of
,
neither different treatments of the mass-loss rates in the
evolutionary tracks nor different velocity laws in the computation of
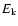 and
and 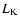 ,
which would presumably increase the
range of possible values. So, a more careful analysis, based on a
self-consistent comparison of the multiwavelength spectral energy
distribution and a complete set of observables of Mrk 33 with the model
predictions is necessary to derive any firmer conclusion.
,
which would presumably increase the
range of possible values. So, a more careful analysis, based on a
self-consistent comparison of the multiwavelength spectral energy
distribution and a complete set of observables of Mrk 33 with the model
predictions is necessary to derive any firmer conclusion.
4 Predictions on optical emission lines intensities: H and
He II
and
He II
The H equivalent width has been used by many authors in the last
years as a reliable indicator of the evolutionary status of a starburst,
since it relates the most massive stellar population (main contributors to
the gas ionization) with the total population in the cluster, which
produces the optical continuum (see Copetti et al. 1986 or Mas-Hesse & Kunth 1999
as an example). Other emission lines have been proposed as age indicators,
like [O III] ones by Stasinska & Leitherer (1996). Additionally, the strong soft
X-ray flux produced by the hot diffuse gas and SNR will contribute to
harden the overall ionizing continuum, potentially affecting the ratios of
different emission lines.
equivalent width has been used by many authors in the last
years as a reliable indicator of the evolutionary status of a starburst,
since it relates the most massive stellar population (main contributors to
the gas ionization) with the total population in the cluster, which
produces the optical continuum (see Copetti et al. 1986 or Mas-Hesse & Kunth 1999
as an example). Other emission lines have been proposed as age indicators,
like [O III] ones by Stasinska & Leitherer (1996). Additionally, the strong soft
X-ray flux produced by the hot diffuse gas and SNR will contribute to
harden the overall ionizing continuum, potentially affecting the ratios of
different emission lines.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{CMHKf5.eps} \medskip
\end{figure}](/articles/aa/full/2002/34/aa2257/Timg89.gif) |
Figure 5:
W(H )
evolution as a function of the metallicity for a
model where the X-ray emission is not taken into account and a model
with a value of )
evolution as a function of the metallicity for a
model where the X-ray emission is not taken into account and a model
with a value of
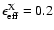 and its corresponding
and its corresponding
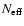 (W(H (W(H )) in units of )) in units of
 and
and
 (W(H (W(H )) values. )) values. |
| Open with DEXTER |
We show in Fig. 5 the evolution with time of W(H )
as a
function of the metallicity for a model where X-ray emission (neither SNR
nor mechanical energy reprocessed in X-rays) is not taken into account
(standard) and a model with a value of
)
as a
function of the metallicity for a model where X-ray emission (neither SNR
nor mechanical energy reprocessed in X-rays) is not taken into account
(standard) and a model with a value of
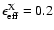 .
It
can be seen that the presence of hot gas may affect the predicted
W(H
.
It
can be seen that the presence of hot gas may affect the predicted
W(H )
values after the first 6 Myr of evolution, i.e., when the
ionizing continuum of the massive stars decreases
)
values after the first 6 Myr of evolution, i.e., when the
ionizing continuum of the massive stars decreases![[*]](/icons/foot_motif.gif) .
A first implication of these results is that W(H
.
A first implication of these results is that W(H )
becomes a very
uncertain age indicator for values below about 10 Å. A similar
conclusion has been obtained by Van Bever et al. (1999) based only on the effect
of binary systems, but in their case, the additional ionizing flux comes
both from the donor star of the binary system, that becomes (depending on
the mass-transfer scenario) a WR star, and from the gainer star, that
becomes more massive hence hotter than before the mass-transfer episode.
They obtain a higher value for a reliable use of W(H
)
becomes a very
uncertain age indicator for values below about 10 Å. A similar
conclusion has been obtained by Van Bever et al. (1999) based only on the effect
of binary systems, but in their case, the additional ionizing flux comes
both from the donor star of the binary system, that becomes (depending on
the mass-transfer scenario) a WR star, and from the gainer star, that
becomes more massive hence hotter than before the mass-transfer episode.
They obtain a higher value for a reliable use of W(H )
(i.e. not
dominated by binary systems) around 75 Å.
)
(i.e. not
dominated by binary systems) around 75 Å.
Additionally, the dispersion of W(H )
when the X-ray emission is
taken into account becomes larger than the one without such hot gas
emission. It is due to the intrinsic uncertainty of the X-ray emission
itself (i.e. the small number of effective sources). It also means that
the age determination of systems with low W(H
)
when the X-ray emission is
taken into account becomes larger than the one without such hot gas
emission. It is due to the intrinsic uncertainty of the X-ray emission
itself (i.e. the small number of effective sources). It also means that
the age determination of systems with low W(H )
values is an intrinsically difficult task, as far as the possible ionizing sources
are not only massive stars, but also diffuse hot gas.
)
values is an intrinsically difficult task, as far as the possible ionizing sources
are not only massive stars, but also diffuse hot gas.
While the inclusion of the soft X-ray flux in the ionizing budget does not
affect only weakly the total intensity of the H line, it can
affect more significantly other emission lines
with higher ionization potentials, like
[O III]
line, it can
affect more significantly other emission lines
with higher ionization potentials, like
[O III] 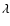 5007 Å. At 54.9 eV, the soft X-ray flux might
become the dominant contribution to the ionizing continuum, affecting
significantly the expected intensity of the line.
5007 Å. At 54.9 eV, the soft X-ray flux might
become the dominant contribution to the ionizing continuum, affecting
significantly the expected intensity of the line.
The nebular He II 4686 Å emission line has been detected in few
Star Forming Galaxies (SFG) (Conti 1991; Schaerer et al. 1999), but is apparently absent
in most of them. The average ratio of the observed intensity of
He II over the intensity of H ,
I(He II)/I(H
,
I(He II)/I(H ),
is around 0.02 (French 1980). Massive stars are not hot enough to produce
the hard ionizing continuum required for such relatively large ratios,
except perhaps during the WR phase, as discussed by Schaerer & Vacca (1998).
Nevertheless, no clear correlation has been found between the detection of
the line and the presence of WR stars in the region. Additional, harder
contributions to the ionizing continuum are therefore required to explain
the observed ratios.
),
is around 0.02 (French 1980). Massive stars are not hot enough to produce
the hard ionizing continuum required for such relatively large ratios,
except perhaps during the WR phase, as discussed by Schaerer & Vacca (1998).
Nevertheless, no clear correlation has been found between the detection of
the line and the presence of WR stars in the region. Additional, harder
contributions to the ionizing continuum are therefore required to explain
the observed ratios.
We have explored the effects associated with the reprocessing of mechanical
energy in the interstellar medium and the X-ray emission of SNR. The
results are shown in Fig. 6.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{CMHKf6.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg90.gif) |
Figure 6:
I(He II)/I(H )
ratio as a function of age and
metallicity for a model where the X-ray emission is not taken into
account and a model with a value of )
ratio as a function of age and
metallicity for a model where the X-ray emission is not taken into
account and a model with a value of
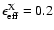 and
its corresponding
and
its corresponding
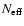 (I(He II)/I(H (I(He II)/I(H )) in
units of )) in
units of
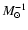 and
and 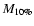 (I(He II)/I(H (I(He II)/I(H ))
values. ))
values. |
| Open with DEXTER |
The ionization by hard photons produced by the diffuse gas heated by the
release of mechanical energy into the medium can lead to significantly
higher values of the I(He II)/I(H )
ratio specially for low
metallicity clusters. As has been shown by Schaerer & Vacca (1998), for solar
metallicity starburst, a value of the ratio of 0.01 can be explained only
with the presence of WR stars, but such value is never reached in low
metallicity clusters. We show here that it is possible to obtain such ratio
if the soft X-ray emission is included.
)
ratio specially for low
metallicity clusters. As has been shown by Schaerer & Vacca (1998), for solar
metallicity starburst, a value of the ratio of 0.01 can be explained only
with the presence of WR stars, but such value is never reached in low
metallicity clusters. We show here that it is possible to obtain such ratio
if the soft X-ray emission is included.
However there are some points we would like to note here:
- The extension of the ionized region emitting the He II
4686 Å line is generally much smaller than the region over which
H
 is emitted, as shown by Maíz-Apellániz et al. (1998) in NGC 4214. To
properly compare with the predictions of synthesis models, the observed
He II 4686 Å flux has to be divided by the H
is emitted, as shown by Maíz-Apellániz et al. (1998) in NGC 4214. To
properly compare with the predictions of synthesis models, the observed
He II 4686 Å flux has to be divided by the H intensity
integrated over the whole ionized area. Such integrated ratios can be
smaller by almost an order of magnitude than the ratios measured just
locally. Another illustrative example can be found in Luridiana et al. (1999)
where the authors apply a photoionization model to NGC 2363 with the aim
of explain with a single model all the observations of the region
obtained by other authors using different apertures. Whereas the observed
I(He II)/I(H
intensity
integrated over the whole ionized area. Such integrated ratios can be
smaller by almost an order of magnitude than the ratios measured just
locally. Another illustrative example can be found in Luridiana et al. (1999)
where the authors apply a photoionization model to NGC 2363 with the aim
of explain with a single model all the observations of the region
obtained by other authors using different apertures. Whereas the observed
I(He II)/I(H )
ratios varies from 0.010 to 0.004, the global
I(He II)/I(H
)
ratios varies from 0.010 to 0.004, the global
I(He II)/I(H )
ratio of the model that fit all the
observations has a value of 0.001;
)
ratio of the model that fit all the
observations has a value of 0.001;
- Our models compute the predicted soft X-ray emission assuming the
released mechanical energy is reprocessed immediately into high energy
photons. A more realistic scenario would imply that the mechanical energy
is first accumulated in the form of energetic gas outflows, being
released in the form of soft X-rays only when this expanding gas
interacts with static interstellar clouds. Therefore, at some stages, the
soft X-ray contributions to the ionizing continuum could be stronger than
values predicted by our models;
- The hard ionizing flux intrinsically has a big dispersion. Its value
is controlled by a small number of effective sources (WR stars, hot gas
clouds or binary systems), hence suffers from severe statistic problems.
In order to support the last items, we show in Fig. 7 the
90% confidence limits obtained from the
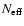 (I(He II)/I(H
(I(He II)/I(H )) value for a cluster with a
metallicity Z=0.001 and different amount of gas transformed into stars.
)) value for a cluster with a
metallicity Z=0.001 and different amount of gas transformed into stars.
We therefore conclude that the additional hard ionizing photons produced by
the diffuse gas can explain, at least partially, the intensities of
He II 4686 Å observed in low metallicity star forming regions.
However, at this point it is impossible to establish the source(s) of the
He II 4686 Å. From a theoretical point of view, it is necessary
to include other sources of X-ray emission that were not considered in this
work, and establish their statistical relevance. From the
observational point of view, more observations in different wavelengths
domains are needed to constrain the sampling effects due to the
discreteness of the stellar population. They must be unaffected by
additional aperture effect biases.
5 Star-formation processes in Seyfert galaxies
We have compared the predictions of our models with the multiwavelength
data for a sample of AGNs (QSO, Seyfert 1 and Seyfert 2) and SFGs compiled
by Mas-Hesse et al. (1995). We show in Fig. 8 the predicted evolution
of the 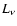 (0.1-3.5 keV) over
(0.1-3.5 keV) over 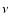
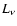 (1450 Å) ratio for
(1450 Å) ratio for
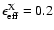 and different metallicities. The model
predictions correspond to a Salpeter IMF. We have also plotted the highest
(0.040 metallicity with
and different metallicities. The model
predictions correspond to a Salpeter IMF. We have also plotted the highest
(0.040 metallicity with
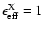 )
and the lowest
(0.001 metallicity with
)
and the lowest
(0.001 metallicity with
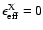 including the SNR
component only) values of the ratio, and the corresponding
90% CL for a 105
including the SNR
component only) values of the ratio, and the corresponding
90% CL for a 105 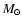 cluster, so that, for a given age, both solid
lines (and bands) represent the upper and lower limits we should expect
associated to a star-formation episode. Data points are from SFG in
Mas-Hesse et al. (1995) compilation. We have determined the ages of the plotted
objects from the W(H
cluster, so that, for a given age, both solid
lines (and bands) represent the upper and lower limits we should expect
associated to a star-formation episode. Data points are from SFG in
Mas-Hesse et al. (1995) compilation. We have determined the ages of the plotted
objects from the W(H )
values taken from the literature, but it can
be seen that in any case the results are weakly dependent on the assumed
age. UV data have not been corrected for internal extinction, so that the
plotted ratios have to be taken as upper values and should be indeed
intrinsically lower by factors between 2 and 5, approximately
(Mas-Hesse & Kunth 1999).
)
values taken from the literature, but it can
be seen that in any case the results are weakly dependent on the assumed
age. UV data have not been corrected for internal extinction, so that the
plotted ratios have to be taken as upper values and should be indeed
intrinsically lower by factors between 2 and 5, approximately
(Mas-Hesse & Kunth 1999).
From Fig. 8 we see that almost all galaxies fall within the
predictions of synthesis models. It is important to stress that some
conversion of mechanical energy into X-rays is always required. Otherwise
the models would severely underestimate the observed X-ray/UV ratios.
Additionally, some galaxies fall outside the model limits. It can be due to
statistical effects and/or the presence of binary systems that will
increase the X-ray emission and/or the underestimation of the observed UV
flux due to extinction effects. We want to point out that the effect of
the extinction in our sample has not been considered. Even a moderate
extinction would significantly affect the UV continuum, putting so the
X-ray/UV ratio within the model limits without additional X-ray sources.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{CMHKf7.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg93.gif) |
Figure 7:
90%
confidence levels of the I(He II)/I(H )
ratio as a
function of age for a Z=0.001 model with a value of )
ratio as a
function of age for a Z=0.001 model with a value of
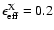 for a cluster where 104, 105 and
106
for a cluster where 104, 105 and
106 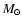 have been transformed into stars. We also show the mean
value.
have been transformed into stars. We also show the mean
value. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{CMHKf8.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg94.gif) |
Figure 8:
Ratio 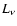 (0.1-3.5 keV) over (0.1-3.5 keV) over 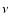 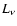 (1450 Å)
computed for an efficiency in the reprocessing of mechanical energy into
soft X-rays emission of (1450 Å)
computed for an efficiency in the reprocessing of mechanical energy into
soft X-rays emission of
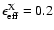 and different
metallicities (with lines as in Fig. 6). In grey, the
90% CL for a cluster where 105
and different
metallicities (with lines as in Fig. 6). In grey, the
90% CL for a cluster where 105 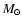 have been transformed into
stars for two extreme metallicities and
have been transformed into
stars for two extreme metallicities and
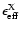 values. Data points are from SFG in Mas-Hesse et al. (1995) compilation. Note
that the UV continuum of the data points has not been corrected from
internalextinction.
values. Data points are from SFG in Mas-Hesse et al. (1995) compilation. Note
that the UV continuum of the data points has not been corrected from
internalextinction. |
| Open with DEXTER |
Note that our models compute only the persistent X-ray emission form
single-stellar populations. Transient sources like Be/X-ray binaries and SN
explosions may increase the X-ray emission in these galaxies, but only
during very short periods of time. In the case of Be/X-ray binaries the
component may be highly variable and would affect only the soft X-ray
emission.
In order to disentangle the relative contribution of (circum-)nuclear
star-formation processes to the total energy budget of low activity AGNs,
we have compared their 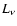 (0.1-3.5 keV) over
(0.1-3.5 keV) over 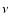
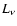 (1450 Å)
ratios with the predictions of our synthesis models. We show in Fig.
9 the corresponding histograms for the Sey 1, Sey 2 and SFGs
taken from the Mas-Hesse et al. (1995) sample. The vertical line corresponds to
the maximum value predicted by the models, as shown in Fig. 8.
(1450 Å)
ratios with the predictions of our synthesis models. We show in Fig.
9 the corresponding histograms for the Sey 1, Sey 2 and SFGs
taken from the Mas-Hesse et al. (1995) sample. The vertical line corresponds to
the maximum value predicted by the models, as shown in Fig. 8.
The segregation of Sey 1 and star-forming galaxies becomes evident at first
glance: while most of the SFGs in the sample fall below the predicted upper
value, all Seyfert 1 galaxies show clearly higher values, by one to two
orders of magnitude. Therefore, while the physical processes assumed to
take place in star-forming galaxies may explain their observational
properties, other high energy sources are required in the case of
Seyferts 1, as expected.
The case for Seyfert 2 galaxies is more interesting: while some of them are
located on the plot in the region associated to starbursts, some others
show a clear X-ray excess with respect to star-formation dominated objects.
The presence of star-formation regions in or around the nuclei of some
Seyfert 2 galaxies has become evident in the last years. Heckman et al. (1997)
showed that around 70% of the UV continuum in some Seyfert 2 galaxies were
contributed by young, massive stars, with only a small contribution being
associated to the nuclear active source. Colina et al. (1997) estimated that
only 1-10% of the UV flux in 4 Seyfert 2 galaxies imaged with the HST was
originated by the nuclear source, while the rest was due to young hot stars
recently formed around the nuclei. The contribution of star-forming
regions to the budget energy distribution of AGNs was also pointed out some
years ago by Mas-Hesse et al. (1995) based in multivawelength analysis of these
type of galaxies, and by Cid-Fernandes & Terlevich (1995).
Our results show that not only the UV continuum seems to be strongly
contaminated by the emission associated to starburst episodes in Seyfert 2
galaxies, but also their soft X-ray emission. This result is consistent
with the scenario assumed for Seyfert 2 galaxies, since the opaque torus
surrounding the nucleus would hide not only the UV emission associated to
the active source but also a significant part of its soft X-ray emission
due to absorption by neutral hydrogen. For example, a detailed analysis of
the UV and X-ray emission of NGC 1068 shows that a significant fraction of
its soft X-ray emission
could originate from the starburst episodes present around
its nucleus. On the other hand, the hard X-ray flux would be
underestimated by
our models by more than two orders of magnitude, indicating that it is
mostly contributed by the active source (Jiménez-Bailón et al., in
preparation). A more extended analysis of some Seyfert 2 galaxies will be
![\begin{figure}
\par\includegraphics[width=5cm,clip]{CMHKf9.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg95.gif) |
Figure 9:
Histograms for the ratio 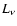 (0.1-3.5 keV) over (0.1-3.5 keV) over
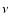 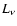 (1450 Å) for different types of emission line galaxies.
Data taken from Mas-Hesse et al. (1995). The UV continuum of the galaxy sample
has not been corrected from internal extinction. The solid line
corresponds to the upper value predicted by our evolutionary synthesis
models, as explained in the text. (1450 Å) for different types of emission line galaxies.
Data taken from Mas-Hesse et al. (1995). The UV continuum of the galaxy sample
has not been corrected from internal extinction. The solid line
corresponds to the upper value predicted by our evolutionary synthesis
models, as explained in the text. |
| Open with DEXTER |
presented elsewhere.
6 Conclusions
In this work we have explored the X-ray emission originated in a
star-forming region with only single stellar populations. The mechanical
energy injected into the interstellar medium by stellar winds and supernova
explosions will heat the diffuse gas to very high temperatures, and will be
finally reprocessed into soft X-ray emission. We have found that the X-ray
emission observed in starburst galaxies can be well explained assuming that
a moderate fraction of the mechanical energy is finally reprocessed into
X-ray emission. The rest of the mechanical energy released leads to the
expansion of the gas, creating bubbles and gas flows at galactic scales.
An interesting implication is that the age deduced from kinematical studies
will result systematically lower than the one obtained from the analysis of
the emission line spectrum if the heating of the gas and the X-ray emission
is not taken into account. Additionally, the inclusion of X-ray transient
systems, like SN explosions and Be/X-ray binaries showing bursts of X-ray
emission, may lead to some degree of variability in the high energy
emission of starburst galaxies.
We have computed the expected intensity of the nebular He II
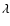 4686 Å, including the additional ionization of the gas by the
soft X-ray emission originated in the diffuse gas. The observational
values of the He II/H
4686 Å, including the additional ionization of the gas by the
soft X-ray emission originated in the diffuse gas. The observational
values of the He II/H ratios can be reproduced by our models
assuming moderate efficiencies (about 20%) in the reprocessing of
mechanical energies into X-ray emission. Alternatively, the mechanical
energy reprocessing could not be a continuous process. This energy released
by the massive stars could be "accumulated'' in the form of accelerated
gas flows, which would release all this accumulated energy only when the
outflowing gas interacts with the static interstellar medium. Under this
scenario the soft X-ray emission originated by the shocked gas would
provide enough additional ionizing power to explain the observed
He II/H
ratios can be reproduced by our models
assuming moderate efficiencies (about 20%) in the reprocessing of
mechanical energies into X-ray emission. Alternatively, the mechanical
energy reprocessing could not be a continuous process. This energy released
by the massive stars could be "accumulated'' in the form of accelerated
gas flows, which would release all this accumulated energy only when the
outflowing gas interacts with the static interstellar medium. Under this
scenario the soft X-ray emission originated by the shocked gas would
provide enough additional ionizing power to explain the observed
He II/H ratios. We have also shown that such ratios have a
high intrinsic dispersion and that a deeper statistical study is necessary
to investigate the source of the nebular He II
ratios. We have also shown that such ratios have a
high intrinsic dispersion and that a deeper statistical study is necessary
to investigate the source of the nebular He II 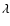 4686 Å
line.
4686 Å
line.
We have compared the predicted soft X-ray emission with observational
values for a sample of star-forming and Seyfert galaxies, aiming to
disentangle the contribution of star-formation episodes to the total energy
budget of low activity galaxies. We have found that while the high energy
emission of Seyfert 1 galaxies is clearly above the predictions of
starburst models, both the UV and soft X-ray emissions of many Seyfert 2
galaxies are apparently associated mostly to the (circum-)nuclear starburst
episodes known to be present in these objects. The active source in
Seyfert 2 galaxies would dominate therefore only at harder X-rays.
Acknowledgements
We want to acknowledge the referee, Onno Pols, for his valuable sugestions
that have allowed to improve the clarity of this paper. Useful comments
have been provided by María de Santos and Pedro
Rodríguez-Pascual. MC wants to acknowledge Daniel Schaerer for
useful comments about the models and evolutionary tracks, Valentina
Luridiana for useful comments about the manuscript, Roland Diehl and
Stephan Plüschke for coments about superbubble evolution and
Gra
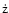 yna Stasinska for very useful comments about the
dispersion in the emission lines. MC wants to acknowledge the Instituto de Astrofísica de Andalucía for logistic support.
We want also to thank Eduardo Fernandes Vieira and Carlos Rodrigo Blanco
for useful comments. This work has been supported by Spanish CICYT
ESP-95-0389-C02-02. MC has been supported by an INTA "Rafael Calvo
Rodés'' predoctoral grant, an ESA postdoctoral grant and a MPE grant.
yna Stasinska for very useful comments about the
dispersion in the emission lines. MC wants to acknowledge the Instituto de Astrofísica de Andalucía for logistic support.
We want also to thank Eduardo Fernandes Vieira and Carlos Rodrigo Blanco
for useful comments. This work has been supported by Spanish CICYT
ESP-95-0389-C02-02. MC has been supported by an INTA "Rafael Calvo
Rodés'' predoctoral grant, an ESA postdoctoral grant and a MPE grant.
- Arnault, Ph., Kunth, D., & Schild, H.
1989, A&A, 224, 73
In the text
NASA ADS
- Aschenbach, B.
1998, IAU Coll. 101 (Cambridge University Press), 99
In the text
- Buzzoni, A. 1989, ApJS, 71, 871
In the text
- Castor, J., Weaver, R., & McCray,
R. 1975, ApJ, 200, L107
In the text
NASA ADS
- Cerviño, M., & Mas-Hesse, J. M. 1994, A&A, 284, 749 (CMH)
In the text
NASA ADS
- Cerviño, M., Knödlseder,
J., Schaerer, D., von Ballmoos, P., & Meynet, G. 2000, A&A, 363, 970
In the text
NASA ADS
- Cerviño, M., Luridiana, V., &
Castander, F. 2000b, A&A, 360, L5
NASA ADS
- Cerviño, M., Vals-Gabaud,
D., Luridiana, V., & Mas-Hesse, J. M. 2002, A&A, 381, 51
In the text
NASA ADS
- Cerviño, M.,
Gómez-Flechoso, M. A., Castander, F. J., et al. 2001, A&A, 376, 422
In the text
NASA ADS
- Chlebowski, T., Harnden, F. R.,
& Sciortino, S. 1989, ApJ, 341, 427
In the text
NASA ADS
- Chlebowski, T., & Garmany, C. D.
1991, ApJ, 368, 241
In the text
NASA ADS
- Chu, Y.-H., & Mac Low, M.-M.
1990, ApJ, 365, 510
In the text
NASA ADS
- Cid-Fernandes, R., &
Terlevich, R. 1995, MNRAS, 272, 423
In the text
NASA ADS
- Colina, L., García-Vargas,
M. L., Mas-Hesse, J. M., Alberdi, A., & Krabbe, A. 1997,
ApJ, 488, L71
In the text
NASA ADS
- Conti, P. S. 1991, ApJ, 377, 115
In the text
NASA ADS
- Copetti, M. V. F., Pastoriza, M. G.,
& Dottori, M. A. 1986, A&A, 156, 111
In the text
NASA ADS
- Cox, D. P. 1972, ApJ, 178, 169
In the text
NASA ADS
- Dickel, J., Norton, L.,
& Gensheimer, P. 1990, IAU Coll., 115, 168
In the text
- Dickow, R., Hensler, G.,
& Junkes, N. 1996, The interplay between massive star formation,
the IMS and Galaxy Evolution ed. D. Kunth, B. Guiderdoni,
M. Heydari-Malayeri, & T. X. Thuan (Éditions Frontières), 383
In the text
- French, H. B. 1980, ApJ, 240, 41
In the text
NASA ADS
- González-Delgado, R. M.,
Heckman, T., Leitherer, C., et al. 1998, ApJ, 505, 174
In the text
NASA ADS
- Heckman, T. M., Dahlem, M., Lehnert, M.,
et al.
1995, ApJ, 448, 98
In the text
NASA ADS
- Heckman, T. M., Dahlem, M.,
Eales, S. A., Fabbiano, G., & Weaver, K. 1996, ApJ, 457, 616
In the text
NASA ADS
- Heckman, T. M.,
González-Delgado, R. M., Leitherer, C., et al. 1997, ApJ, 482, 114
In the text
NASA ADS
- Kennicutt, R. C. Jr. 1992, ApJ, 388, 310
NASA ADS
- Kunth, D., & Joubert, M.
1985, A&A, 142, 411
NASA ADS
- Kurucz, R. L. 1991, in Stellar Atmospheres: Beyond
Classical Limits, ed. L. Crivellari, I. Hubeny, & D. G. Hummer (Dordrecht:
Kluwer), 441
In the text
- Legrand, F., Kunth, D.,
Mas-Hesse, J. M., & Lequeux, J. 1997, A&A, 326, 929
In the text
NASA ADS
- Leitherer, C., Robert, C.,
& Drissen, L. 1992, ApJ, 401, 596
In the text
NASA ADS
- Lequeux, J., Kunth, D.,
Mas-Hesse, J. M., & Sargent, W. L. W. 1985, A&A, 301, 18
In the text
NASA ADS
- Luridiana, V., Peombert, M., &
Leitherer, C. 1999, ApJ, 527, 110
In the text
NASA ADS
- Maíz-Apellániz,
J., Mas-Hesse, J. M., Muñoz-Tuñón, C., Vílchez, J. M., &
Castañeda, H. O. 1998, A&A, 329, 409
In the text
NASA ADS
- Mas-Hesse, J. M., & Kunth, D.
1991, A&AS, 88, 399 (MHK)
In the text
NASA ADS
- Mas-Hesse, J. M. 1992, A&A, 253, 49
In the text
NASA ADS
- Mas-Hesse, J. M.,
Rodríguez-Pascual, P. M., Sanz-Fernandéz de Córdoba, L.,
et al.
1995, A&A, 298, 22
In the text
NASA ADS
- Mas-Hesse, J. M., & Kunth, D.
1998, A&A, 349, 765
In the text
NASA ADS
- Meynet, G., Maeder, A.,
Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97
In the text
NASA ADS
- Persic, M., & Rephaeli, Y.
2002, A&A, 382, 843
In the text
NASA ADS
-
Plüschke, S. 2001, Ph.D. Thesis, MPE, Germany
In the text
- Raymond, J. C., & Smith, B. W.
1997, ApJS, 35, 419
In the text
NASA ADS
- Schaerer, D., & De Koter, A.
1997, A&A, 322, 598
In the text
NASA ADS
- Schaerer, D., & Vacca, W. D.
1998, ApJ, 497, 618
In the text
NASA ADS
- Schaerer, D., Contini, T., &
Pindao, M. 1999, ApJS, 136, 35
In the text
- Schaller, G., Schaerer, D.,
Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
In the text
NASA ADS
- Schmutz, W., Leitherer, C.,
& Gruenwald, R. 1992, PASP, 104, 1164
In the text
NASA ADS
- Silich, S. A., Tenorio-Tagle, G.,
Terlevich, R., Terlevich, E., & Netzer, H. 2001, MNRAS, 324, 191
In the text
NASA ADS
- Stasinska, G., &
Leitherer, C. 1996, ApJS, 107, 661
In the text
NASA ADS
- Stevens, I. R., &
Strickland, D. K. 1998a, MNRAS, 294, 523
In the text
NASA ADS
- Stevens, I. R., &
Strickland, D. K. 1998b, MNRAS, 301, 215
NASA ADS
- Strickland, D. K., &
Stevens, I. R. 1999, MNRAS, 306, 43
In the text
NASA ADS
- Strickland, D. K., &
Stevens, I. R. 2000, MNRAS, 314, 511
In the text
NASA ADS
- Summers, L. K., Stevens, I. R., &
Strickland, D. K. 2001, MNRAS, 327, 385
In the text
NASA ADS
- Van Bever, J., Belkus, H.,
Vanbeveren, D., & van Rensbergen, W. 1999, New Astron., 4, 173
In the text
- Van Bever, J., &
Vanbeveren, D. 2000, A&A, 358, 462
In the text
NASA ADS
- Wang, Q. D., & Helfand, D. J.
1991, ApJ, 370, 541
In the text
NASA ADS
- Wang, Q. D.
1999, ApJ, 510, L139
In the text
NASA ADS
- Woltjer, L. 1972, ARA&A, 10, 129
In the text
NASA ADS
- Woosley, S. E., Langer,
N., & Weaver, T. 1995, ApJ, 448, 315
In the text
NASA ADS
- Woosley, S. E., & Weaver, T. 1995,
ApJS, 101, 181
In the text
NASA ADS
Copyright ESO 2002
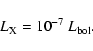
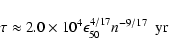
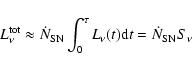
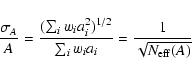
![\begin{figure}
\par\includegraphics[width=18cm,clip]{CMHKf1.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg58.gif)
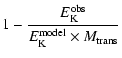
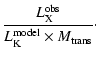
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{CMHKf3a.eps}\includegraphics[width=8.4cm,clip]{CMHKf3b.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{CMHKf2.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg87.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{CMHKf4.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{CMHKf5.eps} \medskip
\end{figure}](/articles/aa/full/2002/34/aa2257/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{CMHKf6.eps} \end{figure}](/articles/aa/full/2002/34/aa2257/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{CMHKf7.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg93.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{CMHKf8.eps}\end{figure}](/articles/aa/full/2002/34/aa2257/Timg94.gif)