A&A 391, 1173-1184 (2002)
DOI: 10.1051/0004-6361:20020901

Studies on the E2-transition in CoXVII

H. Ray

Indian Institute of Astrophysics, Koramangala, Bangalore 560034, India

Received 4 March 2002 / Accepted 4 June 2002

Abstract
The spectrum of the solar corona, plasma spectra, astrophysical objects and fusion devices exhibit forbidden lines in alkali-like ions. Ions belonging to the iron group are particularly important in this respect. More accurate data for term values, line strengths and transition probabilities are reported for electric quadrupole (E2) transitions in the highly stripped ion CoXVII using highly correlated relativistic wavefunctions obtained by coupled cluster theory. The present results are consistent with the findings of the earlier theoretical data. Some of the data are reported for the first time.

Key words: astrophysics, abundances, corona, stellar, forbidden E2-transition probability, highly stripped ion


1 Introduction

The study of atomic transitions is a subject of considerable interests in many fields. The extremely hot environment of the stars (for instance, the corona of the sun, planetary nebulae etc.) show abundances (Feldman 1992) of highly stripped ions. With the advent of high resolution spectrographs, observations of weak or forbidden transition lines become possible and they are of great astrophysical interests. Many astrophysical phenomena like coronal heating, evolution of chemical composition in stellar envelopes, determination of the chemistry in the planetary nebulae precursor's envelope are believed to be explained largely by these forbidden lines.

In astrophysics, the study of transition probabilities plays an important role in the determination of atomic abundances. In controlled thermonuclear reactions, atomic radiation is one of the primary loss mechanism. In laboratory tokamak plasmas and in various astronomical objects, suitably chosen electric quadrupole (E2) forbidden lines serve as a basis for reliable electron density and/or temperature diagnostics (Biemont et al. 1996). Accurate estimates of radiative transition probabilities among multiplet states are an important source for successful experimental identification of the spectra of astrophysical and laboratory plasmas. Probabilities of magnetic dipole and electric quadrupole transitions, in particular, are important in plasma diagnostics, but experimental determination of these quantities is difficult and only accurate theoretical calculation can provide important information.

A number of theoretical calculations on electric and magnetic multipole transition rates have been performed in recent years using various approximations (Huang 1985; Johnson et al. 1995; Safronova et al. 1999; Avgoustoglou et al. 1998; Beck 1998; Ishikawa et al. 2001; Ray 2002a; Ray 2002b; Ray & Das 2002), and it has become evident that accurate, correlated wave functions must be employed to evaluate the transition rates accurately. For the electric-dipole forbidden transitions in high-Z ions, electric-quadrupole (E2) transition rates are dominant over magnetic-dipole (M1) rates. High precision calculation of transition energies as well as of wave functions are necessary because E2 transition rates involve a fifth power dependence on transition energy. A relativistic description is required for describing the highly stripped ions where the orbital electrons probe the regions of space with high potential energy near the atomic nuclei. The primary effect of this relativistic description is to include changes in spatial and momentum distributions, spin-orbit interactions, quantum electrodynamic corrections such as Lamb shift and vacuum polarization whereas the secondary effect in many electron system is the modification of orbitals due to shielding of the other electrons in penetrating orbits.

In the present article we are interested in studying the electric quadrupole transition properties of the Na-like highly stripped ion CoXVII with higher accuracy. Tull et al. (1971) have mentioned the additional need for both theoretical and experimental work on such systems. The present availability of intense tunable radiation sources has made it feasible to measure transition probabilities of electric quadrupole (E2) transitions. However no experimental E2 transition data (Charro et al. 2001) for the present system is available in the literature. Very recently Charro et al. (2001) have reported line strength data using the quasi-relativistic RQDO-method. We have compared our E2-transition probability data with the existing theoretical data of Fuhr et al. (1988).

The Dirac-Hartree-Fock method adapted in numerical MCDF GRASP-code by Parpia (1992) is able to generate only the bound orbitals due to the boundary conditions imposed to solve the differential equation; it creates convergence problems to generate higher orbitals. The Gaussian basis set expansion method is able to generate both the bound and continuum orbitals solving the Dirac-Hartree-Fock equation, but these orbitals are highly dependent on two arbitrary parameters, known in the literature as $\alpha_0$ and $\beta$; there is a great debate on the choice of these two parameters. So there is the utmost necessity of a suitable basis set with both the bound and continuum orbitals including all the required physical effects. Majumder et al. (2001) have prescribed a new methodology for generating the basis set combining the numerical and more accurate GRASP bound orbitals with the continuum Gaussian orbitals and satisfying all the important physics through orthonormalisation in Fock space. They also verified its utility by applying it in different systems (Majumder et al. 2001). We have followed their methodology for generating the present basis orbitals. The motivation is to make the basis orbitals as close as possible to the more physical GRASP-orbitals to get better accuracy in a limited finite basis. However, the Slater determinant formed by these orbitals to represent the atomic state function (ASF) is deficient from the physical point of view due to the lack of correlation effects which is approximated by an equivalent single particle potential in the Dirac-Hartree-Fock theory. How these correlation effects can be included properly in a many-electron-system is a great challenge to quantum chemists, atomic and molecular physicists.

One of the most advanced method for treating this problem is the coupled cluster method (Bishop et al. 1987). It is a quantum many-body method in which the wavefunction is decomposed in terms of amplitudes for exciting clusters of a finite number of particles. The development of this theory was started in the nuclear physics community by Coester & Kümmel (Coester 1958; Coester et al. 1960) and was later introduced in quantum chemistry by Cizek and co-workers (Paldus et al. 1978; Paldus 1983); it was applicable mainly to closed shell systems. Subsequent development of this theory using the idea of complete model spaces (Lindgren 1978; Ey 1978; Mukherjee 1986; Lingren et al. 1987) and a Hermitian formulation (Lindgren 1991) of the coupled cluster method have led to connected cluster operators and an effective Hamiltonian, even for an incomplete model space.

2 Theory

2.1 Coupled cluster method (CCM)

The idea of the coupled cluster method (CCM) is as follows: two particles in the filled Fermi sea interact with each other and lift themselves out of the Fermi sea, so that after the interaction both particles are in orbitals that in the previous simplified picture were unoccupied. This process may be described by a quantum mechanical operator $\vec{S}_2$ which acts on the Fermi sea wavefunction (say $\vert\Phi\rangle$) to produce the wavefunction $\vec{S}_2\vert\vec{\Phi}\rangle$, which describes two particles outside the Fermi sea and consequently two holes inside it and all remaining N-2 particles are in their previous orbitals, where N is the total number of electrons present in the atom.

It may also happen that two pairs of particles do this completely independently. This process may be described by applying this operator $\vec{S}_2$ twice and so on, with the proviso that we must include the proper weighting factor. By the principle of linear superposition, the total amplitude for excitation of an arbitrary number m (including zero) of independent pairs is

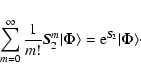\begin{displaymath}\sum_{m=0}^{\infty} \frac{1}{m!} \vec{S}_2^m \vert\vec{\Phi}\rangle = {\rm e}^{ \vec{S}_2}\vert\vec{\Phi}\rangle\cdot \end{displaymath} (1)

Simultaneous excitation of three particles can be described by a contribution $\vec{S}_3\vert\vec{\Phi}\rangle$ to the exact wavefunction and the simultaneous excitation of n independent triplets will be $(1/n!) \vec{S}_3^n\vert\vec{\Phi}\rangle$. We must also count the possibility of simultaneous excitation of pairs and triplets. Again by linear superposition, the amplitude for simultaneous excitation of "m'' pairs and "n'' triplets from the Fermi sea is $(1/m! n!) \vec {S}_2^m \vec{S}_3^n\vert\vec{\Phi}\rangle$. Here $\vec{S}_2$ and $\vec{S}_3$ are independent processes, so they commute and we need not worry about their ordering. Summing over all possible values of "m'' and "n'' leads to the amplitude e $^{(\vec{S}_2+\vec{S}_3)}\vert\vec{\Phi}\rangle$ for the total effect of all pair and triplet excitations. Proceeding in this way with the excitation of clusters of 4, 5,..., N particles we arrive at a wavefunction

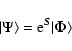\begin{displaymath}\vert\Psi\rangle = {\rm e}^{\vec{S}}\vert\vec{\Phi}\rangle \end{displaymath} (2)

where

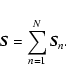\begin{displaymath}\vec{S} = \sum_{n=1}^N \vec{S}_n. \end{displaymath} (3)

Here $\vec{S}_n$ indicates excitation of n-particles at a time. John Hubbard (Hubbard 1957) noticed first that the operator generating the wavefunction of a quantum many-body system has an exponential form. This exponential representation may be regarded as an expansion of the exact wavefunction in a complete orthonormal basis. But we have to keep always in mind the arguments we have used. Such an interpretation of the wavefunction is very useful in practical application of CCM. It may be considered a universal theory for including correlation in many body physics, due to its wide range of applicability in different fields of many-body systems of both bosons and fermions, quite regardless of the type and range of interaction, and because it yields high-precision results for the ground state as well as for low-energy excited states.

The CCM equations for the amplitudes of $\vec{S}_n$ are easily obtained by projecting the Schrödinger equation

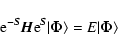\begin{displaymath}{\rm e}^{-\vec{S}} \vec{H}{\rm e}^{\vec{S}}\vert\vec{\Phi}\rangle = E\vert\vec{\Phi}\rangle \end{displaymath} (4)

onto the complete N-body space spanned by the Fermi sea states and those states obtained by creating "n'' general particle-hole excitations out of it. This yields a series of coupled equations, each of which contains a finite number of terms. The excitation operators can be written as:

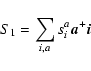\begin{displaymath}S_1 = \sum_{i,a} s_i^a \vec{a}^{+}\vec{i} \end{displaymath} (5)


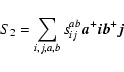\begin{displaymath}S_2 = \sum_{i,j,a,b} s_{ij}^{ab} \vec{a}^{+} \vec{i}\vec{b}^+ \vec{j} \end{displaymath} (6)

and so on. Here i, j are the hole annihilation; $\vec{a}^+$, $\vec{b}^+$ are the particle creation operators and sia, sijab are the amplitudes for single-particle, two-particle excitations repectively.

The first equation in the series yields an expression for E. Due to the special form of the above Schrödinger equation, the remaining equations do not involve the energy E or other macroscopic terms, and represent a truly microscopic decomposition of the Schrödinger equation into a set of coupled equations that describe the dynamics of the n-body clusters. These equations are intrinsically nonlinear. We consider all the single, double and partial triple excitations from the core in the present calculation.

2.2 Matrix element for electric quadrupole transition

The matrix element for electric quadrupole transitions is

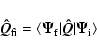\begin{displaymath}\vec{\hat Q}_{\rm fi} = \langle\vec{\Psi}_{\rm f}\vert \vec{\hat Q}\vert\vec{\Psi}_{\rm i}\rangle \end{displaymath} (7)

where $\vert\vec{\Psi}_{\rm i}\rangle$ and $\vert\vec{\Psi}_{\rm f}\rangle$ denote respectively the initial and final atomic state functions. Here electric quadrupole operator $\vec{\hat Q}$ is a rank two tensor and may be written as

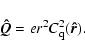\begin{displaymath}\vec{\hat Q} = e r^2 C^2_{\rm q}(\vec{\hat r}). \end{displaymath} (8)

The line strength is defined as

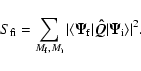\begin{displaymath}S_{\rm fi} = \sum_{M_{\rm f},M_{\rm i}} \vert\langle \vec{\Ps... ... f}\vert \vec{\hat Q} \vert \vec{\Psi}_{\rm i}\rangle\vert^2. \end{displaymath} (9)

Applying the Wigner-Eckart theorem, the above expression transforms to

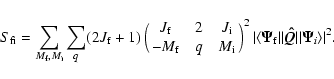\begin{displaymath}S_{\rm fi} = \sum_{M_{\rm f},M_{\rm i}} \sum_q (2J_{\rm f}+1... ...vert\vert \vec{\hat Q} \vert\vert \vec{\Psi}_i\rangle\vert^2 . \end{displaymath} (10)

The transition probability (in s-1) for present E2 transition is related with the line strength (in atomic or e $^2a_{\circ}^4$ unit) by the relation

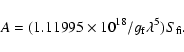\begin{displaymath}A = (1.11995\times 10^{18}/g_{\rm f}\lambda^5) S_{\rm fi}. \end{displaymath} (11)

Here $\lambda $ is the wavelength (in Å) of the associated electromagnetic radiation, "A'' is the transition probability and $g_{\rm f}$ is the degeneracy of the final state.

 
Table 1a: Term values of CoXVII in cm-1.
Levels J-values DHF$^{\bf a}$ CCM$^{\bf b}$ Tull et al.$^{\bf c}$ Observed %error$^{\bf a}$ %error$^{\bf b}$ %error$^{\bf c}$

3s

 1/2 0 0 0 0      
3p 1/2 295 647 294 704 294 600 294 480 -0.396 -0.076 -0.041
  3/2 321 576 320 755 318 230 319 930 -0.514 -0.258 0.531
3d 3/2 723 113 721 691 721 400 720 170 -0.409 -0.211 -0.171
  5/2 727 106 725 779 725 580 723 890 -0.444 -0.261 -0.233
4s 1/2 2 076 768 2 080 058 2 077 880 2 079 500 0.131 -0.027 0.078
4p 1/2 2 194 404 2 197 376 2 195 140 2 196 500 0.095 -0.040 0.062
  3/2 2 204 651 2 207 580 2 204 470 2 206 580 0.087 -0.045 0.096
4d 3/2 2 352 284 2 355 393 2 352 760 2 353 630 0.057 -0.075 0.037
  5/2 2 354 095 2 357 238 2 354 560 2 355 220 0.048 -0.086 0.028
4f 5/2 2 417 357 2 421 445 2 418 980 2 419 640 0.094 -0.075 0.027
  7/2 2 417 992 2 422 087 2 419 620 2 420 300 0.095 -0.074 0.028
5s 1/2 2 927 810 2 969 518 2 966 590        
5p 1/2 2 992 485 3 027 462 3 024 510 3 026 090 1.110 -0.045 0.052
  3/2 3 028 318 3 032 495 3 029 120 3 030 760 0.081 -0.057 0.054
5d 3/2 3 099 618 3 103 934 3 100 750 3 102 130 0.081 -0.058 0.044
  5/2 3 100 564 3 104 896 3 101 680 3 102 970 0.077 -0.062 0.042
5f 5/2 3 132 408 3 137 113 3 134 070 3 135 400 0.095 -0.055 0.042
  7/2 3 132 736 3 137 444 3 134 400 3 135 740 0.096 -0.054 0.043
5g 7/2 3 135 657 3 140 960          
  9/2 3 135 852 3 141 155          
6s 1/2 3 182 818 3 431 664 3 428 410        
6p 1/2 3 288 104 3 464 394 3 461 130 3 463 320 5.059 -0.031 0.063
  3/2 3 462 528 3 467 239 3 463 740 3 466 200 0.106 -0.030 0.071
6d 3/2 3 502 483 3 507 284 3 503 880 3 505 580 0.088 -0.049 0.048
  5/2 3 503 035 3 507 844 3 504 420 3 506 060 0.086 -0.051 0.047
6f 5/2 3 521 259 3 526 254 3 522 950 3 524 430 0.090 -0.052 0.042
  7/2 3 521 449 3 526 447 3 523 150 3 524 460 0.085 -0.056 0.037
6g 7/2 3 523 377 3 528 720          
  9/2 3 523 490 3 528 833          
7s 1/2 3 484 622 3 702 333 3 698 910        
7p 1/2 3 570 493 3 722 589 3 719 160        
  3/2 3 719 373 3 724 352 3 720 780        
7d 3/2 3 744 030 3 749 067 3 745 560 3 747 520 0.093 -0.041 0.052
  5/2 3 744 378 3 749 421 3 745 890 3 747 990 0.096 -0.038 0.056
8s 1/2 3 680 514 3 874 415 3 870 890        
8p 1/2 3 753 437 3 887 807 3 884 280        
  3/2 3 883 847 3 888 975 3 885 350        
8d 3/2 3 900 138 3 905 304 3 901 730        
  5/2 3 900 371 3 905 542 3 901 950 3 903 900 0.090 -0.042 0.050
9s 1/2 3 813 452 3 990 580 3 986 990        
9p 1/2 3 879 615 3 999 890 3 996 300        
  3/2 3 995 487 4 000 703 3 997 050        
9d 3/2 4 006 810 4 012 056 4 008 430        
  5/2 4 006 974 4 012 223 4 008 590        


2.3 Computation using CCM

The expression for the present E2 transition using CCM is

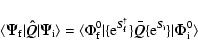\begin{displaymath}\langle \vec{\Psi}_{\rm f}\vert\vec{\hat Q}\vert\vec{\Psi}_{\... ...\rm e}^{\vec{S}_{\rm i}}\}\vert \vec{\Phi}_{\rm i}^{0}\rangle \end{displaymath} (12)

with

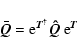\begin{displaymath}\vec{\bar Q} = {\rm e}^{\vec{T}^{\dag }}\vec{\hat Q}\ {\rm e}^{\vec{T} } \end{displaymath} (13)

where T, $\vec{S}_{\rm i}$ and $\vec{S}_{\rm f}$ are the cluster operators for excitations from the core and the valence orbitals in the initial and final states respectively. The connected parts of Eqs. (12) and (13) will contribute and hence we compute only those parts in our quadrupole matrix element calculation.

Here $\vert\vec{\Phi}_{\rm i}^0\rangle $ and $\vert\vec{\Phi}_{\rm f}^0\rangle $ are the Slater determinants obtained by using the Dirac Hartree Fock single particle orbitals. We have considered a large basis set of twelve(12) s-orbitals, eleven(11) of each of the p(1/2), p(3/2), d(3/2), d(5/2), f(5/2), f(7/2) orbitals; ten(10) of each of the g(7/2) and g(9/2) orbital: a total of 98 orbitals. It should be noted that our basis orbitals include both the bound and continuum states; however due to limited computer resources we are forced to confine our continuum orbitals to within a maximum energy of 500 a.u.

3 Results and discussion

We present the theoretical data for term values, E2-transition line strengths and transition probabilities which are far more accurate than the previous theoretical results. Firstly, we have used fully relativistic Dirac-Hartree-Fock (DHF) orbitals and secondly, we have included the effect of Coulomb correlation through an ab-initio all order many-body coupled-cluster theory. It should be noted that the present coupled-cluster theory is equivalent to an all order many-body perturbation theory. We have included all the single, double and partially triple excitations from the atomic core in our calculation. In Table 1a, we have compared our term values obtained by using CCM with fully relativistic Dirac-Hartree Fock orbitals, with the corresponding available experimental data of Feldman et al. (1971) and the theoretical data of Tull et al. (1971). In their calculation of term values, Tull et al. have included the relativistic effect through first order perturbation theory on the non-relativistic frozen core type Hartree-Fock orbitals. The percentage errors with respect to the observed values are presented in the same Table for both the theoretical results and the simple Dirac-Hartree-Fock (DHF) term values. A negative sign before the percentage error indicates that the experimental values are lower than the theoretical values and vice versa. The effect of the Coulomb correlation interaction can be understood by comparing rows a and b in Table 1a. All our theoretical results indicate the importance of correlation in such system. The effect of correlation is more in low lying states and in all the p-orbitals. Again it should be noted that the effect of correlation has changed all the errors to negative which means that the improved term values are slightly higher than the observed values. The low lying p(3/2) and d(3/2,5/2) deviate more strongly. The percentage error is $\sim$10-1 whereas in other cases it is $\sim$10-2. In Table 1b, a few of our line strength data are compared with the existing non-relativistic data of Tull et al. (1971) and a quasi-relativistic RQDO-data of Charro et al. (2001). Similarly in Table 1c, a few of our transition probability data are compared with the relativistic E2-transition probability data of Fuhr et al. (1988). All the present data are in consistency with other theoretical values.

In Table 2, the present detailed data for E2-transition line strengths and transition probabilities for CoXVII are reported with both the experimental and the theoretical transition energies which are available in the electronic version of the paper. All line strength results are in close agreement with the relativistic results of Charro et al. (2001) and the non-relativistic results of Tull et al. (1971). Our line strength data in Table 2 need a multiplicative factor of $1/{\sqrt{2}}$ to compare with others. All our transition probality data are also in agreement with Fuhr et al. (1988). Some of the data reported here are completely new.


 
Table 1b: Comparison of present line strengths (a.u.) with available theoretical data ( Charro et al. 2001; Tull et al. 1971) for CoXVII.
Transition Line strength Line strength Line strength
  Present calculation Charro et al. Tull et al.
$n^{\prime}{l^{\prime}}\rightarrow nl$ l-1/2 l+1/2 Sum Sum Non-relativistic
3s $\rightarrow $3d 0.094 0.142 0.236 0.236 0.227
3s $\rightarrow $4d 0.067 0.100 0.167 0.153 0.169
3s $\rightarrow $5d 0.009 0.013 0.022 0.021 0.022
4s $\rightarrow $4d 1.459 2.193 3.652 3.53 3.51
4s $\rightarrow $5d 0.455 0.678 1.133 1.05 1.15
3p(1/2) $\rightarrow $4f 0.250        
3p(3/2) $\rightarrow $4f 0.073 0.440 0.764 0.776 0.736
3p(1/2) $\rightarrow $4p   0.048      
3p(3/2) $\rightarrow $4p 0.052 0.050 0.150 0.148 0.145
3d(3/2) $\rightarrow $4d 0.048 0.021      
3d(5/2) $\rightarrow $4d 0.021 0.082 0.172 0.171 0.164
4f(5/2) $\rightarrow $5f 0.637 0.106      
4f(7/2) $\rightarrow $5f 0.107 0.886 1.736 1.660 1.650



 
Table 1c: Comparison of present transition probabilities with the available theoretical data by Fuhr et al. (1988) in units of 108 s-1 for CoXVII. The quantities within third brackets indicate the powers of 10.
Transition Present E2-transition E2-transition probabilities
  probabilities Fuhr et al.
$n^{\prime}{l^{\prime}}\rightarrow nl$ l-1/2 l+1/2 Sum l-1/2 l+1/2 Sum
3s $\rightarrow $3d 7.30[-3] 7.56[-3] 1.49[-2] 7.40[-3] 7.60[-3] 1.50[-2]
3s $\rightarrow $4d 1.93[0] 1.92[0] 3.85[0] 2.10[0] 2.05[0] 3.85[0]
3s $\rightarrow $5d 1.03[0] 1.03[0] 2.06[0]   1.00[0]  
4s $\rightarrow $4d 9.14[-4] 9.47[-4] 1.86[-3] 9.10[-4] 9.40[-4] 1.85[-3]
4s $\rightarrow $5d 2.03[-1] 2.02[-1] 4.05[-1] 2.20[-1] 2.16[-1] 4.36[-1]
3p(1/2) $\rightarrow $4f 2.86[0]     2.97[0]    
3p(3/2) $\rightarrow $4f 7.92[-1] 3.57[0] 7.22[0] 8.00[-1] 3.61[0] 7.38[0]
3p(1/2) $\rightarrow $4p   4.86[-1]     5.20[-1]  
3p(3/2) $\rightarrow $4p 9.65[-1] 4.78[-1] 1.93[0] 9.40[-1] 4.80[-1] 1.94[0]
3d(3/2) $\rightarrow $4d 2.21[-1] 6.36[-2]   2.20[-1] 6.50[-2]  
3d(5/2) $\rightarrow $4d 9.50[-2] 2.52[-1] 6.32[-1] 9.70[-2] 2.60[-1] 6.42[-1]
4f(5/2) $\rightarrow $5f 3.16[-2] 3.97[-3]   3.20[-2] 3.99[-3]  
4f(7/2) $\rightarrow $5f 5.28[-3] 3.29[-2] 7.375[-2] 5.30[-3] 3.30[-2] 7.43[-2]



 
Table 2: E2-transition properties for CoXVII. General E-format is used to express the data.
Transition   Transition Energy (a.u.)   Transition Properties
$n^{\prime}{l^{\prime}}\rightarrow nl$   Experimental Present CCM   Line strength (a.u.) Probability (s-1)

3s(1/2) $\rightarrow $ 3d(3/2)

   3.2814E+00 3.2883E+00   0.13313E+00 0.730E+06
3s(1/2) $\rightarrow $ 4d(3/2)   1.0724E+01 1.0732E+01   0.95146E-01 0.193E+09
3s(1/2) $\rightarrow $ 5d(3/2)   1.4134E+01 1.4143E+01   0.12789E-01 0.103E+09
3s(1/2) $\rightarrow $ 6d(3/2)   1.5973E+01 1.5980E+01   0.38722E-02 0.575E+08
3s(1/2) $\rightarrow $ 7d(3/2)   1.7075E+01 1.7082E+01   0.16756E-02 0.347E+08
3s(1/2) $\rightarrow $ 8d(3/2)     1.7794E+01   0.86469E-03 0.220E+08
3s(1/2) $\rightarrow $ 9d(3/2)     1.8280E+01   0.38575E-03 0.112E+08
3s(1/2) $\rightarrow $ 3d(5/2)   3.2983E+01 3.3069E+01   0.20108E+00 0.756E+06
3s(1/2) $\rightarrow $ 4d(5/2)   1.0731E+01 1.0740E+01   0.14167E+00 0.192E+09
3s(1/2) $\rightarrow $ 5d(5/2)   1.4138E+01 1.4147E+01   0.19127E-01 0.103E+09
3s(1/2) $\rightarrow $ 6d(5/2)   1.5975E+01 1.5983E+01   0.57967E-02 0.575E+08
3s(1/2) $\rightarrow $ 7d(5/2)   1.7077E+01 1.7084E+01   0.25097E-02 0.347E+08
3s(1/2) $\rightarrow $ 8d(5/2)   1.7788E+01 1.7795E+01   0.12953E-02 0.220E+08
3s(1/2) $\rightarrow $ 9d(5/2)     1.8281E+01   0.57719E-03 0.112E+08
4s(1/2) $\rightarrow $ 4d(3/2)   1.2490E+00 1.2545E+00   0.20636E+01 0.914E+05
4s(1/2) $\rightarrow $ 5d(3/2)   4.6595E+00 4.6652E+00   0.64455E+00 0.203E+08
4s(1/2) $\rightarrow $ 6d(3/2)   6.4977E+00 6.5030E+00   0.87155E-01 0.145E+08
4s(1/2) $\rightarrow $ 7d(3/2)   7.6001E+00 7.6046E+00   0.26198E-01 0.950E+07
4s(1/2) $\rightarrow $ 8d(3/2)     8.3165E+00   0.11163E-01 0.633E+07
4s(1/2) $\rightarrow $ 9d(3/2)     8.8029E+00   0.49575E-02 0.374E+07
4s(1/2) $\rightarrow $ 4d(5/2)   1.2563E+00 1.2629E+00   0.31024E+01 0.947E+05
4s(1/2) $\rightarrow $ 5d(5/2)   4.6633E+00 4.6695E+00   0.95943E+00 0.202E+08
4s(1/2) $\rightarrow $ 6d(5/2)   6.4978E+00 6.5055E+00   0.13055E+00 0.145E+08
4s(1/2) $\rightarrow $ 7d(5/2)   7.6023E+00 7.6062E+00   0.39350E-01 0.952E+07
4s(1/2) $\rightarrow $ 8d(5/2)   8.3126E+00 8.3176E+00   0.16795E-01 0.636E+07
4s(1/2) $\rightarrow $ 9d(5/2)     8.8037E+00   0.74652E-02 0.375E+07
5s(1/2) $\rightarrow $ 5d(3/2)     6.1245E-01   0.14733E+02 0.181E+05
5s(1/2) $\rightarrow $ 6d(3/2)     2.4502E+00   0.29135E+01 0.367E+07
5s(1/2) $\rightarrow $ 7d(3/2)     3.5519E+00   0.38432E+00 0.310E+07
5s(1/2) $\rightarrow $ 8d(3/2)     4.2638E+00   0.11273E+00 0.226E+07
5s(1/2) $\rightarrow $ 9d(3/2)     4.7502E+00   0.43707E-01 0.151E+07
5s(1/2) $\rightarrow $ 5d(5/2)     6.1683E-01   0.22132E+02 0.188E+05
5s(1/2) $\rightarrow $ 6d(5/2)     2.4528E+00   0.43295E+01 0.365E+07
5s(1/2) $\rightarrow $ 7d(5/2)     3.5535E+00   0.57455E+00 0.309E+07
5s(1/2) $\rightarrow $ 8d(5/2)     4.2649E+00   0.16896E+00 0.227E+07
5s(1/2) $\rightarrow $ 9d(5/2)     4.7510E+00   0.65584E-01 0.151E+07
6s(1/2) $\rightarrow $ 6d(3/2)     3.4455E-01   0.69765E+02 0.483E+04
6s(1/2) $\rightarrow $ 7d(3/2)     1.4462E+00   0.10214E+02 0.921E+06
6s(1/2) $\rightarrow $ 8d(3/2)     2.1581E+00   0.13034E+01 0.870E+06
6s(1/2) $\rightarrow $ 9d(3/2)     2.6445E+00   0.35781E+00 0.660E+06
7s(1/2) $\rightarrow $ 7d(3/2)     2.1294E-01   0.25402E+03 0.159E+04
7s(1/2) $\rightarrow $ 8d(3/2)     9.2481E-01   0.29975E+02 0.289E+06
7s(1/2) $\rightarrow $ 9d(3/2)     1.4112E+00   0.36332E+01 0.290E+06
8s(1/2) $\rightarrow $ 8d(3/2)     1.4074E-01   0.76920E+03 0.606E+03
8s(1/2) $\rightarrow $ 9d(3/2)     6.2714E-01   0.76528E+02 0.106E+06
9s(1/2) $\rightarrow $ 9d(3/2)     9.7853E-02   0.20375E+04 0.261E+03
6s(1/2) $\rightarrow $ 6d(5/2)     3.4710E-01   0.10474E+03 0.502E+04
6s(1/2) $\rightarrow $ 7d(5/2)     1.4478E+00   0.15164E+02 0.917E+06
6s(1/2) $\rightarrow $ 8d(5/2)     2.1592E+00   0.19466E+01 0.868E+06
6s(1/2) $\rightarrow $ 9d(5/2)     2.6452E+00   0.53565E+00 0.659E+06



 
Table 2: continued.
Transition   Transition Energy (a.u.)   Transition Properties
$n^{\prime}{l^{\prime}}\rightarrow nl$   Experimental Present CCM   Line strength (a.u.) Probability (s-1)
7s(1/2) $\rightarrow $ 7d(5/2)     2.1455E-01   0.38124E+03 0.165E+04
7s(1/2) $\rightarrow $ 8d(5/2)     9.2590E-01   0.44466E+02 0.288E+06
7s(1/2) $\rightarrow $ 9d(5/2)     1.4120E+00   0.54212E+01 0.289E+06
8s(1/2) $\rightarrow $ 8d(5/2)     1.4183E-01   0.11541E+04 0.629E+03
8s(1/2) $\rightarrow $ 9d(5/2)     6.2790E-01   0.11345E+03 0.105E+06
9s(1/2) $\rightarrow $ 9d(5/2)     9.8614E-02   0.30564E+04 0.271E+03
3d(3/2) $\rightarrow $ 4s(1/2)   6.1936E+00 6.1892E+00   0.50948E-01 0.132E+08
3d(3/2) $\rightarrow $ 5s(1/2)     1.0242E+01   0.20821E-02 0.669E+07
3d(3/2) $\rightarrow $ 6s(1/2)     1.2348E+01   0.47846E-03 0.392E+07
3d(3/2) $\rightarrow $ 7s(1/2)     1.3581E+01   0.18752E-03 0.247E+07
3d(3/2) $\rightarrow $ 8s(1/2)     1.4365E+01   0.94182E-04 0.164E+07
3d(3/2) $\rightarrow $ 9s(1/2)     1.4894E+01   0.54425E-04 0.114E+07
4d(3/2) $\rightarrow $ 5s(1/2)     2.7981E+00   0.76179E+00 0.373E+07
4d(3/2) $\rightarrow $ 6s(1/2)     4.9039E+00   0.26316E-01 0.213E+07
4d(3/2) $\rightarrow $ 7s(1/2)     6.1372E+00   0.55024E-02 0.137E+07
4d(3/2) $\rightarrow $ 8s(1/2)     6.9212E+00   0.20254E-02 0.917E+06
4d(3/2) $\rightarrow $ 9s(1/2)     7.4505E+00   0.94537E-03 0.619E+06
5d(3/2) $\rightarrow $ 6s(1/2)     1.4933E+00   0.53510E+01 0.113E+07
5d(3/2) $\rightarrow $ 7s(1/2)     2.7265E+00   0.16164E+00 0.694E+06
5d(3/2) $\rightarrow $ 8s(1/2)     3.5106E+00   0.31113E-01 0.473E+06
5d(3/2) $\rightarrow $ 9s(1/2)     4.0399E+00   0.10562E-01 0.324E+06
6d(3/2) $\rightarrow $ 7s(1/2)     8.8872E-01   0.25096E+02 0.397E+06
6d(3/2) $\rightarrow $ 8s(1/2)     1.6728E+00   0.68113E+00 0.254E+06
6d(3/2) $\rightarrow $ 9s(1/2)     2.2021E+00   0.12049E+00 0.178E+06
7d(3/2) $\rightarrow $ 8s(1/2)     5.7113E-01   0.90760E+02 0.157E+06
7d(3/2) $\rightarrow $ 9s(1/2)     1.1004E+00   0.22426E+01 0.103E+06
8d(3/2) $\rightarrow $ 9s(1/2)     3.8855E-01   0.27293E+03 0.689E+05
3p(1/2) $\rightarrow $ 3p(3/2)   1.1596E-01 1.1870E-01   0.16763E+00 0.563E-01
3p(1/2) $\rightarrow $ 4p(3/2)   8.7122E+00 8.7158E+00   0.67838E-01 0.486E+08
3p(1/2) $\rightarrow $ 5p(3/2)   1.2467E+01 1.2474E+01   0.61985E-02 0.267E+08
3p(1/2) $\rightarrow $ 6p(3/2)   1.4451E+01 1.4455E+01   0.17362E-02 0.156E+08
3p(1/2) $\rightarrow $ 7p(3/2)     1.5627E+01   0.73465E-03 0.976E+07
3p(1/2) $\rightarrow $ 8p(3/2)     1.6377E+01   0.37555E-03 0.631E+07
3p(1/2) $\rightarrow $ 9p(3/2)     1.6886E+01   0.18472E-03 0.362E+07
4p(1/2) $\rightarrow $ 4p(3/2)   4.5928E-02 4.6493E-02   0.22287E+01 0.690E-02
4p(1/2) $\rightarrow $ 5p(3/2)   3.8012E+00 3.8051E+00   0.67361E+00 0.766E+07
4p(1/2) $\rightarrow $ 6p(3/2)   5.7852E+00 5.7860E+00   0.53733E-01 0.497E+07
4p(1/2) $\rightarrow $ 7p(3/2)     6.9575E+00   0.13885E-01 0.323E+07
4p(1/2) $\rightarrow $ 8p(3/2)     7.7076E+00   0.55328E-02 0.215E+07
4p(1/2) $\rightarrow $ 9p(3/2)     8.2166E+00   0.24493E-02 0.131E+07
5p(1/2) $\rightarrow $ 5p(3/2)   2.1278E-02 2.2932E-02   0.15332E+02 0.139E-02
5p(1/2) $\rightarrow $ 6p(3/2)   2.0053E+00 2.0038E+00   0.38727E+01 0.178E+07
5p(1/2) $\rightarrow $ 7p(3/2)     3.1753E+00   0.28133E+00 0.129E+07
5p(1/2) $\rightarrow $ 8p(3/2)     3.9254E+00   0.68022E-01 0.904E+06
5p(1/2) $\rightarrow $ 9p(3/2)     4.4344E+00   0.24326E-01 0.595E+06
6p(1/2) $\rightarrow $ 6p(3/2)   1.3122E-02 1.2963E-02   0.71838E+02 0.375E-03
6p(1/2) $\rightarrow $ 7p(3/2)     1.1845E+00   0.16067E+02 0.534E+06
6p(1/2) $\rightarrow $ 8p(3/2)     1.9345E+00   0.10858E+01 0.419E+06
6p(1/2) $\rightarrow $ 9p(3/2)     2.4436E+00   0.24107E+00 0.299E+06
7p(1/2) $\rightarrow $ 7p(3/2)     8.0329E-03   0.26109E+03 0.125E-03



 
Table 2: continued.
Transition   Transition Energy (a.u.)   Transition Properties
$n^{\prime}{l^{\prime}}\rightarrow nl$   Experimental Present CCM   Line strength (a.u.) Probability (s-1)

7p(1/2) $\rightarrow $ 8p(3/2)

     7.5812E-01   0.53438E+02 0.191E+06
7p(1/2) $\rightarrow $ 9p(3/2)     1.2672E+00   0.33620E+01 0.157E+06
8p(1/2) $\rightarrow $ 8p(3/2)     5.3218E-03   0.79177E+03 0.482E-04
8p(1/2) $\rightarrow $ 9p(3/2)     5.1440E-01   0.15077E+03 0.774E+05
9p(1/2) $\rightarrow $ 9p(3/2)     3.7043E-03   0.21039E+04 0.209E-04
3p(3/2) $\rightarrow $ 4p(1/2)   8.5504E+00 8.5506E+00   0.16819E+00 0.113E+00
3p(3/2) $\rightarrow $ 5p(1/2)   1.2330E+01 1.2333E+01   0.74022E-01 0.965E+08
3p(3/2) $\rightarrow $ 6p(1/2)   1.4322E+01 1.4324E+01   0.64146E-02 0.522E+08
3p(3/2) $\rightarrow $ 7p(1/2)     1.5500E+01   0.17656E-02 0.304E+08
3p(3/2) $\rightarrow $ 8p(1/2)     1.6253E+01   0.74036E-03 0.189E+08
3p(3/2) $\rightarrow $ 9p(1/2)     1.6763E+01   0.37589E-03 0.122E+08
4p(3/2) $\rightarrow $ 5p(1/2)   3.7340E+00 3.7357E+00   0.22398E+01 0.139E-01
4p(3/2) $\rightarrow $ 6p(1/2)   5.7262E+00 5.7265E+00   0.73160E+00 0.152E+08
4p(3/2) $\rightarrow $ 7p(1/2)     6.9029E+00   0.55123E-01 0.968E+07
4p(3/2) $\rightarrow $ 8p(1/2)     7.6557E+00   0.13946E-01 0.623E+07
4p(3/2) $\rightarrow $ 9p(1/2)     8.1664E+00   0.54889E-02 0.412E+07
5p(3/2) $\rightarrow $ 6p(1/2)   1.9709E+00 1.9679E+00   0.15403E+02 0.278E-02
5p(3/2) $\rightarrow $ 7p(1/2)     3.1443E+00   0.42004E+01 0.353E+07
5p(3/2) $\rightarrow $ 8p(1/2)     3.8971E+00   0.28804E+00 0.252E+07
5p(3/2) $\rightarrow $ 9p(1/2)     4.4078E+00   0.68098E-01 0.175E+07
6p(3/2) $\rightarrow $ 7p(1/2)     1.1635E+00   0.72155E+02 0.754E-03
6p(3/2) $\rightarrow $ 8p(1/2)     1.9163E+00   0.17413E+02 0.106E+07
6p(3/2) $\rightarrow $ 9p(1/2)     2.4270E+00   0.11100E+01 0.818E+06
7p(3/2) $\rightarrow $ 8p(1/2)     7.4476E-01   0.26220E+03 0.251E-03
7p(3/2) $\rightarrow $ 9p(1/2)     1.2554E+00   0.57877E+02 0.378E+06
8p(3/2) $\rightarrow $ 9p(1/2)     5.0537E-01   0.79524E+03 0.967E-04
3p(3/2) $\rightarrow $ 4p(3/2)   8.5963E+00 8.5971E+00   0.71350E-01 0.478E+08
3p(3/2) $\rightarrow $ 5p(3/2)   1.2352E+01 1.2356E+01   0.62859E-02 0.258E+08
3p(3/2) $\rightarrow $ 6p(3/2)   1.4335E+01 1.4336E+01   0.17367E-02 0.150E+08
3p(3/2) $\rightarrow $ 7p(3/2)     1.5508E+01   0.72913E-03 0.932E+07
3p(3/2) $\rightarrow $ 8p(3/2)     1.6258E+01   0.37036E-03 0.600E+07
3p(3/2) $\rightarrow $ 9p(3/2)     1.6767E+01   0.17942E-03 0.339E+07
4p(3/2) $\rightarrow $ 5p(3/2)   3.7553E+00 3.7586E+00   0.70387E+00 0.753E+07
4p(3/2) $\rightarrow $ 6p(3/2)   5.7393E+00 5.7395E+00   0.53940E-01 0.479E+07
4p(3/2) $\rightarrow $ 7p(3/2)     6.9110E+00   0.13707E-01 0.308E+07
4p(3/2) $\rightarrow $ 8p(3/2)     7.6611E+00   0.54065E-02 0.203E+07
4p(3/2) $\rightarrow $ 9p(3/2)     8.1701E+00   0.23668E-02 0.123E+07
5p(3/2) $\rightarrow $ 6p(3/2)   1.9840E+00 1.9808E+00   0.40331E+01 0.175E+07
5p(3/2) $\rightarrow $ 7p(3/2)     3.1524E+00   0.28084E+00 0.125E+07
5p(3/2) $\rightarrow $ 8p(3/2)     3.9024E+00   0.66627E-01 0.860E+06
5p(3/2) $\rightarrow $ 9p(3/2)     4.4115E+00   0.23518E-01 0.560E+06
6p(3/2) $\rightarrow $ 7p(3/2)     1.1715E+00   0.16697E+02 0.525E+06
6p(3/2) $\rightarrow $ 8p(3/2)     1.9216E+00   0.10800E+01 0.403E+06
6p(3/2) $\rightarrow $ 9p(3/2)     2.4307E+00   0.23483E+00 0.284E+06
7p(3/2) $\rightarrow $ 8p(3/2)     7.5008E-01   0.55452E+02 0.188E+06
7p(3/2) $\rightarrow $ 9p(3/2)     1.2591E+00   0.33354E+01 0.151E+06
8p(3/2) $\rightarrow $ 9p(3/2)     5.0907E-01   0.15631E+03 0.762E+05
3p(1/2) $\rightarrow $ 4f(5/2)   9.6830E+00 9.6902E+00   0.35270E+00 0.286E+09
3p(1/2) $\rightarrow $ 5f(5/2)   1.2944E+01 1.2951E+01   0.14074E-01 0.487E+08
3p(1/2) $\rightarrow $ 6f(5/2)   1.4717E+01 1.4724E+01   0.18082E-02 0.119E+08



 
Table 2: continued.
Transition   Transition Energy (a.u.)   Transition Properties
$n^{\prime}{l^{\prime}}\rightarrow nl$   Experimental Present CCM   Line strength (a.u.) Probability (s-1)

4p(1/2) $\rightarrow $ 4f(5/2)

   1.0167E+00 1.0209E+00   0.19618E+01 0.207E+05
4p(1/2) $\rightarrow $ 5f(5/2)   4.2780E+00 4.2818E+00   0.23869E+01 0.327E+08
4p(1/2) $\rightarrow $ 6f(5/2)   6.0505E+00 6.0549E+00   0.18056E+00 0.140E+08
5p(1/2) $\rightarrow $ 5f(5/2)   4.9806E-01 4.9961E-01   0.18718E+02 0.554E+04
5p(1/2) $\rightarrow $ 6f(5/2)   2.2706E+00 2.2727E+00   0.10192E+02 0.587E+07
6p(1/2) $\rightarrow $ 6f(5/2)   2.7844E-01 2.8186E-01   0.98586E+02 0.167E+04
3p(3/2) $\rightarrow $ 4f(5/2)   9.5671E+00 9.5715E+00   0.10371E+00 0.792E+08
3p(3/2) $\rightarrow $ 5f(5/2)   1.2828E-01 1.2832E-01   0.38784E-02 0.128E+08
3p(3/2) $\rightarrow $ 6f(5/2)   1.4601E-01 1.4605E-01   0.46881E-03 0.296E+07
4p(3/2) $\rightarrow $ 4f(5/2)   9.7078E-01 9.7445E-01   0.56141E+00 0.469E+04
4p(3/2) $\rightarrow $ 5f(5/2)   4.2320E+00 4.2353E+00   0.70686E+00 0.916E+07
4p(3/2) $\rightarrow $ 6f(5/2)   6.0046E+00 6.0084E+00   0.51220E-01 0.381E+07
5p(3/2) $\rightarrow $ 5f(5/2)   4.7678E-01 4.7668E-01   0.53612E+01 0.125E+04
5p(3/2) $\rightarrow $ 6f(5/2)   2.2493E+00 2.2497E+00   0.30335E+01 0.166E+07
6p(3/2) $\rightarrow $ 6f(5/2)   2.6532E-01 2.6889E-01   0.28256E+02 0.378E+03
3p(3/2) $\rightarrow $ 4f(7/2)   9.5701E+00 9.5745E+00   0.62289E+00 0.357E+09
3p(3/2) $\rightarrow $ 5f(7/2)   1.2830E+01 1.2834E+01   0.23463E-01 0.582E+08
3p(3/2) $\rightarrow $ 6f(7/2)   1.4601E+01 1.4606E+01   0.28585E-02 0.135E+08
4p(3/2) $\rightarrow $ 4f(7/2)   9.7379E-01 9.7737E-01   0.33736E+01 0.214E+05
4p(3/2) $\rightarrow $ 5f(7/2)   4.2336E+00 4.2368E+00   0.42370E+01 0.412E+08
4p(3/2) $\rightarrow $ 6f(7/2)   6.0048E+00 6.0092E+00   0.30807E+00 0.172E+08
5p(3/2) $\rightarrow $ 5f(7/2)   4.7833E-01 4.7819E-01   0.32199E+02 0.574E+04
5p(3/2) $\rightarrow $ 6f(7/2)   2.2495E+00 2.2506E+00   0.18168E+02 0.748E+07
6p(3/2) $\rightarrow $ 6f(7/2)   2.6545E-01 2.6977E-01   0.16966E+03 0.173E+04
4f(5/2) $\rightarrow $ 5f(5/2)   3.2613E+00 3.2608E+00   0.90112E+00 0.316E+07
4f(5/2) $\rightarrow $ 6f(5/2)   5.0338E+00 5.0339E+00   0.50512E-01 0.155E+07
5f(5/2) $\rightarrow $ 6f(5/2)   1.7726E+00 1.7731E+00   0.65707E+01 0.109E+07
4f(7/2) $\rightarrow $ 5f(5/2)   3.2583E+00 3.2579E+00   0.15126E+00 0.528E+06
4f(7/2) $\rightarrow $ 6f(5/2)   5.0308E+00 5.0310E+00   0.84951E-02 0.260E+06
5f(7/2) $\rightarrow $ 6f(5/2)   1.7710E+00 1.7716E+00   0.11048E+01 0.183E+06
4f(5/2) $\rightarrow $ 4f(7/2)   3.0072E-03 2.9252E-03   0.34655E+00 0.530E-09
4f(5/2) $\rightarrow $ 5f(7/2)   3.2628E+00 3.2624E+00   0.15061E+00 0.397E+06
4f(5/2) $\rightarrow $ 6f(7/2)   5.0340E+00 5.0348E+00   0.85080E-02 0.196E+06
5f(5/2) $\rightarrow $ 5f(7/2)   1.5492E-03 1.5082E-03   0.33983E+01 0.190E-09
5f(5/2) $\rightarrow $ 6f(7/2)   1.7727E+00 1.7739E+00   0.10993E+01 0.138E+06
6f(5/2) $\rightarrow $ 6f(7/2)   1.3669E-04 8.7938E-04   0.18357E+02 0.686E-10
4f(7/2) $\rightarrow $ 5f(7/2)   3.2598E+00 3.2594E+00   0.12527E+01 0.329E+07
4f(7/2) $\rightarrow $ 6f(7/2)   5.0310E+00 5.0319E+00   0.70220E-01 0.161E+07
5f(7/2) $\rightarrow $ 6f(7/2)   1.7711E+00 1.7724E+00   0.91314E+01 0.114E+07
3d(3/2) $\rightarrow $ 5g(7/2)     1.1023E+01   0.21782E+00 0.253E+09
3d(3/2) $\rightarrow $ 6g(7/2)     1.2790E+01   0.78987E-01 0.193E+09
4d(3/2) $\rightarrow $ 5g(7/2)     3.5793E+00   0.72792E+01 0.305E+08
4d(3/2) $\rightarrow $ 6g(7/2)     5.3461E+00   0.82242E-03 0.256E+05
5d(3/2) $\rightarrow $ 5g(7/2)     1.6870E-01   0.14632E+02 0.143E+02
5d(3/2) $\rightarrow $ 6g(7/2)     1.9355E+00   0.38433E+02 0.744E+07
6d(3/2) $\rightarrow $ 6g(7/2)     9.7670E-02   0.11236E+03 0.712E+01
3d(5/2) $\rightarrow $ 5g(7/2)     1.1004E+01   0.24376E-01 0.280E+08
3d(5/2) $\rightarrow $ 6g(7/2)     1.2771E+01   0.88212E-02 0.214E+08
4d(5/2) $\rightarrow $ 5g(7/2)     3.5709E+00   0.81159E+00 0.336E+07
4d(5/2) $\rightarrow $ 6g(7/2)     5.3377E+00   0.11958E-03 0.369E+04



 
Table 2: continued.
Transition   Transition Energy (a.u.)   Transition Properties
$n^{\prime}{l^{\prime}}\rightarrow nl$   Experimental Present CCM   Line strength (a.u.) Probability (s-1)

5d(5/2) $\rightarrow $ 5g(7/2)

     1.6432E-01   0.16238E+01 0.139E+01
5d(5/2) $\rightarrow $ 6g(7/2)     1.9311E+00   0.42911E+01 0.821E+06
6d(5/2) $\rightarrow $ 6g(7/2)     9.5119E-02   0.12473E+02 0.692E+00
5g(7/2) $\rightarrow $ 6d(3/2)     1.6691E+00   0.85506E+00 0.158E+06
5g(7/2) $\rightarrow $ 7d(3/2)     2.7708E+00   0.45817E-01 0.107E+06
5g(7/2) $\rightarrow $ 8d(3/2)     3.4826E+00   0.96807E-02 0.707E+05
5g(7/2) $\rightarrow $ 9d(3/2)     3.9690E+00   0.34732E-02 0.488E+05
6g(7/2) $\rightarrow $ 7d(3/2)     1.0040E+00   0.79048E+01 0.115E+06
6g(7/2) $\rightarrow $ 8d(3/2)     1.7159E+00   0.40691E+00 0.863E+05
6g(7/2) $\rightarrow $ 9d(3/2)     2.2023E+00   0.83852E-01 0.619E+05
5g(9/2) $\rightarrow $ 6d(5/2)     1.6708E+00   0.11773E+01 0.146E+06
5g(9/2) $\rightarrow $ 7d(5/2)     2.7715E+00   0.63325E-01 0.984E+05
5g(9/2) $\rightarrow $ 8d(5/2)     3.4817E+00   0.13392E-01 0.652E+05
5g(9/2) $\rightarrow $ 9d(5/2)     3.9689E+00   0.48062E-02 0.450E+05
6g(9/2) $\rightarrow $ 7d(5/2)     1.0051E+00   0.10887E+02 0.106E+06
6g(9/2) $\rightarrow $ 8d(5/2)     1.7164E+00   0.56273E+00 0.797E+05
6g(9/2) $\rightarrow $ 9d(5/2)     2.2025E+00   0.11608E+00 0.572E+05
3d(3/2) $\rightarrow $ 4d(3/2)   7.4427E+00 7.4438E+00   0.67779E-01 0.221E+08
3d(3/2) $\rightarrow $ 5d(3/2)   1.0853E+01 1.0854E+01   0.48162E-02 0.103E+08
3d(3/2) $\rightarrow $ 6d(3/2)   1.2691E+01 1.2692E+01   0.12002E-02 0.564E+07
3d(3/2) $\rightarrow $ 7d(3/2)   1.3794E+01 1.3794E+01   0.47922E-03 0.341E+07
3d(3/2) $\rightarrow $ 8d(3/2)     1.4506E+01   0.24234E-03 0.222E+07
3d(3/2) $\rightarrow $ 9d(3/2)     1.4992E+01   0.14227E-03 0.154E+07
4d(3/2) $\rightarrow $ 5d(3/2)   3.4104E+00 3.4106E+00   0.74729E+00 0.492E+07
4d(3/2) $\rightarrow $ 6d(3/2)   5.2487E+00 5.2484E+00   0.51017E-01 0.290E+07
4d(3/2) $\rightarrow $ 7d(3/2)   6.3511E+00 6.3501E+00   0.12199E-01 0.180E+07
4d(3/2) $\rightarrow $ 8d(3/2)     7.0620E+00   0.46998E-02 0.118E+07
4d(3/2) $\rightarrow $ 9d(3/2)     7.5484E+00   0.22476E-02 0.785E+06
5d(3/2) $\rightarrow $ 6d(3/2)   1.8383E+00 1.8378E+00   0.43787E+01 0.131E+07
5d(3/2) $\rightarrow $ 7d(3/2)   2.9406E+00 2.9395E+00   0.28342E+00 0.887E+06
5d(3/2) $\rightarrow $ 8d(3/2)     3.6513E+00   0.64743E-01 0.599E+06
5d(3/2) $\rightarrow $ 9d(3/2)     4.1377E+00   0.23410E-01 0.405E+06
6d(3/2) $\rightarrow $ 7d(3/2)   1.1024E+00 1.1016E+00   0.18191E+02 0.421E+06
6d(3/2) $\rightarrow $ 8d(3/2)     1.8135E+00   0.11197E+01 0.313E+06
6d(3/2) $\rightarrow $ 9d(3/2)     2.2999E+00   0.24091E+00 0.221E+06
7d(3/2) $\rightarrow $ 8d(3/2)     7.1187E-01   0.60294E+02 0.157E+06
7d(3/2) $\rightarrow $ 9d(3/2)     1.1983E+00   0.35177E+01 0.124E+06
8d(3/2) $\rightarrow $ 9d(3/2)     4.8640E-01   0.16950E+03 0.658E+05
3d(3/2) $\rightarrow $ 3d(5/2)   1.6950E-02 1.8626E-02   0.50367E-01 0.107E-05
3d(3/2) $\rightarrow $ 4d(5/2)   7.4499E+00 7.4522E+00   0.29131E-01 0.636E+07
3d(3/2) $\rightarrow $ 5d(5/2)   1.0857E+01 1.0859E+01   0.21009E-02 0.301E+07
3d(3/2) $\rightarrow $ 6d(5/2)   1.2693E+01 1.2695E+01   0.52827E-03 0.166E+07
3d(3/2) $\rightarrow $ 7d(5/2)   1.3796E+01 1.3795E+01   0.21217E-03 0.101E+07
3d(3/2) $\rightarrow $ 8d(5/2)   1.4506E+01 1.4507E+01   0.10775E-03 0.658E+06
3d(3/2) $\rightarrow $ 9d(5/2)     1.4993E+01   0.63455E-04 0.457E+06
4d(3/2) $\rightarrow $ 4d(5/2)   7.2446E-03 8.4065E-03   0.88298E+00 0.352E-06
4d(3/2) $\rightarrow $ 5d(5/2)   3.4143E+00 3.4150E+00   0.32089E+00 0.142E+07
4d(3/2) $\rightarrow $ 6d(5/2)   5.2509E+00 5.2510E+00   0.22231E-01 0.844E+06
4d(3/2) $\rightarrow $ 7d(5/2)   6.3532E+00 6.3517E+00   0.53577E-02 0.526E+06



 
Table 2: continued.
Transition   Transition Energy (a.u.)   Transition Properties
$n^{\prime}{l^{\prime}}\rightarrow nl$   Experimental Present CCM   Line strength (a.u.) Probability (s-1)

4d(3/2) $\rightarrow $ 8d(5/2)

   7.0636E+00 7.0631E+00   0.20748E-02 0.347E+06
4d(3/2) $\rightarrow $ 9d(5/2)     7.5491E+00   0.99622E-03 0.232E+06
5d(3/2) $\rightarrow $ 5d(5/2)   3.8273E-03 4.3832E-03   0.65911E+01 0.101E-06
5d(3/2) $\rightarrow $ 6d(5/2)   1.8405E+00 1.8404E+00   0.18804E+01 0.377E+06
5d(3/2) $\rightarrow $ 7d(5/2)   2.9428E+00 2.9411E+00   0.12367E+00 0.259E+06
5d(3/2) $\rightarrow $ 8d(5/2)   3.6532E+00 3.6524E+00   0.28516E-01 0.176E+06
5d(3/2) $\rightarrow $ 9d(5/2)     4.1385E+00   0.10382E-01 0.120E+06
6d(3/2) $\rightarrow $ 6d(5/2)   2.1871E-03 2.5516E-03   0.31871E+02 0.329E-07
6d(3/2) $\rightarrow $ 7d(5/2)   1.1045E+00 1.1033E+00   0.78134E+01 0.121E+06
6d(3/2) $\rightarrow $ 8d(5/2)   1.8149E+00 1.8146E+00   0.48929E+00 0.915E+05
6d(3/2) $\rightarrow $ 9d(5/2)     2.3007E+01   0.10643E+00 0.652E+05
3d(5/2) $\rightarrow $ 4d(3/2)   7.4257E+00 7.4251E+00   0.29529E-01 0.950E+07
3d(5/2) $\rightarrow $ 5d(3/2)   1.0836E+01 1.0840E+01   0.20935E-02 0.446E+07
3d(5/2) $\rightarrow $ 6d(3/2)   1.2674E+01 1.2674E+01   0.52237E-03 0.244E+07
3d(5/2) $\rightarrow $ 7d(3/2)   1.3777E+01 1.3775E+01   0.20882E-03 0.148E+07
3d(5/2) $\rightarrow $ 8d(3/2)     1.4487E+01   0.10572E-03 0.962E+06
3d(5/2) $\rightarrow $ 9d(3/2)     1.4973E+01   0.61962E-04 0.665E+06
4d(5/2) $\rightarrow $ 5d(3/2)   3.4032E+00 3.4022E+00   0.32611E+00 0.212E+07
4d(5/2) $\rightarrow $ 6d(3/2)   5.2415E+00 5.2400E+00   0.22251E-01 0.125E+07
4d(5/2) $\rightarrow $ 7d(3/2)   6.3438E+00 6.3417E+00   0.53311E-02 0.780E+06
4d(5/2) $\rightarrow $ 8d(3/2)     7.0536E+00   0.20578E-02 0.512E+06
4d(5/2) $\rightarrow $ 9d(3/2)     7.5400E+00   0.98557E-03 0.342E+06
5d(5/2) $\rightarrow $ 6d(3/2)   1.8344E+00 1.8334E+00   0.19134E+01 0.565E+06
5d(5/2) $\rightarrow $ 7d(3/2)   2.9368E+00 2.9351E+00   0.12402E+00 0.385E+06
5d(5/2) $\rightarrow $ 8d(3/2)     3.6470E+00   0.28448E-01 0.262E+06
5d(5/2) $\rightarrow $ 9d(3/2)     4.1334E+00   0.10329E-01 0.178E+06
6d(5/2) $\rightarrow $ 7d(3/2)   1.1002E+00 1.0991E+00   0.79539E+01 0.182E+06
6d(5/2) $\rightarrow $ 8d(3/2)     1.8110E+00   0.49089E+00 0.136E+06
6d(5/2) $\rightarrow $ 9d(3/2)     2.2974E+00   0.10623E+00 0.969E+05
3d(5/2) $\rightarrow $ 4d(5/2)   7.4329E+00 7.4335E+00   0.11666E+00 0.252E+08
3d(5/2) $\rightarrow $ 5d(5/2)   1.0840E+01 1.0840E+00   0.82850E-02 0.118E+08
3d(5/2) $\rightarrow $ 6d(5/2)   1.2677E+01 1.2676E+01   0.20651E-02 0.642E+07
3d(5/2) $\rightarrow $ 7d(5/2)   1.3779E+01 1.3777E+01   0.82449E-03 0.389E+07
3d(5/2) $\rightarrow $ 8d(5/2)   1.4489E+01 1.4488E+01   0.41689E-03 0.253E+07
3d(5/2) $\rightarrow $ 9d(5/2)     1.4974E+01   0.24424E-03 0.175E+07
4d(5/2) $\rightarrow $ 5d(5/2)   3.4070E+00 3.4066E+00   0.12855E+01 0.561E+07
4d(5/2) $\rightarrow $ 6d(5/2)   5.2437E+00 5.2426E+00   0.87767E-01 0.330E+07
4d(5/2) $\rightarrow $ 7d(5/2)   6.3460E+00 6.3433E+00   0.20987E-01 0.205E+07
4d(5/2) $\rightarrow $ 8d(5/2)   7.0564E+00 7.0546E+00   0.80856E-02 0.134E+07
4d(5/2) $\rightarrow $ 9d(5/2)     7.5407E+00   0.38650E-02 0.896E+06
5d(5/2) $\rightarrow $ 6d(5/2)   1.8366E+00 1.8360E+00   0.75277E+01 0.149E+07
5d(5/2) $\rightarrow $ 7d(5/2)   2.9389E+00 2.9367E+00   0.48728E+00 0.101E+07
5d(5/2) $\rightarrow $ 8d(5/2)   3.6493E+00 3.6480E+00   0.11132E+00 0.684E+06
5d(5/2) $\rightarrow $ 9d(5/2)     4.1341E+00   0.40255E-01 0.462E+06
6d(5/2) $\rightarrow $ 7d(5/2)   1.1023E+00 1.1007E+00   0.31259E+02 0.480E+06
6d(5/2) $\rightarrow $ 8d(5/2)   1.8127E+00 1.8121E+00   0.19243E+01 0.357E+06
6d(5/2) $\rightarrow $ 9d(5/2)     2.2981E+00   0.41408E+00 0.252E+06
7d(5/2) $\rightarrow $ 8d(5/2)   7.1038E-01 7.1135E-01   0.10358E+03 0.179E+06
7d(5/2) $\rightarrow $ 9d(5/2)     1.1974E+00   0.60438E+01 0.141E+06
8d(5/2) $\rightarrow $ 9d(5/2)     4.8608E-01   0.29112E+03 0.751E+05


4 Conclusions

The continuing developments in astrophysical and astronomical observations demand accurate theoretical transition data to determine the stellar chemical composition. Our theoretical values obtained from the highly correlated many-body coupled-cluster method using fully relativistic Dirac-Fock orbitals generated by an improved methodology of forming basis sets, are definitely very accurate for the highly stripped Na-like iron group ion CoXVII and can partially meet the present requirements.

Acknowledgements
The author likes to thank Dr. B. P. Das for introducing many-body CCM theory and his group members for their co-operation. The author is thankful to the Indian Institute of Astrophysics, Bangalore, India for providing a research associateship. She is grateful to Dr. Jet Katgert and Dr. (Mrs.) Kiran Jain for their valuable help to improve the final manuscript.

References

 

Copyright ESO 2002