A&A 391, L11-L15 (2002)
DOI: 10.1051/0004-6361:20021003

A high-resolution study of the evolution of the Lyman $\alpha $ forest in the redshift interval 0.9 < z < 1.7[*]

E. Janknecht - R. Baade - D. Reimers

Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany

Received 15 April 2002 / Accepted 6 July 2002

Abstract
Spectroscopy with HST/STIS Echelle and VLT/UVES of the bright QSO HE 0515-4414 ( $z_{\rm em} =1.73, B = 15.0$) offers for the first time the opportunity to study the Lyman $\alpha $ forest in the redshift range 0.9 < z < 1.7 at a resolution $\leq$10 kms-1. The number density evolution of the Lyman $\alpha $ lines is well described by the power law approach d $n/{\rm d}z \propto (1+z)^\gamma$. We derive $\gamma = 2.23 \pm 1.21$ for the strong lines ( $13.64 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 16.00$), in agreement with the Lyman $\alpha $ forest evolution for z > 1.7. The expected slow-down in their evolution does not appear earlier than $z \sim 1$. For the weak lines ( $13.10 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 14.00$) we find that the HE 0515-4414 data for z > 1 follow the trend with $\gamma = 1.40$known from z > 1.7 observations, i.e. we confirm the difference in evolution between weak and strong lines. We use the two-point velocity correlation function (TPCF) to search for clustering of the Lyman $\alpha $ lines, yet we detect no excess in the TPCF on scales up to 10000 kms-1.

Key words: cosmology: observations - intergalactic medium - quasars: Ly $\alpha $ forest - quasars: individual: HE0515-4414


1 Introduction

The evolution of the Lyman $\alpha $ absorption lines per unit redshift d $n/{\rm d}z$ has been a subject of observational studies since many years. At high redshift (z>1.6) the evolution is steep with dn/d $z \propto (1+z)^{\gamma}$and $\gamma = 2$-3 for strong Lyman $\alpha $ lines (i.e. log $N_{\rm H{\sc i}} > 14$; Rauch 1998). Observations of the Lyman $\alpha $ forest at low redshift with HST/FOS, at first in 3C273 (Bahcall et al. 1991), showed that the number of Lyman $\alpha $ lines was far in excess of the expected number according to an extrapolation from high z. As a final result from the HST QSO absorption line key project Weymann et al. (1998) found $\gamma = 0.1$-0.3 for z < 1.5. They also claimed a break in the evolutionary behaviour from a steep evolutionary law for z > 1.6 to a flat one for z < 1.5. The apparently rather abrupt break in the evolutionary law just at the transition from high-resolution optical data to low-resolution UV data immediately raised the suspicion that this behaviour might not be real. Owing to the insufficient FOS resolution (230- $270 \ {\rm km\,s}^{-1}$) the number counts might be underestimated due to line blending (Weymann et al. 1998). It is obvious, that this open question can be addressed only by UV observations of very bright QSOs at Echelle resolution. A further unsettled question which requires high-resolution UV spectra is the different evolutionary behaviour of strong compared to weak Lyman $\alpha $ lines. It has been found from high-resolution optical spectra for z > 1.6 that apparently weak lines evolve much slower than strong lines (Kim et al. 1997). Is that also true for z < 1.5?

In this paper we use the first UV spectra of the bright intermediate redshift QSO HE 0515-4414 (z = 1.73, B = 15.0, Reimers et al. 1998) at STIS/Echelle resolution (10 kms-1) for addressing the above discussed open questions.

2 Observations

HE0515-4414 was observed with STIS between January 31 and February 2, 2000 with the medium-resolution NUV echelle mode (E230M) and a $0.2 \times 0.2$ aperture. The overall exposure time was 31500 s resulting in a typical signal-to-noise ratio of 10 depending on the order and on the position within the orders. The resolution of the spectra is FWHM$\, \simeq$ 10 kms-1. The data reduction was performed by the HST pipeline completed by an additional inter-order background correction and by coadding the separate subexposures.

The optical spectra were obtained between October 7, 2000 and January 3, 2001 using the UV-Visual Echelle Spectrograph (UVES) at the VLT/Kueyen telescope. The overall exposure time was 31500 s. The slit width was 0.8 arcsec resulting in a spectral resolution of FWHM$\, \simeq$ 6 kms-1. After reduction by the UVES pipeline and conversion to vacuum baryocentric wavelengths, the individual spectra were coadded and exhibit a S/N $\simeq 10$-50 in the investigated spectral region.

3 Data analysis

The combined HST and VLT data provide the spectral range of the Lyman $\alpha $ forest of HE0515-4414 from z=0.87 up to z=1.73, the quasar's Lyman $\alpha $ emission redshift. To avoid the proximity effect we exclude a region of about 5000 km s-1from the quasar leading to an investigated spectral range $\lambda = 2278{-}3260$ Å or z = 0.87-1.68. We normalize the spectrum fitting polynomials to line-free regions and dividing the flux by this background continuum.

The spectrum of HE0515-4414 is strewn with metal lines and lines of molecular hydrogen (H2) from its damped Lyman $\alpha $ system which has been studied in detail by de la Varga et al. (2000). The main difficulty in the line identification was the extraction of the Lyman $\alpha $ lines from this real H2 forest dominating the short-wavelength region of the HST spectrum and thus suggesting to ignore this region in our analysis of the weak Lyman $\alpha $ lines (see below). The molecular hydrogen of the DLA will be the topic of a forthcoming paper.

In a first approximation, we detected about 400 lines as Lyman $\alpha $ candidates in the whole spectrum. These lines were fitted with the FITLYMAN code in the MIDAS package (Fontana & Ballester 1995) using Voigt profiles convolved with the instrumental profile. FITLYMAN adjusts three independent parameters per line by $\chi ^2$ minimization. These parameters are the redshift of an absorption line z, its H I column density $N_{\rm H{\sc i}}$, and its Doppler parameter b, comprising the thermal and the turbulent broadening of the lines. The general fitting strategy, especially for blends, was to start with a single line and to add a further component to the ensemble if the $\chi ^2$ decreased with this second line. For each of the Lyman $\alpha $ candidates we calculated the significance level $S = \frac {W}{\sigma_{W}}$, where W denotes the observed equivalent width of the line and $\sigma_{W}$ the $1\, \sigma$ error of W implying both the fit error and the continuum error. With the selection criteria $S \ga 1$ and $b \ga 10$ kms-1, we reduced the original sample to 235 Lyman $\alpha $ lines. The full fit parameter list for all recognized hydrogen absorption lines is available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.12.85) via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?/A+A/391/L11.

4 Discussion

4.1 Simultaneous fits with Lyman $\beta $

An important fitting constraint is given for the stronger Lyman $\alpha $ lines for which we tried to detect the higher order lines of the Lyman series followed by a simultaneous fit, if possible. We compared the H I parameters inferred from Ly $\alpha $ profile fitting with the parameters determined with a simultaneous fit with the accompanying Ly $\beta $ counterparts. Figure 1 shows a rather small systematic effect in the column densities. We derive $\langle\, N_{\rm H{\sc i}}^{\rm sim} / N_{\rm H{\sc i}}^{\rm single} \rangle = 1.145$ for the mean proportion of the Ly $\alpha $/Ly $\beta $ fit column densities and the column densities based solely on Ly $\alpha $ fitting. The same holds for b ( $\langle\,b_{\rm sim} / b_{\rm single}\rangle = 1.03$). This is in contrast to the recently suggested strong dependence of the fit parameters on the fit strategy (single-component fit versus simultaneous Ly $\alpha $-Ly $\beta $ fit; e.g., Hurwitz et al. 1998; Shull et al. 2000). Our 15 per cent deviation of the inferred column densities is at variance with the above cited studies. Obviously, the improved data quality leads to more consistent fit results. The remaining discrepancy may be attributed to the unphysical assumption of Voigt profile fitting. Indeed, the interpretation of the line-broadening velocity as unresolved stochastic motions is probably an oversimplification (e.g., Levshakov & Kegel 1997).

  \begin{figure} \centering \includegraphics[width=8.8cm]{Ed153_fig1.eps}\end{figure} Figure 1: Column densities of individually treated Lyman $\alpha $ lines versus column densities of simultaneous Ly $\alpha $/Ly $\beta $ fits. We present the results for all detected pairs.
Open with DEXTER

4.2 Column density distribution function

The differential column density distribution function $f(N_{\rm H{\sc i}})$ is defined as the number of Lyman $\alpha $ absorption lines per unit column density and per unit absorption distance path (Tytler 1987):

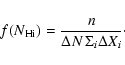\begin{displaymath}% f(N_{\rm H{\sc i}}) = \frac {n}{\Delta N \, \Sigma_{i}\Delta X_{i}}\cdot \end{displaymath} (1)

For q0 = 0, $X(z) = \frac {1}{2}\,\, [(1+z)^{2} - 1]$, so that $\Delta X = (1~+~z)\, \Delta z$. For the spectral range investigated we get $\Delta z = 0.808$, $z = \overline{z} = 1.278$, and hence $\Delta X = 1.841$.


  \begin{figure} \centering \includegraphics[width=8.8cm]{Ed153_fig2.eps} % \end{figure} Figure 2: The column density distribution function for the Lyman $\alpha $ lines. For the best fit only lines with log ${\sl N}_{\rm H{\sc i}} > 13.00$ were included due to the limited S/N of the spectra.
Open with DEXTER

Usually, $f(N_{\rm H{\sc i}})$ is fitted by a power law of the form $f(N_{\rm H{\sc i}}) = A\, N_{\rm H{\sc i}}^{-{\beta}}$. The distribution function for all 232 lines with log $N_{\rm H{\sc i}} \leq 15.70$ is plotted in Fig. 2. The squares show the observed log f values, while the solid line represents the best fit for all lines with log $N_{\rm H{\sc i}} \geq 13.00$. We have chosen this lower boundary because the distribution follows the power law down to this value. Assuming the general validity of the power law the sample is obviously not complete below log $N_{\rm H{\sc i}} \la 13.00$. The best fit yields log $A = 9.62\, \pm\, 0.58$ and $\beta = 1.61 \pm 0.04$. Considering exclusively the STIS lines in the same column density range, the result is very similar: log $A = 9.47 \pm 0.59$ and $\beta = 1.60 \pm 0.04$. In contrast, the slope of the distribution function for the UVES lines is much flatter (log $A = 4.60 \,\pm\, 0.72$, $\beta = 1.24 \pm 0.05$). The distribution of the UVES lines can be approximated very well with a single power law for an even wider column density range ( $12.50 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 15.70$) due to the better resolution of UVES. The flatter slope of the higher redshifted UVES lines indicates that stronger absorbers have evolved away faster than weaker ones. This will be discussed in more detail in Sect. 4.3.

Our result is in accordance with other analyses in comparable redshift ranges. For example, Dobrzycki et al. (2002) found $\beta \leq 1.6$-1.7, deriving the exponent from a curve of growth analysis. Hu et al. (1995) obtained $\beta = 1.46$ for $12.3 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 14.5$, while Kim et al. (2001) determined $\beta $ for various column density ranges to 1.70-1.74.

4.3 Number density evolution

The evolution of the number density per unit redshift of Lyman $\alpha $ clouds can be well approximated by the power law

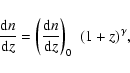\begin{displaymath}% \frac{\rm d \it n}{\rm d \it z} = \left(\frac{\rm d \it n}{\rm d \it z} \right)_{0} \,\, (1 + z)^ {\gamma}, \end{displaymath} (2)

where $\left(\frac{\rm d \it n}{\rm d \it z}\right)_{0}$ is the local comoving number density and the exponent $\gamma$ includes the cosmological evolution as well as the intrinsic evolution of the absorbers. For a non-evolving population in the standard Friedmann universe with the cosmological constant $\Lambda = 0$ and with q0 = 0the exponent becomes $\gamma = 1$. Because there exist a lot of hints that weaker and stronger Lyman $\alpha $ clouds evolve differently, it is convenient to distinguish between two subsamples. We use the column density range $13.10 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 14.00$ for the weak lines, while the interval $13.64 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 16.00$ defines the strong ones. These boundaries are frequently used in the literature (Weymann et al. 1998; Kim et al. 2001; Dobrzycki et al. 2002) allowing a direct comparison.


  \begin{figure} \centering \includegraphics[width=8.8cm]{Ed153_fig3.eps} % \end{figure} Figure 3: The number density evolution of the Lyman $\alpha $ forest for weak lines ( $13.10 < {\sl N}_{\rm H{\sc i}} < 14.00$). The data points are binned with $\Delta z = 0.1$. The best fit was obtained by $\chi ^2$ minimization. The dotted curves represent the 95% confidence band.
Open with DEXTER


  \begin{figure} \centering \includegraphics[width=8.8cm]{Ed153_fig4.eps} % \end{figure} Figure 4: Same as in Fig. 3, for $13.64 < {\sl N}_{\rm H{\sc i}} < 16.00$.
Open with DEXTER

In Figs. 3 and 4 we present the line numbers per unit redshift plotted over the redshift for the weak and for the strong lines, respectively. While for the strong lines we could exploit the whole wavelength region, we omit the spectral range $\lambda \la 2415$ Å for the weak lines to avoid misidentification due to the H2 lines, retaining an effective redshift range $1.0 \la z \la 1.7$. The diagrams show the data points and the best fit for which we obtain $\gamma = 0.01 \pm 0.64$ for $13.10 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 14.00$, suggesting that there is little evolution in the weak lines in the redshift interval 1.0 < z < 1.7. Considering a broader redshift range (Fig. 5, upper part) demonstrates that our STIS data follow the earlier optical observations (z > 1.6), i.e. the number density evolution is consistent with $\gamma = 1.40$ over the whole redshift range $1 \leq z \leq 3.7$. It should be noted that $\gamma = 1.40$ lies within the 2$\sigma $ confidence band of our data points (see Fig. 3). The transition to a flat ( $\gamma = 0$) evolution curve probably occurs around z = 1. In contrast, the strong Lyman $\alpha $ lines show a steeper gradient in the evolution diagram (Fig. 4). We detect an obvious correlation between the evolution and the line strength, i.e., the high column density absorbers evolve with $\gamma = 2.23 \pm 1.21$. This disagrees with the results of Penton et al. (2000) and Dobrzycki et al. (2002) who found no or only marginal evidence for a different evolution, respectively. We cannot recognize a slow-down in the evolution of the stronger absorbers. Therefore, we conclude that this break does not occur earlier than at $z \sim 1$rather than at $z \sim 1.5$-1.7 as previously claimed (Impey et al. 1996; Weymann et al. 1998; Dobrzycki et al. 2002). The large spread of our data points result from the poor statistics of a single line of sight. For example, omitting the two outliers in the plot for the strong lines lying beyond the 95% confidence limit our result ( $\gamma = 1.88 \pm 0.57$) becomes more robust. The lower panel of Fig. 5 demonstrates the difference between the Weymann et al. (1998) data points and our values. Indeed, the former ones do not indicate any change in the evolution until $z \sim 1.5$, while the results of HE 0515-4414 suggest a change of the slope at much lower z.


  \begin{figure} \centering \includegraphics[width=7cm]{Ed153_fig5.eps} % \end{figure} Figure 5: The number density evolution of the Lyman $\alpha $ forest, comparison of different studies. Shown are the results for the column density range ${\sl N}_{\rm H{\sc i}} = 10^{13.10 - 14.00}~{\rm cm}^{-2}$ (upper panel) and ${\sl N}_{\rm H{\sc i}} = 10^{13.64 - 16.00}~{\rm cm}^{-2}$ (lower panel). The filled circles are from our study, for the other symbols see legend. It should be noted that the data points from Penton et al. (2000) and Savaglio et al. (1999) in the lower panel apply to ${\sl N}_{\rm H{\sc i}} > 10^{14.00}~{\rm cm}^{-2}$.
Open with DEXTER

4.4 Two-point velocity correlation function

To study the clustering properties of the Lyman $\alpha $ forest, we introduce the two-point velocity correlation function $\xi \, (\Delta v)$where the number of observed line pairs in a given velocity separation bin $\Delta v$, $n_{\rm obs}$, is compared with the number of expected pairs $n_{\rm exp}$ determined in the same velocity difference bin in a randomly produced spectrum:

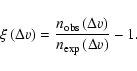\begin{displaymath}% \xi\, (\Delta v) = \frac{n_{\rm obs}\, (\Delta v)}{n_{\rm exp}\, (\Delta v)} - 1. \end{displaymath} (3)

Having two absorbers at z1 and z2 the velocity splitting in the rest frame at mean redshift reads

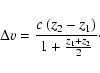\begin{displaymath}% \Delta v = \frac {c\,(z_{2} - z_{1})}{1 + \frac {z_{1} + z_{2}}{2}}\cdot \end{displaymath} (4)

We derived $n_{\rm exp}$ from Monte Carlo simulations distributing our line sample - in accordance with the determined number density evolution - randomly over the spectrum, counting the line pairs for varying velocity splittings and repeating this procedure 1000 times. Various studies have found at least marginal evidence for clustering on scales $\Delta v \leq 500\ {\rm km\,s}^{-1}$. For example, Cristiani et al. (1995) derived $\xi = 0.89 \pm 0.18$ and $\xi = 1.02 \pm 0.26$ (for two different QSOs) for ${\rm log}\, N_{\rm H{\sc i}} > 13.8$ and a redshift interval 0 < z < 3.66 at a velocity separation of $\Delta v = 100\ {\rm km\,s}^{-1}$, while Kim et al. (2001) found $\xi = 0.4 \pm 0.1$ for ${\rm log}\, N_{\rm H{\sc i}} > 12.7$and 1.5 < z < 2.4 at the same velocity splitting. Penton et al. (2000) and Kulkarni et al. (1996) also detected a weak clustering signal in their data. In addition, the occurence of clustering on different scales is also supported by a number of theoretical studies (e.g., Cirkovic & Lanzetta 2000; Pando et al. 1998). We have examined the clustering separately for the weak and strong lines (the latter is shown in Fig. 6). Up to a velocity separation of $\Delta v = 1000\ {\rm km\,s}^{-1}$ we detect no signal exceeding the 2$\sigma $ level and only a marginal one above the 1$\sigma $ level. For example, for the strong lines we derive $\xi\,\left(\overline{\Delta v}=50\, {\rm km\,s}^{-1}\right) = 1.14$with a 1$\sigma $ poisson error of 1.13 in accordance with Fig. 6. For ${\rm log}\, N_{\rm H{\sc i}} > 13.8$ we obtain $\xi\, (50\, {\rm km\,s}^{-1}) = 1.63$ (1$\sigma $ poisson error 1.60) and $\xi\, (150\, {\rm km\,s}^{-1}) = 1.23$ (1$\sigma $ poisson error 1.36), so we cannot confirm the Cristiani et al. (1995) result. For ${\rm log}\, N_{\rm H{\sc i}} > 12.7$, $\xi\, (50\, {\rm km\,s}^{-1}) = 0.10$ (1$\sigma $ poisson error 0.16) and $\xi\, (150\, {\rm km\,s}^{-1}) = -0.01$ (1$\sigma $ poisson error 0.15) not being consistent with the weak clustering seen by Kim et al. (2001) in a comparable redshift range. There is also no excess in $\xi$ on much larger velocity separations (up to 10000 km s-1) in our data. We do not find any dependence of $\xi$ on the redshift either. Thus we cannot confirm the result of weak clustering of the Lyman $\alpha $ lines as suggested in the above cited studies. However, the small number of lines in a single line of sight does not allow a final assessment.
  \begin{figure} \centering \includegraphics[width=7.7cm]{aaedf6.eps}\end{figure} Figure 6: Two-point correlation function $\xi \, (\Delta v)$ (solid line), in 100 kms-1 bins, for higher column density absorbers ( $13.64 \leq {\rm log}\, N_{\rm HI} \leq 16.00$). Dashed and dot-dashed lines represent the 1$\sigma $ and 2$\sigma $ Poisson errors, respectively.
Open with DEXTER

5 Conclusions

We have analyzed the evolution of the Lyman $\alpha $ forest in the redshift range 0.9 < z < 1.7 using combined high-resolution HST/STIS and VLT/UVES data. The main results are summarized as follows:

1.
The recently claimed dependence of the hydrogen fit parameters on the fit strategy (single Ly $\alpha $ fit or simultaneous Ly $\alpha $-Ly $\beta $ fit) cannot be confirmed by our results.

2.
The column density distribution of our Lyman $\alpha $ line sample can be approximated over several orders of magnitude ( $13.00 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 15.70$) by a power law. The (negative) slope is described by $\beta = 1.61\, \pm\, 0.04$ for $\overline{z} \sim 1.3$, consistent with recent results.
3.

The evolution of strong and weak lines is distinctly different. The high column density ( $13.64 \leq {\rm log}\, N_{\rm H{\sc i}} \leq 16.00$) absorbers evolve according to $(1+z)^{\gamma}$ with $\gamma = 2.23\, \pm\,1.21$ for 0.9 < z < 1.7, and the expected slow-down in the evolution does not appear down to $z \sim 1$. The evolution of the weaker lines over the same redshift range is consistent with $\gamma = 1.40$, thus we have a continuation of the trend seen at higher redshifts. Again, the transition to non-evolution probably occurs around z=1. More lines of sight are necessary to confirm our results.

4.

We detect no significant clustering of neither the weak nor the strong Lyman $\alpha $ lines on scales up to 10000 kms-1, so we are unable to confirm most of the previous studies reporting a weak clustering signal for $\Delta v \leq 150$ kms-1.

Acknowledgements
This research has been supported by the Verbundforschung of the BMBF/DLR under Grant No. 50 OR 9911 1. We thank the anonymous referee for his very helpful report.

References

 

Copyright ESO 2002