A&A 391, 749-756 (2002)
DOI: 10.1051/0004-6361:20020866
On electron acceleration at CIR related shock waves
G. Mann1
- H. T. Classen1
- E. Keppler 2
- E. C. Roelof3
1 - Astrophysikalisches Institut Potsdam,
An der Sternwarte 16, 14482 Potsdam, Germany
2 -
Max-Planck-Institut für Aeronomie,
Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
3 -
Applied Physics Laboratory, John Hopkins University,
Laurel, MD 20723, USA
Received 15 March 2002 / Accepted 15 May 2002
Abstract
The interaction of fast and slow speed
solar wind streams leads to the formation of
so-called corotating interaction regions (CIRs) in the heliosphere. These
CIRs are often associated with shock waves, at which
electrons are accelerated as observed by the Ulysses
spacecraft.
A correlation between the ratio of energetic electron fluxes at the
crossing of CIR related shocks to those in the far upstream region
of these shocks and the magnetic field compression of
the associated shocks has been revealed by analysing the data of
the HISCALE instrument aboard Ulysses.
This result can be explained by a model of electron acceleration
at shock waves, where the electrons gain energy due to multiple
reflections at large amplitude magnetic field fluctuations occurring
in the vicinity of the shock transition.
Key words: acceleration of particles - sun: solar wind - shock waves
The Sun is a source of a permanent stream of charged particles (e.g. electrons,
protons and heavy ions) penetrating into the interplanetary space. It is
the so-called solar wind forming the heliosphere due to its interaction
with the interstellar wind (Parker 1958). The solar wind was originally
discovered by in-situ measurements
of the Mariner 2 spacecraft in 1962 (Neugebauer 1966).
It is temporally and spatially structured (see Schwenn 1990 as a review).
There are high and slow speed solar wind streams.
The coronal holes with open magnetic field structures are the sources of
the high speed streams, whereas the slow solar wind is coming from regions
with closed magnetic field structures located around the equatorial plane
(Schwenn 1990). Due to the rotation of the Sun the fast and slow solar
wind streams interact with each other, leading to the formation
of a so-called corotating interaction region (CIR) (Pizzo 1978).
An interface is located within the CIR. It is a contact discontinuity
dividing the fast solar wind plasma
from that of the slow solar wind stream. In many cases
a pair of forward and reverse shocks
forms the boundaries of CIRs. The forward shocks are propagating into
the slow solar wind towards the equatorial plane whereas
the reverse shocks are travelling pole-ward into the fast solar wind stream
(Gosling & Pizzo 1999).
The formation of CIRs mainly takes place at distances beyond 1 AU. Since
the Ulysses spacecraft was exploring the three-dimensional heliosphere
between 1 and 5 AU during the declining period of solar activity
(Marsden et al. 1996), the Ulysses mission is highly appropriate to study all
phenomena related to CIRs.
The shock waves associated with CIRs are able to generate
energetic electrons, protons and heavy ions, as well-known from
the observations of the Pioneer and Voyager spacecraft (McDonald et al. 1976;
Barnes & Simpson 1976).
The basic features of energetic particles associated with CIRs have been
summarized by Mason & Sanderson (1999). As an example, Fig. 1
offers the
energetic particle and plasma data recorded by the Ulysses spacecraft
during its
passage through the CIR No. 5 occurring during the days 282-286 in 1992.
(The numbering of CIRs observed by Ulysses
was originally introduced by Bame et al. 1993.)
![\begin{figure}
\par\includegraphics[width=13cm,clip]{ms2482f1.ps}\par\end{figure}](/articles/aa/full/2002/32/aa2482/Timg10.gif) |
Figure 1:
HISCALE data of energetic protons (top panel) and electrons
(2nd panel from top) as well as
the behaviour of the proton number density N (4th panel), the proton temperature T (5th panel), the solar wind
velocity
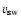 (6th panel) and the magnetic field in polar coordinates
(three panels at the bottom) during the passage of the CIR No. 5 by
the ULYSSES spacecraft.
(6th panel) and the magnetic field in polar coordinates
(three panels at the bottom) during the passage of the CIR No. 5 by
the ULYSSES spacecraft. |
The plasma and magnetic field data
were provided by the solar wind plasma instrument (SWOOPS)
(Bame et al. 1992) and the VHM/FGM magnetometer (Balogh et al. 1992)
aboard Ulysses, respectively. The location of
CIR is evidently identified in the data of the solar wind speed and magnitude
of the magnetic field as indicated by the dashed vertical lines
in Fig. 1. The forward and reverse shocks
have Alfvén-Mach numbers
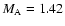 and
and
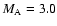 as well as
jumps of the magnetic field
B2/B1 = 1.40 and
B2/B1 = 2.30(Balogh et al. 1995; Classen et al. 1998), respectively.
Here, B1 and B2 denote the up- and downstream magnetic field
of the shock, respectively.
The two panels at the top of Fig. 1 present the
proton and electron fluxes in different channels covering
the range
0.61-19 MeV and 38-315 keV, respectively,
as measured by the HISCALE (Lanzerotti et al. 1992) and the COSPIN
instrument (Simpson et al. 1992)
aboard Ulysses. Whereas the flux of energetic protons increases at few orders
of magnitudes at both the forward and reverse shock, the flux of energetic
electrons is essentially more enhanced at the reverse shock (see Fig. 1).
The evolution of energetic electrons and ions has been discussed
by Simnett & Roelof (1995) and Roelof et al. (1996) for the
period of the first southbound journey of the Ulysses spacecraft.
At low heliospheric latitudes
both energetic electrons and ions were simultaneously seen with the
occurrence of the forward (FS) and reverse (RS) shocks (Keppler et al. 1996).
The last shock pair (CIR No. 15) was observed at a distance
of 4.58 AU and a latitude of
as well as
jumps of the magnetic field
B2/B1 = 1.40 and
B2/B1 = 2.30(Balogh et al. 1995; Classen et al. 1998), respectively.
Here, B1 and B2 denote the up- and downstream magnetic field
of the shock, respectively.
The two panels at the top of Fig. 1 present the
proton and electron fluxes in different channels covering
the range
0.61-19 MeV and 38-315 keV, respectively,
as measured by the HISCALE (Lanzerotti et al. 1992) and the COSPIN
instrument (Simpson et al. 1992)
aboard Ulysses. Whereas the flux of energetic protons increases at few orders
of magnitudes at both the forward and reverse shock, the flux of energetic
electrons is essentially more enhanced at the reverse shock (see Fig. 1).
The evolution of energetic electrons and ions has been discussed
by Simnett & Roelof (1995) and Roelof et al. (1996) for the
period of the first southbound journey of the Ulysses spacecraft.
At low heliospheric latitudes
both energetic electrons and ions were simultaneously seen with the
occurrence of the forward (FS) and reverse (RS) shocks (Keppler et al. 1996).
The last shock pair (CIR No. 15) was observed at a distance
of 4.58 AU and a latitude of
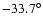 ,
while the reverse shocks were
directly seen by Ulysses for several more solar rotations (Gosling et al. 1993).
The relationship between particle acceleration at CIR-related shocks and their
magnetohydrodynamic (MHD) parameters was studied by Desai et al. (1998) and
Classen et al. (1998). Classen et al. (1998) analysed
a sample of 18 CIRs associated with 33 shocks. They found that shocks
accelerate predominantly electrons and protons if the Alfvén-Mach number
,
while the reverse shocks were
directly seen by Ulysses for several more solar rotations (Gosling et al. 1993).
The relationship between particle acceleration at CIR-related shocks and their
magnetohydrodynamic (MHD) parameters was studied by Desai et al. (1998) and
Classen et al. (1998). Classen et al. (1998) analysed
a sample of 18 CIRs associated with 33 shocks. They found that shocks
accelerate predominantly electrons and protons if the Alfvén-Mach number
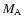 and the angle
and the angle
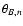 between the upstream magnetic field
and the shock normal simultaneously fulfilled the conditions
between the upstream magnetic field
and the shock normal simultaneously fulfilled the conditions
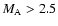 and
and
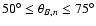 .
.
The aim of the present paper is to investigate the efficiency of electron
acceleration at CIR related shocks (see Mann 1999 for a
preliminary study). Note that the generation of energetic
electrons has also been observed at shocks in the solar corona
(Wild & McCready 1950; Cane et al. 1981; Cairns & Robinson 1987),
at travelling interplanetary shocks (Tsurutani & Lin 1985; Lopate 1989), and
at the Earth's bow shock (Anderson et al. 1969; Scarf et al. 1971).
The electron fluxes used in the present paper has been provided by
the HISCALE instrument (Lanzerotti et al. 1992) in the range 30-50 keV
aboard the Ulysses spacecraft. The electron fluxes
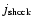 at the shock crossing are compared with those j0
measured during quiet solar wind periods before and after the
CIR (see Sect. 2). Furthermore, the ratios
at the shock crossing are compared with those j0
measured during quiet solar wind periods before and after the
CIR (see Sect. 2). Furthermore, the ratios
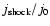 are related to the magnetic field compression
B2/B1
of the associated shock.
Mann & Classen (1995)
proposed a mechanism of generation of energetic electrons
at collisionless shocks. It is well-known that super-critical
shocks are accompanied with large amplitude magnetic field fluctuations
in the vicinity of the shock transition (Kennel et al. 1985). Electrons can be
reflected and subsequently accelerated at these fluctuations. Due to
multiple encounters of electrons with these fluctuations they receive
a considerable acceleration (Mann & Classen 1995). This
special acceleration mechanism will be introduced in a quantitative manner
in Sect. 3, and subsequently adopted to explain the relations
between the flux ratios
are related to the magnetic field compression
B2/B1
of the associated shock.
Mann & Classen (1995)
proposed a mechanism of generation of energetic electrons
at collisionless shocks. It is well-known that super-critical
shocks are accompanied with large amplitude magnetic field fluctuations
in the vicinity of the shock transition (Kennel et al. 1985). Electrons can be
reflected and subsequently accelerated at these fluctuations. Due to
multiple encounters of electrons with these fluctuations they receive
a considerable acceleration (Mann & Classen 1995). This
special acceleration mechanism will be introduced in a quantitative manner
in Sect. 3, and subsequently adopted to explain the relations
between the flux ratios
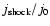 and jumps of the magnetic
field
B2/B1 of the associated shocks in Sect. 4.
and jumps of the magnetic
field
B2/B1 of the associated shocks in Sect. 4.
The HISCALE instrument (Lanzerotti et al. 1992) aboard Ulysses
is able to measure the fluxes of
energetic electrons in four different channels, i.e. DE1: 30-50 keV,
DE2: 50-90 keV, DE3: 90-165 keV, and DE4:
165-300 keV.
The data recorded in the channel DE1 are employed to compare
the electron fluxes
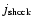 at the shock crossing with those j0,
which are determined during quiet conditions of the solar wind stream
related with the corresponding
shock. It should be recalled, that the forward and reverse shocks are
travelling into the slow and fast speed solar wind (Pizzo 1978), respectively.
at the shock crossing with those j0,
which are determined during quiet conditions of the solar wind stream
related with the corresponding
shock. It should be recalled, that the forward and reverse shocks are
travelling into the slow and fast speed solar wind (Pizzo 1978), respectively.
The data analysis can be demonstrated for example in Fig. 1.
The energetic electron fluxes j0 of
quiet solar wind conditions are chosen to be at day 281 and 293
for the forward and reverse shock in this particular case, respectively.
These days have been chosen because the particle, plasma and
magnetic field data show no strong and rapid changes, i.e. there were
really quiet solar wind conditions.
The results of the whole data analysis are summarized in Table 1.
CIRs Nos. 1-18 (Bame et al. 1993) have been employed for this study.
But only a sub-sample of
15 CIR related shocks could be used for investigating the efficiency of
electron acceleration, since the energetic electron fluxes
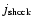 and j0 can reliably
determined only at these shocks presented in Table 1. The parameters of the
associated shocks were given by Balogh et al. (1995) and Classen et al. (1998).
N1, T1, N2, and T2 are the particle number densities
and temperatures in the up- and downstream region, respectively.
The upstream regions of the CIR related shocks (Classen et al. 1998)
have the mean values of the following plasma parameters:
and j0 can reliably
determined only at these shocks presented in Table 1. The parameters of the
associated shocks were given by Balogh et al. (1995) and Classen et al. (1998).
N1, T1, N2, and T2 are the particle number densities
and temperatures in the up- and downstream region, respectively.
The upstream regions of the CIR related shocks (Classen et al. 1998)
have the mean values of the following plasma parameters:
| upstream magnetic field |
B1 = 0.9 nT |
| upstream density |
N1 = 0.25 cm-3 |
| upstream temperature |
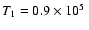 K K |
| upstream plasma beta |
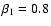 . . |
These values will be used as typical upstream parameters of CIR related
shocks in Sect. 4.
The angle
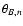 between the upstream magnetic field
and the shock normal varies between
between the upstream magnetic field
and the shock normal varies between
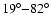 with a mean value
of
with a mean value
of
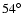 for these shocks (Classen et al. 1998),
i.e. CIR related shocks are mainly quasi-perpendicular,
(
for these shocks (Classen et al. 1998),
i.e. CIR related shocks are mainly quasi-perpendicular,
(
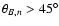 ).
The correlation between the ratios
).
The correlation between the ratios
 and the jump
of the magnetic field
B2/B1 is depicted for all 15 CIR related shocks
(Table 1) in Fig. 2.
and the jump
of the magnetic field
B2/B1 is depicted for all 15 CIR related shocks
(Table 1) in Fig. 2.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ms2482f2.eps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg57.gif) |
Figure 2:
Correlation between the ratios
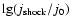 and
the jump of the magnetic field
B2/B1 for 15 CIR related shocks
(Table 1). The full line represents the theoretical result
obtained by means of Eq. (22).
The dashed-dotted line shows the line of linear regression.
and
the jump of the magnetic field
B2/B1 for 15 CIR related shocks
(Table 1). The full line represents the theoretical result
obtained by means of Eq. (22).
The dashed-dotted line shows the line of linear regression. |
The dashed dotted line represents the linear regression with a correlation
coefficient of 0.649 and a standard deviation of 0.594.
Therefore, the efficiency of electron acceleration expressed by
the ratios
 is increasing for shocks with a
stronger jump of the magnetic field
B2/B1 (Fig. 2).
This result can be explained by a model of
electron acceleration at collisionless shocks as described in Sect. 3.
is increasing for shocks with a
stronger jump of the magnetic field
B2/B1 (Fig. 2).
This result can be explained by a model of
electron acceleration at collisionless shocks as described in Sect. 3.
As already mentioned the CIR related shocks are usually quasi-perpendicular,
i.e.
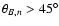 .
For a plasma-beta
.
For a plasma-beta
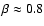 such shocks
are super-critical, if their Alfvén-Mach number is greater than 2.0
(Kennel et al. 1985).
That is mostly the case of the shocks considered in this paper (see Table 1).
Figure 3 shows the behaviour
of the magnitude of the magnetic field during the crossing of the CIR related
shock No. 7F as measured by the magnetometer (Balogh et al. 1992)
aboard the Ulysses spacecraft.
such shocks
are super-critical, if their Alfvén-Mach number is greater than 2.0
(Kennel et al. 1985).
That is mostly the case of the shocks considered in this paper (see Table 1).
Figure 3 shows the behaviour
of the magnitude of the magnetic field during the crossing of the CIR related
shock No. 7F as measured by the magnetometer (Balogh et al. 1992)
aboard the Ulysses spacecraft.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2482f3.ps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg59.gif) |
Figure 3:
Behaviour of the magnitude of the magnetic field during
the crossing of the CIR related shock No. 7F as measured by the
magnetometer aboard the ULYSSES spacecraft. |
As seen in Fig. 3 quasi-perpendicular, super-critical shocks
are accompanied with strong magnetic field fluctuations,
especially in the downstream region. Furthermore, they show
a so-called overshoot
at the shock transition, i.e., the magnetic field compression
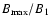 is locally stronger than the jump
B2/B1
of the magnetic field according to
the Rankine-Hugoniot relations (Kennel et al. 1985),
i.e.,
is locally stronger than the jump
B2/B1
of the magnetic field according to
the Rankine-Hugoniot relations (Kennel et al. 1985),
i.e.,
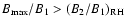 ,
where
,
where 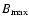 denotes the maximum magnitude of the magnetic field.
These large amplitude magnetic
field fluctuations can be considered as nonlinear
magnetohydrodynamic waves. Such waves have the property
that their velocity
denotes the maximum magnitude of the magnetic field.
These large amplitude magnetic
field fluctuations can be considered as nonlinear
magnetohydrodynamic waves. Such waves have the property
that their velocity
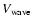 is a monotonically increasing function of the
magnetic field compression
is a monotonically increasing function of the
magnetic field compression
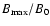 (Mann 1995)
where B0 denotes the magnitude of the undisturbed ambient magnetic field.
Thus, two neighbouring magnetic field fluctuations with different
magnetic field compressions have consequently a non-vanishing relative
velocity. They are establishing a system of converging magnetic mirrors,
which are able to accelerate particles, as originally proposed
by Fermi (1949).
(Mann 1995)
where B0 denotes the magnitude of the undisturbed ambient magnetic field.
Thus, two neighbouring magnetic field fluctuations with different
magnetic field compressions have consequently a non-vanishing relative
velocity. They are establishing a system of converging magnetic mirrors,
which are able to accelerate particles, as originally proposed
by Fermi (1949).
Now, the movement of an electron between two neighbouring mirrors
is considered in detail, following the way described
by Chen (1984) and Mann & Classen (1995).
The computations are lengthy, but straightforward. Thus, only the main line
of thought will be presented. The mirrors M1 and M2 (see Fig. 4)
are accompanied with magnetic field compressions BM1 and BM2
with
BM1 > BM2 and have the velocities V1and V2 with
V1 > V2, respectively.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{ms2482f4.eps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg65.gif) |
Figure 4:
Scheme of converging magnetic mirrors M1 and M2. |
Since energetic electrons with an energy of about 40 keV are
considered, this treatment can be done in a nonrelativistic manner, i.e.
the required relation
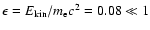 (
(
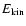 ,
kinetic energy;
,
kinetic energy; 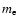 ,
electron mass; c, velocity of light)
is well fulfilled.
The two mirrors are initially separated by a distance Ln (see Fig. 4).
The electron with an initial velocity Vn parallel to the ambient
magnetic field and a pitch angle
,
electron mass; c, velocity of light)
is well fulfilled.
The two mirrors are initially separated by a distance Ln (see Fig. 4).
The electron with an initial velocity Vn parallel to the ambient
magnetic field and a pitch angle
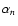 starts at the mirror M1
and moves towards the mirror M2, which is reached after a distance
starts at the mirror M1
and moves towards the mirror M2, which is reached after a distance
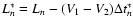 and a time
and a time
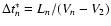 (see Fig. 4).
At the mirror M2 it is reflected and, subsequently,
it returns towards the mirror M1 with the velocity
(see Fig. 4).
At the mirror M2 it is reflected and, subsequently,
it returns towards the mirror M1 with the velocity
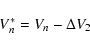 |
(1) |
parallel to the magnetic field. The velocity gain
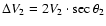 results from the shock drift
acceleration at the mirror M2 (Toptygin 1980; Holman & Pesses 1983;
Decker 1988). Here,
results from the shock drift
acceleration at the mirror M2 (Toptygin 1980; Holman & Pesses 1983;
Decker 1988). Here,
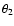 denotes
the angle between the undisturbed ambient magnetic field
denotes
the angle between the undisturbed ambient magnetic field
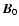 and the
propagation direction of the mirror M2. During the reflection process
at the mirror M2 the pitch angle is changed according to
and the
propagation direction of the mirror M2. During the reflection process
at the mirror M2 the pitch angle is changed according to
![\begin{displaymath}\alpha_{n}^{\ast} = \arctan \left [\frac{V_{n} \cdot \tan \alpha_{n}}{V_{n} - \Delta V_{2}} \right ] \cdot
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img76.gif) |
(2) |
After this reflection at the mirror M2 the electron moves back towards
the mirror M2, which is reached after a time period of
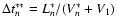 .
There, the electron is reflected again and gets a final velocity
.
There, the electron is reflected again and gets a final velocity
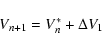 |
(3) |
parallel to the magnetic field and a pitch angle
![\begin{displaymath}\alpha_{n+1} = \arctan \left [\frac{V_{n}^{\ast} \cdot \tan \alpha_{n}^{\ast}}{V_{n}^{\ast} + \Delta V_{1}} \right]\cdot
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img79.gif) |
(4) |
Here,
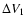 is given by
is given by
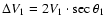 ,
where
,
where
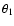 denotes
the angle between the undisturbed ambient field and the propagation direction
of the mirror M1. Thus, the nth revolution lasts
denotes
the angle between the undisturbed ambient field and the propagation direction
of the mirror M1. Thus, the nth revolution lasts
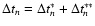 whereas
the distance between the two mirrors is diminished to
whereas
the distance between the two mirrors is diminished to
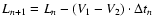 (see Fig. 4).
(see Fig. 4).
Concerning this process it is generally assumed that the electrons are
adiabatically reflected at the magnetic field compressions
acting as magnetic mirrors. This assumption is justified
if the gyroradius 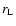 of the electron is essentially smaller than the
characteristic length scale of the magnetic field compressions.
This length scale is typically 10 ion inertial
lengths (Mann et al. 1994).
Since electrons in the energy range 30-50 keV have a typical gyroradius of
1.3 ion inertial lengths under plasma conditions near CIRs (see Sect. 2),
the required condition is well fulfilled in the case considered here.
of the electron is essentially smaller than the
characteristic length scale of the magnetic field compressions.
This length scale is typically 10 ion inertial
lengths (Mann et al. 1994).
Since electrons in the energy range 30-50 keV have a typical gyroradius of
1.3 ion inertial lengths under plasma conditions near CIRs (see Sect. 2),
the required condition is well fulfilled in the case considered here.
Since the mirrors in terms of two neighbouring large amplitude magnetic
field compressions cannot penetrate each other, the distance between
them can be reduced only up to a minimum one 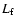 .
Consequently, the acceleration process is finished either if
.
Consequently, the acceleration process is finished either if
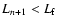 or if the electron leaves the region between the mirrors,
since the pitch angle
or if the electron leaves the region between the mirrors,
since the pitch angle
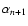 becomes
becomes
![$\alpha_{n+1} < \alpha_{\rm f} = \arctan [(B_{0}/B_{M2})^{1/2}]$](/articles/aa/full/2002/32/aa2482/img89.gif) .
The movement
of an electron between these two mirrors leads finally to a nonuniform
acceleration as illustrated in Fig. 5. In this special example
the particle has an initial velocity
.
The movement
of an electron between these two mirrors leads finally to a nonuniform
acceleration as illustrated in Fig. 5. In this special example
the particle has an initial velocity
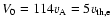 (
(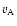 ,
Alfvén speed;
,
Alfvén speed;
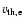 ,
thermal
electron velocity) parallel to
the ambient magnetic field and an initial pitch angle
,
thermal
electron velocity) parallel to
the ambient magnetic field and an initial pitch angle
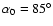 .
The distance between the two mirrors is diminished from
L0 = 50diup to
.
The distance between the two mirrors is diminished from
L0 = 50diup to
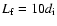 .
The mirrors M1 and M2 are moving with
the velocities
.
The mirrors M1 and M2 are moving with
the velocities
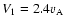 and
and
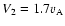 ,
respectively.
The magnetic field compression at the mirror M2 is assumed to be
BM2/B0 = 2.8 resulting in a final pitch angle
,
respectively.
The magnetic field compression at the mirror M2 is assumed to be
BM2/B0 = 2.8 resulting in a final pitch angle
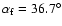 .
Adopting
.
Adopting
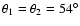 as typical values
for CIR related shocks,
as typical values
for CIR related shocks,
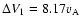 and
and
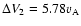 is found.
The result of the numerically evaluated Eqs. (1)-(4) is presented in
Fig. 5.
is found.
The result of the numerically evaluated Eqs. (1)-(4) is presented in
Fig. 5.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms2482f5.eps}\end{figure}](/articles/aa/full/2002/32/aa2482/Timg100.gif) |
Figure 5:
Velocity-time diagram
of a special example of the mirror acceleration. The chosen parameters
are introduced in Sect. 3. The velocity and the time are normalized
to the Alfvén speed 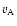 and the inverse proton cyclotron frequency
and the inverse proton cyclotron frequency
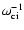 . . |
Here, the temporal
coordinate is normalized to the inverse of the proton cyclotron frequency
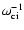 leading to a normalization of the velocities with respect
to the Alfvén speed
leading to a normalization of the velocities with respect
to the Alfvén speed 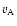 .
The particle is nonuniformly accelerated in a discrete manner up to
a final velocity
.
The particle is nonuniformly accelerated in a discrete manner up to
a final velocity
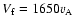 during a time of
during a time of
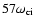 corresponding to a final energy of 33 keV, where
corresponding to a final energy of 33 keV, where
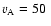 km s-1 and
km s-1 and
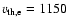 km s-1 have been used as typical values
of the Alfvén speed and thermal electron velocity in the quiet solar wind,
respectively. These values correspond to the mean plasma parameters
found in the upstream region of CIR related shocks (see Sect. 2).
km s-1 have been used as typical values
of the Alfvén speed and thermal electron velocity in the quiet solar wind,
respectively. These values correspond to the mean plasma parameters
found in the upstream region of CIR related shocks (see Sect. 2).
Since the electrons move much faster than the mirrors,
the acceleration process might be considered
as a continuous one (see Fig. 5), i.e. the relationship
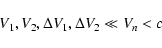 |
(5) |
is well fulfilled for the cases under consideration.
Then, the acceleration defined by
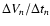 with
with
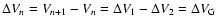 and
and
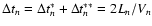 may be taken as a differential equation
may be taken as a differential equation
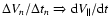
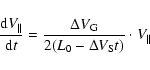 |
(6) |
with the initial condition
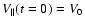 .
Here,
.
Here,
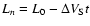 with
with
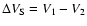 has been used in deriving Eq. (6).
Note, that the mirrors are initially separated at a distance L0.
The solution of Eq. (6) is found to be
has been used in deriving Eq. (6).
Note, that the mirrors are initially separated at a distance L0.
The solution of Eq. (6) is found to be
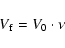 |
(7) |
with
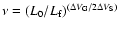 (Chen 1984; Mann & Classen 1995).
In order to derive a differential equation for the evolution
of the pitch angle Eqs. (1)-(4) will be employed
taking into account the relationship (5).
Then,
(Chen 1984; Mann & Classen 1995).
In order to derive a differential equation for the evolution
of the pitch angle Eqs. (1)-(4) will be employed
taking into account the relationship (5).
Then,
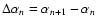 can be
calculated to be
can be
calculated to be
![\begin{displaymath}\Delta \alpha_{n} = \arctan \left [(-1) \cdot \frac{\Delta V_...
...{V_{n}} \cdot
\sin \alpha_{n} \cdot \cos \alpha_{n} \right ]
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img117.gif) |
(8) |
leading to a differential equation according to
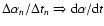 ,
i.e.,
,
i.e.,
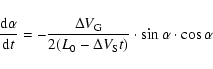 |
(9) |
with the initial condition
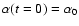 .
The solution is given by
.
The solution is given by
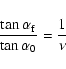 |
(10) |
relating the initial pitch angle
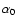 and final one
and final one
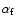 .
.
Thus, the solutions
of Eqs. (6) and (9) describe the evolution of the particle in
the velocity space
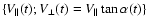 during the acceleration between
t0 = 0 and
during the acceleration between
t0 = 0 and
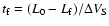 (see Fig. 6).
Here,
(see Fig. 6).
Here, 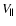 and
and 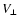 denote the particle velocity parallel
and perpendicular to the ambient magnetic field, respectively.
Now, an ensemble of particles is regarded in the velocity space.
All particles initially located on the path determined by
denote the particle velocity parallel
and perpendicular to the ambient magnetic field, respectively.
Now, an ensemble of particles is regarded in the velocity space.
All particles initially located on the path determined by
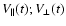 in the velocity space are accelerated and receive
the final velocity
in the velocity space are accelerated and receive
the final velocity
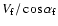 and final pitch angle
and final pitch angle
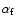 ,
i.e.,
all particles with pitch angles
,
i.e.,
all particles with pitch angles
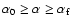 receive an acceleration.
Then, the total number of accelerated particles can be calculated by
receive an acceleration.
Then, the total number of accelerated particles can be calculated by
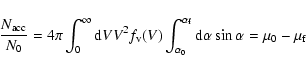 |
(11) |
with
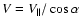 ,
,
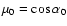 ,
and
,
and
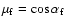 .
Here,
.
Here, 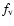 denotes the distribution function in the velocity space.
It is normalized to unity.
Now, it is intended to calculate
the total number of particles
denotes the distribution function in the velocity space.
It is normalized to unity.
Now, it is intended to calculate
the total number of particles
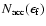 accelerated
up to a final (maximum) energy
accelerated
up to a final (maximum) energy
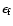 .
.
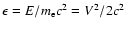 (
(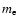 ,
electron mass;
c, velocity of light) denotes the kinetic energy E
normalized to the rest energy
,
electron mass;
c, velocity of light) denotes the kinetic energy E
normalized to the rest energy
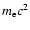 .
Consequently, the final energy
.
Consequently, the final energy
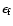 is given by
is given by
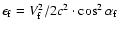 .
In order to obtain
.
In order to obtain
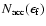 the integral (11) must be
carried out as an area integral over the dashed region depicted in Fig. 6.
the integral (11) must be
carried out as an area integral over the dashed region depicted in Fig. 6.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2482f6.eps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg140.gif) |
Figure 6:
Scheme of the area integration of the integral (12)
in the 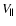 - -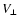 space.
space. |
This is conveniently done not in the 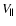 -
-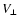 space but in the
space but in the
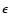 -
-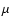 space with
space with
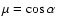 .
In carrying out this area integration
.
In carrying out this area integration
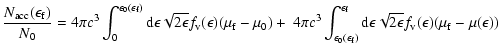 |
|
|
(12) |
results for the total number
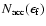 of particles accelerated up to a final energy
of particles accelerated up to a final energy
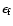 .
In the
.
In the 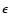 -
-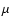 space
the function
space
the function
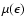 defines the path of an electron, which is
accelerated from the initial energy
defines the path of an electron, which is
accelerated from the initial energy
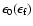 with an initial pitch angle
with an initial pitch angle
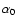 (or
(or 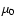 )
up to the final one
)
up to the final one
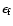 with the final pitch angle
with the final pitch angle
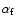 (or
(or
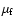 )
by the considered mechanism.
By means of Eqs. (7) and (10) the initial energy
)
by the considered mechanism.
By means of Eqs. (7) and (10) the initial energy
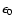 is related to the final one
is related to the final one
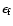 by
by
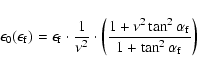 |
(13) |
resulting to
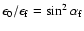 in the case
in the case 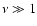 (Chen 1984).
Furthermore,
(Chen 1984).
Furthermore,
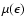 can be deduced to be
can be deduced to be
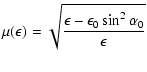 |
|
|
(14) |
from Eqs. (7) and (10).
Finally, the particle distribution function
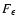 in the energy space can be found by
in the energy space can be found by
![\begin{displaymath}F_{\epsilon}(\epsilon) = \frac{{\rm d}}{{\rm d}\epsilon}
\left [\frac{N_{\rm acc}(\epsilon)}{N_{0}} \right ]
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img155.gif) |
(15) |
for the accelerated particles. This expression will be employed to compute the
differential fluxes of energetic electrons at CIR related shocks
as discussed in the next section. This approach has recently been
generalized for relativistic electrons by Mann et al. (2001).
Now, the mechanism of electron acceleration as introduced in the previous
Section is used to explain the correlation between the ratios
 and the jump of the magnetic field
B2/B1as deduced for CIR related shocks from the HISCALE data (see Fig. 2).
and the jump of the magnetic field
B2/B1as deduced for CIR related shocks from the HISCALE data (see Fig. 2).
The differential flux j(E) is related to the distribution function
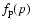 in the momentum space by
in the momentum space by
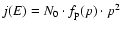 (Landau & Lifschitz 1975).
Here, the distribution function
(Landau & Lifschitz 1975).
Here, the distribution function
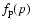 is normalized to unity.
If
is normalized to unity.
If
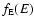 denotes the distribution function in the energy space,
the conservation of the particle number density in the phase space, i.e.,
denotes the distribution function in the energy space,
the conservation of the particle number density in the phase space, i.e.,
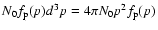 d
d
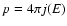 d
d
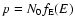 dE, leads to
dE, leads to
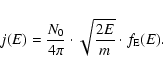 |
(16) |
Here N0 denotes the undisturbed particle number density.
Then, the distribution function 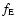 in the energy space
is related to that
in the energy space
is related to that 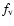 in the velocity space by
in the velocity space by
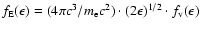 .
.
Now the flux
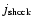 of accelerated electrons at the shock crossing is compared
with that j0 in the undisturbed upstream region.
In order to do this a so-called kappa distribution is assumed to
exist for velocity distribution function
of accelerated electrons at the shock crossing is compared
with that j0 in the undisturbed upstream region.
In order to do this a so-called kappa distribution is assumed to
exist for velocity distribution function
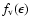 in the undisturbed solar wind, i.e. upstream of
CIR related shock waves. A kappa distribution is defined by
in the undisturbed solar wind, i.e. upstream of
CIR related shock waves. A kappa distribution is defined by
![\begin{displaymath}f_{\rm v}(E) = C_{\kappa} \left [1+\frac{E}{\kappa E_{\kappa}} \right ]^{-\kappa-1}
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img166.gif) |
(17) |
with the normalization constant
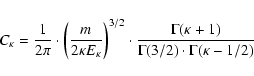 |
(18) |
(Krauss-Varban & Burgess 1991).
It behaves like a Maxwellian distribution
for
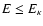 and a power law one for
and a power law one for
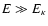 .
The temperature T can be defined in a kinetic manner, i.e.
as the mean energy
.
The temperature T can be defined in a kinetic manner, i.e.
as the mean energy 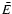 of an ensemble
average with respect to the kappa distribution, resulting in
of an ensemble
average with respect to the kappa distribution, resulting in
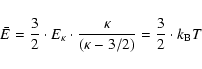 |
(19) |
(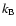 ,
Boltzmann's constant). Thus, the kappa distribution
(see Eq. (17)) is unambiguously determined by fixing the temperature T and
the parameter
,
Boltzmann's constant). Thus, the kappa distribution
(see Eq. (17)) is unambiguously determined by fixing the temperature T and
the parameter 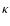 .
Inserting the distribution function (Eq. (17) into Eq. (16))
.
Inserting the distribution function (Eq. (17) into Eq. (16))
![\begin{displaymath}j_{0}(E) = \frac{N_{1}c^{4}}{m_{\rm e}c^{2}} \cdot C_{\kappa,...
...rac{\epsilon}{\kappa\epsilon_{\kappa,1}} \right ]^{-\kappa-1}
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img174.gif) |
(20) |
results for the undisturbed flux
with
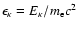 .
Consequently, N1 denotes again the upstream particle number density.
Here, the quantities
.
Consequently, N1 denotes again the upstream particle number density.
Here, the quantities
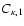 and
and
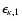 are determined
by the temperature in the upstream region.
In particular, the 3D plasma instrument aboard the Wind spacecraft is able
to measure the electron distribution function under quiet solar wind
conditions in the heliosphere at 1 AU. These measurements can be fitted
by kappa distributions with
are determined
by the temperature in the upstream region.
In particular, the 3D plasma instrument aboard the Wind spacecraft is able
to measure the electron distribution function under quiet solar wind
conditions in the heliosphere at 1 AU. These measurements can be fitted
by kappa distributions with
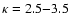 (Lin et al. 1996).
Thus, a kappa distribution with
(Lin et al. 1996).
Thus, a kappa distribution with
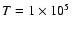 K (see Sect. 2)
and
K (see Sect. 2)
and
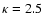 is assumed to be an appropriate electron distribution
in the upstream region of CIR related shock waves, although the CIRs
occur mainly at heliospheric distances of 4-5 AU.
is assumed to be an appropriate electron distribution
in the upstream region of CIR related shock waves, although the CIRs
occur mainly at heliospheric distances of 4-5 AU.
The flux of the accelerated electrons at the shock crossing is determined by
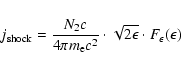 |
(21) |
taking into account
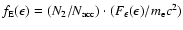 .
.
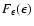 is numerically calculated by means of Eqs. (12)-(15). Then, the kappa distribution of the downstream
region must be inserted into Eq. (12), i.e.
is numerically calculated by means of Eqs. (12)-(15). Then, the kappa distribution of the downstream
region must be inserted into Eq. (12), i.e.
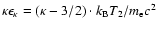 is to be inserted.
is to be inserted.
Now the results theoretically obtained from the presented electron
acceleration mechanism are compared with the observations summarized
in Fig. 2. In order to do this the plasma parameters usually found
upstream of CIR related shocks (see Sect. 2) will be employed.
The jumps of the particle number
density
N2/N1, of the magnetic field
B2/B1, and
of the temperature
T2/T1 are related to the Alfven-Mach number
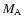 by the well-known Rankine-Hugoniot relations (Kennel et al. 1985)
as depicted in Fig. 7.
by the well-known Rankine-Hugoniot relations (Kennel et al. 1985)
as depicted in Fig. 7.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ms2482f7.eps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg185.gif) |
Figure 7:
Dependence of the jump of the temperature
T2/T1,
the particle number density
N2/N1, and the magnetic field
B2/B1 across the shock on the Alfven-Mach number 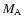 according to the Rankine-Hugoniot
relationships (Kennel et al. 1985).
An angle
according to the Rankine-Hugoniot
relationships (Kennel et al. 1985).
An angle
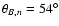 between the
upstream magnetic field and the shock normal, a plasma beta
between the
upstream magnetic field and the shock normal, a plasma beta
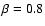 and an adiabatic index of 5/3 has been used.
and an adiabatic index of 5/3 has been used. |
Here, a plasma beta of 0.8 and an angle
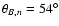 (see Sect. 2) have been adopted.
Using Eqs. (20) and (21) the ratio
(see Sect. 2) have been adopted.
Using Eqs. (20) and (21) the ratio
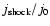 can be expressed by
can be expressed by
![\begin{displaymath}\frac{j_{\rm shock}}{j_{0}} = \frac{1}{4\pi c^{3}} \cdot \fra...
...\epsilon}{\kappa\epsilon_{\kappa,1}} \right ]^{\kappa +1}\cdot
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img186.gif) |
(22) |
Firstly, it is seen that the jump of the density
N2/N1 and
the temperature
T2/T1 appear in the second factor of
the ratio
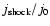 and in the ratio of the normalization
constants
and in the ratio of the normalization
constants
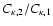 ,
respectively. Thus, a variation
of these shock parameters influences immediately the ratio
,
respectively. Thus, a variation
of these shock parameters influences immediately the ratio
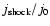 .
Furthermore, the variation of the jump of the magnetic field
B2/B1influences this ratio in another way.
As already mentioned large
amplitude magnetic field fluctuations appear in the vicinity of the shock
transition. Here, the maximum of the magnetic field compression is
assumed to be
.
Furthermore, the variation of the jump of the magnetic field
B2/B1influences this ratio in another way.
As already mentioned large
amplitude magnetic field fluctuations appear in the vicinity of the shock
transition. Here, the maximum of the magnetic field compression is
assumed to be
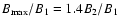 ,
for example (Kennel et al. 1985).
Then, the final pitch angle is given by
,
for example (Kennel et al. 1985).
Then, the final pitch angle is given by
![$\alpha_{\rm f} = \arcsin[(1.4B_{2}/B_{1})^{-1/2}]$](/articles/aa/full/2002/32/aa2482/img189.gif) .
Furthermore, the distance between
the two mirrors is assumed to be diminished from
.
Furthermore, the distance between
the two mirrors is assumed to be diminished from
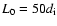 up to
up to
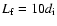 .
The velocities V1 and V2 of the mirrors M1
and M2 are regarded to be
.
The velocities V1 and V2 of the mirrors M1
and M2 are regarded to be
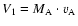 and
and
![$V_{2} = [1 + (M_{\rm A}-1)/2] \cdot v_{\rm A}$](/articles/aa/full/2002/32/aa2482/img192.gif) ,
i.e.
,
i.e.
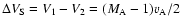 ,
leading to
,
leading to
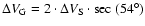 (
(
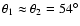 )
and
)
and
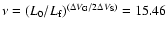 as well as to the initial pitch angle
as well as to the initial pitch angle
![$\alpha_{0} = \arctan[\nu \cdot \tan(\alpha_{\rm f})]$](/articles/aa/full/2002/32/aa2482/img197.gif) (see Eq. (10)).
Because of
(see Eq. (10)).
Because of
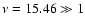 Eq. (13) reduces to
Eq. (13) reduces to
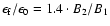 .
All quantities just
described are directly or indirectly influenced
by the variation of the jump
B2/B1of the magnetic field.
In Fig. 2 the full line represents the dependence of the
ratio
.
All quantities just
described are directly or indirectly influenced
by the variation of the jump
B2/B1of the magnetic field.
In Fig. 2 the full line represents the dependence of the
ratio
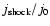 numerically calculated by Eq. (22)
on the jump of the magnetic field
B2/B1taking into account the results of the Rankine-Hugoniot relations
(see Fig. 7). As evidently seen in Fig. 2
the theoretically obtained results can explain the correlation deduced from
the data provided by the HISCALE instruments aboard the ULYSSES spacecraft.
numerically calculated by Eq. (22)
on the jump of the magnetic field
B2/B1taking into account the results of the Rankine-Hugoniot relations
(see Fig. 7). As evidently seen in Fig. 2
the theoretically obtained results can explain the correlation deduced from
the data provided by the HISCALE instruments aboard the ULYSSES spacecraft.
The study of the enhancements
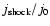 of energetic electron fluxes
in the range 30-40 keV during the crossing of CIR related shocks reveals
a relationship between the ratio
of energetic electron fluxes
in the range 30-40 keV during the crossing of CIR related shocks reveals
a relationship between the ratio
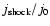 and the jump
B2/B1of the magnetic field of the associated shock as shown in Fig. 2.
This relationship
has been explained by an electron acceleration mechanism, which acts
as an interaction of electrons with the large amplitude magnetic field
fluctuations in the vicinity of the shock transition. The enhancements of
the energetic electron fluxes are caused by the heating of the electrons
as a result of the shock crossing and
the subsequent acceleration due to their interaction with the magnetic field
fluctuations in the downstream region. Since the large amplitude magnetic field
fluctuations, which are necessary for the electron acceleration, appear mainly
in the vicinity of the shock transition for quasi-perpendicular
shocks, the proposed acceleration mechanism acts very locally and fast
for electrons at spatial and temporal scales of few ion inertial lengths
and inverse proton cyclotron frequencies, respectively.
In contrast to the shock drift acceleration (Holman & Pesses 1983;
Krauss-Varban & Wu 1989; Kraus-Varban et al. 1989),
where the energy gain is limited
because of a single shock encounter and only efficient at nearly
perpendicular shocks, the mechanism presented is much more efficient
since the electrons accumulate energy due to the multiple reflections
at the large amplitude magnetic field fluctuations. Furthermore, this
mechanism is a deterministic one, unlike diffuse shock acceleration
(Axford et al. 1977), which is a stochastical process acting in the whole
up- and downstream region of the associated shock.
Recently, Classen et al. (1999) reported on
a high correlation between the fluxes of 1 MeV protons and the
low frequency magnetic field turbulence in the downstream region of CIR
related shocks,
especially in the vicinity immediately after the shock transition.
This result implies that wave-particle interactions in the
downstream region even after the shock transition
play an important role for acceleration of particles at CIR-related shock
waves. This observational result confirms additionally the acceleration
mechanism proposed in this paper.
and the jump
B2/B1of the magnetic field of the associated shock as shown in Fig. 2.
This relationship
has been explained by an electron acceleration mechanism, which acts
as an interaction of electrons with the large amplitude magnetic field
fluctuations in the vicinity of the shock transition. The enhancements of
the energetic electron fluxes are caused by the heating of the electrons
as a result of the shock crossing and
the subsequent acceleration due to their interaction with the magnetic field
fluctuations in the downstream region. Since the large amplitude magnetic field
fluctuations, which are necessary for the electron acceleration, appear mainly
in the vicinity of the shock transition for quasi-perpendicular
shocks, the proposed acceleration mechanism acts very locally and fast
for electrons at spatial and temporal scales of few ion inertial lengths
and inverse proton cyclotron frequencies, respectively.
In contrast to the shock drift acceleration (Holman & Pesses 1983;
Krauss-Varban & Wu 1989; Kraus-Varban et al. 1989),
where the energy gain is limited
because of a single shock encounter and only efficient at nearly
perpendicular shocks, the mechanism presented is much more efficient
since the electrons accumulate energy due to the multiple reflections
at the large amplitude magnetic field fluctuations. Furthermore, this
mechanism is a deterministic one, unlike diffuse shock acceleration
(Axford et al. 1977), which is a stochastical process acting in the whole
up- and downstream region of the associated shock.
Recently, Classen et al. (1999) reported on
a high correlation between the fluxes of 1 MeV protons and the
low frequency magnetic field turbulence in the downstream region of CIR
related shocks,
especially in the vicinity immediately after the shock transition.
This result implies that wave-particle interactions in the
downstream region even after the shock transition
play an important role for acceleration of particles at CIR-related shock
waves. This observational result confirms additionally the acceleration
mechanism proposed in this paper.
- Anderson, K. A. 1969, J. Geophys. Res., 73, 2387
In the text
- Axford, W. I., Leer, E., & Skadron, G. 1977,
Proc. Int. Conf. Cosmic Rays 15th, 11, 132
In the text
- Balogh, A., Beek, T. J., Forsyth, J. R.,
et al. 1992, A&AS, 92, 271 T
In the text
-
Balogh, A., Gonzalez, J. A., Forsyth, R. J., et al. 1995,
Space Sci. Rev., 72, 171
In the text
NASA ADS
-
Bame, S. J., McComas, D. J., Barraclough, B. I., et al. 1992,
A&AS, 92, 237
In the text
NASA ADS
-
Bame, S. J., Goldstein, B. E., Gosling, J. T., et al. 1993,
Geophys. Res. Lett., 20, 2323
In the text
NASA ADS
-
Barnes, C. W., & Simpson, J. A. 1976,
ApJ, 210, L91
In the text
NASA ADS
-
Cairns, I. H., & Robinson, R. D. 1987,
Solar Phys., 111, 356
In the text
- Cane, H. V., Stone, R. G., Fainberg, J. L.,
Stewart, R. T., & Steinberg, J. L. 1981,
Geophys. Res. Lett., 8, 1285
In the text
NASA ADS
-
Chen, F. F. 1984,
Introduction to Plasma Physics and Controlled Fusion:
Plasma Physics vol. 1 (Kluwer, Dordrecht), 30
In the text
-
Classen, H.-T., Mann, G., & Keppler, E. 1998, A&A, 335, 1001
In the text
-
Classen, H.-T., Mann, G., Forsyth, R. J., & Keppler, E. 1999, A&A, 347, 313
In the text
NASA ADS
-
Decker, R. B. 1988,
Space Sci. Rev., 48, 195
In the text
NASA ADS
-
Desai, M. I., Marsden, R. G., Sanderson, T. R., et al. 1998, J. Geophys. Res., 103, 2, 003
In the text
- Fermi, E. 1949, Phys. Rev., 75, 1149
In the text
-
Gosling, J. T., & Pizzo, V. J. 1999,
in Corotating Interaction Regions,
ed. A. Balogh, J. T. Gosling, J. R. Jokipii, R. Kallenbach, &
H. Kunow (Kluwer Academic Publishers, Dordrecht), 21
In the text
-
Gosling, J. T., Bame, S., Feldman, W. C., et al. 1993, Geophys. Res. Lett., 21, 2335
In the text
-
Holman, G. D., & Pesses, M. E. 1983, ApJ, 267, 837
In the text
NASA ADS
-
Kennel, C. F., Edmiston, J. P., & Hada, T. 1985,
in Collisionless Shocks in the Heliosphere: A Tutorial Review,
ed. B. T. Stone, & R. G. Stone,
Geophysical Monographs GN-34 (AGU, Washington DC), 1
In the text
-
Keppler, E., Drolias, B., Fraenz, M., et al. 1996, A&A, 316, 464
In the text
NASA ADS
-
Krauss-Varban, D., & Wu, C. S. 1989, J. Geophys. Res., 94, 15, 367
In the text
NASA ADS
-
Krauss-Varban, D., Burgess, D., & Wu, C. S. 1989, J. Geophys. Res., 94, 15, 089
NASA ADS
-
Krauss-Varban, D., & Burgess, D. 1991, J. Geophys. Res., 96, 143
In the text
NASA ADS
-
Landau, L. D., & Lifshitz, E. M. 1975,
The classical field theory of fields (Pergamon Press, Oxford), 264
In the text
-
Lanzerotti, L. J., Gold, R. E., Anderson, K. A., et al. 1992, A&AS, 92, 349
In the text
NASA ADS
-
Lin, R. P., Larson, D., McFadden, J., et al. 1996,
Geophys. Res. Lett., 23, 1211
In the text
NASA ADS
-
Lopate, N. 1989, J. Geophys. Res., 94, 9, 995
In the text
NASA ADS
- Mann, G. 1995, J. Plasma Phys., 53, 109
In the text
- Mann, G. 1999, in Corotating Interaction Regions,
ed. A. Balogh, J. T. Gosling, J. R. Jokipii, R. Kallenbach,
& H. Kunow (Kluwer Academic Publishers, Dordrecht), 389
In the text
-
Mann, G., & Classen, H. T. 1995, A&A, 304, 576
NASA ADS
-
Mann, G., Lühr, H., & Baumjohann, W. 1994, J. Geophys. Res., 99, 13, 315
In the text
-
Mann, G., Classen, H.-T., & Motschmann, U. 2001, J. Geophys. Res., 106, 25, 323
In the text
-
Marsden, R. G., Smith, E. J., Cooper, J. F., & Tranquille, C. 1996,
A&A, 316, 279
In the text
NASA ADS
-
Mason, G. M., & Sanderson, T. R. 1999,
in Corotating Interaction Regions,
ed. A. Balogh, J. T. Gosling, J. R. Jokipii, R. Kallenbach, &
H. Kunow (Kluwer Academic Publishers, Dordrecht), 77
In the text
-
McDonald, F. B., Teegarden, B. J., Trainor, J. H., von Rosenvinge, T. T.,
& Weber, W. R. 1976, ApJ, 203, L149
In the text
NASA ADS
-
Neugebauer, M. C., & Snyder, C. W. 1966, J. Geophys. Res., 71, 4469
In the text
-
Parker, E. N. 1958, ApJ, 128, 664
In the text
NASA ADS
-
Pizzo, V. J. 1978, J. Geophys. Res., 83, 5, 563
In the text
-
Roelof, E. C., Simnett, G. M., & Tappin, S. J. 1966, A&A, 316, 481
In the text
NASA ADS
-
Scarf, F. L., Fredricks, R. W., Frank, L. A., & Neugebauer, M. 1971,
J. Geophys. Res., 76, 5162
In the text
-
Schwenn, R. 1990, in Physics of the Inner Heliosphere,
ed. R. Schwenn, & E. Marsch (Springer Verlag, Berlin), 99
In the text
-
Simpson, J. A., et al. 1992, A&AS, 92, 365
In the text
NASA ADS
-
Simnett, G. M., & Roelof, E. C. 1995, Space Sci. Rev., 72, 302
In the text
-
Toptygin, I. N. 1980, Space Sci. Rev., 26, 157
In the text
NASA ADS
-
Tsurutani, B. T., & Lin, R. P. 1985, J. Geophys. Res., 90, 1
In the text
NASA ADS
-
Wild, J. P., & McCready, L. L. 1950,
Austr. J. Sci. Res., Ser. A, 3, 387
In the text
Copyright ESO 2002
![]() at the shock crossing are compared with those j0
measured during quiet solar wind periods before and after the
CIR (see Sect. 2). Furthermore, the ratios
at the shock crossing are compared with those j0
measured during quiet solar wind periods before and after the
CIR (see Sect. 2). Furthermore, the ratios
![]() are related to the magnetic field compression
B2/B1
of the associated shock.
Mann & Classen (1995)
proposed a mechanism of generation of energetic electrons
at collisionless shocks. It is well-known that super-critical
shocks are accompanied with large amplitude magnetic field fluctuations
in the vicinity of the shock transition (Kennel et al. 1985). Electrons can be
reflected and subsequently accelerated at these fluctuations. Due to
multiple encounters of electrons with these fluctuations they receive
a considerable acceleration (Mann & Classen 1995). This
special acceleration mechanism will be introduced in a quantitative manner
in Sect. 3, and subsequently adopted to explain the relations
between the flux ratios
are related to the magnetic field compression
B2/B1
of the associated shock.
Mann & Classen (1995)
proposed a mechanism of generation of energetic electrons
at collisionless shocks. It is well-known that super-critical
shocks are accompanied with large amplitude magnetic field fluctuations
in the vicinity of the shock transition (Kennel et al. 1985). Electrons can be
reflected and subsequently accelerated at these fluctuations. Due to
multiple encounters of electrons with these fluctuations they receive
a considerable acceleration (Mann & Classen 1995). This
special acceleration mechanism will be introduced in a quantitative manner
in Sect. 3, and subsequently adopted to explain the relations
between the flux ratios
![]() and jumps of the magnetic
field
B2/B1 of the associated shocks in Sect. 4.
and jumps of the magnetic
field
B2/B1 of the associated shocks in Sect. 4.
![]() at the shock crossing with those j0,
which are determined during quiet conditions of the solar wind stream
related with the corresponding
shock. It should be recalled, that the forward and reverse shocks are
travelling into the slow and fast speed solar wind (Pizzo 1978), respectively.
at the shock crossing with those j0,
which are determined during quiet conditions of the solar wind stream
related with the corresponding
shock. It should be recalled, that the forward and reverse shocks are
travelling into the slow and fast speed solar wind (Pizzo 1978), respectively.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ms2482f2.eps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg57.gif)
![]() .
For a plasma-beta
.
For a plasma-beta
![]() such shocks
are super-critical, if their Alfvén-Mach number is greater than 2.0
(Kennel et al. 1985).
That is mostly the case of the shocks considered in this paper (see Table 1).
Figure 3 shows the behaviour
of the magnitude of the magnetic field during the crossing of the CIR related
shock No. 7F as measured by the magnetometer (Balogh et al. 1992)
aboard the Ulysses spacecraft.
such shocks
are super-critical, if their Alfvén-Mach number is greater than 2.0
(Kennel et al. 1985).
That is mostly the case of the shocks considered in this paper (see Table 1).
Figure 3 shows the behaviour
of the magnitude of the magnetic field during the crossing of the CIR related
shock No. 7F as measured by the magnetometer (Balogh et al. 1992)
aboard the Ulysses spacecraft.
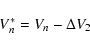
![\begin{displaymath}\alpha_{n}^{\ast} = \arctan \left [\frac{V_{n} \cdot \tan \alpha_{n}}{V_{n} - \Delta V_{2}} \right ] \cdot
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img76.gif)
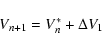
![\begin{displaymath}\alpha_{n+1} = \arctan \left [\frac{V_{n}^{\ast} \cdot \tan \alpha_{n}^{\ast}}{V_{n}^{\ast} + \Delta V_{1}} \right]\cdot
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img79.gif)
![]() of the electron is essentially smaller than the
characteristic length scale of the magnetic field compressions.
This length scale is typically 10 ion inertial
lengths (Mann et al. 1994).
Since electrons in the energy range 30-50 keV have a typical gyroradius of
1.3 ion inertial lengths under plasma conditions near CIRs (see Sect. 2),
the required condition is well fulfilled in the case considered here.
of the electron is essentially smaller than the
characteristic length scale of the magnetic field compressions.
This length scale is typically 10 ion inertial
lengths (Mann et al. 1994).
Since electrons in the energy range 30-50 keV have a typical gyroradius of
1.3 ion inertial lengths under plasma conditions near CIRs (see Sect. 2),
the required condition is well fulfilled in the case considered here.
![]() .
Consequently, the acceleration process is finished either if
.
Consequently, the acceleration process is finished either if
![]() or if the electron leaves the region between the mirrors,
since the pitch angle
or if the electron leaves the region between the mirrors,
since the pitch angle
![]() becomes
becomes
![]() .
The movement
of an electron between these two mirrors leads finally to a nonuniform
acceleration as illustrated in Fig. 5. In this special example
the particle has an initial velocity
.
The movement
of an electron between these two mirrors leads finally to a nonuniform
acceleration as illustrated in Fig. 5. In this special example
the particle has an initial velocity
![]() (
(![]() ,
Alfvén speed;
,
Alfvén speed;
![]() ,
thermal
electron velocity) parallel to
the ambient magnetic field and an initial pitch angle
,
thermal
electron velocity) parallel to
the ambient magnetic field and an initial pitch angle
![]() .
The distance between the two mirrors is diminished from
L0 = 50diup to
.
The distance between the two mirrors is diminished from
L0 = 50diup to
![]() .
The mirrors M1 and M2 are moving with
the velocities
.
The mirrors M1 and M2 are moving with
the velocities
![]() and
and
![]() ,
respectively.
The magnetic field compression at the mirror M2 is assumed to be
BM2/B0 = 2.8 resulting in a final pitch angle
,
respectively.
The magnetic field compression at the mirror M2 is assumed to be
BM2/B0 = 2.8 resulting in a final pitch angle
![]() .
Adopting
.
Adopting
![]() as typical values
for CIR related shocks,
as typical values
for CIR related shocks,
![]() and
and
![]() is found.
The result of the numerically evaluated Eqs. (1)-(4) is presented in
Fig. 5.
is found.
The result of the numerically evaluated Eqs. (1)-(4) is presented in
Fig. 5.
![]() with
with
![]() and
and
![]() may be taken as a differential equation
may be taken as a differential equation
![]()
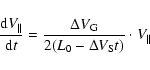
![]() .
Here,
.
Here,
![]() with
with
![]() has been used in deriving Eq. (6).
Note, that the mirrors are initially separated at a distance L0.
The solution of Eq. (6) is found to be
has been used in deriving Eq. (6).
Note, that the mirrors are initially separated at a distance L0.
The solution of Eq. (6) is found to be
![]() (Chen 1984; Mann & Classen 1995).
In order to derive a differential equation for the evolution
of the pitch angle Eqs. (1)-(4) will be employed
taking into account the relationship (5).
Then,
(Chen 1984; Mann & Classen 1995).
In order to derive a differential equation for the evolution
of the pitch angle Eqs. (1)-(4) will be employed
taking into account the relationship (5).
Then,
![]() can be
calculated to be
can be
calculated to be
![\begin{displaymath}\Delta \alpha_{n} = \arctan \left [(-1) \cdot \frac{\Delta V_...
...{V_{n}} \cdot
\sin \alpha_{n} \cdot \cos \alpha_{n} \right ]
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img117.gif)
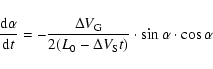
![]() .
The solution is given by
.
The solution is given by
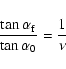
![]() and final one
and final one
![]() .
.
![]() during the acceleration between
t0 = 0 and
during the acceleration between
t0 = 0 and
![]() (see Fig. 6).
Here,
(see Fig. 6).
Here, ![]() and
and ![]() denote the particle velocity parallel
and perpendicular to the ambient magnetic field, respectively.
Now, an ensemble of particles is regarded in the velocity space.
All particles initially located on the path determined by
denote the particle velocity parallel
and perpendicular to the ambient magnetic field, respectively.
Now, an ensemble of particles is regarded in the velocity space.
All particles initially located on the path determined by
![]() in the velocity space are accelerated and receive
the final velocity
in the velocity space are accelerated and receive
the final velocity
![]() and final pitch angle
and final pitch angle
![]() ,
i.e.,
all particles with pitch angles
,
i.e.,
all particles with pitch angles
![]() receive an acceleration.
Then, the total number of accelerated particles can be calculated by
receive an acceleration.
Then, the total number of accelerated particles can be calculated by
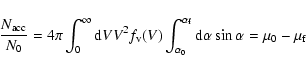
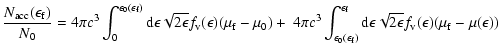
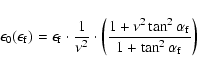
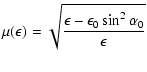
![\begin{displaymath}F_{\epsilon}(\epsilon) = \frac{{\rm d}}{{\rm d}\epsilon}
\left [\frac{N_{\rm acc}(\epsilon)}{N_{0}} \right ]
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img155.gif)
![]() and the jump of the magnetic field
B2/B1as deduced for CIR related shocks from the HISCALE data (see Fig. 2).
and the jump of the magnetic field
B2/B1as deduced for CIR related shocks from the HISCALE data (see Fig. 2).
![]() in the momentum space by
in the momentum space by
![]() (Landau & Lifschitz 1975).
Here, the distribution function
(Landau & Lifschitz 1975).
Here, the distribution function
![]() is normalized to unity.
If
is normalized to unity.
If
![]() denotes the distribution function in the energy space,
the conservation of the particle number density in the phase space, i.e.,
denotes the distribution function in the energy space,
the conservation of the particle number density in the phase space, i.e.,
![]() d
d
![]() d
d
![]() dE, leads to
dE, leads to
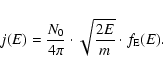
![]() of accelerated electrons at the shock crossing is compared
with that j0 in the undisturbed upstream region.
In order to do this a so-called kappa distribution is assumed to
exist for velocity distribution function
of accelerated electrons at the shock crossing is compared
with that j0 in the undisturbed upstream region.
In order to do this a so-called kappa distribution is assumed to
exist for velocity distribution function
![]() in the undisturbed solar wind, i.e. upstream of
CIR related shock waves. A kappa distribution is defined by
in the undisturbed solar wind, i.e. upstream of
CIR related shock waves. A kappa distribution is defined by
![\begin{displaymath}f_{\rm v}(E) = C_{\kappa} \left [1+\frac{E}{\kappa E_{\kappa}} \right ]^{-\kappa-1}
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img166.gif)
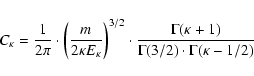
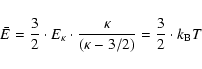
![\begin{displaymath}j_{0}(E) = \frac{N_{1}c^{4}}{m_{\rm e}c^{2}} \cdot C_{\kappa,...
...rac{\epsilon}{\kappa\epsilon_{\kappa,1}} \right ]^{-\kappa-1}
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img174.gif)
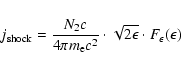
![]() by the well-known Rankine-Hugoniot relations (Kennel et al. 1985)
as depicted in Fig. 7.
by the well-known Rankine-Hugoniot relations (Kennel et al. 1985)
as depicted in Fig. 7.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ms2482f7.eps} \end{figure}](/articles/aa/full/2002/32/aa2482/Timg185.gif)
![\begin{displaymath}\frac{j_{\rm shock}}{j_{0}} = \frac{1}{4\pi c^{3}} \cdot \fra...
...\epsilon}{\kappa\epsilon_{\kappa,1}} \right ]^{\kappa +1}\cdot
\end{displaymath}](/articles/aa/full/2002/32/aa2482/img186.gif)
![]() of energetic electron fluxes
in the range 30-40 keV during the crossing of CIR related shocks reveals
a relationship between the ratio
of energetic electron fluxes
in the range 30-40 keV during the crossing of CIR related shocks reveals
a relationship between the ratio
![]() and the jump
B2/B1of the magnetic field of the associated shock as shown in Fig. 2.
This relationship
has been explained by an electron acceleration mechanism, which acts
as an interaction of electrons with the large amplitude magnetic field
fluctuations in the vicinity of the shock transition. The enhancements of
the energetic electron fluxes are caused by the heating of the electrons
as a result of the shock crossing and
the subsequent acceleration due to their interaction with the magnetic field
fluctuations in the downstream region. Since the large amplitude magnetic field
fluctuations, which are necessary for the electron acceleration, appear mainly
in the vicinity of the shock transition for quasi-perpendicular
shocks, the proposed acceleration mechanism acts very locally and fast
for electrons at spatial and temporal scales of few ion inertial lengths
and inverse proton cyclotron frequencies, respectively.
In contrast to the shock drift acceleration (Holman & Pesses 1983;
Krauss-Varban & Wu 1989; Kraus-Varban et al. 1989),
where the energy gain is limited
because of a single shock encounter and only efficient at nearly
perpendicular shocks, the mechanism presented is much more efficient
since the electrons accumulate energy due to the multiple reflections
at the large amplitude magnetic field fluctuations. Furthermore, this
mechanism is a deterministic one, unlike diffuse shock acceleration
(Axford et al. 1977), which is a stochastical process acting in the whole
up- and downstream region of the associated shock.
Recently, Classen et al. (1999) reported on
a high correlation between the fluxes of 1 MeV protons and the
low frequency magnetic field turbulence in the downstream region of CIR
related shocks,
especially in the vicinity immediately after the shock transition.
This result implies that wave-particle interactions in the
downstream region even after the shock transition
play an important role for acceleration of particles at CIR-related shock
waves. This observational result confirms additionally the acceleration
mechanism proposed in this paper.
and the jump
B2/B1of the magnetic field of the associated shock as shown in Fig. 2.
This relationship
has been explained by an electron acceleration mechanism, which acts
as an interaction of electrons with the large amplitude magnetic field
fluctuations in the vicinity of the shock transition. The enhancements of
the energetic electron fluxes are caused by the heating of the electrons
as a result of the shock crossing and
the subsequent acceleration due to their interaction with the magnetic field
fluctuations in the downstream region. Since the large amplitude magnetic field
fluctuations, which are necessary for the electron acceleration, appear mainly
in the vicinity of the shock transition for quasi-perpendicular
shocks, the proposed acceleration mechanism acts very locally and fast
for electrons at spatial and temporal scales of few ion inertial lengths
and inverse proton cyclotron frequencies, respectively.
In contrast to the shock drift acceleration (Holman & Pesses 1983;
Krauss-Varban & Wu 1989; Kraus-Varban et al. 1989),
where the energy gain is limited
because of a single shock encounter and only efficient at nearly
perpendicular shocks, the mechanism presented is much more efficient
since the electrons accumulate energy due to the multiple reflections
at the large amplitude magnetic field fluctuations. Furthermore, this
mechanism is a deterministic one, unlike diffuse shock acceleration
(Axford et al. 1977), which is a stochastical process acting in the whole
up- and downstream region of the associated shock.
Recently, Classen et al. (1999) reported on
a high correlation between the fluxes of 1 MeV protons and the
low frequency magnetic field turbulence in the downstream region of CIR
related shocks,
especially in the vicinity immediately after the shock transition.
This result implies that wave-particle interactions in the
downstream region even after the shock transition
play an important role for acceleration of particles at CIR-related shock
waves. This observational result confirms additionally the acceleration
mechanism proposed in this paper.