A&A 391, 725-739 (2002)
DOI: 10.1051/0004-6361:20020837
Seismic tests for solar models with
tachocline mixing
A. S. Brun1,2 - H. M.
Antia3 - S. M. Chitre4 - J.-P. Zahn2
1 - JILA, University of Colorado, Boulder,
CO 80309-0440, USA
2 - LUTH, Observatoire de Paris-Meudon, 92195 Meudon, France
3 - Tata Institute of Fundamental
Research, Homi Bhabha road, Mumbai 400005, India
4 - Department of Physics, University of
Mumbai, Mumbai 400098, India
Received 24 February 2002 / Accepted 31 May 2002
Abstract
We have computed accurate 1-D solar models
including both a macroscopic mixing process in the solar
tachocline as well as up-to-date microscopic physical
ingredients. Using sound speed and density profiles inferred
through primary inversion of the solar oscillation
frequencies coupled with the equation of thermal equilibrium,
we have extracted the temperature and hydrogen abundance
profiles. These inferred quantities place strong constraints
on our theoretical models in terms of the extent and strength
of our macroscopic mixing, on the photospheric heavy elements
abundance, on the nuclear reaction rates such as S11and S34 and on the efficiency of the microscopic
diffusion. We find a good overall agreement between the
seismic Sun and our models if we introduce a macroscopic
mixing in the tachocline and allow for variation within their
uncertainties of the main physical ingredients. From our
study we deduce that the solar hydrogen abundance at the
solar age is
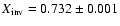 and that based on
the 9Be photospheric depletion, the maximum extent of mixing
in the tachocline is 5% of the solar radius. The nuclear reaction
rate for the fundamental pp reaction is found to be
and that based on
the 9Be photospheric depletion, the maximum extent of mixing
in the tachocline is 5% of the solar radius. The nuclear reaction
rate for the fundamental pp reaction is found to be
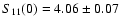 10-25 MeV barns, i.e., 1.5%
higher than the present theoretical determination. The
predicted solar neutrino fluxes are discussed in the light
of the new SNO/SuperKamiokande results.
10-25 MeV barns, i.e., 1.5%
higher than the present theoretical determination. The
predicted solar neutrino fluxes are discussed in the light
of the new SNO/SuperKamiokande results.
Key words: Sun: abundances - Sun: interior - Sun: oscillations - neutrinos
Over the past decade our understanding of the solar interior has improved
significantly. Today with the precise helioseismic data available from the GONG
(Global Oscillation Network Group) ground based instruments and the SOHO
(SOlar and Heliospheric Observatory) space experiments
(Gough et al. 1996; Thompson et al. 1996; Fröhlich et al. 1997;
Gabriel et al. 1997; Schou et al. 1998), the detailed internal structure and
complex dynamics of our star can be inferred with reasonable
accuracy using inversion techniques. In addition to sound speed
c and density  profiles, the internal rotation rate
profiles, the internal rotation rate
 can also be inferred. It reveals that on the top of an almost
uniformly rotating radiation zone (with a rotation period of about 28 days), the
bulk of the convection zone is differentially rotating with properties close to
what is deduced from sunspot tracking, i.e., a period at the equator of 25 days
and at the pole of 33 days corresponding to a contrast
can also be inferred. It reveals that on the top of an almost
uniformly rotating radiation zone (with a rotation period of about 28 days), the
bulk of the convection zone is differentially rotating with properties close to
what is deduced from sunspot tracking, i.e., a period at the equator of 25 days
and at the pole of 33 days corresponding to a contrast
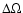 of 30%.
The sharp transition region between these two distinct zones, located around
of 30%.
The sharp transition region between these two distinct zones, located around
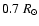 ,
has been called the tachocline (Spiegel & Zahn 1992);
it is thought to play an important role in determining the structure and the
chemical evolution of the Sun (Brun et al. 1999; Elliott
& Gough 1999).
,
has been called the tachocline (Spiegel & Zahn 1992);
it is thought to play an important role in determining the structure and the
chemical evolution of the Sun (Brun et al. 1999; Elliott
& Gough 1999).
Indeed, it appears that the solar structure deduced from
helioseismology and the observed photospheric compositions can
not be explained adequately without invoking some mixing
in the radiative interior (Brun et al. 1999). This conclusion has been
drawn after a careful study of the microscopic processes present in
solar models (Christensen-Dalsgaard et al. 1996; Morel et al. 1997;
Bahcall et al. 1998a;
Brun et al. 1998). More precisely, in the early 90's,
after significant improvements in the description of the solar plasma
through better equation of state, opacities and nuclear reaction rates,
helioseismic studies have established the need for
microscopic diffusion of helium and heavy elements in the
radiative interior (Christensen-Dalsgaard et al. 1993). But it was soon realized that
models including only microscopic diffusion exhibit sharp composition
gradients below the base of the convection zone which are not
consistent with helioseismic data; these favour instead smoother
composition profiles within this region (Basu & Antia 1994).
In spite of further improvements in solar models, this discrepancy
still persists around 0.7 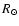 (Christensen-Dalsgaard et al. 1996; Brun et al. 1998), suggesting that some extra mixing
must be implemented in the models.
(Christensen-Dalsgaard et al. 1996; Brun et al. 1998), suggesting that some extra mixing
must be implemented in the models.
Further, using primary inversions for sound speed and density and
the equations of thermal equilibrium, Antia & Chitre (1998) have inferred
the hydrogen abundance profile in the radiative interior. This
profile confirms the presence of such mixing in the Sun, as the
hydrogen abundance appears to be almost constant in the
region
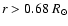 .
.
Another evidence for mixing occurring in that
region comes from the photospheric light elements composition.
Purely microscopic processes cannot reproduce the under
abundance of lithium observed in the Sun
and in open clusters (Grevesse et al. 1996; Cayrel 1998;
Richard et al. 1996; Turcotte et al. 1998; Brun et al. 1999).
We are thus compelled to introduce some mixing processes in the stably
stratified radiative interior. The possible causes of instabilities leading to
such mixing are the solar rotation, the magnetic field or
penetrative convection (Zahn 1998). The recent study of Balachandran & Bell
(1998) on the photospheric light elements abundance of 7Li and 9Be puts
strong constraints on the extent, amplitude and location of such instabilities.
It is now believed that only the lithium is significantly depleted, by more
than a factor of 100 in comparison to the meteoritic composition, while the
beryllium has varied by only 10% over the last 4.6 Gyr. The temperatures at
which these two species are destroyed by nuclear burning are respectively 
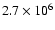 K (at
K (at
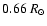 )
and
)
and 
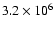 K (at
K (at
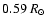 ), which are relatively close to the temperature at the base of the
convection zone
), which are relatively close to the temperature at the base of the
convection zone 
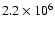 K at
K at
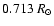 (Christensen-Dalsgaard et al. 1991).
This implies that any macroscopic processes for such lithium destruction have
to be located near the top of the radiation zone and cannot extend deeper than
(
(Christensen-Dalsgaard et al. 1991).
This implies that any macroscopic processes for such lithium destruction have
to be located near the top of the radiation zone and cannot extend deeper than
( 8%) in solar radius without producing an excessive destruction of
9Be.
8%) in solar radius without producing an excessive destruction of
9Be.
This requirement is satisfied if the mixing is confined in the tachocline.
For this reason, Brun et al. (1999) calculated the mixing occurring in that
layer, based on Spiegel & Zahn's hydrodynamical description of the
tachocline. They found indeed that such mixing
improved the agreement between the models and the Sun, provided the secular
variation of the tachocline
was taken into account. Alternative approaches based on gravity waves
(Montalban & Schatzman 1996) and magnetic field (Barnes et al. 1999) have also been studied.
In this paper we intend to go further in understanding the influence of
tachocline mixing on the solar internal structure and composition by using the
powerful seismic diagnostic. In particular, we examine the cumulative effect of
varying, within their intrinsic uncertainties, the basic microscopic ingredients
such as the nuclear reaction cross sections, the microscopic diffusion coefficients, etc.
Seismic probing of the solar structure has been improved to
a level where it can be used to constrain physical processes, since the Sun
provides a ready-made cosmic laboratory for testing various aspects of physics.
For example, there have been some attempts to constrain the nuclear reaction
rate for pp reaction using helioseismic data (Antia & Chitre 1998, 1999;
Degl'Innocenti et al. 1998; Schlattl et al. 1999).
These studies indicate that the cross-section for pp reaction needs to be
increased by a few percent over the currently accepted value (Adelberger et al. 1998). Using a similar approach Weiss et al. (2001) found
that enhancing the electron screening by about 5% improves the agreement
between solar model and helioseismically inferred sound speed. Therefore,
we would like to revise, among other quantities, the pp cross-section deduced
from helioseismology, by using in our solar models either the weak (Salpeter 1954)
or intermediate (Mitler 1977) treatment for electron screening. We also deduce
the photospheric hydrogen abundance
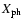 ,
the maximum
extent h of the tachocline mixing allowed in a solar model and predict the
theoretical neutrino fluxes in light of the recent SNO results (Ahmad et al. 2001, 2002).
,
the maximum
extent h of the tachocline mixing allowed in a solar model and predict the
theoretical neutrino fluxes in light of the recent SNO results (Ahmad et al. 2001, 2002).
We have organised our paper as follows. In Sect. 2, we briefly recall
how we compute our 1-D solar models with or without the presence of
tachocline mixing, describe our inversion techniques of the solar
acoustic frequencies and demonstrate the need for further progress in
solar modelling. In Sect. 3, we present our latest results on the sound
speed, density, hydrogen abundance and temperature profiles obtained with our
modified solar tachocline models and discuss the resulting neutrino fluxes.
Finally in Sect. 4, we comment on our findings and outline our
conclusions.
In order to model the Sun, we use the CESAM code (Morel 1997), which solves the
structure equations (Kippenhahn & Weigert 1994) in time and space for
a spherically symmetric star of one solar mass (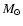 )
in
mechanical and thermal equilibrium.
Once the evolved structure of a given model
reaches the age of 4.6 Gyr, including a pre main sequence (PMS) phase of
)
in
mechanical and thermal equilibrium.
Once the evolved structure of a given model
reaches the age of 4.6 Gyr, including a pre main sequence (PMS) phase of 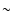 50 Myr, it is
calibrated to the solar radius
50 Myr, it is
calibrated to the solar radius 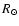 ,
luminosity
,
luminosity 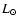 and surface heavy elements abundance
and surface heavy elements abundance
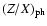 to within an accuracy
of 10-5 (see Table 1). This is done by modifying the
mixing length parameter
to within an accuracy
of 10-5 (see Table 1). This is done by modifying the
mixing length parameter 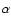 ,
the initial helium Y0 and heavy
elements Z0 abundances. This accurate calibration of solar values is
crucial and allows us to test different solutions in our
search for the best agreement between our models and the Sun.
We refer to Brun et al. (1998) for a more detailed description of our solar models.
,
the initial helium Y0 and heavy
elements Z0 abundances. This accurate calibration of solar values is
crucial and allows us to test different solutions in our
search for the best agreement between our models and the Sun.
We refer to Brun et al. (1998) for a more detailed description of our solar models.
The macroscopic mixing present in the tachocline is modelled by adding to the equation
for chemical evolution an effective time dependent diffusion coefficient
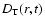 ,
based on the hydrodynamical description of the tachocline
developed by Spiegel & Zahn (1992). In their study they invoked the anisotropy of the
turbulence in a stratified medium to explain the thinness of this
layer. We refer to Brun et al. (1999) for a complete description of
the different steps followed to deduce from their model the effective
turbulent diffusivity
,
based on the hydrodynamical description of the tachocline
developed by Spiegel & Zahn (1992). In their study they invoked the anisotropy of the
turbulence in a stratified medium to explain the thinness of this
layer. We refer to Brun et al. (1999) for a complete description of
the different steps followed to deduce from their model the effective
turbulent diffusivity
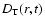 used in this work. This coefficient depends on two parameters:
used in this work. This coefficient depends on two parameters:
 the tachocline thickness at the solar age, h (or the closely related quantity
the tachocline thickness at the solar age, h (or the closely related quantity 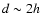 ),
a relatively well-known quantity (Antia et al. 1998; Corbard et al. 1999, see Table 1),
),
a relatively well-known quantity (Antia et al. 1998; Corbard et al. 1999, see Table 1),
 the Brunt-Väisälä frequency
the Brunt-Väisälä frequency
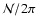 ,
which varies with
depth and is taken as constant in this model, representing some average
over the tachocline; furthermore, it depends on the extent of overshoot
and its value is therefore somewhat uncertain.
,
which varies with
depth and is taken as constant in this model, representing some average
over the tachocline; furthermore, it depends on the extent of overshoot
and its value is therefore somewhat uncertain.
The time dependence of the angular velocity is based on the Skumanich law (Skumanich 1972), e.g.,
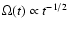 .
This law is not adequate for the early phases of
the solar evolution when the star contracts and/or exchanges angular momentum with its
accretion disk (see Piau & Turck-Chièze 2001).
Nevertheless, for this study concerned mainly with the present day Sun, it is satisfactory.
.
This law is not adequate for the early phases of
the solar evolution when the star contracts and/or exchanges angular momentum with its
accretion disk (see Piau & Turck-Chièze 2001).
Nevertheless, for this study concerned mainly with the present day Sun, it is satisfactory.
To test and constrain the solar models, we compare their sound speed,
density, temperature and hydrogen abundance profiles with seismically
deduced ones. The sound speed and density profiles are inferred using a
Regularised Least Squares (RLS) inversion technique (Antia 1996). This
primary inversion is based only on the equations of mechanical equilibrium,
and has been tested through extensive
comparisons (e.g., Gough et al. 1996). For these primary
inversions, we use a set of modes in the range of harmonic degree
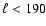 ,
obtained from the
first 360 days of operation of the Michelson Doppler Imager (MDI) (Schou et al. 1998). The inversion results in the central region depend
on the set of low degree acoustic modes used (i.e.,
,
obtained from the
first 360 days of operation of the Michelson Doppler Imager (MDI) (Schou et al. 1998). The inversion results in the central region depend
on the set of low degree acoustic modes used (i.e.,
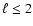 ,
Basu et al. 2000) but not
to the extent of modifying the conclusions of this work.
To infer secondary quantities such as temperature and chemical
composition within the Sun, we follow the treatment given by
Antia & Chitre (1998).
,
Basu et al. 2000) but not
to the extent of modifying the conclusions of this work.
To infer secondary quantities such as temperature and chemical
composition within the Sun, we follow the treatment given by
Antia & Chitre (1998).
Apart from evolutionary solar models, we also construct some static
ones, using a composition profile calculated by the evolutionary
stellar structure code CESAM. These models
use the same physical inputs as the evolutionary models, but include a
different treatment of atmosphere, using the atmospheric model of
Vernazza et al. (1981) as well as the opacity tables from Kurucz (1991)
at low temperatures
and the formulation of Canuto & Mazzitelli (1991) to calculate the
convective flux. Because of these differences the surface layers in the
Sun are better represented in these static models.
Before introducing any new modifications in our evolutionary solar
models, let us recall what are the strengths and weaknesses of
the tachocline models of Brun et al. (1999).
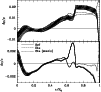 |
Figure 1:
The relative difference in sound speed and density profiles between
the Sun and solar models is shown as a
function of fractional radius. Model ref including only microscopic diffusion
is represented with a solid line and the mixed models Btz and its static
equivalent with respectively a short-dashed and long-dashed lines.
Superimposed on model ref is the 1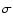 error envelope coming from the helioseismic inversion.
error envelope coming from the helioseismic inversion. |
In Fig. 1 we represent the relative sound speed and
density differences
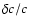 and
and
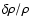 between the seismic Sun obtained using the inversion procedure
described above and our purely microscopic diffusive model, hereafter referred to
as ref model or a typical tachocline model of Brun et al. (1999), namely, model Btz.
A first quick look reveals that the mixed model Btz shows a better overall
agreement both for density and sound speed compared to the reference
one. For both these quantities, the transition at the base of the
homogeneous convection zone is smoother, resulting in an almost
disappearance of the pronounced peak seen in
between the seismic Sun obtained using the inversion procedure
described above and our purely microscopic diffusive model, hereafter referred to
as ref model or a typical tachocline model of Brun et al. (1999), namely, model Btz.
A first quick look reveals that the mixed model Btz shows a better overall
agreement both for density and sound speed compared to the reference
one. For both these quantities, the transition at the base of the
homogeneous convection zone is smoother, resulting in an almost
disappearance of the pronounced peak seen in
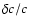 of
model ref. Further, the hydrogen abundance in the convective
envelope is slightly closer to the seismic one, due mainly to the
limiting action of the macroscopic mixing on the gravitational settling
of the chemical elements (see Table 3). Brun et al. (1999) found that macroscopic
mixing at the base of the convection zone reduces by 25% the
microscopic diffusion in comparison to a purely microscopic model such
as ref. Moreover, as we shall see in Sect. 3.3,
the hydrogen abundance profile is smoother and does not exhibit
any sharp gradient just below the base of the convection zone.
Further, the lithium depletion achieved in the
mixed model is significant, of the order of 100, and follows
quantitatively well the open cluster observations, such as in the
Hyades, or older clusters such as NGC 752. On the other hand, model ref
burns its lithium mainly in the PMS phase with only a tiny fraction
being depleted during the main sequence evolution due to gravitational
settling.
of
model ref. Further, the hydrogen abundance in the convective
envelope is slightly closer to the seismic one, due mainly to the
limiting action of the macroscopic mixing on the gravitational settling
of the chemical elements (see Table 3). Brun et al. (1999) found that macroscopic
mixing at the base of the convection zone reduces by 25% the
microscopic diffusion in comparison to a purely microscopic model such
as ref. Moreover, as we shall see in Sect. 3.3,
the hydrogen abundance profile is smoother and does not exhibit
any sharp gradient just below the base of the convection zone.
Further, the lithium depletion achieved in the
mixed model is significant, of the order of 100, and follows
quantitatively well the open cluster observations, such as in the
Hyades, or older clusters such as NGC 752. On the other hand, model ref
burns its lithium mainly in the PMS phase with only a tiny fraction
being depleted during the main sequence evolution due to gravitational
settling.
In Fig. 1 we also compare the sound speed and density profiles of a
typical static model which has been constructed using the same physical
inputs as in model Btz including its composition profiles as well.
In the interior, the sound speed of the static model is almost the same
as that of the evolutionary model, while in the outer layers
it represents better that of the Sun. This improvement is most probably
due to better treatment of surface layers in the static model through
the use of a different prescription to calculate convective flux and
also the adoption of a better atmospheric model.
Despite all the positive aspects,
solar models including tachocline mixing still need further
improvements. Model Btz, for example, shows significant
departure from the seismic Sun in its density profile, even though this
quantity is in better agreement in comparison to model ref.
Further, it assumes a photospheric value for the heavy elements,
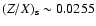 which is somewhat higher than the observed value.
The reason is that a model
calibrated to
which is somewhat higher than the observed value.
The reason is that a model
calibrated to
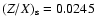 ,
such as model Bt in Brun et al. (1999),
is not as close to the seismic Sun as model Btz, because of a smaller
Z content and to the resulting variation of the opacities in the
radiative interior. Therefore, we would like to reach between our
new models and the Sun an agreement in density and sound speed better
than that with model Btz, but without having to relax the
,
such as model Bt in Brun et al. (1999),
is not as close to the seismic Sun as model Btz, because of a smaller
Z content and to the resulting variation of the opacities in the
radiative interior. Therefore, we would like to reach between our
new models and the Sun an agreement in density and sound speed better
than that with model Btz, but without having to relax the
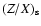 constraint in the calibration process. Finally, the
lithium depletion in the PMS phase is overestimated, indicating the
need for a better treatment of this early phase of evolution. All the
cited improvements can come both from a better treatment of the
mixing at the top of the radiation zone or by a better microscopic description. We
refer to Piau & Turck-Chièze (2001) for a careful study of the PMS
lithium depletion problem and focus our attention on the present Sun.
We propose to keep for most of our models the same
treatment for the tachocline mixing as introduced in Brun et al. (1999)
but to allow for variations within uncertainties of the main
physical ingredients, in order to see if any improvements can be obtained
before introducing a new description of the tachocline mixing.
constraint in the calibration process. Finally, the
lithium depletion in the PMS phase is overestimated, indicating the
need for a better treatment of this early phase of evolution. All the
cited improvements can come both from a better treatment of the
mixing at the top of the radiation zone or by a better microscopic description. We
refer to Piau & Turck-Chièze (2001) for a careful study of the PMS
lithium depletion problem and focus our attention on the present Sun.
We propose to keep for most of our models the same
treatment for the tachocline mixing as introduced in Brun et al. (1999)
but to allow for variations within uncertainties of the main
physical ingredients, in order to see if any improvements can be obtained
before introducing a new description of the tachocline mixing.
3 Improved solar models
3.1 Model parameters
We see from the foregoing discussion that there is still need to
improve our mixed tachocline models. In this section we outline the modifications
and models computed for this study, which for the sake of clarity are
also summarised in Table 2 with their designation and the corresponding
choice of parameters.
Note: The parameters,
d and
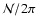
,
represent twice the extent of the tachocline
h and the
Brunt-Väisälä frequency (in
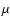
Hz) in the overshoot region and are related to our
effective macroscopic coefficient
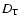
(cf., Brun et al.
1999).
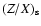
,
S11,
S33,
S34,
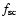
and
Di are respectively, the surface ratio of heavy elements to hydrogen abundances
of the models at the solar age, the variation applied in the nuclear cross section of
pp,
3He-
3He and
3He-
4He, the screening prescription used in the model
(either Weak or Intermediate) and the variation of the microscopic diffusive coefficient.
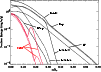 |
Figure 2:
Contribution to the nuclear energy generation of the main pp-chain and CNO cycles nuclear reactions as
a function of the normalised solar radius. |
 pp nuclear reaction: when dealing with the properties of the solar core
one is inevitably led to the nuclear reaction rates and
their intrinsic uncertainties (Brun et al. 1998; Bahcall et al. 1998a; Morel et al. 1999).
Unfortunately, the fundamental nuclear reaction in the pp-chain, i.e.,
pp nuclear reaction: when dealing with the properties of the solar core
one is inevitably led to the nuclear reaction rates and
their intrinsic uncertainties (Brun et al. 1998; Bahcall et al. 1998a; Morel et al. 1999).
Unfortunately, the fundamental nuclear reaction in the pp-chain, i.e.,
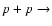 D
D
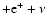 ,
is an electroweak interaction and
its cross section has not been determined via direct experimentation. Recent
theoretical works give an uncertainty of about 1-2% in the
determination of S11 (Adelberger et al. 1998). But a seismic
calibration of this cross section indicated that up to a 4% increase is
favoured (Antia & Chitre 1998). We have therefore decided to allow in our models for a
variation up to 4% of this dominant cross-section and will also determine
which value of S11(0) gives the best agreement with helioseismic inversion.
,
is an electroweak interaction and
its cross section has not been determined via direct experimentation. Recent
theoretical works give an uncertainty of about 1-2% in the
determination of S11 (Adelberger et al. 1998). But a seismic
calibration of this cross section indicated that up to a 4% increase is
favoured (Antia & Chitre 1998). We have therefore decided to allow in our models for a
variation up to 4% of this dominant cross-section and will also determine
which value of S11(0) gives the best agreement with helioseismic inversion.
Aside the fundamental pp nuclear reaction, other reactions can possibly
modify the central structure of the Sun. In Fig. 2 we plot the
energy production of the dominant nuclear reactions from the pp chains as well as
the three main reactions from the CNO cycle. These reactions are
the following: D
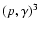 He, 3He
He, 3He
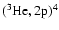 He,
3He
He,
3He
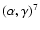 Be, 7Li
Be, 7Li
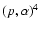 He from the pp chains and
13C
He from the pp chains and
13C
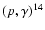 N, 14N
N, 14N
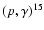 O
O
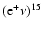 N,
15N
N,
15N
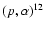 C from the CNO cycle. To plot these curves we
have used the internal structure of ref model for the present Sun.
C from the CNO cycle. To plot these curves we
have used the internal structure of ref model for the present Sun.
Not all the nuclear reactions displayed in Fig. 2 are
expected to modify the thermal structure of the solar core. We
can already discard some of them by considering either their importance
in the energy budget or the time they require to reach equilibrium.
 CNO cycle nuclear reactions: because the Sun is a low mass star, we
don't expect the CNO nuclear reactions to significantly influence the solar central region
since the cycle contributes to less than 2% of the total
nuclear energy production (Clayton 1968; Bahcall 1989; Bahcall et al. 2001). We have therefore not introduced any
modification of these reactions in our models and refer to
Turck-Chièze et al. (2001) for a discussion of their influence on the solar structure.
CNO cycle nuclear reactions: because the Sun is a low mass star, we
don't expect the CNO nuclear reactions to significantly influence the solar central region
since the cycle contributes to less than 2% of the total
nuclear energy production (Clayton 1968; Bahcall 1989; Bahcall et al. 2001). We have therefore not introduced any
modification of these reactions in our models and refer to
Turck-Chièze et al. (2001) for a discussion of their influence on the solar structure.
 D-p and 7Li-p nuclear reactions: because the lifetime of deuterium
and lithium is very short, these elements quickly reach equilibrium abundance in the temperature
and density range prevailing in the solar core. Consequently, these
reactions do not have a significant impact on the core structure even
though they are very energetic. We refer to Gautier & Morel (1997) for a
discussion of the important D/H astrophysical ratio and to Brun et al. (1999) for
a study of the influence of the 7Li-p cross section on photospheric lithium abundance.
We will adopt in all our models the cross sections proposed by the NACRE compilation (Angulo
et al. 1999).
D-p and 7Li-p nuclear reactions: because the lifetime of deuterium
and lithium is very short, these elements quickly reach equilibrium abundance in the temperature
and density range prevailing in the solar core. Consequently, these
reactions do not have a significant impact on the core structure even
though they are very energetic. We refer to Gautier & Morel (1997) for a
discussion of the important D/H astrophysical ratio and to Brun et al. (1999) for
a study of the influence of the 7Li-p cross section on photospheric lithium abundance.
We will adopt in all our models the cross sections proposed by the NACRE compilation (Angulo
et al. 1999).
 3He- 3He and 3He-4He nuclear reactions:
these nuclear cross sections play a crucial role in determining the branching between
the ppI and the ppII and ppIII chains and thus directly influence the
high energy neutrino production.
3He- 3He is one of the most energetic reactions in the pp-chain along with D-p.
Unlike deuterium and lithium, 3He does not reach its
equilibrium value on a very short time scale but instead slowly builds up
for temperatures less than
3He- 3He and 3He-4He nuclear reactions:
these nuclear cross sections play a crucial role in determining the branching between
the ppI and the ppII and ppIII chains and thus directly influence the
high energy neutrino production.
3He- 3He is one of the most energetic reactions in the pp-chain along with D-p.
Unlike deuterium and lithium, 3He does not reach its
equilibrium value on a very short time scale but instead slowly builds up
for temperatures less than
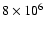 K (Clayton 1968).
In a solar model, the resulting theoretical 3He abundance profile peaks
around
K (Clayton 1968).
In a solar model, the resulting theoretical 3He abundance profile peaks
around
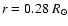 with a characteristic bell-like curve due
to the competition respectively between its creation and its
destruction in the outer and in the inner regions of the solar
core. At the same time, being one of the most energetic reactions in
the pp chains and reaching equilibrium gradually in the outer parts of
the nuclear region, this cross section is expected to have an influence on
the thermal structure of the solar core at a level where seismic inversions can detect it.
Even though the 3He-4He nuclear reaction does not contribute much to the
solar energy budget, the fact that it involves both 3He and 4He chemical elements
makes it also an important reaction to study. The experimental uncertainty of S33 and
S34 are respectively
with a characteristic bell-like curve due
to the competition respectively between its creation and its
destruction in the outer and in the inner regions of the solar
core. At the same time, being one of the most energetic reactions in
the pp chains and reaching equilibrium gradually in the outer parts of
the nuclear region, this cross section is expected to have an influence on
the thermal structure of the solar core at a level where seismic inversions can detect it.
Even though the 3He-4He nuclear reaction does not contribute much to the
solar energy budget, the fact that it involves both 3He and 4He chemical elements
makes it also an important reaction to study. The experimental uncertainty of S33 and
S34 are respectively 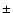 8% and
8% and 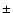 10% (Adelberger et al. 1998).
10% (Adelberger et al. 1998).
 Intermediate screening: we use the intermediate screening prescription
of Mitler (1977) in all our models except one that uses the classical weak screening of Salpeter (1954).
It should be recognised that the screening in stellar nuclear reaction rates is a sensitive
issue which is not yet completely understood (Dzitko et al. 1995; Wilets et al. 2000).
Depending on the solar thermodynamical conditions and the chemical species interacting
in the nuclear reaction considered, one has to introduce the adequate screening factor,
Intermediate screening: we use the intermediate screening prescription
of Mitler (1977) in all our models except one that uses the classical weak screening of Salpeter (1954).
It should be recognised that the screening in stellar nuclear reaction rates is a sensitive
issue which is not yet completely understood (Dzitko et al. 1995; Wilets et al. 2000).
Depending on the solar thermodynamical conditions and the chemical species interacting
in the nuclear reaction considered, one has to introduce the adequate screening factor,
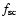 ,
coming from the surrounding particles present in the solar plasma which in general differ
from the screening effect evaluated by nuclear physicist in their experiments. There are thus
several sources of uncertainties in evaluating the cross sections and
screening effects for any given nuclear reaction that we intend to consider in this work.
,
coming from the surrounding particles present in the solar plasma which in general differ
from the screening effect evaluated by nuclear physicist in their experiments. There are thus
several sources of uncertainties in evaluating the cross sections and
screening effects for any given nuclear reaction that we intend to consider in this work.
 Opacities, microscopic diffusion and heavy elements abundance Z:
the structure of solar radiative zone is very sensitive to these two physical processes and
to the heavy elements abundance. These are all closely related since a change
in Z leads to a change in the opacity
Opacities, microscopic diffusion and heavy elements abundance Z:
the structure of solar radiative zone is very sensitive to these two physical processes and
to the heavy elements abundance. These are all closely related since a change
in Z leads to a change in the opacity 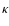 and in the microscopic diffusion,
which in turn modify Z as a consequence of the iterative calibration process.
The opacity is accurately computed (error
and in the microscopic diffusion,
which in turn modify Z as a consequence of the iterative calibration process.
The opacity is accurately computed (error  5%)
for temperatures greater than 104 K (Iglesias & Rogers 1996), their main sources of
uncertainties come from the relative composition and the ionisation degree
of the heavy elements as well as quantum effects (Rogers & Iglesias 1998).
In this work we will leave
5%)
for temperatures greater than 104 K (Iglesias & Rogers 1996), their main sources of
uncertainties come from the relative composition and the ionisation degree
of the heavy elements as well as quantum effects (Rogers & Iglesias 1998).
In this work we will leave 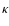 unchanged and will concentrate instead on
the heavy elements abundance Z and on the amplitude of the microscopic coefficients Di.
From a detailed comparison with the work of Turcotte et al. (1998), Brun et al. (1998)
have confirmed that the analytical expressions for the microscopic diffusion
coefficients given by Michaud & Proffitt (1993) are accurate enough to deal with the solar case.
For the Sun, these uncertainties are at most 15%. In order to reduce the
chemical composition gradient present at the base of the convection zone, which
has been found to be too large in model ref compared to the
seismically deduced one, we have run one model with Di reduced by 10%.
The heavy elements abundance of our models has been calibrated to the observed value
of Grevesse et al. (1996), i.e.,
unchanged and will concentrate instead on
the heavy elements abundance Z and on the amplitude of the microscopic coefficients Di.
From a detailed comparison with the work of Turcotte et al. (1998), Brun et al. (1998)
have confirmed that the analytical expressions for the microscopic diffusion
coefficients given by Michaud & Proffitt (1993) are accurate enough to deal with the solar case.
For the Sun, these uncertainties are at most 15%. In order to reduce the
chemical composition gradient present at the base of the convection zone, which
has been found to be too large in model ref compared to the
seismically deduced one, we have run one model with Di reduced by 10%.
The heavy elements abundance of our models has been calibrated to the observed value
of Grevesse et al. (1996), i.e.,
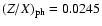 (see Table 1).
Model Btz introduced earlier has been computed
with an initial heavy elements abundance
Z0=0.01959=Zref that leads to
(see Table 1).
Model Btz introduced earlier has been computed
with an initial heavy elements abundance
Z0=0.01959=Zref that leads to
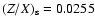 or 4% higher than
or 4% higher than
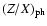 .
.
 Mixing: it is very tempting to introduce a
mild mixing in the nuclear region, for example very close to the 3He peak,
in order to improve the solar model structure and to reduce the predicted neutrino fluxes
(Haxton 1997; Brun et al. 1998).
However, the presence of a mixing in the solar core can be rejected on account of
the helioseismic constraints, due to the huge disagreement in the central region that
it generates (of the order of few % in
Mixing: it is very tempting to introduce a
mild mixing in the nuclear region, for example very close to the 3He peak,
in order to improve the solar model structure and to reduce the predicted neutrino fluxes
(Haxton 1997; Brun et al. 1998).
However, the presence of a mixing in the solar core can be rejected on account of
the helioseismic constraints, due to the huge disagreement in the central region that
it generates (of the order of few % in
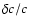 ).
This seismic evidence along with the recent results of the SNO neutrino experiment
(Ahmad et al. 2001, 2002), strongly disfavour a "macroscopic mixing'' as the source of
the electron neutrino deficit seen on Earth's detectors but instead support
the idea of neutrino flavour oscillations.
).
This seismic evidence along with the recent results of the SNO neutrino experiment
(Ahmad et al. 2001, 2002), strongly disfavour a "macroscopic mixing'' as the source of
the electron neutrino deficit seen on Earth's detectors but instead support
the idea of neutrino flavour oscillations.
Therefore we limited ourselves to the tachocline
region for which we have better evidence for mixing
and a relatively more elaborate physical description available.
We used the parameters of model
Btz (e.g.,
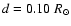 and
and
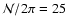
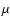 Hz),
which have been proven to give a reasonable agreement with seismic constraints and
light elements photospheric abundance (cf. Sect. 2.3 and Brun et al. 1999). For one case we have
assumed a wider mixing zone, i.e.,
Hz),
which have been proven to give a reasonable agreement with seismic constraints and
light elements photospheric abundance (cf. Sect. 2.3 and Brun et al. 1999). For one case we have
assumed a wider mixing zone, i.e.,
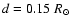 ,
in order to limit even more the gravitational settling and therefore
reduce the steep gradients seen in the sound speed, density and composition profile
at the base of the convection zone. We have also used the prescription
introduced by Elliott & Gough (1999), namely a constant diffusion
coefficient
,
in order to limit even more the gravitational settling and therefore
reduce the steep gradients seen in the sound speed, density and composition profile
at the base of the convection zone. We have also used the prescription
introduced by Elliott & Gough (1999), namely a constant diffusion
coefficient
 operating over a small domain
operating over a small domain
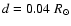 .
It is not our intention to reevaluate this coefficient,
but just to compare both mixing prescriptions.
.
It is not our intention to reevaluate this coefficient,
but just to compare both mixing prescriptions.
Having introduced all these modifications in our evolution code we
derive the profiles of sound speed, density, hydrogen abundance
and temperature that we discuss in the following subsections.
We first consider the relative differences in the sound speed and density between the
Sun and our new modified solar models.
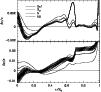 |
Figure 3:
The relative difference in sound speed and density profiles between
the Sun and solar models as a function of fractional radius.
Model ref including
only microscopic diffusion and the mixed models Btz,
N0 and N (the latter two with increased pp cross section),
are represented respectively with solid, short-dashed,
dash-dotted and long-dashed lines.
Superimposed on model ref is the 1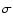 error envelope coming from the helioseismic inversion.
error envelope coming from the helioseismic inversion. |
In Fig. 3 we display two new models, N0 and N, which include
respectively an enhanced pp nuclear cross section by 2% and 3.5%, along with
the older models ref and Btz already presented in Fig. 1.
Clearly the relative differences in the sound speed and density between
the Sun and model N, and to a lesser extent model N0, are smaller in comparison to
model ref and the mixed model Btz. This is really encouraging because contrary to model
Btz, both models N0 and N have been calibrated to the exact value of
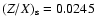 used
in model ref. This indicates that the effect of Z via the opacity
used
in model ref. This indicates that the effect of Z via the opacity
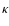 can be compensated by a small variation of the S11.
Thus a variation of the order of a few percent of
either the heavy elements abundance or the fundamental pp nuclear reaction rate seems to
have the same effect on the model sound speed profile in the upper part of the radiative
region but not below
can be compensated by a small variation of the S11.
Thus a variation of the order of a few percent of
either the heavy elements abundance or the fundamental pp nuclear reaction rate seems to
have the same effect on the model sound speed profile in the upper part of the radiative
region but not below
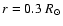 where contrary to case Btz, model N departs from ref.
For the density, a variation of S11 modifies the profile everywhere resulting in a
significantly better agreement for case N, at least above
where contrary to case Btz, model N departs from ref.
For the density, a variation of S11 modifies the profile everywhere resulting in a
significantly better agreement for case N, at least above
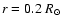 .
Thus it is very useful to assess the accuracy of a model by considering both the sound speed and
the density profiles, because it allows one to distinguish
the impact of different physical processes on solar structure. In this
particular case an increase of S11 by 3.5% seems to be favoured by
helioseismology, as opposed to an increase of S11 by 2% or of
.
Thus it is very useful to assess the accuracy of a model by considering both the sound speed and
the density profiles, because it allows one to distinguish
the impact of different physical processes on solar structure. In this
particular case an increase of S11 by 3.5% seems to be favoured by
helioseismology, as opposed to an increase of S11 by 2% or of
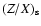 .
.
It may be noticed that in Fig. 3 the agreement in sound speed inside
the convection zone is much better as compared to that for the same
models in Fig. 1. This improvement arises because we have scaled the
solar radius in the models by a factor of 1.0003 before forming the
difference with the seismically deduced sound speed and density
profiles. This scaling of the radius appears to remove most of the
discrepancy in the upper convection zone, but does not affect the interior.
This may be expected since a correction of
0.03% in radial distance is only a small fraction of scale height in
the interior, while it can become comparable to the scale height in the
photospheric layers, resulting in significant differences in outer regions.
A better agreement with the Sun is also obtained in the outer convective zone
in the case of a static model (Fig. 1), which assumes a different treatment
of the surface layers. It would appear that uncertainties in
treatment of these layers are responsible for the discrepancy in the
outer convection zone. In standard solar models the surface is normally defined as the
layer where the temperature equals the effective temperature.
Because of significant uncertainties in treatment of surface layers,
the position of the surface may not be correctly estimated in a solar
model. Thus, we believe that the scaling of radius effectively corrects
for this error.
In all subsequent figures we have used this scaled radius when comparing the solar models
with profiles inferred from inversions.
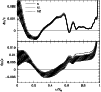 |
Figure 4:
The relative difference in sound speed and density profiles between
the Sun and solar models as a function of fractional radius, showing the effect
of modifying the cross sections S33 and S34.
The mixed models N, N1 and N2 are represented respectively with
solid, short-dashed and long-dashed lines. Superimposed on model N is
the 1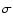 error envelope coming from the helioseismic inversion.
error envelope coming from the helioseismic inversion. |
We have just seen that a small change in S11 can significantly
improve the agreement between solar models and the seismic Sun when
combined with a treatment of the solar tachocline. In the same spirit we have
computed a sequence of models including
modifications of S33 and S34 nuclear reaction cross sections (cf. Sect. 3.1).
Models N1 and N2 share the same tachocline macroscopic
treatment, calibration of heavy elements to
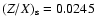 and increase of
S11 by 3.5% as model N, but differ by having respectively an increase of S33 by
8% and a decrease of S34 by 10% (see Table 2).
and increase of
S11 by 3.5% as model N, but differ by having respectively an increase of S33 by
8% and a decrease of S34 by 10% (see Table 2).
In Fig. 4 we plot the relative differences in density and sound speed between
the Sun and models N, N1 and N2. We first notice that the
applied modifications of the cross section S33 and S34
improve the core structure both in density and sound speed. A
variation of S34 by 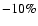 seems to affect more the very central
region than a variation of S33 by
seems to affect more the very central
region than a variation of S33 by 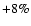 does, even if we take into
account the fact that S33 has been varied by a smaller amount.
For model N2 the agreement in
does, even if we take into
account the fact that S33 has been varied by a smaller amount.
For model N2 the agreement in
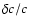 in the core improves by a
factor 2 with respect to model N,
whereas for model N1 it does only by 20% or so. For
in the core improves by a
factor 2 with respect to model N,
whereas for model N1 it does only by 20% or so. For
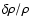 ,
the influence of these two cross sections is more modest and results in a small
gradual change of the profile over the solar radius.
,
the influence of these two cross sections is more modest and results in a small
gradual change of the profile over the solar radius.
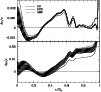 |
Figure 5:
The relative difference in sound speed and density profiles between
the Sun and solar models as a function of fractional radius, showing the effect
of modifying the cross sections S33 and S34.
The mixed models N0, N02 and N03 are represented respectively with solid,
short-dash-long-dashed and dash-dotted lines. Superimposed on model N0
is the 1 error envelope coming from the helioseismic inversion.
error envelope coming from the helioseismic inversion. |
We now turn to models N02 and N03 displayed in Fig. 5 along
with model N0 as reference. Models N02 and N03 are identical to model N0
except that they respectively include a decrease of S34 by 10% and the cumulative
opposite variations of the nuclear cross sections S33 by 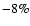 and S34 by
and S34 by 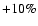 (see Table 2), in order to modify the pp branching ratio such as to
increase the high energy neutrino flux. Model N02 exhibits a better core profile than
model N0 does by having both relative differences closer to zero.
However, these two models do not differ from each other
as much as their counterpart models N and N2 do and are within the
(see Table 2), in order to modify the pp branching ratio such as to
increase the high energy neutrino flux. Model N02 exhibits a better core profile than
model N0 does by having both relative differences closer to zero.
However, these two models do not differ from each other
as much as their counterpart models N and N2 do and are within the 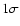 error bar.
In overall the decrease of S34 represents in this case a small progress toward a better
agreement with the seismic data. On the contrary, model N03 that has been computed on purpose
with opposite variations of S33 and S34 is almost everywhere in better agreement than model N0 is.
Its density profile is significantly closer to the Sun.
The main exception is in the very central part of the solar core,
where the
error bar.
In overall the decrease of S34 represents in this case a small progress toward a better
agreement with the seismic data. On the contrary, model N03 that has been computed on purpose
with opposite variations of S33 and S34 is almost everywhere in better agreement than model N0 is.
Its density profile is significantly closer to the Sun.
The main exception is in the very central part of the solar core,
where the
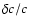 is quite off and the
is quite off and the
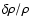 exhibits a pronouncedly curved shape.
Model N03 is an interesting solar model but our variation of the S33 and S34 cross sections
is certainly too large and goes in the wrong direction for the central parts.
In summary, these new sets of results confirm that it is possible to improve
the overall agreement between the models and the seismic Sun by modifying, within
their uncertainties, the rates of important nuclear reactions such as S33 and S34. Here it appears
that the seismic data favour a decrease of S34 and an increase of S33 rather than the opposite.
exhibits a pronouncedly curved shape.
Model N03 is an interesting solar model but our variation of the S33 and S34 cross sections
is certainly too large and goes in the wrong direction for the central parts.
In summary, these new sets of results confirm that it is possible to improve
the overall agreement between the models and the seismic Sun by modifying, within
their uncertainties, the rates of important nuclear reactions such as S33 and S34. Here it appears
that the seismic data favour a decrease of S34 and an increase of S33 rather than the opposite.
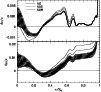 |
Figure 6:
The relative difference in sound speed and density profiles between
the Sun and solar models as a function of fractional radius,
showing the effect of changing the nuclear screening.
The mixed models N2, N02 and
N0W are represented respectively with solid, short-dashed and
long-dashed lines. Superimposed on model N2
is the 1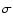 error envelope coming from the helioseismic inversion.
error envelope coming from the helioseismic inversion. |
We would like now to characterise the influence of the nuclear screening on the
solar model sound speed and density profiles. We have therefore changed the
screening prescription from intermediate to weak (cf. Sect. 3.1), on the top of
all the modifications already introduced in one model, that we have chosen to
be N02, and called that new model N0W.
In Fig. 6 we compare results obtained for models N2, N02 and N0W,
in order to quantify the influence of the nuclear screening on the solar core.
In the very central part of model N0W the agreement seems to
not be as good as in model N02. The relative sound speed difference profile
between the Sun and model N0W for
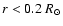 reaches a value of the
same order as model N0 in Fig. 5 and thus the change of nuclear screening seems to
compensate the change by 10% in S34 made in model N02. The density
profile of model N0W is in better agreement with the Sun than model N02 above
0.3
reaches a value of the
same order as model N0 in Fig. 5 and thus the change of nuclear screening seems to
compensate the change by 10% in S34 made in model N02. The density
profile of model N0W is in better agreement with the Sun than model N02 above
0.3 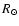 .
We should be careful in evaluating the effect on the
core structure of using a different screening prescription, because
model N0W includes an increase of S11(0) already calibrated on
the intermediate screening, but the inversion seems to indicate that a
smaller increase of S11 is favoured if one has to use a weak nuclear
screening instead (cf., Table 3).
.
We should be careful in evaluating the effect on the
core structure of using a different screening prescription, because
model N0W includes an increase of S11(0) already calibrated on
the intermediate screening, but the inversion seems to indicate that a
smaller increase of S11 is favoured if one has to use a weak nuclear
screening instead (cf., Table 3).
As already stated in Sect. 3.1, we are interested in a reduction of the steep
composition gradient at the base of the convection zone, which implies a
decrease of the microscopic diffusion coefficients Di. Model NDincludes such a decrease by 10% of Di along with other variations
identical to model N2. It is obvious from Fig. 7, that a reduction of
microscopic diffusion is not appropriate, since model NDsystematically departs more from the seismic Sun in the radiation
zone than model N2. It is well known that microscopic diffusion
modifies and improves the stratification in the radiation zone
(Christensen-Dalsgaard et al. 1993). Based on the sound speed and density profiles,
an increase of Di is favoured rather than a decrease as in model ND.
However an increase of Di would make the composition gradient
at the base of the convective zone even steeper. Thus it seems quite
unlikely that the microscopic diffusion is the remaining source of the
discrepancies seen in a solar model like N2.
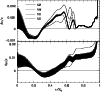 |
Figure 7:
The relative difference in sound speed and density profiles between
the Sun and solar models. The mixed models N2, NM, NE and ND are
represented respectively with solid, short-dashed, long-dashed and
dash-dotted lines. Superimposed on model N2 is the 1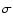 error envelope
coming from the helioseismic inversion.
error envelope
coming from the helioseismic inversion. |
In the sequence of models we have just discussed, we were only concerned with
the influences on the solar structure of variations
in the nuclear and atomic input data. We are now interested in
assessing the impact on
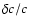 and
and
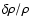 of
varying the macroscopic parameters used for the solar tachocline. In
Fig. 7 we also display models NM and
NE which include the same microscopic ingredients as
model N2 but with respectively, a broader mixing region with
of
varying the macroscopic parameters used for the solar tachocline. In
Fig. 7 we also display models NM and
NE which include the same microscopic ingredients as
model N2 but with respectively, a broader mixing region with
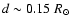 (i.e., tachocline thickness
(i.e., tachocline thickness
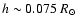 )
and another macroscopic
treatment for the tachocline (Elliott & Gough 1999),
over a shorter distance
)
and another macroscopic
treatment for the tachocline (Elliott & Gough 1999),
over a shorter distance
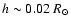 (see Table 2).
We clearly see that model NE does not reduce the bump in
(see Table 2).
We clearly see that model NE does not reduce the bump in
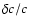 or the steep gradient in
or the steep gradient in
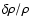 at the base of the
convection zone seen in model ref in Fig. 3 as
much as the two other models N2 and NM. Even though model NE
includes the same nuclear cross section modifications, it is
further away from the seismic Sun. One reason for this poorer
agreement is that the tachocline mixing is too shallow. The value of
0.02
at the base of the
convection zone seen in model ref in Fig. 3 as
much as the two other models N2 and NM. Even though model NE
includes the same nuclear cross section modifications, it is
further away from the seismic Sun. One reason for this poorer
agreement is that the tachocline mixing is too shallow. The value of
0.02 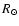 adopted in model NE for the extent of the mixing has been calibrated by
Elliott & Gough using a static model of the Sun at the present age
and by convolving with the inversion kernels afterward. This
convolution procedure using the inversion kernels makes the effective
thickness of the mixing broader, mainly because of their overlapping
radial resolution, and as a consequence Elliott & Gough
found that
adopted in model NE for the extent of the mixing has been calibrated by
Elliott & Gough using a static model of the Sun at the present age
and by convolving with the inversion kernels afterward. This
convolution procedure using the inversion kernels makes the effective
thickness of the mixing broader, mainly because of their overlapping
radial resolution, and as a consequence Elliott & Gough
found that 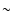 0.02
0.02 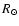 was large enough to get
rid of the bump in
was large enough to get
rid of the bump in
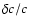 .
It is quite puzzling that the
introduction of their mixing in our evolutionary model does not give at
all the same result. Indeed model NE is significantly different from
models N2 or NM, that we believe are in quite good agreement
with the seismic Sun. It can be seen in Fig. 7 that an
increase of the extent of the mixing region in model NM does not
affect that much the density and sound speed profiles except for
the slight modification close to the base of the convection zone. We
therefore conclude that not all prescriptions for "tachocline mixing''
give the same result and that ours is quite efficient in suitably
modelling this transition region.
.
It is quite puzzling that the
introduction of their mixing in our evolutionary model does not give at
all the same result. Indeed model NE is significantly different from
models N2 or NM, that we believe are in quite good agreement
with the seismic Sun. It can be seen in Fig. 7 that an
increase of the extent of the mixing region in model NM does not
affect that much the density and sound speed profiles except for
the slight modification close to the base of the convection zone. We
therefore conclude that not all prescriptions for "tachocline mixing''
give the same result and that ours is quite efficient in suitably
modelling this transition region.
3.3 Hydrogen abundance profile and photospheric composition
We have so far addressed the question of the influence of mixing and microscopic
variations on the primary inversion quantities such as the sound speed
and the density. We would now like to assess what are the consequences
of such changes on the profile and photospheric value of the
hydrogen abundance
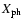 .
Using the secondary inversion procedure introduced by Antia & Chitre
(1998), we have compared the hydrogen abundance profile in the Sun with that predicted by our new
set of solar models. By assuming the Z profile of the models we have calculated the
difference of X between each model and the Sun.
.
Using the secondary inversion procedure introduced by Antia & Chitre
(1998), we have compared the hydrogen abundance profile in the Sun with that predicted by our new
set of solar models. By assuming the Z profile of the models we have calculated the
difference of X between each model and the Sun.
In Fig. 8 we represent the absolute difference
in hydrogen abundance profile 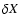 between the solar models ref, Btz,
N0 and N (cf., Table 2) and the Sun. As with
between the solar models ref, Btz,
N0 and N (cf., Table 2) and the Sun. As with
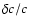 and
and
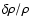 displayed in Fig. 3, it is quite clear that the mixed models are closer to the
inferred solar hydrogen abundance than the purely
microscopic model ref is. This improvement occurs mainly
close to the base of the convection zone and in the convection
zone itself (i.e., indicating a closer photospheric value) as expected
by the introduction of our shallow tachocline mixing. The reason for
such an improvement is twofold:
displayed in Fig. 3, it is quite clear that the mixed models are closer to the
inferred solar hydrogen abundance than the purely
microscopic model ref is. This improvement occurs mainly
close to the base of the convection zone and in the convection
zone itself (i.e., indicating a closer photospheric value) as expected
by the introduction of our shallow tachocline mixing. The reason for
such an improvement is twofold:
 Firstly, by introducing a macroscopic mixing at the base of the
convection zone, we hinder the gravitational settling of the chemical
species and as a result there are relatively more helium and heavy
elements in the convection zone, thus reducing the hydrogen
contribution in the plasma composition mixture to a value closer to the
seismically inferred one.
Firstly, by introducing a macroscopic mixing at the base of the
convection zone, we hinder the gravitational settling of the chemical
species and as a result there are relatively more helium and heavy
elements in the convection zone, thus reducing the hydrogen
contribution in the plasma composition mixture to a value closer to the
seismically inferred one.
 Secondly, the existence of an extended/mixed plateau of the
chemical composition due to the presence of a macroscopic mixing at
the base of the convection zone is in better agreement with the
seismically inferred X profile.
Secondly, the existence of an extended/mixed plateau of the
chemical composition due to the presence of a macroscopic mixing at
the base of the convection zone is in better agreement with the
seismically inferred X profile.
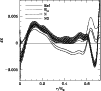 |
Figure 8:
The absolute difference in hydrogen abundance profile between the models
and the Sun is shown as a function of fractional radius. Model ref including
only microscopic diffusion and the mixed models BtzN0 and N are represented respectively with solid, short-dashed,
dash-dotted and long-dashed lines.
Superimposed on model ref is the 1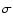 error envelope coming
from the helioseismic inversion.
error envelope coming
from the helioseismic inversion. |
This result, along with the improved sound speed and density profiles
discussed in the previous subsection, confirms the presence of macroscopic
mixing at the base of the convection zone and the necessity to
introduce this process in
solar models. Figure 8 also reveals
that a small increase by less than 4% of the cross-section of the fundamental
nuclear reaction pp is favoured as
well. Indeed models N0 and N are significantly closer to the inferred
hydrogen abundance over the whole radiative interior (except for a
small region between 0.35 and 0.5 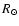 )
than either of the two
other models shown.
Further, Fig. 8 shows that the photospheric hydrogen content
of model N (
)
than either of the two
other models shown.
Further, Fig. 8 shows that the photospheric hydrogen content
of model N (
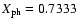 see Table 3) and model N0
are closer to the seismically inferred value of
see Table 3) and model N0
are closer to the seismically inferred value of
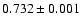 than both models Btz and ref.
Thus the effect of varying the nuclear cross section S11 is to change the
hydrogen surface abundance in the model via the calibration procedure,
the maximum amplitude of such modification being located in
the central region, leading to an improvement of the agreement between
the Sun and model N by at least a factor 2.
than both models Btz and ref.
Thus the effect of varying the nuclear cross section S11 is to change the
hydrogen surface abundance in the model via the calibration procedure,
the maximum amplitude of such modification being located in
the central region, leading to an improvement of the agreement between
the Sun and model N by at least a factor 2.
Table 3:
Seismic inference on hydrogen abundance and S11.
| Models |
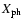 |
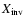 |
S11 |
| Ref |
0.7392 |
0.7311 |
4.053 |
| Btz |
0.7304 |
0.7269 |
4.053 |
N0 |
0.7338 |
0.7322 |
4.066 |
| N02 |
0.7339 |
0.7322 |
4.054 |
| N03 |
0.7334 |
0.7323 |
4.085 |
| N0W |
0.7337 |
0.7322 |
4.017 |
| N |
0.7333 |
0.7323 |
4.067 |
| N1 |
0.7334 |
0.7323 |
4.060 |
| N2 |
0.7336 |
0.7323 |
4.054 |
| ND |
0.7321 |
0.7327 |
4.057 |
| NM |
0.7329 |
0.7324 |
4.055 |
| NE |
0.7362 |
0.7317 |
4.048 |
Note:
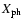 and
and
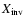 correspond respectively to
the photospheric hydrogen abundance achieved in the model and
deduced by seismic inversion. The seismically deduced pp
reaction cross-section S11 for each models is given in unit
of 10-25 MeV barns.
correspond respectively to
the photospheric hydrogen abundance achieved in the model and
deduced by seismic inversion. The seismically deduced pp
reaction cross-section S11 for each models is given in unit
of 10-25 MeV barns.
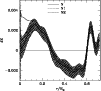 |
Figure 9:
The absolute difference in hydrogen abundance profile between
solar models and the Sun as a function of fractional radius. The mixed models N, N1 and N2 are
represented respectively with solid, short-dashed and long-dashed
lines. Superimposed on model N is the 1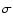 error envelope from
the helioseismic inversion.
error envelope from
the helioseismic inversion. |
While determining the X profile through inversions
we also get an estimate of pp reaction cross-section, S11 that is
required to match the observed solar luminosity. Table 3
lists the values obtained by assuming the Z profile of each of the models
considered in this study. It is clear that this estimate is not
sensitive to other properties of the model, except for the treatment of
the plasma screening. Beside model N0W, all other models yields a value
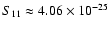 MeV Barns, which is 1.5% higher
than the value given by Adelberger et al. (1998). This is somewhat
less than the value given by Antia & Chitre (1999) or by
Degl'Innocenti et al. (1998). This difference is due to different
treatment of the plasma screening in calculating nuclear energy generation rates.
If one uses weak, intermediate or strong screening for the solar plasma, the resulting
increase in the pp cross section S11 found by seismic inversion
will vary respectively between 0.5% and 4%. Anyway all
screening treatments seem to indicate a higher value of S11 than currently calculated
by nuclear physicists.
However, it appears that with our intermediate screening (e.g., Mitler 1977),
an increase of S11 by 3.5% pushes the value of the pp cross section
beyond what is required from seismic constraints, but nevertheless we keep these models as they
amplify the effect of increasing S11 and are in rather good agreement with
the primary inversions of the sound speed and density.
MeV Barns, which is 1.5% higher
than the value given by Adelberger et al. (1998). This is somewhat
less than the value given by Antia & Chitre (1999) or by
Degl'Innocenti et al. (1998). This difference is due to different
treatment of the plasma screening in calculating nuclear energy generation rates.
If one uses weak, intermediate or strong screening for the solar plasma, the resulting
increase in the pp cross section S11 found by seismic inversion
will vary respectively between 0.5% and 4%. Anyway all
screening treatments seem to indicate a higher value of S11 than currently calculated
by nuclear physicists.
However, it appears that with our intermediate screening (e.g., Mitler 1977),
an increase of S11 by 3.5% pushes the value of the pp cross section
beyond what is required from seismic constraints, but nevertheless we keep these models as they
amplify the effect of increasing S11 and are in rather good agreement with
the primary inversions of the sound speed and density.
Apart from S11 Table 3 also gives the seismically inferred photospheric hydrogen
abundance (
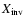 ). Again this value is not sensitive
to small differences in the Z profile, but is mainly determined by the photospheric Z value.
Thus all models other than Btz give
). Again this value is not sensitive
to small differences in the Z profile, but is mainly determined by the photospheric Z value.
Thus all models other than Btz give
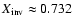 which is only slightly less than the value in the corresponding solar
model (
which is only slightly less than the value in the corresponding solar
model (
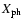 ). Further, this value will yield helium abundance,
). Further, this value will yield helium abundance,
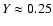 ,
which is also close to the independently inferred
value using seismic inversions in the convection zone (Basu 1998; DiMauro et al. 2002).
Thus the photospheric helium abundances obtained using different
techniques are consistent with each other.
,
which is also close to the independently inferred
value using seismic inversions in the convection zone (Basu 1998; DiMauro et al. 2002).
Thus the photospheric helium abundances obtained using different
techniques are consistent with each other.
We now consider the effect of a variation of the 3He-3He and 3He-4He
reaction rates on the hydrogen abundance via their influence on the
creation and destruction of helium in the solar core. In Fig.
9 we display the absolute difference 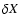 between the
mixed models N, N1 and N2 and the Sun. As we previously
did, we prefer to use the mixed model N for comparison in this plot,
since model N is significantly closer to the seismic Sun than model ref is.
The absolute differences
between the
mixed models N, N1 and N2 and the Sun. As we previously
did, we prefer to use the mixed model N for comparison in this plot,
since model N is significantly closer to the seismic Sun than model ref is.
The absolute differences 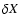 for the three models shown are all very close to zero.
We find that as with the sound speed profile, variations of the nuclear reaction
cross section S34 modifies relatively more the hydrogen abundance
profile than variations of S33, but obviously less than modifications that
variations of S11 can produce.
But for the quantity
for the three models shown are all very close to zero.
We find that as with the sound speed profile, variations of the nuclear reaction
cross section S34 modifies relatively more the hydrogen abundance
profile than variations of S33, but obviously less than modifications that
variations of S11 can produce.
But for the quantity 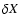 ,
model N gives a better agreement with the Sun
than models N1 and N2.
,
model N gives a better agreement with the Sun
than models N1 and N2.
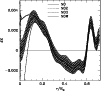 |
Figure 10:
The absolute difference in hydrogen abundance profile between
solar models and the Sun. The mixed models N0, N02, N03 and N0W are
represented respectively with solid, short-dashed, long-dashed
and dot-dashed lines. Superimposed on model N0 is the 1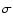 error envelope from
the helioseismic inversion.
error envelope from
the helioseismic inversion. |
In Fig. 10 we display the difference in hydrogen abundance
between the sequence of mixed models N0, N02,
N03 and N0W and the Sun. A first small difference with the previous figure
is that an increase of pp by +2% does not reduce as much the disagreement with the
inferred hydrogen abundance profiles than an increase by 3.5% does. As for model N2,
the hydrogen abundance profile of model N02 is only slightly affected in the inner central part.
This seems to indicate that the variation of 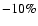 of S34 is too large.
Model N03, with opposite variations of S33 and S34 cross sections,
is shifted downward by -0.0005 compared to model N0 over most of the radiative zone and
its core profile is way off. All these models confirm the feeling that
the effects of the S33 and S34 cross section are mixed, in the sense
that in some regions the agreement is improved while in other regions it
becomes worse. Thus it is difficult to conclude if the variation of
these cross sections is justified basing one's argument on seismic inversion of the hydrogen abundance.
of S34 is too large.
Model N03, with opposite variations of S33 and S34 cross sections,
is shifted downward by -0.0005 compared to model N0 over most of the radiative zone and
its core profile is way off. All these models confirm the feeling that
the effects of the S33 and S34 cross section are mixed, in the sense
that in some regions the agreement is improved while in other regions it
becomes worse. Thus it is difficult to conclude if the variation of
these cross sections is justified basing one's argument on seismic inversion of the hydrogen abundance.
For model N0W, computed with a weak nuclear screening instead of
intermediate as in model N02, the result is a very small downward
shift of 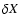 compared to model N02, but no significant improvement
otherwise. It is thus unlikely that the screening effect will correct near
the solar core the remaining discrepancy seen in the hydrogen abundance
profiles obtained in our mixed models.
compared to model N02, but no significant improvement
otherwise. It is thus unlikely that the screening effect will correct near
the solar core the remaining discrepancy seen in the hydrogen abundance
profiles obtained in our mixed models.
Finally in Fig. 11 we display the difference in hydrogen abundance
between the solar models and the Sun for cases NM and NEthat include different macroscopic parameters and case ND with
reduced microscopic diffusion along with case N2.
For model ND the effect of the microscopic diffusion is subtle to be appreciated
because it modifies non uniformly the hydrogen abundance. The model seems
to possess the closest hydrogen surface abundance
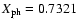 relative to
the inferred value
relative to
the inferred value
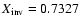 ,
and the smallest composition gradient
at the base of the convection zone, thus justifying the use of a smaller
microscopic diffusion coefficient Di. But the reduction seems overestimated
because model ND is the only solar model to exhibit a smaller hydrogen
photospheric abundance
,
and the smallest composition gradient
at the base of the convection zone, thus justifying the use of a smaller
microscopic diffusion coefficient Di. But the reduction seems overestimated
because model ND is the only solar model to exhibit a smaller hydrogen
photospheric abundance
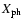 than the seismically inferred one.
Further, deeper down in the radiative interior the hydrogen
abundance profile departs too much from the inferred profile. Therefore, as
for the sound speed, a reduction of Di seems to be discarded by present
helioseismic inversions.
than the seismically inferred one.
Further, deeper down in the radiative interior the hydrogen
abundance profile departs too much from the inferred profile. Therefore, as
for the sound speed, a reduction of Di seems to be discarded by present
helioseismic inversions.
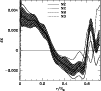 |
Figure 11:
The absolute difference in hydrogen abundance profile between
solar models and the Sun as a function of fractional radius. The mixed models N2, NE, NM and
ND are represented respectively with solid, short-dashed, long-dashed,
and dot-dashed lines. Superimposed on model N2 is the 1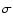 error
envelope coming from the helioseismic inversion.
error
envelope coming from the helioseismic inversion. |
The effect of a broader mixing on 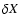 (i.e., model NM) is to reduce the
composition gradient and to extend the mixed plateau, properties that seem to
be in better agreement with the inferred X profile. Moreover,
(i.e., model NM) is to reduce the
composition gradient and to extend the mixed plateau, properties that seem to
be in better agreement with the inferred X profile. Moreover,
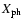 is closer to
is closer to
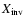 in models NM and ND than for example model N2.
Deeper down the improvement is not as obvious and
considering the fact that the extent of the tachocline mixing is
certainly over estimated in this model, we can hardly conclude
that it constitutes a better solution than, say, models N or N2. Model
NE is clearly worse in X as well as in
in models NM and ND than for example model N2.
Deeper down the improvement is not as obvious and
considering the fact that the extent of the tachocline mixing is
certainly over estimated in this model, we can hardly conclude
that it constitutes a better solution than, say, models N or N2. Model
NE is clearly worse in X as well as in
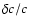 and
and
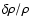 compared to
other mixed models. Whereas its profile deep in the radiative interior
is in reasonable agreement with the seismically inferred one, while it is clearly not
the case for the upper part (
compared to
other mixed models. Whereas its profile deep in the radiative interior
is in reasonable agreement with the seismically inferred one, while it is clearly not
the case for the upper part (
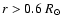 ). The resulting composition gradient is too steep and
the hydrogen abundance in the convective envelope too high.
). The resulting composition gradient is too steep and
the hydrogen abundance in the convective envelope too high.
To summarise our findings about the hydrogen abundance
profile, it can be stated that "tachocline mixing''
is very likely to occur in the Sun,
and that an increase of S11 is clearly
favoured by current helioseismic data, with an amplitude of the order of a few %.
Less obvious are the effects of the two others dominant nuclear cross sections, i.e., S33 and
S34, although they can lead to some improvement as well. On the other
side, neither the microscopic diffusion nor the screening effect seem
to cause significant changes. However, the screening prescription has been found to modify
significantly the value of the cross section of the pp nuclear reaction inferred by seismic inversion.
Our last two models NE and NM including variations of the macroscopic
parameters are not favoured by our study, because with model NE, the mixing is
too shallow and does not vary with time and with model NM the mixing is too broad.
We thus find that the seismically inferred photospheric hydrogen abundance is
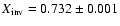 ,
but the value change quite a bit depending on the
value of heavy elements abundance assumed.
,
but the value change quite a bit depending on the
value of heavy elements abundance assumed.
We would like now to briefly discuss the new photospheric composition obtained
by our models at the solar age, with particular emphasis on light
elements depletion. As already stressed, the
mixed models exhibit a better overall chemical composition, say
compared to models with only microscopic diffusion such as ref. One chemical
element, namely the lithium, is crucial to assess the efficiency and
time dependence of macroscopic mixing. With the presence of an
effective macroscopic mixing at the base of the convection zone, all
the models presented in this study are expected to deplete a fair
amount of 7Li. All models, except NE, burn indeed a
substantial quantity of 7Li both in the PMS and in the main
sequence phases, thus reaching a photospheric abundance at the solar
age, Li ,
significantly smaller than the initial/meteoritic value,
Li0, i.e.,
,
significantly smaller than the initial/meteoritic value,
Li0, i.e.,
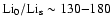 ,
in reasonable agreement with the
observations of Grevesse et al. (1996),
,
in reasonable agreement with the
observations of Grevesse et al. (1996),
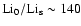 .
Model
NE depletes a large amount of lithium as well
(
.
Model
NE depletes a large amount of lithium as well
(
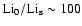 ), but most of it (
), but most of it ( 90%) in the PMS
phase, which is not realistic when compared with open cluster
observations. This comes about because the macroscopic coefficient
90%) in the PMS
phase, which is not realistic when compared with open cluster
observations. This comes about because the macroscopic coefficient
 used in this model, following Elliott & Gough treatment of
the tachocline, does not include any time dependence. Brun et al. (1999) have demonstrated
that a proper time dependence of
used in this model, following Elliott & Gough treatment of
the tachocline, does not include any time dependence. Brun et al. (1999) have demonstrated
that a proper time dependence of  causes
significant lithium burning along the main sequence as well. Another important
constraint is provided by the beryllium abundance,
which requires that the mixing must be shallow in order not to destroy this element by more than
10% (see Brun et al. 1999; Bell et al. 2001).
With either of the two diffusion coefficients used in this study,
causes
significant lithium burning along the main sequence as well. Another important
constraint is provided by the beryllium abundance,
which requires that the mixing must be shallow in order not to destroy this element by more than
10% (see Brun et al. 1999; Bell et al. 2001).
With either of the two diffusion coefficients used in this study,
 or
or
 ,
we easily achieve this goal, i.e., all the models but one deplete 9Be
by less than 10%. Model NM, which has been computed with the broadest tachocline mixing
(i.e.,
,
we easily achieve this goal, i.e., all the models but one deplete 9Be
by less than 10%. Model NM, which has been computed with the broadest tachocline mixing
(i.e.,
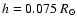 ), leads to an underabundance of 9Be of 20%, thus confirming that in
this model the mixing extends too deep inside the radiative zone. We interpret this result
as an indication that the tachocline mixing can not be broader than 5% in solar radius.
Thus using this upper limit for the tachocline extent, we are
quite confident about the efficiency of our macroscopic time dependent coefficient
), leads to an underabundance of 9Be of 20%, thus confirming that in
this model the mixing extends too deep inside the radiative zone. We interpret this result
as an indication that the tachocline mixing can not be broader than 5% in solar radius.
Thus using this upper limit for the tachocline extent, we are
quite confident about the efficiency of our macroscopic time dependent coefficient
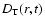 to
model the tachocline region and to lead not only to the proper
photospheric composition at the solar age but also in the earlier phases.
However, as already stated with model Btz, with our prescription the lithium
depletion is still too big in the PMS, even though it is reasonably distributed over the whole temporal
evolution compared, say, to model NE.
to
model the tachocline region and to lead not only to the proper
photospheric composition at the solar age but also in the earlier phases.
However, as already stated with model Btz, with our prescription the lithium
depletion is still too big in the PMS, even though it is reasonably distributed over the whole temporal
evolution compared, say, to model NE.
It has been known for more than thirty years that standard solar
models and neutrino experiments on Earth disagree on the amount of
neutrinos produced in the thermonuclear core of the Sun,
the former predicting always a flux in excess (Bahcall 1989).
A number of ingenious suggestions have been given to either explain
the discrepancy from revised and "non-standard'' solar models or by invoking neutrino flavour
oscillations from the electron neutrino
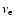 ,
generated in the pp
chains and CNO cycles, to its siblings the muon
,
generated in the pp
chains and CNO cycles, to its siblings the muon 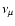 and tau
and tau
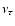 neutrinos or to the so-called "sterile neutrino'' (Haxton 1995;
Bahcall et al. 1998b). Here we intend to use the seismic diagnosis to
constrain as much as possible the theoretical neutrino flux, which is very
sensitive to the central temperature.
neutrinos or to the so-called "sterile neutrino'' (Haxton 1995;
Bahcall et al. 1998b). Here we intend to use the seismic diagnosis to
constrain as much as possible the theoretical neutrino flux, which is very
sensitive to the central temperature.
Figure 12 represents the relative temperature difference between solar models
ref, Btz, N, N0, N02 and N03 and the Sun. The overall agreement of the six
models is quite satisfactory, with model ref being the least accurate in the
tachocline region as expected.
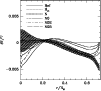 |
Figure 12:
The relative temperature difference between solar models ref, Btz, N, N0, N02 and N03 and the Sun. Note the somewhat larger uncertainties for this variable in
the neutrino production region (
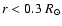 )
compared for example to the sound speed ones. )
compared for example to the sound speed ones. |
We can indeed notice that the introduction of a macroscopic mixing in the tachocline improves
the profile of all the models by at least a factor 2 above
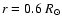 ,
over model ref, thus confirming the importance of taking into account the mixing
present in this transition region.
In the bulk of the radiative zone, some improvement comes from the increase of the pp
cross section and results in a flattening of
,
over model ref, thus confirming the importance of taking into account the mixing
present in this transition region.
In the bulk of the radiative zone, some improvement comes from the increase of the pp
cross section and results in a flattening of
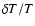 and a slightly closer agreement
with the Sun.
For the very central part, where the neutrinos are produced, the secondary seismic inversion of the temperature is less accurate with an error bar of
and a slightly closer agreement
with the Sun.
For the very central part, where the neutrinos are produced, the secondary seismic inversion of the temperature is less accurate with an error bar of
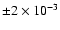 ,
and thus does not constrain the solar models as much.
Models ref and Btz are surprisingly good there.
Model N is quite satisfying except in this very central part.
This can be interpreted as an excessive increase of the pp cross section.
Models N0 and N03 seem to be our best models in the range [0,0.7]
,
and thus does not constrain the solar models as much.
Models ref and Btz are surprisingly good there.
Model N is quite satisfying except in this very central part.
This can be interpreted as an excessive increase of the pp cross section.
Models N0 and N03 seem to be our best models in the range [0,0.7]  .
While this could have been expected from model N0, based on the inversion of the sound speed
and density profiles (Sect. 3.2), it was not so for model N03 that has been computed with opposite
variation of the nuclear cross sections S33 and S34.
Effectively, it seems that for the temperature profile, the decrease of S34 by 10%, as in
model N02, does not lead to any progress in the central part while an increase does.
This conclusion is at odd with what we learnt from the sound speed inversion.
This could mean that either the secondary inversion of the temperature is not as reliable as
the sound speed (that is in part true but unsatisfactory) or that the temperature varies
differently with modifications of the main physical ingredients than the sound speed does,
due for example to a compensatory change of the central composition.
So, we have to be cautious in our conclusions regarding the very central part since this
is the region where the inversions are the least reliable.
Nevertheless, we still consider that for the temperature profile models ref, Btz,
N0, N03 and more marginally, model N, all represent seismically acceptable solutions
of the solar core. As a result, what one can expect to be the impact on the neutrino fluxes
of such diverse temperature profiles?
.
While this could have been expected from model N0, based on the inversion of the sound speed
and density profiles (Sect. 3.2), it was not so for model N03 that has been computed with opposite
variation of the nuclear cross sections S33 and S34.
Effectively, it seems that for the temperature profile, the decrease of S34 by 10%, as in
model N02, does not lead to any progress in the central part while an increase does.
This conclusion is at odd with what we learnt from the sound speed inversion.
This could mean that either the secondary inversion of the temperature is not as reliable as
the sound speed (that is in part true but unsatisfactory) or that the temperature varies
differently with modifications of the main physical ingredients than the sound speed does,
due for example to a compensatory change of the central composition.
So, we have to be cautious in our conclusions regarding the very central part since this
is the region where the inversions are the least reliable.
Nevertheless, we still consider that for the temperature profile models ref, Btz,
N0, N03 and more marginally, model N, all represent seismically acceptable solutions
of the solar core. As a result, what one can expect to be the impact on the neutrino fluxes
of such diverse temperature profiles?
Table 4:
Neutrino fluxes at Earth.
| |
Detector |
| Models |
71Ga |
37Cl |
Water |
| Ref |
127.1 |
7.04 |
4.99 |
| Btz |
127.1 |
7.04 |
4.99 |
| N0 |
123.7 |
6.41 |
4.48 |
| N03 |
128.2 |
7.08 |
4.99 |
| N0W |
121.4 |
6.10 |
4.25 |
| N |
122.5 |
6.18 |
4.29 |
| N1 |
121.3 |
6.0 |
4.16 |
| N2 |
119.3 |
5.7 |
3.93 |
| ND |
118.7 |
5.59 |
3.85 |
Note: The
71Ga,
37Cl and Water columns correspond respectively to
the predicted solar neutrinos fluxes for the gallium, chlorine and water
experiments (cf., Table
1). The gallium and chlorine neutrino
fluxes are given in SNU whereas the water (SNO/SuperKamiokande) ones
are in 10
6 cm
-2 s
-1.
To answer that question we have summarised in Table 4 the neutrinos fluxes of
the most significant models. By comparing for example models ref and N2, we find
that for the latter the Gallium flux is reduced by 8 SNU, the Chlorine by 1.34 SNU and
the 8B by 106 cm-2 s-1 down to
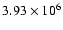 cm-2 s-1.
Such theoretical fluxes are still too high compared to the neutrino experiment on Earth (cf., Table 1),
if no other modifications are introduced either in the model or in the quantum properties of the neutrinos.
For example, the production of the 8B neutrinos is directly sensitive to the p-7Be nuclear
cross section. The value used in this study is
S17(0)=19.1+4-2 eV barns
(Adelberger et al. 1998), and corresponds to an intermediate value compared to the
recent estimate of Davids et al. (2001) (i.e.,
S17(0)=17.8+1.4-1.2 eV barns)
or of Junghans et al. (2002) (i.e.,
cm-2 s-1.
Such theoretical fluxes are still too high compared to the neutrino experiment on Earth (cf., Table 1),
if no other modifications are introduced either in the model or in the quantum properties of the neutrinos.
For example, the production of the 8B neutrinos is directly sensitive to the p-7Be nuclear
cross section. The value used in this study is
S17(0)=19.1+4-2 eV barns
(Adelberger et al. 1998), and corresponds to an intermediate value compared to the
recent estimate of Davids et al. (2001) (i.e.,
S17(0)=17.8+1.4-1.2 eV barns)
or of Junghans et al. (2002) (i.e.,
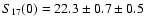 eV barns).
Thus we can conservatively consider that the error bar in S17 nuclear cross section
is at least of the order of
eV barns).
Thus we can conservatively consider that the error bar in S17 nuclear cross section
is at least of the order of 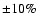 .
Such an uncertainty, results in an increase or
decrease of our 8B flux by
.
Such an uncertainty, results in an increase or
decrease of our 8B flux by 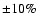 as well.
as well.
By taking into account most of the uncertainties
present in a solar model to calculate the neutrino fluxes, such as the nuclear
reactions cross sections, the screening, the heavy elements abundance,
the absorption cross sections for gallium and chlorine experiments,
the amount of microscopic and macroscopic diffusion, etc. (see Turck-Chièze et al. 2001),
we end up with the following fluxes (errors have been obtained by quadratic sum of
the individual contributions assumed to be independent):
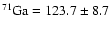 SNU,
SNU,
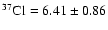 SNU and
SNU and
Water
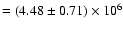 cm-2 s-1.
cm-2 s-1.
These values are a bit lower than Bahcall et al. (2001) and Turck-Chièze et al. (2001), but remain
within the  error range. However, they are still significantly larger than the observations,
unless one invokes non standard neutrino properties.
Such evidence for neutrino flavour oscillation have been recently given by Ahmad et al. (2001)
based on the careful study of the high energy neutrino fluxes detected by the SNO detector and
by the SuperKamiokande experiments (Fukuda et al. 1998).
Since then SNO has also measured the 8B neutrino flux using the
neutral current channel, which is equally sensitive to all neutrino
flavours (Ahmad et al. 2002).
The resulting 8B flux, is found to be
error range. However, they are still significantly larger than the observations,
unless one invokes non standard neutrino properties.
Such evidence for neutrino flavour oscillation have been recently given by Ahmad et al. (2001)
based on the careful study of the high energy neutrino fluxes detected by the SNO detector and
by the SuperKamiokande experiments (Fukuda et al. 1998).
Since then SNO has also measured the 8B neutrino flux using the
neutral current channel, which is equally sensitive to all neutrino
flavours (Ahmad et al. 2002).
The resulting 8B flux, is found to be
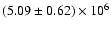 cm-2 s-1,
which is within the error bars of the current solar neutrino prediction.
Our helioseismic study seems to favour more the lower range of the detection than the upper range.
cm-2 s-1,
which is within the error bars of the current solar neutrino prediction.
Our helioseismic study seems to favour more the lower range of the detection than the upper range.
In this work our goal was to assess the effect of uncertainties in
nuclear reaction rates, atomic data and diffusion coefficients on solar models,
which we have compared with the results of helioseismic inversions.
We have concluded in Sect. 3 that a variation of the nuclear reaction rates
can have a
significant impact on the solar structure and that current
modelling coupled with seismic data favours some change of the accepted
central value of three important nuclear reaction rates, pp, 3He-3He and
3He-4He.
While the pp reaction rates needs to be increased by about 1.5% over
the currently accepted value from Adelberger et al. (1998), the
constraints on other reaction rates are less clear.
Even the increase of pp rate involved in this study is less
than that inferred by Antia & Chitre (1999) and Degl'Innocenti et al. (1998)
and the difference can be attributed to different treatment of
nuclear energy generation in CESAM as compared to the version of Bahcall's energy
routine used in earlier estimates.
More precisely, most of the discrepancy comes from the different screening
prescriptions used. In the previous study of Antia & Chitre (1999), the screening
formulation of Graboske et al. (1973) was assumed as opposed to Salpeter (1954) or
Mitler (1977) in this new study. We refer to Dzitko et al. (1995) and Wilets et al. (2000)
for a detailed comparison of several weak, intermediate and strong, screening prescriptions.
Our work confirms the result of Brun et al. (1999) that the implementation
of macroscopic mixing in the tachocline improves the agreement between
solar models and seismic Sun (Sect. 3.2). In particular, direct comparison
of hydrogen abundance profiles between our models and the Sun
as inferred from seismic inversions has demonstrated that the models
with tachocline mixing are in much better agreement with the Sun
in tachocline region. Comparison of hydrogen abundance profile
in solar models with inferred profiles show that there is still
a discrepancy of about 0.003 (Sect. 3.3). The largest discrepancies occur in
the region close to the tachocline and at about
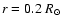 ,
where
the sound speed also shows maximum discrepancy. Thus it appears
that there is still some scope for improving the formulation
for calculating the mixing in tachocline region.
We were not able to achieve any significant improvement compared
to the results of Brun et al. (1999) by adjusting the parameters
of the tachocline model. With some modifications the agreement improves
in the tachocline region, like in model NM, but it tends to worsen in
other places.
We have found as well that based on the 9Be photospheric depletion,
the maximum extent of the mixing in the tachocline is 5% of solar radius.
It is quite possible that a major part of the remaining
discrepancies (about 0.1% in sound speed, 1% in density and 0.003 in X) in
our improved models may be due to uncertainties in input physics, like the
opacities or equation of state.
,
where
the sound speed also shows maximum discrepancy. Thus it appears
that there is still some scope for improving the formulation
for calculating the mixing in tachocline region.
We were not able to achieve any significant improvement compared
to the results of Brun et al. (1999) by adjusting the parameters
of the tachocline model. With some modifications the agreement improves
in the tachocline region, like in model NM, but it tends to worsen in
other places.
We have found as well that based on the 9Be photospheric depletion,
the maximum extent of the mixing in the tachocline is 5% of solar radius.
It is quite possible that a major part of the remaining
discrepancies (about 0.1% in sound speed, 1% in density and 0.003 in X) in
our improved models may be due to uncertainties in input physics, like the
opacities or equation of state.
Comparing the surface hydrogen abundance in solar models and
those obtained by inversions (Table 3) with the abundance inferred directly
from seismic data (Basu 1998), we again find a difference of 0.001.
This suggests that discrepancies of this order are
present in the input physics which is used in inferring these
independent measurements of surface hydrogen abundance.
The helium abundance drawn from the structure of the ionisation zones
is particularly sensitive to the equation of state (Basu & Antia 1995),
while its abundance inferred from the solar models depends on the whole
input physics used in constructing those.
Similarly, the seismically inferred hydrogen abundance
profile is sensitive to opacity as well as to the Z profile used
in inversion. Thus the discrepancy between these three independent
estimates of surface hydrogen abundance probably gives an estimate
of errors in input physics. The difference between solar models
with tachocline mixing and seismically inferred profiles is of the
same order and could be due also to remaining uncertainties in input
physics.
As seen in Fig. 1 the evolutionary solar models show a significant
departure from seismic inferences inside the convection zone.
We find that scaling the radius of these models by 1.0003 before
taking the differences with inverted profile removes most of the
discrepancy in the convection zone. We believe that this is due
to uncertainties in the treatment of surface layers.
In the solar models the surface is defined by the layer where the
temperature equals effective temperature and it is quite possible
that because of uncertainties in surface layers the location of
this point has an error of about 200 km in our evolutionary models.
We would like to point out that adjusting the solar radius in the
model by 200 km does not remove this discrepancy, since even in the
new model the position of the surface has the same uncertainty.
Thus this scaling of radius has no relation to uncertainty in
solar radius itself.
The calculated neutrino fluxes in solar models with tachocline
mixing are found to be somewhat lower than those in standard
solar model of Bahcall et al. (2001), but within the 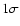 error limits (Sect. 3.4). The main reason for reduction is the increase in
pp reaction rate, which reduces the central temperature
required to generate the solar luminosity. Recently,
using both the charged and neutral current channels, SNO has measured the total
8B neutrino flux of
error limits (Sect. 3.4). The main reason for reduction is the increase in
pp reaction rate, which reduces the central temperature
required to generate the solar luminosity. Recently,
using both the charged and neutral current channels, SNO has measured the total
8B neutrino flux of
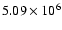 cm-2 s-1 (Ahmad et al. 2002).
This is somewhat larger than the value we find in our
models. In the modified models
N1, N2 the neutrino fluxes are much lower, because we have
chosen to modify the nuclear reaction rates to reduce these fluxes.
If instead as with model N03 we had modified S33 and S34
in opposite directions the neutrino fluxes would have increased and it would be possible
to get values close to that inferred by Ahmad et al. (2002).
Also our increase of pp reaction rate by 3.5% in some of
these models is probably an overestimate, since seismic models with same input
physics appear to need an increase by only 1.5% to produce the
required solar luminosity. When almost all the sources of uncertainties are taken
into account in evaluating the theoretical neutrino fluxes, our result is
within 1
cm-2 s-1 (Ahmad et al. 2002).
This is somewhat larger than the value we find in our
models. In the modified models
N1, N2 the neutrino fluxes are much lower, because we have
chosen to modify the nuclear reaction rates to reduce these fluxes.
If instead as with model N03 we had modified S33 and S34
in opposite directions the neutrino fluxes would have increased and it would be possible
to get values close to that inferred by Ahmad et al. (2002).
Also our increase of pp reaction rate by 3.5% in some of
these models is probably an overestimate, since seismic models with same input
physics appear to need an increase by only 1.5% to produce the
required solar luminosity. When almost all the sources of uncertainties are taken
into account in evaluating the theoretical neutrino fluxes, our result is
within 1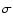 of the other published theoretical neutrino fluxes and the recent
SNO compilation. It will be interesting in the near future, when the
SNO collaboration results will have been integrated over a longer time
to see if the helioseismic tool
will be able to constrain even more efficiently the main nuclear cross sections, via
a careful analysis of the neutrino spectrum, and also delineate the parameter
space for mass-squared difference-mixing angle plane.
of the other published theoretical neutrino fluxes and the recent
SNO compilation. It will be interesting in the near future, when the
SNO collaboration results will have been integrated over a longer time
to see if the helioseismic tool
will be able to constrain even more efficiently the main nuclear cross sections, via
a careful analysis of the neutrino spectrum, and also delineate the parameter
space for mass-squared difference-mixing angle plane.
Acknowledgements
We thank the anonymous referee for constructive comments
and suggestions which have led to a considerable improvement in the final version of the paper.
ASB would like to thank S. Turck-Chièze for useful discussions and the Service
d'Astrophysique, for access to their computers. This work was partly
supported by NASA through grants NAG5-2256 and NAG5-8133.
SMC is grateful to DAE-BRNS for support under the Senior Scientist Scheme.
- Adelberger, E. G., Austin, S. M., Bahcall, J. N., et al. 1998, Rev. Mod. Phys., 70, 1265
In the text
NASA ADS
- Ahmad, Q. R., Allen, R. C., Andersen, T. C., et al. 2001, Phys. Rev. Lett., 87, 071301
(SNO collaboration)
In the text
- Ahmad, Q. R., Allen, R. C., Andersen, T. C., et al. 2002, Phys. Rev. Lett., 89, 011 301
(SNO collaboration)
In the text
- Angulo, C., Arnould, M., Rayet, M.,
& the NACRE collaboration 1999, Nucl. Phys. A, 656, 3
In the text
NASA ADS
- Antia, H. M. 1996, A&A, 307, 609
In the text
NASA ADS
- Antia, H. M., & Chitre, S. M. 1998, A&A, 339, 239
NASA ADS
- Antia, H. M., & Chitre, S. M. 1999, A&A, 347, 1000
In the text
NASA ADS
- Antia, H. M., Basu, S., & Chitre, S. M. 1998, MNRAS, 298, 543
In the text
NASA ADS
- Bahcall, J. N. 1989, Neutrino Astrophysics (Cambridge University Press)
In the text
- Bahcall, J. N., Basu, S., & Pinsonneault, M. H. 1998a, Phys. Lett. B, 433, 1
In the text
NASA ADS
- Bahcall, J. N., Krastev, P. I., & Smirnov, A. Yu. 1998b, Phys. Rev. D, 58, 096016
In the text
- Bahcall, J. N., Pinsonneault, M. H., & Basu, S. 2001, ApJ, 555, 990
In the text
NASA ADS
- Balachandran, S., & Bell, R. A. 1998, Nature, 392, 791
In the text
NASA ADS
- Barnes, G., Charbonneau, P., & MacGregor, K. B. 1999, ApJ, 511, 466
In the text
NASA ADS
- Basu, S. 1998, MNRAS, 298, 719
In the text
NASA ADS
- Basu, S., & Antia, H. M. 1994, MNRAS, 269, 1137
In the text
NASA ADS
- Basu, S., & Antia, H. M. 1995, MNRAS, 276, 1402
In the text
NASA ADS
- Basu, S., Turck-Chièze, S., Berthomieu, G., et al. 2000, ApJ, 535, 1078
In the text
NASA ADS
- Bell, R. A., Balachandran, S., & Bautista, M. 2001, ApJ, 546, L65
In the text
NASA ADS
- Brun, A. S., Turck-Chièze, S., & Morel, P. 1998, ApJ, 506, 913
In the text
NASA ADS
- Brun, A. S., Turck-Chièze, S., & Zahn, J.-P. 1999, ApJ, 525, 1032
In the text
NASA ADS
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295
In the text
NASA ADS
- Cayrel, R. 1998, Space Sci. Rev., 84, 145
In the text
NASA ADS
- Christensen-Dalsgaard, J., Berthomieu, G. 1991, in Solar interior and atmosphere,
ed. A. N. Cox, W. C. Livingston & M. Matthews (University of Arizona
Press), 401
- Christensen-Dalsgaard, J., Gough, D. O., & Thompson, M. J. 1991, ApJ, 378, 413
In the text
NASA ADS
- Christensen-Dalsgaard, J., Proffitt, C. R., & Thompson, M. J. 1993, ApJ, 403, L75
In the text
NASA ADS
- Christensen-Dalsgaard, J., Däppen, W., et al. 1996, Science, 272, 1286
In the text
NASA ADS
- Clayton, D. D. 1968, Principles of Stellar Evolution and Nucleosynthesis (University of Chicago Press)
In the text
- Corbard, T., Blanc-Féraud, L., Berthomieu, G., & Provost, J. 1999, A&A, 344, 696
In the text
NASA ADS
- Davids, B., Austin, S. M., Bazin, D., et al. 2001, Phys. Rev. Lett., 86, 2750
In the text
NASA ADS
- Degl'Innocenti, S., Fiorentini, G., & Ricci, B. 1998, Phys. Lett. B, 416, 365
NASA ADS
- Di Mauro, M. P., Christensen-Dalsgaard, J., Rabello-Soares, M. C., & Basu, S. 2002, A&A, 384, 666
In the text
NASA ADS
- Dzitko, H., Turck-Chièze, S., Delbourgo-Salvador, P., & Lagrange, G. 1995, ApJ, 447, 428
In the text
NASA ADS
- Elliott, J. R., & Gough, D. O. 1999, ApJ, 516, 475
In the text
NASA ADS
- Fröhlich, C., Andersen, B. N., Appourchaux, T., et al. 1997, Sol. Phys., 170, 1
In the text
NASA ADS
- Fukuda, Y., Hayakawa, T., Ichihara, E., et al. 1998, Phys. Rev. Lett., 81, 1158 (SuperKamiokande Collaboration)
In the text
- Gabriel, A. H., Charra, J., Grec, G., et al. 1997, Sol. Phys., 175(2), 207
In the text
NASA ADS
- Gautier, D., & Morel, P. 1997, A&A, 323, L9
In the text
NASA ADS
- Gough, D. O., Kosovichev, A. G., Toomre, J., et al. 1996, Science, 272, 1296
In the text
NASA ADS
- Graboske, H. C., DeWitt, H. E., Grossman, A. S., & Cooper, M. S. 1973, ApJ, 181, 457
In the text
NASA ADS
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, in Cosmic Abundances, ed. S. S. Holt, & G. Sonneborn (San Francisco: ASP), 117
In the text
- Haxton, W. C. 1995, ARA&A, 33, 459
In the text
NASA ADS
- Haxton, W. C. 1997 [nucl-th/9704052]
In the text
- Iglesias, C., & Rogers, F. J. 1996, ApJ, 464, 943
In the text
NASA ADS
- Junghans, A. R., Mohrmann, E. C., Snover, K. A., et al. 2002 [nucl-ex/0111014]
In the text
- Kippenhahn, R., & Weigert, A. 1994, Stellar Structure and Evolution (Springer-Verlag, Berlin)
In the text
- Kurucz, R. L., Stellar Atmospheres: Beyond classical models, ed. L. Crivellari, I. Hubeny, & D. G. Hummer, NATO ASI Ser. (Kluwer, Dordrecht), 1991
- Michaud, G., & Proffitt, C. R. 1993, Inside the stars IAU 137, ed. W. W. Weiss, & A. Baglin (San Francisco: ASP), 246
In the text
- Mitler, H. E. 1977, ApJ, 212, 513
In the text
NASA ADS
- Montalban, J., & Schatzman, E. 1996, A&A, 305, 513
In the text
NASA ADS
- Morel, P. 1997, A&AS, 124, 597
In the text
NASA ADS
- Morel, P., Provost, J., & Berthomieu, G. 1997, A&A, 327, 349
NASA ADS
- Morel, P., Pichon, B., Provost, J., & Berthomieu, G. 1999, A&A, 350, 275
In the text
NASA ADS
- Piau, L., & Turck-Chièze, S. 2002, ApJ, 566, 419
NASA ADS
- Richard, O., Vauclair, S., Charbonnel, C., & Dziembowski, W. A. 1996, A&A, 312, 1000
In the text
NASA ADS
- Rogers, F. J., & Iglesias, C. 1998, Space Sci. Rev., 85, 61
In the text
NASA ADS
- Salpeter, E. E. 1954, Aust. J. Phys., 7, 373
In the text
- Schlattl, H., Bonanno, A., & Paternó, L. 1999, Phys. Rev. D, 60, 113002
In the text
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390
In the text
NASA ADS
- Skumanich, A. 1972, ApJ, 171, 565
In the text
NASA ADS
- Spiegel, E. A., & Zahn, J.-P. 1992, A&A, 265, 106
In the text
NASA ADS
- Thompson, M. J., Toomre, J., Anderson, E. R., et al. 1996, Science, 272, 1300
In the text
NASA ADS
- Turck-Chièze, S. 1998, Space Sci. Rev., 85, 125
NASA ADS
- Turck-Chièze, S., Couvidat, S., Kosovochev, A. G., et al. (GOLF team E) 2001, ApJ, 555, L69
In the text
NASA ADS
- Turcotte, S., Richer, J., Michaud, G., Iglesias, C. A.,
& Rogers, F. J. 1998, ApJ, 504, 539
In the text
NASA ADS
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635
In the text
NASA ADS
- Weiss, A., Flaskamp, M., & Tsytovich, V. N. 2001, A&A, 371, 1123
In the text
NASA ADS
- Wilets, L., Giraud, B. G., Watrous, M. J., & Rehr, J. J. 2000, ApJ, 530, 504
In the text
NASA ADS
- Zahn, J.-P. 1998, Space Sci. Rev., 85, 79
In the text
NASA ADS
Copyright ESO 2002











