A&A 391, 795-799 (2002)
DOI: 10.1051/0004-6361:20020897

Research Note

The effects of blending on the light curve shape of Cepheids

E. Antonello

Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, Italy

Received 18 February 2002 / Accepted 4 June 2002

Abstract
A short analysis is presented of the effects on the cepheid light curve shape, i.e. on the Fourier parameters usually adopted for its description, of the blending of the stellar image with other close stars. The conclusion is that, within reasonable error, the effects are in general small and the Fourier decomposition is confirmed to be a useful tool for pulsation mode discrimination. A large effect has been found on the phase differences in a narrow period range corresponding to the known resonance centers between pulsation modes.

Key words: stars: oscillations - stars: variables: Cepheids - galaxies: stellar content


1 Introduction

Cepheids are primary distance indicators for external galaxies and those used for this application pulsate in the fundamental mode. First overtone mode Cepheids are brighter by about 0.4 mag than fundamental mode pulsators with the same period. Since the period-luminosity relation has an intrinsic dispersion, which depends on several parameters (e.g. different effective temperature or color, different reddening, contribution from stellar companions), it is essential to remove the contaminating stars that are pulsating in a different mode. The large surveys of the Magellanic Clouds performed by MACHO (e.g. Welch et al. 1997), EROS (e.g. Beaulieu et al. 1995) and OGLE (e.g. Udalski et al. 1999) projects proved that the Fourier decomposition is a good technique for discriminating the mode among short period ($P \la 6$ d) Cepheids. More recently, the technique began to be applied to Cepheids of farther galaxies in the Local Group, such as IC 1613 (e.g. Antonello et al. 1999; Dolphin et al. 2001) and M 33 (Mochejska et al. 2001).

The large surveys offered also the opportunity of discussing the problems related to blending. Mochejska et al. (2000) define the blending as the close projected association of a Cepheid with one or more intrinsically luminous stars, which cannot be detected within the observed point-spread function by the photometric analysis. There is some debate about the implications for the distance determination related to the blending and more generally to poor resolution of the stellar images in these galaxies. The blending also has other effects on the light and the color curves. Mochejska et al. (2000) note that in the case of a red or blue companion the light curve exhibits a flatter minimum. As regards binaries, it is well-known that the observed amplitude of the light curve is affected by the luminosity of a bright companion. Could it be that the blending, apart from producing a lower amplitude, also mimics a different pulsation mode? Recently, we recalled that in principle such an effect on the Fourier parameters is small in the context of mode identification (Antonello et al. 2002). Here we report the results of simulations that support this conclusion, and we discuss some unexpected characteristics.


  \begin{figure} \par\includegraphics[width=6cm,clip]{MS2382f1.eps} \smallskip \end{figure} Figure 1: Lower panel: blending effect on the V light curve of a Cepheid, for different values of the luminosity of the companion star ($L_{\rm c}$). Upper panel: comparison between the light curve for $L_{\rm c}=0$ (continuous line) and $L_{\rm c}=4<L>$ (dotted line) scaled to the same amplitude.
Open with DEXTER

2 Analysis

The problem by itself would not be important if we adopt intensities instead of magnitudes to measure stellar brightness. Indeed, an increased intensity due to a close star, assuming no measurement error, would produce a light curve with a similar shape to that without such a close star. The average intensity would be larger, the absolute amplitude would be the same, and the relative amplitude would be of course decreased. Let <L> be the average stellar intensity (that is, the average number of collected photons), $\Delta{L}$ the absolute amplitude, $A=\Delta{L}/<L>$ the relative amplitude, and $\epsilon \sim \sqrt{<L>}$ the mean absolute error on the measurement. Let us assume a close constant star with intensity a<L>. The relative amplitude of the system will be $A_1=\Delta{L}/[(a+1)<L>]$ and the mean absolute error $\epsilon_1 \sim \sqrt{(a+1)<L>}$. A close star has the effect of decreasing the relative amplitude and increasing the absolute error. This implies a lower order of fit of the reliable Fourier decomposition of the intensity curve, and larger formal errors of the Fourier parameters; however, the parameters themselves are unchanged (within the formal errors).

The nonlinearity of the relation between intensity and magnitude introduces some changes. The simplest method for studying them is by means of simulations. We considered light curves of some stars pulsating in the fundamental or first overtone mode (e.g. X Cyg, DT Cyg) observed by Moffett & Barnes (1984; data retrieved from McMaster Cepheid Photometry and Radial Velocity Data Archive), and we adopted the best fitting curve as a synthetic light curve. We simulated several time series, adopting the original observing dates, and changing the synthetic light curve by introducing the contribution of a close constant star, and different mean errors of the measurement. In Fig. 1 we show the effects of increasing luminosity on the synthetic light curve of X Cyg. In the upper panel one can see the changes of light curve shape due to a four times brighter companion; the two curves are scaled to the same amplitude. The flattening of the minimum does not appear very prominent, even in this case where the magnitude difference between the Cepheid and the blended image is large, 1.75 mag.

The time series were constructed applying a random number generator for a Gaussian error distribution. The series were then Fourier decomposed and the resulting Fourier parameters are plotted in Fig. 2 for the case of X Cyg, as an example. One can see clearly that the increasing blending implies a decreasing order of the reliable fit.

When performing the simulations, we also analyzed some OGLE stars in the SMC, and we noted different trends with respect to the above Cepheids. We suspected some dependence on the P, therefore we decided to analyze all the Cepheids in OGLE database of the SMC (Udalski et al. 1999). The fitting curves of the Fourier decomposed I-band light curves were modified by introducing the contribution of a companion star with $L_{\rm c}=2<L>$, then they were analyzed and we computed the difference between the Fourier parameters for $L_{\rm c}=2<L>$ and $L_{\rm c}=0$. The results for the lowest order are shown in Figs. 3 and 4 for the fundamental and first overtone mode, respectively. Although the effect on the amplitude ratio is always small, the trend with P is confirmed. The unexpected result is the large effect on the phase difference very close to the resonance centers at $P \sim 10$ d for the fundamental mode, and $P \sim 2.2$ d for the first overtone mode. Outside these narrow P ranges the effect is small.

3 Discussion and conclusion


  \begin{figure} \par\includegraphics[width=5.7cm,clip]{MS2382f2.eps} \end{figure} Figure 2: The plots show how the Fourier parameters and light curve amplitude of a Cepheid change according to the luminosity of a companion star ( $L_{\rm c}/<L>$ is the ratio of the luminosity of the companion to the average value of the Cepheid). The symbols indicate different values of the mean error $\sigma $ of measurements adopted in the simulations: filled circle: $\sigma =0$, filled triangle: $\sigma =0.02$; open circle: $\sigma =0.05$; open triangle: $\sigma =0.1$ mag. The errorbar indicates the formal error of the respective parameter. $\Delta {mag}$ is the average magnitude difference between the Cepheid and the blended image.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=5cm,clip]{MS2382f3.eps} \end{figure} Figure 3: Simulated blending effect on the I-band light curves of all the OGLE fundamental mode Cepheids in the SMC. The plots show the difference of R21 and $\phi _{21}$ between the light curves for $L_{\rm c}=2<L>$ and $L_{\rm c}=0$.
Open with DEXTER

The cases discussed here concern reasonable light curves; we do not consider the problems related to very faint variables, which can hardly be detected at minimum light. The requirement is that in the P interval where it is possible to find stars pulsating in different modes, the Fourier parameters must allow us to make the discrimination. It is known that this occurs for $P \la 6$ d for the fundamental and the first overtone mode, using only light curves parameters. The results of the simulations show that in this P range the blending has a negligible effect when we compare the differences introduced by it with the size of the parameters themselves. In particular, a blended fundamental mode pulsator will have slightly larger amplitude ratios than a non-blended one; we recall that the amplitude ratios of fundamental mode pulsators are intrinsically larger than those of first overtone mode ones in this P range. The same occurs for a first overtone mode pulsator compared with a second overtone one, for $P \la 1.3$ d. On the other hand, a heavily blended first overtone pulsator increases its R21 value, but in general not so much so as to be confused with a fundamental mode pulsator. In conclusion, the blending due to various reasons is not an issue for the pulsation mode discrimination.

The color of the companion stars is not relevant for the present discussion, as long as their contribution is constant; some (second order) effects could be related to their intrinsic variability, both in terms of photometric variability and/or Doppler shift. The influence of the photometric variability of the companion itself can be usually accurately estimated, since an adequate time series analysis is sufficient to disentangle the different contributions, because of the different periodicities or timescales involved. Also in this case, however, it is wise to work with intensities rather than with magnitudes. Variable seeing conditions could have some effect on the estimate of the intensity through the PSF fitting procedure; however in this case we would expect just an increased error in the measurement.

The plots in Figs. 3 and 4 suggest some interesting considerations. A light curve with an altered value of the mean luminosity, such as that depicted in Fig. 1, or expressed with a different, nonlinear mathematical function (e.g. the intensity instead of the magnitude) is characterized of course by (usually slightly) different Fourier parameters. If we estimate the differences related to these changes, we note that the largest ones are for the phases of the Fourier components with smaller amplitude; for example, at about 10 d some stars have R21 < Ri1, for i from 3 up to 6 or more. The large differences are not due to errors or to uncertainties, since here we are not dealing with observed data but with synthetic light curves (i.e. the fitting curves), which are in principle error-free. In other words the differences are intrinsically real and reflect directly the change of the shape introduced by the different mathematical function. The interpretation of this feature is reported in the Appendix; from that, we conclude that the observed dispersion is strictly related to the smallness of the Fourier component involved. In our example, the small second Fourier component has changed its phase value by several tenths of a radian, while for the other components the change is much smaller. For the same reason we should expect an analogous results for $\phi _{41}$, i.e. we should have some dispersion at $P \sim 7$ d, where R41 is small since another resonance, P0/P4=3, should be operating there (e.g. Antonello 1994). Indeed this is shown in Fig. 5; note also that the discontinuity of  $\Delta{R_{21}}$ located at 10 d is replaced by that of  $\Delta{R_{41}}$ at about 7 d. In a certain sense, plots such as those shown in Figs. 3-5 are better indicators of resonance effects than the classical ones, because they are free of subjective corrections of the phase differences by $\pm{2\pi}$, which could be uncertain, mainly for the higher orders. Finally, it is possible to note two minima in the lower panel of Fig. 3, one at the resonance center, and the other at $\log P \sim 1.5$. Kanbur et al. (2002) noted the structural change of the light curves at this P; these features still await a theoretical interpretation.

Last but not least, we remark further that several problems with the time series analysis of stellar luminosities would be simplified by adopting intensity scales instead of magnitude scales. This statement is not new, of course. Our comment is just further support to the proposal of abandoning the magnitudes. In fact, the blending has no effect on the light curve shape when we use intensity light curves, and this is an advantage, since one is always dealing with observed parameters which are affected by errors.

  \begin{figure} \par\includegraphics[width=5.2cm,clip]{MS2382f4.eps} \end{figure} Figure 4: Simulated blending effect on the I-band light curves of all the OGLE first overtone mode Cepheids in the SMC. The plots showthe difference of R21 and $\phi _{21}$ between the light curves for $L_{\rm c}=2<L>$ and $L_{\rm c}=0$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=5cm,clip]{MS2382f5.eps} \end{figure} Figure 5: The difference of R41 and $\phi _{41}$ between the simulated light curves for $L_{\rm c}=2<L>$ and $L_{\rm c}=0$ of fundamental mode Cepheids. It should be compared with Fig. 3.
Open with DEXTER

Appendix A: Intensity and magnitudes

Note that the increasing blending produces a light curve, expressed in magnitudes, with a shape which is similar to the shape of the intensity light curve. That is, for very large $L_{\rm c}$, the amplitude becomes very small, and the Fourier parameters become those of the intensity-light curve (for the phase differences one has to consider the different sign). The diagrams of the differences between intensity- and magnitude-light curves of the SMC Cepheids look similar to those of the diagrams shown in Figs. 3-5, but with slightly different ranges of the ordinate; for example, the range of  $\Delta{R_{21}}$ values would be about $\pm$0.05 instead of about $\pm$0.035 as indicated by Fig. 3.

In this Appendix we will use some approximations to understand the effect seen near the resonances between pulsation modes of Cepheids, or more generally the effect on the smaller Fourier components, given by different mathematical descriptions of the light curve. In this context, the intensity-light curve could be considered, in a certain sense, as a magnitude-light curve for an extremely large blending value.

Let us assume that the intensity curve is expressed by

\begin{displaymath}L = L_{\rm o} + x = L_{\rm o} + \sum\left[A_i\cos(i\omega{t}) + B_i\sin(i\omega{t})\right], \end{displaymath} (A.1)

where $L_{\rm o}$ is the mean intensity value, which may include the contribution from a companion star or blending, and $\omega$ is the pulsation frequency. The observed light curve can be written as

\begin{displaymath}V = -2.5 \log(L) + k_1, \end{displaymath} (A.2)

where k1 is an appropriate constant. By considering the natural logarithm, we can write

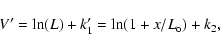\begin{displaymath}V' = {\rm ln} (L) + k_1' = {\rm ln} (1 + x/L_{\rm o}) + k_2, \end{displaymath} (A.3)

where V'=-V/1.0857 and $k_2 = - k_1/1.0857 + {\rm ln}(L_{\rm o})$. We assume a relatively small amplitude, and expand (A.3) in the series

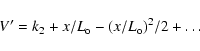\begin{displaymath}V' = k_2 + x/L_{\rm o} - (x/L_{\rm o})^2/2 + \ldots \end{displaymath} (A.4)

where the Fourier series of espression (A.1) is introduced, and we assume for simplicity that $i \le 3$. After some manipulation, we get the following expressions for the coefficients of the cosine terms, from i=1 to i=6,
$\displaystyle A_1/L_{\rm o} - (A_1A_2 + B_1B_2 + A_2A_3 + B_2B_3)/2L_{\rm o}^2$     (A.5)
$\displaystyle A_2/L_{\rm o} - (A_1A_3 + B_1B_3 + A_1^2/2 + B_1^2/2)/2L_{\rm o}^2$     (A.6)
$\displaystyle A_3/L_{\rm o} - (A_1A_2 - B_1B_2)/2L_{\rm o}^2$     (A.7)
$\displaystyle - (A_1A_3 - B_1B_3 + A_2^2/2 - B_2^2/2)/2L_{\rm o}^2$     (A.8)
$\displaystyle - (A_2A_3 - B_2B_3)/2L_{\rm o}^2$     (A.9)
$\displaystyle - (A_3^2/2 - B_3^2/2)/2L_{\rm o}^2,$     (A.10)

respectively. Six Fourier components are needed instead of just three to describe the V' light curve. Analogously for the sine terms we get
$\displaystyle B_1/L_{\rm o} - (A_1B_2 - B_1A_2 + A_2B_3 - B_2A_3)/2L_{\rm o}^2$     (A.11)
$\displaystyle B_2/L_{\rm o} - (A_1B_1 + A_1B_3 - B_1A_3)/2L_{\rm o}^2$     (A.12)
$\displaystyle B_3/L_{\rm o} - (A_1B_2 + B_1A_2)/2L_{\rm o}^2$     (A.13)
$\displaystyle - (A_1B_3 + B_1A_3 + A_2B_2)/2L_{\rm o}^2$     (A.14)
$\displaystyle - (A_2B_3 + B_2A_3)/2L_{\rm o}^2$     (A.15)
$\displaystyle - (A_3B_3)/2L_{\rm o}^2,$     (A.16)

and the correcting term for the mean value:

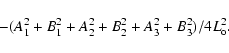\begin{displaymath}-(A_1^2 + B_1^2 + A_2^2 + B_2^2 + A_3^2 + B_3^2)/4L_{\rm o}^2. \end{displaymath} (A.17)

If we had considered a further cubic power of x in the expansion (A.4), the previous expressions for the coefficients would have included another correcting term containing cubic power and cross-products of Ai and Bi multiplied by 1/3 $L_{\rm o}^3$, and the number of Fourier components would have been nine.

We will assume that the absolute values of the coefficients A2, B2 are much smaller than those of A1, B1 and A3, B3, that is, the second Fourier component is very small with respect to the first and third ones. We note that here we are not dealing with the nonlinear oscillator problem (e.g. Antonello 1994a, 1994b). In the coefficient of the second cosine and sine term, (A.6) and (A.12), the first elements, $A_2/L_{\rm o}$ and  $B_2/L_{\rm o}$ are, according to our assumption, small in comparison with the absolute value of the correcting terms which contain squares and cross-products of  A1, A3, B1, B3. On the other hand, for the same reason the corrections of the coefficients of the first and third cosine and sine terms are small. In other words, while the first and third Fourier components are only slightly changed, we must expect a very different second component of the Fourier decomposed V' light curve from that of the L light curve. This conclusion applies, of course, to any value of blending.

References

 
Copyright ESO 2002