A&A 391, 781-787 (2002)
DOI: 10.1051/0004-6361:20020853
Hydrodynamic stability in accretion disks under the combined
influence of shear and density stratification
G. Rüdiger1 - R. Arlt1
- D. Shalybkov1,2
1 - Astrophysikalisches Institut Potsdam,
An der Sternwarte 16, 14482 Potsdam, Germany
2 -
A.F. Ioffe Institute for Physics and Technology, 194021,
St. Petersburg, Russia
Received 18 February 2002 / Accepted 4 June 2002
Abstract
The hydrodynamic stability of accretion disks is considered.
The particular question is whether the combined action of a (stable) vertical
density stratification and a (stable) radial differential rotation gives rise
to a new instability for nonaxisymmetric modes of disturbances.
The existence of such an instability is not suggested by the
well-known Solberg-Høiland criterion. It is also not suggested by
a local analysis for disturbances in general stratifications
of entropy and angular momentum which is presented in our Sect. 2.
This confirms the results of the Solberg-Høiland criterion also for
nonaxisymmetric modes within the frame of ideal hydrodynamics but
only in the frame of a short-wave
approximation for small m. As a necessary condition for stability we
find that only conservative external forces are allowed to influence the stable disk. As magnetic forces are never conservative, linear disk instabilities
should only exist in the magnetohydrodynamical regime which indeed contains the magnetorotational instability as a much-promising candidate.
To overcome some of the used approximations in a numerical approach, the equations of the compressible adiabatic
hydrodynamics are integrated, imposing initial nonaxisymmetric velocity perturbations
with m=1 to m=200. Only solutions with decaying kinetic energy
are found. The system always settles in a vertical equilibrium
stratification according to pressure balance with the gravitational
potential of the central object.
Key words: accretion, accretion disks - hydrodynamic -
instabilities - turbulence
According to the Rayleigh criterion, Keplerian disks are
hydrodynamically stable configurations, because the angular momentum
per unit mass,
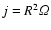 ,
increases with radius, i.e.
,
increases with radius, i.e.
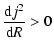 |
|
|
(1) |
with R being the distance from the rotation axis. They are
unstable configurations, however, under the influence of a (weak) magnetic
field if the disk plasma has a sufficiently
high conductivity (Balbus & Hawley 1991; Balbus 1995; Brandenburg et al. 1995;
Ziegler & Rüdiger 2000). There remains the question whether
also other, nonmagnetic
influences exist which in combination with the basic (negative) shear
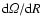 allow instabilities in the linear regime. We recall three
recent discussions. Urpin & Brandenburg (1998) consider the destabilizing
action of any vertical dependence of
allow instabilities in the linear regime. We recall three
recent discussions. Urpin & Brandenburg (1998) consider the destabilizing
action of any vertical dependence of
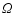 on z which may more than
compensate the stabilization of the positive radial gradient of j.
There is also the suggestion of Klahr & Bodenheimer (2001) that
the negative radial entropy
stratification in thin Keplerian disks may act in the sense of a
destabilization. Note that with the standard-alpha description of
accretion disks one finds the positive value
on z which may more than
compensate the stabilization of the positive radial gradient of j.
There is also the suggestion of Klahr & Bodenheimer (2001) that
the negative radial entropy
stratification in thin Keplerian disks may act in the sense of a
destabilization. Note that with the standard-alpha description of
accretion disks one finds the positive value
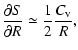 |
|
|
(2) |
indicating, however, stability.
Molemaker et al. (2001) and Yavnesh et al. (2001)
recently pointed out that a vertical density stratification in the Taylor-Couette flow
may have a similar destabilizing effect as a global vertical magnetic field for an electrically conducting fluid. The sufficient condition that a (nonaxisymmetric) disturbance will be unstable is given to be the same as for an unstratified
ideal MHD Taylor-Couette flow in the presence of a vertical magnetic field, i.e.
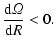 |
|
|
(3) |
If this were also true for nonmagnetic accretion disks - which always have vertical density stratifications - they would be hydrodynamically unstable, so that a turbulence can develop transporting the angular momentum outwards.
There is indeed some analogy between accretion disks and experimental Taylor-Couette
flows. But the question remains why such a hydrodynamic "radial-shear+vertical-stratification''
instability might exist in accretion disks even though the extensive
numerical simulations in local shearing-box systems have always shown that
Keplerian disks![[*]](/icons/foot_motif.gif) are stable to infinitesimal and finite disturbances (Balbus et al. 1996).
Most of the mentioned discussions are covered by the Solberg-Høiland
conditions for dynamic stability which, for the geometrical constellation studied here,
take the form
are stable to infinitesimal and finite disturbances (Balbus et al. 1996).
Most of the mentioned discussions are covered by the Solberg-Høiland
conditions for dynamic stability which, for the geometrical constellation studied here,
take the form
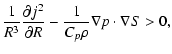 |
|
|
(4) |
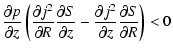 |
|
|
(5) |
(Tassoul 2000). If
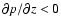 (as is usual for accretion
disks), the latter relation turns into
(as is usual for accretion
disks), the latter relation turns into
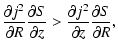 |
|
|
(6) |
which for Keplerian disks with
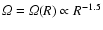 simply
leads to the usual Schwarzschild criterion,
simply
leads to the usual Schwarzschild criterion,
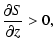 |
|
|
(7) |
for stability. However, if the angular velocity
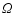 depends on
the vertical coordinate z then Eq. (6) allows instability
in the standard case of positive
depends on
the vertical coordinate z then Eq. (6) allows instability
in the standard case of positive
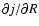 and
and
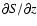 in case they are large enough.
Equation (4) becomes
in case they are large enough.
Equation (4) becomes
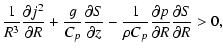 |
|
|
(8) |
which with (7) and for
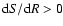 ensures stability.
Here we have used
ensures stability.
Here we have used
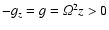 .
In the opposite case of a negative entropy gradient one at least needs
.
In the opposite case of a negative entropy gradient one at least needs
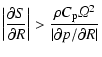 |
|
|
(9) |
in order to violate Eq. (8) in the most optimistic case of vertical
isentropy.
If, on the other hand, the standard stratifications of accretion disks are j =
j(R) and S=S(z), with
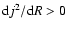 then the
Solberg-Høiland criterion for stability reduces to
then the
Solberg-Høiland criterion for stability reduces to
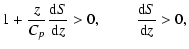 |
|
|
(10) |
(in the upper hemisphere). Obviously
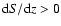 is a sufficient condition for stability of Kepler disks
after the Solberg-Høiland criterion also for the combined
action of vertical density stratification and differential Kepler rotation.
The same result have been derived in earlier papers by Livio & Shaviv
(1977), Abramowicz et al. (1984) and Elstner et al. (1989). The local
analysis for ring-like disturbances by Elstner et al.
demonstrates in all details that in the framework of an ideal
hydrodynamics, i.e. for vanishing Shakura-Sunyaev alpha, the traditional
Schwarzschild criterion
is a sufficient condition for stability of Kepler disks
after the Solberg-Høiland criterion also for the combined
action of vertical density stratification and differential Kepler rotation.
The same result have been derived in earlier papers by Livio & Shaviv
(1977), Abramowicz et al. (1984) and Elstner et al. (1989). The local
analysis for ring-like disturbances by Elstner et al.
demonstrates in all details that in the framework of an ideal
hydrodynamics, i.e. for vanishing Shakura-Sunyaev alpha, the traditional
Schwarzschild criterion
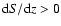 ensures stability for the Kepler disk.
If the disk can be considered as isothermal in the vertical direction then it follows
ensures stability for the Kepler disk.
If the disk can be considered as isothermal in the vertical direction then it follows
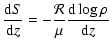 |
|
|
(11) |
which is always positive for the typical density stratification, i.e. the disk should always be stable.
In this section a local stability analysis of the equations of
ideal hydrodynamics in cylindrical coordinates (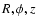 )
is presented. Self-gravitation phenomena are excluded.
Sound waves and nonaxisymmetric disturbances, however, are in particular allowed to
exist.
The three components of the momentum equation are
)
is presented. Self-gravitation phenomena are excluded.
Sound waves and nonaxisymmetric disturbances, however, are in particular allowed to
exist.
The three components of the momentum equation are
The mass conservation reads
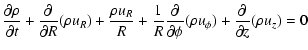 |
|
|
(15) |
and the energy equation is
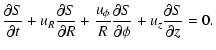 |
|
|
(16) |
As usual 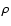 is the density, p is the pressure, S is the specific
entropy,
is the density, p is the pressure, S is the specific
entropy,
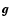 is the vector of any acceleration.
The unperturbed state is assumed to be
uR,0=uz,0=0,
is the vector of any acceleration.
The unperturbed state is assumed to be
uR,0=uz,0=0,
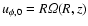 ,
,
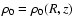 ,
p0=p0(R,z),
S0=S0(R,z),
gR=gR(R,z),
,
p0=p0(R,z),
S0=S0(R,z),
gR=gR(R,z), 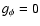 ,
gz=gz(R,z).
The only non-zero equations of the system (12)-(16)
are Eqs. (12) and (14) which take the form
,
gz=gz(R,z).
The only non-zero equations of the system (12)-(16)
are Eqs. (12) and (14) which take the form
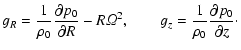 |
|
|
(17) |
Finally, the ideal gas equation of state is used
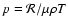 ,
,
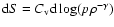 with
with
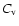 as the specific heat at constant volume, and
as the specific heat at constant volume, and
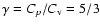 .
.
The perturbations in the force are neglected.
The perturbations uR,
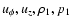 to the basic state
are assumed small and the linearized system (12)-(16) is
to the basic state
are assumed small and the linearized system (12)-(16) is
In the frame of our local approximation the equations are
considered only in small volume near some reference
point (
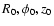 ). The coefficients
in the equations are thus constant taken at
(
). The coefficients
in the equations are thus constant taken at
(
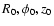 ). As usual both the
short-wave approximation and the small-m approximation, i.e.
). As usual both the
short-wave approximation and the small-m approximation, i.e.
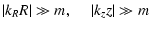 |
|
|
(23) |
are applied (cf. Meinel 1983).
In this approximation all perturbations can be expressed by
the modal representation
![${\rm exp}[{\rm i}(k_RR+m\phi+k_zz-\omega t)]$](/articles/aa/full/2002/32/aa2380/img51.gif) and the equations take the final form
and the equations take the final form
Generally, it is
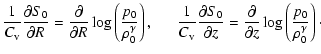 |
|
|
(29) |
The epicyclic frequency 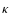 and the adiabatic sound speed
and the adiabatic sound speed
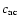 are
are
 |
|
|
(30) |
The determinant of the above homogeneous fifth order
system must vanish and the resulting dispersion relation is
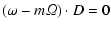 |
|
|
(31) |
with
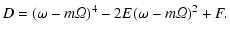 |
|
|
(32) |
Here we have introduced the expressions
![$\displaystyle E={1\over2} \left[ (k_R^2+k_z^2)c_{\rm ac}^2
+{1 \over \rho_0^2}{...
...ial p_0 \over \partial z}
{\partial \rho_0 \over \partial z} + \kappa^2 \right]$](/articles/aa/full/2002/32/aa2380/img63.gif) |
|
|
(33) |
and
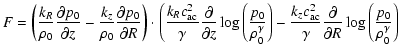 |
|
|
|
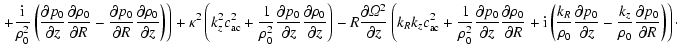 |
|
|
(34) |
For axisymmetric modes we simply have to
replace
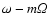 by
by 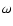 .
This procedure influences the
frequencies rather than the stability.
The stability of axisymmetric
and nonaxisymmetric perturbations is thus defined by the same stability
criterion in the approximation used.
The first factor in (31) describes the waves with
.
This procedure influences the
frequencies rather than the stability.
The stability of axisymmetric
and nonaxisymmetric perturbations is thus defined by the same stability
criterion in the approximation used.
The first factor in (31) describes the waves with
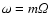 and will not be considered below. The stability is
defined by the factor D. The roots of D are
and will not be considered below. The stability is
defined by the factor D. The roots of D are
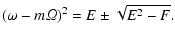 |
|
|
(35) |
According to (33) the coefficient E is real.
The flow is thus always unstable for negative E and complex F.
Positive E and real F are, therefore, the necessary conditions
for stability.
According to (34), F is real if and only if
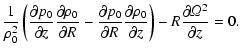 |
|
|
(36) |
Inserting (36) in (17),
we find
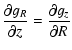 |
|
|
(37) |
as the immediate consequence. Without forces this relation is always fulfilled.
Any conservative force is
a particular solution of (37). If - as it is in accretion disks - the gravity
balances the pressure and the centrifugal force, then Eq. (36) is automatically fulfilled.
Note that
after the Poincare theorem for rotating media with potential force and
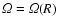 both the density and the pressure can be written as
functions of the generalized potential so that (36) is always fulfilled.
Generally, the magnetic field is not conservative and can never
fulfill the condition (37). This is the basic explanation for the
existence of the magnetorotational instability which is driven by (weak)
magnetic fields. That instability is typically obtained in a
short-wavelength approximation too, but is largely independent of the
assumptions made.
both the density and the pressure can be written as
functions of the generalized potential so that (36) is always fulfilled.
Generally, the magnetic field is not conservative and can never
fulfill the condition (37). This is the basic explanation for the
existence of the magnetorotational instability which is driven by (weak)
magnetic fields. That instability is typically obtained in a
short-wavelength approximation too, but is largely independent of the
assumptions made.
Now we can suppose that the necessary condition (36) is fulfilled.
The flow is stable if both roots in (35) are real and
positive. The sufficient conditions for stability are therefore
 |
|
|
(38) |
Inserting (36) into (34) we find F to be positive if
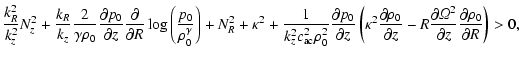 |
|
|
(39) |
where
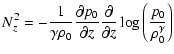 |
|
|
(40) |
and
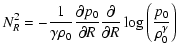 |
|
|
(41) |
are components of the Brunt-Väisälä frequency.
In our short-wave approximation (see (23)) we can neglect the last
term on the left hand side of (39). The expression (39) is thus a simple
quadratic expression in kR / kz. Two conditions will ensure its positivity: i) the expression is positive
for some value kR / kz and ii) the expression has no real roots i.e.
the discriminant is negative.
The first condition is fulfilled if
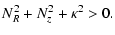 |
|
|
(42) |
This is the Schwarzschild criterion for stability in
the presence of rotation. The second condition leads to
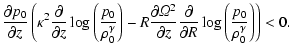 |
|
|
(43) |
Equations (42) and (43) are exactly equivalent to the
Solberg-Høiland conditions (4) and
(5).
The Schwarzschild criterion (42) ensures
that E>0 and the short-wave approximation ensures that F<E2 and
these relations do not yield any additional conditions.
The Solberg-Høiland conditions (4) and (5)
can also be obtained in the Boussinesq approximation. Goldreich & Schubert
(1967) have already formulated the dispersion relation within the framework of
the Boussinesq approximation.
Nevertheless, our more general consideration allows to find
the new necessary condition for stability (36).
Let us consider two interesting limiting cases.
Without rotation the Schwarzschild criterion (4) takes the form
where NR and Nz are given by (40) and (41).
The stratification is thus always stable if p0 and S0 have
opposite stratifications - which indeed is the standard case.
Nevertheless, Eq. (44) allows the stability also for the case
when p0 and S0 have the same stratifications in one direction
and opposite stratifications in another. Note that according to
(44) the situation with pressure stratification without
any density stratification is always unstable.
Without density stratification the sufficient stability condition (4)
for a rotating flow is
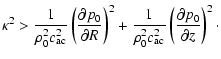 |
|
|
(45) |
This is the classical Rayleigh criterion (1) for stability generalized to
the compressible case. Obviously, the right-hand side is positive
and the criterion (45) is more restrictive than the standard one.
The main shortcoming in our presentation is the
short-wave assumption (23) under which all the above considerations
are only valid. Without this assumption, Fourier modes are no longer
solutions of the linearized equations and we have to switch to much more
complicated mathematics involving integral equations
(see Rüdiger & Kitchatinov 2000). We prefer to present numerical
simulations for the stability of (isothermal) density-stratified Keplerian
disks under the influence of finite disturbances. Along this way also
finite-amplitude disturbances can be considered within the framework of
a nonideal hydrodynamics.
The above analytical study has shown that stratified disks are stable;
under the assumption of a small scale in perturbations compared with
the disk dimensions. We present a few numerical integrations of the
hydrodynamic equations for the unrestricted case. The computations are
based on the work of Arlt & Rüdiger (2001) which required a stable,
stratified Keplerian disk as a prerequisite. We adapt these simulations
with adiabatic evolution and relatively strong nonaxisymmetric
perturbations.
The setup for our three-dimensional simulations applies a
global, cylindrical computational
domain with full azimuthal range, dimensionless radii from 4 to 6,
and a vertical extent of 2 density scale heights on average,
which is -1 to +1 in dimensionless units.
The ZEUS-3D code (developed by Stone & Norman 1992a,b; Stone et al. 1992)
was used for the integration of the hydrodynamic equations. The modifications
to the code are very close to those given in Arlt & Rüdiger (2001);
the induction equation is naturally not integrated here.
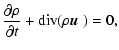 |
|
|
(46) |
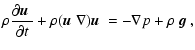 |
|
|
(47) |
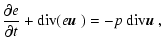 |
|
|
(48) |
where
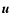 ,
,
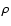 ,
e, and p have the usual meanings of
velocity, density, energy density per unit volume, and pressure. The source of gravitation
is that of a point mass M=105 at R=0. The simulations are
performed in a non-rotating reference frame; they do not include
self-gravity in the disk. The polytrophic exponent is
,
e, and p have the usual meanings of
velocity, density, energy density per unit volume, and pressure. The source of gravitation
is that of a point mass M=105 at R=0. The simulations are
performed in a non-rotating reference frame; they do not include
self-gravity in the disk. The polytrophic exponent is
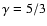 .
The original ZEUS code provides artificial viscosities for
improved shock evolution; we have put these terms to zero here.
The advection interpolation is the second order van-Leer scheme.
The conditions for the vertical boundaries are stress-free;
no matter can exit the computational domain in vertical direction
and the vertical derivatives of uR and
.
The original ZEUS code provides artificial viscosities for
improved shock evolution; we have put these terms to zero here.
The advection interpolation is the second order van-Leer scheme.
The conditions for the vertical boundaries are stress-free;
no matter can exit the computational domain in vertical direction
and the vertical derivatives of uR and 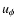 vanish.
The radial boundaries are also closed for the flow, and the radial
derivative of uz vanishes. For the azimuthal flow, we have to
adopt a modified boundary condition though. A Keplerian rotation
profile is maintained into the boundary zones, based on the last
zone of the integration domain. If the first azimuthal velocity
of the computational domain is denoted by
vanish.
The radial boundaries are also closed for the flow, and the radial
derivative of uz vanishes. For the azimuthal flow, we have to
adopt a modified boundary condition though. A Keplerian rotation
profile is maintained into the boundary zones, based on the last
zone of the integration domain. If the first azimuthal velocity
of the computational domain is denoted by
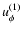 ,
we use
,
we use
The outer radial boundary is treated accordingly for
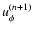 and
and
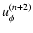 .
The azimuthal boundary conditions are periodic.
.
The azimuthal boundary conditions are periodic.
A rough representation of a stratified disk with radius-independent
density scale-height, was used for the initial conditions. We leave
this configuration for free development under the influence of the
gravitational potential. The initial conditions also involve
a non-axisymmetric velocity perturbation of the form
| uz |
= |
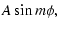 |
(51) |
| uR |
= |
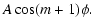 |
(52) |
The amplitude A is - in terms of the Keplerian velocity in the
middle of the annulus, 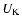 - about
- about
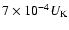 .
We have run two models with m=1 and different resolutions and
two additional with m=10 and m=200 in order to test short-wave
perturbations. The models are summarized in Table 1.
The initial configuration is isothermal with an energy density of
.
We have run two models with m=1 and different resolutions and
two additional with m=10 and m=200 in order to test short-wave
perturbations. The models are summarized in Table 1.
The initial configuration is isothermal with an energy density of
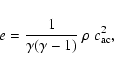 |
(53) |
where the sound speed
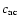 is 7% of the Keplerian velocity
is 7% of the Keplerian velocity
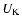 ,
and the polytrope exponent is
,
and the polytrope exponent is
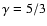 .
.
Table 1:
Overview of simulation configurations. The quantity
m denotes the azimuthal mode of the initial perturbation.
| Model |
Resolution |
m |
| I |
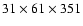 |
1 |
| II |
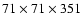 |
1 |
| III |
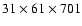 |
10 |
| IV |
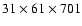 |
200 |
Figure 1 shows the evolution of the directional kinetic energies
for the z- and r-components. A gradual decay of fluid motion
is observed. Velocity fluctuations can also be measured in terms
of the correlation tensor element 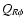 which is non-dimensionalized
with the average pressure giving the Shakura-Sunyaev parameter
which is non-dimensionalized
with the average pressure giving the Shakura-Sunyaev parameter
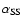 (cf. Arlt & Rüdiger 2001). Figure 2 shows the evolution of
(cf. Arlt & Rüdiger 2001). Figure 2 shows the evolution of
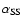 during
30 rotation periods at the inner disk radius. A clear relaxation
of the flow is seen. The initially strong velocity fluctuations
settle the correct density stratification for the gravitational
potential of the point mass (central star). The fluctuations in the
vertical direction reach
during
30 rotation periods at the inner disk radius. A clear relaxation
of the flow is seen. The initially strong velocity fluctuations
settle the correct density stratification for the gravitational
potential of the point mass (central star). The fluctuations in the
vertical direction reach 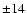 % of the Keplerian velocity
% of the Keplerian velocity 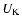 .
Those in the radial direction even reach -27%. They are thus not
small at all, and even a nonlinear instability might be noticed
if existing.
.
Those in the radial direction even reach -27%. They are thus not
small at all, and even a nonlinear instability might be noticed
if existing.
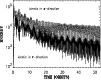 |
Figure 1:
Kinetic energies in the vertical and radial components of the
flow from the run with
 grid points (Model I).
The solid line is the energy of the r-direction, the dashed
line that of the z-direction. Times are given in revolutions of
the inner boundary of the computational domain.
grid points (Model I).
The solid line is the energy of the r-direction, the dashed
line that of the z-direction. Times are given in revolutions of
the inner boundary of the computational domain. |
| Open with DEXTER |
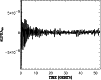 |
Figure 2:
Shakura-Sunyaev parameter
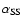 from the same
model as in Fig. 1 (Model I). Times are again
in orbital periods of the inner boundary of the domain.
from the same
model as in Fig. 1 (Model I). Times are again
in orbital periods of the inner boundary of the domain. |
| Open with DEXTER |
We can read an approximate decay time
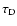 from
Fig. 1. On average, it amounts to an e-folding time of about 20 orbital
periods or
from
Fig. 1. On average, it amounts to an e-folding time of about 20 orbital
periods or
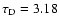 in non-dimensional
units. As the main relaxation motions
are vertical, we use the density scale-height for the length scale
and obtain a viscosity of 0.03 caused by the finite resolution of
the numerical grid. In terms of Reynolds numbers, we achieve
in non-dimensional
units. As the main relaxation motions
are vertical, we use the density scale-height for the length scale
and obtain a viscosity of 0.03 caused by the finite resolution of
the numerical grid. In terms of Reynolds numbers, we achieve
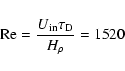 |
(54) |
near the inner edge of the annulus where the Keplerian velocity
is
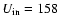 .
The density-scale height at the inner edge
is
.
The density-scale height at the inner edge
is
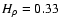 in the initial configuration.
A second run with significantly higher resolution - in
vertical direction in particular - is shown in Fig. 3.
No change in the decaying nature of the perturbation
is found.
An increase in azimuthal wave number of the perturbation does
not provide instability either. Figure 4 is the result
of a simulation with a perturbation of very high wave number,
in the initial configuration.
A second run with significantly higher resolution - in
vertical direction in particular - is shown in Fig. 3.
No change in the decaying nature of the perturbation
is found.
An increase in azimuthal wave number of the perturbation does
not provide instability either. Figure 4 is the result
of a simulation with a perturbation of very high wave number,
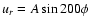 ,
,
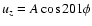 ,
and doubled azimuthal resolution. The gas again settles towards an
equilibrium state and very low kinetic energies in the radial and vertical
components.
,
and doubled azimuthal resolution. The gas again settles towards an
equilibrium state and very low kinetic energies in the radial and vertical
components.
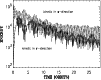 |
Figure 3:
Kinetic energies in the vertical (dashed) and radial
(solid) components of the flow. The resolution of the model
is
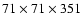 grid points (Model II). Times are again
in orbital periods of the inner boundary of the domain. grid points (Model II). Times are again
in orbital periods of the inner boundary of the domain. |
| Open with DEXTER |
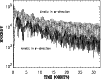 |
Figure 4:
Kinetic energies in the vertical (dashed) and radial
(solid) components for the model with m=200 in the
initial perturbation (Model IV). The resolution of the computational
domain is
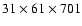 . . |
| Open with DEXTER |
We have shown in Sect. 1 that the Solberg-Høiland conditions (4)
and (5) answer the question whether the combined action of stable (radial)
shear and stable (vertical) density stratification can produce a new instability.
The clear answer is No, but uncertainties remain about validity of the
Solberg-Høiland criterion for the case of nonaxisymmetric disturbances
of the compressible accretion disk material. Indeed, in Sect. 2 we were able to
reproduce the Solberg-Høiland criterion in the well-known formulation
but only with a short-wave approximation and a small-m approximation applied
formulated in (23).
Self-gravitation (i.e. density waves) has been excluded from the consideration but
sound waves have been included. Our dispersion relation (32) is of fourth order contrary to the dispersion relation of second order resulting from the Boussinesq approximation (Goldreich & Schubert 1967) and contrary to the dispersion relation of fifth order resulting from nonideal hydrodynamics (Abramowicz et al. 1984, 1990). Along this way a new necessary condition for stability results which requires the external force which balances pressure and centrifugal force to be a conservative one, i.e. to possess a potential (cf. (36)).
It is interesting to note that in the Boussinesq approximation for nonideal
fluids the Solberg-Høiland criterion changes to the
Goldreich-Schubert-Fricke criterion (Goldreich & Schubert 1967; Smith &
Fricke 1975; Urpin & Brandenburg 1998) which no longer allows the existence of a vertical shear for
stability, i.e.
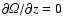 .
And, indeed, even in thin
accretion disks there is always such a (weak) vertical shear
.
And, indeed, even in thin
accretion disks there is always such a (weak) vertical shear
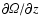 the meaning of which remains open. We have thus numerically
simulated the stability of such accretion disks using the ZEUS-3D code. The
numerical integration of the nonlinear adiabatic equations of the fully
compressible hydrodynamics with initially nonaxisymmetric velocity perturbations
does not lead to the onset of instability although the disk, of course, does
possess a small vertical shear. An overview of the simulated configurations
can be found in Table 1 which shows that we indeed have also considered very
high values of the azimuthal "quantum'' number m which do not fulfil the short-wave condition (23).
Based on our numerical simulations, we thus cannot support findings
about a fast, hydrodynamic instability
in stratified disk flows.
Similar simulations including magnetic fields showed the
magneto-rotational instability with growth rates near
the meaning of which remains open. We have thus numerically
simulated the stability of such accretion disks using the ZEUS-3D code. The
numerical integration of the nonlinear adiabatic equations of the fully
compressible hydrodynamics with initially nonaxisymmetric velocity perturbations
does not lead to the onset of instability although the disk, of course, does
possess a small vertical shear. An overview of the simulated configurations
can be found in Table 1 which shows that we indeed have also considered very
high values of the azimuthal "quantum'' number m which do not fulfil the short-wave condition (23).
Based on our numerical simulations, we thus cannot support findings
about a fast, hydrodynamic instability
in stratified disk flows.
Similar simulations including magnetic fields showed the
magneto-rotational instability with growth rates near
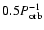 .
Our hydrodynamic runs cover 30-50 orbits of
the inner disk and show only decay in velocity fluctuations.
Angular momentum transport hovers at
.
Our hydrodynamic runs cover 30-50 orbits of
the inner disk and show only decay in velocity fluctuations.
Angular momentum transport hovers at
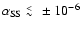 ;
the temporal average in Fig. 2 is
;
the temporal average in Fig. 2 is
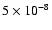 .
.
-
Abramowicz, M. A., Livio, M., Piran, T., & Wiita, P. J. 1984, ApJ, 279, 367
In the text
NASA ADS
-
Abramowicz, M. A., Livio, M., Soker, N., & Szuszkiewicz, E. 1990, A&A, 239, 399
In the text
NASA ADS
-
Arlt, R., & Rüdiger, G. 2001, A&A, 374, 1035
In the text
NASA ADS
-
Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214
In the text
NASA ADS
-
Balbus, S. A. 1995, ApJ, 453, 380
In the text
NASA ADS
-
Balbus, S. A., Hawley, J. F., & Stone, J. M. 1996, ApJ, 467, 76
In the text
NASA ADS
-
Brandenburg, A., Nordlund, Å., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741
In the text
NASA ADS
-
Elstner, D., Rüdiger, G., & Tschäpe, R. 1989, GAFD, 48, 235
In the text
-
Goldreich, P., & Schubert, G. 1967, ApJ, 150, 571
In the text
NASA ADS
-
Klahr, H., & Bodenheimer, P. 2001, Turbulence in Accretion Discs, The Global
Baroclinic Instability, in Astronomische Gesellschaft Abstract Ser., 18, 38
In the text
-
Livio, M., & Shaviv, G. 1977, A&A, 55, 95
In the text
NASA ADS
-
Meinel, R. 1983, Astron. Nachr., 304, 65
In the text
NASA ADS
-
Molemaker, M., McWilliams, J., & Yavneh, I. 2001, Phys. Rev. Lett., 86, 5270
In the text
NASA ADS
-
Rüdiger, G., & Kitchatinov, L. L. 2000, Astron. Nachr., 321, 181
In the text
NASA ADS
-
Smith, C. R., & Fricke, K. J. 1975, MNRAS, 172, 577
In the text
-
Stone, J. M., & Norman, M. L. 1992a, ApJS, 80, 753
In the text
NASA ADS
-
Stone, J. M., & Norman, M. L. 1992b, ApJS, 80, 791
NASA ADS
-
Stone, J. M., Mihalas, D., & Norman, M. L. 1992, ApJS, 80, 819
In the text
NASA ADS
-
Tassoul, J.-L. 2000, Stellar Rotation (Cambridge Univ. Press, Cambridge)
In the text
-
Urpin, V. A., & Brandenburg, A. 1998, MNRAS, 294, 399
In the text
NASA ADS
-
Yavneh, I., McWilliams, J., & Molemaker, M. 2001, J. Fluid Mech., 448, 1
In the text
-
Ziegler, U., & Rüdiger, G. 2000, A&A, 356, 1141
In the text
NASA ADS
Copyright ESO 2002
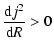
![]() are stable to infinitesimal and finite disturbances (Balbus et al. 1996).
Most of the mentioned discussions are covered by the Solberg-Høiland
conditions for dynamic stability which, for the geometrical constellation studied here,
take the form
are stable to infinitesimal and finite disturbances (Balbus et al. 1996).
Most of the mentioned discussions are covered by the Solberg-Høiland
conditions for dynamic stability which, for the geometrical constellation studied here,
take the form
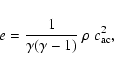


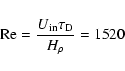


![]() .
And, indeed, even in thin
accretion disks there is always such a (weak) vertical shear
.
And, indeed, even in thin
accretion disks there is always such a (weak) vertical shear
![]() the meaning of which remains open. We have thus numerically
simulated the stability of such accretion disks using the ZEUS-3D code. The
numerical integration of the nonlinear adiabatic equations of the fully
compressible hydrodynamics with initially nonaxisymmetric velocity perturbations
does not lead to the onset of instability although the disk, of course, does
possess a small vertical shear. An overview of the simulated configurations
can be found in Table 1 which shows that we indeed have also considered very
high values of the azimuthal "quantum'' number m which do not fulfil the short-wave condition (23).
Based on our numerical simulations, we thus cannot support findings
about a fast, hydrodynamic instability
in stratified disk flows.
Similar simulations including magnetic fields showed the
magneto-rotational instability with growth rates near
the meaning of which remains open. We have thus numerically
simulated the stability of such accretion disks using the ZEUS-3D code. The
numerical integration of the nonlinear adiabatic equations of the fully
compressible hydrodynamics with initially nonaxisymmetric velocity perturbations
does not lead to the onset of instability although the disk, of course, does
possess a small vertical shear. An overview of the simulated configurations
can be found in Table 1 which shows that we indeed have also considered very
high values of the azimuthal "quantum'' number m which do not fulfil the short-wave condition (23).
Based on our numerical simulations, we thus cannot support findings
about a fast, hydrodynamic instability
in stratified disk flows.
Similar simulations including magnetic fields showed the
magneto-rotational instability with growth rates near
![]() .
Our hydrodynamic runs cover 30-50 orbits of
the inner disk and show only decay in velocity fluctuations.
Angular momentum transport hovers at
.
Our hydrodynamic runs cover 30-50 orbits of
the inner disk and show only decay in velocity fluctuations.
Angular momentum transport hovers at
![]() ;
the temporal average in Fig. 2 is
;
the temporal average in Fig. 2 is
![]() .
.