

Up: Astrometry of five major 1995-1997
Subsections
Numerical integration has been used very effectively in generating
ephemerides of natural satellites. A numerical integration can provide
a powerful way for checking the validity of the analytical theory
before making any fit to real observations (see, for example,
Sinclair & Taylor 1985; Harper et al. 1989). In this paper,
we explore the use of numerical integration in producing an
ephemeris of the five major Uranian satellites, which can also
be used in our calibration calculation as an alternative to an
analytical theory.
As concerns numerical integration methods, Hadjifotinou & Harper
(1995) and Hadjifotinou & Ichtiaroglou (1997) studied the behaviour
of two numerical integration methods, the 10th-order Gauss-Jackson
backward difference and the 12th-order Runge-Kutta-Nyström method
(RKN12(10)17M formulae of Brankin et al. 1989). They concluded
that when using the first method,
an instability occurs in the integration of the equations for the
partial derivatives when the step-size is larger than 1/76 of the
orbital period of the innermost satellite. In contrast, the RKN
method is stable and can achieve very good accuracy with step-sizes
much larger than the critical step-sizes of the Gauss-Jackson method.
Therefore the RKN method is preferable than Gauss-Jackson.
Taylor (1998) computed the ephemerides of the five major Uranian
satellites by numerical integration using all available Earth-based
observations. His excellent work provided the newest physical
parameters for the integration of the Uranian satellite system, the most
of which have been retained in our calculation. The main parameters
that we used are given as follows:
Mass of Uranus =
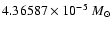
Mass of Miranda:
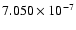
Mass of Titania:
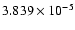
Mass of Oberon:
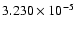
J2 = 0.003365
Equatorial radius of Uranus = 26 200 km.
These parameters come from fitting to all of the data, including those from
the spacecraft mission, and are taken from Taylor (1998).
Mass of Ariel:
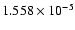
Mass of Umbriel:
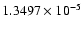 .
.
The masses of Ariel and Umbriel come from Jacobson et al. (1992).
The masses of the satellites given above are all expressed in units of
the mass of Uranus.
Coordinates of the pole of Uranus:
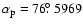 ,
,
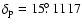 .
.
The reference is the Earth's Mean Equator and Equinox of B1950.
J4 = -0.0000321.
Both the pole of Uranus and J4 were taken from
French et al. (1988).
The equatorial plane of Uranus is chosen as the reference plane for
the numerical integration. The integration equations were formulated
in Cartesian coordinates with the x-axis directed at the ascending
node of the equator of Uranus w.r.t. Earth's equator of B1950.0
(JED 2433282.423), and the origin at the center of mass of Uranus.
For simplification of reduction, no planetary and solar perturbations
were included in our numerical integration. From trial computation we
found no significant loss of accuracy by omitting them. The position
of Uranus itself was given from the ephemerides DE406.
A numerical integration was iteratively fitted to the GUST86 theory over
a span of 128 days in order to obtain a first set of initial positions and
velocities at the epoch JED 2449948.5, which is close to the middle of
the time span covered by the observations.
Next, the numerical integration was iteratively fitted to the observations.
The resulting initial positions and velocities are given in Table 3.
The RKN integration method calculates the step-size adaptively, but
an initial estimate is required to start the process. A value of 0.0625
days was used. In the fitting of integration to the observations, good
convergence was obtained after only three iterations.
The observed-minus-computed residuals of inter-satellite positions
from numerical integration,
in separation (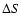 )
and position angle (
)
and position angle (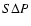 ),
are given also in Table 4. Oberon is excepted, as it was used as
a reference. The rejection level that we used was
),
are given also in Table 4. Oberon is excepted, as it was used as
a reference. The rejection level that we used was
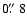 .
.


Up: Astrometry of five major 1995-1997
Copyright ESO 2002