A&A 391, 633-639 (2002)
DOI: 10.1051/0004-6361:20020867
Behaviour of the periods in double mode RR Lyrae, V26 in M15
M. Paparó1 -
B. Szeidl1 -
S. M. Saad2 -
Z. Kolláth1 -
M. S. Abu Elazm2
1 - Konkoly Observatory, 1525 Budapest XII, PO Box 67, Hungary
2 - Helwan Institute of Astronomy and Geophysics, Cairo, Egypt
Received 3 September 2001/ Accepted 30 April 2002
Abstract
The changes in the periods of the fundamental and first overtone pulsation
of the variable V26 in the globular cluster M15 are studied. The analysis
was based on published observations. The method of investigation was
outlined in our previous paper (Paparó et al. 1998). The Fourier
phase diagrams for both frequencies have been constructed. General
guidelines concerning the cycle counting problems are discussed.
In both periods a sudden increase took place around JD 2431500 ( 1945)
and the changes
were the same in sign but slightly different in magnitude. The period
change behaviour of the fundamental mode
was noticed for the first time. Before the abrupt change the fundamental
and first overtone periods were
1945)
and the changes
were the same in sign but slightly different in magnitude. The period
change behaviour of the fundamental mode
was noticed for the first time. Before the abrupt change the fundamental
and first overtone periods were
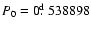 and
and
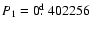 days and after it
days and after it
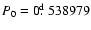 and
and
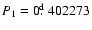 days. Although the
fundamental component is very weak, there is
a remarkable concordance between our period after the abrupt change and
the period derived by
Clement & Walker (1991). The disagreement between the observed period
changes and the expectation of stellar evolutionary theory strongly suggest
that period changes are dominated by short term changes governed by the physics
of the star.
Fast changes in oscillation frequency such as in V26/M15 cannot take
place without sudden changes in the stellar structure. The
possible physical processes are the mixing events in a small part of the
semiconvective zone (Sweigart & Renzini 1979) or the dredge up
of a small amount of helium by occasional convection overshooting
(Cox 1998).
days. Although the
fundamental component is very weak, there is
a remarkable concordance between our period after the abrupt change and
the period derived by
Clement & Walker (1991). The disagreement between the observed period
changes and the expectation of stellar evolutionary theory strongly suggest
that period changes are dominated by short term changes governed by the physics
of the star.
Fast changes in oscillation frequency such as in V26/M15 cannot take
place without sudden changes in the stellar structure. The
possible physical processes are the mixing events in a small part of the
semiconvective zone (Sweigart & Renzini 1979) or the dredge up
of a small amount of helium by occasional convection overshooting
(Cox 1998).
Key words: stars: individual: V26 in M15 - stars: oscillations - stars: variables:
RR Lyrae - globular cluster: individual: M15
1 Introduction
The study of period changes of RR Lyrae stars in globular clusters is considered
to be a powerful test of the evolutionary theories of horizontal branch stars.
As stellar evolution results in slow changes in the star's physical parameters
(e.g. in stellar radius), one may expect that the
accumulation of subtle changes in the periods might reveal the trend and the
size of the period changes.
On the one hand the period changes observed often differ in sign and in rate
from the theoretically predicted values, and on the other hand the complex
structure of the O-C diagram of some RR Lyrae stars suggests that some
kind of "noise'' may be superimposed on the secular variations of the
periods. Abrupt changes in the periods are also characteristic of some of the
stars (Szeidl 1975; Smith & Sandage 1981). The
source of
"noise'' and the abrupt changes have been attributed to discrete mixing events in
the semiconvective zones (Sweigart & Renzini 1979) or they may have a
hydromagnetic origin (Stothers 1980).
Theoretical and evolutionary consideration suggested that the relative
changes in the period of the fundamental and first overtone of an RR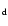 star (
star (
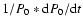 and
and
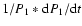 )
should be of the same sign and about
the same rate. Paparó et al. (1998) (Paper I) have demonstrated that no strict
correlation exists between the changes in the periods of the two
pulsational modes of an RR
)
should be of the same sign and about
the same rate. Paparó et al. (1998) (Paper I) have demonstrated that no strict
correlation exists between the changes in the periods of the two
pulsational modes of an RR star, neither in rate nor in sign. Thus,
these investigations questioned the
simple idea that the linear period changes reflect the evolution of RR
Lyrae stars on the horizontal branch (HB). All the stars studied in Paper I,
have shown slow linear changes in their dominant (first overtone) frequency
(except V54, which showed a small period jump as well). V26 was not included
in the previous investigation because its first overtone frequency had a
large abrupt
change around 1945 or JD 2 431 500 (Silbermann & Smith 1995a) and
its preliminary study (Paparó et al. 1997) also indicated that the
frequency of the fundamental mode was subject to a sudden change around the
same time. In view of this, V26 deserves special attention.
star, neither in rate nor in sign. Thus,
these investigations questioned the
simple idea that the linear period changes reflect the evolution of RR
Lyrae stars on the horizontal branch (HB). All the stars studied in Paper I,
have shown slow linear changes in their dominant (first overtone) frequency
(except V54, which showed a small period jump as well). V26 was not included
in the previous investigation because its first overtone frequency had a
large abrupt
change around 1945 or JD 2 431 500 (Silbermann & Smith 1995a) and
its preliminary study (Paparó et al. 1997) also indicated that the
frequency of the fundamental mode was subject to a sudden change around the
same time. In view of this, V26 deserves special attention.
2 Data
The investigation of RR Lyrae stars in M15 was started by
Bailey (1919)
in 1896.
The definition of variable stars in M15 as variable (V or v) and the
running number of Bailey's list (26 in our case) has been accepted in all
catalogues (e.g. Sawyer Hogg 1973).
In the ensuing nine decades a great number of photographic
observations have been obtained by different observers. Between 1896 and 1908 Bailey's
observations were rather sporadic and scarce. Since 1915, however, there
have been very many photographic observations and they are relatively
uniform.
We have made extensive use of the observation of Bailey (1919),
Barlai (1989), Bingham et al. (1984),
Filippenko & Simon (1981),
Fritze (1963), Grubissich (1956), Sandage et al. (1981)
and Wesselink (1974). The observations of
Makarova & Akimova (1965)
were left out of consideration because these observations were given in an
unusual photometric system; Gordenko et al. (1984) did not
publish individual observations for the stars they studied.
Recently we have seen the beginning of a new era in observational
techniques: Silbermann &
Smith (1995b) started CCD observations of the variables in M15 in the
early 1990s. Unfortunately no CCD photometric data on V26 have been
obtained since the star was out of the CCD frame (Silbermann 2001).
Table 1:
Distribution of observations used in the present work.
|
Year |
Number of observations |
Source |
| |
in pg/B band |
in V band |
|
|
1915 |
35 pg |
|
Bailey (1919) |
| 1916 |
27 pg |
|
" |
| 1925 |
33 pg |
|
Fritze (1963) |
| 1933 |
13 pg |
|
" |
| 1937 |
29 pg |
|
Barlai (1989) |
| 1938 |
86 pg |
|
" |
| 1939 |
14 pg |
|
" |
| 1940 |
11 pg |
|
" |
| 1941 |
18 pg |
|
" |
| 1950 |
5 pg |
|
" |
| 1951 |
80 pg |
|
" |
| 1952 |
15 pg |
|
" |
| 1953 |
5 pg |
|
" |
| 1954 |
154 pg |
|
Grubissich (1956) |
| 1955 |
34 pg |
|
" |
| |
1 pg |
|
Barlai (1989) |
| 1956 |
16 pg |
|
" |
| 1957 |
25 pg |
|
" |
| |
3 B |
6 V |
Sandage et al. (1981) |
| 1958 |
42 B |
42 V |
" |
| 1959 |
17 B |
16 V |
" |
| 1963 |
25 pg |
|
Barlai (1989) |
| 1966 |
15 pg |
|
" |
| |
7 B |
|
Wesselink (1974) |
| 1967 |
20 B |
|
" |
| 1968 |
19 B |
|
" |
| 1973 |
|
1 V |
Bingham et al. (1984) |
| 1974 |
9 B |
12 V |
" |
| 1975 |
4 B |
2 V |
" |
| 1976 |
|
31 V |
Filippenko & Simon (1981) |
| 1977 |
|
60 V |
" |
| |
9 B |
8 V |
Bingham et al. (1984) |
| 1978 |
|
107 V |
Filippenko & Simon (1981) |
| |
8 B |
16 V |
Bingham et al. (1984) |
| 1979 |
14 B |
14 V |
" |
Table 1 summarizes the number and photometric band of
observations of the different years discussed in this paper. The distribution of
data used are shown in Fig. 1 (filled squares: pg/B
observations, open circles: V observations). The separation into
segments is given later in Table 4.
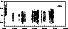 |
Figure 1:
Distribution of data. Squares indicate photographic (or B)
observations, open circles V observations. The ordinate scale is given in
magnitude and the abcissa is time in days JD - 2 400 000. |
| Open with DEXTER |
Over the past 90 years observations have been carried out by
a variety of techniques,
telescopes of different size and focal ratio, etc., which may have
serious effects on the photometry. Generally speaking reduction of the
data to the
same photometric system is not an easy task albeit the magnitudes of
comparison stars used by different observers are known. However, in our
case the magnitude scale of the different photometric systems are
insignificant: only the zero points show slight differences.
The photographic light curves of most observers are
well-matched, so all the mpg and B data are treated together and used as
a coherent data set. The zero point in each case is treated as a free
parameter in
our investigation.
As we see in Fig. 1 the mean values from the different
observational tracks are
the same except for the observations of Bailey
which are brighter by about 0.6 mag. We may say as an explanation that
the photographic technique was in its early stages compared with the later
generally-accepted sensitivity range of emulsion. However, in this case all the
other stars in M15 measured by Bailey on the same set of plates should show
a similar difference in the mean value compared with his other
observations. As is shown by the
distribution of data of other double mode RR Lyrae stars (Fig. 1 in
Paper I) there is not such a large
difference
in the mean light level for the other stars. Bailey (1919) used the same set of
standard stars for all variables except for V28.
The Hungarian photographic plates were carefully checked for possible
contamination by a faint star near to V26 but contamination was ruled out
as an explanation.
V26 has no specific position
in the cluster. It is not near the center of the cluster which would
make questionable the precise photometry. At present, it would seem that
there is no acceptable explanation for Bailey's observation for the mean
light level of V26.
We accepted the mean error of the
observations as 0.15 mag throughout our analysis, which is characteristic
of the photographic observations, but overestimates the error of the
high-quality data of Sandage et al. (1981) and Bingham et al. (1984).
3 Analysis
The available observational data do not readily lend themselves to an analysis
of the changes in the frequencies of both pulsational modes by the usual
techniques (traditional O-C, Fourier, PDM). Therefore the
method of analysis (Fourier phase method)
described in detail in Paper I was used to derive the
changes in the fundamental and first overtone period of V26/M15.
The main point of the method is that by fixing the frequencies and amplitudes
(aij) only the 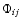 phases are left as free parameters in the Fourier
decomposition of the light curve:
phases are left as free parameters in the Fourier
decomposition of the light curve:
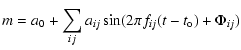 |
|
|
(1) |
where fij is the linear combination of the fundamental (f0) and first
overtone (f1) frequencies. The zero point is marked by a0. The phase,
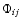 is calculated from an epoch (t0).
is calculated from an epoch (t0).
In this way the reduced numbers of free parameters allowed us to use more
sporadic observations as well. The method is not sensitive to small changes
in the amplitude (tested in Paper I). For V26 the errors of the phase due
to the errors in amplitude determination are very small:
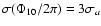 and
and
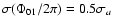 ,
where
,
where 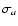 is in magnitudes. This means that a 0.02 mag error in a0
results in an error of 0.06 in the phase of the fundamental mode.
During the investigation the amplitudes of fundamental mode and first
overtone were fixed at
a10 = 0.034 and
a01 = 0.183 mag that
we obtained from a least squares fit for the whole data set. This resulted
in a 1:5-1:6 amplitude ratio.
The variations in the phases
is in magnitudes. This means that a 0.02 mag error in a0
results in an error of 0.06 in the phase of the fundamental mode.
During the investigation the amplitudes of fundamental mode and first
overtone were fixed at
a10 = 0.034 and
a01 = 0.183 mag that
we obtained from a least squares fit for the whole data set. This resulted
in a 1:5-1:6 amplitude ratio.
The variations in the phases 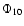 and
and 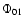 reflect the changes in the frequencies if the fixed values of the frequencies
are precise enough or the cycle counting problem can be treated
appropriately.
The zero point
reflect the changes in the frequencies if the fixed values of the frequencies
are precise enough or the cycle counting problem can be treated
appropriately.
The zero point 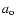 was also
treated as a free parameter - as permitted by the Fourier method.
was also
treated as a free parameter - as permitted by the Fourier method.
Table 2:
Period derived by different authors.
|
P1 |
P0 |
Source |
Remark |
| days |
days |
|
|
|
0.402326 |
|
Bailey (1919) |
|
| 0.402270 |
|
Grubissich (1956) |
|
| 0.4023068 |
|
Fritze (1962) |
|
| 0.402278 |
|
Wesselink (1974) |
|
| 0.402270 |
|
Smith & Sandage (1981) |
|
| 0.4023 |
0.5430 |
Hodson & Cox (1982) |
SKS |
| |
0.5398 |
" |
FS |
| 0.402275 |
0.5430 |
Cox et al. (1983) |
SKS |
| 0.402260 |
0.53913 |
Nemec (1985) |
SKS |
| 0.402268 |
0.53892 |
Jurcsik & Barlai (1990) |
|
| 0.402272 |
0.538990 |
Clement & Walker (1991) |
G+SKS |
| 0.402280 |
0.53896 |
" |
BCDF |
| |
|
|
|
| Remarks: SKS: only Sandage et al.'s (1981) data, |
| FS: only Filippenko & Simon's (1981) data, |
| G+SKS: only Grubissich (1956) and
Sandage et al.'s (1981) data, |
| BCDF: only Bingham et al.'s (1984) data |
It is well known that the period changes of single mode RR Lyrae stars
given by the O-C diagram can be studied when the periods are
precisely known.
The rate of period change over 30-40 years results in changes of 10-6
days (Hoffmeister et al. 1985).
We should expect that in order to investigate period changes for double mode
RR Lyrae stars one needs as precise period determinations as for single
mode RR Lyrae stars.
However, the possibility of obtaining as precise periods for double mode RR Lyrae stars as for
single mode RR Lyrae stars is not an easy task. Even
for the same length of observation, the increased number of parameters decreases
the precision of the determination. The interaction of modes has only a slight
effect on the larger amplitude mode whereas the effect is much stronger for the
smaller amplitude modes.
There is general agreement on the first overtone period of V26/M15 derived
by the authors (listed in Table 2) of up to 10-5 days.
Since the total amplitude of
the fundamental oscillation is much less
than that of the first overtone pulsation (about a quarter of that published in
the literature), the result from determining the
frequency of the fundamental mode is somewhat doubtful using shorter data
sets. In fact, the
fundamental oscillation of V26/M15 sometimes became insignificant (e.g. in
1938) and the star did not show a measurable double mode nature in the set of
Babelsberg observations (Jurcsik & Barlai 1990;
Purdue et al. 1995). However, on analysing
the observations of Sandage et al. (1981) and
Filippenko & Simon (1981), Hodson & Cox (1982) came to the conclusion that the ratio of
the amplitudes of the first overtone to fundamental mode pulsation of V26/M15
had remained unchanged within the error limits. Because of the very small
fundamental component in the star's pulsation,
Kovács et al. (1986) left it out of their analysis.
Clement & Walker (1991), Jurcsik & Barlai (1990) and
Nemec (1985) included the star in their thorough analysis. Their
investigations led to concordant results for both the fundamental and the first
overtone oscillation.
The general agreement on the fundamental mode period of V26/M15
(see Table 2) is much weaker than for the
first overtone. Differences are up to 10-3, 10-4 or
10-5 days depending on the length of the data set involved in the analysis.
In this overview we have tried to emphasize how important the precise value of
a period determination is if we are interested in a meaningful period change
interpretation.
Incidentally, in connection with V26/M15 we can show the strength of the
Fourier phase method in finding the precise true period and what the
range of discrepancy is in the period where the method is still usable. For
V26/M15 the accepted starting values of
the modes were taken from
the paper by
Nemec (1985).
The value of 0.402260 days for the first overtone proved to be
an appropriate starting
value since the resulting phase values immediately showed similar regular
structures (see in Fig. 3). However, his less precise 0.53913
day value for the fundamental mode illustrated how the phase values
suffered from the cycle counting problem.
There are two parameters that
influence the appearance of the phase diagram, viz.
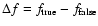 representing the correction to get the true frequency
and
representing the correction to get the true frequency
and 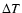 ,
given the time interval that we use for obtaining a certain phase
value. A specific time interval, marked by
,
given the time interval that we use for obtaining a certain phase
value. A specific time interval, marked by
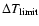 ,
is defined
by
,
is defined
by
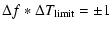 |
|
|
(2) |
where 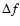 is given in cycle/day,
is given in cycle/day,
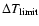 is given in days.
Equation (2) shows
that the difference between the true and false periods accumulates
and beyond the
is given in days.
Equation (2) shows
that the difference between the true and false periods accumulates
and beyond the
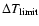 time interval it reaches a full cycle. This means
that we have to solve the serious problem of cycle counting for a gapped
data set. In Fig. 2 we present some test cases calculated with
different
time interval it reaches a full cycle. This means
that we have to solve the serious problem of cycle counting for a gapped
data set. In Fig. 2 we present some test cases calculated with
different 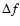 and
and 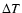 values. The phases were calculated using the
fundamental period of V26 shifted by the
values. The phases were calculated using the
fundamental period of V26 shifted by the 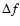 values. At a given
values. At a given 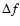 value if our choice is too large,
value if our choice is too large,
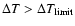 ,
then the phase values show a distribution where
one or more cycles are missing between each phase point (panel a).
In this case there is no way to
reconstruct a continuous phase diagram. Since for the test case we knew the
number of missing cycles, we reconstructed the straight line
for illustration purposes. This covers a phase range of 8 cycles, thereby showing the
very inaccurate value of the period used. The interpretation of such a diagram
(left side),
as no regular period change is apparently present, is misleading. In this case
we see only the
poor treatment of the cycle counting problem. Our suggestion is that
,
then the phase values show a distribution where
one or more cycles are missing between each phase point (panel a).
In this case there is no way to
reconstruct a continuous phase diagram. Since for the test case we knew the
number of missing cycles, we reconstructed the straight line
for illustration purposes. This covers a phase range of 8 cycles, thereby showing the
very inaccurate value of the period used. The interpretation of such a diagram
(left side),
as no regular period change is apparently present, is misleading. In this case
we see only the
poor treatment of the cycle counting problem. Our suggestion is that
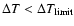 is applicable.
is applicable.
We should go further in our limitation. Our aim is to have 2 or 3 phase
values between 0 and 1 without missing any cycle. These phase values will
define a line with a definite slope. To get
2 or 3 phase values in the
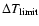 interval we have to use
interval we have to use
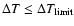 /2 or /3 time interval. In practice the
/2 or /3 time interval. In practice the
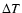 time intervals do not need to be exactly the same but their sum
must not exceed
time intervals do not need to be exactly the same but their sum
must not exceed
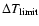 .
Even for a single straight
line, with a longer compact data set (panel b), the other
phase values can be arranged
along a continuous straight line increasing or decreasing the resulting
phase values by
.
Even for a single straight
line, with a longer compact data set (panel b), the other
phase values can be arranged
along a continuous straight line increasing or decreasing the resulting
phase values by 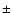 1, 2, etc. (right side panels). Obviously more than
one straight line
facilitates the arrangement (panel c). We should say
that the lowest possible value of
1, 2, etc. (right side panels). Obviously more than
one straight line
facilitates the arrangement (panel c). We should say
that the lowest possible value of 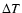 is desirable but the lower limit is strongly connected
with the distribution of observations and the noise level. If the data
are scarce
there may be no way to find 2 or 3 *
is desirable but the lower limit is strongly connected
with the distribution of observations and the noise level. If the data
are scarce
there may be no way to find 2 or 3 * 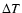 time intervals
within the
time intervals
within the
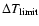 .
In this case there is also no way to overcome the cycle
counting problem.
.
In this case there is also no way to overcome the cycle
counting problem.
In the case of V26/M15 2-3 years were chosen as 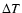 ,
not equally
long for each group of data. Three straight line sections were observed. However,
at the beginning or at the end where observations were scarce, the
,
not equally
long for each group of data. Three straight line sections were observed. However,
at the beginning or at the end where observations were scarce, the
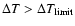 was used and each phase value had a missing cycle between
one and the next. The three straight sections allowed us to
reconstruct a continuous
straight line unambiguously.
was used and each phase value had a missing cycle between
one and the next. The three straight sections allowed us to
reconstruct a continuous
straight line unambiguously.
The value of the other parameter (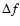 )
is not known in advance. We should
consider the effect of the different
)
is not known in advance. We should
consider the effect of the different 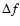 at a fixed
at a fixed
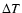 .
If
.
If 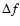 is too large then we have the same effect as in the
case of too large
is too large then we have the same effect as in the
case of too large 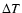 and the cycle counting problem is untreatable
(panel a).
To check whether the cycle counting problem is present, it is
suggested that
and the cycle counting problem is untreatable
(panel a).
To check whether the cycle counting problem is present, it is
suggested that
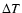 be decreased (as in panel b). If a smaller
be decreased (as in panel b). If a smaller 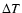 reproduces the straight line section
then the cycle counting problem is treatable. If there are no straight
lines then a new starting value for the frequency is suggested.
Bearing in mind that the
period of
RR
reproduces the straight line section
then the cycle counting problem is treatable. If there are no straight
lines then a new starting value for the frequency is suggested.
Bearing in mind that the
period of
RR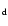 stars is precise up to 10-2 or 10-3 days, the cycle/month
(
stars is precise up to 10-2 or 10-3 days, the cycle/month
(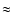 0.03 c/d), cycle/year (
0.03 c/d), cycle/year (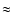 0.0027 c/d) or cycle/3 years
(
0.0027 c/d) or cycle/3 years
(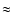 0.009 c/d) aliases of the period used can serve as a new starting
value (panels d and e). As soon as the starting value is close to the true period (
0.009 c/d) aliases of the period used can serve as a new starting
value (panels d and e). As soon as the starting value is close to the true period (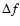 is small enough) the straight line sections of the phase values appear and
the cycle counting problem becomes treatable. The inclination of the
continuous straight line gives the final correction of the starting value,
i.e.
the new, true period of the pulsation. If the
is small enough) the straight line sections of the phase values appear and
the cycle counting problem becomes treatable. The inclination of the
continuous straight line gives the final correction of the starting value,
i.e.
the new, true period of the pulsation. If the 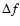 value is sufficiently small,
then regular behaviour of the phase diagram immediately appears, if
it exists.
We give a word of warning here: it is strongly recommended that
before making any attempt to interpret O-C or Fourier phase diagrams
one should make trials to solve the cycle counting problem.
value is sufficiently small,
then regular behaviour of the phase diagram immediately appears, if
it exists.
We give a word of warning here: it is strongly recommended that
before making any attempt to interpret O-C or Fourier phase diagrams
one should make trials to solve the cycle counting problem.
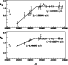 |
Figure 3:
Fourier phase diagram for the fundamental (upper panel) and
first overtone (lower panel) modes. Possible explanation for the deviating
points is given in the text. |
| Open with DEXTER |
For V26/M15 no correction was applied for the first overtone but 0.00043625
c/d correction was applied for the fundamental mode starting value given by
Nemec (1985). This correction was obtained from a straight line
in a range of phases between 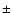 6. On repeating the phase counting
procedure with the corrected new value a similar regular distribution of
phases between 0 and 1 appeared for the fundamental mode that we had found for
the first overtone.
6. On repeating the phase counting
procedure with the corrected new value a similar regular distribution of
phases between 0 and 1 appeared for the fundamental mode that we had found for
the first overtone.
As a final test the frequency spectrum was checked. After prewhitening with
the first overtone and its harmonics, and linear combinations, the
closely spaced peaks near to the new
value of the fundamental mode were used to obtain the Fourier phase diagrams.
The closely spaced peaks (cycle/many years aliases) produced a less clean
Fourier phase diagram than the given f0 value. On changing the values
between the half width of the given peak some improvement occurred. The
finally accepted Fourier phase diagram with the new value is presented
in Fig. 3. Table 4 contains the JD dates of the
first and last points in each data group used to calculate the phases.
The phases and errors correspond to Fig. 3.
Table 3:
Frequencies of the fundamental and first overtone modes before and
after the abrupt change.
|
Frequencies |
Before |
After |
| |
cycle/day |
cycle/day |
|
fundamental f0 |
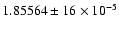 |
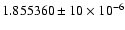 |
| overtone f1 |
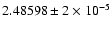 |
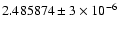 |
Table 4:
Fourier phases and their standard deviations. JD1 and
JD2 are the Julian dates of the first and last data points in each
data group used to calculate the phases.
|
JD1 |
JD2 |
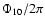 |
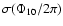 |
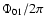 |
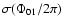 |
|
20724.65 |
20725.99 |
0.60 |
0.10 |
0.82 |
0.02 |
| 21099.72 |
21184.54 |
0.17 |
0.04 |
0.68 |
0.02 |
| 24381.55 |
24474.26 |
-0.11 |
0.17 |
0.73 |
0.02 |
| 27334.42 |
27384.37 |
0.07 |
0.20 |
0.93 |
0.06 |
| 28774.39 |
29187.32 |
0.09 |
0.07 |
1.16 |
0.01 |
| 29518.31 |
29546.28 |
0.34 |
0.15 |
1.21 |
0.04 |
| 29877.38 |
29879.45 |
0.31 |
0.17 |
1.30 |
0.05 |
| 30259.32 |
30261.43 |
0.75 |
0.26 |
1.29 |
0.03 |
| 33502.44 |
33502.53 |
1.05 |
0.10 |
1.39 |
0.07 |
| 33858.43 |
33895.54 |
1.21 |
0.06 |
1.40 |
0.01 |
| 34238.53 |
34270.51 |
1.18 |
0.09 |
1.43 |
0.03 |
| 34573.46 |
34606.59 |
1.20 |
0.31 |
1.63 |
0.11 |
| 34973.51 |
35407.28 |
1.34 |
0.04 |
1.38 |
0.01 |
| 35720.32 |
35725.53 |
1.55 |
0.03 |
1.42 |
0.02 |
| 36068.50 |
36407.98 |
1.42 |
0.03 |
1.38 |
0.01 |
| 36783.79 |
36840.76 |
1.23 |
0.09 |
1.42 |
0.02 |
| 38259.42 |
38289.56 |
1.22 |
0.06 |
1.38 |
0.02 |
| 39350.47 |
39434.57 |
1.29 |
0.07 |
1.41 |
0.03 |
| 39736.69 |
40153.57 |
1.27 |
0.06 |
1.38 |
0.01 |
| 42274.51 |
42309.38 |
1.10 |
0.12 |
1.45 |
0.03 |
| 42715.33 |
42752.27 |
1.35 |
0.21 |
1.44 |
0.05 |
| 43392.33 |
43401.41 |
1.00 |
0.10 |
1.39 |
0.03 |
| 43756.44 |
44168.38 |
1.19 |
0.11 |
1.42 |
0.02 |
The deviation of Bailey's phases from the straight line is obvious. No cycle
counting shift can solve the discrepancy. A possible explanation is that an abrupt
period change took place at around 1914. However, this conclusion is not
well-established since it is based on only two closely spaced observations.
 |
Figure 4:
Folded light curves of V26 according to f0 and f1, before
and after the break, for the starting and new values. |
| Open with DEXTER |
It was known from previous studies
(Silbermann & Smith 1995a) that the P1 primary period (first
overtone period) had an abrupt change around 1945 ( JD 2431500),
and since that time it has been more or less constant. Our present
investigation shows that
an abrupt change characterizes both frequencies around 1945. The exact date
cannot be precisely determined because the time interval is not properly covered
by observations. The period change behaviour of the fundamental mode of V26 was
noticed for the first time. The large
error bars before the sudden jump of the fundamental period indicate
the poorer quality of the data tracks.
The frequencies of both modes before and after the abrupt
change are given in Table 3. The periods obtained after the
abrupt change (
P0 = 0.538979 day and
P1 = 0.402273 day) are very close to
the values derived by Clement & Walker (1991). It is very
reassuring that in such a difficult case as V26/M15 where the fundamental
component is hardly noticeable, different techniques produce the same result.
In Fig. 4 the folded light curves of V26 according to the phase
of the fundamental mode (upper four panels) and the first overtone (bottom
four panels) can be seen. The data are divided before and after
the break. Both the starting and new values are used. Since the amplitude ratio
of the first overtone to the fundamental mode is high, the improvement is
more remarkable in the first overtone.
JD 2431500),
and since that time it has been more or less constant. Our present
investigation shows that
an abrupt change characterizes both frequencies around 1945. The exact date
cannot be precisely determined because the time interval is not properly covered
by observations. The period change behaviour of the fundamental mode of V26 was
noticed for the first time. The large
error bars before the sudden jump of the fundamental period indicate
the poorer quality of the data tracks.
The frequencies of both modes before and after the abrupt
change are given in Table 3. The periods obtained after the
abrupt change (
P0 = 0.538979 day and
P1 = 0.402273 day) are very close to
the values derived by Clement & Walker (1991). It is very
reassuring that in such a difficult case as V26/M15 where the fundamental
component is hardly noticeable, different techniques produce the same result.
In Fig. 4 the folded light curves of V26 according to the phase
of the fundamental mode (upper four panels) and the first overtone (bottom
four panels) can be seen. The data are divided before and after
the break. Both the starting and new values are used. Since the amplitude ratio
of the first overtone to the fundamental mode is high, the improvement is
more remarkable in the first overtone.
4 Discussion
For the stars situated in the instability strip of the HR
diagram the evolutionary changes lead to small increases or decreases
in their pulsation period. The changes are far too slow to be perceptible
on human time scales. Nevertheless, the hope still exists that the
period changes that were observed might reveal the speed and direction of
their evolution if the
database is extensive enough.
Long-term monitoring projects have been carried out over the
last century. Nowadays the length of the database is around 50-70 years for
most kinds of pulsating variable stars. Besides the traditionally used O-C
technique, new approaches have recently been published (Koen 1996;
Paparó et al. 1998). Period changes are widely discussed in the
literature for each kind of pulsating star.
The Joint Discussion, "Stellar Evolution in Real Time: Stellar Evolution
on Human Time Scales'' (Guinan & Koch 1999) nicely summarized
the present state of our knowledge from both observational and theoretical
sides, in other words, the contradictory results from observation
compared with the theory.
All types of period change, period decrease, increase or constant period
may occur in each type of pulsating variable.
Some of the Cepheids show practically no period change, though
most of them show a period change in agreement with the theoretical ones
(Percy 1999; Szabados, private communication). The
fairly good agreement for the Cepheids is a consequence of crossing the
instability strip five times with a different period change rate
each time. It is easy to find
an evolutionary stage with period change sign and rate obtained by observation.
According to the investigation of Breger (1999) equal numbers of stars
with small positive and negative changes in period have been found for
Pop I  Scuti stars. The period changes of many Pop II
Scuti stars. The period changes of many Pop II 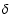 Scuti (SX Phe) stars are characterized by a sudden jump
(Breger & Pamyatnykh 1998). The actual situation for
Scuti (SX Phe) stars are characterized by a sudden jump
(Breger & Pamyatnykh 1998). The actual situation for 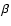 Cep
stars is more complicated than is expected from theory
(Jerzykiewicz 1990).
Cep
stars is more complicated than is expected from theory
(Jerzykiewicz 1990).
In the most remarkable cases period changes of more than one mode have
been investigated and have shown period changes of different sign for
simultaneously excited modes (AI Vel: Walraven et al. 1992
(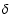 Scuti type),
Scuti type), 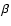 CMa: Shobbrook 1973 and
12 (DD) Lacertae: Pigulski 1994 (
CMa: Shobbrook 1973 and
12 (DD) Lacertae: Pigulski 1994 (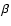 Cephei type) and
v53/M15: Paparó et al. 1998 (RR Lyrae type)).
Cephei type) and
v53/M15: Paparó et al. 1998 (RR Lyrae type)).
It can be concluded that the observed period changes are not in agreement with
those expected from a smooth stellar evolution, and we strongly suspect that
the period changes are dominated by short term changes governed by the
physics of the star.
The investigation of the evolution-pulsation link is still in its
infancy. Period changes are estimated by the instant linear periods
of static models representing different stages of evolution. This
approximation can be valid for smooth and slow evolutionary changes,
however for abrupt and transient-like variations, a dynamic approach
is needed.
It was shown very recently that pulsation and evolution
can be modelled together with the help of amplitude equations
(Kolláth & Buchler 2001; Buchler & Kolláth 2001).
From a finite number of nonlinear
pulsation calculations the pulsation behaviour can be mapped on
the Hertzsprung-Russell diagram, and then the period changes can be calculated for any
evolutionary path. This formalism, together with slow and regular
evolutionary sequences, cannot produce sudden changes (or perhaps
only at bifurcations like mode switching). Sudden changes in
the stellar structure are necessary to induce fast changes in
the oscillation frequency, as in V26/M15. Only a couple of processes are known
that can induce changes in the stellar envelope structure on
a short time scale.
Sweigart & Renzini (1979)
proposed that mixing events in a small part of the semiconvective zone
can produce the observed period changes. Mixing events (labelled type B
in Sweigart and Renzini's paper) confined to the semiconvective zone cause
an increase in the period. A sudden increase in the period (or decrease in the
frequency) is observable if some mixing events of that type have taken
place within a short time interval (within some years). Since the periods of
both modes in V26/M15 changed in a similar way, the ideas of Sweigart & Renzini
seem to have observational support. As
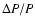 is on the order of
10-5 for both
modes, mixing elements amounting to
is on the order of
10-5 for both
modes, mixing elements amounting to
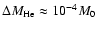 can
produce the observed period change.
can
produce the observed period change.
Another possible mechanism for changes in the stellar envelope is the
dredge up of a small amount of helium by occasional convection
overshooting (Cox 1998). Since this event occurs on a short time
scale, i.e. the convection turnover time, some composition
inhomogeneity should be a prerequisite for this type of
structure change. From the values of Table I of Cox (1998), one can
estimate the necessary change in the surface helium content
to be 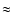 10-4 to match the observed period changes.
Whether the accretion of interstellar matter has a noticeable
effect on surface composition is still an open question.
10-4 to match the observed period changes.
Whether the accretion of interstellar matter has a noticeable
effect on surface composition is still an open question.
The main difference between the Sweigart & Renzini type of
structure changes and that of Cox is their location. While the dredge up
on the
surface can be characterized by one time scale given by the
convection, mixing in the core induces changes in the star
on multiple levels. After a mixing event in the semiconvective
zone the radius of the star varies on the dynamic time scale,
i.e. the order of the pulsation period. However, the long scale
readjustment of the envelope occurs on the thermal time scale,
which results in long-term period changes.
For double mode stars the interaction of modes may provide an
additional time scale. These effects together make the
interpretation of period changes a nontrivial problem (Szabó et al. 2001).
From the theoretical point of view the period ratio of the fundamental and
first overtone is a critical point for mass determination. It is worthwhile
to check whether the abrupt period change of V26 modified the period ratio
of the excited modes. Judging from the new period values
the period ratio slightly decreased after the abrupt change in the periods.
Before the event it was
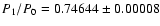 and after it
and after it
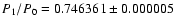 .
If this effect were real, it would
slightly modify our view about the mass - period ratio relation. The errors
in determining the period ratios before and after the abrupt
period changes, however, do not preclude the constancy of the period ratio.
.
If this effect were real, it would
slightly modify our view about the mass - period ratio relation. The errors
in determining the period ratios before and after the abrupt
period changes, however, do not preclude the constancy of the period ratio.
Recent studies (Kolláth & Buchler 2001) indicate
that the difference between the nonlinear and linear period
ratios of RR Lyrae models is of the order of 0.1%. The actual
value depends on the amplitudes, and for typical RR Lyrae
models less than 10% change in the amplitudes results in
a 10-4 shift in P1/P0.
If the observed
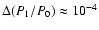 shift is real
and it is mostly induced by amplitude changes due to the
evolution of the star, then the amount of amplitude changes should
be a few percent. Such a small amplitude variation cannot be
detected in the observations with any degree of significance. The
Fourier phase method is
not sensitive to such a small amplitude variation.
shift is real
and it is mostly induced by amplitude changes due to the
evolution of the star, then the amount of amplitude changes should
be a few percent. Such a small amplitude variation cannot be
detected in the observations with any degree of significance. The
Fourier phase method is
not sensitive to such a small amplitude variation.
Thorough investigations of period changes of double mode RR Lyrae stars in other
globular clusters by the Fourier phase method are strongly suggested. With
more, well-studied cases, there is a greater chance of distinguishing
between the
period changes caused by occasional changes in the physics of the star and
the evolutionary changes.
Acknowledgements
Research grants, OTKA Nos. T 030955, T 038440 and T 025288 are gratefully
acknowledged. The authors are indebted to Dr. N. A. Silbermann for her very
thorough referee report and helpful comments.
-
Bailey, S. I. 1919, Harvard Ann., 78, 195
In the text
-
Barlai, K. 1989, Commun. Konkoly Obs., 10, No. 92, 143
In the text
NASA ADS
-
Bingham, E. A., Cacciari, C., Dickens, R. J., & Fussi Pecci, F. 1984, MNRAS, 209, 765
In the text
NASA ADS
-
Breger, M. 1999, New Astron. Rev., 43, 441
In the text
NASA ADS
-
Breger, M., & Pamyatnykh, A. A. 1998, A&A, 332, 958
In the text
NASA ADS
-
Buchler, J. R., & Kolláth, Z. 2001, ApJ, submitted
In the text
-
Clement, C. M., & Walker, I. R. 1991, AJ, 101, 1352
In the text
NASA ADS
-
Cox, A. N. 1998, ApJ, 496, 246
In the text
NASA ADS
-
Cox, A. N., Hodson, S. W., & Clancy, S. P. 1983, ApJ, 266, 94
NASA ADS
-
Filippenko, A. V., & Simon, R. S. 1981, AJ, 86, 671
In the text
NASA ADS
-
Fritze, K. 1963, Astron. Nachr., 287, 79
In the text
NASA ADS
-
Gordenko, A. F., Klabukova, A. V., & Fashchevskij, N. N. 1984, Prob. Kosmicheskoj Fiz., 19, 93
In the text
-
Grubissich, C. 1956, Mem. Soc. Astr. It., 27, 391
In the text
NASA ADS
-
Guinan, E. F., & Koch, R. H. 1999, New Astron. Rev., 43, vii
In the text
-
Hodson, S. W., & Cox, A. N. 1982, in Pulsation in Classical and Cataclysmic Variable Stars, ed. J. P. Cox, & C. J. Hansen (JILA, Boulder), 201
In the text
-
Hoffmeister, C., Richter, G., & Wenzel, W. 1985, Variable Stars
(Springer-Verlag, Berlin, Heidelberg, New York, Tokyo)
In the text
-
Jerzykiewicz, M. 1999, New Astron. Rev., 43, 455
In the text
NASA ADS
-
Jurcsik, J., & Barlai, K. 1990, in Confrontation Between Stellar Pulsation and Evolution, ed. C. Cacciari, & G. Clementini, 112
In the text
-
Koen, C. 1996, MNRAS, 283, 471
In the text
NASA ADS
-
Kolláth, Z., & Buchler, J. R. 2001, in Stellar Pulsation - Nonlinear Studies, ed. M. Takeuti, & D. D. Sasselov, ASSL, 257, 29
In the text
-
Kovács, G., Shlosman, I., & Buchler, J. R. 1986, ApJ, 307, 593
In the text
NASA ADS
-
Makarova, V. A., & Akimova, V. P. 1965, Perem. Zvezdy, 15, 350
In the text
-
Nemec, J. M. 1985, AJ, 90, 240
In the text
NASA ADS
-
Paparó, M., Saad, S. M., Szeidl, B., et al. 1998, A&A, 332, 102 (Paper I)
In the text
NASA ADS
-
Paparó, M., Saad, S. M., Szeidl, B., Kolláth, Z., & Abu Elazm 1997,
in Sounding Solar and Stellar Interiors, Poster papers,
ed. J. Provost, & F.-X. Schmider, IAU Symp., 181, 275
In the text
-
Percy, J. R. 1999, New Astron. Rev., 43, 449
In the text
NASA ADS
-
Pigulski, A. 1994, A&A, 292, 183
In the text
NASA ADS
-
Purdue, P., Silbermann, N. A., Gay, P., & Smith, H. A. 1995, AJ, 110, 1712
In the text
NASA ADS
-
Sandage, A., Katem, B., & Sandage, M. 1981, ApJS, 46, 41
In the text
NASA ADS
-
Sawyer Hogg, H. 1973, Publ. David Dunlap Obs., 3, No. 6
In the text
NASA ADS
-
Silbermann, N. A. 2001, private communication
In the text
-
Silbermann, N. A., & Smith, H. A. 1995a, AJ, 109, 1119
In the text
NASA ADS
-
Silbermann, N. A., & Smith, H. A. 1995b, AJ, 110, 704
In the text
NASA ADS
-
Smith, H. A., & Sandage, A. 1981, AJ, 86, 1870
In the text
NASA ADS
-
Shobbrook, R. R. 1973, MNRAS, 161, 257
In the text
NASA ADS
-
Stothers, R. 1980, PASP, 92, 475
In the text
NASA ADS
-
Sweigart, A. V., & Renzini, A. 1979, A&A, 71, 66
In the text
NASA ADS
-
Szabados, L. 2000, private communication
-
Szabó, R., Kolláth, Z., Csubry, Z., & Buchler, J. R. 2001, in
Astrophysical Ages and Time scales, ed. T. von Hippel, N. Manset, & C.
Simpson, ASP Conf. Ser., 245, 373
In the text
-
Szeidl, B. 1975, in Variable Stars and Stellar Evolution, ed. V. E. Sherwood, & L. Plaut (Reidel, Dordrecht) IAU Symp., 67, 545
In the text
-
Walraven, Th., Walraven, J., & Balona, L. A. 1992, MNRAS, 254, 59
In the text
NASA ADS
-
Wesselink, A. J. 1974, A&A, 36, 163
In the text
NASA ADS
Copyright ESO 2002