The integrated ![]() 6 cm radio flux density
6 cm radio flux density
![]() (Tables 5 and 6)
is correlated with the integrated
(Tables 5 and 6)
is correlated with the integrated
![]() m far-infrared flux
density
m far-infrared flux
density
![]() (Tables 1 and 2) as shown in Fig. 2.
The correlation coefficient is
(Tables 1 and 2) as shown in Fig. 2.
The correlation coefficient is
![]() .
NGC 1559 lies well above the fitted line,
i.e., its radio emission is "too high'' compared with its far-infrared
emission (cf. Sect. 5.2). This is possibly also true for NGC 1097.
NGC 986 and NGC 7552 are "too radio-faint'', possibly due to
the incomplete uv coverage of our observations.
.
NGC 1559 lies well above the fitted line,
i.e., its radio emission is "too high'' compared with its far-infrared
emission (cf. Sect. 5.2). This is possibly also true for NGC 1097.
NGC 986 and NGC 7552 are "too radio-faint'', possibly due to
the incomplete uv coverage of our observations.
The radio-far-infrared correlation has been studied in detail for large
samples of barred and non-barred galaxies. The average flux density ratio
![]() (where
(where
![]() is measured in mJy and
is measured in mJy and
![]() in Jy) is
in Jy) is ![]() for the RC2 galaxies in the sample of
de Jong et al. (1985) and
for the RC2 galaxies in the sample of
de Jong et al. (1985) and ![]() for the 134 galaxies observed by
Unger et al. (1989, scaled to
for the 134 galaxies observed by
Unger et al. (1989, scaled to ![]() 6 cm). The slope of the fitted
line in our Fig. 2 is
6 cm). The slope of the fitted
line in our Fig. 2 is ![]() ,
in agreement with these results.
The radio continuum luminosity of spiral galaxies is also closely related
to the far-infrared luminosity (Condon 1992; Niklas 1997).
,
in agreement with these results.
The radio continuum luminosity of spiral galaxies is also closely related
to the far-infrared luminosity (Condon 1992; Niklas 1997).
Unger et al. found no significant difference in the radio/far-infrared ratio
either between Hubble classes or between barred and non-barred galaxies. The average
value of
![]() in our sample also indicates no general excess
of radio emission from barred galaxies.
in our sample also indicates no general excess
of radio emission from barred galaxies.
A close correlation between radio continuum emission and dust emission
in the far-infrared has been found within many galaxies
(Bicay & Helou 1990; Hoernes et al. 1998),
and between radio continuum and the mid-infrared emission (
![]() m)
in the spiral galaxy NGC 6946 at all spatial scales
(Frick et al. 2001).
ISOCAM images at
m)
in the spiral galaxy NGC 6946 at all spatial scales
(Frick et al. 2001).
ISOCAM images at
![]() m and
m and
![]() m are available for several
galaxies in our sample: NGC 1097, 1365, 1433, 1672, 4535 and 7552
(Roussel et al. 2001a). The similarity to our radio maps
is striking and shows that the relationship holds not only for the integrated
flux densities and luminosities, but also for spatial scales down to our
resolution.
m are available for several
galaxies in our sample: NGC 1097, 1365, 1433, 1672, 4535 and 7552
(Roussel et al. 2001a). The similarity to our radio maps
is striking and shows that the relationship holds not only for the integrated
flux densities and luminosities, but also for spatial scales down to our
resolution.
As synchrotron emission dominates at radio wavelengths longer than about
![]() 3 cm, the radio-infrared correlation cannot be explained
solely by thermal processes. Various interpretations are dicussed by
Hoernes et al. (1998). As suggested by Niklas & Beck
(1997), the radio-[far-]infrared correlation for bright galaxies
holds if the magnetic field is connected to the star formation rate
where the gas clouds may serve as the physical link.
For radio-weak galaxies, however, the far-infrared emission is dominated by cold dust
heated by the general radiation field which is not related with recent
star formation (Hoernes et al. 1998). Most of the galaxies
in our sample are bright enough to ensure that their far-infrared emission
is indeed a measure of star formation intensity.
3 cm, the radio-infrared correlation cannot be explained
solely by thermal processes. Various interpretations are dicussed by
Hoernes et al. (1998). As suggested by Niklas & Beck
(1997), the radio-[far-]infrared correlation for bright galaxies
holds if the magnetic field is connected to the star formation rate
where the gas clouds may serve as the physical link.
For radio-weak galaxies, however, the far-infrared emission is dominated by cold dust
heated by the general radiation field which is not related with recent
star formation (Hoernes et al. 1998). Most of the galaxies
in our sample are bright enough to ensure that their far-infrared emission
is indeed a measure of star formation intensity.
In normal spiral galaxies, cool gas and magnetic fields are compressed in various shocks, followed by an increase in star formation. However, large-scale shock fronts in a galaxy do not always enhance star formation. For example, the non-barred spiral galaxy NGC 2276 interacts with some external (intracluster) gas, so that a large-scale shock front forms on the leading side producing a ridge of strong total and regular magnetic field without significant effect on star formation (Hummel & Beck 1995). As a consequence, this galaxy deviates from the radio-far-infrared correlation.
Barred galaxies also host large-scale shock fronts, identified with dust lanes.
However, shock fronts in bars are non-standard shocks in that they have enhanced
velocity shear across them, similar to bow shocks. If the shear rate
![]() exceeds the inverse time for star formation,
the gas density enhancement in the shock does not trigger star formation.
If the magnetic field is compressed in the shock, the ratio of
radio/far-infrared flux densities would be higher than normal.
However, for our sample this ratio and the average total field strengths
(Sect. 5.3) are similar to those of non-barred galaxies.
This indicates that large-scale field compression in the bar is generally small
and that the magnetic field is not frozen into the flow in the regions of
strong compression and shear (the dust lanes).
Nevertheless, the average surface brightness in radio continuum
and far-infared increases with increasing bar length (see Sect. 5.2).
exceeds the inverse time for star formation,
the gas density enhancement in the shock does not trigger star formation.
If the magnetic field is compressed in the shock, the ratio of
radio/far-infrared flux densities would be higher than normal.
However, for our sample this ratio and the average total field strengths
(Sect. 5.3) are similar to those of non-barred galaxies.
This indicates that large-scale field compression in the bar is generally small
and that the magnetic field is not frozen into the flow in the regions of
strong compression and shear (the dust lanes).
Nevertheless, the average surface brightness in radio continuum
and far-infared increases with increasing bar length (see Sect. 5.2).
Several quantitative measures of bar
strength have been suggested. Most of them are based
on purely geometric parameters such as the bar axial
ratio, where a smaller value of b/a means a stronger bar
(Martin 1995; Aguerri 1999;
Chapelon et al. 1999;
Abraham & Merrifield 2000).
Smallest values of b/a in our sample are
found in NGC 1300, 1433, 1493, 1559, 3059, 3359 and 7552
(see Tables 1 and 2),
but only NGC 1559
and NGC 7552 have a high surface brightness in radio continuum
(see Tables 5 and 6) and far-infrared.
NGC 1365 has the highest radio flux density
![]() in our sample, although the aspect ratio of its bar is
relatively small (b/a=0.51). However, it hosts the longest bar
(
in our sample, although the aspect ratio of its bar is
relatively small (b/a=0.51). However, it hosts the longest bar
(![]() 29 kpc)
in the sample. NGC 1559, 1672 and 7552 are fainter mainly because they are
smaller.
Their (distance-independent) radio surface bightness values
29 kpc)
in the sample. NGC 1559, 1672 and 7552 are fainter mainly because they are
smaller.
Their (distance-independent) radio surface bightness values
![]() (measured in
(measured in ![]() Jy/beam area) are similar to or even larger than that of
NGC 1365
(see Col. 11 in Tables 5 and 6),
and the same is true for the typical
far-infrared surface brightness, which is
a measure of star formation rate per surface area.
Figure 3 confirms that the radio surface brightness
Jy/beam area) are similar to or even larger than that of
NGC 1365
(see Col. 11 in Tables 5 and 6),
and the same is true for the typical
far-infrared surface brightness, which is
a measure of star formation rate per surface area.
Figure 3 confirms that the radio surface brightness
![]() is uncorrelated with the aspect ratio b/a (correlation coefficient
of
is uncorrelated with the aspect ratio b/a (correlation coefficient
of
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2373fig2a.eps}\end{figure}](/articles/aa/full/2002/31/aa2373/Timg80.gif) |
Figure 3:
Variation of the radio surface brightness
|
A physically motivated measure of the bar strength has been introduced by
Buta & Block (2001) and Block et al. (2001)
based, following Combes & Sanders (1981),
on the maximum amplitude of
the tangential gravitational force relative to the mean axisymmetric radial
force. Thus defined, the strength parameter ![]() is sensitive
not only to the bar ellipticity, but also to its size and mass, and is
related to the quadrupole moment of the bar potential
(P. Englmaier, priv. comm.).
A reliable estimation of
is sensitive
not only to the bar ellipticity, but also to its size and mass, and is
related to the quadrupole moment of the bar potential
(P. Englmaier, priv. comm.).
A reliable estimation of ![]() involves careful analysis
of near-infrared galactic images (Quillen et al. 1994).
Buta & Block (2001) and Block et al. (2001)
determine
involves careful analysis
of near-infrared galactic images (Quillen et al. 1994).
Buta & Block (2001) and Block et al. (2001)
determine ![]() for a selection of galaxies, but only six
of them belong to our sample. Therefore, we consider a simpler
(and admittedly incomplete) measure of the bar strength described
in what follows.
for a selection of galaxies, but only six
of them belong to our sample. Therefore, we consider a simpler
(and admittedly incomplete) measure of the bar strength described
in what follows.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2373fig2b.eps}\end{figure}](/articles/aa/full/2002/31/aa2373/Timg82.gif) |
Figure 4:
Variation of the radio surface brightness
|
The quadrupole moment, with respect to the major axis,
of a homogeneous triaxial ellipsoid with semi-axes
![]() and c is given by
and c is given by
![]() where M is the mass of the ellipsoid (Landau & Lifshitz 1976).
Assuming that the
vertical scale height of the bar is much smaller than its size
(
where M is the mass of the ellipsoid (Landau & Lifshitz 1976).
Assuming that the
vertical scale height of the bar is much smaller than its size
(
![]() )
(e.g.,
Buta & Block 2001), the quadrupole moment normalized to
M25R254 (with M25 the mass within the radius
R25) is given by
)
(e.g.,
Buta & Block 2001), the quadrupole moment normalized to
M25R254 (with M25 the mass within the radius
R25) is given by
Since ![]() depends strongly on the relative bar length 2a/d25, we
can reasonably expect that radio emission is correlated
with this parameter. This expectation is confirmed by
the high correlation between the radio surface brightness
depends strongly on the relative bar length 2a/d25, we
can reasonably expect that radio emission is correlated
with this parameter. This expectation is confirmed by
the high correlation between the radio surface brightness
![]() at
at
![]() and the relative bar length
(correlation coefficient of
and the relative bar length
(correlation coefficient of
![]() ,
with NGC 1559 excluded
- see below), confirmed by Student's t test.
Figure 4 shows this correlation in logarithmic scales.
Although the scatter is stronger than that in Fig. 2,
the correlation is not weaker than other correlations
discussed for barred galaxies in the current literature
(cf. Chapelon et al. 1999). We conclude that a stronger bar results
in an overall enhancement of the total radio emission in the bar region despite
a relatively weak compression of the regular magnetic field
near the dust lanes, as discussed in Sect. 5.1.
As noted by Block et al. (2001), longer bars can
produce more extensive deviations form axial symmetry in the gas velocity
because the relative tangential force is stronger when the end of the bar is
farther from the (axisymmetric) bulge;
this may be the physical reason for the correlation
shown in Fig. 4.
,
with NGC 1559 excluded
- see below), confirmed by Student's t test.
Figure 4 shows this correlation in logarithmic scales.
Although the scatter is stronger than that in Fig. 2,
the correlation is not weaker than other correlations
discussed for barred galaxies in the current literature
(cf. Chapelon et al. 1999). We conclude that a stronger bar results
in an overall enhancement of the total radio emission in the bar region despite
a relatively weak compression of the regular magnetic field
near the dust lanes, as discussed in Sect. 5.1.
As noted by Block et al. (2001), longer bars can
produce more extensive deviations form axial symmetry in the gas velocity
because the relative tangential force is stronger when the end of the bar is
farther from the (axisymmetric) bulge;
this may be the physical reason for the correlation
shown in Fig. 4.
With the most strongly deviating galaxy excluded
(NGC 1559), the data shown in Fig. 4
can be fitted with a power law
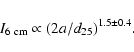
We have been unable to
include the dependence on the surface mass densities into our
measure of the bar strength, and this plausibly contributes
into the scatter of the data points around the fit. It
is difficult to say whether or not
![]() is
correlated with 2a/d25. If
is
correlated with 2a/d25. If
![]() is
independent of 2a/d25, the above fit implies an
approximate scaling
is
independent of 2a/d25, the above fit implies an
approximate scaling
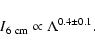
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2373fig10.eps}\hspace*{2.4...
...s}\hspace*{2.4mm}
\includegraphics[width=8.8cm,clip]{2373fig13.eps}
\end{figure}](/articles/aa/full/2002/31/aa2373/Timg98.gif) |
Figure 7:
Total intensity contours and the observed B-vectors of polarized emission
of NGC 1365, overlayed onto an optical image taken at the ESO
3.6 m telescope by Lindblad (1999).
The basic contour levels are 700, 500, 200 and 100 |
On the other hand, NGC 1300, 1433 and 3992 are radio-weak in spite
of their relatively long bars (Fig. 4). Their far-infrared flux
density and thus their star formation rate is low.
Apart from an usually small value of
![]() for these galaxies, other reasons for these deviations are concievable.
Martinet & Friedli (1997) argue that some galaxies
with strong bars have settled into a quiescent state after an episode of
vigorous star formation which has transformed most of the gas into stars.
Alternatively, Tubbs (1982) and Reynaud & Downes
(1998)
found indications for suppression of star formation in fast flows of the
gas along the bar.
The field strength should be low in the first case, because there is not enough
gas to hold the field or the dynamo is not able to maintain a strong
magnetic field. In the second case the field should be strong, but the galaxy
does not host enough cosmic-ray electrons to generate strong synchrotron radiation.
This can be verified by comparing regular magnetic field strengths
deduced from Faraday rotation and polarized intensity
from further radio observations with higher
sensitivity.
for these galaxies, other reasons for these deviations are concievable.
Martinet & Friedli (1997) argue that some galaxies
with strong bars have settled into a quiescent state after an episode of
vigorous star formation which has transformed most of the gas into stars.
Alternatively, Tubbs (1982) and Reynaud & Downes
(1998)
found indications for suppression of star formation in fast flows of the
gas along the bar.
The field strength should be low in the first case, because there is not enough
gas to hold the field or the dynamo is not able to maintain a strong
magnetic field. In the second case the field should be strong, but the galaxy
does not host enough cosmic-ray electrons to generate strong synchrotron radiation.
This can be verified by comparing regular magnetic field strengths
deduced from Faraday rotation and polarized intensity
from further radio observations with higher
sensitivity.
Measurements of the star formation efficiency SFE may also help:
In the first case, the content of molecular gas should be low, with a SFE
similar to that in spiral galaxies, while in the second case the SFE
should be exceptionally small.
Existing data seem to favour a higher SFE
in barred galaxies compared to non-barred ones (Young 1993), but
the infrared luminosity is dominated by the central region
where star formation is triggered by gas inflow (see Roussel et al. 2001b).
The SFE in the bar itself (and its possible suppression by a fast gas flow)
should be subject to future investigations.
The estimates of the total magnetic field strength in our Galaxy, derived from
![]() -ray data and the local cosmic-ray energy density (Strong et al. 2000), agree well with equipartition
values from radio continuum data (Berkhuijsen, in Beck 2001),
so that the equipartition assumption is a useful estimate, at least on scales
of more than a few kpc.
-ray data and the local cosmic-ray energy density (Strong et al. 2000), agree well with equipartition
values from radio continuum data (Berkhuijsen, in Beck 2001),
so that the equipartition assumption is a useful estimate, at least on scales
of more than a few kpc.
From the integrated flux density
![]() at
at ![]() 6 cm and the
solid angle
of the integration area, the surface brightness
6 cm and the
solid angle
of the integration area, the surface brightness
![]() and the corresponding
equipartition strength of the total magnetic field
and the corresponding
equipartition strength of the total magnetic field
![]() were computed
(Tables 5 and 6), assuming for all
galaxies a thermal contribution to the surface brightness
at
were computed
(Tables 5 and 6), assuming for all
galaxies a thermal contribution to the surface brightness
at ![]() cm of 20% and a spectral index
cm of 20% and a spectral index
![]() of the nonthermal emission of 0.85, which is the mean value
for spiral galaxies of type Sb and later (Niklas et al. 1997).
of the nonthermal emission of 0.85, which is the mean value
for spiral galaxies of type Sb and later (Niklas et al. 1997).
Spectral indices ![]() between
between ![]() cm and
cm and ![]() cm
(
cm
(
![]() )
can be computed from our VLA data (given in Table 5).
The values lie in the range 0.71 and 0.97 which is in the range typical
of normal spiral galaxies (Niklas 1995).
Nonthermal spectral indices
)
can be computed from our VLA data (given in Table 5).
The values lie in the range 0.71 and 0.97 which is in the range typical
of normal spiral galaxies (Niklas 1995).
Nonthermal spectral indices
![]() cannot be
determined with data at only two frequencies.
cannot be
determined with data at only two frequencies.
We adopted the standard cosmic-ray proton-to-electron ratio K of 100, a pathlength
through the disc of 1 kpc/![]() ,
and assumed that
the regular field is in the galaxy's plane and
the random field is statistically isotropic. Uncertainties in any of these
parameters of
,
and assumed that
the regular field is in the galaxy's plane and
the random field is statistically isotropic. Uncertainties in any of these
parameters of ![]() 50% lead to an error of
50% lead to an error of ![]() 13% in
13% in
![]() .
We estimate the total error in
.
We estimate the total error in
![]() to be about 30%. The relative errors
between galaxies are smaller because some of the input parameters
(e.g. the proton-to-electron ratio) are not expected to vary strongly
from one galaxy to another.
to be about 30%. The relative errors
between galaxies are smaller because some of the input parameters
(e.g. the proton-to-electron ratio) are not expected to vary strongly
from one galaxy to another.
With the above assumptions,
![]() is related to the
average synchrotron volume emissivity
is related to the
average synchrotron volume emissivity ![]() and surface brightness I (neglecting a term weakly varying with inclination i) by
and surface brightness I (neglecting a term weakly varying with inclination i) by

The average total magnetic field strength
![]() ,
according to
Tables 5 and 6
(representing the average synchrotron emissivity), is
a function of neither Hubble type (SBb-SBc) nor luminosity class (I-III),
which has also been found for a much larger sample of barred and non-barred
spiral galaxies (Hummel 1981). The average total field strength
,
according to
Tables 5 and 6
(representing the average synchrotron emissivity), is
a function of neither Hubble type (SBb-SBc) nor luminosity class (I-III),
which has also been found for a much larger sample of barred and non-barred
spiral galaxies (Hummel 1981). The average total field strength
![]() is
is
![]() for our sample,
similar to the average minimum-energy field strength of
for our sample,
similar to the average minimum-energy field strength of
![]() for the large galaxy sample (Hummel et al. 1988) and
to the mean equipartition value of
for the large galaxy sample (Hummel et al. 1988) and
to the mean equipartition value of
![]() of the sample of 146 late-type
galaxies calculated by Fitt & Alexander (1993),
corrected to K=100.
Niklas (1995) derived a mean equipartition value of
of the sample of 146 late-type
galaxies calculated by Fitt & Alexander (1993),
corrected to K=100.
Niklas (1995) derived a mean equipartition value of
![]() for his sample of 74 spiral galaxies.
Hummel (1981) also found no significant emissivity difference
between barred and non-barred galaxies.
for his sample of 74 spiral galaxies.
Hummel (1981) also found no significant emissivity difference
between barred and non-barred galaxies.
The following galaxies have the strongest total magnetic field in our sample, as evidenced by their high radio surface brightness: NGC 1365, 1559, 1672 and 7552 (see Tables 5 and 6). This indicates that the total field strength is highest for galaxies with the (relatively) longest bars, with the exception of NGC 1559 that has a short bar (see Fig. 4).
The last column in Tables 5 and 6 gives
the average equipartition strength
![]() of the resolved regular magnetic field, derived from the
polarized surface brightness averaged over the galaxy.
of the resolved regular magnetic field, derived from the
polarized surface brightness averaged over the galaxy.
![]() ,
in contrast to
,
in contrast to
![]() ,
depends on
the linear resolution within a galaxy and thus on its physical size, its
distance and its inclination.
However,
,
depends on
the linear resolution within a galaxy and thus on its physical size, its
distance and its inclination.
However,
![]() and
and
![]() in Tables 5 and
6 do not correlate with distance of the galaxy.
As a test, we smoothed the
in Tables 5 and
6 do not correlate with distance of the galaxy.
As a test, we smoothed the ![]() 6 cm map of NGC 1097 by enlarging the beam size
from 30
6 cm map of NGC 1097 by enlarging the beam size
from 30
![]() to 60
to 60
![]() and to 90
and to 90
![]() which corresponds to
increasing the galactic distance by factors 2 and 3. The
degree of polarization decreased from 8.5% to 7% and 6%,
respectively, and the strength of the resolved regular magnetic field decreased
from 4.3 to 4.0 and
which corresponds to
increasing the galactic distance by factors 2 and 3. The
degree of polarization decreased from 8.5% to 7% and 6%,
respectively, and the strength of the resolved regular magnetic field decreased
from 4.3 to 4.0 and
![]() ,
respectively,
remaining above the sample average.
Hence the values of
,
respectively,
remaining above the sample average.
Hence the values of
![]() and
and
![]() in Tables 5 and 6
seem to depend only weakly on distance to the galaxies,
implying that our observations generally resolve most of the structure
in the regular magnetic field, at least for large galaxies and
at distances of up to about 40 Mpc.
in Tables 5 and 6
seem to depend only weakly on distance to the galaxies,
implying that our observations generally resolve most of the structure
in the regular magnetic field, at least for large galaxies and
at distances of up to about 40 Mpc.
Average polarized surface brightness (and thus
![]() )
values
are similar for the galaxies of our sample. The exceptions are NGC 1097
and NGC 1559 with
)
values
are similar for the galaxies of our sample. The exceptions are NGC 1097
and NGC 1559 with
![]() ,
above the average of
,
above the average of
![]() .
NGC 1097 probably drives a strong dynamo where field amplification is supported
by shear in the velocity field (Moss et al. 2001, Paper II). The
degree of polarization at
.
NGC 1097 probably drives a strong dynamo where field amplification is supported
by shear in the velocity field (Moss et al. 2001, Paper II). The
degree of polarization at ![]() 6 cm, signature of the
degree of uniformity of the resolved field, is also high in NGC 1097
(see Fig. 25). NGC 1559, 1672 and 7552 are similar
candidates for a strong dynamo, but the present radio observations (Fig. 26) have
insufficient linear resolution at the relatively large distances of these galaxies
to reveal the true strength of the regular fields and their detailed structure.
6 cm, signature of the
degree of uniformity of the resolved field, is also high in NGC 1097
(see Fig. 25). NGC 1559, 1672 and 7552 are similar
candidates for a strong dynamo, but the present radio observations (Fig. 26) have
insufficient linear resolution at the relatively large distances of these galaxies
to reveal the true strength of the regular fields and their detailed structure.
NGC 1300, NGC 3992 and NGC 4535 have the highest degrees of
polarization but only low total surface brightness. They host weak
but ordered magnetic fields with spiral patterns, similar
to those in non-barred galaxies (Beck 2000).
A classification system of barred galaxies was
introduced by Martinet & Friedli (1997), based on the
axis ratio b/a (see Tables 1 and 2) and on the
star formation rate (SFR) measured by the far-infrared luminosity.
Galaxies with large b/a are generally weak in star formation (class I),
but some have a high SFR (class II). Galaxies with small b/a have a large
spread in SFR: from high (class III) to weak (class IV).
Galaxies of class IV in Martinet & Friedli
have strong bars, but low SFR (see Sect. 5.2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2373fig44.eps}
\end{figure}](/articles/aa/full/2002/31/aa2373/Timg117.gif) |
Figure 17:
Total intensity contours
of NGC 1433, overlayed onto an optical image from the Digitized
Sky Surveys. The contours are 1, 2, 3, 4, 6, 8
|
Here we propose that there are basic differences among barred galaxies concerning their magnetic field structure and strength which may reflect physical properties of barred galaxies like the gas flow, the shock strength in the bar and the presence of a circumnuclear ring.
Firstly, barred galaxies can have low radio luminosity because they are small (NGC 1313, 1493 and 5068), or because their gas content and star formation activity is small in spite of their large bars (NGC 1300 and 1433). Little or no polarization is detected in these galaxies. In galaxies with small bars the radio continuum morphology is formed as a result of star formation in the spiral arms, as in NGC 2336, 3359, 3953, 3992, 4535, 5643, and also M 83 observed previously by Beck (2000). The bar is of little importance for the overall radio properties of these galaxies. The average degree of radio polarization (i.e., the degree of field regularity) seems to be controlled by the spiral structure rather than the bar, being low in flocculent spirals and high when massive spiral arms are present. Regular fields are often enhanced in interarm regions between optical spiral arms, e.g. in NGC 3359, NGC 4535 and M 83, similar to non-barred galaxies.
Secondly, galaxies with long bars and strong star formation
have a high radio luminosity and a strong total magnetic field
(
![]() )
(NGC 1097, 1365, 1672, 2442 and 7552, and
also NGC 3627 observed previously by Soida et al. 2001).
NGC 1097, 1365, 1672 and 7552 have a
high polarization surface brightness and a strong regular field which is
enhanced upstream of the shock fronts in the bar.
The magnetic field lines upstream of the dust
lanes are oriented at large angles with respect to the bar and turn
smoothly towards the dust lanes along the major axis of the bar.
This is accompanied by large-scale field enhancements associated with, e.g.,
strong shear in the velocity field and/or strong dynamo action rather than
enhanced gas density.
Gas inflow along the bar may lead to circumnuclear rings which have been
detected already in NGC 1097 (Hummel et al. 1987;
Gerin et al. 1988), NGC 2442 (Mihos & Bothun 1997),
NGC 7552 (Forbes et al. 1994a, 1994b)
and possibly in NGC 1365 (Sandqvist et al. 1995),
and should be searched for in the other
radio-bright galaxies.
)
(NGC 1097, 1365, 1672, 2442 and 7552, and
also NGC 3627 observed previously by Soida et al. 2001).
NGC 1097, 1365, 1672 and 7552 have a
high polarization surface brightness and a strong regular field which is
enhanced upstream of the shock fronts in the bar.
The magnetic field lines upstream of the dust
lanes are oriented at large angles with respect to the bar and turn
smoothly towards the dust lanes along the major axis of the bar.
This is accompanied by large-scale field enhancements associated with, e.g.,
strong shear in the velocity field and/or strong dynamo action rather than
enhanced gas density.
Gas inflow along the bar may lead to circumnuclear rings which have been
detected already in NGC 1097 (Hummel et al. 1987;
Gerin et al. 1988), NGC 2442 (Mihos & Bothun 1997),
NGC 7552 (Forbes et al. 1994a, 1994b)
and possibly in NGC 1365 (Sandqvist et al. 1995),
and should be searched for in the other
radio-bright galaxies.
NGC 7479 is anomalous in the radio range as it possesses a nuclear "jet'' (Laine & Gottesman 1998). Indications of a weaker nuclear jet have been found in NGC 1365 by Sandqvist et al. (1995).
For NGC 986, 1559 and 3059
the resolution and sensitivity of the present observations
are insufficient to reveal their detailed field structure.
NGC 7552 is a special case. Its radio surface brightness is high (i.e., the total magnetic field is strong, see Table 6), but still too low to be consistent with its far-infrared flux density (see Fig. 2). NGC 7552 hosts a starburst ring and may drive a "galactic superwind'' (Forbes et al. 1994a). As a member of a galaxy group, it may be subject to tidal interactions. It seems possible that the magnetic field is still not strong enough to hold the large number of cosmic-ray electrons produced due to the high star formation activity. However, major distortions of our radio map by instrumental effects cannot be excluded. Further radio observations are required.
Copyright ESO 2002