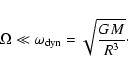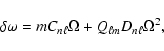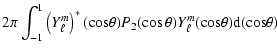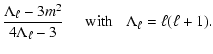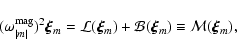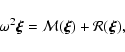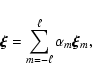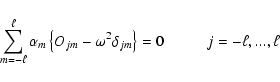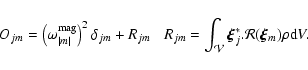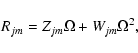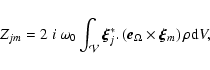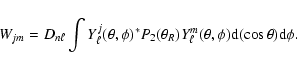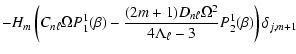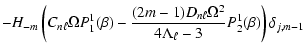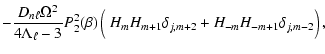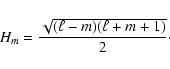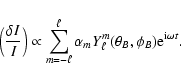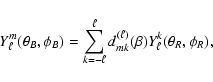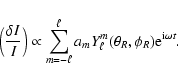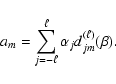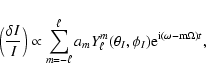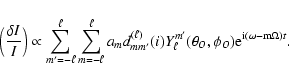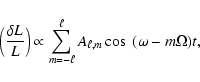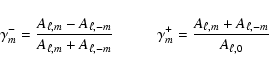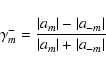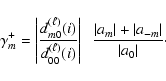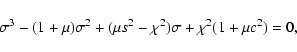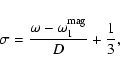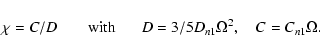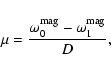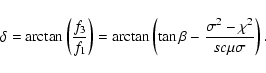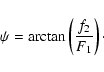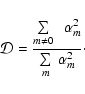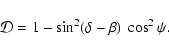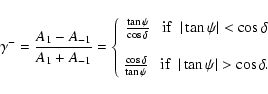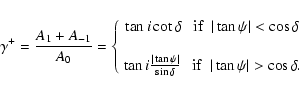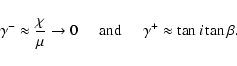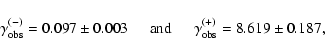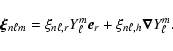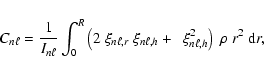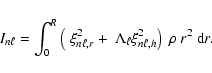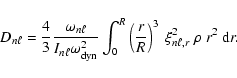A&A 391, 235-245 (2002)
DOI: 10.1051/0004-6361:20020824
The oblique pulsator model revisited
L. Bigot1,2 - W. A. Dziembowski3
1 - Département Cassini, UMR CNRS 6529, Observatoire de la Côte
d'Azur, BP 4229, 06304 Nice Cedex 4, France
2 - Niels Bohr Institute for Astronomy, Physics and Geophysics,
Juliane Maries Vej 30, DK-2100 Copenhagen Ø, Denmark
3 - Warsaw University Observatory,
Al Ujazdowskie 4, 00-478 Warszawa, Poland; N. Copernicus Astronomical
Center, Polish Academy of Science, Bartycka 18, 00-716 Warszawa, Poland
Received 7 September 2001 / Accepted 23 May 2002
Abstract
The oblique pulsator model accounts for most of the pulsation
properties of the rapidly oscillating Ap (roAp) stars. The model predicts that modes are seen
as equidistant multiplets separated by the angular frequency of rotation. The relative amplitudes
of the components may be calculated and directly compared with observations. The effects of rotation
introduce amplitude asymmetry, that is peaks corresponding to azimuthal numbers m and -m are unequal.
In this paper we propose improvements to the model that
consist of including effects of the centrifugal force and in using a
non-perturbative treatment of the magnetic field influence. We show that in roAp stars
the centrifugal force is the primary source of the rotational frequency shift. Although
the amplitude asymmetry arises from the Coriolis force, its size is strongly affected by
the centrifugal force. For dipole modes (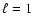 )
we develop a simple geometrical picture
of pulsation in the presence of rotation and a magnetic field. We provide some numerical
results for a representative model of roAp stars which is applied to the case of HR 3831.
We find that the mode that agrees with the observed amplitude ratios in this star
significantly departs from alignment with the magnetic axis. We discuss problems posed
by the observational data of HR 3831, emphasizing difficulties of the standard oblique
pulsator model which assumes that the excited mode is nearly aligned with the magnetic field.
)
we develop a simple geometrical picture
of pulsation in the presence of rotation and a magnetic field. We provide some numerical
results for a representative model of roAp stars which is applied to the case of HR 3831.
We find that the mode that agrees with the observed amplitude ratios in this star
significantly departs from alignment with the magnetic axis. We discuss problems posed
by the observational data of HR 3831, emphasizing difficulties of the standard oblique
pulsator model which assumes that the excited mode is nearly aligned with the magnetic field.
Key words: stars: oscillations - stars: magnetic fields - stars: rotation
The rapidly oscillating Ap (roAp) stars are high order p-mode pulsators.
The pulsation periods are in the 5-15 min range which
is nearly the same as that of the solar oscillations. However, the mode
amplitudes in roAp stars, with typical values of one millimagnitude,
are higher by three orders of magnitude than those in the Sun. Kurtz (1982)
argued that the magnetic field must play an essential role in roAp oscillations as
the maxima of the oscillation amplitudes coincide with the maxima of the
longitudinal field.
The properties of the magnetic field in roAp
stars are similar to that in the whole group of Ap stars. The observed field
is predominantly dipolar and has a kiloGauss strength.
Since their discovery two decades ago (Kurtz 1978), the number of
roAp stars has grown to 32. Most of the pulsation data in roAp stars
may be interpreted in terms of
rotating dipole modes that Kurtz assumed to be symmetric around the magnetic axis.
The model provides a natural explanation of the
observed multiplets in the spectrum of the oscillations in which the
components are split by exactly the frequency of rotation.
Dziembowski & Goode (1985) generalized the oblique pulsator
model by taking into account effects of the Coriolis force. The
signature of this effect is an inequality in the amplitudes of the side peaks, which is in fact observed.
In this model, the amplitude differences
depend on the ratio of rotational to magnetic frequency perturbation.
Hence the amplitudes yield a constraint on the internal magnetic
field. The generalized model was further developed by Kurtz &
Shibahashi (1986) who gave analytical relations between
amplitudes of the multiplets in the case of a dominating magnetic
field over rotational effects. Some additional improvements have been brought by
Shibahashi & Takata (1993) and Takata & Shibahashi (1995).
In all these works, effects of the centrifugal force were ignored
and those of the magnetic field were treated as a small perturbation.
Neither of these approximations are justified in the case of roAp stars.
Our aim here
is to eliminate these shortcomings.
In Sect. 2, we consider the dynamical effects of the magnetic field
and rotation on arbitrary oscillation modes. We treat effects of
rotation as a perturbation of magneto-acoustic modes. Since rotation
couples nearly degenerate states of different m values, the
degenerate perturbation formalism is used. It leads to a matrix
eigenvalue problem for mode frequencies and relative amplitudes of
spherical harmonics of different m's. In
Sect. 3,
we consider individual modes in the observer's system.
Each mode is seen as a multiplet with 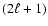 components. We determine their relative amplitudes. In Sect. 4, we explore
the consequences of these improvements for the mode properties in the special case of
components. We determine their relative amplitudes. In Sect. 4, we explore
the consequences of these improvements for the mode properties in the special case of 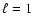 .
Finally in Sect. 5,
we apply these results to a representative model of roAp stars. We also discuss problems posed by
the roAp star HR 3831 for which the inequality of the side peaks is clearly seen.
In roAp stars the observed surface magnetic fields have kiloGauss intensities.
Even at these large values, the field has almost no dynamical effect on
acoustic wave propagation except in a thin layer at the surface of the star
(one or two percent in radius), where the magnetic pressure is comparable to (or
larger than)
the gas pressure. Therefore, in this thin layer the magnetic field effect
cannot be
treated as a perturbation. Non-perturbative treatments
of the effects of a magnetic field on oscillations in roAp stars
were developed by Dziembowski & Goode (1996),
Bigot et al. (2000) and Cunha & Gough (2000).
It is known from these previous studies that the magnetic field
distorts the modes so that the angular dependence
is in general described by a linear combination of spherical harmonics of
different
.
Finally in Sect. 5,
we apply these results to a representative model of roAp stars. We also discuss problems posed by
the roAp star HR 3831 for which the inequality of the side peaks is clearly seen.
In roAp stars the observed surface magnetic fields have kiloGauss intensities.
Even at these large values, the field has almost no dynamical effect on
acoustic wave propagation except in a thin layer at the surface of the star
(one or two percent in radius), where the magnetic pressure is comparable to (or
larger than)
the gas pressure. Therefore, in this thin layer the magnetic field effect
cannot be
treated as a perturbation. Non-perturbative treatments
of the effects of a magnetic field on oscillations in roAp stars
were developed by Dziembowski & Goode (1996),
Bigot et al. (2000) and Cunha & Gough (2000).
It is known from these previous studies that the magnetic field
distorts the modes so that the angular dependence
is in general described by a linear combination of spherical harmonics of
different 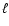 's and the same m (as long as the field is
axisymmetric). For a pure dipole field
the combination involves only
's and the same m (as long as the field is
axisymmetric). For a pure dipole field
the combination involves only 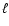 's of the same parity.
We adopt
here the approach developed by Bigot et al. (2000) with one additional
simplification. This simplification consists of assuming that the angular
dependence for individual modes may be approximated by a single
spherical harmonic in the magnetic reference system.
The effects of rotation on p-mode oscillations may be regarded
as small perturbations. For the rotation periods of roAp stars, which are of
the order of days or more, the angular velocity of rotation,
's of the same parity.
We adopt
here the approach developed by Bigot et al. (2000) with one additional
simplification. This simplification consists of assuming that the angular
dependence for individual modes may be approximated by a single
spherical harmonic in the magnetic reference system.
The effects of rotation on p-mode oscillations may be regarded
as small perturbations. For the rotation periods of roAp stars, which are of
the order of days or more, the angular velocity of rotation,
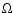 ,
satisfies the strong inequality
,
satisfies the strong inequality
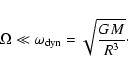 |
(1) |
If the rotation is the only non-spherical perturbation, then in the coordinate system with the polar
axis aligned with the rotation axis, each of the individual modes is described by a single spherical harmonic.
In that case the frequency shift due to rotation may be written in the following form
(e.g. Gough & Thompson 1990; Dziembowski & Goode 1992)
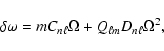 |
(2) |
where
The first term in Eq. (2) is due to the Coriolis force. The coefficient 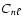 is called the Ledoux constant (Ledoux 1951). The coefficient
is called the Ledoux constant (Ledoux 1951). The coefficient 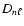 represents the radial integral
of the effect of the centrifugal distortion of the star on the mode (see Appendix). We made two
approximations regarding the quadratic term. First, we ignore spherical change of the star due to the
surface average of the centrifugal force. It causes a small m-independent frequency shift, which
is not of interest to us. The second approximation is to include only the effect of the centrifugal distortion,
which is much larger than the second-order effect of the Coriolis force.
The reason why in roAp stars, which are rather slow
rotators, the quadratic term of rotation may exceed the linear one
is a consequence of high radial order n of p-modes
excited in these stars. For such modes we
have approximately
represents the radial integral
of the effect of the centrifugal distortion of the star on the mode (see Appendix). We made two
approximations regarding the quadratic term. First, we ignore spherical change of the star due to the
surface average of the centrifugal force. It causes a small m-independent frequency shift, which
is not of interest to us. The second approximation is to include only the effect of the centrifugal distortion,
which is much larger than the second-order effect of the Coriolis force.
The reason why in roAp stars, which are rather slow
rotators, the quadratic term of rotation may exceed the linear one
is a consequence of high radial order n of p-modes
excited in these stars. For such modes we
have approximately 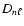
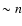 and
and
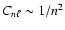 .
The
ratio of the second to the first term in Eq. (2) is
.
The
ratio of the second to the first term in Eq. (2) is
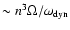 and is
greater than 1 for all roAp stars for which we have data to
evaluate it.
The previous approach to calculate the effects of rotation is not directly
applicable to roAp stars. The reason is that in most of these stars
the magnetic and rotation axes are tilted by a certain angle
and is
greater than 1 for all roAp stars for which we have data to
evaluate it.
The previous approach to calculate the effects of rotation is not directly
applicable to roAp stars. The reason is that in most of these stars
the magnetic and rotation axes are tilted by a certain angle 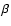 ,
called
the obliquity.
The combined magnetic and rotational perturbations do not have axial
symmetry.
It will be convenient for us to consider this joint perturbation in the
reference system with the polar axis aligned with the magnetic axis, which
we will call the magnetic system.
We allow the rotational frequency perturbation to be of the same order as
the frequency separations between magnetic eigenmodes of different m's. The
perturbation due to rotation is non-axisymmetric which implies coupling
of modes of different m's. We are thus in the situation requiring the use of a degenerate
perturbation theory.
Individual eigenmodes are no longer described by a single value of m.
Simultaneous effects of rotation and inclined magnetic field have
already been investigated (e.g. Dicke 1982;
Dziembowski & Goode 1985; Gough & Thompson 1990). In this
paper, we will follow the approach of Dziembowski & Goode but we
improve it in two different respects. The magnetic field effects
are treated with a non-perturbative approach. We also take into account the effect of the centrifugal
distortion of the star for the reasons already mentioned.
,
called
the obliquity.
The combined magnetic and rotational perturbations do not have axial
symmetry.
It will be convenient for us to consider this joint perturbation in the
reference system with the polar axis aligned with the magnetic axis, which
we will call the magnetic system.
We allow the rotational frequency perturbation to be of the same order as
the frequency separations between magnetic eigenmodes of different m's. The
perturbation due to rotation is non-axisymmetric which implies coupling
of modes of different m's. We are thus in the situation requiring the use of a degenerate
perturbation theory.
Individual eigenmodes are no longer described by a single value of m.
Simultaneous effects of rotation and inclined magnetic field have
already been investigated (e.g. Dicke 1982;
Dziembowski & Goode 1985; Gough & Thompson 1990). In this
paper, we will follow the approach of Dziembowski & Goode but we
improve it in two different respects. The magnetic field effects
are treated with a non-perturbative approach. We also take into account the effect of the centrifugal
distortion of the star for the reasons already mentioned.
In this subsection, we use the reference system with the polar axis aligned with the magnetic axis.
The zeroth order equation is
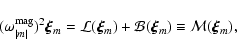 |
(4) |
where
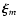 represents the displacement,
represents the displacement,
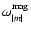 the magnetic eigenfrequency,
the magnetic eigenfrequency,
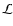 the usual adiabatic oscillation operator and
the usual adiabatic oscillation operator and 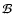 the Lorentz force operator (see e.g. Unno et al. 1989).
The
the Lorentz force operator (see e.g. Unno et al. 1989).
The 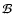 operator introduces a dependence on |m|. Indeed, the
degeneracy with respect to m which exists in absence of symmetry breaking agents is partially removed
by the magnetic field since it breaks the spherical symmetry of the star.
To simplify notation, we do not put the
operator introduces a dependence on |m|. Indeed, the
degeneracy with respect to m which exists in absence of symmetry breaking agents is partially removed
by the magnetic field since it breaks the spherical symmetry of the star.
To simplify notation, we do not put the 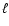 and n subscripts.
Numerical solutions of Eq. (4) for more-or-less
realistic models of
roAp stars were obtained by Bigot et al. (2000) and by Cunha & Gough (2000) for polytropic models.
The eigenfrequencies are complex.
The non-Hermitian nature of the operator is a consequence of the
boundary condition applied at the base of the magnetic
layer which implicitly assumes an efficient dissipation of the
downward propagating Alfvénic waves. This complex nature of the
problem will be ignored in our considerations here. In fact, the
only quantities obtained from Eq. (4) that we will use here
are differences between eigenfrequencies
and n subscripts.
Numerical solutions of Eq. (4) for more-or-less
realistic models of
roAp stars were obtained by Bigot et al. (2000) and by Cunha & Gough (2000) for polytropic models.
The eigenfrequencies are complex.
The non-Hermitian nature of the operator is a consequence of the
boundary condition applied at the base of the magnetic
layer which implicitly assumes an efficient dissipation of the
downward propagating Alfvénic waves. This complex nature of the
problem will be ignored in our considerations here. In fact, the
only quantities obtained from Eq. (4) that we will use here
are differences between eigenfrequencies
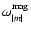 at specified
at specified  and n. As we have already pointed out, we
assume a single spherical harmonic dependence for individual
magneto-sonic modes.
Now we consider effects of rotation. The
eigenvalue equation becomes
and n. As we have already pointed out, we
assume a single spherical harmonic dependence for individual
magneto-sonic modes.
Now we consider effects of rotation. The
eigenvalue equation becomes
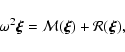 |
(5) |
where 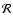 denotes the perturbing rotational operator.
In agreement with the properties of Ap stars we assume that the rotation and magnetic axes are tilted, hence the
perturbation due to rotation is non-axisymmetric. This leads to coupling of the magnetic states corresponding
to different azimuthal
orders m. The strength of the coupling depends on the size of the rotational
shift of the frequency relative to the
frequency differences,
denotes the perturbing rotational operator.
In agreement with the properties of Ap stars we assume that the rotation and magnetic axes are tilted, hence the
perturbation due to rotation is non-axisymmetric. This leads to coupling of the magnetic states corresponding
to different azimuthal
orders m. The strength of the coupling depends on the size of the rotational
shift of the frequency relative to the
frequency differences,
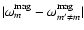 .
Even with typical magnetic fields
found in roAp stars, such as 1 kG, the rotational shift of frequency,
dominated by the centrifugal distortion, can be comparable to the above frequency differences. Therefore,
a standard perturbation theory cannot be applied in this model.
We have to use a degenerate perturbation theory as Dziembowski & Goode (1985) did in the same context. We then
consider the following displacement vector
.
Even with typical magnetic fields
found in roAp stars, such as 1 kG, the rotational shift of frequency,
dominated by the centrifugal distortion, can be comparable to the above frequency differences. Therefore,
a standard perturbation theory cannot be applied in this model.
We have to use a degenerate perturbation theory as Dziembowski & Goode (1985) did in the same context. We then
consider the following displacement vector
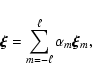 |
(6) |
which takes into account the 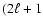 )
coupled magnetic levels. The
)
coupled magnetic levels. The
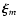 are solutions of
Eq. (4) and
are solutions of
Eq. (4) and 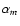 are coefficients to be determined. The sum involves only nearly degenerate modes, which in the adopted
approximation are
described by a single value of
are coefficients to be determined. The sum involves only nearly degenerate modes, which in the adopted
approximation are
described by a single value of 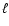 .
The orthogonality of
.
The orthogonality of
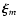 follows
from orthogonality of
follows
from orthogonality of
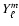 .
We assume the completeness of the set of
.
We assume the completeness of the set of
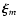 .
Using Eq. (6) in Eq. (5), after
multiplication by
.
Using Eq. (6) in Eq. (5), after
multiplication by
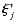 and
integration over the
volume, we get the eigensystem,
and
integration over the
volume, we get the eigensystem,
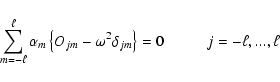 |
(7) |
with
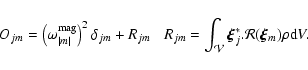 |
(8) |
The
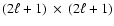 symmetric matrix O is a sum of a
diagonal matrix built with eigenvalues of Eq. (4) and a matrix whose elements are
projections of the operator
symmetric matrix O is a sum of a
diagonal matrix built with eigenvalues of Eq. (4) and a matrix whose elements are
projections of the operator 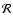 onto the base
onto the base
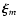 .
Therefore, to calculate the effect of an oblique rotation on magnetic states, one has to
find the (
.
Therefore, to calculate the effect of an oblique rotation on magnetic states, one has to
find the (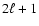 )
eigenfrequencies
)
eigenfrequencies 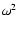 and the
corresponding eigenvectors
and the
corresponding eigenvectors
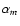 of the matrix O. The condition for non-trivial solutions requires
that the determinant of Eq. (7) vanishes. This condition yields the eigenfrequencies.
of the matrix O. The condition for non-trivial solutions requires
that the determinant of Eq. (7) vanishes. This condition yields the eigenfrequencies.
The elements of matrix 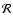 are given by
are given by
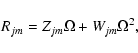 |
(9) |
where
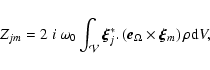 |
(10) |
with 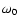 the frequency in absence of magnetic field and rotation,
the frequency in absence of magnetic field and rotation,
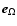 a unit vector along rotation axis, and
a unit vector along rotation axis, and
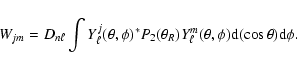 |
(11) |
In the last expression 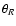 is the polar angle in the rotation system.
is the polar angle in the rotation system.
The Zjm coefficients couple components with
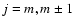 because
because
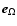 expressed in magnetic system contains only terms proportional either to
expressed in magnetic system contains only terms proportional either to 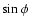 or
or 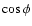 .
Using the
complex spherical harmonic property
.
Using the
complex spherical harmonic property
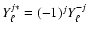 ,
it is easy to show that
,
it is easy to show that
The Wjm coefficients couple components with j=m, 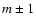 ,
,
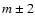 because
because
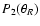 expressed
in the magnetic system generates harmonics with
expressed
in the magnetic system generates harmonics with 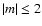 .
The property of the integral in Eq. (11)
leads to the relation
.
The property of the integral in Eq. (11)
leads to the relation
After integration the explicit expression for Rjm becomes
where
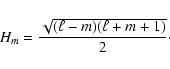 |
(15) |
The
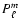 's are the usual associated Legendre functions.
This matrix is non-diagonal
as long as the rotation and
magnetic axes are not aligned (
's are the usual associated Legendre functions.
This matrix is non-diagonal
as long as the rotation and
magnetic axes are not aligned (
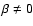 ).
).
In the calculation of the Rjm elements we made an additional
approximation which consists in neglecting the contribution
from the thin magnetic layer to the radial integrals in the
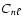 and
and 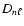 coefficients.
coefficients.
In order to calculate fluctuations of luminosity in the observer's system,
we now express the eigensolutions of Eq. (7) in the reference system with the polar axis
directed towards the observer. Following Dziembowski & Goode (1985),
we assume that the intensity fluctuation
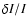 has the same angular dependence as
fluctuation of photospheric pressure
has the same angular dependence as
fluctuation of photospheric pressure
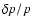 .
In the magnetic reference system the intensity fluctuations is written
.
In the magnetic reference system the intensity fluctuations is written
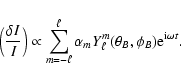 |
(16) |
From the well-known relation for spherical harmonic transformation (e.g. Edmonds 1960)
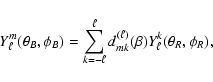 |
(17) |
we write the intensity fluctuations in the rotation system
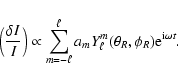 |
(18) |
The coefficients am and 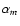 obey the relation
obey the relation
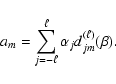 |
(19) |
The expression for the luminosity fluctuations in observer's system is then obtained by two transformations. One consists in writing the fluctuations in an inertial reference system with
the same polar axis as the rotation axis but which differs by
the longitudes, i.e.
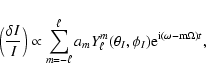 |
(20) |
where we adopted
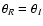 and
and
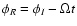 .
The final transformation
consists in a rotation of the coordinate system so that the new
polar axis coincides with the line of sight
.
The final transformation
consists in a rotation of the coordinate system so that the new
polar axis coincides with the line of sight
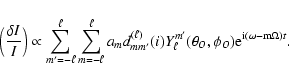 |
(21) |
The subscripts B,R,I,O refer to the magnetic, rotational, inertial
and observer systems, respectively. In the last expression i denotes
the angle between the rotation axis and the line of sight.
Finally, each eigenmode is seen by an observer as a 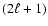 - component multiplet. In the time domain,
such a mode will be observed as an amplitude modulated pulsation with a modulation period equal to
- component multiplet. In the time domain,
such a mode will be observed as an amplitude modulated pulsation with a modulation period equal to
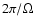 .
Unfortunately, from observations we can get only an averaged
luminosity over the visible disk. Then, only the components with m'=0 survive in the
disk-average intensity fluctuations. Thus, the relative luminosity change seen by the observer has the from
of the multiplet
.
Unfortunately, from observations we can get only an averaged
luminosity over the visible disk. Then, only the components with m'=0 survive in the
disk-average intensity fluctuations. Thus, the relative luminosity change seen by the observer has the from
of the multiplet
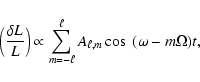 |
(22) |
where the amplitudes are given by
 |
(23) |
The mode is represented by a multiplet as long as its geometry is described by more than one value of m in the rotation system.
It is convenient to use the following amplitude ratios (Kurtz & Shibahashi 1986),
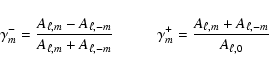 |
(24) |
which are the observables of interest. In order to evaluate these observables, we need a stellar model
as well as information about rotation and magnetic field. We now have pretty good ideas about the model
for specific stars. The rotation rate 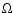 is the most accurately determined parameter, but the inclination
angle i is never reliably known. Regarding the magnetic field, we are in a worse situation. In all
calculations of magnetic effects on oscillations of roAp stars a simple dipole model has adopted. In this
case the field is fully characterized by its polar value at the surface,
is the most accurately determined parameter, but the inclination
angle i is never reliably known. Regarding the magnetic field, we are in a worse situation. In all
calculations of magnetic effects on oscillations of roAp stars a simple dipole model has adopted. In this
case the field is fully characterized by its polar value at the surface, 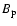 ,
and the obliquity angle
,
and the obliquity angle
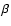 .
We have observational assessments of
.
We have observational assessments of 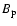 but with uncertainties. The only justification for
using a dipole model of the magnetic field is its simplicity. Therefore the main application of our
observables is to subject the model to an observational test.
From Eq. (23) we get for the amplitude ratios,
but with uncertainties. The only justification for
using a dipole model of the magnetic field is its simplicity. Therefore the main application of our
observables is to subject the model to an observational test.
From Eq. (23) we get for the amplitude ratios,
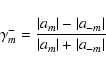 |
(25) |
and
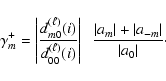 |
(26) |
Note that
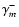 measures the
departure from equality of side peak amplitudes at +m and -m. It is important to note here that
the asymmetry of the amplitudes Am in the observer's system
comes from the asymmetry of the coefficients of the coupling,
measures the
departure from equality of side peak amplitudes at +m and -m. It is important to note here that
the asymmetry of the amplitudes Am in the observer's system
comes from the asymmetry of the coefficients of the coupling,
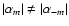 .
Neither the magnetic field nor the centrifugal distortion can
explain this inequality since they affect the components +m and -m in the same way. In our problem,
only the Coriolis force affects in a different way these two
components. Ignoring this force, the problem would have a
mirror symmetry that is invariant
to the transformation
.
Neither the magnetic field nor the centrifugal distortion can
explain this inequality since they affect the components +m and -m in the same way. In our problem,
only the Coriolis force affects in a different way these two
components. Ignoring this force, the problem would have a
mirror symmetry that is invariant
to the transformation
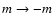 .
The formal proof follows from Eq. (13) which implies that in absence of the Coriolis force
.
The formal proof follows from Eq. (13) which implies that in absence of the Coriolis force
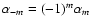 and thereby
and thereby
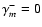 .
The symmetry
of
.
The symmetry
of
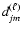 implies the same relation for the am-coefficients. The value of
implies the same relation for the am-coefficients. The value of
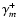 depends both on the aspect angle i (first factor) and relative role of rotation and magnetic field
(second factor).
depends both on the aspect angle i (first factor) and relative role of rotation and magnetic field
(second factor).
The dipole mode is of special importance because it is dominant in roAp stars. Furthermore, these modes admit
a simple geometrical interpretation.
In the present case, equating to zero the determinant of Eq. (7) leads to the following cubic
equation for eigenfrequencies
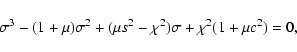 |
(27) |
where
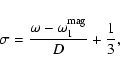 |
(28) |
and
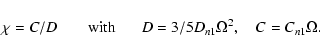 |
(29) |
The obliquity angle appears in
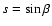 and
and
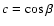 .
The magnetic
field effects come only through the parameter
.
The magnetic
field effects come only through the parameter
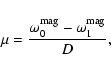 |
(30) |
which, according to the results in Bigot et al. (2000), is always negative. We should stress that
Cunha & Gough (2000) found situations where 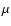 is positive. We are unable to explain this disagreement.
The geometrical picture of the
is positive. We are unable to explain this disagreement.
The geometrical picture of the 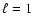 modes is a displacement of the sphere representing the stellar surface. In the absence of a magnetic field, the m=0 modes represent displacements along the rotation axis, z. The
modes is a displacement of the sphere representing the stellar surface. In the absence of a magnetic field, the m=0 modes represent displacements along the rotation axis, z. The 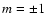 modes represent motions of the sphere along a circle in the (x,y) plane with two
opposite directions. To describe the modification of the geometrical picture due to the combined effect
of magnetic field and rotation, we consider radial component of the displacement
modes represent motions of the sphere along a circle in the (x,y) plane with two
opposite directions. To describe the modification of the geometrical picture due to the combined effect
of magnetic field and rotation, we consider radial component of the displacement
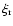 at the star surface.
Since we are in the framework of the linear pulsation theory the horizontal displacement is irrelevant.
We oriented the axes so that the magnetic field axis lies in the (x,z)-plane. The radial displacement
has the same angular and temporal dependence as in Eq. (18). In Cartesian coordinates (x,y,z),
this is written
at the star surface.
Since we are in the framework of the linear pulsation theory the horizontal displacement is irrelevant.
We oriented the axes so that the magnetic field axis lies in the (x,z)-plane. The radial displacement
has the same angular and temporal dependence as in Eq. (18). In Cartesian coordinates (x,y,z),
this is written
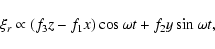 |
(31) |
where,
The displacement vector described Eq. (31) lies in a
plane whose normal makes an angle 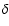 with the rotation axis
and is given by
with the rotation axis
and is given by
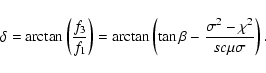 |
(33) |
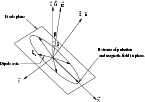 |
Figure 1:
Representation of the dipole mode geometry. During one
periode of oscillation, the maximum of the displacement vector
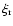 describes an ellipse in the mode plane whose normal
describes an ellipse in the mode plane whose normal
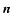 makes an angle
makes an angle 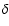 with the
rotation axis. The line which joins the two angular extrema of
with the
rotation axis. The line which joins the two angular extrema of
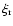 is the axis of symmetry of the dipole mode. The thick
arrows correspond to different positions of the dipole axis during
the pulsation cycle. The magnetic and rotation axes are in the
same plane (X,Z) but they are tilted by the angle
is the axis of symmetry of the dipole mode. The thick
arrows correspond to different positions of the dipole axis during
the pulsation cycle. The magnetic and rotation axes are in the
same plane (X,Z) but they are tilted by the angle 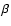 .
For
this figure we plot .
For
this figure we plot 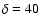 deg and
deg and 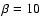 deg which are
the values found for HR 3831, see Sect. 5.
For clarity, we draw on this plot an ellipticity
deg which are
the values found for HR 3831, see Sect. 5.
For clarity, we draw on this plot an ellipticity 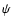 that is
much larger than the one found for HR 3831 (
that is
much larger than the one found for HR 3831 (
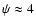 deg).
For each period of oscillation, the maxima of the dipole mode and
the magnetic field are in phase when the mode axis crosses the
plane formed by the magnetic and rotation axes, i.e. the (X,Z)
plane. deg).
For each period of oscillation, the maxima of the dipole mode and
the magnetic field are in phase when the mode axis crosses the
plane formed by the magnetic and rotation axes, i.e. the (X,Z)
plane. |
| Open with DEXTER |
The inclination of the plane is mainly determined by the relative size of the centrifugal and
magnetic shifts. Indeed, in roAp stars only the centrifugal distortion effects can be
comparable to the magnetic ones. The role of the Coriolis force is marginal
regarding the inclination of the mode.
We now rotate the coordinate system around the y-axis by the angle 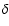 .
In the new coordinate system
(X,y,Z) the displacement is writen
.
In the new coordinate system
(X,y,Z) the displacement is writen
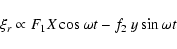 |
(34) |
with,
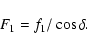 |
(35) |
During the pulsation cycle, the maximum of the displacement vector describes an ellipse in the (X,y) plane.
The three solutions of Eq. (27) correspond to three different polarizations of the motion which
are described by the parameter
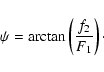 |
(36) |
Its value does not depend on the choice of the reference system. The special cases are:
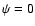 - linear polarization along the X-axis,
- linear polarization along the X-axis,
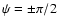 - linear polarization along the y-axis,
- linear polarization along the y-axis,
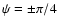 - circular polarization.
- circular polarization.
The geometry of the problem is illustrated in Fig.
1.
The Coriolis force plays an essential role in the polarization of the displacement vector. Indeed, as we have
already mentioned only this force creates unequal coefficients for the components 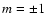 and thereby
and thereby
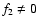 ,
which leads to an elliptical polarization. When it is neglected (f2=0), we have three linearly polarized modes along the three orthogonal
axes of the reference system except for the singularity at F1=0, as we have for
,
which leads to an elliptical polarization. When it is neglected (f2=0), we have three linearly polarized modes along the three orthogonal
axes of the reference system except for the singularity at F1=0, as we have for 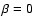 .
In absence of rotation two modes are degenerate with the same frequency,
.
In absence of rotation two modes are degenerate with the same frequency,
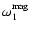 .
If we take
into account only the effect of the centrifugal distortion as a manifestation of the rotation, it would raise
this degeneracy as long as
.
If we take
into account only the effect of the centrifugal distortion as a manifestation of the rotation, it would raise
this degeneracy as long as
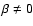 ,
but it would also lead to equal amplitudes for the coefficients
,
but it would also lead to equal amplitudes for the coefficients
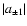 since the centrifugal distortion does not introduce asymmetry. These two modes would be therefore
linearly polarized along two orthogonal axes.
The effects of the Coriolis force and the mode ellipticity decrease if the rotation axis is approaching the mode plane
(
since the centrifugal distortion does not introduce asymmetry. These two modes would be therefore
linearly polarized along two orthogonal axes.
The effects of the Coriolis force and the mode ellipticity decrease if the rotation axis is approaching the mode plane
(
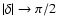 ). When the rotation axis is inside the mode plane (
). When the rotation axis is inside the mode plane (
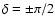 ),
the effects of the Coriolis force vanish and the mode is linearly polarized.
),
the effects of the Coriolis force vanish and the mode is linearly polarized.
The three dipole modes are completely characterized by the
(
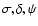 )
parameters. In Fig. 2
these parameters are plotted as functions of the obliquity angle
)
parameters. In Fig. 2
these parameters are plotted as functions of the obliquity angle
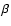 for three different values of
for three different values of 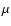 which depends on magnetic field strength. For better visualization, we have selected
which depends on magnetic field strength. For better visualization, we have selected 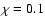 ,
though the
realistic values for roAp stars are generally smaller
(
,
though the
realistic values for roAp stars are generally smaller
(
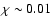 ). The fourth quantity
). The fourth quantity 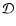 will be introduced in Sect. 4.2.
will be introduced in Sect. 4.2.
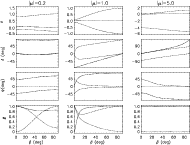 |
Figure 2:
Plots of the mode parameters for (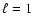 )
as functions
of the obliquity angle )
as functions
of the obliquity angle 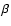 .
The dimensionless frequency .
The dimensionless frequency
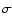 ,
the inclination of the mode ,
the inclination of the mode 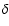 ,
the polarization
angle ,
the polarization
angle 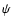 and the quantity
and the quantity
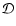 are plotted on the
four rows of the graph. Each column corresponds to a specific
magnetic regime represented by three values of
are plotted on the
four rows of the graph. Each column corresponds to a specific
magnetic regime represented by three values of 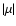 .
The left
column corresponds to a rotation dominating regime ( .
The left
column corresponds to a rotation dominating regime (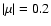 )
in which two modes (dotted and dashed) can be nearly aligned
( )
in which two modes (dotted and dashed) can be nearly aligned
(
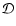 )
with the magnetic axis. For a dominating magnetic
regime plotted in the right column ( )
with the magnetic axis. For a dominating magnetic
regime plotted in the right column (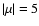 ), only one mode
(dashed) is aligned with the magnetic axis. ), only one mode
(dashed) is aligned with the magnetic axis. |
| Open with DEXTER |
The efficiency of the coupling between m-components of the mode by rotation depends on the size of the
frequency separation of the unperturbed magnetic modes compared with
the rotational shift (Coriolis + centrifugal). Two regimes exist depending on the value of 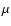 .
.
For small values of
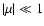 ,
the rotational (centrifugal) effects
dominate over the magnetic effects. In the frame with the polar axis aligned with the rotation axis, each
eigenmode is represented by a single spherical harmonic. One mode is linearly polarized along the rotation axis
(
,
the rotational (centrifugal) effects
dominate over the magnetic effects. In the frame with the polar axis aligned with the rotation axis, each
eigenmode is represented by a single spherical harmonic. One mode is linearly polarized along the rotation axis
(
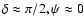 )
whereas the two other modes are circularly polarized
in two opposite senses (
)
whereas the two other modes are circularly polarized
in two opposite senses (
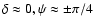 )
in the rotational equatorial plane.
For large values of
)
in the rotational equatorial plane.
For large values of
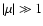 ,
the magnetic effects dominate over
the rotational ones. In that case, this axisymmetric harmonic (m=0), defined in the system with the polar axis aligned with the magnetic axis, is not coupled with the non-axisymmetric ones
,
the magnetic effects dominate over
the rotational ones. In that case, this axisymmetric harmonic (m=0), defined in the system with the polar axis aligned with the magnetic axis, is not coupled with the non-axisymmetric ones 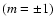 .
The axisymmetric mode is linearly polarized along the magnetic axis. As shown in Fig. 2 two modes are circularly
polarized (
.
The axisymmetric mode is linearly polarized along the magnetic axis. As shown in Fig. 2 two modes are circularly
polarized (
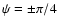 )
for
)
for 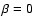 and tend to be linearly polarized as
and tend to be linearly polarized as
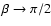 since the effects of the Coriolis force decrease. For almost perpendicular rotation and magnetic axes,
since the effects of the Coriolis force decrease. For almost perpendicular rotation and magnetic axes,
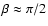 ,
the three dipoles modes are linearly polarized along the three orthogonal axes of
the magnetic system.
In the intermediate regime,
,
the three dipoles modes are linearly polarized along the three orthogonal axes of
the magnetic system.
In the intermediate regime,
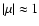 ,
the situation is more
complex. In that case the centrifugal and magnetic effects are comparable which
leads to an inclination of the mode system between magnetic and rotation axes.
,
the situation is more
complex. In that case the centrifugal and magnetic effects are comparable which
leads to an inclination of the mode system between magnetic and rotation axes.
It is generally believed that modes excited in roAp
stars are nearly aligned with the magnetic axis. In principle, as long as
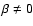 ,
none of the three dipole
modes is
strictly aligned with the magnetic field. Let us note that the strict alignment requires
,
none of the three dipole
modes is
strictly aligned with the magnetic field. Let us note that the strict alignment requires
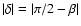 and
and 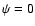 .
From the three modes,
we would like to select the one which is the most aligned with the magnetic axis.
A convenient measure of the departure from strict alignment is the quantity
.
From the three modes,
we would like to select the one which is the most aligned with the magnetic axis.
A convenient measure of the departure from strict alignment is the quantity 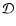 defined as follows
defined as follows
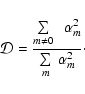 |
(37) |
For a pure axisymmetric mode (
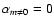 )
we have
)
we have
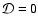 ,
and in the opposite case for a pure
non-axisymmetric mode (
,
and in the opposite case for a pure
non-axisymmetric mode (
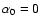 )
we have
)
we have
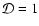 .
For dipole modes, with the help of Eqs. (19), (32), (33) and (36), we can
express
.
For dipole modes, with the help of Eqs. (19), (32), (33) and (36), we can
express 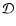 in terms of the polarization angles
(
in terms of the polarization angles
(
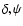 )
defined in the rotation system, as follows
)
defined in the rotation system, as follows
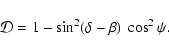 |
(38) |
This quantity is plotted in Fig. 2 as function of the obliquity angle
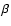 and the magnetic strength parameter
and the magnetic strength parameter 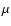 .
For large magnetic fields,
.
For large magnetic fields,
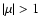 ,
we see that there is a mode which for all values of
,
we see that there is a mode which for all values of 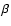 remains linearly polarized along the
magnetic axis (
remains linearly polarized along the
magnetic axis (
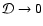 ). At weaker fields (
). At weaker fields (
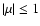 )
various modes may approach
)
various modes may approach
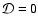 and at the same time have significant values of
and at the same time have significant values of 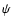 implying elliptical polarizations. The case of the mode
represented by the dashed line is quite interesting for large
implying elliptical polarizations. The case of the mode
represented by the dashed line is quite interesting for large 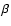 .
The geometrical picture is that the mode
moves the sphere along an elongated ellipse whose major axis is close to the magnetic
axis.
These results show that generally speaking, for reasonable values of
.
The geometrical picture is that the mode
moves the sphere along an elongated ellipse whose major axis is close to the magnetic
axis.
These results show that generally speaking, for reasonable values of 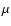 and for
and for
![$\beta \neq 0 ~[\pi/2]$](/articles/aa/full/2002/31/aa1896/img156.gif) ,
none of the three dipole modes is linearly polarized along the magnetic axis (
,
none of the three dipole modes is linearly polarized along the magnetic axis (
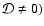 .
.
As it follows from Sect. 3, each of the three 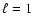 eigenmodes is seen as a triplet with peaks separated
exactly by the rotation rate,
eigenmodes is seen as a triplet with peaks separated
exactly by the rotation rate,  .
Further, the inequality of the side peaks,
.
Further, the inequality of the side peaks, 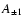 ,
arises only from the Coriolis force. From Eqs. (23) and (25) we have
,
arises only from the Coriolis force. From Eqs. (23) and (25) we have
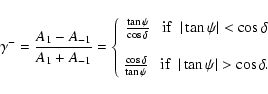 |
(39) |
The role of the Coriolis force is essential for this inequality since it modifies the ellipticity 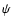 of the mode
which determines the size of
of the mode
which determines the size of 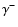 .
The sign of
.
The sign of 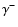 is related to the sense of polarization. Negative
values means counter-clockwise elliptical polarization. Note that
is related to the sense of polarization. Negative
values means counter-clockwise elliptical polarization. Note that
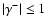 .
The value of
.
The value of
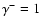 corresponds to A-1=0 and
corresponds to A-1=0 and
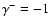 to A1=0.
This equation emphasizes also the role of centrifugal force in determining the inequality of side peaks through the
angle
to A1=0.
This equation emphasizes also the role of centrifugal force in determining the inequality of side peaks through the
angle 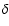 .
.
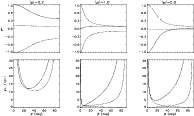 |
Figure 3:
Plots of the amplitude ratios 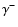 (top) and
(top) and 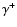 (bottom) as
functions of the obliquity angle
(bottom) as
functions of the obliquity angle 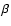 and for different magnetic regimes
and for different magnetic regimes 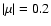 (left), 1.0 (middle) and 5.0 (right). The curves correspond to the three dipole modes. The notation remains the
same as in Fig. 2.
(left), 1.0 (middle) and 5.0 (right). The curves correspond to the three dipole modes. The notation remains the
same as in Fig. 2. |
| Open with DEXTER |
The sum of the side peak amplitudes to central peak ratio, 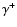 ,
depends on two effects as we have already discussed in Sect. 3. For
,
depends on two effects as we have already discussed in Sect. 3. For 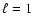 ,
Eq. (26) becomes
,
Eq. (26) becomes
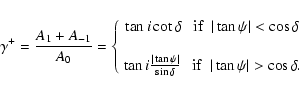 |
(40) |
The value of 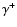 is determined by the inclination of the mode plane to the rotation axis and the inclination
of the rotation axis to the line of sight.
In Fig. 3 we plot
is determined by the inclination of the mode plane to the rotation axis and the inclination
of the rotation axis to the line of sight.
In Fig. 3 we plot 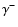 and
and
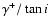 as functions of
as functions of 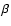 and for the same values
of
and for the same values
of 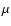 used in Fig. 2. Note the rapid decline of
used in Fig. 2. Note the rapid decline of
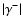 with
with 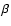 that corresponds to
a decreasing effect of the Coriolis force as discussed in Sect. 4.1.
In the strong magnetic field regime,
that corresponds to
a decreasing effect of the Coriolis force as discussed in Sect. 4.1.
In the strong magnetic field regime,
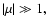 we find for the mode which is the most aligned with the magnetic
field axis (
we find for the mode which is the most aligned with the magnetic
field axis (
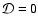 ), the well-known relations for amplitude ratios of the oblique pulsator model
(e.g. Kurtz & Shibahashi 1986; Unno et al. 1989),
), the well-known relations for amplitude ratios of the oblique pulsator model
(e.g. Kurtz & Shibahashi 1986; Unno et al. 1989),
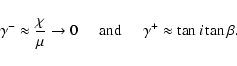 |
(41) |
In the weak magnetic field regime,
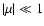 ,
the triplet reduces to a single dominant peak. Indeed, for the
mode linearly polarized along the rotation axis (
,
the triplet reduces to a single dominant peak. Indeed, for the
mode linearly polarized along the rotation axis (
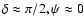 )
we have
)
we have
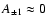 and
and
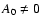 .
For the two circularly polarized modes in the rotational equatorial plane
(
.
For the two circularly polarized modes in the rotational equatorial plane
(
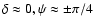 ), we have
), we have
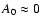 .
One of the two amplitudes A1 or A-1 also
vanishes depending on the mode that we consider (
.
One of the two amplitudes A1 or A-1 also
vanishes depending on the mode that we consider (
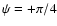 or
or 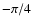 ). This situation is the worse for
asteroseismology since we lose information about the triplet.
Here we see the role of the centrifugal force in the side peak inequality because it is this force that determines
the value of
). This situation is the worse for
asteroseismology since we lose information about the triplet.
Here we see the role of the centrifugal force in the side peak inequality because it is this force that determines
the value of 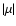 and then the regime to consider.
and then the regime to consider.
5 Application to a representative model of roAp star
We select a model characterized by the following parameters
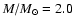 ,
,
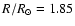 ,
,
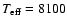 K,
K,
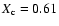 .
These parameters are not far from those adopted for HR 3831 - the roAp star with accurately measured unequal side peak amplitudes. The rotation period of this star is
.
These parameters are not far from those adopted for HR 3831 - the roAp star with accurately measured unequal side peak amplitudes. The rotation period of this star is
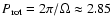 d and the central peak frequency of the multiplet is 1.428 mHz. Unfortunately our calculations are not applicable to this object if the polar
d and the central peak frequency of the multiplet is 1.428 mHz. Unfortunately our calculations are not applicable to this object if the polar 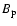 value of 14 kG, as inferred by Bagnulo et al. (1999), is true. The validity of our theory cannot be much extended beyond a 1 kG field. This is illustrated in Fig. 4 which shows in particular that the assumption of single
value of 14 kG, as inferred by Bagnulo et al. (1999), is true. The validity of our theory cannot be much extended beyond a 1 kG field. This is illustrated in Fig. 4 which shows in particular that the assumption of single 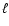 at fields above 1 kG is incorrect. The
at fields above 1 kG is incorrect. The 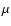 dependence on
dependence on 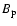 is complicated and it would be foolish to extrapolate the results by 1 order of magnitude.
Let us stress that the value of
is complicated and it would be foolish to extrapolate the results by 1 order of magnitude.
Let us stress that the value of
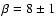 deg determined by Bagnulo et al. (1999) is very different from that assumed by Kurtz for modelling light variations in this star (e.g. Kurtz 1992). We also emphasize that it is quite surprising to see any inequality of the side peaks if the mode is aligned with the magnetic axis and if
deg determined by Bagnulo et al. (1999) is very different from that assumed by Kurtz for modelling light variations in this star (e.g. Kurtz 1992). We also emphasize that it is quite surprising to see any inequality of the side peaks if the mode is aligned with the magnetic axis and if 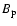 is as large as Bagnulo et al. (1999) found since the effects of the Coriolis force would be negligible compared to the magnetic ones.
is as large as Bagnulo et al. (1999) found since the effects of the Coriolis force would be negligible compared to the magnetic ones.
 |
Figure 4:
(Left panel) Plots of the magnetic parameter 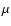 as
function of the photospheric magnetic strength
as
function of the photospheric magnetic strength 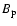 obtained with
the stellar model given in the text, for three different periods of rotation,
obtained with
the stellar model given in the text, for three different periods of rotation,
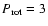 d (full line), =6 d (dotted), =12 d (dashed). The frequency is d (full line), =6 d (dotted), =12 d (dashed). The frequency is 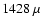 Hz.
Note that these ratios are always negative. When Hz.
Note that these ratios are always negative. When 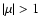 the magnetic effects dominate
over the rotational (centrifugal) effects. (Right panel) Plots of the relative kinetic
energies of each
the magnetic effects dominate
over the rotational (centrifugal) effects. (Right panel) Plots of the relative kinetic
energies of each 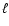 -components of the mode generated by the magnetic field, as functions of -components of the mode generated by the magnetic field, as functions of 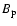 .
In all cases m=0, k=1 (full line), k=3 (dashed line), k=5 (dot-dashed line) and k=7 (dotted line), see Bigot et al. (2000) for more details.
For .
In all cases m=0, k=1 (full line), k=3 (dashed line), k=5 (dot-dashed line) and k=7 (dotted line), see Bigot et al. (2000) for more details.
For
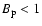 kG, the k=1 component dominates and the mode is almost a dipole. kG, the k=1 component dominates and the mode is almost a dipole. |
| Open with DEXTER |
In view of the controversial data about magnetic field in HR 3831 we have arbitrarily assumed
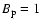 kG to calculate
kG to calculate 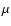 shown in Fig. 5. Note that our values are always negative. In the same figure we show corresponding values of
shown in Fig. 5. Note that our values are always negative. In the same figure we show corresponding values of 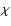 .
At the fastest rotation and the adopted value of
.
At the fastest rotation and the adopted value of 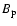 we are in the
we are in the 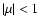 regime (first column in
Fig. 2). As soon as we depart from
regime (first column in
Fig. 2). As soon as we depart from 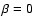 the alignment of the mode with the magnetic axis is lost. At the lowest rotation, we are in the
the alignment of the mode with the magnetic axis is lost. At the lowest rotation, we are in the
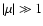 regime (third column in Fig. 2). At all values of
regime (third column in Fig. 2). At all values of 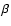 one mode is aligned with the magnetic axis,
one mode is aligned with the magnetic axis,
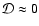 .
We may suppose that with the
Bagnulo et al. (1999) value of
.
We may suppose that with the
Bagnulo et al. (1999) value of 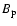 we will be in the same regime.
One sees that even at the longest rotational period the value of
we will be in the same regime.
One sees that even at the longest rotational period the value of 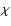 is below 0.1 that we have adopted in
Fig. 2. The centrifugal distortion is thus always the dominant rotational effect in determining
the orientation of the mode plane,
is below 0.1 that we have adopted in
Fig. 2. The centrifugal distortion is thus always the dominant rotational effect in determining
the orientation of the mode plane, 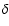 .
.
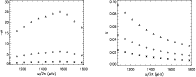 |
Figure 5:
The values of the parameter 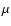 ,
see Eq. (30), and ,
see Eq. (30), and 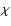 ,
see Eq. (29), are plotted
against mode frequencies for three values of rotational periods, ,
see Eq. (29), are plotted
against mode frequencies for three values of rotational periods,
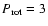 d (*), 6 d ( d (*), 6 d (
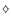 ), 12 d ( ), 12 d (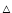 ). The value of ). The value of
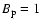 kG is assumed. The parameters of the adopted Main Sequence star model of 2 kG is assumed. The parameters of the adopted Main Sequence star model of 2 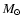 are given in the text.
are given in the text. |
| Open with DEXTER |
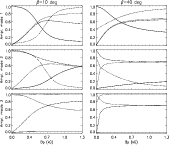 |
Figure 6:
Plots of the amplitudes A0 (full line) A1 (dashed
line) and A-1 (dot-dashed line) of the
triplet as functions of the magnetic field strength 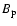 and for two values of the obliquity angle
and for two values of the obliquity angle 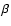 .
Each row corresponds to one of the three dipole mode solutions of Eq. (7). The amplitudes are normalized by
(A02+A12+A-12)1/2. The dotted line corresponds to the quantity .
Each row corresponds to one of the three dipole mode solutions of Eq. (7). The amplitudes are normalized by
(A02+A12+A-12)1/2. The dotted line corresponds to the quantity 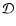 that measures the mode inclination with the magnetic field (
that measures the mode inclination with the magnetic field (
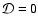 means alignment). The aspect angle is i=80 deg.
means alignment). The aspect angle is i=80 deg. |
| Open with DEXTER |
The two angles that are related to the side peak inequality are 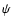 and
and 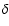 .
When looking at
Figs. 2 and 3 we have to keep in mind that we have used here the value of
.
When looking at
Figs. 2 and 3 we have to keep in mind that we have used here the value of 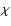 which is at least one order of magnitude larger than the values seen in Fig. 5, which
are realistic. Qualitatively the pattern remains the same, however the values of
which is at least one order of magnitude larger than the values seen in Fig. 5, which
are realistic. Qualitatively the pattern remains the same, however the values of 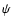 stay close to 0 or
stay close to 0 or
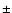
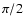 through much wider range of
through much wider range of 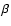 .
Such values of
.
Such values of 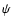 imply linear polarizations.
In Fig. 6 we plot the amplitudes of the triplet (
A0,A1,A-1) as functions of the magnetic field. It is clear that the structure of the triplet is strongly affected by the magnetic field's configuration (
imply linear polarizations.
In Fig. 6 we plot the amplitudes of the triplet (
A0,A1,A-1) as functions of the magnetic field. It is clear that the structure of the triplet is strongly affected by the magnetic field's configuration (
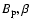 ).
In the weak field regime, the triplet reduces to a single peak, since in rotation system each eigenmode is
represented by a single spherical harmonics. In the strong field regime, the tendency is to have almost equal
side peaks,
).
In the weak field regime, the triplet reduces to a single peak, since in rotation system each eigenmode is
represented by a single spherical harmonics. In the strong field regime, the tendency is to have almost equal
side peaks,
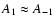 ,
for the mode nearly aligned with the magnetic field (
,
for the mode nearly aligned with the magnetic field (
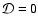 ).
For the mode verifying
).
For the mode verifying
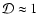 ,
the inequality of the side peaks increases with the magnetic field
strength,
,
the inequality of the side peaks increases with the magnetic field
strength, 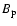 ,
since as we have already emphasized in Sect. 4.1, the ellipticity of the mode increases.
,
since as we have already emphasized in Sect. 4.1, the ellipticity of the mode increases.
This inequality of side peaks increases when 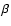 decreases since in that case the Coriolis effects are
stronger.
For HR 3831, the measured values of the
decreases since in that case the Coriolis effects are
stronger.
For HR 3831, the measured values of the 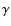 's are
's are
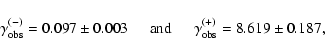 |
(42) |
(Kurtz et al. 1997). We made an attempt to reproduce the observed values allowing wide ranges of 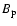 ,
,
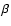 and i values. The value of
and i values. The value of 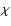 is 0.012. Following the standard assumption, we first considered modes with
is 0.012. Following the standard assumption, we first considered modes with
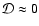 ,
i.e. nearly aligned with the magnetic field. None of the combination of the three parameters brought us even close to the observational data. We have succeeded only for a mode which is well inclined to the magnetic axis. In view of the geometrical picture, this dipole mode moves the sphere along a very elongated ellipse (
,
i.e. nearly aligned with the magnetic field. None of the combination of the three parameters brought us even close to the observational data. We have succeeded only for a mode which is well inclined to the magnetic axis. In view of the geometrical picture, this dipole mode moves the sphere along a very elongated ellipse (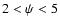 deg) in a plane which is very inclined from the magnetic axis (
deg) in a plane which is very inclined from the magnetic axis (
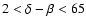 deg).
The range of the parameters leading to
deg).
The range of the parameters leading to 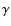 's consistent with observations
are
's consistent with observations
are
![$B_{\rm p} \in [1{-}2]$](/articles/aa/full/2002/31/aa1896/img195.gif) kG,
kG,
![$\beta \in [4{-}19 ]$](/articles/aa/full/2002/31/aa1896/img196.gif) deg and
deg and
![$i \in [75{-}87]$](/articles/aa/full/2002/31/aa1896/img197.gif) deg.
These large ranges of parameters are reduced if we fix one of these, e.g. the inclination angle i. If we
consider that i=84 deg, we get more precise values:
deg.
These large ranges of parameters are reduced if we fix one of these, e.g. the inclination angle i. If we
consider that i=84 deg, we get more precise values:
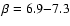 deg,
deg,
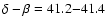 deg,
deg,
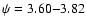 deg and
deg and
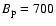 G. We cannot determine them more precisely
because of the error bars in the observations of the
G. We cannot determine them more precisely
because of the error bars in the observations of the 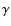 's. They also depend on the stellar model that we consider which is subject to uncertainties.
This inclination of the mode axis is very
different from the common interpretation of the oscillations in roAp stars in terms of a mode axis aligned, or nearly aligned, with the
magnetic axis. The role of centrifugal force in producing this mode geometry is essential. Only
with this force, we have modes which are nearly linearly polarized
along an inclined
axis in the plane formed by the magnetic and rotation axes.
There are two observational constraints
generally accepted to discuss the geometry of the mode in roAp stars. The first one is the phase jump by
's. They also depend on the stellar model that we consider which is subject to uncertainties.
This inclination of the mode axis is very
different from the common interpretation of the oscillations in roAp stars in terms of a mode axis aligned, or nearly aligned, with the
magnetic axis. The role of centrifugal force in producing this mode geometry is essential. Only
with this force, we have modes which are nearly linearly polarized
along an inclined
axis in the plane formed by the magnetic and rotation axes.
There are two observational constraints
generally accepted to discuss the geometry of the mode in roAp stars. The first one is the phase jump by
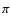 radians of the oscillation at
the amplitude minimum. This is clearly seen in HR 3831 (e.g. Kurtz et al. 1997).
This indicates that the mode is a dipole, or very close to a dipole, say with two
hemispheres shifted by
radians of the oscillation at
the amplitude minimum. This is clearly seen in HR 3831 (e.g. Kurtz et al. 1997).
This indicates that the mode is a dipole, or very close to a dipole, say with two
hemispheres shifted by 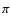 radians, one in contraction and one in expansion. For any inclination
of the mode axis, except when the mode is aligned with the
rotation axis (
radians, one in contraction and one in expansion. For any inclination
of the mode axis, except when the mode is aligned with the
rotation axis (
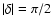 ), a phase shift occurs as the star
rotates since we see alternatively the two hemispheres.
The second observational fact is the "apparent'' coincidence between the times of
magnetic and pulsation maxima, e.g. Kurtz et al. (1992) for HR 3831.
In fact, for a near coincidence of the envelope of the
luminosity-variation curve and magnetic field maxima, it suffices that
the pulsation axis stays close to the plane that is formed by the magnetic axis and the
rotation axis. This condition is fulfilled with our small value of
), a phase shift occurs as the star
rotates since we see alternatively the two hemispheres.
The second observational fact is the "apparent'' coincidence between the times of
magnetic and pulsation maxima, e.g. Kurtz et al. (1992) for HR 3831.
In fact, for a near coincidence of the envelope of the
luminosity-variation curve and magnetic field maxima, it suffices that
the pulsation axis stays close to the plane that is formed by the magnetic axis and the
rotation axis. This condition is fulfilled with our small value of 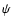 .
In short, the inclined dipole mode that we found is consistent with these observational constraints.
.
In short, the inclined dipole mode that we found is consistent with these observational constraints.
The aim behind our project was to improve the oblique pulsator model and the hope was that this would solve problems
posed by the pulsation data of the roAp star HR 3831.
We have shown that the hitherto ignored effect of centrifugal force in modelling pulsations in roAp stars is quite
important. In fact, the contribution of the Coriolis force to the total rotational frequency shift is two orders
of magnitude less than that of the centrifugal force. Another improvement is the treatment of the magnetic field
effects by a non-perturbative approach. However, the adopted treatment is still approximate and needs further
improvements.
The observables of interest have been the relative amplitudes of the 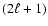 components of the multiplet in observer's system. We showed that the inequality of side peak amplitudes is determined by the Coriolis force. Only this force can make a difference between prograde and retrograde components of the mode, which is essential for the inequality of amplitudes. Even if the centrifugal force is not responsible for that inequality, at the quantitative level it is very significant.
In greater detail we have discussed the case of
components of the multiplet in observer's system. We showed that the inequality of side peak amplitudes is determined by the Coriolis force. Only this force can make a difference between prograde and retrograde components of the mode, which is essential for the inequality of amplitudes. Even if the centrifugal force is not responsible for that inequality, at the quantitative level it is very significant.
In greater detail we have discussed the case of 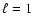 modes - the most important ones for modelling pulsations in roAp stars. We have developed a simple geometrical picture for these modes in the presence of rotation and a magnetic field. We have shown that during the pulsation cycle these dipole modes displace the star in general along an ellipse whose orientation in the stellar reference system is determined mostly by the balance between the centrifugal distortion and the magnetic field effects. We also showed that the shape of this ellipse is determined by the Coriolis force. The amplitude ratios in the observer's system are given in terms of the geometrical properties of this ellipse, i.e. orientation and eccentricity.
modes - the most important ones for modelling pulsations in roAp stars. We have developed a simple geometrical picture for these modes in the presence of rotation and a magnetic field. We have shown that during the pulsation cycle these dipole modes displace the star in general along an ellipse whose orientation in the stellar reference system is determined mostly by the balance between the centrifugal distortion and the magnetic field effects. We also showed that the shape of this ellipse is determined by the Coriolis force. The amplitude ratios in the observer's system are given in terms of the geometrical properties of this ellipse, i.e. orientation and eccentricity.
We did not succeed in solving problems of HR 3831 within the
framework of the standard version the
oblique pulsator model in which the mode is nearly aligned with the magnetic field. Indeed, we found that the
observed mode in HR 3831 is significantly inclined from the magnetic axis; this then is in contradiction with the common idea of aligned magnetic and pulsation axes. Perhaps our failure is due to inadequacies of our treatment
of the magnetic field. Still, we would like to point out that we succeeded in reproducing the observed amplitude
ratios with this mode inclined to the magnetic field. The maxima of pulsation amplitude for this mode occur close to the plane determined by
the rotation and magnetic axes. Such a mode geometry is possible only if effects
of centrifugal force are taken into account.
The Coriolis force is much weaker and hardly influences the inclination. However, it is responsible for small
departure of the maxima from that plane and for the observed inequality of the side-peaks. Such a possibility of a
dipole mode inclined with respect to the magnetic axis deserves some consideration in view of the fact that the
problem of mode selection in roAp stars is far from being understood. Balmforth et al. (2001) explained
preferential excitation of the mode aligned with the magnetic field by invoking an inhibiting effect of the
magnetic field on convection and an inhibiting effect of convection on oscillations. Both effects are very
difficult to study and this explanation must be regarded only as a possibility.
Acknowledgements
Most of the results presented in this paper were obtained during
the visits of L.B. in the Copernicus Center
in Warsaw and W.A.D. in the Observatoire de la Côte d'Azur within the framework of the CNRS/PAN program
Jumelage Astrophysique. This research was partially supported by the KBN grant No. 5P03D 012 20. L.B. thanks the "Société
de Secours des Amis des Sciences'' for their financial support.
We deeply acknowledge Don Kurtz for a careful reading of the
manuscript.
L.B. thanks Janine Provost and Gabrielle Berthomieu for their
comments during the preparation of the manuscript.
For our application, we use the standard expression for eigenvectors in a non-rotating and non-magnetic star.
These are defined by
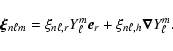 |
(A.1) |
The radial eigenfunctions,
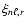 and
and
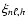 ,
which in general must be determined only
numerically, are m-independent (e.g. Unno et al. 1989).
The Ledoux constant is given by
,
which in general must be determined only
numerically, are m-independent (e.g. Unno et al. 1989).
The Ledoux constant is given by
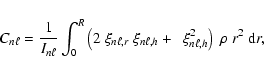 |
(A.2) |
where
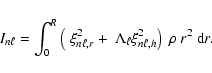 |
(A.3) |
At 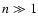 we have
we have
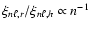 .
However, we have
.
However, we have
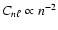 because the contribution from the leading term in
because the contribution from the leading term in
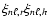 vanishes upon integration.
vanishes upon integration.
The distortion coefficient has a more complex form but for high radial order
p-modes, a good approximation is (Dziembowski & Goode 1992)
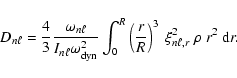 |
(A.4) |
With
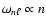 we roughly have
we roughly have
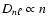 .
.
-
Bagnulo, S., Landolfi, M., & Landi Degl'Innocenti, M. 1999, A&A, 343, 865
In the text
NASA ADS
-
Balmforth, N. J., Cunha, M. S., Dolez, N., Gough, D. O., & Vauclair, S. 2001, MNRAS, 323, 362
In the text
NASA ADS
-
Bigot, L., Provost, J., Berthomieu, G., Dziembowski, W. A., & Goode, P. R. 1999,
A&A, 356, 218
NASA ADS
-
Cunha, M. S., & Gough, D. 2000, MNRAS, 319, 1020
In the text
NASA ADS
-
Dicke, R. H. 1982, Nature, 300, 693
In the text
NASA ADS
-
Dziembowski, W. A., & Goode, P. R. 1985, ApJL, 296, L27
In the text
NASA ADS
-
Dziembowski, W. A., & Goode, P. R. 1992, ApJ, 394, 670
In the text
NASA ADS
-
Dziembowski, W. A., & Goode, P. R. 1996, ApJ, 458, 338
In the text
NASA ADS
-
Edmonds, A. R. 1960, Angular Momentum in Quantum Mechanics, second
edition (Princeton Univ. Press)
In the text
-
Gough, D. O., & Thompson, M. J. 1990, MNRAS, 242, 25
In the text
NASA ADS
-
Kurtz, D. W. 1978, Inf. Bull. Var. Stars, No. 1436
In the text
-
Kurtz, D. W. 1982, MNRAS, 200, 807
In the text
NASA ADS
-
Kurtz, D. W., Kanaan, A., Martinez, P., & Tripe, P. 1992, MNRAS,
255, 289
In the text
NASA ADS
-
Kurtz, D. W., van Wyk, F., Roberts, G., et al. 1997, MNRAS, 287, 69
In the text
NASA ADS
-
Kurtz, D. W., & Shibahashi, H. 1986, MNRAS, 223, 557
In the text
NASA ADS
-
Ledoux, P. 1951, ApJ, 114, 373
In the text
NASA ADS
-
Shibahashi, H., & Takata, M. 1993, PASJ, 45, 617
In the text
NASA ADS
-
Takata, M., & Shibahashi, H. 1995, PASJ, 47, 219
In the text
NASA ADS
-
Unno, W., Osaki, Y., Ando, H., & Shibahashi, H. 1989,
Non-radial oscillations of stars, second edition
(University of Tokyo Press)
In the text
Copyright ESO 2002