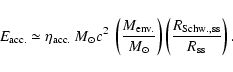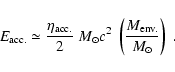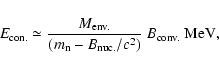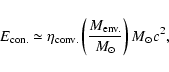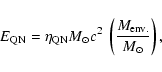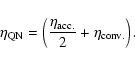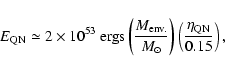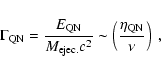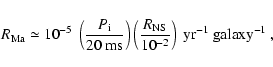A&A 390, L39-L42 (2002)
DOI: 10.1051/0004-6361:20020982
Quark-Nova
R. Ouyed1 -
J. Dey2 -
M. Dey 3
1 - Nordic Institute for Theoretical Physics, Blegdamsvej 17,
DK-2100 Copenhagen, Denmark
2 -
Department of Physics, Maulana Azad
College, Calcutta 700 013, India
3 -
Department of Physics, Presidency
College, Calcutta 700 073, India
Received 14 May 2002 / Accepted 1 July 2002
Abstract
We explore the scenario where
the core
of a neutron star (having experienced
a transition to an up and down quark phase)
shrinks into the equilibrated quark object after reaching
strange quark matter saturation density (where
a composition of up, down and strange quarks is the favored state of matter).
The overlaying (envelope) material free-falls following the core
contraction releasing upto
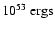 in energy as radiation,
partly as a result of the conversion of envelope material to quarks. This
phenomena, we named Quark-Nova, leads to a wide
variety of ejectae ranging form the Newtonian, "dirty"
to the ultra-relativistic fireball.
The mass range of the corresponding compact remnant
(the quark star) ranges from less than
in energy as radiation,
partly as a result of the conversion of envelope material to quarks. This
phenomena, we named Quark-Nova, leads to a wide
variety of ejectae ranging form the Newtonian, "dirty"
to the ultra-relativistic fireball.
The mass range of the corresponding compact remnant
(the quark star) ranges from less than
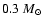 up to a solar mass.
We discuss the connection between Quark-Novae and Gamma ray bursts and
suggest the recently studied GRB011211 event as a plausible Quark-Nova
candidate.
up to a solar mass.
We discuss the connection between Quark-Novae and Gamma ray bursts and
suggest the recently studied GRB011211 event as a plausible Quark-Nova
candidate.
Key words: dense matter - gamma ray: bursts - stars: interior
Recent and fresh observational
data collected by the new generation of X-ray and  -ray
satellites suggest that the compact
objects associated with the X-ray pulsars, the X-ray bursters,
particularly the SAX J1808.4-3658 (Li et al. 1999)
are good quark stars candidates.
If quark stars do exist in nature then how do they form?
They have been speculated to form directly during
or shortly after some supernova (SN) explosion
when the central density of the proto-neutron star
is high enough to induce phase conversion to quark matter
(e.g., Dai et al. 1995; Xu et al. 2000).
Another plausible scenario involves converting neutron stars into
quark stars (Olinto 1987; Cheng & Dai 1996; Bombaci & Datta 2000).
Here we explore the scenario where the quark matter
core contracts and shrinks to the corresponding
stable compact/quark object.
While this has already been considered in the literature
(e.g., Rosenhauer et al. 1992; Ma & Xie 1996),
in our model the core shrinks as to physically separate from the overlaying
material (we refer to as the envelope).
This approach, also leading to quark star formation, offers a new and richer
dynamics and allows us to develop the concept of Quark-Nova (QN).
-ray
satellites suggest that the compact
objects associated with the X-ray pulsars, the X-ray bursters,
particularly the SAX J1808.4-3658 (Li et al. 1999)
are good quark stars candidates.
If quark stars do exist in nature then how do they form?
They have been speculated to form directly during
or shortly after some supernova (SN) explosion
when the central density of the proto-neutron star
is high enough to induce phase conversion to quark matter
(e.g., Dai et al. 1995; Xu et al. 2000).
Another plausible scenario involves converting neutron stars into
quark stars (Olinto 1987; Cheng & Dai 1996; Bombaci & Datta 2000).
Here we explore the scenario where the quark matter
core contracts and shrinks to the corresponding
stable compact/quark object.
While this has already been considered in the literature
(e.g., Rosenhauer et al. 1992; Ma & Xie 1996),
in our model the core shrinks as to physically separate from the overlaying
material (we refer to as the envelope).
This approach, also leading to quark star formation, offers a new and richer
dynamics and allows us to develop the concept of Quark-Nova (QN).
Strange matter, or (u, d, s), mixture (a composition of up,
down and strange quarks, hereafter SQM)
is traditionally modeled with
an equation of state (EOS) based on the MIT-bag model
(Farhi & Jaffe 1984). Here, for
illustration purposes, we choose to use the EOS as suggested in
Dey et al. (1998) with the binding energy
versus density of such a system shown in Fig. 1. One finds that from
about 3
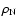 to 7
to 7
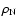 (
(
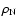 is the
nuclear matter saturation density) the (u, d, s) mixture has more binding
energy than 56Fe saturating around
is the
nuclear matter saturation density) the (u, d, s) mixture has more binding
energy than 56Fe saturating around
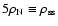 with an energy about
with an energy about
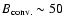 MeV per baryon less than
56Fe and is therefore very stable.
MeV per baryon less than
56Fe and is therefore very stable.
The possible existence of quark stars
(specifically of strange star; SSs), is a direct consequence of the
above described conjecture that SQM may be the absolute ground
state of strong interacting matter rather than 56Fe
(Bodmer 1971; Witten 1984; Alcock et al. 1986).
Figure 2 shows the SS mass-radius plane resulting from the EOS described in
Dey et al. (1998). SSs can acquire masses up to
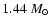 ,
with radii up to 7.06 km (for non-rotating stars).
However there is no lower limit on their
size (mass) since they would be bound by the
strong interaction even in the absence of gravity.
Among their features
(Alcock et al. 1986; Glendenning 1997) that are relevant to our present model:
,
with radii up to 7.06 km (for non-rotating stars).
However there is no lower limit on their
size (mass) since they would be bound by the
strong interaction even in the absence of gravity.
Among their features
(Alcock et al. 1986; Glendenning 1997) that are relevant to our present model:
i) The density at the surface changes abruptly from zero to
 .
The abrupt change (the thickness of the quark surface) occurs within
about 1 fm, which is a typical strong interaction length scale.
.
The abrupt change (the thickness of the quark surface) occurs within
about 1 fm, which is a typical strong interaction length scale.
ii) The electrons being bound to the quark matter by the electro-magnetic
interaction and not by the strong
force, are able to move freely across the quark surface
extending up to  103 fm above the surface of the star.
Associated with this electron layer is a
strong electric field (
103 fm above the surface of the star.
Associated with this electron layer is a
strong electric field (
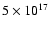 V/cm)
which would prevent ionized matter from coming into
direct contact with the surface of the star.
Note that free neutrons (or neutral matter
in general) can easily penetrate the
Coulomb barrier and gravitate to the surface of
the star; they are readily absorbed and converted to quark matter.
V/cm)
which would prevent ionized matter from coming into
direct contact with the surface of the star.
Note that free neutrons (or neutral matter
in general) can easily penetrate the
Coulomb barrier and gravitate to the surface of
the star; they are readily absorbed and converted to quark matter.
From the calculations by Gentile et al. (1993), the phase transition
to a state with the up and down quarks would take place in the inner core
(with mass
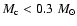 and radius
and radius
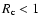 km)
where matter is homogeneous (
km)
where matter is homogeneous (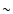
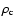 ); it is this portion
of the star which we discuss next.
); it is this portion
of the star which we discuss next.
Take a neutron star (hereafter NS, of mass
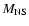 )
which
experienced an increase in their central density
above deconfinement values
(
)
which
experienced an increase in their central density
above deconfinement values
(
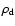 ;
that is
;
that is
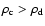 )
- following a spin-down
history or as a direct result of a SN
explosion (see Ma 2002 for a recent discussion).
Conversion of (u, d)
matter to (u, d, s) takes place via weak interactions where
non-leptonic (for example,
)
- following a spin-down
history or as a direct result of a SN
explosion (see Ma 2002 for a recent discussion).
Conversion of (u, d)
matter to (u, d, s) takes place via weak interactions where
non-leptonic (for example,
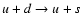 )
process is of greater
rate (Anand et al. 1997; Olinto 1987; Heiselberg et al. 1991).
If the density of the core does not exceed
)
process is of greater
rate (Anand et al. 1997; Olinto 1987; Heiselberg et al. 1991).
If the density of the core does not exceed
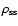 then it will never
undergo transition into the lower energy branch of the matter.
The NS remains a contaminated stable neutron star namely, a hybrid star
with a core density lying between
then it will never
undergo transition into the lower energy branch of the matter.
The NS remains a contaminated stable neutron star namely, a hybrid star
with a core density lying between
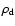 and
and
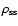 (e.g.
Chap. 8 in Glendenning 1997). Only when
(e.g.
Chap. 8 in Glendenning 1997). Only when
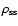 is
reached can a QN occur.
We mention that while in the case of a proto-NS the
trapped neutrinos will shift the possible onset of the phase transition
to SQM to higher densities, with respect to the case of a cold and
neutrino-free NS, the basic idea presented below remains the same.
is
reached can a QN occur.
We mention that while in the case of a proto-NS the
trapped neutrinos will shift the possible onset of the phase transition
to SQM to higher densities, with respect to the case of a cold and
neutrino-free NS, the basic idea presented below remains the same.
The speed of propagation of the conversion/contamination front and its
dynamics are limited by the low weak rate of
at which the quarks diffuse. As such, the front propagation might
be considered slow compared to the conversion
(the conversion into SQM occurs within a very short period
of time 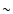 10-7 s; Dai et al. 1995) leading to the
interesting situation where the core density exceeds
10-7 s; Dai et al. 1995) leading to the
interesting situation where the core density exceeds
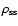 much before the rest (upper layers) of the star. A
scenario where the core would shrink to the corresponding stable
bare SQM object.
much before the rest (upper layers) of the star. A
scenario where the core would shrink to the corresponding stable
bare SQM object.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{Ee141_f1.eps}\end{figure}](/articles/aa/full/2002/30/aaee141/Timg19.gif) |
Figure 1:
Energy per baryon for SQM
in terms of the density as modeled
by Dey et al. (1998). The horizontal dotted line shows the
energy per baryon in 56Fe.
At high density (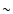
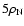 ), SQM
with its lower energy is the preferred state of matter. ), SQM
with its lower energy is the preferred state of matter. |
| Open with DEXTER |
The radius of the contracted core we can estimate
as
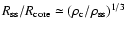 .
Given our fiducial values
.
Given our fiducial values
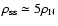 and
and
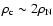 (for a canonical
(for a canonical
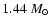 and standard 10 km radius generic
neutron star) the core of the NS would shrink by as much as 30%.
The maximum gravitational energy released is thus
and standard 10 km radius generic
neutron star) the core of the NS would shrink by as much as 30%.
The maximum gravitational energy released is thus
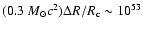 ergs; although
very large
ergs; although
very large![[*]](/icons/foot_motif.gif) would be mostly
carried out by neutrinos and only a very tiny part of it
would be released as radiation (Janka & Ruffert 1996).
would be mostly
carried out by neutrinos and only a very tiny part of it
would be released as radiation (Janka & Ruffert 1996).
Because of the density contrast between the core
and the overlaying material (
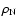 ), the envelope
free-fall time (
), the envelope
free-fall time (
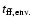 )
is longer than the core
contraction time (
)
is longer than the core
contraction time (
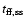 ).
Simple considerations imply
).
Simple considerations imply
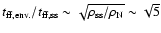 and the core physically separates from the overlaying material.
The infalling envelope material would consist
of the neutral part (
and the core physically separates from the overlaying material.
The infalling envelope material would consist
of the neutral part (
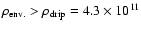 g/cc with
g/cc with
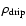 the neutron drip density)
the ionized plasma part
of the envelope material
(
the neutron drip density)
the ionized plasma part
of the envelope material
(
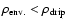 )
and the upper solid layers
(the crust).
The Coulomb barrier of the newly formed
quark star which is of the order of
)
and the upper solid layers
(the crust).
The Coulomb barrier of the newly formed
quark star which is of the order of
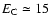 MeV
(Alcock et al. 1986) makes the QN collapse very intricate.
Indeed, the charged envelope material (including the crust)
will be subject to the tremendous Coulomb polarizing force.
One might argue that the kinetic
energy of a proton when accreted (
MeV
(Alcock et al. 1986) makes the QN collapse very intricate.
Indeed, the charged envelope material (including the crust)
will be subject to the tremendous Coulomb polarizing force.
One might argue that the kinetic
energy of a proton when accreted (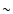
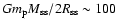 MeV where
MeV where
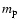 is the proton mass and G the gravitational constant) is large enough
to overcome such a barrier, however, it is likely that the kinetic
energy will be radiated away via heat (Frank et al. 1992) before
reaching the neutron drip sphere.
In this case the energy per accreted proton
is reduced below the Coulomb barrier as to halt
the infalling material leaving it suspended ("polarized up")
a few hundred Fermi above the surface of the SQM core.
As we show below, the energy released during conversion of the
neutrons is enough to expel any ionized material
that might have been left
suspended above the newly formed SS as to leave it naked/bare.
is the proton mass and G the gravitational constant) is large enough
to overcome such a barrier, however, it is likely that the kinetic
energy will be radiated away via heat (Frank et al. 1992) before
reaching the neutron drip sphere.
In this case the energy per accreted proton
is reduced below the Coulomb barrier as to halt
the infalling material leaving it suspended ("polarized up")
a few hundred Fermi above the surface of the SQM core.
As we show below, the energy released during conversion of the
neutrons is enough to expel any ionized material
that might have been left
suspended above the newly formed SS as to leave it naked/bare.
During envelope collapse we shall have tremendous energy release as radiation.
First, is the gravitational binding energy which
is released during the first stage of the collapse
(onto the neutron drip line), followed by the conversion energy.
The neutrons not subject to the Coulomb barrier
will continue their fall and be be converted to SQM;
the envelope is essentially squeezed out of its neutral component.
The accretion energy can be written as,
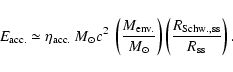 |
(1) |
In general,
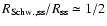 (Fig. 2) which leave
us with,
(Fig. 2) which leave
us with,
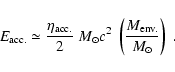 |
(2) |
Since the drip line radius does not refer to a "hard'' surface but only
to a region into which matter can fall before it is squeezed out of
its neutrons, it is far from clear on the value of
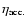 one needs
to adopt. It might seem appropriate as a first approximation to take
the accretion efficiency of SSs to lie close to that of
black holes (
one needs
to adopt. It might seem appropriate as a first approximation to take
the accretion efficiency of SSs to lie close to that of
black holes (
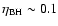 )
and of neutron stars (
)
and of neutron stars (
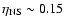 ); that is
); that is
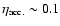 .
.
Each neutron converted to SQM is accompanied by a
photon of energy
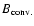 .
The conversion energy is therefore
.
The conversion energy is therefore
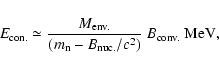 |
(3) |
where 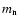 is
the baryon mass and
is
the baryon mass and
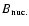 the nuclear binding energy. Equation above is best written as
the nuclear binding energy. Equation above is best written as
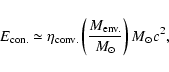 |
(4) |
where
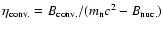 is the strangeness conversion efficiency
estimated to be
is the strangeness conversion efficiency
estimated to be
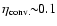 given
given
 MeV.
MeV.
The energy released in the QN is thus
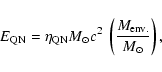 |
(5) |
where
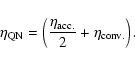 |
(6) |
Thus,
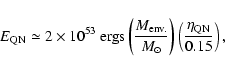 |
(7) |
which can be as high
as
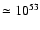 ergs.
ergs.
The fireball's radiation energy density a T4 (
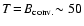 MeV) by far exceeds that of the gravitational energy density
in the envelope (
MeV) by far exceeds that of the gravitational energy density
in the envelope (
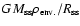 ).
Some envelope material and any matter that might ended suspended
above the neutron drip sphere is thus loaded into the fireball
making up the QN ejecta.
The corresponding Lorentz factor can be written as
).
Some envelope material and any matter that might ended suspended
above the neutron drip sphere is thus loaded into the fireball
making up the QN ejecta.
The corresponding Lorentz factor can be written as
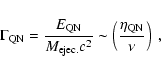 |
(8) |
where 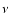 defines the amount of ejected material (
defines the amount of ejected material (
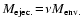 ).
The QN ejecta could lead
to a wide variety of ejectae (with different Lorentz factors) ranging from a
Newtonian, "dirty" to an ultra-relativistic fireball.
).
The QN ejecta could lead
to a wide variety of ejectae (with different Lorentz factors) ranging from a
Newtonian, "dirty" to an ultra-relativistic fireball.
The compact remnant (the quark star) mass is mainly dependent on
the amount of envelope material that falls
onto the core and acquires a mass in the
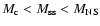 range.
An efficient envelope extraction would
lead to a light star with
range.
An efficient envelope extraction would
lead to a light star with
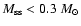 .
Note that any fallback material from the QN ejecta
would end up as a fossil disk material
.
Note that any fallback material from the QN ejecta
would end up as a fossil disk material![[*]](/icons/foot_motif.gif) which if channeled to the polar caps could later form a crust
(recall that the disk material is globally charged, Xu et al. 2000).
which if channeled to the polar caps could later form a crust
(recall that the disk material is globally charged, Xu et al. 2000).
The QN rate can be expressed as
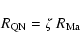 |
(9) |
where
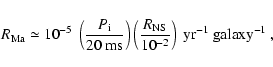 |
(10) |
is the rate at which NSs undergo a phase transition
to quark matter in the core (see Ma 2002).
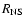 is the neutron star birth rate and
is the neutron star birth rate and 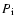 the initial spin of a neutron star.
The factor
the initial spin of a neutron star.
The factor 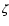 represents the fraction of
neutron stars that will undergo
the transition to the
represents the fraction of
neutron stars that will undergo
the transition to the
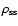 density following deconfinement
in the core. We expect
density following deconfinement
in the core. We expect 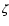 to be small making the QN a very rare
event. A value for
to be small making the QN a very rare
event. A value for 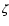 is suggested below.
is suggested below.
The QN as we have seen would lead
to the formation of hot quark stars (the collapse and conversion
process would heat up the star to high temperatures).
In Ouyed & Sannino (2002) and Ouyed (2002, for a recent review)
we explained how Gamma ray bursts (GRBs)
might result from the evaporation of such stars into photons.
Such a process as we showed is triggered when
quark matter phase transitions come into play at the surface
of the star.
As the quark star (with surface temperatures above
a few tens of MeV) cools it enters the
so-called 2 flavor color superconductivity (2SC) phase
where glueballs decay into photons (the fireball;
Ouyed & Sannino 2001) consuming most of the star in this process.
It is interesting to note from Eq. (10) that
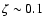 would imply QN rate of one per million year per galaxy
in agreement with the GRB rate derived from
BATSE
would imply QN rate of one per million year per galaxy
in agreement with the GRB rate derived from
BATSE![[*]](/icons/foot_motif.gif) measurements. This might be an indication that this
aspect of our model warrants further study.
measurements. This might be an indication that this
aspect of our model warrants further study.
If deconfinement (and later
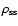 )
happens late following a
spin-down history then the collapse would occur much after the SN event
with no QN-SN interaction. On the other hand,
if deconfinement happens during or shortly after the SN event
(e.g. for very massive progenitors),
the SN is then expected to be followed by the QN.
The time delay between the two events (the time it takes the core
to reach the critical density
)
happens late following a
spin-down history then the collapse would occur much after the SN event
with no QN-SN interaction. On the other hand,
if deconfinement happens during or shortly after the SN event
(e.g. for very massive progenitors),
the SN is then expected to be followed by the QN.
The time delay between the two events (the time it takes the core
to reach the critical density
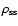 )
could
vary from seconds to days depending on the conditions
in the core of the proto-NS before contraction (such as the temperature and
density) and the details of the spread
of contamination/conversion front.
)
could
vary from seconds to days depending on the conditions
in the core of the proto-NS before contraction (such as the temperature and
density) and the details of the spread
of contamination/conversion front.
Eventually, the QN-ejecta catches up with the dense SN-ejecta which is
heated up producing emission.
QNe would thus be detected indirectly by their effect on the preceding
SNe ejectae. In the case where the QN-ejecta
consists of a hot fireball (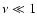 )
and the
QN occurs within a few days after the SN, the latter
is caught up when the expanding QN-ejecta is in its X-ray phase
(the fireball afterglow phase; Piran 1999).
The dense SN-ejecta when heated up would then produce X-ray emission.
Such a signature might have been observed in the
GRB011211 case (Reeves et al. 2002) where the authors
conclude that the measured X-ray emission is best explained as
an emission from SN material illuminated by a GRB which occurred a few days
following the SN explosion. Given its features,
we are tempted to suggest GRB011211 as a plausible QN candidate.
)
and the
QN occurs within a few days after the SN, the latter
is caught up when the expanding QN-ejecta is in its X-ray phase
(the fireball afterglow phase; Piran 1999).
The dense SN-ejecta when heated up would then produce X-ray emission.
Such a signature might have been observed in the
GRB011211 case (Reeves et al. 2002) where the authors
conclude that the measured X-ray emission is best explained as
an emission from SN material illuminated by a GRB which occurred a few days
following the SN explosion. Given its features,
we are tempted to suggest GRB011211 as a plausible QN candidate.
Acknowledgements
We are grateful to an anonymous referee for the remarks that helped improve this work.
- Alcock, C., Farhi, E., & Olinto, A. 1986,
ApJ, 310, 261
In the text
NASA ADS
- Anand, J. D., Goyal, A., Gupta, V. K., & Singh, S.
1997, ApJ, 481, 954
In the text
NASA ADS
- Bodmer, A. R. 1971, Phys. Rev. D, 4, 1601
In the text
NASA ADS
- Bombaci, I, & Datta, B. 2000, ApJ, 530, L69
In the text
NASA ADS
- Cheng, K. S., & Dai, Z. G. 1996, Phys.
Rev. Lett., 77, 1210
In the text
NASA ADS
- Dai, Z. G., Peng, Q. H., & Lu, T. 1995, ApJ, 440, 815
In the text
NASA ADS
- Dey, M., Bombaci, I., Dey, J., Ray, S., & Samanta, B. C.
1998, Phys. Lett. B, 438, 123
In the text
NASA ADS
- Farhi, E., & Jaffe, R. L. 1984, Phys. Rev. D, 30, 2379
In the text
NASA ADS
- Frank, J., King, A. R., & Raine, D. J. 1992,
Accretion power in
astrophysics (Cambridge Univ. Press)
In the text
- Gentile, N. A., Aufderheide, M. B., Mathews, G. J., et al. 1993, ApJ, 414, 701
In the text
NASA ADS
- Glendenning, N. K. 1997, Compact stars (Springer)
In the text
- Heiselberg, H., Baym, G., & Pethick, C. J. 1991, Nucl. Phys.
B (proc. Suppl.), 24B, 144
In the text
- Janka, H.-Th., & Ruffert, M. 1996, A&A, 307, L33
In the text
NASA ADS
- Li, X-D., Bombaci, I., Dey, M., Dey, J., & van den
Heuvel, E. P. J. 1999, Phys. Rev. Lett., 83, 3776
In the text
NASA ADS
- Ma, F., & Xie, B. 1996, ApJ, 462, L63
In the text
NASA ADS
- Ma, F. 2002 [astro-ph/0202040]
In the text
- Olinto, A. 1987, Phys. Lett. B, 192, 71
In the text
- Ouyed, R. 2002, in
Compact Stars in the QCD Phase Diagram, Proc.
[astro-ph/0201408]
In the text
- Ouyed, R., & Sannino, F. 2001, Phys. Lett. B,
511, 66
In the text
NASA ADS
- Ouyed, R., & Sannino, F. 2002, A&A, 387, 725
In the text
NASA ADS
- Piran, T. 1999, Phys. Rev., 314, 575
In the text
- Reeves, J. N., Watson, D., Osborne, J. P.,
et al. 2002, Nature, 416, 512
In the text
NASA ADS
- Rosenbauer, A., Staubo, E. F., Csernai, L. P.,
Øvergård, T., & Østgaard, E. 1992, Nucl. Phys. A, 540, 630
In the text
- Witten, E. 1984, Phys. Rev. D, 30, 272
In the text
NASA ADS
- Xu, R. X., Zhang, B., & Qiao, G. J. 2001, Astro. Part.
Phys., 15, 101
In the text
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{Ee141_f1.eps}\end{figure}](/articles/aa/full/2002/30/aaee141/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{Ee141_f2.eps}\end{figure}](/articles/aa/full/2002/30/aaee141/Timg33.gif)