A&A 390, L31-L34 (2002)
DOI: 10.1051/0004-6361:20020939

Nucleosynthesis in $\gamma-$ray bursts outflows

M. Lemoine

Institut d'Astrophysique de Paris, GReCO, CNRS, 98 bis boulevard Arago, 75014 Paris, France

Received 1 April 2002 / Accepted 19 June 2002

Abstract
It is shown that fusion of neutrons and protons to ⁴He nuclei occurs in $\gamma-$ray burst outflows in a process similar to big-bang nucleosynthesis in the early Universe. Only the surviving free neutrons can then decouple kinematically from the charged fluid so that the multi-GeV neutrino signal predicted from inelastic nuclear n-p collisions is significantly reduced. It is also argued that a sizeable fraction of ultra-high energy cosmic rays accelerated in $\gamma-$ray bursts should be ⁴He nuclei.

Key words: nucleosynthesis - gamma rays: bursts

1 Introduction

Multi-wavelength observations of $\gamma-$ray bursts in the past decade have given increasing evidence in favor of the "expanding fireball'' model (Paczynski 1986, 1990; Goodman 1986, Shemi & Piran 1990; Piran 2000; Mészáros 2002 for reviews), in which a photon - pair plasma loaded with a small admixture of baryons expands relativistically and converts the initial energy into baryon kinetic energy. In the internal/external shock scenario (Rees & Mészáros 1992; Rees & Mészáros 1994; Piran 2000; Mészáros 2002) this kinetic energy is dissipated in shocks, giving rise to the $\gamma-$ray burst phenomenon. The identity of the inner engine, the source of energy and the mechanism of collimation remain however unknown.

One should not expect that only protons are injected in the accelerating wind. As a matter of fact, all theoretical proposals for the progenitor involve compact objects, e.g. neutron stars/black hole mergers, or imploding massive stars, in which the baryon load must be neutron rich. This has triggered recent interest in the study of phenomenological consequences of neutron loading in $\gamma-$ray bursts (e.g. Derishev et al. 1999a,b; Bahcall & Mészáros 2000; Fuller et al. 2000; Mészáros & Rees 2000).

One possible consequence is nucleosynthesis of neutrons and protons to heavier nuclei. A recent study argued that nucleosynthesis should not take place as the dynamical timescale (taken to be $t_{\rm dyn}\approx10^{-5}$ s) is too short (Derishev et al. 1999). However this particular value rather constitutes a strict lower limit to the dynamical timescale since it implies a source size $\lesssim$3 km. This timescale is nonetheless bounded from above by the shortest variability timescale observed $\approx$10^-2 s (Piran 1999).

The purpose of this Letter is to show that nucleosynthesis to ⁴He can occur and is generically efficient, provided the dynamical timescale $\gtrsim$10^-4 s (Sect. 2). Most available neutrons and protons are then bound into ⁴He and only the surviving neutrons can decouple kinematically from the charged fluid component (Sect. 3). Thus this significantly weakens the 5-15 GeV neutrino signal expected from ${\rm n\!-\!p}$ inelastic collisions (Derishev et al. 1999; Bahcall & Mészáros 2000; Mészáros & Rees 2000). Furthermore, if $\gamma-$ray bursts accelerate particles to ultra-high energies $\gtrsim$10²⁰ eV (Levinson & Eichler 1993; Vietri 1995; Waxman 1995; Waxman 2001 for a review), the ultra-high energy cosmic ray spectrum should comprise a sizeable fraction of ⁴He nuclei (Sect. 3).

   
2 Nucleosynthesis

The fireball wind can be modeled as a pair plasma with luminosity $L= L_{50}\times10^{50}$ ergs/s injected into a solid angle $\Omega=4\pi\theta^2$, where $\theta^2\equiv\left(1-\cos\theta_{1/2}\right)$ represents the effect of beaming into two jets of half-opening angle $\theta_{1/2}$. Observations suggest a roughly uniform $L_{50}\sim1$among $\gamma-$ray bursts and a varying $\theta$ with mean value $\theta\sim0.1$ (Frail et al. 2001; Panaitescu & Kumar 2001; Piran et al. 2001); for a wind of typical duration $\sim$10 s, this yields a total equivalent isotropic output energy $\sim$10⁵³ ergs. The bulk Lorentz factor is written $\Gamma$, and its saturation value $\eta\equiv L/\dot{M}c^2$ is the ratio of total luminosity to baryon outflow (Mészáros et al. 1992). Injection takes place at radius $r_{\rm o}=r_{\rm o,7}\times10^7$ cm, with initial temperature $T_0\simeq 0.93~L_{50}^{1/4}\theta^{-1/2}_{0.1}r_{\rm o,7}^{-1/2}$ MeV $/k_{\rm B}$, using 11/2 for the number of degrees of freedom (photons + pairs). In the wind frame the ejecta is indeed similar to the early Universe before big-bang nucleosynthesis (Shemi & Piran 1990). However the physical conditions are very different: in a $\gamma-$ray burst ejecta, the comoving timescale $\sim$10^-3 s and the photon to baryon ratio $n_\gamma/n_{\rm b}\simeq 4.1\times 10^4 L_{50}^{-1/4}\theta^{1/2}_{0.1}r_{\rm o,7}^{1/2}\eta_{300}$, with $\eta_{300}\equiv\eta/300$, to be compared with $t_{\rm dyn}\sim 100$ s and $n_\gamma/n_{\rm b}\sim10^{10}$ for the early Universe. A large dynamical timescale favors nucleosynthesis but a high entropy acts against. Big-bang nucleosynthesis is also hampered by a small neutron to proton ratio due to neutron decay and late freeze-out of the weak interactions that interconvert protons and neutrons. Here one expects equal n, p mass fractions $X_{\rm n}\!\sim\! X_{\rm p}$ if baryons come from photodissociated nuclei, and neutron decay is insignificant on a millisecond timescale. If $T_0\!\gtrsim\! 6.5~{\rm MeV}~ (t_{\rm dyn}/10^{-3}~{\rm s})^{-1/5}$, the rate of weak interactions becomes larger than the fireball expansion rate and the neutron to proton ratio achieves equilibrium independently of the initial composition, $X_{\rm n}/X_{\rm p}\rightarrow\exp[(m_{\rm p}-m_{\rm n})c^2/k_{\rm B}T_0]\sim~1$. However this occurs for $\theta\lesssim 0.02r_{\rm o,6}^{-1}L_{50}^{1/2}(t_{\rm dyn}/10^{-3}~{\rm s})^{2/5}$, i.e. for the most highly beamed or compact $\gamma-$ray bursts, or those with the longest dynamical timescales (see also Fuller et al. 2000 for a discussion of the impact of a neutrino flux on the initial chemical composition of the outflow).

Adiabaticity during the acceleration phase implies that the bulk Lorentz factor $\Gamma$ and the temperature T evolve as $T\propto \Gamma^{-1}\propto r^{-1}$, with r the radial coordinate in the lab frame. If the flow can be approximated as quasi-one dimensional, the relativistic Bernoulli equation further implies $\Gamma\propto\theta r$ (Blandford & Rees 1974). In particular Mészáros et al. (1993) use $\Gamma\approx\theta r/r_{\rm o}$, which is obviously valid only in the limit $r\gg \theta^{-1}r_{\rm o}$. The exact numerical prefactor in this relation depends on the details of the injection phase at radius $r\!\sim\! r_{\rm o}$. In what follows, the early behavior will be phenomenologically modeled as $\Gamma=(1 + \theta r/r_{\rm o})$, with $T\propto \Gamma^{-1}$, which approaches the twin exhaust model of Blandford & Rees (1974), in which the flow is collimated by outside pressure forces and accelerates to relativistic velocity through a de Laval nozzle. A more exact solution requires solving the complex problem of injection and collimation in the early phase of the flow. Steps in this direction have been accomplished recently by Levinson & Eichler (2000) who studied the hydrodynamic collimation of a $\gamma-$ray burst outflow by a wind emanating from a torus. Their solution indeed reproduces a nozzle with nearly constant cross-section at small radii similarly to the Blandford & Rees (1974) model.

The dependence of the bulk Lorentz factor on r is important as it gives the dynamical expansion timescale $t_{\rm dyn}\equiv r/\Gamma c$. Interestingly in this context the scaling $\Gamma\propto\theta r$ suggests that highly beamed outflows have a longer dynamical timescale, hence should not show variations on short timescales due to erasure of inhomogeneities on scales smaller than the sound horizon $\lesssim$ $c t_{\rm dyn}/\sqrt{3}$. Nevertheless, in order to circumvent uncertainties related to the modeling of the early evolution of the bulk Lorentz factor, all results that follow will be shown as a function of dynamical timescale $t_{\rm dyn}$ instead of $\Gamma$. This is justified as $t_{\rm dyn}$ and the entropy are the two parameters that control the efficiency of nucleosynthesis. Moreover it was checked that a spherically symmetric wind with the simple expansion law $\Gamma=r/r_{\rm o}$ gives the same result than a jet with respect to nucleosynthesis provided the dynamical timescale and entropy are the same.

In the ultra-relativistic regime $\Gamma\gg1$ the temperature decreases exponentially fast with comoving time $\propto$ $\log(r/r_{\rm o})$. In the outflow thermal equilibrium is ensured between all species all along nucleosynthesis, and neutrons remain coupled to protons through nuclear scattering with velocity averaged cross-section $\langle\sigma_{\rm n-p} v\rangle\sim30$ mb c (Derishev et al. 1999). Decoupling occurs when $1/n_{\rm p}\langle\sigma_{\rm n-p}v\rangle > t_{\rm dyn}$, at temperature $T\approx 2~ L_{50}^{-1/12}\theta_{0.1}^{1/6}r_{\rm o,7}^{1/6}\eta_{300}^{1/3}(t_{\rm dyn}/10^{-3}~{\rm s})^{-1/3}~{\rm keV}/k_{\rm B}$, i.e., well after nucleosynthesis has taken place (see below).

	Figure 1: Mass fractions vs. radius for the case $r_{\rm o}=3\times 10^6$ cm, $\theta =0.1$ ( $\Omega /4\pi =10^{-2}$), dynamical timescale $t_{\rm dyn}=10^{-3}$ s, L=1050 ergs s-1 and initial mass composition $X_{\rm n}=0.54$, $X_{\rm p}=0.46$.
Open with DEXTER

In order to estimate the final abundances of nuclei synthesized, use was made of a big-bang nucleosynthesis numerical code whose time and entropy evolutions were modified accordingly. This code accounts successfully for synthesis of elements up to ⁷Be when compared to other big-bang nucleosynthesis calculations. An example of the outcome of nucleosynthesis is shown in Fig. 1 for a $\gamma-$ray burst with fiducial parameters $r_{\rm o,7}=0.3$, $\theta =0.1$, L₅₀=1, initial composition $X_{\rm n}=0.54$, $X_{\rm p}=0.46$ (photodissociated ⁵⁶Fe nuclei) and dynamical timescale $t_{\rm dyn}\simeq10^{-3}$ s. The final mass fractions of elements produced are $X_4\simeq0.84$ (for ⁴He), $X_{\rm n}\simeq0.12$, $X_{\rm p}\simeq0.04$, $X_{\rm D}\simeq0.005$ and other elements are produced only in traces. Although the numerical code used cannot deal with elements beyond mass 9, estimates of the triple $\alpha$ reaction and $\alpha(\alpha~ {\rm n},\gamma)^9$Be $(\alpha,{\rm n})^{12}$C necessary to bridge the mass gaps to ¹²C and beyond suggest that these three-body reactions do not have sufficient time to produce heavy elements in abundance (see however Sect. 3).

	Figure 2: Contours of the final 4He mass fraction as a function of photon to baryon number density $n_\gamma /n_{\rm b}$ and comoving dynamical timescale $\tau _{\rm dyn}$.
Open with DEXTER

The bulk of nucleosynthesis occurs at temperature $T_{\rm nuc}\sim0.1$-0.2 MeV $/k_{\rm B}$, corresponding to $\Gamma\sim 10\!-\!100$ depending on the parameters, and is over by $T_{\rm nuc}\sim0.06~$MeV $/k_{\rm B}$. Nucleosynthesis is favored by a large $t_{\rm dyn}$ and a small $n_\gamma /n_{\rm b}$, and it is thus more efficient as $\eta$ decreases (meaning higher baryon density), as $\theta$ decreases, or as $r_{\rm o}$ increases if $t_{\rm dyn}\propto r_{\rm o}$ (since a large expansion timescale is more critical to nucleosynthesis than a small entropy). Obviously the efficiency of nucleosynthesis is maximal for $X_{\rm n}/X_{\rm p}=1$ initially, and less efficient as this ratio departs from unity. A contour plot of the final mass fraction of ⁴He produced is shown in Fig. 2 as a function of $t_{\rm dyn}$ and $n_\gamma /n_{\rm b}$. In this figure, it was assumed that initially $X_{\rm n}/X_{\rm p}=1$. It shows that nucleosynthesis is efficient in most of parameter space: most available neutrons and protons are bound into ⁴He provided the dynamical timescale $t_{\rm dyn}\gtrsim10^{-4}$ s if $n_\gamma/n_{\rm b}\lesssim 10^4$, or $t_{\rm dyn}\gtrsim10^{-3}$ s if $n_\gamma/n_{\rm b}\lesssim 10^5$. One can understand analytically these results by comparing the expansion rate $t_{\rm dyn}^{-1}$ to the deuterium formation rate at temperature T ( $n_{\rm b}\propto T^{-3}$): $R_{{\rm p}({\rm n},\gamma){\rm d}}=\langle\sigma_{{\rm p}({\rm n},\gamma){\rm d... ...eta_{0.1}^{-1/2}L_{50}^{1/4}\eta_{300}^{-1} X_{\rm n}(1-X_{\rm n})~{\rm s}^{-1}$. Indeed deuterium production occurs if $t_{\rm dyn}\gtrsim10^{-4}$ s. The dependence on the entropy comes through the reverse photodisintegration rate which inhibits the production of deuterium hence of heavier elements.

One expects nucleosynthesis to be more efficient than above if, for instance, magnetic energy represents a significant fraction $x_{\rm B}$ of the total energy. The photon number density hence $n_\gamma /n_{\rm b}$are then smaller by $(1-x_{\rm B})^{3/4}$ while the initial temperature is only reduced by $(1-x_{\rm B})^{1/4}$. The present calculation also assumes a homogeneous steady wind, but inhomogeneities in the wind, e.g. shells or blobs, would increase the efficiency of nucleosynthesis, as $n_\gamma/n_{\rm b}\propto E^{-1/4}$ where E is the local energy content.

  
3 Discussion

The feedback of nuclear binding energy release on the fireball evolution has been neglected in the above calculations. This is justified since the ratio of entropy density released to total entropy density (assuming this latter is dominated by the photons) if all neutrons and protons are instantaneously converted to ⁴He at $T\!\approx\!0.1$ MeV $/k_{\rm B}$ reads ${\rm d}S/S \approx 20 (k_{\rm B}T/0.1~{\rm MeV})^{-1} (n_\gamma/n_{\rm b})^{-1}$, with ${\rm d}S=n_{\rm b}B_4/4k_{\rm B}T$ and B₄=28.3 MeV the ⁴He binding energy. Note that in some rather extreme parts of parameter space, the prerequisite conditions for successful r-process nucleosynthesis could be satisfied: initial electron fraction $Y_{\rm e}\equiv X_{\rm p}<0.5$, $t_{\rm dyn}\gtrsim10^{-3}$ s, $n_\gamma/n_{\rm b}\!\sim\!10^2$ and initial temperature $T_0\!\sim\! 1$ MeV $/k_{\rm B}$(e.g. Hoffman et al. 1997; Meyer & Brown 1997). This presumably requires a highly beamed ejecta $\theta < 0.1$ from a compact source $r_{\rm o}\lesssim 10^6~$cm, with a significant fraction of magnetic energy, and/or a low limiting Lorentz factor $\eta$. This latter condition can be fulfilled in the outer parts of a jet with inhomogeneous baryon load as proposed recently (Zhang & Mészáros 2002). Successful r-process nucleosynthesis might thus be able to operate in $\gamma-$ray bursts outflows, and further studies using dynamical r-process codes appear mandatory. Other connections between the site r-process site and $\gamma-$ray bursts have been proposed by Eichler et al. (1989), Levinson & Eichler (1993) and Cameron (2001).

An important consequence of successful nucleosynthesis to ⁴He is to keep neutrons tied to protons and prevent their kinematical decoupling when nuclear scattering becomes ineffective. As shown by Bahcall & Mészáros (2000) and Mészáros & Rees (2000), such decoupling occurs before the Lorentz factor has saturated to its limiting value $\eta$ provided $\eta\gtrsim 480 L_{50}^{1/4}\theta_{0.1}^{-1/2}r_{\rm o,7}^{-1/4}Y_{\rm e}^{1/4}$ and leads to relative velocities between neutrons and protons $\sim$c; in turn this leads to pion production in inelastic collisions and thus to a 5-15 GeV neutrino signal. Mészáros & Rees (2000) have further shown that transverse diffusion of neutrons in inhomogeneously baryon loaded fireballs can lead to an appreciable multi-GeV neutrino signal for lower values of $\eta$. However these studies assumed that nucleosynthesis did not occur. In fact, the inelastic collisions occur in these scenarii at large radii well after nucleosynthesis, hence only the surviving free neutrons will be able to decouple.

Consider first an homogeneous fireball. In the absence of nucleosynthesis, the neutrino signal is proportional to $X_{\rm p}X_{\rm n}\equiv Y_{\rm e}\left(1-Y_{\rm e}\right)$, and is thus maximal when $Y_{\rm e}\sim0.5$. The neutron-⁴He collision cross-section is higher than the n-p cross-section by the geometrical factor 4^2/3 but there are only X₄/4 ⁴He nuclei per baryon (X₄ denotes as before the mass fraction). The neutrino signal produced after nucleosynthesis ($X_4\neq0$) is then a factor r of that produced when X₄=0 (no nucleosynthesis) with:

$$r\simeq \frac{2\left(1-Y_{\rm e}\right)-X_4}{4Y_{\rm e}\left(1-Y_{\rm e}\right)}\left(2Y_{\rm e} - 0.685X_4\right);$$

it was assumed that the outcome of nucleosynthesis is only n, p and ⁴He. This reduction factor takes the following values: for $Y_{\rm e}\simeq0.5$, $r\simeq0.33$ for X₄=0.5, $r\simeq0.09$ for X₄=0.80. If $Y_{\rm e}>0.5$ and nucleosynthesis is maximally efficient, all neutrons are bound into ⁴He and obviously r=0. By combining the above relation with Fig. 2 it is possible to obtain estimates of r for various $\gamma-$ray bursts parameters. As an example, $\eta=500$ (so that kinematical decoupling of free neutrons occurs before saturation), L=10⁵⁰ ergs s^-1, $\theta =0.1$, $r_{\rm o}=0.3\times10^7$ cm and $t_{\rm dyn}=10^{-3}$ s gives $X_4\simeq0.70$ and the neutrino signal is reduced by a factor $\approx6.4$. Note that even a small reduction factor is significant as the neutrino signal predicted is of the order a few events per year for a km³ neutrino telescope and does not exceed a dozen events per year.

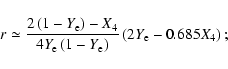
If the jet is inhomogenous, say made of an inner baryon poor jet surrounded by a baryon rich outer shell (Eichler & Levinson 1999; Mészáros & Rees 2001), the above discussion still applies if the outer baryonic wind originates from the central engine with a temperature $T\sim~{\cal O}~({\rm MeV})$ similar to that of the central jet. In effect nucleosynthesis is then very efficient in the outer shell since its Lorentz factor and entropy are both lower than in the jet. If the surrounding shell is "cold'', or if it is neutron rich and the inner jet proton rich (or vice-versa) one can circumvent the above argument. However in the case of a jet punching its way through a collapsar progenitor atmosphere Mészáros & Rees (2000) have shown that it leads to a very low neutrino signal.

Finally, if ultra-high energy cosmic rays are accelerated in $\gamma-$ray bursts (Levinson & Eichler 1993; Vietri 1995; Waxman 1995; Waxman 2001 and references), one expects in the present context a significant fraction of these particles to be ⁴He nuclei. However nuclei are subject to photodisintegration with cross-section $\sim$a few mb for photon energies $\gtrsim$20 MeV in the nucleus rest frame, and during acceleration in internal shocks and production of the $\gamma-$ray signal a fraction of them will be disrupted.

The calculation of the fraction of nuclei dissociated as a function of their energy and shock radius is in itself similar to that performed by Waxman & Bahcall (1997), Guetta et al. (2001) for the production of a 100 TeV neutrino signal from pion production of accelerated protons. At the highest energies $E_{{\rm He}}\gtrsim10^{15}$ eV (observer frame), one can thus write the photodisintegration rate $R\equiv A^{-1}{\rm d}A/{\rm d}t\simeq U_\gamma c \eta \langle\sigma_{\gamma{\rm He}}\rangle/ A\epsilon_{\rm b}$, where $U_\gamma\equiv L_\gamma / 4\pi\theta^2 r^2\eta^2c$ is the photon energy density, $\epsilon_{\rm b}\approx 1~$MeV is the observed break energy in the $\gamma-$ray spectrum, and $\langle\sigma_{\gamma{\rm He}}\rangle$ is the inverse energy weighted photodisintegration cross-section, $\langle\sigma_{\gamma{\rm He}}\rangle\simeq 2.8$ mb accounting for 1 and 2 nucleon loss with respective branching ratios 80%, 20%. The optical depth to photodisintegration thus reads $\tau\approx Rt_{\rm dyn}\approx L_{50}\theta_{0.1}^{-2}r_{14}^{-1}\eta_{300}^{-2}(\epsilon_{\rm b}/1~{\rm MeV})^{-1}$, with $r_{14}\equiv r/10^{14}~{\rm cm}$ the radius of emission.

Since features of temporal width $\delta t\equiv\delta t_{-2}~\times~ 10^{-2}$ s are emitted at radius $r_{14}\simeq0.6\delta t_{-2}\eta_{300}^2$, this optical depth is unity where features of width $\delta t\sim10^{-2}$ s are emitted. High energy nuclei accelerated in shocks at smaller radii are photodisintegrated, while those accelerated at larger radii are unharmed. One can also show that low energy nuclei are not photodisintegrated even at small radii. The overall ⁴He nuclei energy spectrum is thus subject to photodisintegration, acceleration and reacceleration in shocks and adiabatic losses. Acceleration at large radii is in any case crucial to overcome expansion losses (Waxman 2001). It thus seems reasonable to expect that a sizeable fraction of ⁴He nuclei would be present in the escaping ultra-high energy radiation and the measurement of the chemical composition might provide further information on the nuclear processes at work in the $\gamma-$ray burst. Detailed signatures of these ultra-high energy ⁴He nuclei will be presented elsewhere.

Note added in proof: While this paper was being refereed, a similar study by Pruet et al. (2002) appeared, with similar conclusions as to the efficiency of nucleosynthesis.

Acknowledgements

It is a pleasure to thank R. Mochkovitch, G. Pelletier and E. Waxman for useful comments and suggestions.

References

 
• Bahcall, J. N., & Mészáros, P. 2000, Phys. Rev. Lett., 85, 1362 In the text NASA ADS  
• Blandford, R., & Rees, M. J. 1974, MNRAS, 169, 395 In the text NASA ADS  
• Cameron, A. G. W. 2001, ApJ, 562, 456 In the text NASA ADS  
• Derishev, E. V., Kocharovsky, V. V., & Kocharovsky, Vl. V. 1999a, A&A, 345, L51 In the text NASA ADS  
• Derishev, E. V., Kocharovsky, V. V., & Kocharovsky, Vl. V. 1999b, ApJ, 521, 640 In the text NASA ADS  
• Eichler, D., & Levinson, A. 1999, ApJ, 521, L117. In the text NASA ADS  
• Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 In the text NASA ADS  
• Frail, D. A., et al. 2001, ApJ, 562, L55 In the text NASA ADS  
• Fuller, G. M., Pruet, J., & Abazajian, K. 2000, Phys. Rev. Lett., 85, 2673 In the text NASA ADS  
• Guetta, D., Spada, M., & Waxman, E. 2001, ApJ, 559, 101 In the text NASA ADS  
• Goodman, J. 1986 ApJ, 308, L47 In the text NASA ADS  
• Hoffmann, R. D., Woosley, S. E., & Qian, Y.-Z. 1997, ApJ, 482, 951 In the text NASA ADS  
• Levinson, A., & Eichler, D. 1993, ApJ 418, 386 In the text NASA ADS  
• Levinson, A., & Eichler, D. 2000, Phys. Rev. Lett., 85, 236 In the text NASA ADS  
• Mészáros, P., Laguna, P., & Rees, M. J. 1993, ApJ, 415, 181 In the text NASA ADS  
• Mészáros, P., & Rees, M. J. 2000, ApJ, 541, L5 In the text NASA ADS  
• Mészáros, P. 2002, ARA&A, in press, [astro-ph/0111170] In the text  
• Meyer, B. S., & Brown, J. S. 1997, ApJS, 112, 199 In the text NASA ADS  
• Paczynski, B. 1986, ApJ, 308, L43 In the text NASA ADS  
• Paczynski, B. 1990, ApJ, 363, 218 In the text NASA ADS  
• Panaitescu, A., & Kumar, P. 2001, ApJ, 560, L49 In the text NASA ADS  
• Piran, T. 2000, Phys. Rep., 333, 529 In the text NASA ADS  
• Piran, T., Kumar, P., Panaitescu, A., & Piro, L. 2001, ApJ, 560, L167 In the text NASA ADS  
• Pruet, J., Guiles, S., & Fuller, G. M. 2002, ApJ, submitted, [astro-ph/0205056] In the text  
• Rees, M. J., & Mészáros, P. 1992, MNRAS, 258, 41 In the text  
• Rees, M. J., & Mészáros, P. 1994, ApJ, 430, L93 In the text NASA ADS  
• Shemi, A., & Piran, T. 1990, ApJ, 365, L55 In the text NASA ADS  
• Vietri, M. 1995, ApJ, 453, 883 In the text NASA ADS  
• Waxman, E. 1995, Phys. Rev. Lett., 75, 386 In the text NASA ADS  
• Waxman, E. 2001, in Physics and Astrophysics of Ultra-High Energy Cosmic Rays, ed. M. Lemoine, & G. Sigl (Springer-Verlag, Lecture Notes in Physics), 122 In the text  
• Zhang, B., & Mészáros, P. 2002, ApJ, in press [astro-ph/0112118] In the text