| (6) |
To estimate pulsation masses, we made use of the PMR relations of Wood (1990) for the
fundamental mode and of those of Wood et al. (1983) for the first overtone. Calculated
for oxygen-rich LPVs, they were already applied by Groenewegen & de Jong (1994) to
LPVs in the LMC, either oxygen-rich or carbon-rich. For the fundamental, we thus adopted the
period
| (6) |
| (7) |
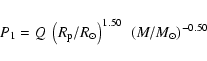 |
(8) |
| (9) |
| G | m | n |
|
|
|
|
|
g' |
|
Comments | |
| HC3 | F | 1 | 125 | 75 | 0.26: | -3.15 | 3945 | 61: | 13: | 0.3: | C3938=V CrA |
| HC4 | F | 1 | 110 | 93 | 0.47: | -3.65 | 3865 | 59: | 15: | 0.5: | C3319=TT CVn; CH |
| HC5 | F | 5 | 0.53 | -4.18 | 3400 | 13 | 5.6 | ||||
| O | 2 | 0.68 | -3.76 | 3460 | 26: | 10: | |||||
| CV1 | F | 6 | 0.46 | -3.60 | 3300 | 13 | 5.3 | ||||
| O | 8 | 0.59 | -3.76 | 3290 | 15 | 6.4 |
|
||||
| CV2 | F | 13 | 1.05 | -4.42 | 3050 | 7.5 | 5.0 | ||||
| O | 16 | 0.94 | -4.34 | 3020 | 7.6 | 4.8 | |||||
| CV3 | F | 10 | 1.52 | -4.58 | 2880 | 6.6 | 5.1 | ||||
| O | 12 | 1.62 | -4.73 | 2910 | 5.9 | 4.9 | |||||
| CV4 | F | 14 | 1.74 | -4.77 | 2770 | 6.5 | 5.4 | ||||
| O | 8 | 2.16 | -4.96 | 2780 | 4.7 | 4.6 |
|
||||
| CV5 | F | 13 | 1.68 | -4.40 | 2670 | 5.6 | 4.8 | ||||
| F | 10 | 3.15 | -4.91 | 2670 | 5.4 | 6.0 | without 3 underluminous stars | ||||
| F | 3 | 423: | 188: | 0.48 | -3.28 | 2645 | 7.3 | 3.7 | 0.5: | underlum.: RU Pup, T Lyn, RZ Peg | |
| O | 15 | 2.14 | -4.76 | 2660 | 4.0 | 4.1 | |||||
| O | 14 | 2.25 | -4.87 | 2660 | 3.6 | 3.9 | without 1 underluminous star | ||||
| O | 1 | 217: | 220: | 0.45 | -3.61 | 2675 | 4.2 | 2.5 | 0.5: | underlum.: AC Pup | |
| CV6 | F | 13 | 4.67 | -4.86 | 2460 | 4.3 | 5.6 | ||||
| O | 4 | 2.78 | -4.58 | 2465 | 3.7 | 4.3 | |||||
| O |
7 | 3.97 | -5.88 | 2250 | 0.84 | 1.8 | O |
||||
| CV7 | O |
7 |
|
8.24 | -5.72 | 1970 | 0.73 | 2.1 | 8.2: | O |
|
| SCV | F | 1 | 365: | 406: | 3.83: | -5.49 | 2880 | 5.7: | 6.4: | V346 Aur | |
| O |
3 | 227: | 533: | 5.04: | -5.83 | 2995 | 3.3: | 4.9: | 4.7: | O |
The available data is practically limited to the HC5, SCV and CV1-CV7 photometric groups, some
of them being poorly documented. The adopted period (either fundamental mode or first overtone)
is the mean of individual values in the sample. The mean radius was obtained from the values of
the
![]() -coefficient as described in Sects. 3.1 and 4 of Paper III. The results were
given in Table
-coefficient as described in Sects. 3.1 and 4 of Paper III. The results were
given in Table
![]() of Paper III. The mean pulsation mass increases along the
sequence of groups from
of Paper III. The mean pulsation mass increases along the
sequence of groups from ![]()
![]() at HC5-CV1 to
at HC5-CV1 to ![]()
![]() at CV6-CV7.
at CV6-CV7.
The mean pulsation periods are quoted for each mode,
identified as described in Sect. 2. The adopted mode is doubtful for a few percent of the data
that might prove to be misclassified later on, but the mean values should not be seriously
affected.
The mean values of photospheric radii are given for variables pulsating in either mode. They can
differ from values quoted in Table 3 of Paper III which includes all the carbon giants of our
initial sample, even if they are not LPVs (e.g. even for irregular variables). It was shown in
Table 4 of Paper III that, on average, the SR- and Mira-variables are slightly brighter than
the Lb-ones. We have also operated a detailed comparison, group per group, with the conclusion:
there is no significant difference in terms of
![]() between the irregular Lb-stars and
the whole sample. The difference noted in Table 4 of Paper III is actually an artifact of
the concentration of irregular variables in earlier (thus less luminous) photometric groups
(say HC5 to CV3) than SRs and Miras (see Fig. 8 of Paper II).
between the irregular Lb-stars and
the whole sample. The difference noted in Table 4 of Paper III is actually an artifact of
the concentration of irregular variables in earlier (thus less luminous) photometric groups
(say HC5 to CV3) than SRs and Miras (see Fig. 8 of Paper II).
Small mean pulsation masses are found in the groups HC5 and CV1. One is tempted to question the applicability of the PMR relations as written in Sect. 3.1. They were established for oxygen-rich variables, and the effect of opacities specific for carbon-rich atmospheres on such models remains to be investigated. We however note that
An interesting question comes from the underluminous carbon giants already found when studying
the period-luminosity diagrams of the present Galactic carbon stars (Sample 3 of Bergeat et al.
1998), and those of their analogues in the LMC. Those CV5-CV6 stars are found at
![]() that is about 1.4 mag below the locus of standard
CV5-stars (say
that is about 1.4 mag below the locus of standard
CV5-stars (say
![]() ). Samples without underluminous stars
have been also considered, resulting in increased estimates of mean masses. The mean mass
deduced for 4 underluminous CV5-stars, namely RU Pup, T Lyn, RZ Peg and AC Pup, amounts to
). Samples without underluminous stars
have been also considered, resulting in increased estimates of mean masses. The mean mass
deduced for 4 underluminous CV5-stars, namely RU Pup, T Lyn, RZ Peg and AC Pup, amounts to
![]() a value again compatible with a practically stripped
core. Such underluminous giants are also observed in the LMC (Bergeat et al. 1998).
Spurious results from HIPPARCOS may accidentally contribute but their existence seems
beyond doubt. The above mean mass we found suggests that they experienced strong mass loss,
evolving from standard CV-stars. We note that their mean masses, luminosities and radii are
similar to those of the CV1- or HC5-group, the main difference lying in mean effective
temperatures about 650 to 800 K higher in the latter groups. More speculatively, they could be
low-luminosity "interpulse'' objects or post-TP AGB stars evolving toward HC5-CV1 at nearly
constant luminosity. Such a possibility is suggested by theoretical tracks (e.g. Lattanzio
1987; Sackman et al. 1993). Many RCB variables and HdC stars with
similar low masses are considered as born-again objects (Sect. 7.2 of Paper III).
The results in Table
a value again compatible with a practically stripped
core. Such underluminous giants are also observed in the LMC (Bergeat et al. 1998).
Spurious results from HIPPARCOS may accidentally contribute but their existence seems
beyond doubt. The above mean mass we found suggests that they experienced strong mass loss,
evolving from standard CV-stars. We note that their mean masses, luminosities and radii are
similar to those of the CV1- or HC5-group, the main difference lying in mean effective
temperatures about 650 to 800 K higher in the latter groups. More speculatively, they could be
low-luminosity "interpulse'' objects or post-TP AGB stars evolving toward HC5-CV1 at nearly
constant luminosity. Such a possibility is suggested by theoretical tracks (e.g. Lattanzio
1987; Sackman et al. 1993). Many RCB variables and HdC stars with
similar low masses are considered as born-again objects (Sect. 7.2 of Paper III).
The results in Table
![]() can be summarized as follows;
(1) a marked increase of mean masses along the HC5-CV7 sequence, to be discussed later,
(2) the absence of large systematic differences between mean values deduced from both modes,
(3) the consistency of extreme mean values (0.5-
can be summarized as follows;
(1) a marked increase of mean masses along the HC5-CV7 sequence, to be discussed later,
(2) the absence of large systematic differences between mean values deduced from both modes,
(3) the consistency of extreme mean values (0.5-
![]() )
with prediction from
evolutionary tracks and mass loss operating,
(4) the mean stellar density steadily decreases along the sequence as expected,
and (5) the mean surface gravity is practically constant, close to 0.005 SI that is 0.5 CGS
)
with prediction from
evolutionary tracks and mass loss operating,
(4) the mean stellar density steadily decreases along the sequence as expected,
and (5) the mean surface gravity is practically constant, close to 0.005 SI that is 0.5 CGS
![]()
Copyright ESO 2002