A&A 390, 1049-1061 (2002)
DOI: 10.1051/0004-6361:20020741
J.-C. Bouret1 - M. Deleuil1,2 - T. Lanz3,4 - A. Roberge5 - A. Lecavelier des Etangs6 - A. Vidal-Madjar6
1 - Laboratoire d'Astrophysique de Marseille, Traverse du Siphon,
BP 8, 13376 Marseille Cedex 12, France
2 -
Université de Provence, Centre de Mathématiques et d'Informatique,
39 rue J. Curie, 13453 Marseille Cedex 13, France
3 -
Laboratory for Astronomy and Solar Physics, Code 681, NASA Goddard
Space Flight Center, Greenbelt MD 20771, USA
4 -
Department of Astronomy, University of Maryland, College Park,
MD 20742, USA
5 -
Department of Physics and Astronomy, Johns Hopkins University,
3400 N. Charles St., Baltimore MD 21218, USA
6 -
Institut d'Astrophysique de Paris, CNRS, 98bis Bd Arago, 75014
Paris, France
Received 5 March 2002 / Accepted 22 April 2002
Abstract
We investigate a chromospheric scenario to explain the
characteristics of the far-UV emission lines of ![]() Pictoris, revealed by FUSE
spectra of this famous circumstellar disk system.
The model assumes a thin region heated up to a few 105 K located close
to the stellar photosphere.
The resonance lines of C III at 977 Å and O VI at 1032-1037 Å,
seen in emission, are produced in this chromosphere-transition region
complex. Using complementary data in the mid and near UV (specifically, a
resonance doublet of C IV at 1548-1550 Å and Mg II h & k),
we show that the whole dataset is remarquably well reproduced
by the model.
In addition, we investigate the properties of the C III* multiplet at
1176 Å and conclude that this line likely forms in a weak warm wind,
originating from the prominent circumstellar disk of
Pictoris, revealed by FUSE
spectra of this famous circumstellar disk system.
The model assumes a thin region heated up to a few 105 K located close
to the stellar photosphere.
The resonance lines of C III at 977 Å and O VI at 1032-1037 Å,
seen in emission, are produced in this chromosphere-transition region
complex. Using complementary data in the mid and near UV (specifically, a
resonance doublet of C IV at 1548-1550 Å and Mg II h & k),
we show that the whole dataset is remarquably well reproduced
by the model.
In addition, we investigate the properties of the C III* multiplet at
1176 Å and conclude that this line likely forms in a weak warm wind,
originating from the prominent circumstellar disk of ![]() Pictoris.
Finally, radiative losses have been calculated and have provided
estimates of the
amount of non radiative energy dissipated in the external atmosphere of
Pictoris.
Finally, radiative losses have been calculated and have provided
estimates of the
amount of non radiative energy dissipated in the external atmosphere of ![]() Pictoris,
which is a measure of the star's activity level.
Such behavior for an A5 V star presents a challenge for both evolution
and activity models since the former predict that main-sequence A stars
should not be active, while the latter are unable to quantitatively account
for the characteristics of the chromospheric heating of
Pictoris,
which is a measure of the star's activity level.
Such behavior for an A5 V star presents a challenge for both evolution
and activity models since the former predict that main-sequence A stars
should not be active, while the latter are unable to quantitatively account
for the characteristics of the chromospheric heating of ![]() Pictoris.
Pictoris.
Key words: line: profiles - stars: atmospheres - stars: chromospheres - stars: activity - stars: winds, outflows
Recent studies have confirmed that ![]() Pictoris is a
Pictoris is a ![]() Myr old
A5 star, arriving at the main-sequence (Barrado y Navascues et al. 1999). This star has been long known to host a massive
debris disk of dust and gas, seen nearly edge-on (Smith & Terrile
1984).
Spectroscopic observations have shown that many ionization states are present
in the circumstellar (CS) gas associated with the disk, and they produce numerous
variable absorption features, interpreted
in terms of star-grazing comets in the Falling Evaporating Bodies (hereafter
FEBs) scenario of Lagrange et al. (1988).
Myr old
A5 star, arriving at the main-sequence (Barrado y Navascues et al. 1999). This star has been long known to host a massive
debris disk of dust and gas, seen nearly edge-on (Smith & Terrile
1984).
Spectroscopic observations have shown that many ionization states are present
in the circumstellar (CS) gas associated with the disk, and they produce numerous
variable absorption features, interpreted
in terms of star-grazing comets in the Falling Evaporating Bodies (hereafter
FEBs) scenario of Lagrange et al. (1988).
Besides derivation of the fundamental stellar parameters, the star itself
attracted little interest for further studies, as main-sequence A-type stars
like ![]() Pictoris are not expected to be chromospherically active. Indeed,
according to the standard theory of stellar evolution, main-sequence mid
A-type stars with intermediate masses, possess at the very best, very thin
outer convection zones unable to sustain magnetic activity.
Moreover, chromospheric emission lines had never been detected in the
spectroscopic data accumulated for years, supporting the conclusion that
Pictoris are not expected to be chromospherically active. Indeed,
according to the standard theory of stellar evolution, main-sequence mid
A-type stars with intermediate masses, possess at the very best, very thin
outer convection zones unable to sustain magnetic activity.
Moreover, chromospheric emission lines had never been detected in the
spectroscopic data accumulated for years, supporting the conclusion that
![]() Pictoris is not an active star. In this context, the
recent detection of strong emission lines of O VI and C III
with the Far Ultraviolet Spectroscopic Explorer (FUSE) by Deleuil et
al. (2001) is very surprising.
Pictoris is not an active star. In this context, the
recent detection of strong emission lines of O VI and C III
with the Far Ultraviolet Spectroscopic Explorer (FUSE) by Deleuil et
al. (2001) is very surprising.
Only collisional processes can produce these ions, the stellar FUV of
![]() Pictoris being much too weak to ionize a significant fraction of atoms into
such high ionization states. This implies that densities and
temperatures high enough for collisional processes to dominate
are reached in the line formation regions.
Such conditions, with electron densities ranging from a few 106 cm-3 to about 1010 cm-3 are easily obtained in the FEBs framework,
through collisions in shock waves surrounding infalling comet-like bodies.
They have been invoked to explain the presence of time variable
Al III
and C IV absorption lines in
Pictoris being much too weak to ionize a significant fraction of atoms into
such high ionization states. This implies that densities and
temperatures high enough for collisional processes to dominate
are reached in the line formation regions.
Such conditions, with electron densities ranging from a few 106 cm-3 to about 1010 cm-3 are easily obtained in the FEBs framework,
through collisions in shock waves surrounding infalling comet-like bodies.
They have been invoked to explain the presence of time variable
Al III
and C IV absorption lines in ![]() Pictoris spectrum (Beust & Tagger 1993).
Pictoris spectrum (Beust & Tagger 1993).
However, this model is unable to explain FUSE
observations of O VI and C III. First,
the large blueshift of the C III* ![]() 1175 line, contrasted with the
small redshift of the O VI lines and C III
1175 line, contrasted with the
small redshift of the O VI lines and C III ![]() 977, is
statistically unlikely, as shown recently by Beust & Morbidelli (2000).
Second, since emission lines arising from highly ionized species are
expected to be produced from infalling bodies that are very close to the
star, the emission lines should all be redshifted by several hundreds of km s-1 and should vary rapidly (within hours). FUSE spectra of
977, is
statistically unlikely, as shown recently by Beust & Morbidelli (2000).
Second, since emission lines arising from highly ionized species are
expected to be produced from infalling bodies that are very close to the
star, the emission lines should all be redshifted by several hundreds of km s-1 and should vary rapidly (within hours). FUSE spectra of ![]() Pictoris taken
at different times (2000 March 18, 2001 March 1, and 2001 March 3 and, more
recently, in october 2001) show no significant variation in the emission line
fluxes or redshifts, on a timescale of a few days.
Pictoris taken
at different times (2000 March 18, 2001 March 1, and 2001 March 3 and, more
recently, in october 2001) show no significant variation in the emission line
fluxes or redshifts, on a timescale of a few days.
On the other hand, it is now observationally well established that
several A stars show such an activity. The onset of stellar activity
for these objects is however limited to spectral type A7 or later.
FUV emission lines from O VI, N V,
C III, Si III, C II, and H I have been observed
on ![]() Aql (Altair) and
Aql (Altair) and ![]() Cep (both of A7 V spectral type) using
IUE, HST/GHRS, ORFEUS-SPAS II and FUSE
(e.g. Freire Ferrero et al. 1995; Simon & Landsman 1997;
Simon & Ayres 1998; Gouttebroze et al. 1999; Redfield
et al. 2002).
These emission lines are observed at similar strengths in the solar spectrum.
In the latter case, it is well known that they are produced in the chromosphere
and/or in the transition zone between the chromosphere and the corona.
Furthermore, chromospheric models have been proposed recently for
Cep (both of A7 V spectral type) using
IUE, HST/GHRS, ORFEUS-SPAS II and FUSE
(e.g. Freire Ferrero et al. 1995; Simon & Landsman 1997;
Simon & Ayres 1998; Gouttebroze et al. 1999; Redfield
et al. 2002).
These emission lines are observed at similar strengths in the solar spectrum.
In the latter case, it is well known that they are produced in the chromosphere
and/or in the transition zone between the chromosphere and the corona.
Furthermore, chromospheric models have been proposed recently for
![]() Aql and
Aql and ![]() Cep that successfully account for the shapes and
intensities of several emission lines including Ly
Cep that successfully account for the shapes and
intensities of several emission lines including Ly![]() and the
C II resonance doublet (Gouttebroze et al. 1999).
Non-standard physical mechanisms are now being proposed to solve the
problem of the generation of strong magnetic fields that could drive
stellar activity in the absence of a significant convective envelope (see
e.g. Vigneron et al. 1990; Tout & Pringle 1995;
Lignières et al. 1996).
and the
C II resonance doublet (Gouttebroze et al. 1999).
Non-standard physical mechanisms are now being proposed to solve the
problem of the generation of strong magnetic fields that could drive
stellar activity in the absence of a significant convective envelope (see
e.g. Vigneron et al. 1990; Tout & Pringle 1995;
Lignières et al. 1996).
Such signs of chromospheric and transition region activity were not
expected for main-sequence A5 stars, before FUSE observations of ![]() Pictoris.
In this specific case, the flux levels measured by Deleuil et al.
(2001) for the emission lines seem compatible with formation
in a solar-like chromosphere-transition region (see Table 2).
Therefore, we decided to investigate a similar scenario for
Pictoris.
In this specific case, the flux levels measured by Deleuil et al.
(2001) for the emission lines seem compatible with formation
in a solar-like chromosphere-transition region (see Table 2).
Therefore, we decided to investigate a similar scenario for ![]() Pictoris
in which the observed emission lines originate in a chromosphere-like
region located within a few tenths of stellar radii above the photosphere.
Using non-LTE radiative transfer techniques together with semiempirical
atmosphere models, line profiles have been computed and compared to observed
ones.
The atmospheric structure deduced from this modeling has been compared to
that of main-sequence A stars of later type as well as to that of the
pre-main-sequence Herbig Ae stars, both cases where chromospheric activity is
commonly observed.
Pictoris
in which the observed emission lines originate in a chromosphere-like
region located within a few tenths of stellar radii above the photosphere.
Using non-LTE radiative transfer techniques together with semiempirical
atmosphere models, line profiles have been computed and compared to observed
ones.
The atmospheric structure deduced from this modeling has been compared to
that of main-sequence A stars of later type as well as to that of the
pre-main-sequence Herbig Ae stars, both cases where chromospheric activity is
commonly observed.
This allows us to address the question of the evolution with time of the activity of A-type stars, and related to this, the question of the driving mechanisms that sustain the activity.
The goal of the modeling work presented in this paper is to explain the
characteristics of the emission lines of ![]() Pictorisobserved by FUSE. In
addition to C III lines (977 Å and 1776 Å) and O VI
resonance doublet (1032-1037 Å), we have included in this analysis the
modeling of the C IV resonance lines. These UV lines are
sensitive to the location, size and temperature of the chromosphere
above the photosphere, as demonstrated in the case of the prototypical
Herbig Ae star AB Aur by Bouret & Catala (1998). We have
computed line profiles for all these ions that probe different
regions and physical conditions in the chromospheric model. Finally,
we have calculated the Mg II h and k resonance lines
predicted for our chromospheric models to assess the influence of
the chromosphere. Indeed,
Pictorisobserved by FUSE. In
addition to C III lines (977 Å and 1776 Å) and O VI
resonance doublet (1032-1037 Å), we have included in this analysis the
modeling of the C IV resonance lines. These UV lines are
sensitive to the location, size and temperature of the chromosphere
above the photosphere, as demonstrated in the case of the prototypical
Herbig Ae star AB Aur by Bouret & Catala (1998). We have
computed line profiles for all these ions that probe different
regions and physical conditions in the chromospheric model. Finally,
we have calculated the Mg II h and k resonance lines
predicted for our chromospheric models to assess the influence of
the chromosphere. Indeed, ![]() Pictoris reveals purely photospheric
Mg II resonance lines (a weak chromospheric core might be washed out
due to relatively fast rotation).
The Mg II lines could thus constrain the chromospheric models,
setting a limit on the depth of the region where the chromospheric
temperature rise could start.
Pictoris reveals purely photospheric
Mg II resonance lines (a weak chromospheric core might be washed out
due to relatively fast rotation).
The Mg II lines could thus constrain the chromospheric models,
setting a limit on the depth of the region where the chromospheric
temperature rise could start.
Hereafter, we briefly recall (and update when necessary) the conclusions concerning the apparent structure of the lines profiles that are relevant to our study, as they have been discussed in Vidal-Madjar et al. (1994) and Deleuil et al. (2001). Table 1 summarizes the observations.
| Instrument | Date | Exposure Time |
| (s) | ||
| STIS-E230H..... | December 6 1997 | 360 |
| STIS-E140H..... | December 6 1997 | 900 |
| FUSE............... | March 1/3, 2001 |
|
The March 2001 dataset that we discuss here has been reprocessed using the
version 2.0.4 of calfuse, the FUSE pipeline processing
software. This version provides a better calibration and corrects for
the sign error in the calfuse heliocentric velocity
calculation. The stellar continuum, which is only detected
down to ![]() 1100 Å, is well reproduced by a Kurucz model for
1100 Å, is well reproduced by a Kurucz model for ![]() Pictoris
(see Lanz et al. 1995).
Comparing the position of a few C I photospheric lines predicted
by this Kurucz model to those observed on the Lif 2a spectrum near 1140 Å,
we checked the absolute wavelength scale of our FUSE spectra. The resulting
uncertainty in the wavelength calibration is less than 20 km s-1.
Finally, we overplotted Sic 1a and Lif 1a channels and checked that they
match within 5 km s-1, the comparison being achieved in the wings of
O VI
Pictoris
(see Lanz et al. 1995).
Comparing the position of a few C I photospheric lines predicted
by this Kurucz model to those observed on the Lif 2a spectrum near 1140 Å,
we checked the absolute wavelength scale of our FUSE spectra. The resulting
uncertainty in the wavelength calibration is less than 20 km s-1.
Finally, we overplotted Sic 1a and Lif 1a channels and checked that they
match within 5 km s-1, the comparison being achieved in the wings of
O VI ![]() 1032 line, which has the highest signal to noise ratio
in this wavelength range.
This operation ensures that the absolute wavelength calibration
in Sic and Lif channels is well established.
1032 line, which has the highest signal to noise ratio
in this wavelength range.
This operation ensures that the absolute wavelength calibration
in Sic and Lif channels is well established.
Table 2 summarizes some of the major properties of the emission lines (in order of increasing ionization), that we discuss hereafter.
The C III resonance line at 977 Å appears as a broad, non Gaussian
emission feature, with a total width of about 950 km s-1 (Fig. 1).
Absorption components, whose origin and nature are not clear, are
superimposed on the emission profile.
A deep, broad (0.2 Å) depression affects the center of the profile at
977.15 Å. This component is seen on both Sic 1b and Sic 2a channels.
The wavelength of this absorption component corresponds to a redshift
with respect to the stellar velocity of 30 km s-1 (Fig. 1).
Both the important velocity shift and intensity
of this central component make it unlikely to be of interstellar origin.
Indeed, few local ISM absorption features are seen toward ![]() Pictoris in
Fe II or other lines in STIS spectra; they are weak and are
measured at -9 km s-1 with respect to the stellar velocity.
A second absorption component is seen at 976.5 Å on the Sic 2a spectrum,
but is less obvious on the Sic 1b spectrum, suggesting that it may be
an observational artefact. The wavelength of this absorption corresponds to
a blueshift of -200 km s-1 with respect to the stellar velocity
(Fig. 1).
Pictoris in
Fe II or other lines in STIS spectra; they are weak and are
measured at -9 km s-1 with respect to the stellar velocity.
A second absorption component is seen at 976.5 Å on the Sic 2a spectrum,
but is less obvious on the Sic 1b spectrum, suggesting that it may be
an observational artefact. The wavelength of this absorption corresponds to
a blueshift of -200 km s-1 with respect to the stellar velocity
(Fig. 1).
The C III UV4 multiplet (a blend of six components at ![]() 1174.933,
1174.933,
![]() 1175.263,
1175.263, ![]() 1175.59,
1175.59, ![]() 1175.711,
1175.711, ![]() 1175.987,
1175.987, ![]() 1176.37) is well
detected in both Lif 1b and Lif 2a spectra. Unlike the complex profile of
the ion C III resonance line, the shape of this multiplet is
Gaussian-like and the fit shows that the line is blueshifted by about
220 km s-1 relative to the stellar velocity (Fig. 1).
This global blueshift is further confirmed by looking at the
individual components of the multiplet, each of them being
blueshifted by 220 km s-1 in the star's rest frame. The peak of the
observed feature corresponds to the
1176.37) is well
detected in both Lif 1b and Lif 2a spectra. Unlike the complex profile of
the ion C III resonance line, the shape of this multiplet is
Gaussian-like and the fit shows that the line is blueshifted by about
220 km s-1 relative to the stellar velocity (Fig. 1).
This global blueshift is further confirmed by looking at the
individual components of the multiplet, each of them being
blueshifted by 220 km s-1 in the star's rest frame. The peak of the
observed feature corresponds to the ![]() 1175.711 transition, the
strongest of the multiplet.
1175.711 transition, the
strongest of the multiplet.
A weak emission line at 1035.8 Å, blended with the blue wing of the
O VI ![]() 1037, most likely corresponds to the C II
resonance line at 1036.3 Å blueshifted by 130 km s-1.
On the other hand,
the detection of both this resonance line and the excited line at 1037 Å
in absorption at their rest wavelength is much more uncertain, though they
might correspond to the weak absorption troughs on the blue wing of
O VI
1037, most likely corresponds to the C II
resonance line at 1036.3 Å blueshifted by 130 km s-1.
On the other hand,
the detection of both this resonance line and the excited line at 1037 Å
in absorption at their rest wavelength is much more uncertain, though they
might correspond to the weak absorption troughs on the blue wing of
O VI ![]() 1037. Observing them as two independent components
suggests an interstellar or circumstellar, rather than stellar, origin for
these lines. Indeed, if formed close to the star, they would be affected by
the high rotation rate of
1037. Observing them as two independent components
suggests an interstellar or circumstellar, rather than stellar, origin for
these lines. Indeed, if formed close to the star, they would be affected by
the high rotation rate of ![]() Pictoris and they would merge and create
an artificial broad absorption feature, which is not the case (see e.g.
Deleuil et al. 2001, Fig. 3).
Pictoris and they would merge and create
an artificial broad absorption feature, which is not the case (see e.g.
Deleuil et al. 2001, Fig. 3).
The O VI doublet lines have symmetrical profiles and could be reproduced
by Gaussian profiles. A Gaussian fit has been made for both components,
using a standard minimization procedure.The wavelength separation of the two
components was the only fixed parameter. The line ratio ![]() 1037/
1037/![]() 1032 measured
from the fit is equal to the theoretical ratio, showing that the
gas is optically thin in this wavelength range. Should the
absorption trough seen at 1037.1 Å be caused by C II
interstellar absorption, the wavelength scale in the Lif 1a channel
would be further confirmed to be good within 5 km s-1.
Compared to the previous analysis (Deleuil et al. 2001), this
calibration revealed a much smaller velocity shift
of 10 km s-1 (instead of 46 km s-1) for the two lines, relative to the star.
1032 measured
from the fit is equal to the theoretical ratio, showing that the
gas is optically thin in this wavelength range. Should the
absorption trough seen at 1037.1 Å be caused by C II
interstellar absorption, the wavelength scale in the Lif 1a channel
would be further confirmed to be good within 5 km s-1.
Compared to the previous analysis (Deleuil et al. 2001), this
calibration revealed a much smaller velocity shift
of 10 km s-1 (instead of 46 km s-1) for the two lines, relative to the star.
For the present work, we have used HST/STIS high resolution echelle spectra
showing the spectral range around the C IV ![]() 1548-1550 and
Mg II
1548-1550 and
Mg II ![]() 2796-2803 resonance doublets (E140H and E230H gratings,
respectively). These spectra have been described in Roberge et al.
(2000). Errors
in the velocity determination are about 1 km s-1, given the high accuracy
in the absolute wavelength calibration of STIS. The reader is referred to
Roberge et al. (2000) for more details about data processing.
2796-2803 resonance doublets (E140H and E230H gratings,
respectively). These spectra have been described in Roberge et al.
(2000). Errors
in the velocity determination are about 1 km s-1, given the high accuracy
in the absolute wavelength calibration of STIS. The reader is referred to
Roberge et al. (2000) for more details about data processing.
These lines have been extensively observed in the past, though at lower spectral resolution and signal to noise. They appear always in absorption. In addition to the photospheric absorption lines, centered at rest wavelengths, there are time-variable, redshifted (up to 300 km s-1) components that are produced by the evaporation of FEBs (Vidal-Madjar et al. 1994).
The two components of the doublet appear in absorption and are redshifted by 4 km s-1,
with additional redshifted (![]() 300 km s-1) components. The time variability
of the latter has been revealed by IUE (Deleuil et al. 1993), despite
a quite low stellar flux and S/N ratio. These obervations had been
further confirmed with HST/GHRS observations (Vidal-Madjar et al. 1994).
The two redshifted components have similar strengths, indicating that they are
saturated.
300 km s-1) components. The time variability
of the latter has been revealed by IUE (Deleuil et al. 1993), despite
a quite low stellar flux and S/N ratio. These obervations had been
further confirmed with HST/GHRS observations (Vidal-Madjar et al. 1994).
The two redshifted components have similar strengths, indicating that they are
saturated.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2439f1.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg14.gif) |
Figure 1:
FUSE spectrum of |
| Open with DEXTER | |
| Line |
|
|
|
Ratio | |
| (Å) | (km s-1) | (ergs cm-2 s-1) | (10-7) | ||
| C II
|
1036 | -130 |
|
0.05 | 0.18 |
| C III
|
977 | ... |
|
2.03 | 1.40 |
| C III* | 1176 | -220 |
|
0.23 | 0.37 |
| O VI | 1032 | 10 |
|
0.59 | 0.81 |
| O VI | 1037 | 10 |
|
0.28 | 0.45 |
|
|
Using HST/GHRS observations combined with stellar atmosphere modeling
and spectral synthesis techniques, Lanz et al. (1995) derived reliable
parameters for ![]() Pictoris:
Pictoris:
![]() K,
log
K,
log
![]() ,
,
![]()
![]() and
and
![]() .
From these values, a
straightforward estimate of the stellar radius is
.
From these values, a
straightforward estimate of the stellar radius is
![]() .
These authors also showed that elemental abundances are solar-like and
that the rotation velocity of the star is v sin i = 140 km s-1, which we
adopted throughout this work.
.
These authors also showed that elemental abundances are solar-like and
that the rotation velocity of the star is v sin i = 140 km s-1, which we
adopted throughout this work.
We further assume that ![]() Pictoris photosphere is adequately described
by a classical Kurucz model atmosphere, in radiative and hydrostatic
equilibria, with the above-mentioned parameters.
Pictoris photosphere is adequately described
by a classical Kurucz model atmosphere, in radiative and hydrostatic
equilibria, with the above-mentioned parameters.
We adopted
![]() km s-1 as a conservative value for the microturbulent
velocity of the model.
Other values have been tested, always lower than the sound speed in the
photosphere (
km s-1 as a conservative value for the microturbulent
velocity of the model.
Other values have been tested, always lower than the sound speed in the
photosphere (
![]() km s-1 for
km s-1 for ![]() Pictoris) but, because of the high
rotational broadening, this parameter has no visible effect
on the synthetic profiles.
Pictoris) but, because of the high
rotational broadening, this parameter has no visible effect
on the synthetic profiles.
We will always adopt the same description of the photospheric layers, making a comparison between our different models (photosphere+chromosphere+transition region) dependent only on the physical conditions in the outer atmosphere.
Our modeling of the hot region surrounding ![]() Pictoris is
directly inspired from the semi-empirical approach developed by
Bouret & Catala (1998, 2000)
to study the activity of Herbig Ae/Be stars. On the top of
the photosphere, a model for the extended heated region where C III,
C IV and O VI are expected to form is appended.
Adopting a solar analogy, we will refer to the different parts of this zone as
chromosphere and transition region (hereafter TR), to distinguish the formation
region of C III and C IV resonance lines on the one hand and the
one of O VI resonance lines on the other hand.
We assume this region to be spherically symmetric when calculating the various
quantities describing the model.
Pictoris is
directly inspired from the semi-empirical approach developed by
Bouret & Catala (1998, 2000)
to study the activity of Herbig Ae/Be stars. On the top of
the photosphere, a model for the extended heated region where C III,
C IV and O VI are expected to form is appended.
Adopting a solar analogy, we will refer to the different parts of this zone as
chromosphere and transition region (hereafter TR), to distinguish the formation
region of C III and C IV resonance lines on the one hand and the
one of O VI resonance lines on the other hand.
We assume this region to be spherically symmetric when calculating the various
quantities describing the model.
The temperature law from the Kurucz model is adopted in the photosphere
until it reaches a specified minimum
![]()
![]() .
Since, obviously, this parameter has no influence on the line
profiles of the highly ionized species we are interested in here, we fixed
it once for all, after studying its effect on photospheric lines.
.
Since, obviously, this parameter has no influence on the line
profiles of the highly ionized species we are interested in here, we fixed
it once for all, after studying its effect on photospheric lines.
In the chromosphere and transition region, we adopted temperature laws
sharply rising outside the photosphere and
extending radially for a few tenths of stellar radii.
Using different lines of different ions with different formation
conditions allowed us to tightly constrain the temperature law required
to reproduce the shapes and intensities of the observed line profiles.
More precisely, temperature regimes in the
chromosphere have been constrained through the analysis of C II,
C III and C IV resonance lines. They probe
temperatures roughly ranging from 17 000 to 100 000 K.
We first built a model with a constant temperature gradient, from the bottom
(
![]() )
to the top (T=130 000 K) of the chromosphere. This maximum
temperature was determined as the upper limit above which the ionization
equilibrium shifts from C IV to C V.
The location of the outer chromospheric point was chosen such that, if the
gas is on Keplerian orbits around the star, the linear velocity on the
corresponding radius is three times v sin i as suggested from the width of C III
and O VI lines. This model failed to reproduce C II,
C III and C IV lines as observed.
Models with variable temperature gradients were then explored.
)
to the top (T=130 000 K) of the chromosphere. This maximum
temperature was determined as the upper limit above which the ionization
equilibrium shifts from C IV to C V.
The location of the outer chromospheric point was chosen such that, if the
gas is on Keplerian orbits around the star, the linear velocity on the
corresponding radius is three times v sin i as suggested from the width of C III
and O VI lines. This model failed to reproduce C II,
C III and C IV lines as observed.
Models with variable temperature gradients were then explored.
Furthermore, the mere presence of O VI lines in a stellar spectrum indicates a temperature higher than 160 000 K in the line formation region. The temperature law in the transition region has been built as follow: at the bottom of the TR, the first point of the temperature is the upper point of the chromospheric model giving the best agreement with the carbon ions lines. The outside most point of the TR was fixed such that after this point, whatever temperature law is adopted, no visible contribution is made to the O VI lines already modeled. The simplest TR model, including a single, constant gradient throughout the whole region had to be rejected because no satisfactory agreement could be found with the observed O VI doublet profiles. As for the chromosphere case, models with two gradients in the TR were explored.
In summary, the principal free parameters describing the line formation
regions are their size and location and the temperature gradients
between the photosphere and the external point of the TR.
In the remainder of the paper, we will
use the column mass
![]() to conveniently locate the different
zones of the temperature law. Locations of the different temperature
gradients have been fixed successively, starting from the base of the
chromosphere and proceeding outwards, so as to fit our sample of
lines. Varying the steepness of the gradient and the size of the
region over which this gradient is applied makes it possible to study
the effect of an accumulation of gas at formation temperatures of a
given line.
to conveniently locate the different
zones of the temperature law. Locations of the different temperature
gradients have been fixed successively, starting from the base of the
chromosphere and proceeding outwards, so as to fit our sample of
lines. Varying the steepness of the gradient and the size of the
region over which this gradient is applied makes it possible to study
the effect of an accumulation of gas at formation temperatures of a
given line.
The density distribution ![]() in the chromosphere-transition
region complex is obtained by extrapolating the hydrostatic equilibrium
structure of the underlying photosphere Kurucz model. We then compute the
velocity law through the continuity equation
v(r) =
in the chromosphere-transition
region complex is obtained by extrapolating the hydrostatic equilibrium
structure of the underlying photosphere Kurucz model. We then compute the
velocity law through the continuity equation
v(r) = ![]() /
/
![]() ,
where
,
where ![]() is the a free parameter describing the outflow rate in the model.
With density decreasing monotonically outwards, this equation shows that the
velocity law is an increasing function of the radial distance r from the
stellar center.
A smooth connection bewteen the velocity law in the chromosphere-TR and the
photosphere is obtained by requiring that at the connecting point, we have:
is the a free parameter describing the outflow rate in the model.
With density decreasing monotonically outwards, this equation shows that the
velocity law is an increasing function of the radial distance r from the
stellar center.
A smooth connection bewteen the velocity law in the chromosphere-TR and the
photosphere is obtained by requiring that at the connecting point, we have:
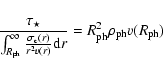 |
(1) |
For all the models, we adopted a canonical ![]() that we obtained as
follow.
Assuming that the gas in the chromospheric region is fully ionized, we wrote
that
that we obtained as
follow.
Assuming that the gas in the chromospheric region is fully ionized, we wrote
that
![]() where
where ![]() and
and ![]() are the
mass of an hydrogen atom and the electron density, respectively.
Then,
are the
mass of an hydrogen atom and the electron density, respectively.
Then, ![]() was determined from the flux ratio
f1176/f977which is well known to be sensitive to electron density over the
range
was determined from the flux ratio
f1176/f977which is well known to be sensitive to electron density over the
range
![]() (Bathia & Kastner 1993).
No C III* line, close to its rest wavelength, is seen on the FUSE
data; therefore, we could only estimate an upper limit on the flux ratio
(Bathia & Kastner 1993).
No C III* line, close to its rest wavelength, is seen on the FUSE
data; therefore, we could only estimate an upper limit on the flux ratio
![]() .
Using theoretical curves from Bathia & Kastner (1993) for a
standard formation temperature for ion C III (log T=4.8,
Simon & Ayres 1998), we concluded that log
.
Using theoretical curves from Bathia & Kastner (1993) for a
standard formation temperature for ion C III (log T=4.8,
Simon & Ayres 1998), we concluded that log
![]() .
For a velocity of a few tens of kilometer per second, corresponding to the
thermal speed for the adopted temperature, we obtained:
.
For a velocity of a few tens of kilometer per second, corresponding to the
thermal speed for the adopted temperature, we obtained:
![]()
![]()
![]() yr-1.
This value is consistent with the theoretical work of Babel (1995)
on the mass loss rates of main-sequence A-type stars and with the observations
of Bruhweiler et al. (1991) on
yr-1.
This value is consistent with the theoretical work of Babel (1995)
on the mass loss rates of main-sequence A-type stars and with the observations
of Bruhweiler et al. (1991) on ![]() Pictoris. It is also compatible with
what was found by Beust et al. (2001), when studying the
interaction between an outflowing wind and infalling evaporating cometary
bodies. They showed that the upper limit above which no spectral signatures
for such bodies could be detected in the
Pictoris. It is also compatible with
what was found by Beust et al. (2001), when studying the
interaction between an outflowing wind and infalling evaporating cometary
bodies. They showed that the upper limit above which no spectral signatures
for such bodies could be detected in the ![]() Pictoris system is
Pictoris system is
![]()
![]()
![]() yr-1.
Note that such an upper limit on the mass loss rate was found by
Lanz & Catala (1992) when searching for traces of stellar winds
in H
yr-1.
Note that such an upper limit on the mass loss rate was found by
Lanz & Catala (1992) when searching for traces of stellar winds
in H![]() profiles of a sample of main-sequence AV stars. Furthermore,
as far as the line profiles are concerned, we found no significant differences
for models with
profiles of a sample of main-sequence AV stars. Furthermore,
as far as the line profiles are concerned, we found no significant differences
for models with
![]()
![]()
![]()
![]() yr-1.
yr-1.
Line profiles are calculated with the ETLA code, which solves the radiative transfer equation in the comoving frame of the gas, in the equivalent two-level-atom formulation introduced by Mihalas & Kunasz (1978). NLTE effects for lines and continua of interest are taken into account (Bouret & Catala 2000). In a first step, ETLA solves the transfer equation together with the equations of statistical equilibrium for three successive ionization stages, in the comoving frame formulation. Once this step has been performed, calculations in the observer's frame give the emergent flux in the transitions we are interested in, as well as many other physical quantities, such as the continuum flux.
The atomic model that we have used for carbon is made of 7 levels for C II, 8 levels for C III and C IV and one continuum level for C V. The H I and Mg II models are similar to those used in Bouret & Catala (1998). For the computation of the O VI lines, we have considered 6 levels for O V, 13 levels for O VI and again, one continuum level for O VII.
For all these ions but H I, Doppler profiles have been assumed
(in the atomic rest frame). We have introduced the calculation of the
Stark's wings for the H![]() line, in the observer's frame step.
line, in the observer's frame step.
Auto-ionizations have been neglected but dielectronic recombinations are taken into account. We have assumed complete redistribution for all lines. This latter assumption may not be justified for the case of Mg II h and k lines, since partial redistribution effects have been shown to be potentially significant for some species in static atmospheres (see Mihalas 1978 or Hubeny 1985 for the case of MgII h and k lines). Here however, these effects are likely to be smaller than the effect of Doppler-shift induced by the gas macroscopic motion.
Several chemical species, in various ionization stages, are considered to compute the background continuum. Namely, we used H (bound-free), He I, He II, C I to C IV, N II, N III, N IV, O II, O III, O IV, Ne II, Mg I, Al I, Si I to Si IV. Their contributions are computed assuming LTE.
To compare our predicted line profiles to observations, we need still to properly normalize the theoretical spectra and account for the stellar rotation and the star's radial velocity.
Because of the assumption of spherical symmetry when solving the radiative transfer in the comoving frame, rotation of the envelope can be introduced only in the observer's frame step. Convolution with an analytical rotational profile is performed in order to get line profiles as broad as observed. This operation is acceptable, given that the chromospheric line formation region is very narrow.
The observed profile is corrected for the reddening caused by the interstellar medium, using E(B-V)=0.02 and the reddening curve from Cardelli et al. (1989); this yields the real flux in the emission lines.
The synthetic flux, calculated at the outer limit of the chromospheric region, is converted to flux at earth, adopting a distance of 19.3 pc.
Finally, all the spectra (i.e. FUSE and HST/STIS) have been shifted by -20 km s-1 to take into account the radial velocity of the star.
We focussed on models producing single peak emission profiles for
C III. Double-peaked emission generally forms in rotating circumstellar
envelopes or disks. In this case, the inter-peaks separation is ![]() =
2v sin i.
For
=
2v sin i.
For ![]() Pictoris one would therefore expect
Pictoris one would therefore expect
![]() km s-1.
Measuring the actual separation between the two most intense peaks with our
new wavelength calibration, we find
km s-1.
Measuring the actual separation between the two most intense peaks with our
new wavelength calibration, we find ![]() = 205 km s-1, which therefore
seems to rule out this interpretation.
Even though double-peaked emission profiles can form in chromospheric
models, producing them with their central absorption shifted with respect to
the rest wavelength requires significant mass loss rates as well as high
velocities projected on the line of sight (Bouret & Catala 2000),
in contradiction with our present assumptions.
This lead us to assume that absorbers located outside
the line formation region are responsible for the two absorption components
seen on the line profile. The nature of these absorbers will
be discussed later on.
= 205 km s-1, which therefore
seems to rule out this interpretation.
Even though double-peaked emission profiles can form in chromospheric
models, producing them with their central absorption shifted with respect to
the rest wavelength requires significant mass loss rates as well as high
velocities projected on the line of sight (Bouret & Catala 2000),
in contradiction with our present assumptions.
This lead us to assume that absorbers located outside
the line formation region are responsible for the two absorption components
seen on the line profile. The nature of these absorbers will
be discussed later on.
The minimum of temperature, ![]() ,
was obtained by modeling
the Mg II resonance lines. Line wings of the latter are formed quite
deep in the photosphere while for wavelengths around the line core, the flux
is coming from the upper photosphere, near the temperature minimum. Exploring
the dependance of the synthetic profiles with
,
was obtained by modeling
the Mg II resonance lines. Line wings of the latter are formed quite
deep in the photosphere while for wavelengths around the line core, the flux
is coming from the upper photosphere, near the temperature minimum. Exploring
the dependance of the synthetic profiles with ![]() ,
we obtained a good
agreement between synthetic profiles and observations for
,
we obtained a good
agreement between synthetic profiles and observations for
![]() K.
We also systematically checked that whatever parameters we adopted for the
chromosphere + TR model, the Mg II line profiles remained mostly
unchanged and are similar to those resulting from the Kurucz model
(see Fig. 2).
K.
We also systematically checked that whatever parameters we adopted for the
chromosphere + TR model, the Mg II line profiles remained mostly
unchanged and are similar to those resulting from the Kurucz model
(see Fig. 2).
These profiles agree
reasonably well with the HST/STIS observations, given that the observed
profiles are highly contaminated by non stellar contributions.
In particular, producing
realistic spectra of these lines implies that absorption by the gas of the
massive circumstellar disk of ![]() Pictoris is taken into account. The disk indeed
produces well-known absorption features in the cores of low-excitation metal
lines (Kondo & Bruhweiler 1985; Hobbs et al. 1988;
Vidal-Madjar et al. 1994).
As shown by Lanz et al. (1995), once introduced in the spectrum
modeling, the circumstellar gas absorption allows one
to achieve a remarkably good fit of most of the profiles, with the
exception of the redshifted absorption attributed to FEBs contributions.
Pictoris is taken into account. The disk indeed
produces well-known absorption features in the cores of low-excitation metal
lines (Kondo & Bruhweiler 1985; Hobbs et al. 1988;
Vidal-Madjar et al. 1994).
As shown by Lanz et al. (1995), once introduced in the spectrum
modeling, the circumstellar gas absorption allows one
to achieve a remarkably good fit of most of the profiles, with the
exception of the redshifted absorption attributed to FEBs contributions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2439f2.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg62.gif) |
Figure 2: Mg II: Comparison between HST/STIS profiles (full line) and profiles resulting from Kurucz photospheric model (dashed line). |
| Open with DEXTER | |
The models we discuss hereafter have the same photospheric stucture, obtained
from the modeling of Mg II. The chromospheric temperature laws
start at the minimum of temperature (log m=-3.44,
![]() K).
K).
C II lines form in absorption for models in which the temperature
is higher than T=13 000 K and lower than T=19 000 K for log m=-3.56 and
log m=-3.73 respectively. Below
![]() K, there is almost no
C II left; therefore, with the present data set, we lack information
to constrain the temperature in the deepest, coolest, region of the
chromosphere, connecting the photosphere to the C II formation region.
Because of the higher gas density prevailing in
the deep chromosphere, where these lines form, they are optically thick. As a
consequence, we cannot compare our synthetic profiles to the observed ones
by simply adding them to the the blue wing of the 1036 Å O VI line
(see Sect. 2.1.1).
ETLA is not suitable to treat line blends which prevent us from taking
into account the effect of the underlying line and to compare the
resulting C II line profiles to observations.
K, there is almost no
C II left; therefore, with the present data set, we lack information
to constrain the temperature in the deepest, coolest, region of the
chromosphere, connecting the photosphere to the C II formation region.
Because of the higher gas density prevailing in
the deep chromosphere, where these lines form, they are optically thick. As a
consequence, we cannot compare our synthetic profiles to the observed ones
by simply adding them to the the blue wing of the 1036 Å O VI line
(see Sect. 2.1.1).
ETLA is not suitable to treat line blends which prevent us from taking
into account the effect of the underlying line and to compare the
resulting C II line profiles to observations.
C III resonance line forms in emission in models with temperatures reaching up to 70 000 K at the external border of the heated region. This maximum temperature corresponds to the threshold above which C IV becomes the dominant state of the ionization equilibrium. The size of the emitting region acts on the line intensity through a density effect: the farther (from the photosphere) the external border, the lower the gas density and therefore the number of emitting atoms. Numerically, we found this external border to be at log m=-4.3.
As a consequence of the low electron density in the chromosphere resulting
from the adopted value of ![]() ,
the C III* line is always quite
weak, with a peak of intensity at less than 1.5 times the local continuum.
Computing a detailed model of the underlying photosphere, we found that in the
spectral range bracketting the C III* multiplet, the photospheric
spectrum is dominated by absorption lines of Fe I. The closest to the
C III* wavelength is also the strongest. Once the photospheric spectrum
is convolved with v sin i = 140 km s-1, this line is still quite strong and it can
significantly affect the relative apparent intensity of the C III*
line. We could not calculate the synthetic profile resulting from this blend
with ETLA and compare it to the corresponding observed spectral region,
but we argue that this can explain why no emission line is seen
at C III* rest wavelength on our FUSE data.
Finally, once having fixed the limits for C II and C III lines
formation region, we searched for the conditions to get C IV in
absorption. Models with maximum temperature around 105 000 K and with radial
extension of
,
the C III* line is always quite
weak, with a peak of intensity at less than 1.5 times the local continuum.
Computing a detailed model of the underlying photosphere, we found that in the
spectral range bracketting the C III* multiplet, the photospheric
spectrum is dominated by absorption lines of Fe I. The closest to the
C III* wavelength is also the strongest. Once the photospheric spectrum
is convolved with v sin i = 140 km s-1, this line is still quite strong and it can
significantly affect the relative apparent intensity of the C III*
line. We could not calculate the synthetic profile resulting from this blend
with ETLA and compare it to the corresponding observed spectral region,
but we argue that this can explain why no emission line is seen
at C III* rest wavelength on our FUSE data.
Finally, once having fixed the limits for C II and C III lines
formation region, we searched for the conditions to get C IV in
absorption. Models with maximum temperature around 105 000 K and with radial
extension of ![]() log m=-0.8 (starting at log m=-4.3 for temperatures
around 70 000 K) produce a high enough optical depth in the C IV
formation region for the line to form in absorption.
The theoretical C IV lines only fit the bluest part of each component
of the observed doublet, known to be stable in time (see Fig. 5).
The reddest parts are not reproduced at all, confirming the current
interpretation that they are caused by FEBs.
log m=-0.8 (starting at log m=-4.3 for temperatures
around 70 000 K) produce a high enough optical depth in the C IV
formation region for the line to form in absorption.
The theoretical C IV lines only fit the bluest part of each component
of the observed doublet, known to be stable in time (see Fig. 5).
The reddest parts are not reproduced at all, confirming the current
interpretation that they are caused by FEBs.
As already stated, O VI lines indicate temperatures typically ranging from about 200 000 K to 350 000 K. We have no observational data to constrain the temperature between the region where C III and C IV lines form and the O VI doublet formation zone. An accurate modeling of this region will have to wait for HST/STIS observations of the N V resonance doublet (see Sect. 5.2).
We found that the models in which a steep rise of the temperature
is followed by a much flatter gradient extending up to the top point of
the TR give the best agreement with our observations.
For all these models, we checked that O VI lines are unchanged by
modifications of the parameters of the inner chromosphere, as long as the
location of the bottom of the TR and its temperature to a lesser extent is kept
unchanged. Besides, stronger lines are obtained as temperatures higher than
200 000 K are reached in regions closer to the star's surface, where
the density is higher.
This allowed us to proceed by trial and error to search for a global
model fitting the O VI doublet together with the C III and
C IV lines. Each line profile has been convolved with a rotational
profile with an effective rotational velocity adapted for each element:
![]() km s-1 for C III,
km s-1 for C III,
![]() km s-1 for C IV
and
km s-1 for C IV
and
![]() km s-1 for O VI. Such a super-rotational broadening
is compatible with the assumption that the gas is on a Keplerian orbit
around the star at the distance where the lines form.
We obtained a good agreement with the observed profiles
for a model whose characteritic paramaters are listed in Table 3;
Fig. 3 illustrates the temperature law of this model and shows
the different regions of formation for the lines of interest.
The corresponding profiles are shown in Figs. 2, 4,
5 and 6.
km s-1 for O VI. Such a super-rotational broadening
is compatible with the assumption that the gas is on a Keplerian orbit
around the star at the distance where the lines form.
We obtained a good agreement with the observed profiles
for a model whose characteritic paramaters are listed in Table 3;
Fig. 3 illustrates the temperature law of this model and shows
the different regions of formation for the lines of interest.
The corresponding profiles are shown in Figs. 2, 4,
5 and 6.
| log m | -6.50 | -5.23 | -5.05 | -4.17 | -3.66 | -3.44 |
| T | 400 000 | 260 000 | 100 000 | 68 000 | 26 000 | 5350 |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8.3cm,clip]{MS2439f3.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg68.gif) |
Figure 3: Temperature (K) for the model of Table 3, as a function of the column mass (g cm-2); the upper x-axis shows the radial distance above the star, in photospheric radius units. The location of the different line formation regions are indicated. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2439f4.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg69.gif) |
Figure 4:
Observed profile of C III 977 Å (full line) compared
to the profile obtained with the model from Table 3 (dashed line).
The dotted line shows this synthetic profile + a superimposed absorption
caused by a density column Log
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2439f5.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg70.gif) |
Figure 5: Profiles obtained with the model from Table 3 for C IV doublet (dashed line) compared to the observed profiles (full line). Deep components centered on the rest wavelengths are produced by the chromospheric model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{MS2439f6.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg71.gif) |
Figure 6: The synthetic O VI doublet (dashed line), as obtained from model listed in Table 3, compared to the observed profiles (full line) in the Lif 1a spectrum. The dotted line is for the C II resonance line as produced by the disk-wind model discussed in Sect. 5. This fit suggests that the absorption feature at 1037.1 Å is caused by CS C II (fine structure line) absorption. |
| Open with DEXTER | |
The global shape of the profile of C III resonance line is well reproduced although some discrepancies remain, mainly due to the deep absorption features seen on the profile. As already said in Sect. 2.1.1, the bluest one may be an artefact. Nevertheless, we checked that it cannot be caused by H 2 transitions at 976.55 Å, as it would imply an H 2 column density more than one order of magnitude higher than what was recently measured by Lecavelier des Etangs et al. (2001). Considering the low level of confidence for the real presence of this absorption at -200 km s-1 on C III, we did not investigate in more detail any other possible origin. On the other hand, we have considered several possibilities for the nature and origin of the central absorption feature, unchanged in Sic 2a and Sic 1b spectra.
Unresolved CO bands could be ruled out for two reasons: first, we found that a CO column density 100 times higher than that determined by Roberge et al. (2000) from HST/STIS data is needed to get an absorption component with the right strength for the Q branch from the 977.418 Å band. Second, this band would have to be blueshifted by about 100 km s-1 to fall at the wavelength of the observed central absorption, which we considered unlikely given the conclusions of Roberge et al. (2000).
As shown by Beust & Tagger (1993), highly ionized species such as
Al III or C IV can form in the comae
of FEBs; therefore, some C III must be produced as well. Although very
appealing, this interpretation may be in contradiction with the fact that
the observed absorption does not vary significantly on a short time scale.
The observed trough could as well result from the presence of circumstellar
(within the CS disk) and interstellar C III on the line of sight.
Assuming that the central depression is indeed caused by the
presence of C III on the line of sight, whatever its real origin,
we can derive how much gas is involved. Using simple
(no dynamics or kinematics) assumptions, we were able to reproduce fairly well
the observed profile for a density column Log
![]() and
v=30 km s-1 for the radial velocity of the absorbing gas (Fig. 4).
Remaining differencies, affecting the blue wing of the profile, will
be discussed in Sect. 5.
and
v=30 km s-1 for the radial velocity of the absorbing gas (Fig. 4).
Remaining differencies, affecting the blue wing of the profile, will
be discussed in Sect. 5.
As already stated in Sect. 2.1, both the C II resonance line and C III excited line appear in emission and are blueshifted by 130 and 200 km s-1 respectively. Therefore, they cannot be formed in the chromospheric stucture we have assumed so far; the gas velocity in the chromosphere and in the TR is far from being high enough to induce such a high blueshift.
Although Beust & Morbidelli (2000) have shown that models involving FEBs
can produce blueshifted features, a FEBs origin could easily be ruled out for
these lines. First, the line profiles are symmetric (Gaussian) while
the FEBs model predicts that lines with high velocity shifts are strongly
asymmetric.
Second, the lines do not vary on a short time scale (hours), nor do they on
a long time scale (a few days).
Whatever the mechanism producing the observed blueshift, the FUSE observations
tell us that velocities as high as 200 km s-1 are reached in the line formation
region and that the flow is stable over time.
A simple interpretation of the observed velocity shift is to
assume that the lines form in a flow, blown from the ![]() Pictoris gazeous disk.
This disk wind has to be warm enough to produce C III*. On the other
hand, the maximum temperature in the wind must be low enough that neither
C IV nor O VI components are formed.
If the disk wind hypothesis is correct, the FUSE observations show that the
vertical size of the line formation region (measured perpendicularly to the
disk plane) must be such that it is smaller than the stellar disk. Indeed,
the observed profiles are fully blueshifted, with no extension at redshifted
wavelengths, which shows that if formed in an expanding wind, the receeding
part of the latter does not contribute to the line profile. This has two
straightforward consequences: first,
the temperature for the production of C III must be reached not
far from the disk plane. Second, the density of the wind must decrease
drastically outside the line formation region, such that no blueshifted
absorption lines from
other species, like Fe I, Na I or Balmer lines, are observed,
contrary to the well documented case of FU Ori disk winds (e.g. Calvet et al.
1993; Hartmann & Calvet 1995).
Finally, despite the C II and C III* lines likely forming close to the CS disk, they show
no evidence of rotation, which indicates that the expansion velocity field dominates
over the rotation velocity of the disk, in the line formation region.
Pictoris gazeous disk.
This disk wind has to be warm enough to produce C III*. On the other
hand, the maximum temperature in the wind must be low enough that neither
C IV nor O VI components are formed.
If the disk wind hypothesis is correct, the FUSE observations show that the
vertical size of the line formation region (measured perpendicularly to the
disk plane) must be such that it is smaller than the stellar disk. Indeed,
the observed profiles are fully blueshifted, with no extension at redshifted
wavelengths, which shows that if formed in an expanding wind, the receeding
part of the latter does not contribute to the line profile. This has two
straightforward consequences: first,
the temperature for the production of C III must be reached not
far from the disk plane. Second, the density of the wind must decrease
drastically outside the line formation region, such that no blueshifted
absorption lines from
other species, like Fe I, Na I or Balmer lines, are observed,
contrary to the well documented case of FU Ori disk winds (e.g. Calvet et al.
1993; Hartmann & Calvet 1995).
Finally, despite the C II and C III* lines likely forming close to the CS disk, they show
no evidence of rotation, which indicates that the expansion velocity field dominates
over the rotation velocity of the disk, in the line formation region.
This interpretation is further strengthened by turning back to the C III resonance line profile. The blue side of the theoretical line is not well reproduced by the chromospheric model and some additional emission is seemingly missing. More precisely, there is a peak at 976.37 Å which exactly corresponds to a blueshift of 200 km s-1 for the 977.02 Å C III line. It is very appealing to interpret this additional emission for the C III resonance as being produced in the same region as the C III excited lines.
To test whether this scenario could explain the observed characteristics of the carbon blueshifted lines, we built a model in which a region, much hotter than the surrounding CS gas, is arbitrarily located at ten stellar radii from the star and extends over a few stellar radii along the disk plane.
The adopted temperature law is composed of three distinct parts: first,
a steep rise above the disk plane, then a temperature plateau at ![]() and
finally a regime where the temperature steeply decreases outwards until it
reaches a terminal value T0. The wind therefore ends up with an
isothermal cool region. T0=20 K was adopted, consistent with what is
known of the
and
finally a regime where the temperature steeply decreases outwards until it
reaches a terminal value T0. The wind therefore ends up with an
isothermal cool region. T0=20 K was adopted, consistent with what is
known of the ![]() Pictoris CS gaseous environment (Vidal-Madjar et al. 1998).
Four free parameters (
Pictoris CS gaseous environment (Vidal-Madjar et al. 1998).
Four free parameters (
![]() )
govern this
temperature law, which is expressed as follow:
)
govern this
temperature law, which is expressed as follow:
![\begin{displaymath}T(z)= \left\{\begin{array}{l}
T_{0}+(T_{\max}-T_{0})\exp\left...
...2}\right]\\
{\rm if\ } Z_{\rm p2}\leq z.
\end{array}\right.
\end{displaymath}](/articles/aa/full/2002/30/aa2439/img74.gif) |
(2) |
![\begin{displaymath}Z_{\rm p1}=Z_{\rm D}+\frac{\Delta_{1}}{2(\ln 2)^{1/2}}
\left[...
...frac{T_{\rm max}-T_{0}
}{T_{\rm D}-T_{0}}\right)\right]^{1/2}
\end{displaymath}](/articles/aa/full/2002/30/aa2439/img76.gif) |
(3) |
Afterwards, we adopted a piecewise linear velocity law such that velocities ranging from 150 km s-1 to 250 km s-1 are reached in this region. Then, we integrated the line specific intensity only on rays intercepting the stellar disk. Variation of the line intensity are obtained by varying the temperature and the volume of the emitting region, i.e. extending it on the radial direction.
The electron density in the C III lines formation region was fixed by
measuring the flux ratio
f1176/f977 for the blueshifted observed lines.
The contribution to the line flux f977 from the disk-wind region was
obtained by substracting the theoretical flux from the chromospheric model to
the observed flux. We found
f1176/f977=0.51 which corresponds to
![]() for a gas temperature
for a gas temperature
![]() K, that we used
at this step.
Because of possible opacity effects in the lines, the estimated
density is an upper limit to the true density of the medium.
Assuming that the wind is fully ionized in the line formation region, we can
write:
K, that we used
at this step.
Because of possible opacity effects in the lines, the estimated
density is an upper limit to the true density of the medium.
Assuming that the wind is fully ionized in the line formation region, we can
write:
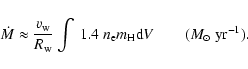 |
(4) |
Results hereabove strongly suggest that a disk-wind is indeed responsible for
the observed blueshifted C II and C III* lines. Although based on simple
assumptions, our modeling implies that the opening angle of the outflow, defined as the angle
between the disk midplane and the maximum latitudinal extent of the outflow,
is small. Such a result is very similar to what was found for the Herbig A0e
star HD 100564 by Viera et al. (1999).
However, in our case, an origin from the CS disk rather than from the star's
surface is favoured for the outflow. First, a stellar wind with the mass loss
rate we derive here would inevitably produce some blueshift in all the lines
produced in the vicinity of the star, which is not observed.
Second, this mass loss rate is rather close to the upper limit
found by Beust et al. (2001) and it would affect the
FEBs signatures, which is again not observed. A flow coming from
regions above the disk mid-plane does not suffer from these problems.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2439f7.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg95.gif) |
Figure 7: C III excited line in the Lif 2a spectrum (full line) compared to the synthetic profile (dashed line) obtained with the disk-wind model discussed in Sect. 5.2. |
| Open with DEXTER | |
The principal issue of this paper is to investigate the relevance of
a chromospheric model to explain the emission spectrum of ![]() Pictoris, newly revealed
by FUSE. The model we propose is able to reproduce not only the FUV emission
features but also absorption lines of Mg II and C IV, spanning a
large domain of wavelengths, in the near-UV.
Pictoris, newly revealed
by FUSE. The model we propose is able to reproduce not only the FUV emission
features but also absorption lines of Mg II and C IV, spanning a
large domain of wavelengths, in the near-UV.
In addition, when calculating the H![]() line profile, we find no differences
between our synthetic profile and what is produced by the Kurucz model of
line profile, we find no differences
between our synthetic profile and what is produced by the Kurucz model of ![]() Pictoris,
once convolved with the stellar v sin i (see Fig. 8).
This comes from the fact that our model, even though it includes high temperature
regions above the photosphere, is much too optically thin to have visible
effect on the H
Pictoris,
once convolved with the stellar v sin i (see Fig. 8).
This comes from the fact that our model, even though it includes high temperature
regions above the photosphere, is much too optically thin to have visible
effect on the H![]() profile. We found that the optical depth ratio between
Ly
profile. We found that the optical depth ratio between
Ly![]() and H
and H![]() is about 106, for the model discussed here.
is about 106, for the model discussed here.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2439f8.ps} \end{figure}](/articles/aa/full/2002/30/aa2439/Timg97.gif) |
Figure 8:
H |
| Open with DEXTER | |
Additional modeling of other lines probing different temperature regimes
is necessary to achieve a better description of the temperature run above
the photosphere. Observing the N V resonance doublet
(1238-1240 Å) or Ly![]() would be most helpful, in this context.
The former line would help constraining the temperature law bewteen the
C IV and O VI formation regions. Likewise, Ly
would be most helpful, in this context.
The former line would help constraining the temperature law bewteen the
C IV and O VI formation regions. Likewise, Ly![]() which is
known to be an excellent diagnostic for chromospheric regions, would
provide reliable information on the temperature regime from 10 000 K to
25 000 K.
Besides these lines, C II resonance line at 1335 Å should also be
observed in emission, if the model is correct.
which is
known to be an excellent diagnostic for chromospheric regions, would
provide reliable information on the temperature regime from 10 000 K to
25 000 K.
Besides these lines, C II resonance line at 1335 Å should also be
observed in emission, if the model is correct.
The model predicts that Ly![]() should intrinsically
appear as a single peak, broad emission feature. When taken into account,
the contamination of this intrinsic profile by the interstellar and circumstellar
Ly
should intrinsically
appear as a single peak, broad emission feature. When taken into account,
the contamination of this intrinsic profile by the interstellar and circumstellar
Ly![]() absorptions will change it into a double-peaked emission profile.
Fitting the observed profile would not only provide information on the
temperature law in the deep chromosphere but also allow us to precisely derive
the H I column density and the micro-turbulent velocity
absorptions will change it into a double-peaked emission profile.
Fitting the observed profile would not only provide information on the
temperature law in the deep chromosphere but also allow us to precisely derive
the H I column density and the micro-turbulent velocity
![]() .
In any case, the changes deduced from Ly
.
In any case, the changes deduced from Ly![]() fitting must be small enough that
they do not change the fits already obtained in the present work.
Note that because of the interstellar contamination, meaningful
comparisons between observed and synthetic Ly
fitting must be small enough that
they do not change the fits already obtained in the present work.
Note that because of the interstellar contamination, meaningful
comparisons between observed and synthetic Ly![]() profiles will be
restricted to the external wings of the emission component.
profiles will be
restricted to the external wings of the emission component.
The ability of our model to explain the properties of the emission
lines in ![]() Pictoris spectrum confirms that this star is undergoing a chromospheric
active phase. Although surprising for a star of this spectral type, this behaviour
has been observed already in more evolved A stars of later spectral type,
like
Pictoris spectrum confirms that this star is undergoing a chromospheric
active phase. Although surprising for a star of this spectral type, this behaviour
has been observed already in more evolved A stars of later spectral type,
like ![]() Aql (Altair) or
Aql (Altair) or ![]() Cep (Freire-Ferrero et al. 1995;
Simon & Landsman 1997; Gouttebroze et al. 1999; Redfield et al. 2002).
Cep (Freire-Ferrero et al. 1995;
Simon & Landsman 1997; Gouttebroze et al. 1999; Redfield et al. 2002).
![]() Pictoris is most likely the earliest A V star for which chromospheric emission has
been observed so far, since the evidence for such an emission in
Pictoris is most likely the earliest A V star for which chromospheric emission has
been observed so far, since the evidence for such an emission in ![]() Eri
is only marginal and would require much deeper exposure for confirmation
(Simon & Landsman 1997). At best, the sample of known main-sequence
mid A-type stars exhibiting conspicuous signs of chromospheric activity is
therefore made of two stars.
On the opposite, a large number of younger objects of same spectral type,
like the Herbig Ae stars, do present spectral signatures of a strong activity.
Assuming that a unique mechanism drives the observed activity
of A-type stars, from the PMS phase to the ZAMS, this suggests
that the efficiency of this mechanism is decaying with time.
In other words, if observed at younger age,
Eri
is only marginal and would require much deeper exposure for confirmation
(Simon & Landsman 1997). At best, the sample of known main-sequence
mid A-type stars exhibiting conspicuous signs of chromospheric activity is
therefore made of two stars.
On the opposite, a large number of younger objects of same spectral type,
like the Herbig Ae stars, do present spectral signatures of a strong activity.
Assuming that a unique mechanism drives the observed activity
of A-type stars, from the PMS phase to the ZAMS, this suggests
that the efficiency of this mechanism is decaying with time.
In other words, if observed at younger age, ![]() Pictoris would exhibit more
activity and vice versa. We might well be witnessing the final stage of
the active phase of a mid A V-type star.
Whatever the mechanism sustaining activity, the
existence of an atmospheric structure including a chromosphere-TR complex
implies that a large amount of non radiative energy is dissipated above
the photosphere of
Pictoris would exhibit more
activity and vice versa. We might well be witnessing the final stage of
the active phase of a mid A V-type star.
Whatever the mechanism sustaining activity, the
existence of an atmospheric structure including a chromosphere-TR complex
implies that a large amount of non radiative energy is dissipated above
the photosphere of ![]() Pictoris. We can estimate it by the calculation of the
radiative losses,
i.e., the amount of energy radiated by the lines and continua that are formed
in the chromosphere and transition region.
We recall here that the radiative losses are defined by:
Pictoris. We can estimate it by the calculation of the
radiative losses,
i.e., the amount of energy radiated by the lines and continua that are formed
in the chromosphere and transition region.
We recall here that the radiative losses are defined by:
In order to calculate E-(r), we need to solve the
radiative transfer equation, that will provide us with
the mean radiation intensity as well as with the source function of the
transitions we are dealing with. The lines that have been used in this work
provide information on the gas physical conditions
throughout the chromosphere and TR, though parts of these regions are poorly
constrained. Therefore, our calculations of the radiative losses only provide
a rough estimate of the energy required to sustain a chromosphere-TR complex
in ![]() Pictoris close environment.
Pictoris close environment.
![]() was calculated by integrating the
radiative losses E-(r) between the two points r1 and r2 where
was calculated by integrating the
radiative losses E-(r) between the two points r1 and r2 where
![]() and
and
![]() respectively:
respectively:
| Transitions |
|
| C II...................... |
|
| C III..................... |
|
| C III*................... |
|
| C IV..................... |
|
| O VI..................... |
|
| C III Cont............ |
|
| C IV Cont............ |
|
| O VI Cont............ |
|
| Total.................... |
|
The ratio of the radiative losses to the bolometric luminosity of the
star is
![]() .
Using the Barnes & Evans (1976) relation, Simon & Landsman
(1997) converted the apparent fluxes measured for a few
chromospheric emission lines into stellar surface fluxes for
.
Using the Barnes & Evans (1976) relation, Simon & Landsman
(1997) converted the apparent fluxes measured for a few
chromospheric emission lines into stellar surface fluxes for
![]() Aql and
Aql and ![]() Cep.
In terms of these chromospheric/TR fluxes,
Cep.
In terms of these chromospheric/TR fluxes, ![]() Pictoris is slightly more active
(by a factor of 4-6) than these stars.
Using Eqs. (5) and (6) for more than 20 transitions
(lines and continua), Bouret & Catala (1998) showed that for
Herbig A0e stars, which are believed to be the progenitors of main-sequence A stars,
the radiative losses in the chromosphere reach up to a few 10-2 of
the stellar bolometric luminosity.
These stars have significant stellar winds (
Pictoris is slightly more active
(by a factor of 4-6) than these stars.
Using Eqs. (5) and (6) for more than 20 transitions
(lines and continua), Bouret & Catala (1998) showed that for
Herbig A0e stars, which are believed to be the progenitors of main-sequence A stars,
the radiative losses in the chromosphere reach up to a few 10-2 of
the stellar bolometric luminosity.
These stars have significant stellar winds (![]() up to
a few 10-8
up to
a few 10-8 ![]() yr-1) and extended chromosphere of moderate temperatures
(
yr-1) and extended chromosphere of moderate temperatures
(
![]() K). The dominant contributors to their radiative losses
are the H
K). The dominant contributors to their radiative losses
are the H![]() line and the Balmer continuum, while the other major lines
and continua (Magnesium and Carbon) produce negligible contributions
(Bouret & Catala 1998).
In the case of the prototypical Herbig Ae star AB Aur,
the highest temperatures are reached in discrete regions produced
by shocks in the wind; in these regions the resonance lines of C IV
and N V dominate the radiative losses.
Obviously, the
line and the Balmer continuum, while the other major lines
and continua (Magnesium and Carbon) produce negligible contributions
(Bouret & Catala 1998).
In the case of the prototypical Herbig Ae star AB Aur,
the highest temperatures are reached in discrete regions produced
by shocks in the wind; in these regions the resonance lines of C IV
and N V dominate the radiative losses.
Obviously, the ![]() Pictoris case is very different for four reasons:
(1) the lower density in the the chromosphere/TR makes the radiative losses
lower -
(2) The physical extent of the emitting regions (chromosphere/TR) is much smaller in
Pictoris case is very different for four reasons:
(1) the lower density in the the chromosphere/TR makes the radiative losses
lower -
(2) The physical extent of the emitting regions (chromosphere/TR) is much smaller in
![]() Pictoris than in Herbig Ae stars; as a comparison, AB Aur chromosphere extends over about
1.6 stellar radii while
Pictoris than in Herbig Ae stars; as a comparison, AB Aur chromosphere extends over about
1.6 stellar radii while ![]() Pictoris chromosphere/TR is only about 0.4
Pictoris chromosphere/TR is only about 0.4
![]() thick -
(3) much higher temperatures are reached in the
thick -
(3) much higher temperatures are reached in the ![]() Pictoris chromosphere/TR -
(4) the chromosphere/TR is not discrete but rather, spherically symmetric.
Therefore, a direct
comparison to Herbig Ae stars is difficult, but we found that
Pictoris chromosphere/TR -
(4) the chromosphere/TR is not discrete but rather, spherically symmetric.
Therefore, a direct
comparison to Herbig Ae stars is difficult, but we found that ![]() Pictoris is
much less active than these PMS objects.
Pictoris is
much less active than these PMS objects.
In the ![]() Aql and
Aql and ![]() Cep case, as well as in many Herbig Ae/Be stars, X-ray
emission has been detected (Schmitt et al. 1985; Zinnecker &
Preibisch 1994).
Cep case, as well as in many Herbig Ae/Be stars, X-ray
emission has been detected (Schmitt et al. 1985; Zinnecker &
Preibisch 1994). ![]() Aql being, from many points of view, similar
to
Aql being, from many points of view, similar
to ![]() Pictoris, some X-ray emission should arise in the latter.
A simple scaling to the activity level measured for
Pictoris, some X-ray emission should arise in the latter.
A simple scaling to the activity level measured for ![]() Aql gives
log
Aql gives
log
![]() for
for ![]() Pictoris.
This is roughly two orders of magnitude smaller than what is measured for
active solar-type stars (Mathioudakis et al. 1995)
and about one order of
magnitude smaller than typical values for early F-type stars like Procyon
(see Drake et al. 1995). In the latter cases, the corona is heated up to
log
Pictoris.
This is roughly two orders of magnitude smaller than what is measured for
active solar-type stars (Mathioudakis et al. 1995)
and about one order of
magnitude smaller than typical values for early F-type stars like Procyon
(see Drake et al. 1995). In the latter cases, the corona is heated up to
log
![]() 6.0-6.2.
As far as
6.0-6.2.
As far as ![]() Aql is concerned, a thourough analysis of the various causes
leading to a low emission measure lead Freire-Ferrero et al. (1995) to
suggest that a warm corona is present close to the star, with
log
Aql is concerned, a thourough analysis of the various causes
leading to a low emission measure lead Freire-Ferrero et al. (1995) to
suggest that a warm corona is present close to the star, with
log
![]() 5.7-5.8.
If the analogy with
5.7-5.8.
If the analogy with ![]() Aql is valid, a warm corona is therefore
expected for
Aql is valid, a warm corona is therefore
expected for ![]() Pictoris, though it cannot be firmly predicted on the basis of the
present dataset. Consequently, the star should have an intrinsic
X-ray emission, originating in this corona.
To our knowledge, no such detection has been claimed for
Pictoris, though it cannot be firmly predicted on the basis of the
present dataset. Consequently, the star should have an intrinsic
X-ray emission, originating in this corona.
To our knowledge, no such detection has been claimed for ![]() Pictoris, which most
likely results from the presence of a large quantity of absorbing gas in the
soft X-ray range around
Pictoris, which most
likely results from the presence of a large quantity of absorbing gas in the
soft X-ray range around ![]() Pictoris.
Pictoris.
The nature of the source of energy that heats the gas is still far from being
determined. Should the solar analogy prevail, the gas heating would be expected to
be caused by magnetic and/or accoustic energy dissipation. This, in turn, implies that
a sub-photospheric convection zone exist in ![]() Pictoris.
Although in contradiction with the standard theory of stellar evolution, this conclusion
is supported by several theoretical works showing that such sub-photospheric convective
regions could exist even in early A-type stars (Zahn 1980; Bohn
1984; Zahn 1993).
Pictoris.
Although in contradiction with the standard theory of stellar evolution, this conclusion
is supported by several theoretical works showing that such sub-photospheric convective
regions could exist even in early A-type stars (Zahn 1980; Bohn
1984; Zahn 1993).
Alternatively, the ultimate origin of this non-radiative energy may be stellar
rotation, through the transformation of rotational energy into turbulent energy
in the star's interior, through shear instabilities (Lignières et al.
1996).
This model, first developed for Herbig Ae/Be stars, assumes that such an energy
transformation is caused by the violent rotational braking that the wind exerts
on the star's surface. The stronger the wind, the higher the amount of energy that
can be extracted. In ![]() Pictoris case, adopting
Pictoris case, adopting ![]() =
=
![]()
![]() yr-1
(see Sect. 3.2),
we found that this mechanism provides an energy reservoir lower than the
radiative losses by about two orders of magnitude:
yr-1
(see Sect. 3.2),
we found that this mechanism provides an energy reservoir lower than the
radiative losses by about two orders of magnitude:
![]() .
However, this model does not take into account the effect of a magnetic field that
should be produced by a dynamo mechanism in the subphotospheric turbulent layers.
In that case, the amount of energy that could be extracted from the turbulent layer is
likely to be larger by two to three orders of magnitudes (Lignières et al.
1996). This
promising approach needs to be completed by its inclusion in a self consistent model of
the coupling of the magnetic field production with the turbulent subphotospheric layers
and may reconcile the energy production rate with our estimates of the radiative losses.
This scenario is especially interesting for our case since our modeling work has
required the introduction of a super-rotational broadening to achieve a good fit
of the emission lines which suggests that rotation is indeed an important component
of the physics of the chromosphere-TR. Because of the high level of differential
rotation between the chromosphere-TR and the photosphere, the torque exerted by
the weak wind of
.
However, this model does not take into account the effect of a magnetic field that
should be produced by a dynamo mechanism in the subphotospheric turbulent layers.
In that case, the amount of energy that could be extracted from the turbulent layer is
likely to be larger by two to three orders of magnitudes (Lignières et al.
1996). This
promising approach needs to be completed by its inclusion in a self consistent model of
the coupling of the magnetic field production with the turbulent subphotospheric layers
and may reconcile the energy production rate with our estimates of the radiative losses.
This scenario is especially interesting for our case since our modeling work has
required the introduction of a super-rotational broadening to achieve a good fit
of the emission lines which suggests that rotation is indeed an important component
of the physics of the chromosphere-TR. Because of the high level of differential
rotation between the chromosphere-TR and the photosphere, the torque exerted by
the weak wind of ![]() Pictoris may efficiently induce subphotospheric turbulence.
Pictoris may efficiently induce subphotospheric turbulence.
Regardless of the nature of this energy source, the heating is apparently effective on
a very thin region above the stellar disk, even when the presence of a potential
corona is taken into account. We already showed that ![]() Pictoris chromosphere/TR complex
is much thinner than those of Herbig Ae stars. On the other hand, it is very
similar to the physical size inferred for
Pictoris chromosphere/TR complex
is much thinner than those of Herbig Ae stars. On the other hand, it is very
similar to the physical size inferred for ![]() Aql and
Aql and ![]() Cep by
Gouttebroze et al. (1999). This may indicate that the efficiency of
the mechanism generating the magnetic field is decaying with time and would
explain why main-sequence A-type stars lack a strong magnetic field. In cooler
stars, the strong magnetic fields trap and heat the gas in closed loop structures
and the energy deposition is weaker at the base of the magnetic structure.
Consequently, the chromosphere and transition region are even thinner than
in
Cep by
Gouttebroze et al. (1999). This may indicate that the efficiency of
the mechanism generating the magnetic field is decaying with time and would
explain why main-sequence A-type stars lack a strong magnetic field. In cooler
stars, the strong magnetic fields trap and heat the gas in closed loop structures
and the energy deposition is weaker at the base of the magnetic structure.
Consequently, the chromosphere and transition region are even thinner than
in ![]() Pictoris (a few percent of stellar radius for the Sun) but their coronae
can extend over more than one stellar radius.
Pictoris (a few percent of stellar radius for the Sun) but their coronae
can extend over more than one stellar radius.
Although unexpected for a mid A V type star like ![]() Pictoris the emission lines
revealed by FUSE are most likely a clue for the existence of a significant
stellar activity.
We have shown that not only these emission lines but also several absorption
lines can be reproduced with a simple model, which involves a chromosphere and
a transition region. This theoretical framework is new for
Pictoris the emission lines
revealed by FUSE are most likely a clue for the existence of a significant
stellar activity.
We have shown that not only these emission lines but also several absorption
lines can be reproduced with a simple model, which involves a chromosphere and
a transition region. This theoretical framework is new for ![]() Pictoris and is most
helpful for interpreting the aforementioned observed characteristics of
the star, which could not be explained in the FEBs framework.
Pictoris and is most
helpful for interpreting the aforementioned observed characteristics of
the star, which could not be explained in the FEBs framework.
The shape and intensity of C III and O VI emission lines have
been used to place constraints on the temperature law and size of the
chromosphere and transition region. The latter were found such that their
presence does not affect purely photospheric profiles, like Mg II
h and k or the H![]() line for instance.
The model predicts that the Ly
line for instance.
The model predicts that the Ly![]() line should appear as a rather
strong intrinsic emission line, on top of which an absorption trough
is formed by the IS hydrogen. Fitting the observations with the theoretical line
will provide a direct and accurate determination of the hydrogen column density
on the line of sight to
line should appear as a rather
strong intrinsic emission line, on top of which an absorption trough
is formed by the IS hydrogen. Fitting the observations with the theoretical line
will provide a direct and accurate determination of the hydrogen column density
on the line of sight to ![]() Pictoris; this however requires HST/STIS observations yet
to come.
Pictoris; this however requires HST/STIS observations yet
to come.
The puzzling blueshift of the C III* line profile has been successfully
interpreted in
terms of a thin warm wind coming from the massive CS disk of ![]() Pictoris. Although
we did not develop a general model of this region, the prescriptions we used
strongly suggest that the gas is flowing with a quite small angle with respect
to the disk plane. This conclusion may relate the
Pictoris. Although
we did not develop a general model of this region, the prescriptions we used
strongly suggest that the gas is flowing with a quite small angle with respect
to the disk plane. This conclusion may relate the ![]() Pictoris case to that of a few
Herbig Ae stars showing the same general behaviour, though observed through
very different ionization conditions.
Pictoris case to that of a few
Herbig Ae stars showing the same general behaviour, though observed through
very different ionization conditions.
Nevertheless, several question remain open, mostly on the theoretical side.
First of all, the origin and nature of the process(es) leading to the energy
deposition responsible for the gas heating in the outer atmosphere of ![]() Pictoris
is still to be clearly identified.
Pictoris
is still to be clearly identified.
Second, the mechanisms driving and heating the disk wind are unknown as well, although a combination of both thermal and radiative pressure might be efficient enough to explain the calculated mass loss rate and observed blueshift.
Finally, assuming that a unique mechanism drives the observed activity of A-type stars from the PMS stage to the ZAMS phase, our results suggest that the effectiveness of this mechanism decays with time, likewise the decay of activity during the main-sequence lifetime of solar-type stars. We might be witnessing here the final active stage of a mid A V star. It is therefore of importance to increase the sample of A stars showing active signature, for different evolutionnary stages.
Acknowledgements
We thank Anne-Marie Lagrange and Hervé Beust for fruitful discussions about the FEBs model. We also wish to warmly thank Andrea Dupree, Michelle Eidelsberg, Rubens Freire-Ferrero and Pierre Gouttebroze for interesting comments on the stellar activity and molecular data of CO. Finally, we acknowledge Thomas Ayres for kindly communicating his lines irradiance measurements to us. This work is based on data obtained for the Guaranteed Time Team by the NASA-CNES-CSA FUSE mission operated by the Johns Hopkins University. Financial support to U. S. participants has been provided by NASA contract NAS5-32985.