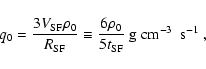A&A 390, 1063-1074 (2002)
DOI: 10.1051/0004-6361:20020731

The evolution of mass loaded supernova remnants

I. Constant and Mach Number dependent mass injection rates

J. E. Dyson¹ - S. J. Arthur² - T. W. Hartquist¹

1 - Department of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK
2 - Instituto de Astronomia, UNAM, Campus Morelia, Apartado Postal 3-72, 58090 Morelia, Michoacán, Mexico

Received 8 February 2002 / Accepted 15 May 2002

Abstract
We describe the evolution of spherically symmetric supernova remnants in which mass addition takes place from embedded clouds. We derive simple approximations to the remnant evolution which can be used for investigating the generation of supernova induced phenomena such as galactic superwinds.

Key words: ISM: kinematics and dynamics - ISM: supernova remnants - galaxies: ISM

   
1 Introduction

The interaction of supernova ejecta with surrounding material notionally proceeds through a sequence of distinct stages. In the initial free expansion (FE) phase, a shock is driven into the ambient gas and a reverse shock accelerates through the ejecta towards the stellar remnant. After most of the explosion energy has been transferred to the ambient gas, the remnant enters the Sedov-Taylor (ST) phase. In this and the FE stage, radiative losses are essentially negligible. Truelove & McKee (1999) have given an exhaustive treatment of this early evolution. Eventually, radiative cooling in the swept-up gas becomes dynamically important and the remnant enters the pressure-driven snowplough (PDS) phase. Depending on circumstances (e.g. Cioffi et al. 1988), a later momentum conserving snowplough phase may occur.

Most treatments of remnant evolution are based on the assumption that surrounding material is smoothly distributed. Hartquist & Dyson (1988) noted that most diffuse astronomical sources (including supernova remnants) result from the injection of energy and/or momentum into multiphase media where clumps of cool gas reside in a substrate of hotter gas. Mass pickup from clumps affects the behaviour and structure of generated flows.

Cowie et al. (1981) numerically modelled the effects of a supernova explosion on a medium where discrete clouds are embedded in a lower density substrate. Cloud material is thermally evaporated into the remnant and the dynamics of the clouds were included. Observations by Chu et al. (1999) of the supernova remnant N63A in the Large Magellanic Cloud reveal dense globules embedded in the hot, shocked gas, which are being evaporated. This is the first clear observational evidence of engulfed cloudlets within a supernova remnant.

Several authors have derived similarity solutions to describe remnant evolution where clouds are treated essentially as continuously distributed mass injection sources. McKee & Ostriker (1977), Chièze & Lazareff (1981) and White & Long (1991) assumed that conductive evaporation drives the mass injection. White & Long (1991) gave solutions that allow for fast and slow evaporation of clouds. Dyson & Hartquist (1987) assumed that material is hydrodynamically ablated into remnants according to a prescription given by Hartquist et al. (1986) (hereafter HDPS).

Arthur (1994) made a preliminary numerical study of the effect of mass loading due to hydrodynamic ablation on supernova remnants in the adiabatic phase. Arthur & Henney (1996) used numerical simulations of mass-loaded supernova remnants to explain the excess soft X-ray emission in bubbles in the Large Magellanic Cloud. They assumed that all the explosions occurred in low density cavities excavated by the progenitor stellar winds and that material was hydrodynamically ablated from clumps embedded in the cavity using the prescription of HDPS. They found that mass loading of these cavity remnants was capable of producing the observed soft X-ray emission over the predicted lifetime of the remnants.

Mass loaded supernova remnants are important in a variety of contexts. A remnant inside a molecular cloud propagates through a multiphase medium with a complex structure partly determined by the interaction of the progenitor star or neighbouring stars with the cloud. The range of the remnant in the cloud is a significant factor in the importance of the remnant for e.g. sequential star formation. On larger scales, the collective effects of supernova explosions drive galactic superwinds (e.g. Chevalier & Clegg 1985; Heckman et al. 1990; Suchkov et al. 1996). Suchkov et al. (1996) showed that the superwind in the starburst galaxy M82 must be mass-loaded to account for the observed X-ray emission. This necessary mass injection can be supplied by conductive or ablative cloud evaporation in the core of M82 (Hartquist et al. 1997). The ranges and radiative energy losses of individual remnants are affected by mass loading and these in turn affect the global wind dynamics and structure.

Quite accurate approximations, confirmed by appropriate numerical modelling, are available to describe remnant evolution in smooth media (Cioffi et al. 1988; Truelove & McKee 1999 and references therein). These approximations represent unified solutions for SNR evolution in the early (Truelove & McKee 1999) and later (Cioffi et al. 1988) stages. Such solutions have the property that only one simulation need be performed for each regime to determine the evolution of all SNRs with the same form of initial ejecta and ambient medium density.

To date, no such approximations have been produced to describe the evolution of remnants with mass loading. In this paper we present some simple approximations for remnant evolution based on extensive numerical modelling.

   
2 The calculations

We here assume that a) mass injection takes place from continuously distributed sources; b) injection takes place at zero velocity relative to the global flow and the injected gas has zero internal energy; c) that injection occurs only within the remnant. (This last assumption might not be appropriate if, for example, massive stars in the vicinity of the supernova, are photoionizing clumps ahead of the blast wave.) In this paper we consider two functional forms for the mass injection: a constant mass injection rate, q, and mass injection whose rate depends on the flow Mach number relative to the clump (cf. HDPS). That is, a mass loading rate of q M^4/3in the subsonic case, where M is the Mach number of the flow, and constant mass loading rate q where the flow is supersonic. In a later paper we will model the evolution of remnants in which mass injection takes place by thermal evaporation (cf. McKee & Ostriker 1977).

We define a fiducial mass loading rate by

$$q_{\rm0} = \frac{3V_{\rm SF} \rho_0}{R_{\rm SF}} \equiv \frac{6 \rho_0}{5 t_{\rm SF}} \ \mbox{g~cm$^{-3}$ ~s$^{-1}$ },$$ (1)

which is simply the mass flux through the blast wave divided by the remnant volume at the onset of thin shell formation. Here, $R_{\rm SF}$ and $V_{\rm SF}$ $( = 2 R_{\rm SF}/5 t_{\rm SF})$ are respectively the remnant radius and expansion speed at the epoch of thin shell formation, $t_{\rm SF}$, for remnant evolution in a homogeneous medium of density $\rho_0$. (They are assumed to follow the Sedov expansion law up to this point.) We adopt the expression for $t_{\rm SF}$ given by Franco et al. (1994)

$$t_{\rm SF} = 2.87 \times 10^4 E_{51}^{3/14} n_{0}^{-4/7} \ \ \mbox{yrs} .$$ (2)

The explosion energy is E ( = 10⁵¹ E₅₁ ergs) and n₀(cm^-3) is the ambient number density. In these units, $q_0 = 2.65 \times 10^{-36} n_0^{11/7} E_{51}^{-3/14}$ g cm^-3 s^-1. We have used mass loading rates q = f q₀, where f = 0, 0.1, 1, 3, 10, 30, 100, and ambient densities n₀ = 0.01, 0.1, 1, 10, 100 cm^-3. The different values of f thus quantify the relative importance of the mass loading. Low values of f mean that mass loading will not dominate in the remnant before the time of onset of thin shell formation, while f > 1 indicates that the ablated mass should become important in the remnant before $t_{\rm SF}$is reached.

It should be noted that this description of the mass loading is for the purely general case and that, in practice, f is determined by the physical situation being studied. Our aim in this paper is to provide simple descriptions of the evolution of mass loaded supernova remnants and to this end we are ignoring details such as clump lifetimes and spatial distributions, which only introduce additional, problem specific, parameters.

All calculations have been carried out using a second order Eulerian Godunov-type code (see e.g., Arthur & Henney 1996), an upwind scheme which solves the conservation equations using a finite volume approach. We assume spherical symmetry. The mass-loading term enters as a source term in the continuity equation. The full set of gas dynamic equations is

$$\frac{\partial \rho}{\partial t} + \frac{1}{r^2} \frac{\partial}{\partial r} r^2 \rho u = q ,$$ (3)

$$\frac{\partial \rho u}{\partial t} + \frac{1}{r^2} \frac{\partial}{\partial r} r^2 (p + \rho u^2) = \frac{2p}{r} ,$$ (4)

$$\frac{\partial e}{\partial t} + \frac{1}{r^2} \frac{\partial}{\partial r} r^2 u ( e + p) = -L ,$$ (5)

where the symbols $\rho$, u, and p have their usual meanings, $e = p/(\gamma - 1) + 0.5 \rho u^2$ is the total energy, L is the radiative cooling term, and q is the mass loading rate discussed above.

Figure 1: a) Logarithm of expansion velocity (km s-1) against logarithm of time in years for n0 = 0.01 cm-3. Upper line (solid) is the case f = 0, middle line (dashed) is f = 10, and lower line (dot-dashed) is f = 100. The vertical dotted lines represent the time at which the remnant is said to merge with an ambient medium at 104 K, while the horizontal bars mark the beginning and end of the QST phase: A corresponds to f = 0; B to f = 10, C to f = 100. b) Logarithm of remnant radius against log(time) for the same cases as a). Constant mass loading rate.

Open with DEXTER

	Figure 2: Same as Fig. 1 but for Mach number dependent mass loading rate.
Open with DEXTER

	Figure 3: Same as Fig. 1 but for n0 = 100 (Constant mass loading rate).
Open with DEXTER

	Figure 4: Same as Fig. 3 but for Mach number dependent mass loading rate.
Open with DEXTER

Radiative cooling is assumed to be collisional ionization equilibrium cooling. We calculate the equilibrium ionization structure in each grid cell from lookup tables. The cooling is found by multiplying the ionization fraction and cooling rate of each ion species by the appropriate elemental abundance. The tables have been generated by considering the detailed atomic physics in a temperature range of 2000 K to 10⁹ K, in the limit of low density ( $n_0 \le 10^4$ cm^-3). In this way we can calculate the cooling for any given set of abundances. Here we use Solar abundances (Anders & Grevesse 1989). The use of lookup tables means that this calculation is not much more costly than the use of a parametrized cooling curve.

The initial conditions used are the injection of $10~M_\odot$ with a supernova energy of 10⁵¹ ergs using the `adiabatic lapse rate' prescription of Gull (1973). This prescription gives the density, velocity and pressure distributions as functions of radius within the ejecta. The rapid expansion of the ejecta means that in a short time the initial thermal energy is converted to kinetic energy (essentially, the pressure within the ejecta becomes negligible). The extent of the remnant within the computational grid is regularly checked and the grid is automatically extended when necessary. Furthermore, there is a periodic regridding of the whole grid when adjacent cells are combined using a simple volume-weighted average. These procedures ensure the most efficient calculation at resolution appropriate to the current evolution of the remnant (see also Appendix A).

Mass loading is assumed to occur only in the part of the remnant that corresponds to swept-up interstellar medium. This avoids unrealistically large mass injection rates at small radii caused by fluctuations in the Mach number due to reflections of secondary shock waves at the center of symmetry of the remnant. The ejected material is traced with a passive scalar.

The definitions of the ends of the FE and ST phases are to some extent arbitrary. Here we define the FE stage as ending when the internal energy of the remnant reaches 60% of the explosion energy. We define the ST phase as ending when the total remnant energy (thermal plus kinetic) drops to 50% of the explosion energy, and because of this, refer to it as the QST ("Quasi-Sedov-Taylor'') phase. The remnants are evolved until they degenerate to an acoustic wave. In the models, the ambient gas has a temperature of 100 K. In many situations, merger into ambient gas at $10^{\rm 4}$ K is probably more appropriate and this has been marked on figures where useful. (In the specific case of superwind generation, merger might take place with gas at even higher temperatures.)

   
3 Results

In Figs. 1a and 1b respectively, we show the evolution of the remnant expansion speed and radius as functions of time up to merger with surrounding gas at a temperature of 10⁴ K for zero mass loading, moderate mass loading (f = 10) and high mass loading (f = 100) for low ambient density ( n₀ = 0.01 cm^-3) for a constant mass loading rate. Figures 2a and 2b give the same information but for the case of Mach number dependent mass loading. In Figs. 3 and  4 the corresponding figures for a high ambient density (n₀ = 100 cm^-3) are plotted. The reductions in expansion velocity and range caused by mass loading are evident and these reductions are quantified later.

Figures 5a-5d give mass fractions of swept up and injected material as functions of time for the moderate and high mass loading cases above in the constant mass loading case. At the end of the FE phase, with moderate mass loading, the swept-up mass dominates the total mass for low n₀, whereas for high n₀, the fractions of swept up and injected mass are comparable. With high mass loading, the fractions are comparable at low n₀ but the ablated mass dominates at high n₀ again at the end of the FE stage. At the end of the QST phase, the injected mass is a few times that of the swept-up mass for both low and high n₀ with moderate mass loading. Injected mass always dominates by at least an order of magnitude at the end of the QST phase with high mass loading. Figures 5e-5h show the corresponding variation of mass fraction with time for the case of Mach number dependent mass loading rate, where the statements above for constant mass loading also hold. The tendency is for the swept-up mass fraction to dominate for a shorter time in the constant mass loading case than in the Mach number dependent case. This is expected since in the constant mass loading case, mass loading occurs equally at all radii, so the mass-loaded mass fraction starts to dominate earlier.

Figure 6a shows the time variation of the total energy of a remnant (as a fraction of the explosion energy) and the remnant thermal and kinetic energies (as fractions of the total energy) for a "standard remnant'' (i.e., one with zero mass loading and n₀ = 1 cm^-3). From Eq. (2), shell formation takes place at $t_{\rm SF} = 2.87 \times 10^4$ years with the parameters given. The sudden loss of thermal energy and increase in the fraction of kinetic energy are clearly seen. Figure 6b gives the same information for low ambient density ( n₀ = 0.01 cm^-3) and moderate constant mass loading respectively (the variation for high mass loading is very similar). The increase in the fraction of kinetic energy during the rapid cooling phase is much less marked than in the standard remnant case. Figure 6c gives the same information for a high ambient density (n₀ = 100 cm^-3) and moderate constant mass loading (again similar to the variation for high mass loading). The variation once again is similar to the standard case. Figures 6d and 6e are for the same parameters as Figs. 6b and 6c but for the Mach number dependent mass loading rate. There is little qualitative difference between the corresponding figures for Mach number dependent and constant mass loading rates.

Figure 5: Mass fractions as functions of logarithm of time in years. In each figure the solid line is the swept up mass fraction, the dashed line is the ablated mass fraction and the dot-dashed line is the ejecta mass fraction. a) n0 = 0.01, f = 10; b) n0 = 0.01, f = 100; c) n0 = 100.0, f = 10; d) n0 = 100.0, f = 100: a)-d) are for constant mass loading rates. e)-h) are the same parameters as a)-d) but for Mach number dependent mass loading rates. The labelled vertical dotted lines denote the end of the free expansion stage (FE), the end of the Quasi-Sedov-Taylor stage (QST), and merger with an ambient medium of temperature 104 K (M).

Open with DEXTER

Figure 6: Thermal energy (dot-dashed line) and kinetic energy (dashed line) as fractions of total energy against logarithm of time in years. Also shown (solid line) is the evolution of the total energy as a fraction of the initial supernova energy. a) n0 = 1, f = 0 ("Standard Remnant''); b) n0 = 0.01, f = 10 (constant mass loading rate); c) n0 = 100, f = 10 (constant mass loading rate); d) n0 = 0.01, f = 10 (Mach number dependent mass loading rate); e) n0 = 100, f = 10 (Mach number dependent mass loading rate). The labelled vertical dotted lines indicate the end of the free expansion stage (FE), the end of the Quasi-Sedov-Taylor stage (QST), and merger with an ambient medium of temperature 104 K (M).

Open with DEXTER

Figure 7: Logarithm of the ratio of half energy time to thin shell formation time ( $\log (t_{1/2}/t_{\rm SF})$) against logarithm of mass loading factor ($\log f$) for full range of densities considered. Heavy solid line, n0 = 0.01; dashed line, n0 = 0.1; dot-dashed line, n0 = 1.0; dotted line, n0 = 10.0; thin solid line, n0 = 100. a) Constant mass loading rate b) Mach number dependent mass loading rate.

Open with DEXTER

In Fig. 7, the ratio of t_1/2(f,n₀) (the time when the total energy of the remnant falls to one half the explosion energy) and $t_{\rm SF}(n_0)$ (the shell formation time defined in Eq. (2)) is shown as a function of the mass loading parameter f for the five values of the ambient density used. Figure 7a shows results for the constant mass loading rate. The ratio is fairly insensitive to the value of n₀ used. In the Mach number dependent mass loading case, Fig. 7b, the ratio is very insensitive to the value of n₀ used. A good approximation for this case is $t_{1/2}(f,n_0)/t_{\rm SF}(n_0) \approx 2 f ^{-3/10}$ for $f \ge 1$. We return to this point in Sect. 4.

Figures 8a and 8b give respectively the density and pressure distributions within a non-mass loaded remnant just at the onset of cooling when the total remnant energy has dropped to 95% of the explosion energy. These are essentially the standard ST distributions. (The large interior density peak is the result of cooling of ejecta that have piled up behind the reverse shock.) These distributions are changed very little up to the inclusion of moderate mass loading over the entire range of n₀. Figures 8c to 8f give the same information respectively for constant and Mach number dependent mass loading. In either case, as the mass loading increases, the density structures in the swept-up gas interior to the blast wave (cf. Figs. 8c and 8e) begin to resemble those given by the injection dominated similarity solutions of Dyson & Hartquist (1987) (for their parameter $\alpha = 0$, i.e., no spatial variation of the mass loading term). That is, the interior density increases steeply after the shock and then smoothly decreases. (This is in contrast to the standard ST solution (cf. Fig. 8a), where the density is at a maximum immediately behind the shock and then monotonically decreases inwards.) However, unsurprisingly, the pressure distributions in all cases are approximately uniform over most of the remnant interiors (see Figs. 8b, 8d and 8f). (In all the pressure plots, the structure that can be seen is the result of waves reflecting between the internal density peak and the blast wave and also between the density peak and the centre of symmetry, and correspond to the "echoes of thunder'' reported by Cioffi et al. 1988.)

   
4 Discussion

   
4.1 The free expansion phase

Figure 8: a) Logarithm of density (cm-3) against radius (pc) for the "Standard Remnant'' (n0 = 1, f = 0) at time when it has radiated 0.05 of its initial energy ( $t = 2.675\times 10^4$ yrs). b) Logarithm of pressure (g cm-1 s-2) against radius (pc) for the same remnant. c) Same as a) but for the case n0 = 0.01, f = 100 constant mass loading rate, $t = 1.132 \times 10^5$ yrs. d) Same as b) but for the same case as c). e) Same as a) but for the case n0 = 0.01, f = 100 Mach number dependent mass loading rate, $t = 8.855 \times 10^4$ yrs. f) Same as b) but for the same case as e).

Open with DEXTER

 

 

Table 1: Total mass in remnant at the end of the free expansion stage for the full range of parameters considered: constant mass injection rates.

	f
n0	0.0	0.1	1.0	3.0	10.0	30.0	100.0
0.01	1.767	1.769	1.771	1.778	1.761	1.725	1.708
0.10	1.759	1.759	1.764	1.756	1.745	1.718	1.700
1.00	1.794	1.770	1.779	1.767	1.755	1.748	1.673
10.0	1.789	1.797	1.786	1.780	1.748	1.735	1.723
100.0	1.796	1.792	1.783	1.791	1.775	1.753	1.734

 

 

Table 2: Total mass in remnant at the end of the free expansion stage for the full range of parameters considered: Mach number dependent mass loading rates.

	f
n0	0.0	0.1	1.0	3.0	10.0	30.0	100.0
0.01	1.767	1.768	1.771	1.776	1.771	1.735	1.701
0.10	1.759	1.759	1.764	1.760	1.749	1.730	1.692
1.00	1.794	1.769	1.777	1.765	1.749	1.738	1.687
10.0	1.789	1.802	1.773	1.781	1.767	1.730	1.690
100.0	1.796	1.798	1.788	1.757	1.731	1.752	1.728

Tables 1 and 2 give the total mass in the remnant at the end of the FE phase for the two types of mass loading. Regardless of its source, this total mass is $57.16 \pm 3.87$ $M_\odot$for the Mach number dependent mass loading rate case and $57.47 \pm 3.73$ $M_\odot$ for the constant mass loading rate case. These two results are in such close agreement because the amount of mass in the remnant is the determining factor in the transition to the QST phase (cf. Gull 1973).

The radius of the remnant, $R_{\rm E}$, at the end of the FE phase (see e.g., Figs. 1, 2, 3 and 4) is found from the equation for mass conservation

$$\frac{\partial M}{\partial t} = \frac{4\pi R_{\rm E}^3 q}{3} + 4\pi R_{\rm E}^2 V_{\rm E} \rho_0 ,$$ (6)

where M is the remnant mass, $R_{\rm E} \equiv V_{\rm E} t_{\rm E}$ is the remnant radius, $V_{\rm E}$ is the expansion velocity (assumed constant) and $t_{\rm E}$ is the elapsed expansion time, and $\rho_0$ is the density of the ambient medium. Integrating Eq. (6) and using the definitions of q and q₀ from Eq. (1), we obtain

$$M - M_0 = \frac{4\pi}{3} R_{\rm E}^3 \rho_0 \left[ \frac{6f}{20}\frac{t_{\rm E}}{t_{\rm SF}} + 1 \right] ,$$ (7)

where M₀ is the ejecta mass and $t_{\rm SF}$ is the shell formation time defined in Eq. (2). Hence, the radius at the end of the free expansion stage, when M = 57 $M_\odot$, is approximately given by

$$R_{\rm E}(f,n_0) = 7.7 n_0^{-1/3} \mu^{-1/3} (1 + \mathcal{F})^{-1/3} \mbox{ pc },$$ (8)

where

$$\mathcal{F} = 0.026 f \mu^{-1/3} n_0^{5/21} V_{3}^{-1} E_{51}^{-3/14} .$$ (9)

Here, the ejecta mass is $10~M_\odot$ and the ejecta velocity is $V_{\rm E} = 3000 V_3$ km s^-1. The mean particle mass in proton masses is $\mu$, taken to be 1.4 in this paper. In deriving this expression, we have taken the expansion time to be $t_{\rm E} = R_{\rm E}(f,n_0)/V_{\rm E} \approx [0.75 (M - M_0)/(\pi \rho_0) ]^{1/3}/V_{\rm E}$.

Figure 9: Logarithm of radius at the end of the free expansion stage against logarithm of ambient density. The symbols represent the results of the numerical simulations and the lines are the analytic approximation of Eq. (8). The triangles and solid line are for a low mass loading rate (f = 0.1) and the diamonds and dashed line are for a high mass loading rate (f = 100). At the resolution of this figure, the results for constant and Mach number dependent mass loading rates are coincident.

Open with DEXTER

In Fig. 9 we plot the variation of $R_{\rm E}$ with ambient density, n₀. In this figure the symbols represent the results from the simulations and the lines are the analytic approximation from Eq. (8). The triangles and solid line represent a low mass loading factor (f = 0.1) while the diamonds and dashed line are for high mass loading (f = 100). The values of $R_{\rm E}(f,n_0)$derived in Eq. (8) agree with the numerical calculations to within 25% in the case of high mass loading and to within 3% for low mass loading (and give the same agreements for both types of mass loading). In all cases the worst agreement corresponds to the highest value of the ambient density. This is because our analytic approximation assumes a constant mass loading rate throughout the remnant volume, whereas in the simulations there is no mass loading in the volume occupied by the ejecta material (see Sect. 2). Thus for the higher density, high mass loading rate cases, the analytic approximation is overestimating the contribution of the mass-loaded material to the remnant mass and hence underestimates the radius $R_{\rm E}$ at the end of this free expansion stage. The assumption that there is no mass loading in the volume occupied by the ejecta means it takes longer for the remnant to achieve the 57 $M_\odot$required to enter the QST phase and hence the radii at the end of the free expansion stage of the remnants in the simulations are larger.

The values of $t_{\rm E}$ agree to about 30% over the mass loading range. We found that a better approximation to $t_{\rm E}$, derived from the numerical results, is to use an expansion law $R \propto t^\eta$, where $\eta \approx 0.75$, over the FE phase and put $V \approx V_{\rm E}/2$ at time $t=t_{\rm E}$. This gives $t_{\rm E} \approx 1.5 R_{\rm E}(f,n_0)/V_{\rm E}$ which agrees to within about 10% (using Eq. (8)) for $R_{\rm E}(f,n_0)$ with the values from the calculations. This procedure, using an underestimate for $t_{\rm E}$ in deriving $R_{\rm E}(f,n_0)$, approximately allows for the fact that mass loading is switched off in the ejecta as mentioned in Sect. 2.

   
4.2 The QST phase

We take this as lasting to time t = t_1/2(f,n₀). Over this phase, using either mass loading prescription, the expansion law is much closer to the usual ST law $R \propto t^{2/5}$ than the t^1/5 law predicted for mass loading dominated solutions found by Dyson & Hartquist (1987). If we adopt the ST variation, the radius $R_{\rm QST}(f,n_0)$ at the end of the QST phase is given by

$$R_{\rm QST}(f,n_0) \approx R_{\rm E}(f,n_0) \left[ \frac{t_{1/2}(f,n_0)}{t_{\rm E}(f,n_0)} \right]^{2/5} ,$$ (10)

where $R_{\rm E}(f,n_0)$ is given by Eq. (8) and we put $t_{1/2}(f,n_0) = 2 f^{-3/10} t_{\rm SF}(n_0)$ (see Sect. 3). We use this variation derived for the case of Mach number dependent mass addition because there is less dispersion in the value of t_1/2(f,n₀) with n₀ for this case and because Mach number dependent mass addition has a more plausible physical basis. The form of this relationship can be understood if we assume that injected mass dominates the interior density <n>so that $<n> \propto fq_0t$ and it is this density which determines the cooling time. If we adopt the standard ST expansion law, assume that t_1/2(f,n₀) has the same density dependence as $t_{\rm SF}(n_0)$, and take a T^-1/2 cooling law (Kahn 1976), then $t_{1/2}(f,n_0)/t_{\rm SF}(n_0) \propto f^{-5/19}$, close to the dependence found. (Of course a T^-1/2 law is only an approximation to the detailed cooling used in the numerical calculations.)

Figure 10: Logarithm of radius at the end of the QST stage against logarithm of ambient density. The symbols represent the results of the numerical simulations and the solid lines are the analytic approximation of Eq. (10). Solid symbols are for constant mass loading rate and open symbols are for Mach number dependent mass loading rate. The triangles, circles and upper solid line are for a low mass loading rate (f = 0.1) and the diamonds, squares and lower solid line are for a high mass loading rate (f = 100). The dashed lines represent fits to $R_{\rm QST}$ obtained from Eq. (11).

Open with DEXTER

In Fig. 10 we plot the values of $R_{\rm QST}$ obtained from the simulations (symbols) together with those derived using Eq. (10) (solid lines) for the cases of low mass loading (f = 0.1) and high mass loading (f = 100.0). We see that Eq. (10) provides a good fit for the high mass loading case but for low mass loading systematically overestimates the radius at the end of the QST phase, although the gradient of the line matches that of the data points. This is because the value of $t_{\rm E}(f,n_0)$ obtained from the simulations is less than the $t_{\rm E}$ obtained from a simple analytical consideration of free expansion (see Sect. 4.1). In the high mass loading case the overall fit is good but the gradient of the analytic solution is steeper than that of the data points. In both cases, the difference between analytic approximation and data points mirrors the fit shown in Fig. 9 but with an offset due to the smaller value of $t_{\rm E}$ obtained from the calculations.

	Figure 11: Logarithm of the ratio of radius at end of Quasi-Sedov-Taylor phase to radius at same point for case f = 0 ( $\log~(R_{\rm QST} /R_{\rm QST}~(f=0))$ against $\log f$ for all n0). Heavy solid line, n0 = 0.01; dashed line, n0 = 0.1; dot-dashed line, n0 = 1.0; dotted line, n0 = 10.0; thin solid line, n0 = 100. a) Constant mass loading rate. b) Mach number dependent mass loading rate.
Open with DEXTER

An alternative approximation to the radii can be obtained from Fig. 11 which shows that there is very little variation of $R_{\rm QST}/R_{\rm QST}(f=0)$ with n₀. An excellent approximation is

$$R_{\rm QST} \approx 0.9 R_{\rm QST}(f=0)(10 \sqrt{f})^{-0.09 \log_{10}f} .$$ (11)

This fit applies to both constant and Mach number dependent mass loading rates. In Fig. 10 we plot this approximation (dashed lines) and show that it is a good fit for both low and high mass loading.

	Figure 12: Ratio of radius at time of merger with an ambient medium of temperature 104 K, R4, to radius at end of Quasi-Sedov-Taylor phase, $R_{\rm QST}$, against $\log f$ for all n0. Heavy solid line, n0 = 0.01; dashed line, n0 = 0.1; dot-dashed line, n0 = 1.0; dotted line, n0 = 10.0; thin solid line, n0 = 100.0. a) Constant mass loading rate; b) Mach number dependent mass loading rate.
Open with DEXTER

However, only a poor estimate of the velocity at the end of the QST phase is given using a standard ST variation because there is a very sudden velocity drop as t approaches $t_{\rm QST}$ (cf. Figs. 1, 2, 3 and 4). In fact, once moderate mass loading is reached or exceeded, the velocity drops so rapidly toward 10 km s^-1 that the supernova range can be taken to be equal to $R_{\rm QST}$ at least for circumstances where the sound speed in the ambient gas is equal to 10 km s^-1. In Fig. 12 we plot the ratio of the radius at the time corresponding to merger with an ambient medium of temperature 10⁴ K to the radius at the end of the QST stage. This figure demonstrates how effectively moderate to high mass loading reduces the SNR range. The reduction is more pronounced for higher ambient densities. This reduction in range is due to a depressurising in the interior of the SNR as the additional mass from the mass loading causes cooling in a greater volume of the remnant interior than in the case of no mass loading. Furthermore, it is evident from the expression for $R_{\rm QST}$ that mass loading greatly reduces the effectiveness of supernovae in pressurising surrounding media. For example, if f=100, a supernova remnant affects less than 1% of the volume a standard remnant in the same ambient density would affect. We finally note that the higher the temperature of the ambient material, the less important mass loading becomes as far as supernova ranges are concerned.

   
4.3 Constant versus Mach number dependent mass loading rate

The essential difference between the two forms of mass loading is that for constant mass loading the mass loading rate is the same at all radii within the remnant, whereas for the Mach number dependent mass loading rate it is highest where the Mach number of the flow within the remnant is closest to unity. This is generally just behind the shock wave and, indeed, drops sharply at smaller radii.

At early times, there is little difference between the results for the two different forms of mass loading (see e.g., Figs. 9, 10 and 11). This is because in the free expansion and QST phases cooling is not important and so the extra mass that is added in the constant mass loading rate case does not have a dynamical effect on the remnant. Once cooling becomes important, at the end of the QST phase, the differences between the two different forms for the mass loading rate become more pronounced. Firstly, from Fig. 5 we see that the ablated mass begins to dominate in the remnant earlier in the constant mass loading rate case. This is an obvious result. In the constant mass loading case, the mass loaded material is distributed throughout the remnant and leads to enhanced cooling rates. Consequently, cooling occurs in a larger volume of the remnant interior in the constant mass loading case than in the Mach number dependent case. This can be seen in Fig. 6 where, at the end of the QST phase, there is a much sharper drop in the thermal energy fraction in the constant mass loading rate case than in the Mach number dependent case. Finally, the times until final merger with an ambient medium at 10² K are slightly shorter for the constant mass loading rate case because the remnant internal pressure decreases more rapidly due to cooling throughout the remnant volume.

   
5 Conclusions

We have investigated the structures and, more specifically, the ranges of supernova remnants where mass loading occurs. We have found simple approximations which fit the evolution of remnants in the free expansion and QST phases where mass loading is either spatially constant or Mach number dependent. The differences between the two cases in these stages of evolution are negligible, given the uncertainties in the physics of mass addition into flows. In future work we will use these results to investigate supernova generated galactic superwinds.

Acknowledgements

SJA would like to acknowledge support from DGAPA-PAPIIT project IN117799, UNAM, Mexico and partial support of a visit to Leeds from PPARC.

   
Appendix A: Numerical method

The code used for solving the gas dynamic equations (Eqs. (3), (4) and (5)) is a second order Eulerian Godunov-type scheme (see e.g., Arthur & Henney 1996). The number of cells in the numerical grid is not constant, being increased when the supernova blast wave moves close to the current grid boundary. Furthermore, the resolution of the spatial grid is dynamic, since it is periodically rescaled using a procedure whereby conserved quantities in neighbouring cells are combined using a simple volume weighted average. This strategy ensures sufficient resolution to follow the initial stages of the remnant evolution accurately but a manageable grid size in the later stages of evolution.

These calculations include radiative cooling, which requires additional considerations. Fortunately, in this work we are not concerned with modeling the detailed emission from the postshock region. However, we do need to be sure that the calculation of global quantities such as the thermal energy as a function of time are not resolution dependent. An important quantity is the postshock cooling length, defined by

$$l_{\rm cool} = \frac{p_{\rm s} v_{\rm s}}{(\gamma - 1)L} ,$$ (A.1)

where $p_{\rm s}$ is the postshock pressure, $v_{\rm s} = 2 V/(\gamma + 1)$ is the postshock velocity (where V is the velocity of the shock) and L is the cooling rate per unit volume. In this paper, the cooling is assumed to be collisional ionization equilibrium cooling, and the abundances are solar, hence the maximum value of the cooling term is $L = 10^{-21} n_{\rm e} n_{\rm H}$ erg cm^-3 s^-1 (see e.g., Sutherland & Dopita 1993) and occurs at a temperature $T = 2.25 \times 10^5$ K. This temperature corresponds to a shock velocity of $V^2 = (\gamma + 1)^2 kT/[2 m_{\rm p}(\gamma -1)]$, where k is Boltzmann's constant and $m_{\rm p} = 1.4 m_{\rm H}$ is the mean particle mass, hence V = 84 km s^-1. The cooling length is therefore $l_{\rm cool} \approx 0.024/n_0$ pc when radiative cooling is at its maximum in the postshock gas. To adequately resolve the details of the cooling region about 10 grid cells are needed per cooling length. Thus, the size of a grid cell should be about 0.0024/n₀ pc.

Obviously, for the lowest densities, this resolution is easily achieved without the number of grid cells becoming too large. However, for the highest densities, for example n₀ = 100, we require a grid cell dimension of $2.4\times 10^{-5}$ pc. This sort of calculation becomes very computationally expensive.

Figure A.1: Thermal energy fraction as a function of time: a) n0 = 0.01, f = 10; b) n0 = 100.0, f = 10. The different line types correspond to three different resolutions: dashed line, low resolution; solid line, medium resolution; dot-dashed line, high resolution. Each resolution differs from the previous one by a factor of two. The horizontal bars mark the end of the free expansion phase (left-most tick mark), the end of the QST phase (central tick mark), and the time of merger with an ambient medium of temperature T = 104 K (right-most tick mark) for each resolution. Constant mass loading rate.

However, it is not necessary to perform the calculations to this level of resolution. As mentioned previously, we are not interested in the detailed emission from the postshock region, only in global quantities. In particular, we are interested in the times when the remnants pass from one stage of evolution to the next, and the sizes of the remnants at these points. In Fig. A.1 we show the evolution of the thermal energy fraction as a function of time for the two cases n₀ = 0.01 cm^-3 and n₀ = 100 cm^-3, with f = 10 in each case, where the mass loading rate is assumed constant. These represent the two extremes of behaviour. In each figure we show the results for calculations at three different resolutions, each differing from the previous by a factor of two. As to be expected, in the low density case (Fig. A.1a) all the results are coincident, since only low resolution is required to resolve the cooling region at this low density. In the high density case (Fig. A.1b) we first note that the free expansion and QST phase boundaries are coincident at all resolutions. Once cooling becomes important the results for all three resolutions are different during the "catastrophic cooling'' stage (Falle 1975, 1981) when secondary shocks are formed following a loss of pressure in the cooling gas. This leads to oscillations in the shock velocity (see Figs. 2 and  4). However, once this highly nonlinear stage is over, the three sets of results are once again the same and the times for merger with a 10⁴ K ambient medium coincide for the two higher resolutions.

In this paper we have used the middle resolution in all the calculations. In addition, the majority of the results derived from the calculations pertain to the free expansion and QST stages, for which it is not crucial to have such a high resolution since cooling is not yet important. For the later stages of evolution, even though for the highest density ambient medium we do not use a resolution high enough to resolve the details in the postshock cooling region, the resolution is high enough to give robust results for the global quantities considered in this paper.

References

 
• Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 In the text  
• Arthur, S. J. 1994, in Numerical Simulations in Astrophysics, ed. J. Franco, S. Lizano, L. Aguilar, & E. Daltabuit (Cambridge: CUP), 210 In the text  
• Arthur, S. J., & Henney, W. J. 1996, ApJ, 457, 752 In the text NASA ADS  
• Chevalier, R., & Clegg, A. 1985, Nature, 317, 44 In the text NASA ADS  
• Chièze, J. P., & Lazareff, B. 1981, A&A, 95, 194 In the text NASA ADS  
• Chu, Y.-H., Caulet, A., Dickel, J., et al. 1999, IAU Symp. 190, New Views of the Magellanic Clouds, ed. Y.-H. Chu, N. Suntzeff, J. Hesser, & D. Bohlender, 143 In the text  
• Cioffi, D. F., McKee, C. F., & Bertschinger, E. 1988, ApJ, 334, 252 In the text NASA ADS  
• Cowie, L. L., McKee, C. F., & Ostriker, J. P. 1981, ApJ, 247, 908 In the text NASA ADS  
• Dyson, J. E., & Hartquist, T. W. 1987, MNRAS, 228, 453 In the text NASA ADS  
• Falle, S. A. E. G. 1975, MNRAS, 172, 55 In the text NASA ADS  
• Falle, S. A. E. G. 1981, MNRAS, 195, 1011 In the text NASA ADS  
• Franco, J., Miller, W. W., Arthur, S. J., Tenorio-Tagle, G., & Terlevich, R. 1994, ApJ, 435, 805 In the text NASA ADS  
• Gull, S. F. 1973, MNRAS, 161, 47 In the text NASA ADS  
• Hartquist, T. W., & Dyson, J. E. 1988, ApSS, 144, 615 In the text  
• Hartquist, T. W., Dyson, J. E., Pettini, M., & Smith, L. J. 1986, MNRAS, 221, 715 (HDPS) In the text NASA ADS  
• Hartquist, T. W., Dyson, J. E., & Williams, R. J. R. 1997, ApJ, 482, 182 In the text NASA ADS  
• Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 73, 833 In the text  
• Kahn, F. D. 1976, A&A, 50, 145 In the text NASA ADS  
• McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 In the text NASA ADS  
• Suchkov, A. A., Berman, V. G., Heckman, T. M., & Balsara, D. S., 1996, ApJ, 463, 528 In the text NASA ADS  
• Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 In the text NASA ADS  
• Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 In the text NASA ADS  
• White, R. L., & Long, K. S. 1991, ApJ, 373, 543 In the text NASA ADS