A&A 390, 937-943 (2002)
DOI: 10.1051/0004-6361:20020748

Red giant branch stars as probes of stellar populations. I.
2MASS calibration and application to 2MASS GC01

V. D. Ivanov1 - J. Borissova2


1 - European Southern Observatory, Ave. Alonso de Cordova 3107, Casilla 19, Santiago 19001, Chile
2 - Institute of Astronomy, Bulgarian Academy of Sciences, and Isaac Newton Institute of Chile, Bulgarian Branch, 72 Tsarigradsko Chaussèe, 1784 Sofia, Bulgaria

Received 16 January 2002 / Accepted 24 April 2002

Abstract
The near-infrared behavior of the red giant branch (RGB hereafter) as a function of abundance is examined with an unprecedented large sample of 27 Galactic globular clusters with Two Micron All Sky Survey photometry. We propose a new simplified analysis, involving the zero point of the RGB slope fit, and derive calibrations for the RGB slope, zero point, and tip. The weak metallicity sensitivity of the zero point leads to a "fan''-like diagram to obtain the abundance distributions in resolved stellar systems, and reddening estimates. 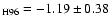Finally, we apply the new calibrations to the recently discovered Galactic globular cluster 2MASS GC01, to derive [Fe/H] $_{\rm H96}=-1.19\pm0.38$ mag. The uncertainty is dominated by the severe foreground contamination. We estimate an extinction of $A_V=21.07\pm2.20$ mag toward the cluster.

Key words: Galaxy: globular clusters: general - Galaxy: abundances - galaxies: abundances - galaxies: distances andredshifts - stars: distances - stars: abundances


1 Introduction

The red giant branch (RGB hereafter) stars are among the brightest red stars in stellar systems, older than a few Gyrs. These stars appear in almost all galaxies, including II Zw 40 (Östlin 2000), considered until recently as the best candidate for a primeval galaxy. Therefore the red giants are a promising tool for probing the parameters of old populations and the history of star formation in any galaxy.

Galactic globular clusters, with their single age and metallicity, are the ideal sites for calibrating the RGB parameters. Since Da Costa & Armandroff (1990) provided the first reliable calibration of the position of the RGB versus metallicity, there has been a significant advancement, both because of the improvement of the astronomical instrumentation and the development of the corresponding theory.

The infrared waveband is particularly compelling for such studies, in comparison with the optical one, because of the potential to probe the stellar populations of systems with high foreground and/or intrinsic extinction. The relatively small size and field of view of the IR arrays have made it more difficult to carry out photometry of large areas, and to compile uniform samples, necessary to calibrate the RGB parameters reliably, in comparison with the optical region. The Two Micron All Sky Survey[*] (2MASS hereafter) offered for the first time such an opportunity.

Previous calibrations suffered a number of drawbacks. Kuchinski et al. (1995) and Kuchinski & Frogel (1995) studied only metal-rich globular clusters, with [Fe/H$]\geq-$1. Later on, Ivanov et al. (2000a) added to their sample three metal-poor globular clusters. Ferraro et al. (2000) used exceptional quality data but in a photometric system, based on unpublished standards by Ian Glass (South African Astronomical Observatory) with no available transformations to any of the other systems. The similarity of their final results to those of Ivanov et al., who used the CIT system, leads to conclusion that the two photometric systems are not radically different.

To expand the basis of the RGB studies, we used high-quality uniform photometry of Galactic globular clusters from the 2MASS point source catalog, and assembled a sample of RGBs of clusters with well known distances and reddening. We calibrated the behavior of the RGB slope, zero point, and tip with metallicity in the 2MASS photometric system. For the first time we offer such calibration in a well defined photometric system with all-sky coverage. We present a "fan'' diagram, suitable for abundance distribution analysis. Our results complement the recent work of Cho & Lee (2001) and Grocholski & Sarajedini (2001) who explored the properties of the RGB bump.

2 2MASS calibration of the RGB parameters

  
2.1 Sample

Infrared photometry of about 80 of the 147 globular clusters, listed in Harris (1996, revision June 22, 1999) is currently available from the First and the Second 2MASS incremental releases. However, many of the observed clusters are rendered unsuitable for this project because they suffer from one or more of the following drawbacks:

1.
Severe foreground contamination. This refers mostly to globular clusters in the general direction of the Galactic center;
2.
The photometry of some distant halo clusters or highly reddened clusters is not sufficiently deep;
3.
Compact globular clusters have unresolved cores, limiting the number statistics, and leading to crowding problems.
After a visual inspection of the luminosity functions and color-magnitude diagrams (CMD hereafter) of all available globular clusters, we selected a subset of 27 objects (Table 1) for which reliable estimates of at least one RGB parameter could be obtained. To calculate the absolute magnitudes, and the intrinsic colors of stars, we adopted the reddening and distance estimates from the compilation of Harris (1996), and the reddening law of Rieke & Lebofsky (1985; used throughout this paper).


 

 
Table 1: Globular cluster sample. The columns give: cluster ID, color excess EB-V, distance modulus, tidal radius $R_{\rm t}$ (all from the compilation of Harris 1996), and abundances in various scales (see the references).
NGCEB-V(m-M)v [Fe/H] [Fe/H][M/H]$R_{\rm t}$
IDmagmag H96 CG97F99$\arcmin$
1040.0413.37 -0.76 -0.70-0.5947.25
2880.0314.69 -1.24 -1.07-0.8512.94
18510.0215.47 -1.22 -1.08-0.8811.70
19040.0115.59 -1.57 -1.37-1.228.34
22980.1415.59 -1.85 -1.74(-1.54)6.48
50240.0216.38 -1.99 (-1.82)(-1.62)21.75
51390.1213.97 -1.62 (-1.38)(-1.18)44.85
54660.0016.15 -2.22 (-2.14)(-1.94)34.24
61210.3612.83 -1.20 -1.19-0.9432.49
61440.3216.06 -1.73 -1.49(-1.29)33.25
61710.3315.06 -1.04 -0.87-0.7017.44
62050.0214.48 -1.54 -1.39-1.1825.18
62730.3715.85 -1.68 (-1.45)(-1.25)14.50
62840.2816.70 -1.32 (-1.10)(-0.90)23.08
63560.2816.77 -0.50 (-0.66)(-0.50)8.97
64410.4416.62 -0.53 (-0.67)(-0.51)8.00
66240.2815.37 -0.42 (-0.64)(-0.48)20.55
66370.1615.16 -0.71 -0.68-0.558.35
66560.3413.60 -1.64 (-1.41)(-1.21)29.97
67150.1417.61 -1.59 (-1.35)(-1.15)7.47
67790.2015.65 -1.94 (-1.75)(-1.55)8.56
68090.0713.87 -1.81 -1.61-1.4116.28
68380.2513.75 -0.73 -0.70-0.499.96
68640.1616.87 -1.32 (-1.10)(-0.90)7.28
70780.1015.37 -2.25 -2.12-1.9121.50
70890.0615.49 -1.62 (-1.38)(-1.18)21.45
70990.0314.62 -2.12 -1.91-1.7118.34


References for [Fe/H]:
H96 - Harris (1996; Zinn scale);
CG97 - Carretta & Gratton (1997);
F99 - Ferraro et al. (1999)


Special care was taken to assure the uniformity of the metallicity data. Harris (1996) based his compilation on the system established by Zinn & West (1984), Zinn (1985), and Armandroff & Zinn (1988). Carretta & Gratton (1997) suggested that this scale may overestimate the abundance of metal-rich globular clusters, and developed a new one. We list their measurements in Table 1 as dwell. Values in brackets are estimates based on the transformation they derive, to the Zinn & West scale (see Eq. (7) of Carretta & Gratton).

Ferraro et al. (1999) argued that the total amount of heavy elements is a better metallicity measurement, because it accounts naturally for the opacity variations, which depend on the total metallicity, not just the iron abundance (Salaris et al. 1993). They developed a new scale, designed to measure this quantity. For the clusters, absent in their sample, we adopted their prescription for 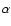$\alpha$-element enhancement (Sect. 3.4 in Ferraro et al.; estimates bracketed in Table 1).

Since the metallicities originate from different sources, and the corresponding uncertainties are often not quoted, we adopted an uniform error of 0.20 dex for all measurements. This is a typical value of the accuracy of the abundance estimates.

The first step before estimating the RGB parameters was to eliminate statistically the foreground contamination. As many stars were removed randomly from the CMD of the globular clusters as the number of stars present in a nearby field with the same area as the globular cluster field. The statistical removal is not reliable in the case of severely contaminated globular clusters, where the number of foreground stars was comparable to the number of cluster members. A subset of CMDs for four clusters is shown in Figs. 1 and 2. In addition, we removed the stars within 15 arcsec of the cluster centers, to minimize the crowding effects.


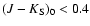  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ivanov01.eps}\end{figure} Figure 1: Color-magnitude diagrams for a subset of metal poor globular clusters. The left panels show the raw data. The right panels show the reddening corrected CMDs, converted to absolute magnitudes. The foreground contamination and stars with $(J-K_{\rm S})_0<0.4$ mag have been removed.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ivanov02.eps}\end{figure} Figure 2: Same as Fig. 1 for metal rich clusters.
Open with DEXTER

  
2.2 RGB slope and zero point

Da Costa & Armandroff (1990) prepared a set of standard RGBs on the V versus V-I CMD, for metallicity estimates of globular clusters in the optical. The technique has been expanded toward the near infrared wavebands, where the giant branch is linear and therefore more obvious and easier to define compared with the optical or optical-infrared CMDs. The slope is related to the effective temperature of the stars along the RGB, and 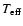$T_{\rm eff}$ in turn depends on the opacity, and the heavy element abundance. The slope is a reddening- and distance-free metallicity indicator. It is significantly less demanding in terms of observing time and telescope collecting area than the spectroscopic methods, but unlike them it can be applied reliably only to uniform groups of stars.

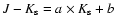We followed the procedure to determine the RGB slope, described in Ivanov et al. (2000a), fitting the RGB on the $[K_{\rm s},(J-K_{\rm s})]$CMD with a linear equation: $J-K_{\rm s}=a\times K_{\rm s}+b$. Only the stars above the horizontal branch were included. We applied a least square method, taking into account the uncertainties along both axes. 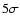Two iterations were performed, and all the stars outside $5\sigma$ from the first fit were removed from the calculations.

For the purpose of fitting the RGB of an individual cluster, the zero point is equivalent to previous calibrations of the RGB colors at fixed K-band magnitude levels (e.g. Ivanov et al. 2000a; Ferraro et al. 2000), although more straightforward. To derive the zero-point relation to the abundance, we used only the clusters that suffer minimal extinction 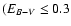$({E}_{B-V}\leq 0.3$ mag).

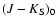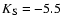Notably, the fit to the zero point shows a very small variation with metallicity: 0.11 mag for [Fe/H] $_{\rm H96}$ varying from -2 to -0.5. For comparison, $(J-K_{\rm S})_0$ at $K_{\rm S}=-5.5$ mag varies by 0.32 mag for the same metallicity range (Ferraro et al. 2000). This result offers the possibility for a more reliable reddening estimate than in case of RGB color calibrations.

The behavior with metallicity of the RGB slope and zero point are demonstrated in Fig. 3. Fitting coefficients for individual cluster RGBs are listed in Table 2.


 

 
Table 2: Linear fits to the RGB in the form of: $J-K_{\rm s}=a\times K_{\rm s}+b$. The radii $R_{\max}$ of the region around the cluster center used in the fit, and the root mean square of the fit are given.
NGC$R_{\max}$abrms
ID$\arcmin$SlopeZero Pointmag
10410-0.125(0.002)0.368(0.004)0.054
2887-0.105(0.006)0.341(0.018)0.048
18515-0.098(0.004)0.399(0.013)0.095
19047-0.081(0.004)0.356(0.017)0.088
22986-0.055(0.005)0.389(0.019)0.104
502411-0.061(0.004)0.417(0.014)0.107
51397-0.085(0.001)0.344(0.005)0.063
546610-0.047(0.008)0.468(0.030)0.082
612110-0.094(0.003)0.360(0.010)0.091
61444-0.066(0.003)0.431(0.014)0.088
61718-0.101(0.003)0.310(0.009)0.096
620510-0.086(0.003)0.354(0.010)0.068
62733-0.074(0.003) 0.099
63562-0.110(0.005)0.311(0.023)0.109
66563-0.059(0.003) 0.074
67153-0.083(0.004)0.343(0.021)0.143
67793-0.048(0.005)0.445(0.020)0.069
680910-0.077(0.004)0.396(0.013)0.064
68383-0.099(0.003)0.352(0.009)0.085
68643-0.078(0.004)0.411(0.020)0.110
70899-0.080(0.003)0.369(0.012)0.090
70998-0.050(0.006)0.450(0.024)0.047


Note: Fitting errors are given in brackets. The Zero
Points for NGC 6273 and 6656 are omitted because
of the large reddening toward this cluster.



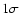  \begin{figure} \par\includegraphics[width=7.3cm,clip]{ivanov03.eps}\end{figure} Figure 3: Relation of the [Fe/H] in various metallicity scales versus RGB slope on $[M_{K_{\rm s}},(J-K_{\rm s})_0]$ diagram. The bars indicate $1\sigma $ uncertainties. The dashed line is the fit of Ferraro et al. (2000) drawn without transformation of colors. The zero point error bars show only the statistical errors from the fits to the RGB, omitting the 0.2 mag added in quadrature to account for the uncertain distance moduli and reddening corrections.
Open with DEXTER

2.3 RGB tip

The tip of the RGB is a well-known distance indicator. Mould & Kristian (1986), Lee (1993) and Lee et al. (1993) pioneered the method in the optical, measuring the corresponding jump in the luminosity function in external galaxies. Later it was applied to number of resolved stellar systems, among the most challenging of which were some Virgo cluster members (Harris et al. 1998) and NGC 3379 (Sakai et al. 1997).

This is a statistically demanding technique, requiring 50-100 stars per bin. The limited size of infrared arrays explains the difficulty applying it in the near infrared. Although it does cover a large area, the 2MASS photometry cannot alleviate the intrinsic problem of the small number of giants in globular clusters. Thus, we assume that the brightest cluster member represents the RGB tip.

In most of the cases the tip is obvious, but sometimes additional criteria had to be applied to determine the brightest stars. We took advantage of the linearity of the RGB in the near infrared, and excluded from the considerations bright stars that deviated from the color of the RGB at a given magnitude level (predicted by the RGB slope fit) by more than 0.5 mag. We also excluded some extremely bright stars, with luminosity higher than the rest of the RGB by 2-3 mag. They were obvious foreground contamination. Finally, the red variables from Clement et al. (2001) were excluded.

The formal uncertainties of the stellar magnitudes given in 2MASS were discarded, since they do not represent well the uncertainty in the tip magnitude. Instead, we adopted the difference in the magnitudes of the two brightest stars, accounting for the possibility that the brightest star may be a non-member. This led to typical error values of 0.2-0.4 mag, much larger than the 2MASS errors.

The RGB tip magnitudes for 20 globular clusters are given in Table 3. The behavior of the RGB tip with metal abundance is shown in Fig. 4.


 

 
Table 3: Estimated RGB tip absolute magnitudes.
NGCJH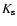$K_{\rm s}$
104-5.616(0.171)-6.372(0.017)-6.862(0.209)
288-5.578(0.621)-6.412(0.610)-6.672(0.656)
1851-5.182(0.083)-6.092(0.024)-6.306(0.040)
1904-5.055(0.189)-5.826(0.231)-5.940(0.211)
5024-5.093(0.049)-5.708(0.006)-5.919(0.035)
5139-5.124(0.106)-5.778(0.040)-6.015(0.003)
6144-5.062(0.294)-5.803(0.318)-5.953(0.280)
6171-5.326(0.605)-6.213(0.565)-6.471(0.711)
6205-5.156(0.050)-5.901(0.092)-6.027(0.020)
6284-5.267(0.277)-6.073(0.133)-6.283(0.156)
6441-5.521(0.246)-6.413(0.235)-6.788(0.288)
6624-5.459(0.019)-6.295(0.027)-6.623(0.072)
6637-5.496(0.474)-6.369(0.401)-6.667(0.426)
6656-5.146(0.023)-5.809(0.067)-5.984(0.059)
6779-5.067(0.050)-5.765(0.036)-5.950(0.054)
6809-5.020(0.385)-5.725(0.335)-5.870(0.367)
6864-5.154(0.072)-6.012(0.047)-6.133(0.007)
7078-4.890(0.136)-5.506(0.211)-5.626(0.087)
7089-4.966(0.046)-5.711(0.072)-5.853(0.076)
7099-5.105(0.183)-5.655(0.134)-5.832(0.142)


Note: The difference between the two brightest
stars is given in brackets.



  \begin{figure} \par\includegraphics[width=7.3cm,clip]{ivanov04.eps}\end{figure} Figure 4: Relation of the [Fe/H] in various metallicity scales versus RGB tip absolute magnitude. The bars indicate 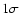$1\sigma $ uncertainties, with the Y-axis errors including the uncertainties due to the reddening and distance. The dashed line is the fit of Ferraro et al. (2000) drawn without transformation of colors.
Open with DEXTER

2.4 Results

The behavior of the derived RGB parameters with metallicity was fitted with linear equations, taking into account the errors along both axes. The coefficients are given in Table 4. Figure 5 shows a "fan''-like grid of RGBs in a reddening and distance corrected CMD, for the three metallicity scales discussed in Sect. 2.1. It demonstrates that the RGB behavior can be reduced to a simple rotation around a nearly-fixed point. This comes as no surprise, since the zero point of the RGB fit is almost independent of the abundance (Sect. 2.2).

The grid allows us to obtain the metallicities of individual stars in resolved systems in the infrared, and to obtain the metallicity distributions as done before in the optical (e.g. Saviane et al. 2000). The linear representation of the RGB in absolute 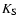$K_{\rm S}$magnitude versus the intrinsic 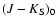$(J-K_{\rm S})_0$ color is:

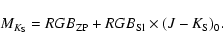\begin{displaymath}M_{K_{\rm S}} = RGB_{\rm ZP} + RGB_{\rm Sl} \times (J-K_{\rm S})_0. \end{displaymath} (1)

Both the slope 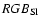$RGB_{\rm Sl}$ and the zero point 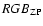$RGB_{\rm ZP}$ were calibrated as functions of the abundance:
$\displaystyle RGB_{\rm Sl} = a_0^{\rm Sl} + a_1^{\rm Sl} \times {\rm [Fe/H]}$     (2)
$\displaystyle RGB_{\rm ZP} = a_0^{\rm ZP} + a_1^{\rm ZP} \times {\rm [Fe/H]}.$     (3)

After substituting Eqs. (2) and (3) in (1), and solving for the stellar metallicity:

\begin{displaymath}{\rm [Fe/H]} = \frac{ M_{K_{\rm S}} - a_0^{\rm Sl}\times (J-K... ... { a_1^{\rm Sl} \times (J-K_{\rm S})_0 + a_1^{\rm ZP} }\cdot \end{displaymath} (4)

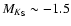This equation should be used with caution. Small photometric errors are crucial for accurate [Fe/H] estimates. The upper part of the infrared CMD is better suited for determining individual metallicities because near the root of the RGB the abundance relation degenerates. The exact faint limit is determined by the quality of the photometry, and by the presence of the horizontal branch at $M_{K_{\rm S}}\sim -1.5$ mag.


 

 
Table 4: Polynomial fits to the metallicity behavior of the RGB slope, zero point, bump, and tip: $Y=a_0+a_1 \times X$.
Variables Coefficients rms $N_{\rm pts}$
XYa0( $\sigma_{{a}_0}$)a1( $\sigma_{{a}_1}$)  
H66 $\it RGB_{Sl}$-0.157(0.009)-0.051(0.006)0.00222
CG97 $\it RGB_{Sl}$-0.158(0.010)-0.058(0.007)0.00222
F99 $\it RGB_{Sl}$-0.149(0.009)-0.060(0.008)0.00222
H66 $\it RGB_{ZP}$+0.277(0.152)-0.070(0.104)0.00720
CG97 $\it RGB_{ZP}$+0.272(0.155)-0.082(0.120)0.00720
F99 $\it RGB_{ZP}$+0.285(0.137)-0.084(0.122)0.00720
H66 $\it J_{tip}$-5.650(0.187)-0.323(0.121)0.02520
CG97 $\it J_{tip}$-5.690(0.210)-0.387(0.151)0.02620
F99 $\it J_{tip}$-5.631(0.191)-0.399(0.158)0.02620
H66 $\it H_{tip}$-6.641(0.186)-0.486(0.121)0.02520
CG97 $\it H_{tip}$-6.712(0.210)-0.594(0.153)0.02420
F99 $\it H_{tip}$-6.631(0.193)-0.620(0.162)0.02420
H66 $\it K_{tip}$-7.032(0.212)-0.615(0.134)0.03220
CG97 $\it K_{tip}$-7.109(0.243)-0.739(0.171)0.03420
F99 $\it K_{tip}$-7.003(0.224)-0.768(0.181)0.03420


Note: Errors are given in brackets. Metallicity notation is the
same as in Table 1.



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ivanov05.eps}\end{figure} Figure 5: "Fan Diagram'' - a grid of RGBs on the reddening and distance corrected color-magnitude diagram, for the three metallicity scales, as indicated.
Open with DEXTER

  
3 2MASS GC01

Hurt et al. (1999, 2000) reported the serendipitous discovery of 2MASS GC01 (hereafter GC01) in 2MASS data. It is a heavily obscured globular cluster, lying in the Milky Way disk, in the general direction of the Galactic center. Ivanov et al. (2000b) determined (m-M)0=12.4-14.0, and AV=20.9-18.8, assuming $\rm [Fe/H]=-0.5$ and -2.0,respectively. The main source of uncertainty in these estimates was the unknown metallicity of the cluster, although the location of GC01 suggested that it might be a metal-rich object.

The first step toward a metallicity estimate of GC01 was to remove the foreground star contamination. Unlike the clusters we used to derive the RGB parameter calibrations, the contamination here is severe, reaching 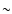$\sim$30% in the RGB region. We performed 2000 foreground substractions, and estimated the RGB slope for each realization separately. This method yields distributions of the RGB slope and tip, and the widths of these distributions measure the respective uncertainties.

To carry out this procedure we defined the CMD area encompassing the RGB: 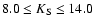$8.0\leq K_{\rm S}\leq14.0$ mag, and 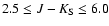$2.5\leq J-K_{\rm S}\leq6.0$ mag. Then we divided it into 0.2 mag square bins. Experiments with different bin sizes indicated that any value between 0.2 and 1.0 mag leads to the same conclusions.

Next, we constructed CMDs for the cluster field, and for a surrounding field with an equal area. To minimize the crowding effects we omitted the stars within 15 arcsec from the cluster center. The outer limit of the cluster field was constrained by the cluster diameter ( 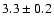$3.3 \pm 0.2$ arcmin, Hurt et al. 1999, 2000). We carried out our calculations to two values of the outer radii: 1.0 and 1.5 arcmin. Smaller values limit the number statistics, and larger ones increase the fraction of the foreground contamination. The foreground field was defined as a circular annulus with 10.49-10.54 or 10.43-10.54 arcmin size respectively for 1.0 and 1.5 armin cluster fields.

Finally we counted the stars in each bin, and subtracted randomly from the "cluster'' bins as many stars as were present in the "field'' bins. If the latter bin had more stars than the former one, we subtracted stars from the nearby bins, again in a random way.

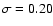We carried out a linear fit on the RGB stars in the foreground-subtracted CMD in the same manner as for the calibration clusters (see Sect. 2.2). For stars without error measurements in 2MASS we adopted $\sigma=0.20$ mag. Using the linearity of the RGB, we imposed a faint limit of the stars, included in the fit, just above the horizontal branch level. The luminosity function of GC01 (Ivanov et al. 2000b, Fig. 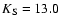5) indicates that the horizontal branch is at $K_{\rm S}=13.0$-13.2 mag. To minimize the uncertainties of the RGB slope, we also imposed color limits on the stars we used in the fit. 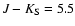The red one was set to $J-K_{\rm S}=5.5$ mag, and has no effect on the slopes because of the negligible number of stars to the red of the RGB. The results are somewhat more sensitive to the blue limit. 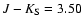We chose to impose $J-K_{\rm S}=3.50$ and 3.80 mag, because of the well-defined limit of the RGB at this colors (Fig. 6).


  \begin{figure} \par\includegraphics[width=8cm,clip]{ivanov06.eps}\end{figure} Figure 6: 2MASS color-magnitude diagram of GC01. Solid dots are stars from 0.25 to 1 arcmin from the cluster center - cluster+foreground. X's indicate the stars within 10.49 to 10.54 arcmin from the center - pure foreground. 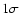$1\sigma $ errors are indicated. The solid line represents the average RGB fit, described in Sect. 3. Clearly, it is dominated by the stars with minimal uncertainties. Dotted lines are the adoptedlimits.
Open with DEXTER

A summary of the results for the RGB slope and zero point GC01 is presented in Fig. 7. The RGB tip is omitted because it is sensitive only to the adopted cluster radius. Clearly, the effects from the assumed parameters are smaller or comparable with the uncertainties originating due to the foreground contamination. We calculated the error-weighted averages for the realizations with 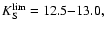$K_{\rm S}^{\rm lim}=12.5{-}13.0,$ to avoid the possible influence of the cluster horizontal brunch. The determined RGB parameters for GC01 are:

  \begin{figure} \par\includegraphics[width=8cm,clip]{ivanov07.eps}\end{figure} Figure 7: Behavior of the RGB slope (top) and zero point (bottom) for different parameters of the foreground subtraction and fits. The horizontal axis is the lower limit of the stars used in the RGB fit. Triangles indicate cluster radius of 1.0 arcmin, and circles indicate 1.5 arcmin. 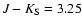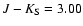Open symbols indicate a blue limit of $J-K_{\rm S}=3.25$ mag, and solid symbols of $J-K_{\rm S}=3.00$ mag. Only some $1\sigma $ errors of individual points are shown to avoid crowding. The solid lines indicate the weighted averages, and the dashed lines indicate their $1\sigma $ errors. The values to the right of the vertical dotted line were discarded because they were affected by the horizontal branch.
Open with DEXTER

1.
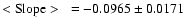
$< {\rm Slope} >~= -0.0965\pm0.0171$
2.
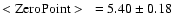
$< {\rm Zero Point} >~ = 5.40\pm0.18$
3.
$< {\rm Tip} >~= 8.87\pm0.13.$
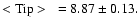
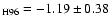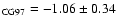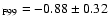Using the equations, given in Table 4 we obtain: [Fe/H] $_{\rm H96}=-1.19\pm0.38$, [Fe/H] $_{\rm CG97}= -1.06\pm 0.34$, and [M/H] $_{\rm F99}= -0.88\pm 0.32$. The errors given here include both the uncertainties in the slope, and in the calibrations. GC01 appears to resemble closely NGC 104.

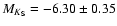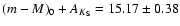The estimated absolute magnitude for the RGB tip for a cluster with such abundance is $M_{K_{\rm S}}= -6.30\pm0.35$ mag, using our new calibration for the Zinn metallicity scale. This leads to a distance modulus of $(m-M)_0+A_{K_{\rm S}}=15.17\pm0.38$ mag consistent with Ivanov et al. (2000b). We refrain from further considerations based on the RGB tip because of the poor statistics at the brighter end of the RGB. 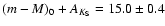Instead, we will adopt $(m-M)_0+A_{K_{\rm S}}=15.0\pm0.4$ mag, a result of interpolation between the values for [Fe/H]=-1.0 and -2.0, in Table 2 of Ivanov et al. (2000b).

We can also verify if the cluster reddening is consistent with the previous estimates. First, we subtract the RGB slope equations, written for the GC01 in apparent and in absolute magnitudes. Respectively:

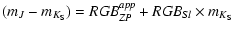$\displaystyle (m_J-m_{K_{\rm S}}) = {\it RGB_{ZP}^{app}} + {\it RGB_{Sl}} \times m_{K_{\rm S}}$     (5)
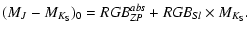$\displaystyle (M_J-M_{K_{\rm S}})_0 = {\it RGB_{ZP}^{abs}} + {\it RGB_{Sl}} \times M_{K_{\rm S}}.$     (6)

Here the notation is the same as in Table 4, and 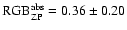${\rm RGB_{ZP}^{abs}}=0.36\pm0.20$ mag, for the [Fe/H] $_{\rm H96}$ given above. The result of the subtraction is:

\begin{displaymath}\!E(J-K_{\rm S}) = {\it RGB_{ZP}^{app}} - {\it RGB_{ZP}^{abs}} + {\it RGB_{Sl}} \times \left[(m-M)_0+A_{K_{\rm S}}\right]\!. \end{displaymath} (7)

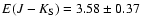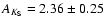Substituting, we obtain: $E(J-K_{\rm S}) = 3.58\pm0.37$ mag, close to the values of 3.49 mag, interpolated as above from Ivanov et al. (2000b). Our new estimate corresponds to $A_V=21.07\pm2.20$ mag, and $A_{K_{\rm S}}=2.36\pm0.25$ mag.

4 Summary

The behavior of the RGB in the infrared was quantified based on an unprecedented large sample of 2MASS photometry of Milky Way globular clusters. The RGBs were fitted by straight lines. We produced new calibrations of the RGB slope, tip, and - for the first time - zero point, as functions of abundance. The introduction of the zero point streamlines greatly the RGB analyses in comparison with the traditional approach where RGB colors at given levels were used. Notably, the zero point is fairly insensitive to the abundance, varying by only 0.11 mag over a range from [Fe/H] 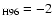$_{\rm H96}=-2$ to -0.5. We present a "fan''-like diagram, suitable for analyses of the metallicity spread in resolved stellar systems.

The derived calibrations were applied to estimate the metal abundance of the recently discovered globular cluster GC01. It is a particularly challenging object because of the severe foreground contamination. We removed it with a random procedure, and used the RGB slope of the remaining pure cluster population to derive [Fe/H] 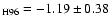$_{\rm H96}=-1.19\pm0.38$. The uncertainty is dominated by the foreground contamination, and albeit large, it allows us to exclude the extremely abundances, expected from the cluster location. GC01 is likely to be moderately metal poor. The RGB tip and zero point yield a distance modulus and extinction consistent with our previous estimates.

Acknowledgements
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center, funded by the National Aeronautics and Space Administration and the National Science Foundation. The authors thank Dr. Ivo Saviane for the useful discussions, and the referee Dr. M. G. Lee for the comments that helped to improve the paper.

References

 

Copyright ESO 2002