A&A 390, 891-915 (2002)
DOI: 10.1051/0004-6361:20020759
N. Bergvall1 - G. Östlin2
1 - Dept. of Astronomy and Space Physics, Box 515, S-75120 Uppsala,
Sweden
2 -
Stockholm Observatory, SCFAB, SE-106 91 Stockholm, Sweden
Received 29 November 2001 / Accepted 15 May 2002
Abstract
We present optical spectroscopy and deep optical/near-IR photometry of 4
luminous metal-poor blue compact galaxies (BCGs) and two of their companions.
With the aid of spectral evolutionary models (SEMs) and structural parameters
derived from the surface photometry we discuss the properties of the central
starbursts and the halo populations of the galaxies. Special attention is paid
to the effects of dust, chemical inhomogeneities and contamination of nebular
emission to the halo light. The optical/near-IR colour index profiles show a
sharp distinction between the starburst and the host. The hosts have luminosity
profiles characteristic of massive ellipticals and remarkably red colours,
typical of a relatively metal-rich stellar population of old age.
These properties are in conflict with the relatively low luminosities. The
situation can best be explained if the hosts have an unusually large amount
of dark matter that can hinder the outflow of metals from the system.The
indicated difference in metallicity between the halo and the young starburst
disproves the recurrent burst scenario and supports different origins of the two
populations. We conclude that these BCGs are undergoing mergers between early
type galaxies/thick disks and gas-rich galaxies or intergalactic HI
clouds, in many respects reminiscent of a retarded formation of massive
ellipticals.
Key words: galaxies: evolution - galaxies: formation - galaxies: starburst - galaxies: dwarfs
Blue compact galaxies (BCGs), sometimes called HII galaxies, are characterized by globally active star formation, low chemical abundances (e.g. Searle & Sargent 1972; Marconi et al. 1994; Kunth & Östlin 2000; Masegosa et al. 1994) and relatively high HI masses (Gordon & Gottesman 1981; Thuan & Martin 1981; Staveley-Smith et al. 1992). These are properties normally associated with young galaxies and indeed there have been claims from time to time (Searle & Sargent 1972; Thuan & Izotov 1997) that some BCGs may be truly young systems. But the most important aspect today is that BCGs constitute an important link to the high redshift universe and the early epoch of galaxy formation.
Observations (e.g. Lilly et al. 1999; Le Fèvre et al. 2000) show that mergers between galaxies are of major importance for the buildup of galaxies at high redshifts. The BCGs and their progenitors (HI clouds, LSB galaxies or other gas-rich dwarfs) that contribute fuel for the starburst may therefore be regarded as the local analogues of the distant subunits participating in the early merger processes. While starbursts of massive galaxies are rare, those induced by mergers of galaxies of intermediate mass may produce a major fraction of the metals observed in the intergalactic medium (IGM) during the buildup processes at high redshifts. A necessary requirement is that the energy input from the exploding supernovae is sufficiently large to overcome the gravitation. This requires masses of the galaxies not much in excess of typical luminous BCGs, making this type of galaxy interesting also from this point of view.
For a better understanding of the star formation processes we want to disentangle the different phases involved in the formation of a BCG by identifying stellar populations and galaxy morphologies of components from different epochs. We also want to know under what conditions a starburst can be triggered. Are the conditions set by external conditions, like the orbital properties of infalling clouds, or is a specific type of galaxy needed to host the burst?
From studies of the central starburst region of BCGs, it is very difficult to rule out that the galaxy is young since the starburst population easily outshines even a relatively massive population of old stars. Therefore, some investigations have focused on the halos of BCGs, where the starburst influence is assumed to be milder. Most BCGs show a regular halo (e.g. Loose & Thuan 1986). Already this fact is a strong argument in favour of a fairly old age because the relaxation time of a system of stars of a typical size of a few kpc is larger than a few times 108 yr. But a regular halo can be formed on a shorter time scale if the medium is viscous. The light may be due to nebular emission, a "Strömgrensphere'' formed by the starburst in the centre. We will elaborate on this a bit further in Sect. 6. If so, the stellar component whose formation may be much delayed relative to the gaseous disk of a protogalaxy, may be quite young.
One of the most debated young galaxy candidates is
IZw18, which belongs to the blue compact dwarfs (BCDs).
These are galaxies in the mass range 107-109
![]() ,
having relatively low luminosities (MB >-17). IZw18
has unique properties in this category, in particular
its record-low oxygen abundance of approximately 1/50 of the solar value
(e.g. Alloin et al. 1978; Izotov & Thuan 1999).
There are however reasons to suspect that winds from massive stars
and supernovae in low-mass galaxies may expel the gas and lower
the chemical abundances in which case
the youth signature may not be more than an artifact (e.g. McLow &
Ferarra 1999; Lequeux et al 1995; Martin 1996).
It is also a bit difficult to cope the relatively low
,
having relatively low luminosities (MB >-17). IZw18
has unique properties in this category, in particular
its record-low oxygen abundance of approximately 1/50 of the solar value
(e.g. Alloin et al. 1978; Izotov & Thuan 1999).
There are however reasons to suspect that winds from massive stars
and supernovae in low-mass galaxies may expel the gas and lower
the chemical abundances in which case
the youth signature may not be more than an artifact (e.g. McLow &
Ferarra 1999; Lequeux et al 1995; Martin 1996).
It is also a bit difficult to cope the relatively low ![]() (HI)/MB
(HI)/MB
![]() 1 in IZw18 (Thuan & Martin 1981) with a recently born
galaxy. As we show below (Fig. 1), already a "simple'' set of
data such as the integrated near-IR colours indicate that this is
an old galaxy. Recent investigations of deep colour-magnitude
diagrams of IZw18, in the optical by Aloisi et al. (1999) and in the
near IR by Östlin (2000), show that the galaxy contains a population
of evolved red stars, indicating an age in excess of 1 Gyr.
Among other young galaxy candidates discussed in the literature
(Bergvall & Jörsäter 1988) is one of the targets
in this project, ESO 400-G43, but as we will show below this galaxy
also seems to contain old stars. Another debated young galaxy candidate is
SBS0335-052 (Thuan & Izotov 1997; Östlin & Kunth 2001).
1 in IZw18 (Thuan & Martin 1981) with a recently born
galaxy. As we show below (Fig. 1), already a "simple'' set of
data such as the integrated near-IR colours indicate that this is
an old galaxy. Recent investigations of deep colour-magnitude
diagrams of IZw18, in the optical by Aloisi et al. (1999) and in the
near IR by Östlin (2000), show that the galaxy contains a population
of evolved red stars, indicating an age in excess of 1 Gyr.
Among other young galaxy candidates discussed in the literature
(Bergvall & Jörsäter 1988) is one of the targets
in this project, ESO 400-G43, but as we will show below this galaxy
also seems to contain old stars. Another debated young galaxy candidate is
SBS0335-052 (Thuan & Izotov 1997; Östlin & Kunth 2001).
Near-IR photometry has proven to be quite powerful in deriving information about the star formation history in galaxies that are dominated by starbursts and seems to support the idea that BCGs are old (e.g. Bergvall et al. 1999; Doublier et al. 2001). Then the interesting question remains what kind of galaxy or galaxies the precursor(s) and the successors could be. Several different scenarios for the ignition of the burst and the types of galaxies involved have been discussed in the literature (e.g. Searle & Sargent 1972; Thuan & Seitzer 1979; Thuan & Martin 1981; Staveley-Smith et al. 1992; Taylor et al. 1994; Telles & Terlevich 1995; Papaderos et al. 1996). One should be careful not to consider all BCDs as starburst galaxies, as is the commonly accepted view. In fact Sage et al. (1992) find that most BCDs are not more efficient in converting gas into stars than are normal spiral galaxies. They appear to be bursting only when compared to other gas-rich dwarfs where the normal star formation rate (SFR) is lower than in massive gas-rich galaxies. It is important to keep in mind that the class of BCGs is quite heterogeneous (Kunth et al. 1988; Kunth & Östlin 2000) and may include objects with different histories. Some galaxies called BCGs by some groups are definitely not BCGs since they easily fit into the extended Hubble classification towards late type disks or normal irregulars (Sandage & Binggeli 1984).
In this work we are dealing with galaxies that have
extremely high star formation efficiencies (SFE). With SFE we mean the
timescale of gas consumption in a closed box scenario, and a short timescale is
equal
to a high SFE. From our spectral
evolutionary models
(SEMs), assuming a Salpeter mass function (1958) and a mass range of
0.1-120
![]() we
find a SFR of
we
find a SFR of ![]() 10
10
![]() yr-1 for a burst with MB between -19 and
-20. Assuming a gas mass of 109
yr-1 for a burst with MB between -19 and
-20. Assuming a gas mass of 109
![]() ,
which is typical for our sample, we
thus obtain a maximum lifetime of
the burst of not more than a few times 108 yr, allowing for a modest fading
of
the burst. Thus, if no fresh gas is supplied the starburst will be a
transient phenomenon during which the properties of the galaxy will change
from what it was before, allowing a morphological metamorphosis to take
place. Based on photometric properties, globular cluster properties, HI
masses, kinematics and chemical abundances (e.g. Bergvall et al.
1998;
Östlin et al. 1998, 2001) we have claimed that
a large fraction of luminous BCGs may form from mergers involving massive gas
rich low surface brightness galaxies or gas clouds and possibly early type
dwarfs. More support in favour of this will be presented below as we discuss
the properties of 4 such massive BCGs. The relationships between H I,
chemical
abundances and photometric properties will be discussed in a paper now in
preparation.
,
which is typical for our sample, we
thus obtain a maximum lifetime of
the burst of not more than a few times 108 yr, allowing for a modest fading
of
the burst. Thus, if no fresh gas is supplied the starburst will be a
transient phenomenon during which the properties of the galaxy will change
from what it was before, allowing a morphological metamorphosis to take
place. Based on photometric properties, globular cluster properties, HI
masses, kinematics and chemical abundances (e.g. Bergvall et al.
1998;
Östlin et al. 1998, 2001) we have claimed that
a large fraction of luminous BCGs may form from mergers involving massive gas
rich low surface brightness galaxies or gas clouds and possibly early type
dwarfs. More support in favour of this will be presented below as we discuss
the properties of 4 such massive BCGs. The relationships between H I,
chemical
abundances and photometric properties will be discussed in a paper now in
preparation.
As noted below, we have observational support for bipolar outflows
from the BCGs
discussed here. An interesting question to ask is under
what conditions and to what extent the metals in these outflows can reach the
escape velocity and be expelled into the ambient intergalactic medium (IGM)
and how much of the metals observed
in Ly![]() and the hot intracluster gas in rich galaxy clusters that can
be explained this way. Outflows will also open channels in the gaseous
halos, making it easier for Ly-continuum photons to escape. Starburst dwarfs may
therefore contribute significantly to the
reionisation of the IGM after recombination.
and the hot intracluster gas in rich galaxy clusters that can
be explained this way. Outflows will also open channels in the gaseous
halos, making it easier for Ly-continuum photons to escape. Starburst dwarfs may
therefore contribute significantly to the
reionisation of the IGM after recombination.
McLow & Ferarra (1999) argue that galaxies with masses exceeding
![]()
![]() (less than a few % of the masses of our targets) will retain
most of their gas indefinitely, while a large fraction of the metals may
be lost. If a bottom-up scenario is relevant for early galaxy formation it could
be argued that most of the pollution of the IGM in the early days were caused
by outflows from starburst dwarfs, similar to the local BCGs. These important
topics deserve a thorough investigation but is not the prime goal of this
paper. Still, as we illustrate below, we have to consider the possibility that
the outflows influence the properties of the halo through polluting the light
with
emission from ionised gas of low temperature.
(less than a few % of the masses of our targets) will retain
most of their gas indefinitely, while a large fraction of the metals may
be lost. If a bottom-up scenario is relevant for early galaxy formation it could
be argued that most of the pollution of the IGM in the early days were caused
by outflows from starburst dwarfs, similar to the local BCGs. These important
topics deserve a thorough investigation but is not the prime goal of this
paper. Still, as we illustrate below, we have to consider the possibility that
the outflows influence the properties of the halo through polluting the light
with
emission from ionised gas of low temperature.
Before entering into the results of this paper, it is enlightening
to have a look at the integrated near-IR properties of BCGs in general.
In Fig. 1 we show the J-H vs. H-K diagram of BCGs,
dIs and dEs with available photometry from the literature. In the
diagram we have also indicated the evolution of a star
forming galaxy with a Salpeter IMF and an exponentially decaying
SFR (e-folding time 14 Gyr). Two tracks are shown, representing different
metallicities
(
![]() and
and ![]() ). The galaxy positions are quite
dispersed in the diagram. As mentioned above, BCGs in general
is a very heterogeneous group of galaxies, composed of subgroups with
different evolutionary histories. Despite the spread in
Fig. 1 it is obvious that most, if not all, galaxies
contain old stars.
). The galaxy positions are quite
dispersed in the diagram. As mentioned above, BCGs in general
is a very heterogeneous group of galaxies, composed of subgroups with
different evolutionary histories. Despite the spread in
Fig. 1 it is obvious that most, if not all, galaxies
contain old stars.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2147f1.ps}\end{figure}](/articles/aa/full/2002/30/aa2147/Timg35.gif) |
Figure 1: The J-H/H-K two colour diagram of BCGs (crosses), luminous irregulars (triangles), HII regions (squares) and dE:s (circles) obtained from Bergvall & Olofsson (1986), Hunter & Gallagher (1985), James (1994) and Thuan (1983). The predicted evolution (Zackrisson et al. 2001) of a star forming galaxy with a Salpeter mass function, an e-folding star formation decay rate of 14 Gyr and two different metallicities (20% solar, solid line; twice solar, dotted line) are also displayed. The evolution starts at the star marked 0 and ends at the large black dot, corresponding to an age of 14.5 Gyr. The position at 1 Gyr is marked with a smaller black dot. The effect of dust reddening and emission are indicated by arrows but note that the nebular emission has been included in the model. The filled triangle at J-H= 0.5, H-K= 0.1 is IZw18. Typical mean errors are indicated on the lower left side. |
| Open with DEXTER | |
Some spread may be due to varying data quality, and differences in metallicity and extinction. However, even when these effects are taken into account, it seems as if the observed distribution is shifted towards slightly redder J-H. The difference can be reduced with 0.1 mag if we assume that the star formation rate declines faster so that the influence from young stars becomes less important. In the cases where the galaxy contains an old population of stars and the starburst is not so strong we would expect that the old stars dominate in the infrared. This is indeed where most of the BCGs are found in the diagram. Only a few BCGs with strong starbursts are located along the evolutionary track with low ages.
| ESO id. | RA1950 | Decl.1950 | Year | Telescope | Filters and integration times (minutes) | Seeing |
| (arcsec) | ||||||
| 338-04 (Tol 1924-416) | 19 24 29.0 | -41 40 36 | 1995 | NTT | H |
1 |
| 1997 | NTT | B(5), V(15), R(15), I(30) | 1 | |||
| 338-04b | 19 24 03 | -41 45 00 | 1997 | NTT | V(5), I(5) | 1 |
| 350-38 (Haro 11) | 00 34 25.7 | -33 49 49 | 1984 | 2.2 m | B(25), V(15),
Gunn |
<1 |
| 1988 | 1.5D | Gunn |
1 | |||
| 1989 | 1.5D | H |
1 | |||
| 400-43 | 20 34 31.0 | -35 39 42 | 1984 | 2.2 m | H |
1 |
| 1989 | 2.2 m | B (30), Gunn |
<1 | |||
| 1995 | NTT | H |
1.5 | |||
| 400-43b | 20 34 31.0 | -35 39 42 | 1989 | 2.2 m | B (5), Gunn |
<1 |
| 480-12 | 02 52 32.8 | -25 18 49 | 1984 | 2.2 m | B(25), V(20), H |
1 |
| 1989 | 2.2 m | B (30), V (20), Gunn |
<1 |
In this paper we focus on luminous BCGs. Such BCGs are likely to have deeper central potential wells and therefore should be more capable retaining the gas than the true dwarfs. In less massive galaxies the metals may be quickly diluted due to winds from high mass stars and could therefore mimic a truly young galaxy. The massive BCGs are more suited for dynamical mass determinations and they are massive enough to show similarities with normal disk galaxies in formation.
There is no commonly-accepted definition of a blue compact galaxy. We have simply chosen luminous galaxies with high central surface brightnesses, blue colours and low chemical abundances from the list of Bergvall & Olofsson (1986). For quite some time we have observed a number of such galaxies and chosen a few for a more detailed study. We have selected those that have metallicities <15% of the solar values, although none of them as low as IZw18. In view of the discussions concerning the possible existence of young galaxies in the local universe we also as a second criterion rejected objects that showed regularity in the central regions. This was done after inspection of CCD images (mostly unpublished data) obtained with the ESO 1.5m telescope of about 15 galaxies from the Bergvall and Olofsson list. Here we discuss the properties of four of these and two of their companions. We hope that by making a more detailed study as presented here and in accompanying papers we can contribute to improving the classification methods for this type of BCG. Throughout this paper we will assume a Hubble parameter of H0= 75 km s-1 Mpc-1.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS2147f2r.eps}\end{figure}](/articles/aa/full/2002/30/aa2147/Timg44.gif) |
Figure 2:
Optical broadband images of ESO 338-IG04 (Tol 1924-426), 338-IG04b,
350-IG38
(Haro 11), 400-G43, 400-G43b and 480-IG12. The filters, indicated after
the abbreviated object name on top of the images, are in the Bessel system
except those marked GR which is the r filter in the Thuan-Gunn
system. A median 3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=10cm,clip]{MS2147f3r.eps}\end{figure}](/articles/aa/full/2002/30/aa2147/Timg45.gif) |
Figure 3:
Johnson |
| Open with DEXTER | |
Spectroscopy was carried out at ESO, La Silla, in 1983 and
1984 using the IDS at the ESO 1.5-m and 3.6-m telescope
and in October 8-10 1986 using the EFOSC1 spectrograph/camera
at the 3.6-m telescope, equipped with an RCA CCD
chip. In the first case we used an aperture of
![]() and a spectral resolution of 12 Å. The spectral
coverage was
and a spectral resolution of 12 Å. The spectral
coverage was ![]() 3600-7700 Å. The aperture was centered on the
maximum intensity in the visual of the central region of the
galaxies. The weather conditions were fair. EFOSC1 was
used with the B300 and O150 grisms, with a wavelength
coverage of 3600-7000 and 3600-5590 Å and a dispersion of
230 and 130 Åmm-1 respectively. Here we will only discuss
some of the results obtained with the B300 grism. We used a
slit size of 2 arcsec. It gives a spectral resolution of
3600-7700 Å. The aperture was centered on the
maximum intensity in the visual of the central region of the
galaxies. The weather conditions were fair. EFOSC1 was
used with the B300 and O150 grisms, with a wavelength
coverage of 3600-7000 and 3600-5590 Å and a dispersion of
230 and 130 Åmm-1 respectively. Here we will only discuss
some of the results obtained with the B300 grism. We used a
slit size of 2 arcsec. It gives a spectral resolution of ![]() 15 Å. The seeing conditions were poor with a mean seeing of
15 Å. The seeing conditions were poor with a mean seeing of ![]() 2 arcsec. At both occasions standard stars were observed each
night to derive the response curves. La Silla mean extinction
was adopted when correcting to zero airmass. Dome flatfields
were obtained with a Tungsten lamp.
The spectra were reduced using
the ESO MIDAS software. Final measurements of the spectra
were made using software developed in Uppsala. When
measuring line strengths, the continuum was defined with a
linear approximation and the line with a gaussian
approximation. The H
2 arcsec. At both occasions standard stars were observed each
night to derive the response curves. La Silla mean extinction
was adopted when correcting to zero airmass. Dome flatfields
were obtained with a Tungsten lamp.
The spectra were reduced using
the ESO MIDAS software. Final measurements of the spectra
were made using software developed in Uppsala. When
measuring line strengths, the continuum was defined with a
linear approximation and the line with a gaussian
approximation. The H![]() line was derived from a
decomposition of two Gaussian approximations of the H
line was derived from a
decomposition of two Gaussian approximations of the H![]() and the [NII]
and the [NII]![]() 6584 line.
6584 line.
| ESO id. | Integration time (seconds) | ||
| J | H |
|
|
| 338-04 | 1000 | 2000 | 3000 |
| 338-04b | 1000 | 2000 | 3000 |
| 358-38 | 1000 | 3000 | 4000 |
| 400-43 | 2000 | 4000 | 5000 |
| 400-43b | 1000 | 1000 | 2000 |
| 480-12 | 1000 | 1000 | 2000 |
Broad and narrowband optical images were obtained at five
occasions in the period 1983-1997. The broadband filters
UBVRI were in the Cousins system and r and i filters also in
the Gunn-Thuan system. Narrowband images were obtained in
H![]() - H
- H![]() .
The bandwidths of these filters were
.
The bandwidths of these filters were ![]() 70 Å. The central wavelengths coincide roughly with the central rest
wavelengths of the lines. Standard stars were obtained during
each night. Colour transformations between Cousins and the Gunn-Thuan systems
were carried out simply by comparing images of the same objects obtained at
different occasions in the two different systems and making the zeropoints
agree with the Cousins system. The colour dependence was thus not taken
into account. From previous calibrations of colour transformation equations
(Rönnback & Bergvall 1994) we estimate that the mean errors in the
colours due to this approximation are less than a few 0.01 mag. The major
conclusions are based on data unaffected by this. Mean extinction coefficients
for La Silla were used
in the photometric corrections to zero airmass. The weather
conditions for photometry were average-excellent. The
observations are summarized in Table 1.
70 Å. The central wavelengths coincide roughly with the central rest
wavelengths of the lines. Standard stars were obtained during
each night. Colour transformations between Cousins and the Gunn-Thuan systems
were carried out simply by comparing images of the same objects obtained at
different occasions in the two different systems and making the zeropoints
agree with the Cousins system. The colour dependence was thus not taken
into account. From previous calibrations of colour transformation equations
(Rönnback & Bergvall 1994) we estimate that the mean errors in the
colours due to this approximation are less than a few 0.01 mag. The major
conclusions are based on data unaffected by this. Mean extinction coefficients
for La Silla were used
in the photometric corrections to zero airmass. The weather
conditions for photometry were average-excellent. The
observations are summarized in Table 1.
JHK![]() observations were carried out with the near-IR camera
IRAC2 at the ESO 2.2-m telescope, equipped with a 256
observations were carried out with the near-IR camera
IRAC2 at the ESO 2.2-m telescope, equipped with a 256![]() 256 pixel2NICMOS detector in August 1993. Of the available field
lenses we chose to work with the C lens, which gives a pixel
size of 0.49 arcsec and a field size of 2 arcmin. The
weather conditions were good with a seeing of 1- 1.5 arcsec. At least 3 different standard stars each night were
used for calibration. For flatfield corrections we used a superflat
constructed from about 10 object frames where the target galaxy had
been shifted to different positions on the chip between the
integrations. A list of integration times in each filter is found
in Table 2.
256 pixel2NICMOS detector in August 1993. Of the available field
lenses we chose to work with the C lens, which gives a pixel
size of 0.49 arcsec and a field size of 2 arcmin. The
weather conditions were good with a seeing of 1- 1.5 arcsec. At least 3 different standard stars each night were
used for calibration. For flatfield corrections we used a superflat
constructed from about 10 object frames where the target galaxy had
been shifted to different positions on the chip between the
integrations. A list of integration times in each filter is found
in Table 2.
Since much of the discussion below focuses on the shape of the profiles at the faintest surface brightness levels, is it crucial to have full control of the error estimates that determine the reliability of the structure parameters. We have good control of the reductions of the optical images, since the field size is considerably larger than the galaxies. In the near-IR images the field size is smaller and the sky background is noisier which makes the sky subtraction more unreliable. We are aware of these problems when we analyze the fainter isophotes in the near-IR profiles.
The profiles were derived in the following way. Firstly we removed hot pixels in the images. This is automatically done when we stack the images in cases where we have several exposures. In other cases, where only one exposure is available, we used the command filter/cosmic in MIDAS. This procedure efficiently and highly selectively removes hot pixels and nearby correlated pixels. Secondly, we approximated the sky background by fitting the sky brightness distribution, measured by integrating in small boxes placed in regions which appeared empty of stars, to a 1-3 degree polynomial. We used a degree as low as possible so that the residuals looked acceptable. To estimate the uncertainty in the final sky level, we calculated the median sky value in each box and the standard deviation of the median values for all the boxes. We use this as a measure of the error of the zeropoint of the sky level. This normally dominates the error sources of the surface luminosities at the faintest isophotes. To further check the stability of the result we in a few cases remade the sky subtraction. Next step was to remove all stars and galaxies in the field by hand and flag these regions not to be included in the following derivation of the profile. Then we determined the centre, inclination and position angle of the outermost profiles and integrated the light in elliptical strips with a width of 1 pixel based on these parameters. We want to point out already here that the profiles displayed in the diagrams presented below have also been corrected for inclination assuming an infinitely thin disk.
The spectral evolutionary models (SEMs) we use in the discussions regarding the stellar content come from an in-house model by Zackrisson et al. (2001), PEGASE2 (Fioc & Rocca-Volmerange 2000) and the model from Worthey (1994). In the spectral analysis we also use a model by Bergvall (Bergvall & Rönnback 1995). The Zackrisson et al. models are based on stellar evolutionary tracks with the major contribution from the Geneva group, synthetic stellar spectra from the compilation by Lejeune et al. (1998) and a nebular component obtained from the Cloudy model (Ferland 1996). In Sect. 6 we use these models to compare between the predicted and observed broadband colours of the halo. We show below that the contribution from ionised gas to the halo light is fairly small, also in the R band, and that the uncertainties due to the nebular emission are not significantly affecting the derived results. This facilitates the analysis and improves the reliability of the method when used for information about the star formation history.
It is important to clarify that we do not intend to discuss the ionisation structure, sources, metallicities and so on in any detail here but rather the reverse - we are content with the situation that we do not need to worry about this component in the halo. If we had the ambition to discuss the star formation history of the central burst the situation would be much more complicated due to the unknown effects of dust, subcondensations in the gas and Lyman photon leakage, just to mention a few problems.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS2147f4.eps}\end{figure}](/articles/aa/full/2002/30/aa2147/Timg51.gif) |
Figure 4:
B-R colour-index maps of
ESO 350-IG38 (upper left), 338-IG04
(upper right), 480-IG12 (lower left)
and 400-G43 (lower right). The colour
coding follows true colours with blue representing young star forming regions.
The dynamical range has been chosen to enhance differences: for 350-38
and 338-04 the range is B-R= 0.2-1.2, while for 480-12 and 400-43 it is
B-R=0.2-1.0.
North is up, east is to the left. The size of each image is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS2147f5.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg53.gif) |
Figure 5:
The images shown are from left to right ESO 350-IG38, 338-IG04
and 400-G43. The upper panel shows deep images in the R window and the
lower panel continuum subtracted H |
| Open with DEXTER | |
| ESO id. | PA |
|
|
|
|
MB | B | B-V | V-R | V-I | V-J | J-H |
|
| 338-04 | 162 | 61 | 0.79 | 42 | 38 | -18.9 | 13.98 | 0.40 | 0.11 | 0.11 | (0.85)1 | (0.51)1 | (0.25)1 |
| 338-04b2 | 135 | 58 | 0.69 | - | 38 | - | - | - | - | 0.58 | 1.58 | 0.57 | 0.04 |
| 350-38 | 120 | 35 | 0.22 | 24 | 82 | -20.0 | 14.57 | 0.58 | 0.18 | 0.39 | 1.10 | 0.63 | 0.60 |
| 400-43 | 163 | 40 | 0.29 | 20 | 77 | -19.6 | 14.89 | 0.62 | 0.00 | - | 0.48 | 0.63 | 0.23 |
| 400-43b3 | 40 | 70 | 1.16 | 26 | 77 | -17.8 | 16.55 | - | - | - | - | 0.38 | 0.36 |
| 480-12 | 20 | 64 | 0.90 | 34 | 60 | -18.9 | 14.96 | 0.37 | 0.13 | 0.44 | 1.00 | 0.70 | 0.14 |
|
1) The Holmberg radius could not be reached in the near-IR so the given
colour is valid for a radius of 30 arcsec.
2) mV= 15.0, MV= -18.3 at 3) B-R= 0.40, B-J= 2.09. |
In Figs. 2, 3 and 4 we present images and colour-index maps of the programme galaxies. The near-IR images are strongly limited by the small field size of the detector but in fact the profiles reach quite far out from the starburst region and it is hard to find corresponding data in the literature. In contrast to normal late type galaxies the BCGs show a strong morphological similarity between the optical and the near-IR. Since the visible light is dominated by young stars, the morphological similarity suggests that young stars (e.g. red supergiants) dominate the near-IR light as well. At intermediate light levels irregular structures, reminiscent of whisps, shells and tails show up. At fainter light levels a somewhat more regular structure is seen but at the faintest levels again we see no firm evidence of an equilibrium system.
Photometry and basic spectroscopic data of most of the galaxies
were presented by Bergvall & Olofsson (1986). A study of
the velocity fields in H![]() all the programme galaxies
has been published (Östlin et al. 1999; Östlin et al.
2001).
all the programme galaxies
has been published (Östlin et al. 1999; Östlin et al.
2001).
This well-known BCG has been discussed by us in two previous papers
(Bergvall et al. 1985; Östlin et al. 1998).
The optical light is dominated by
the central irregular starburst, clearly resolved into compact star
clusters in HST images (Meurer et al. 1995; Östlin et al.
1998). At faint isophotal levels the morphology is that
of a warped disk. In a filtered image (Fig. 6), where
we have made an effort to enhance the faintest structures, a sharp
edge-like structure is seen in the northeastern part of the disk,
possibly indicating a warp or a shell. H![]() derived from
the Fabry-Perot spectroscopy (Östlin et al. 2001) reveal
what may be interpreted as two dynamically separate systems, as if
the galaxy went through a merger. Figure 4 shows a clear
distinction in colour between the starburst and the surrounding
host galaxy. Moreover, there is a blue tail, with peculiar kinematics
(Östlin et al. 2001) extending eastwards from the starburst.
In the H
derived from
the Fabry-Perot spectroscopy (Östlin et al. 2001) reveal
what may be interpreted as two dynamically separate systems, as if
the galaxy went through a merger. Figure 4 shows a clear
distinction in colour between the starburst and the surrounding
host galaxy. Moreover, there is a blue tail, with peculiar kinematics
(Östlin et al. 2001) extending eastwards from the starburst.
In the H![]() (Fig. 5, see also Fig. 7)
we see structures extending perpendicular to the plane, probably
due to nebular emission from bipolar outflows.
(Fig. 5, see also Fig. 7)
we see structures extending perpendicular to the plane, probably
due to nebular emission from bipolar outflows.
This galaxy is of particular interest because it has been shown to host a system of globular clusters, found to have a range of ages, from young ones to old (Östlin et al. 1998). The distribution in age indicates that the galaxy has had a few active starburst periods in the past. The maximum duration of the current burst is estimated from the HST data to be less than 100 Myr or more probable 50 Myr, and the last previous major burst probably occurred about 2 Gyr ago. The centre of the distribution of the globular clusters is offset with respect to the starburst but agrees with that of the underlying red component.
Bergvall (1985) reported an increase in the optical brightness
between 1979 and 1983 and Gondhalekhar (1986) reported an
increase in the UV brightness during the same period. Our new data from
1997 and recent data from Doublier (1999) seem to confirm that
the galaxy is variable in the optical. A comparison between our near-IR
photometry from different epochs shows no variability. Bergvall & Olofsson
(1986) obtained with a diaphragm of 15 arcsec
![]() ,
,
![]() ,
,
![]() as compared to
as compared to
![]() ,
,
![]() and
and
![]() from our integrated surface photometry of
the IRAC2 images in a circular aperture. Variability in the galaxy will
seriously affect the interpretation of the photometry of the central region
discussed below but should not affect the halo data.
from our integrated surface photometry of
the IRAC2 images in a circular aperture. Variability in the galaxy will
seriously affect the interpretation of the photometry of the central region
discussed below but should not affect the halo data.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2147f6.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg65.gif) |
Figure 6:
A deep, median-filtered image of ESO 338-IG04 in V. The arrow on the
left side
indicates what might be a remnant of a disk participating in a merger. The field
size is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS2147f7.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg67.gif) |
Figure 7:
A map of the equivalent width of H |
| Open with DEXTER | |
This is a spectroscopically confirmed companion of the former
galaxy (Bergvall unpublished; see also Östlin et al. 1999).
Morphologically it could be classified as a late type dwarf
irregular, with moderate star formation activity. Contrary to
ESO 338-IG04 it shows regular kinematics, and a dynamical mass
model shows that it contains dark matter (Östlin et al.
1999, 2001). It may have a smaller companion
![]() 40
40![]() westwards (see Fig. 2).
westwards (see Fig. 2).
Three bright condensations are seen in the centre of the galaxy,
which hosts a strong starburst as evident from the high excitation,
large emission line equivalent widths and a strong signature of
emission lines from WR stars in the spectral region around
HeII ![]() 4686. Haro 11 is also an extremely hot IRAS source
(Bergvall et al. 2000). While the broadband images show
three condensations in the centre, Fig. 4 shows
two blue hotspots. However, the
4686. Haro 11 is also an extremely hot IRAS source
(Bergvall et al. 2000). While the broadband images show
three condensations in the centre, Fig. 4 shows
two blue hotspots. However, the
![]() (Fig. 8)
shows that the third condensation has the highest
(Fig. 8)
shows that the third condensation has the highest
![]() 0.
The colourmap shows a gradual transition to redder
colours with distance from centre. The central bent structure can
be followed to faint isophotal levels, which together with the
peculiar kinematics, strongly suggest a merger origin of the starburst
(Östlin et al. 2001).
0.
The colourmap shows a gradual transition to redder
colours with distance from centre. The central bent structure can
be followed to faint isophotal levels, which together with the
peculiar kinematics, strongly suggest a merger origin of the starburst
(Östlin et al. 2001).
Östlin (2000) revealed the presence of a large number of
globular cluster candidates, similar to the ones in ESO 338-IG04.
Faint whisps and indications of shell structures are seen in the faint
outskirts of the mainbody. Approximately perpendicular to the apparent
major axis (which has a position angle ![]() 110
110![]() ), the
H
), the
H![]() is extended, suggesting the presence of bipolar
outflows of ionised gas (Fig. 5). Also
is extended, suggesting the presence of bipolar
outflows of ionised gas (Fig. 5). Also
![]() enhanced
south of the centre, in approximately the same direction (Fig. 8).
enhanced
south of the centre, in approximately the same direction (Fig. 8).
We observed this galaxy in H I with the VLA, the Nancay antenna
and with the Parkes antenna (all unpublished) but only an upper limit
of the H I mass of ![]()
![]() 108
108
![]() could be obtained. With
a
could be obtained. With
a ![]()
![]() /
/![]()
![]() < 0.01, this galaxy seems to be remarkably
devoid of neutral hydrogen.
We made an effort to quantify the conditions in Haro 11 on basis
of observations carried out in the far-IR using the ISO LWS (Bergvall
et al. 2000). We concluded that most of the neutral
H I was located in photodissociated regions. Starting from
the simplified situation discussed in Sect. 5 we may derive an estimate
of the mass of the ionised hydrogen gas. From the spectroscopy we calculate
a central electron
temperature of
< 0.01, this galaxy seems to be remarkably
devoid of neutral hydrogen.
We made an effort to quantify the conditions in Haro 11 on basis
of observations carried out in the far-IR using the ISO LWS (Bergvall
et al. 2000). We concluded that most of the neutral
H I was located in photodissociated regions. Starting from
the simplified situation discussed in Sect. 5 we may derive an estimate
of the mass of the ionised hydrogen gas. From the spectroscopy we calculate
a central electron
temperature of
![]() K and density of
K and density of
![]() cm-3.
The H
cm-3.
The H![]() is
is
![]() W. From this number we derive a
mass of the ionised gas inside 2 scalelengths of
W. From this number we derive a
mass of the ionised gas inside 2 scalelengths of
![]()
![]() ,
assuming a filling factor of 0.01-0.1. The mean HI mass of BCGs of the size
of
Haro11 is
,
assuming a filling factor of 0.01-0.1. The mean HI mass of BCGs of the size
of
Haro11 is
![]()
![]() (Gordon & Gottesman 1981). In Bergvall
et al (2000) we estimate the fraction of molecular gas and the
mass of the gas in the photodissociated regions to be
(Gordon & Gottesman 1981). In Bergvall
et al (2000) we estimate the fraction of molecular gas and the
mass of the gas in the photodissociated regions to be ![]()
![]()
![]() .
These numbers show that a major fraction of the gas may be in ionised and
molecular form.
.
These numbers show that a major fraction of the gas may be in ionised and
molecular form.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS2147f8.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg79.gif) |
Figure 8:
A map of the equivalent width of H |
| Open with DEXTER | |
As Fig. 4 shows, this galaxy has a blue irregular, clumpy
central region and a red regular halo. 2 arcmin east of ESO 400-G43
is a companion galaxy, here named ESO 400-G43b, detected from the HI
observations of the main component (Bergvall & Jörsäter 1988).
Jörsäter & Bergvall (unpublished) observed the main component at the
VLA in the 1415, 4885 and 8414 MHz windows. While the continuum slope in
the low frequency range agrees with that of Bremsstrahlung radiation
from the ionised gas, a component with a steep spectral index
![]() 1.2 (
1.2 (
![]() )
shows up near the centre.
Possible sources are radiosupernovae, SN remnants or possibly a low-mass AGN.
Figure 5 shows a median filtered H
)
shows up near the centre.
Possible sources are radiosupernovae, SN remnants or possibly a low-mass AGN.
Figure 5 shows a median filtered H![]() of the galaxy. The
galaxy has a very extended H
of the galaxy. The
galaxy has a very extended H![]() that can be followed out to 4-5 kpc, or
that can be followed out to 4-5 kpc, or
![]() 2 scalelengths. The
2 scalelengths. The
![]() is shown in Fig. 9.
A longslit spectrum across the galaxy indicates that
the extinction is close to zero throughout the central region (Fig. 11).
is shown in Fig. 9.
A longslit spectrum across the galaxy indicates that
the extinction is close to zero throughout the central region (Fig. 11).
The dynamics and H I content of this galaxy were discussed by Bergvall
& Jörsäter (1988). One of the purposes with that
investigation was to use dynamical information to set upper limits
to the mass of older stellar generations. This mass determination is
particularly important since it is derived from an HI rotation curve
reaching far outside the optical extent of the galaxy and as such is
unique in our sample. The H I mass is ![]()
![]()
![]() and for the companion
and for the companion
![]()
![]() .
A smaller cloud with a mass
of approximately
.
A smaller cloud with a mass
of approximately
![]()
![]() and no optical counterpart was detected
NW of the main component, suggesting that we may be witness to a
merging of a smaller group of galaxies and gas clouds. From best fits
to the rotation curve of the optically bright central region it was
found that the mass was
and no optical counterpart was detected
NW of the main component, suggesting that we may be witness to a
merging of a smaller group of galaxies and gas clouds. From best fits
to the rotation curve of the optically bright central region it was
found that the mass was ![]() 1.
1.
![]()
![]() ,
close to the photometric
mass estimate of young stars
and ionised gas. Moreover, when corrected for internal extinction
(using the H
,
close to the photometric
mass estimate of young stars
and ionised gas. Moreover, when corrected for internal extinction
(using the H![]() /H
/H![]() ratio) the colours (
ratio) the colours (
![]() ;
;
![]() )
correspond to a young stellar population. These observations led
Bergvall and Jörsäter to suggest that ESO 400-G43 could be
a galaxy still in the state of formation. They also
showed that dark matter dominates the dynamics at
r > 15 kpc and that the total mass was >1010
)
correspond to a young stellar population. These observations led
Bergvall and Jörsäter to suggest that ESO 400-G43 could be
a galaxy still in the state of formation. They also
showed that dark matter dominates the dynamics at
r > 15 kpc and that the total mass was >1010
![]() ,
if dynamical
equilibrium was assumed. A distorsion in the transition between the
stellar disk and the H I was interpreted as either an effect of
gas infall or a warp. Östlin et al. (1999, 2001)
mapped the central kinematics in H
,
if dynamical
equilibrium was assumed. A distorsion in the transition between the
stellar disk and the H I was interpreted as either an effect of
gas infall or a warp. Östlin et al. (1999, 2001)
mapped the central kinematics in H![]() - confirmed the complexity of
the velocity field in the nort-eastern part of the central disk,
making dynamical mass determinations of the centre more uncertain.
- confirmed the complexity of
the velocity field in the nort-eastern part of the central disk,
making dynamical mass determinations of the centre more uncertain.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS2147f9.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg88.gif) |
Figure 9:
A map of the equivalent width of H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{MS2147f10.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg89.gif) |
Figure 10:
|
| Open with DEXTER | |
This is the companion of the previously discussed galaxy. It has
properties of an extensively ionised dI galaxy embedded in an H I
cloud with mass
![]()
![]() ,
and a
,
and a ![]() /L ratio that is normal
for dIs. Both the spatial extent and equivalenth width of the H
/L ratio that is normal
for dIs. Both the spatial extent and equivalenth width of the H![]() emission are considerably smaller than for the main component.
The excitation, as measured from the [OIII]
emission are considerably smaller than for the main component.
The excitation, as measured from the [OIII]![]() 5507/H
5507/H![]() ratio
is moderate, and the galaxy is not a strong IRAS source. Hence,
this is not a starburst galaxy.
ratio
is moderate, and the galaxy is not a strong IRAS source. Hence,
this is not a starburst galaxy.
This galaxy has a central condensation and a morphology at the
fainter levels that resemble a warped, distorted disk.
It is the brightest component in a chain of galaxies (see Östlin et al.
2001, Fig. 7). We obtained spectra of three of these (unpublished).
They all have high velocities and thus probably do not belong to the system.
The colour index map (Fig. 4) shows a blue spiral-like structure
slightly off centre. ESO 480-IG12 has the lowest
![]() the BCGs
studied (buth higher than the two companions). Irregular, warp-like
structures are seen in the outer isophotes. Also in this galaxy very faint
structures stretch out in a direction perpendicular
to the disk, indicating that we have bipolar outflows of gas.
Further support for this comes from our Fabry-Perot spectroscopy
(Östlin et al. 1999, 2001).
the BCGs
studied (buth higher than the two companions). Irregular, warp-like
structures are seen in the outer isophotes. Also in this galaxy very faint
structures stretch out in a direction perpendicular
to the disk, indicating that we have bipolar outflows of gas.
Further support for this comes from our Fabry-Perot spectroscopy
(Östlin et al. 1999, 2001).
Comparisons between observations of star forming galaxies and predictions from SEMs are strongly dependent on the reliability of the extinction corrections. In massive star forming galaxies this may become a very severe problem since we may have a radial dependence on metallicity, age and extinction that results in a degeneracy in the information obtained, if the wavelength region covered is not sufficiently extended. The situation is more favourable in studies of BCG as most observations of BCGs point at a low dust content, even in the very central regions (e.g. Terlevich et al. 1991). This is confirmed also for the objects discussed in this article as will be shown below.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{MS2147f11.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg90.gif) |
Figure 11:
The H |
| Open with DEXTER | |
Since we, at this step, are primarily interested in obtaining
information about the halo population, the first thing is to
secure that 1) the extinction is low and 2) the contribution
from nebular emission can be controlled. We will use slit
spectra to determine the extinction from the H![]() /H
/H![]() ratio. Since
the Balmer emission lines are affected by the Balmer absorption
lines from the young stellar population, they have to be
corrected for this before they can be used for extinction
measurements.
As a first approximation, the correction was based on
ratio. Since
the Balmer emission lines are affected by the Balmer absorption
lines from the young stellar population, they have to be
corrected for this before they can be used for extinction
measurements.
As a first approximation, the correction was based on
![]() comparison with
predictions from our SEMs. In Fig. 11 we show the results
from a slitspectrum of one of the programme galaxies, ESO 400-G43.
We show both the measured H
comparison with
predictions from our SEMs. In Fig. 11 we show the results
from a slitspectrum of one of the programme galaxies, ESO 400-G43.
We show both the measured H![]() /H
/H![]() ratio and the same
ratio after correcting for underlying absorption based on
ratio and the same
ratio after correcting for underlying absorption based on
![]() .
From the diagram we see that the corrected H
.
From the diagram we see that the corrected H![]() /H
/H![]() ratio
several times falls significantly below the theoretical ratio
based on Brocklehursts data (Brocklehurst 1971)
which we approximately express
ratio
several times falls significantly below the theoretical ratio
based on Brocklehursts data (Brocklehurst 1971)
which we approximately express
| (1) |
The chemical abundances of nitrogen and oxygen of all galaxies except
ESO 338-IG04 were derived both from IDS spectra and EFOSC1 spectra.
For ESO 338-IG04 Bergvall (1985) derived
![]() ,
whereas Masegosa et al. (1994) and Raimann et al. (2000)
both got
,
whereas Masegosa et al. (1994) and Raimann et al. (2000)
both got
![]() .
.
The intensities of the most prominent emission lines relative to H![]() of the remaining three
BCGs and the two companions are presented in Table 4. For the
brighter central regions of the galaxies the calculation of the
emissivity of the O++ zone was based on a determination of the
electron temperature from the [OIII]
of the remaining three
BCGs and the two companions are presented in Table 4. For the
brighter central regions of the galaxies the calculation of the
emissivity of the O++ zone was based on a determination of the
electron temperature from the [OIII]
![]() /[OIII]
/[OIII]
![]() emission-line ratio. From the first calculation of
emission-line ratio. From the first calculation of ![]() we derived
the theoretical H
we derived
the theoretical H![]() /H
/H![]() recombination value (Brocklehurst
1971)
We then made a reddening correction according to above and
derived a new
recombination value (Brocklehurst
1971)
We then made a reddening correction according to above and
derived a new ![]() .
In this way the extinction and the
temperature in the O++ region were iteratively determined.
In order to calculate the total oxygen abundance one would
like to know also the temperature of the O+ zone. Since useful
lines for such a calculation are either too weak or outside the
spectral window we calculate this temperature from the
metallicity dependent relations derived by Vila-Costas &
Edmunds (1993) on basis of Stasinskas (1990)
models.
If
.
In this way the extinction and the
temperature in the O++ region were iteratively determined.
In order to calculate the total oxygen abundance one would
like to know also the temperature of the O+ zone. Since useful
lines for such a calculation are either too weak or outside the
spectral window we calculate this temperature from the
metallicity dependent relations derived by Vila-Costas &
Edmunds (1993) on basis of Stasinskas (1990)
models.
If ![]() is
expressed in units ot 104 K, the equation we use in this case is
is
expressed in units ot 104 K, the equation we use in this case is
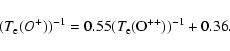 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2147f12.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg100.gif) |
Figure 12: The oxygen abundance of the target galaxies as function of absolute blue magnitude. The open triangles are local group dwarf galaxies and the full drawn line is the regression line. Data are from Skillman (1989). Also shown are the positions of two young galaxy candidates, IZw18 and SBS0335-052. |
| Open with DEXTER | |
A useful piece of information in the interpretation of the difference in
metallicity
between the populations in the different regions of the galaxies
is the size of possible abundance gradients in the ionised gas across the
centre and out into the halo. To check the homogeneity of the oxygen
abundances over the starburst regions we have to work at faint levels in the
spectra, where the standard method cannot be used. For this purpose we
applied the empirical relations based on the
([OII]![]() 3727+[OIII]
3727+[OIII]
![]() 4959,5007)/H
4959,5007)/H![]() line ratio (Pagel et al. 1979; Pagel et al. 1980; Edmunds & Pagel
1984; Skillman 1989). We are not concerned in this
article with systematic differences between the abundances derived from the
temperature sensitive method and the empirical method since we only wish to
set limits on the amplitude of the fluctuations in the abundances. As an
example the result from ESO 400-G43 is shown in Fig. 13. We see
that the variations in the abundances are quite small, and within
the accuracy of the empirical method. The central oxygen
abundances are presented in Table 4 along with the nitrogen abundances as
derived from the [NII]
line ratio (Pagel et al. 1979; Pagel et al. 1980; Edmunds & Pagel
1984; Skillman 1989). We are not concerned in this
article with systematic differences between the abundances derived from the
temperature sensitive method and the empirical method since we only wish to
set limits on the amplitude of the fluctuations in the abundances. As an
example the result from ESO 400-G43 is shown in Fig. 13. We see
that the variations in the abundances are quite small, and within
the accuracy of the empirical method. The central oxygen
abundances are presented in Table 4 along with the nitrogen abundances as
derived from the [NII]![]() 6584 line and the assumption N/H =
(N+/H+)/(O/O+).
6584 line and the assumption N/H =
(N+/H+)/(O/O+).
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{MS2147f13.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg102.gif) |
Figure 13:
The oxygen abundance of ESO 400-G43 as a function
of position along the disk. The position angle is 110 degrees.
The abundances are derived from McGaugh's empirical relations
(McGaugh 1991, 1994), utilizing the [OII], [OIII] and H |
| Open with DEXTER | |
| Line id. | 338-04b | 350-38 | 400-43 | 400-43b | 480-12 | |||||
|
|
|
|
|
|
||||||
| F | F | F | F | F | ||||||
|
OII |
1.73 | 1.74 | 1.76 | 2.02 | 4.68 | 4.39 | 4.82 | 3.98 | 2.40 | 2.54 |
| NeIII |
0.30 | 0.30 | 0.18 | 0.20 | - | - | - | - | 0.36 | 0.37 |
| OIII |
0.033 | 0.030 | 0.050 | 0.051 | 0.058 | 0.054 | - | - | 0.067 | 0.064 |
| HeI |
0.059 | 0.053 | 0.039 | 0.039 | - | - | - | - | 0.043 | 0.041 |
| OIII |
1.25 | 1.02 | 1.19 | 1.05 | 1.14 | 1.05 | 1.00 | 0.83 | 1.46 | 1.22 |
| OIII |
3.69 | 3.00 | 3.80 | 3.30 | 3.32 | 3.06 | 3.24 | 2.68 | 4.64 | 3.86 |
| HeI |
0.16 | 0.11 | 0.15 | 0.11 | 0.17 | 0.15 | - | - | 0.14 | 0.10 |
| OI |
0.16 | 0.11 | 0.068 | 0.047 | 0.20 | 0.18 | - | - | 0.073 | 0.050 |
| H |
4.13 | 2.76 | 4.08 | 2.75 | 3.12 | 2.82 | 3.42 | 2.82 | 4.12 | 2.75 |
| NII |
0.13 | 0.08 | 0.78 | 0.52 | 0.13 | 0.12 | 0.17 | 0.14 | 0.33 | 0.22 |
| HeI |
- | - | 0.0268 | 0.018 | - | - | - | - | - | - |
| SII |
0.54 | 0.36 | 0.25 | 0.16 | 0.39 | 0.36 | - | - | 0.26 | 0.17 |
| SII |
0.44 | 0.30 | 0.13 | 0.086 | 0.25 | 0.22 | - | - | 0.19 | 0.12 |
|
11600 | 13700 | 14400 | - | 14100 | |||||
| log
|
2.3 | 0.8 | 0.8 | - | 1.8 | |||||
|
|
12000 | 13100 | 13400 | - | 13200 | |||||
| log
|
2.3 | -0.2 | -0.2 | - | 1.8 | |||||
|
|
8.0 | 7.9 | 8.0 | 8.21 | 7.9 | |||||
|
|
-1.5 | -0.7 | -1.7 | -1.7 | -1.2 | |||||
|
|
32 | 38 | 65 | 72 | 32 | 38 | 15 | 18 | 43 | 51 |
|
|
5.3 | 12.6 | 416 | 1120 | 39 | 46 | 4.5 | 5.4 | 167 | 366 |
Figures 14 to 16 show the optical/near-IR luminosity and
colour
profiles of the galaxies. We wish to point out that the on-the-spot colours
within the central 1-2 arcsec are not reliable due to seeing effects. To
simplify the presentation we will only show the B luminosity profile (except
for ESO 338-IG04 where we also show the V profile reaching a photometric level
of unique depth) and a few colour index
profiles. This will be sufficient for our main goal here which is to
separate the halo population from the young burst. Of
course there may be many different components in the galaxy if several
mergers have occurred but we will show below that it really is possible to use
a two component distinction. Many investigations of the stellar population in
BCGs are based on BVR surface photometry. A problem when using only BVR data
is that the colour indices, in particular B-V, are fairly insensitive to age
if the metallicity is low. It is thus difficult to use these colours to
discriminate between the burst population and an old halo population. Moreover
the old generation has difficulties to compete with the luminous young
generation. Therefore a combination of optical and near-IR colours is much
more powerful, as is evident the diagrams. In particular in the
![]() profile
which is shown in the diagram, we see a strong trend towards redder colours
as we move outwards. Although this trend is present also in the B-V colours it
is much weaker, despite that we have corrected the colours we show in the
diagrams for internal extinction. This is due to the compensating effect
nebular emission has on "age reddening''. We will call the red stellar
population the "halo population'', clearly distinguished from the starburst
population in the centre.
profile
which is shown in the diagram, we see a strong trend towards redder colours
as we move outwards. Although this trend is present also in the B-V colours it
is much weaker, despite that we have corrected the colours we show in the
diagrams for internal extinction. This is due to the compensating effect
nebular emission has on "age reddening''. We will call the red stellar
population the "halo population'', clearly distinguished from the starburst
population in the centre.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS2147f14.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg114.gif) |
Figure 14:
The surface luminosity profiles of ESO 338-IG04 and ESO 338-IG04b
in
Cousins B and in Cousins/Johnson broadband colour indices.
The luminosity profiles are shown with two different fits. The dashed line
shows
a least square fit to an exponential profile and the solid line a fit to a
Sersic law. Inclination corrections based on a fit to the outer isophotes have
been applied. Likewise reddening corrections based on spectroscopy of the
central region and assuming the column density of the dust to be proportional
to the luminosity density in the broadband image used to derive the upper
luminosity profile, have also been applied. The error bars are 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS2147f15.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg115.gif) |
Figure 15: Luminosity and colour index profiles of ESO 350-IG38 (Haro 11) and ESO 480-IG12. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=10cm,clip]{MS2147f16.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg116.gif) |
Figure 16: Luminosity and colour index profiles of ESO 400-G43 and ESO 400-G43b. |
| Open with DEXTER | |
What we now will do is make a fit to this part of the
luminosity profiles of the deepest images to see what
restrictions we can set to the shape of the profile. In general
(e.g. Sersic 1968; Graham et al. 1996), the luminosity
profiles
of galaxies may be expressed as
![\begin{displaymath}%
I(r)=I_{\rm e}~\exp\big({-b[({r\over r_{\rm e}})^{1/n}-1]}\big)
\end{displaymath}](/articles/aa/full/2002/30/aa2147/img117.gif) |
(3) |
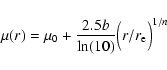 |
(4) |
In an effort to disentangle the photometric parameters of host
galaxies of BCGs, Papaderos et al. (1996) used luminosity
profiles obtained from optical broadband images. When fitting
an exponential disk to the outer part of the profile they found
that the central surface brightness of this hypothetical disk was
brighter than that of typical LSBGs (
![]() ). The conclusion
was that LSBGs were rather improbable as precursors of BCGs.
In the present investigation we reach fainter limiting isophotes
than they obtained in their work. Our luminosity profiles show that this may
make a big difference. We see that the scalelength is more or
less continuously increasing when going to lower surface
luminosity levels. The faintest luminosity profiles of our
galaxies reach
). The conclusion
was that LSBGs were rather improbable as precursors of BCGs.
In the present investigation we reach fainter limiting isophotes
than they obtained in their work. Our luminosity profiles show that this may
make a big difference. We see that the scalelength is more or
less continuously increasing when going to lower surface
luminosity levels. The faintest luminosity profiles of our
galaxies reach ![]() 29-30 mag arcsec-2 (n.b.: after correction
for inclination). As shown in the figures,
we get completely different results if we make a fit out to this
isophote than if we stop at the more commonly used limit,
29-30 mag arcsec-2 (n.b.: after correction
for inclination). As shown in the figures,
we get completely different results if we make a fit out to this
isophote than if we stop at the more commonly used limit,
![]() -26 mag arcsec-2. In fact we have no problem to reach a
central surface brightness as low as that of LSBGs by fitting an
exponential profile to the outer isophotes. The question is however,
whether a disk really is the best and most appropriate fit.
-26 mag arcsec-2. In fact we have no problem to reach a
central surface brightness as low as that of LSBGs by fitting an
exponential profile to the outer isophotes. The question is however,
whether a disk really is the best and most appropriate fit.
To proceed we will make two fits to the outer isophotes,
one where we leave the parameter n (Eq. (4)) free and one where we fix it to
n=1 (exponential disks), in order to facilitate comparisons with LSBGs. The
range of the fit is set by eye inspection where the halo colours start to become
significant. In
Table 5 we summarize the parameters we derive from fits to the outer
parts of the luminosity profiles, within the radial ranges as
indicated as in the figures. The parameters we specify are
the same as in Eq. (4). What is striking is that the n
parameter is very large (![]() 4) when we use good data at large
distances from the centre. Although the baseline of the fit is short, which
will make the solution somewhat unstable, we take this as an
indication that the host galaxy of the burst is of early type since all
galaxies go in the same direction. The fit will not be much worse if we fix n
to be equal to 4 but we see no reason why we should prefer this value to the
best solution value. We obtain an even better fit (measured by the correlation
coefficient) to a power-law if we include more data points closer to the centre.
In the final column of the table we give the maximum
luminosity the power law component can have, simply by assuming that the
brightness follows the power law down to a distance where the model surface
brightness is equal to the observed surface brightness. At shorter radial
distances we have assumed it to be equal to this value.
4) when we use good data at large
distances from the centre. Although the baseline of the fit is short, which
will make the solution somewhat unstable, we take this as an
indication that the host galaxy of the burst is of early type since all
galaxies go in the same direction. The fit will not be much worse if we fix n
to be equal to 4 but we see no reason why we should prefer this value to the
best solution value. We obtain an even better fit (measured by the correlation
coefficient) to a power-law if we include more data points closer to the centre.
In the final column of the table we give the maximum
luminosity the power law component can have, simply by assuming that the
brightness follows the power law down to a distance where the model surface
brightness is equal to the observed surface brightness. At shorter radial
distances we have assumed it to be equal to this value.
There is an exciting consequence of the high n values we derive, should these
values turn out to be firm, once deeper photometry becomes available. Caon et al. (1993) found a correlation between n and galaxy luminosity. The
higher the n value the brighter (and more massive) the galaxy. Similarly,
Graham et al. (1996) found that bright cluster ellipticals typically
have high n values. The highest best fit n values for the luminous galaxies is
typically ![]() .
If a high n signals a high mass it could indicate that
the BCGs in our sample have a high amount of dark matter.
.
If a high n signals a high mass it could indicate that
the BCGs in our sample have a high amount of dark matter.
| Galaxy | Filter | Range |
|
|
|
n |
|
||||||
| (kpc) | (kpc) | (kpc) | |||||||||||
| 338-04 | B | 6-11 | 3.3 | 24.6 | -16.6 | 0.968 | 0.008 | 9.8 | 0.921 | 1.09 | 0.973 | 0.005 | -17.7 |
| 338-04b | V | 6-9 | 2.4 | 24.6 | -15.9 | 0.54 | 0.12 | 19.8 | 8.8e-4 | -39.39 | 0.55 | 0.11 | -17.5 |
| 350-38 | B | 8-16 | 3.2 | 23.5 | -17.6 | 0.978 | 0.009 | 19.8 | 3.2e-5 | -53.95 | 0.982 | 0.008 | -20.0 |
| 400-43 | B | 6-12 | 2.5 | 23.1 | -17.5 | 0.981 | 0.010 | 17.1 | 4.2e-4 | -38.85 | 0.985 | 0.008 | -19.5 |
| 400-43b | B | 5-9 | 2.3 | 22.9 | -17.5 | 0.978 | 0.014 | 1.1 | 3.76 | 22.54 | 0.978 | 0.014 | -17.4 |
| 480-12 | B | 6-11 | 2.4 | 22.8 | -17.7 | 0.988 | 0.006 | 19.7 | 9.0e-5 | -49.18 | 0.996 | 0.002 | -19.3 |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{MS2147f17.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg128.gif) |
Figure 17: The relative contribution from nebular emission to the total emission (stars+gas) in different broadband windows. The colours are based on a model of a continuous star formation rate with a Salpeter mass function and a metallicity of 5% solar. |
| Open with DEXTER | |
In a few cases optical colours of the halos of BCGs have been derived that have been taken as evidence of an old stellar population (Hunter & Gallagher 1985; Kunth et al. 1988). However, one has to be aware of the ambiguities in the interpretation of these data. The analysis of our programme galaxies shows that nebular emission may contribute with a considerable amount to the light from the halo. Possible in situ ionising sources are young stars or old hot stars, i.e. blue horizontal branch stars (BHB) or post-AGB stars (PAGB). If so, it would cause no problem in the following comparisons with SEMs predictions, since the ionising flux from these stars is taken into account and the nebular component is included in the models. But, as we will show below, it is quite possible that gas in the halo is ionised by the central starburst. It is also possible that the expelled gas from the central star forming regions is energetic enough to contribute significantly to the ionisation either mechanically or by conduction. Considering the current debate about what is driving the reionisation of the post-recombination universe it is quite important to identify what is the major important ionising source in luminous BCGs to see if they possibly can contribute significantly to this process.
It seems unlikely that this gas is ionised by stars in situ
because we see no support of the presence of young star clusters in the
region and the large scale morphology in H![]() from
that of the broadband colours (Fig. 5).
We have argued that shocks are important ionisation sources, at least
close to the central region. It is hard to say how much outflows may
contribute to the ionisation at larger
distances but the heat input is probably of importance (e.g. Heckman et al.
2001).
from
that of the broadband colours (Fig. 5).
We have argued that shocks are important ionisation sources, at least
close to the central region. It is hard to say how much outflows may
contribute to the ionisation at larger
distances but the heat input is probably of importance (e.g. Heckman et al.
2001).
Nevertheless we will now also ask whether it is possible for the young
starburst to ionise a halo which has an extent several times larger than the
starburst. We made a calculation to the first approximation of how
realistic such a situation would be assuming that the gas is in
pressure equilibrium and approximately spherically distributed.
The density distribution was assumed to follow King's
approximation
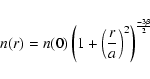 |
(5) |
From our observations we can set limits on the amount of possible excess
radiation from nebular emission in the halo and how
much it contributes to the light. We have used H![]() a probe to make
reasonable estimates. For ESO 338-IG04
we constructed a
a probe to make
reasonable estimates. For ESO 338-IG04
we constructed a
![]() using as continuum a 2000s deep exposure in an H
using as continuum a 2000s deep exposure in an H![]() narrowband (60 Å) filter
designed for a different redshift. The result, Fig. 7), was
first discussed in Sect. 4.2.1. Here
narrowband (60 Å) filter
designed for a different redshift. The result, Fig. 7), was
first discussed in Sect. 4.2.1. Here
![]() below
10 Å in the centre. For ESO 350-IG38, we used the deep R image as "off-line''
to reach a sufficiently faint surface brightness level. Figure 8
(also discussed in Sect. 4.2.3) shows
the resulting
below
10 Å in the centre. For ESO 350-IG38, we used the deep R image as "off-line''
to reach a sufficiently faint surface brightness level. Figure 8
(also discussed in Sect. 4.2.3) shows
the resulting
![]() .
As is seen,
.
As is seen,
![]() at a low level in the
halo. Similarily, as discussed before in Sect. 4.2.4, Fig. 9
shows
at a low level in the
halo. Similarily, as discussed before in Sect. 4.2.4, Fig. 9
shows
![]() ESO 400-G43. We notice rather high values on
the northeastern side. For ESO480-IG12 we do not have access to a deep H
ESO 400-G43. We notice rather high values on
the northeastern side. For ESO480-IG12 we do not have access to a deep H![]() image so here we use a slit spectrum. Figure 10 shows
image so here we use a slit spectrum. Figure 10 shows
![]() a slit in the major axis position. We conclude that also in this case
a slit in the major axis position. We conclude that also in this case
![]() stays at a moderate level, around 50-100 Å although there may be
tendencies for an increase at larger distances.
stays at a moderate level, around 50-100 Å although there may be
tendencies for an increase at larger distances.
We have modelled the colours and fluxes of a pure HII
region in the different wavelengths bands to obtain estimates of how much the
nebular
emission will contribute to the different wavelength bands as the starburst
evolves. Figure 17 shows the relative contribution of the nebular
emission to the total emission from stars and ionised gas. Since H![]() the emission in the R window we can compare the nebular contribution in the Rwindow with the other wavelength bands and then scale with H
the emission in the R window we can compare the nebular contribution in the Rwindow with the other wavelength bands and then scale with H![]() obtain the
actual contributions. The effective band width of the Cousins R window is
obtain the
actual contributions. The effective band width of the Cousins R window is
![]() 1200 Å. Thus, following the results from the spectroscopy and the
narrowband images, which
indicated
1200 Å. Thus, following the results from the spectroscopy and the
narrowband images, which
indicated
![]() ~
~![]() 100 Å, we find that the contribution from nebular
emission to the total flux in any of the
BRIJHK windows is <10% and <15% for V. This will have
a small but not insignificant effect on the
broadband colours when we compare the observations with the predictions. Below
we will return to a discussion about to what extent these data can be used to
constrain the total emission from the outer parts of the halo.
100 Å, we find that the contribution from nebular
emission to the total flux in any of the
BRIJHK windows is <10% and <15% for V. This will have
a small but not insignificant effect on the
broadband colours when we compare the observations with the predictions. Below
we will return to a discussion about to what extent these data can be used to
constrain the total emission from the outer parts of the halo.
| Model | Model | SFH | Z | f | c | ||
| set no. | no. | (Myr) | cm-3 | ||||
| 1 | 1 | const | 0.001 | 14000 | 100 | 1 | 1 |
| 2 | const | 0.001 | 10 | 100 | 1 | 1 | |
| 3 | const | 0.001 | 100 | 100 | 1 | 0.5 | |
| 4 | const | 0.001 | 100 | 100 | 0.1 | 1 | |
| 5 | const | 0.001 | 100 | 1 | 0.1 | 0.5 | |
| 6 | const | 0.001 | 100 | 1 | 1 | 1 | |
| 7 | const | 0.001 | 100 | 100 | 1 | 1 | |
| 8 | expo | 0.001 | 14000 | 100 | 1 | 1 | |
| 9 | expo | 0.001 | 1000 | 100 | 1 | 1 | |
| 2 | 1 | const | 0.001 | 1400 | 100 | 1 | 1 |
| 2 | const | 0.001 | 10 | 100 | 1 | 1 | |
| 3 | const | 0.001 | 100 | 100 | 1 | 0.5 | |
| 4 | const | 0.001 | 100 | 100 | 0.1 | 1 | |
| 5 | const | 0.001 | 100 | 1 | 0.1 | 0.5 | |
| 6 | const | 0.001 | 100 | 1 | 1 | 1 | |
| 7 | const | 0.001 | 100 | 100 | 1 | 1 | |
| 8 | expo | 0.001 | 14000 | 100 | 1 | 1 | |
| 9 | expo | 0.001 | 1000 | 100 | 1 | 1 | |
| 10 | const | 0.004 | 14000 | 100 | 1 | 1 | |
| 11 | const | 0.004 | 10 | 100 | 1 | 1 | |
| 12 | const | 0.004 | 100 | 100 | 1 | 1 | |
| 13 | const | 0.004 | 100 | 100 | 1 | 0 | |
| 14 | expo | 0.004 | 14000 | 100 | 1 | 1 | |
| 15 | expo | 0.004 | 1000 | 100 | 1 | 1 | |
| 16 | const | 0.020 | 10 | 100 | 1 | 1 | |
| 17 | const | 0.020 | 100 | 100 | 1 | 1 | |
| 18 | const | 0.020 | 100 | 100 | 1 | 0 | |
| 19 | expo | 0.020 | 14000 | 100 | 1 | 1 | |
| 20 | expo | 0.020 | 1000 | 100 | 1 | 1 | |
| 21 | const | 0.040 | 10 | 100 | 1 | 1 | |
| 22 | const | 0.040 | 100 | 100 | 1 | 1 | |
| 23 | const | 0.040 | 100 | 100 | 1 | 0 | |
| 24 | expo | 0.040 | 14000 | 100 | 1 | 1 | |
| 25 | expo | 0.040 | 1000 | 100 | 1 | 1 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2147f18.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg134.gif) |
Figure 18:
The predicted evolution of B-V and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2147f19.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg135.gif) |
Figure 19: Similar to Fig. 18 with the difference that the decay rate of the star formation is 14 Gyr (models 1:8 and 1:24 in Table 6). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2147f20.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg136.gif) |
Figure 20:
The diagram shows the predicted evolution from the PEGASE model
(Fioc & Rocca-Volmerange
2000) in B-V and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2147f21.ps} \end{figure}](/articles/aa/full/2002/30/aa2147/Timg137.gif) |
Figure 21: The observed colours of isolated E/S0 galaxies (Bergvall & Johansson 1995; filled dots), M31 globular clusters (Barmby et al. 2000; stars), the mean position of local ellipticals (Pahre 1999; large circle), the disk of the luminous LSBG 0237-0159 (Bell et al. 2000; big star), the low luminosity elliptical ESO 118-G34 (Sadler et al. 2000; diamond). Our BCG data are displayed as in Fig. 18. |
| Open with DEXTER | |
We will now use the colours of the burst and halo regions together with the spectral evolutionary models (SEMs) to constrain the age and metallicity of the stellar populations. The predicted colour evolution of the SEMs depend on the assumed initial mass function (IMF), metallicity and a parameter describing how the SFR changes with time. More sophisticated models also include metallicity evolution and gas flows. There is still on going debate about the slope of the IMF and its possible universality, but within the range consistent with observations (e.g. Salpeter, Scalo, Kroupa et al., Miller-Scalo etc.), varying the IMF has a relatively small impact on colours, except at the very earliest stages. This is because the emitted light will be dominated by the most luminous stars still alive. Sometimes, IMFs truncated at low stellar masses have been proposed for starburst regions. However, at low ages, low mass stars are insignificant contributors to the emitted light, whereas at high ages they are needed to get any light at all. Hence varying the IMF, and its lower and upper mass limits, will affect the mass to light ratio, but have rather small impact on the colour evolution of a stellar population. On the other hand, metallicity and the temporal behaviour of the SFR has a major impact on colours. Assuming that the SFR is constant in time leads to blue colours at high ages, as compared to a short burst. A correct treatment of nebular emission is crucial at low ages, but less important a high ages. Hence, in order to restrict the parameter space, we have chosen to use only models with a "normal'' Salpeter IMF, but instead let the metallicity and star fomation history vary and also and the density, covering factor and filling factors of the ionised gas (with a single, observationally known, metallicity). In Table 6, we give a list of the used parameters in the SEMs.
| Galaxy | Component | Age | MB | B-V | B-R | V-I | V-K | J-H | H-K | MV/L | Mass |
|
|
| (yr) | (
|
mag | mag | ||||||||||
| 338-04 | Halo | -17.70 | 0.31 | 0.69 | 0.70 | 2.83 | 0.68 | 0.12 | |||||
|
|
0.02 | 0.03 | 0.03 | 0.05 | 0.24 | 0.36 | 0.35 | 0.017 | |||||
| Model 1 | 4.5e8 | -16.24 | 0.17 | 0.13 | -0.06 | 0.67 | 0.25 | 0.15 | 0.16 | 5.0e7 | |||
| Model 24 | 7.5e9 | -17.36 | 0.39 | 0.85 | 0.88 | 2.73 | 0.57 | 0.25 | 2.35 | 2.5e9 | |||
| Mix | -17.69 | 0.34 | 0.70 | 0.73 | 2.50 | 0.56 | 0.25 | 1.85 | 2.6e9 | ||||
|
|
-0.01 | -0.03 | -0.01 | -0.03 | 0.33 | 0.12 | -0.13 | 0.017 | 0.032 | |||
| 338-04b | Halo | - | - | - | 0.62 | 2.87 | 0.42 | 0.41 | |||||
|
|
- | - | - | 0.03 | 0.28 | 0.17 | 0.28 | 0.02 | |||||
| Model 9 | 5.0e5 | -16.95 | 0.63 | 0.00 | -1.46 | -0.22 | 0.04 | 0.58 | 0.005 | 4.6e6 | |||
| Model 22 | 6.5e9 | -16.55 | 0.94 | 1.63 | 1.34 | 3.55 | 0.64 | 0.28 | 7.39 | 6.3e9 | |||
| Mix | -17.52 | 0.77 | 0.96 | 0.63 | 2.79 | 0.62 | 0.29 | ||||||
|
|
- | - | - | 0.00 | 0.08 | -0.20 | 0.12 | 0.01 | 0.13 | |||
| 350-38 | Halo | -20.00 | 0.87 | 1.24 | - | 4.16 | - | 0.82 | |||||
|
|
0.03 | 0.26 | 0.12 | - | 0.81 | - | 1.20 | 0.21 | |||||
| Model 9 | 5.0e5 | -19.16 | 0.63 | 0.00 | -1.46 | -0.22 | 0.04 | 0.58 | 0.005 | 3.5e7 | |||
| Model 23 | 14.5e9 | -19.33 | 1.02 | 1.76 | 1.46 | 3.77 | 0.66 | 0.28 | 14.92 | 1.8e11 | |||
| Mix | -20.00 | 0.86 | 1.26 | 1.00 | 3.28 | 0.65 | 0.28 | 9.35 | 1.8e11 | ||||
|
|
0.00 | 0.01 | -0.02 | - | 0.88 | -0.65 | 0.54 | 0.09 | 0.22 | |||
| 400-43 | Halo | -19.50 | 0.92 | 0.74 | - | 3.15 | 0.95 | 0.71 | |||||
|
|
0.03 | 0.19 | 0.19 | - | 0.78 | 0.63 | 0.86 | 0.13 | |||||
| Model 6 | 5.0e5 | -19.15 | 0.65 | -0.03 | -1.50 | -0.25 | 0.04 | 0.58 | 0.005 | 3.6e7 | |||
| Model 22 | 13.5e9 | -18.10 | 1.02 | 1.76 | 1.46 | 3.76 | 0.66 | 0.28 | 13.59 | 5.2e10 | |||
| Mix | -19.50 | 0.76 | 0.80 | 0.44 | 2.66 | 0.63 | 0.29 | 4.73 | 5.2e10 | ||||
|
|
0.00 | 0.15 | -0.07 | - | 0.48 | 0.31 | 0.42 | 0.14 | 0.31 | |||
| 400-43b | Halo | -17.40 | - | 0.89 | - | 2.881 | -0.17 | 0.62 | |||||
|
|
0.05 | - | 0.09 | - | 0.221 | 0.26 | 0.31 | 0.12 | |||||
| Model 4 | 2.5e9 | -17.28 | 0.41 | 0.78 | 0.70 | 2.241 | 0.41 | 0.13 | 1.76 | 1.8e9 | |||
| Model 22 | 10.5e9 | -14.97 | 1.00 | 1.73 | 1.43 | 4.721 | 0.65 | 0.28 | 10.76 | 2.2e9 | |||
| Mix | -17.40 | 0.49 | 0.93 | 0.86 | 2.961 | 0.53 | 0.21 | 3.30 | 4.1e9 | ||||
|
|
0.00 | - | -0.04 | - | -0.08 | -0.70 | 0.41 | 0.16 | 0.19 | |||
| 480-12 | Halo | -19.30 | 0.51 | 0.79 | - | 2.67 | 0.93 | -0.38 | |||||
|
|
0.03 | 0.13 | 0.09 | - | 0.54 | 0.31 | 0.56 | 0.14 | |||||
| Model 9 | 3.5e7 | -18.90 | 0.26 | -0.04 | -0.61 | 0.05 | 0.12 | 0.29 | 0.03 | 9.8e7 | |||
| Model 23 | 14.5e9 | -18.01 | 1.02 | 1.76 | 1.46 | 3.77 | 0.66 | 0.28 | 14.92 | 5.2e10 | |||
| Mix | -19.29 | 0.55 | 0.87 | 0.81 | 2.99 | 0.64 | 0.28 | 7.05 | 5.2e10 | ||||
|
|
-0.01 | -0.04 | -0.08 | - | -0.32 | 0.30 | -0.66 | 0.11 | 0.32 |
Before entering into the detailed modelling of the halo colors, we will have a look at the location of the galaxies in the B-V vs. V-K two colour diagram. In Figs. 18, 19, 20 and 21 we try to show, as simple as possible, the main restrictions we can impose on the stellar populations in the galaxies. The V-K/B-V diagrams show the predicted colour evolution from 0 to 14 Gyr of a star forming galaxy with different star formation histories and metallicities. For comparison we show the results from three different SEMs from three different research groups.
In Fig. 18 we show the predicted evolution of an exponentially
decaying star formation history with timescale of 1 Gyr at two different
metallicities, 5% solar and twice solar (Zackrisson et al. 2001).
Figure 19 shows the same data with the difference that the star
formation decay rate is now 14 Gyr. Hence these represent 4 extreme cases,
and the truth may well lie in between. An instant burst model would differ
from the ![]() Gyr model, only for ages less than a few Gyrs. However,
real galaxies can hardly be truly instantaneous on a global scale, but a
time scale of 1 Gyr is probably more realistic. In Fig. 18
(
Gyr model, only for ages less than a few Gyrs. However,
real galaxies can hardly be truly instantaneous on a global scale, but a
time scale of 1 Gyr is probably more realistic. In Fig. 18
(![]() Gyr) one sees that the the colours of the starburst regions seem
to fall along the metal-poor track, whereas, surprisingly (given the
observed nebular metallicities), the halo colours lie close to the old
ages of the metal-rich track. The same pattern is seen Fig. 19
(
Gyr) one sees that the the colours of the starburst regions seem
to fall along the metal-poor track, whereas, surprisingly (given the
observed nebular metallicities), the halo colours lie close to the old
ages of the metal-rich track. The same pattern is seen Fig. 19
(![]() Gyr), but now the two reddest halos are redder than even the
oldest points in the metal-rich model. Hence, this first simple look at
the halo colours suggests that the halos are old, metal-rich and
formed on relatively short timescales.
Gyr), but now the two reddest halos are redder than even the
oldest points in the metal-rich model. Hence, this first simple look at
the halo colours suggests that the halos are old, metal-rich and
formed on relatively short timescales.
In Fig. 20 we use the predictions from the PEGASE2 model (Fioc & Rocca-Volmerange 2000), in which the recycling of metals in a closed box scenario have been taken into account. Two tracks are displayed - one shows the evolution of a stellar population with zero initial metallicity assuming the star formation rate is kept constant. The other track shows the evolution starting from an initial metallicity of approximately 5% solar (Z=0.001) and then evolving with an exponentially declining SFR and a decay rate of 1 Gyr, as in Fig. 18. In this diagram we also display the predictions of colours of an old stellar population of 3 different metallicities ([Fe/H ]=-1.0, 0.0 and 0.5) from Wortheys (1994) models. On top of this we display the colours of the central region and the halo of our BCGs. Again, it appears that the reddest halos are old and quite metal-rich.
As can be seen, the colours of the central starburst agree very well with the
predictions from the metal-poor model. An important fact to remember is that all
4 BCGs show Wolf-Rayet features in their spectra and have strong Balmer emission
lines and thus must contain a considerable fraction of very young stars, as
is also indicated by the photometry in the UV/blue region and UV spectra
obtained with IUE. What may seem somewhat unexpected perhaps is
that the luminosity weighted ages of the burst populations, as found from the
positions in the diagrams, are quite high, as if the star formation has been
going on continuously for more than 1 Gyr. This cannot be correct because it is
not consistent with the high equivalent widths of the observed emission lines.
The equivalent width of H![]() several hundred Å and the luminosities
correspond
to star formation rates of several
several hundred Å and the luminosities
correspond
to star formation rates of several
![]() yr-1. The available gas budget
of a few times 108
yr-1. The available gas budget
of a few times 108
![]() would be thus consumed in about 108 yr (or even
faster if we have a decaying SFR) unless the IMF is peculiar. The explanation of
the
colours is probably that there is a burst occurring in an old host.
In Figs. 18 and 19
we show the effect on the colours of the transition from a passive old
population to a young burst. Depending on the age and the relative mass of the
burst it may take any position within the region defined by the connecting
lines between the young and old population. Although the optical region
may be little affected by the mixing of the two population we may notice it in
the near-IR, in V-K. A mixed population
with 10% of the V-band luminosity from a population with the same color
as the ones observed in the halos and a 90% from a young (107 yr) model
population gives composite colors which agrees well with those of the central
regions. Thus it is perfectly proper to assume that the ages of the burst
population
are quite low, i.e.
would be thus consumed in about 108 yr (or even
faster if we have a decaying SFR) unless the IMF is peculiar. The explanation of
the
colours is probably that there is a burst occurring in an old host.
In Figs. 18 and 19
we show the effect on the colours of the transition from a passive old
population to a young burst. Depending on the age and the relative mass of the
burst it may take any position within the region defined by the connecting
lines between the young and old population. Although the optical region
may be little affected by the mixing of the two population we may notice it in
the near-IR, in V-K. A mixed population
with 10% of the V-band luminosity from a population with the same color
as the ones observed in the halos and a 90% from a young (107 yr) model
population gives composite colors which agrees well with those of the central
regions. Thus it is perfectly proper to assume that the ages of the burst
population
are quite low, i.e. ![]() 10 Myr.
10 Myr.
Let us now look a bit more detailed at the spectral energy distribution of
the halos and the best fitting SEM predictions from the Zackrisson et al.
(2001) model. For simplicity and considering the large uncertainty
in the near-IR colours of the halo, a few parameters of the SEMs were kept
fixed. Thus we assumed a Salpeter IMF, a mass range between 0.08 and 120
![]() and a constant metallicity.
and a constant metallicity.
We mixed two models where the metallicity in both gas and stars
in one of the models was fixed to 5% of the solar (set No. 1 in Table 6). We think this is a reasonable guess of the metallicity
of the gas used in the burst. It is also at the lower envelope of the
metallicity of the (recently enriched) ISM of gas-rich LSB galaxies
which, as we will argue below, are attractive merger candidates.
Hence this metal-poor component would allow us to simulate contamination
to the halo colours from young stars.
The metallicity of the second
component, which we may associate with the halo population, was allowed to vary
between 5% solar and twice solar (set No. 2 in Table 6). The star formation rate was either assumed to
occur in a burst of constant SFR for ![]() or in an exponentially
declining
mode, SFR
or in an exponentially
declining
mode, SFR ![]() e
e
![]() ,
where t is the age of the burst and
,
where t is the age of the burst and
![]() is the duration of the burst or the SFR decay timescale. Table 6 lists the
parameters of the models we included in the comparison. The optimized mixture of
the two sets of models were fitted to the observed fluxes that were given
weights
in proportion to the square of the inverse of the mean error.
is the duration of the burst or the SFR decay timescale. Table 6 lists the
parameters of the models we included in the comparison. The optimized mixture of
the two sets of models were fitted to the observed fluxes that were given
weights
in proportion to the square of the inverse of the mean error.
Table 7 lists the models that, when optimally mixed, gave the best fits to
the observed broadband fluxes. The table displays predicted colours and the
deviations from the observations. Also inluded are the weighted mean errors
of the observations and the mean error of the fit. The errors refer to the
colours and are based on the weighted errors of the fits to the fluxes.
Although the errors are quite large (we are investigating regions with very
low surface brightneses), the best fits are with a few exceptions obtained
within about ![]() of the observational errors. It is noteworthy
that we find several cases of large deviations with respect to the observed
V-K colours, in the sense that observations are redder than the models.
Hence, increasing the weight of the near IR data would lead to higher
ages and metallicities.
The extremely young ages derived for the metal-poor
component in 2-3 cases is of course unrealistic and should be regarded as
indications of low age only. The important result is that, even as we include
all available photometry in the comparisons, we get consistency with the
conclusions from the previous discussions - the halo components of all
galaxies
have colours that best fit with models of an old metal-rich stellar
population.
of the observational errors. It is noteworthy
that we find several cases of large deviations with respect to the observed
V-K colours, in the sense that observations are redder than the models.
Hence, increasing the weight of the near IR data would lead to higher
ages and metallicities.
The extremely young ages derived for the metal-poor
component in 2-3 cases is of course unrealistic and should be regarded as
indications of low age only. The important result is that, even as we include
all available photometry in the comparisons, we get consistency with the
conclusions from the previous discussions - the halo components of all
galaxies
have colours that best fit with models of an old metal-rich stellar
population.
For comparison, we have also included in the table the mean error of the
best fit to a model including only metal-poor (<20% solar) stellar
populations.
These fits are significanlty worse except for one case, ESO 400-G43b. In
this case the fit is equally good if we assume a low metallicity throughout.
It is interesting to note that this is also the only galaxy in our sample
that has a luminosity profile that fits well with an exponential disk.
It thus has properties similar to LSB galaxies that are thought to have
had a rather constant and low star formation activity over a long time
and are probably not sitting in massive halos.
The other cases typically deviate with 1-3![]() from the observations
and are thus 2-3 times worse when we force the halo to have a low metallicity.
While the errors are large, and the sample is small, the comparison
with the SEMs suggest that the halos are more metal-rich than inferred
from the nebular gas.
from the observations
and are thus 2-3 times worse when we force the halo to have a low metallicity.
While the errors are large, and the sample is small, the comparison
with the SEMs suggest that the halos are more metal-rich than inferred
from the nebular gas.
The predicted photometric masses of the halos, based on the halo luminosities
from Table 5, range from
![]() to
to
![]()
![]() and should
be
regarded
as upper limits. Had we chosen the Scalo (1998) IMF instead of the
Salpeter IMF, the predicted masses would be reduced with a factor
and should
be
regarded
as upper limits. Had we chosen the Scalo (1998) IMF instead of the
Salpeter IMF, the predicted masses would be reduced with a factor ![]() 2.
Moreover, had we used an exponential luminosity profile in estimating the
the total halo luminosities, the mass estimates would go down with up to
a factor of 10.
2.
Moreover, had we used an exponential luminosity profile in estimating the
the total halo luminosities, the mass estimates would go down with up to
a factor of 10.
Now let us have a look at the halo colours and discuss the properties of the host of the starbursts. Let us first recall the most popular alternative star formation scenarios discussed in this context: 1) What we observe is the first star formation epoch in the history of the galaxy. The galaxy is young. 2) This is one of several intermittent bursts taking place in the galaxy. The bursts are caused by infall of cooled gas from the halo, processed in a previous burst. 3) Interaction with a neighbor, causing gas from the outskirts to fall towards the centre, thereby igniting a burst 4) Merger between galaxies or one galaxy (or a few galaxies) and intergalactic gas clouds. We will now discuss these alternatives one by one.
The fact that the chemical abundances are low and
homogeneous agree with a young galaxy but the colours and the morphology of the
halo
population do not. We have shown that the light from the halo is dominated
by stars. Thus the galaxy has to be at least as old as the time it takes for
the stars to relax into a regular structure. This is at least a few crossing
times or a few hundred Myr. The colours of the halo populations are much redder
than
that of metal-poor gas-rich low surface brightness galaxies (BCG halo:
![]() mag. as compared to LSB:
mag. as compared to LSB:
![]() mag.; Bergvall et al. 2000)
and
do not at all agree with a young metal-poor population. The agreement is fine
however,
with a metal-rich
stellar population of an intermediate-high age (
mag.; Bergvall et al. 2000)
and
do not at all agree with a young metal-poor population. The agreement is fine
however,
with a metal-rich
stellar population of an intermediate-high age (![]() 2-15 Gyr). This is
evident
from the
figures where the model predictions are displayed and is consistent with all
three model codes we compare with. Both ESO 350-IG38 and 400-G43 appear to have
old halos while ESO 338-IG04 and 480-IG12 may have halo ages of between 1 Gyr
and a Hubble age, depending on the contribution
of young stars to the halo light.
2-15 Gyr). This is
evident
from the
figures where the model predictions are displayed and is consistent with all
three model codes we compare with. Both ESO 350-IG38 and 400-G43 appear to have
old halos while ESO 338-IG04 and 480-IG12 may have halo ages of between 1 Gyr
and a Hubble age, depending on the contribution
of young stars to the halo light.
In Fig. 21 we compare with different samples of observational data
from the literature. This includes a set of globular clusters in M31 (Barmby
et al. 2000) a sample of seemingly isolated E/SO galaxies (no bright
neighbors in projection; Bergvall & Johansson 1995) and another
sample of mostly cluster ellipticals (Pahre 1999), the distribution of
which is indicated by a large circle in the diagram. The range of metallicities
of the globulars is
![]() Fe/H
Fe/H![]() ,
with mean metallicities slightly
below [Fe/H]=-1.0. This is close to the metallicity of the burst population of
our target
galaxies. Yet they deviate strongly from the colours of the halos. This is in
disagreement with Doublier et al. (2001). They however studied the
global colours and their sample was selected differently. Admittedly
the error bars of the halo colours are quite large but taken together we find
no other reasonable explanation than high age and high metallicity (taking the
risk of generalizing the properties of the halos of the four galaxies). We
have no reason to suspect that we have serious calibration problems and a
comparison
with the few other photometric data available is reassuring. E.g. our photometry
of
the galaxy with the most extraordinary colours, ESO 350-IG38, agree remarkably
well
with those of Vader et al (1993). They obtain MB=-20.2, K=12.08,
J-H=0.62,
H-K=0.62 (
,
with mean metallicities slightly
below [Fe/H]=-1.0. This is close to the metallicity of the burst population of
our target
galaxies. Yet they deviate strongly from the colours of the halos. This is in
disagreement with Doublier et al. (2001). They however studied the
global colours and their sample was selected differently. Admittedly
the error bars of the halo colours are quite large but taken together we find
no other reasonable explanation than high age and high metallicity (taking the
risk of generalizing the properties of the halos of the four galaxies). We
have no reason to suspect that we have serious calibration problems and a
comparison
with the few other photometric data available is reassuring. E.g. our photometry
of
the galaxy with the most extraordinary colours, ESO 350-IG38, agree remarkably
well
with those of Vader et al (1993). They obtain MB=-20.2, K=12.08,
J-H=0.62,
H-K=0.62 (
![]() )
We obtain MB=-20.0, K=12.06, J-H=0.67,
H-K=0.62.
)
We obtain MB=-20.0, K=12.06, J-H=0.67,
H-K=0.62.
In Sect. 6 we concluded that the influence of gas and dust on the colours is
small. How
much and in which direction would the colours be affected if we relax these
constraints? We have discussed some constraints on the H![]() that cover
the
region including the infrared data of ESO 350-IG38, 338-IG04 and 400-G43. In
these two
cases we can rather safely say that the contribution from nebular emission to
the halo light is negligible. But in the other cases we cannot exclude that
the contribution from nebular emission increases as we reach the red regions.
It is therefore motivated to have a look at how nebular emission would affect
the colours. We can derive the colours of a pure HII region (i.e assuming no
stars in the halo so that 100% of the flux is due to the ionised gas)
assuming that the metallicity is the same as that of the ionised gas in the
centre. The colours we obtain are
that cover
the
region including the infrared data of ESO 350-IG38, 338-IG04 and 400-G43. In
these two
cases we can rather safely say that the contribution from nebular emission to
the halo light is negligible. But in the other cases we cannot exclude that
the contribution from nebular emission increases as we reach the red regions.
It is therefore motivated to have a look at how nebular emission would affect
the colours. We can derive the colours of a pure HII region (i.e assuming no
stars in the halo so that 100% of the flux is due to the ionised gas)
assuming that the metallicity is the same as that of the ionised gas in the
centre. The colours we obtain are
![]() and
and
![]() ,
i.e.
significantly bluer than observed. Thus, if anything, the colours of the
stellar population would become redder if we correct for the contribution from
emission from gas ionised by the central source. With the assumptions made in
Sect. 6 the correction in B-V would be marginal while in V-K it would amount
to
0.1-0.2 magnitudes.
,
i.e.
significantly bluer than observed. Thus, if anything, the colours of the
stellar population would become redder if we correct for the contribution from
emission from gas ionised by the central source. With the assumptions made in
Sect. 6 the correction in B-V would be marginal while in V-K it would amount
to
0.1-0.2 magnitudes.
Could the emission be due to warm dust? We may constrain the properties of such
a component from the K band photometry combined with ISOCAM 4-14![]() data of
ESO 350-IG38 from the ISO mission (Bergvall et al., in preparation). The total
fluxes we
obtain from the ISOCAM data are 4.0
data of
ESO 350-IG38 from the ISO mission (Bergvall et al., in preparation). The total
fluxes we
obtain from the ISOCAM data are 4.0![]() :
:
![]() mJy,
6.7
mJy,
6.7![]() :
:
![]() mJy, 9.6
mJy, 9.6![]() :
:
![]() mJy, 14.3
mJy, 14.3![]() :
:
![]() mJy.
If
we assume an emissivity of
mJy.
If
we assume an emissivity of
![]() ,
with
,
with
![]() (Lisenfeld et al. 2000) we obtain a
temperature range of 100-160 K based on these global ISO data. If the heating
is caused by the central burst, 160 K is the maximum temperature we can accept
in the halo. The total K band flux density is 135 mJy. 10% of this emission
originates from the region outside 5 kpc that has a clear red excess. The excess
in
(Lisenfeld et al. 2000) we obtain a
temperature range of 100-160 K based on these global ISO data. If the heating
is caused by the central burst, 160 K is the maximum temperature we can accept
in the halo. The total K band flux density is 135 mJy. 10% of this emission
originates from the region outside 5 kpc that has a clear red excess. The excess
in ![]() relative to a metal-poor stellar population is
relative to a metal-poor stellar population is ![]() 1.4m, or
roughly 80%. If we therefore assume that at least 50% of the
1.4m, or
roughly 80%. If we therefore assume that at least 50% of the ![]() emission,
i.e.
emission,
i.e. ![]() 7 mJy, comes from warm dust we can calculate a minimum
temperature of the dust from the 2
7 mJy, comes from warm dust we can calculate a minimum
temperature of the dust from the 2![]() and the 4
and the 4![]() fluxes. The 4
fluxes. The 4![]() emission outside 5 kpc contributes with
emission outside 5 kpc contributes with ![]() 5% of the total emission in
this frequency band. With these data, the temperature we derive is around
3500 K, which is impossible if the dust is heated by the central burst and
unreasonable if the dust is heated in situ. Warm circumstellar dust with a
temperature of 500 K would contribute with 0.1% of the K flux from the halo if
we scale it with the 4
5% of the total emission in
this frequency band. With these data, the temperature we derive is around
3500 K, which is impossible if the dust is heated by the central burst and
unreasonable if the dust is heated in situ. Warm circumstellar dust with a
temperature of 500 K would contribute with 0.1% of the K flux from the halo if
we scale it with the 4![]() emission. We conclude that the contribution from
dust emission to the halo
emission. We conclude that the contribution from
dust emission to the halo ![]() luminosity is insignificant.
luminosity is insignificant.
Since the dust extinction to the amount that would be
needed for the data to be consistent with a young age, i.e.
![]() mag, probably can be excluded, the only alternative remaining, if we stick
to low metallicities, is that the IMF is odd. But, if so, the only option is a
very low upper mass limit, a highly improbable situation if we can trust the
theoretical models of star formation. The youth hypothesis therefore
can be dismissed.
mag, probably can be excluded, the only alternative remaining, if we stick
to low metallicities, is that the IMF is odd. But, if so, the only option is a
very low upper mass limit, a highly improbable situation if we can trust the
theoretical models of star formation. The youth hypothesis therefore
can be dismissed.
We have shown in a previous paper (Östlin et al. 1998) that at least ESO 338-IG04 has been involved in previous bursts. But if the gas in the present burst originates from expelled gas from a previous burst, the metallicity of the gas must be higher than or comparable to that of the host, not an order of magnitude lower. Following the conclusions from the previous discussion, this is not the case. We can therefore conclude that recurrent bursts, controlled by the cyclic expulsion and later accretion of the ISM, cannot be the explanation of the starburst seen in our BCGs. Previous bursts induced by infall of fresh material, either from gas-rich dwarfs or in the form of intergalactic HI clouds, are however not excluded.
Gas rich galaxies of low to intermediate masses have small abundance gradients. Thus if the starburst is caused by interaction with a neighboring galaxy we still would have to explain why the metallicity of the gas is lower than that of the old stars. Moreover the statistics give no observational support of strong starbursts caused by interaction between low mass galaxies. Only gas-rich LSB galaxies have the required properties of the metal-poor progenitor and it seems to be very difficult to ignite a starburst in such a galaxy (Mihos et al. 1997).
A merger between two galaxies of different metallicities, one gas-rich and one gas-poor, or infall of intergalactic clouds, appear to be the most plausible explanation of the observational results. We have argued in previous papers (Bergvall et al. 1998, 2000) that gas-rich LSB galaxies, and perhaps only this type of galaxy and not normal irregulars, have the required properties of the metal-poor component. One of the arguments was based on the location of these galaxies in the metallicity-luminosity diagram (Fig. 12). If one assumes the progenitor to be a dI, the offset of more than 3 mag in luminosity from the dI relation would require an excessive neutral hydrogen gas mass. LSBGs on the other hand already lie offset from the dI relation, meaning that they need to brighten less, and in addition, the gas mass fractions are much higher than for dIs. Note that also IZw18 and SBS 0335-052 show the same offset from the MB - Z relation in Fig. 12.
The old halo component could be a dwarf elliptical, a massive ellipsoidal
disk or a similar type of galaxy.
If the last interpretation is correct, it would indicate that there should be
cases in which we would find low luminosity early type galaxies hosting HI
clouds or gas-rich galaxies in a state prior to a burst. Sadler et al.
(2000) observed four E/S0 and S0 galaxies with these properties.
Their sample galaxies have luminosities ranging from MB=-17.0 to -19.1,
i.e. similar to
the maximum luminosities of our host galaxies, and contain HI
with masses in the range 108 to 109
![]() .
They found that the HI is
strongly concentrated towards the central region, differing from what is found
in normal early type galaxies. In two of the cases the distribution of the HI
resembles warped disks like in ESO 338-IG04 and ESO 480-IG12. Similar results
were obtained by Lake et al. (1987) for another sample of low
luminosity early type galaxies. James & Mobasher (1999) find star
formation activity most frequent in ellipticals situated in regions of low
density but not completely isolated. Two of the galaxies in the Sadler et al.
sample show clumpy H II emission in the centre with an H
.
They found that the HI is
strongly concentrated towards the central region, differing from what is found
in normal early type galaxies. In two of the cases the distribution of the HI
resembles warped disks like in ESO 338-IG04 and ESO 480-IG12. Similar results
were obtained by Lake et al. (1987) for another sample of low
luminosity early type galaxies. James & Mobasher (1999) find star
formation activity most frequent in ellipticals situated in regions of low
density but not completely isolated. Two of the galaxies in the Sadler et al.
sample show clumpy H II emission in the centre with an H![]() about
a
few percent of what we observe in our BCGs. Interestingly enough, the
optical/near-IR colours are similar to the halos of our disk-like systems,
e.g. their ESO 118-G34 has the colours B-V=0.46 and V-K=2.56, similar to the
halo of ESO 480-IG12 (B-V=0.51, V-K=2.67). It is also interesting
that the halo colours of ESO 338-IG04 and 480-IG12 agree with
the disk colours of a giant LSB galaxy observed by Bell et al. (2000),
believed to have supersolar metallicities from their comparison with SEMs. The
positions of these galaxies have been indicated in Fig. 21.
about
a
few percent of what we observe in our BCGs. Interestingly enough, the
optical/near-IR colours are similar to the halos of our disk-like systems,
e.g. their ESO 118-G34 has the colours B-V=0.46 and V-K=2.56, similar to the
halo of ESO 480-IG12 (B-V=0.51, V-K=2.67). It is also interesting
that the halo colours of ESO 338-IG04 and 480-IG12 agree with
the disk colours of a giant LSB galaxy observed by Bell et al. (2000),
believed to have supersolar metallicities from their comparison with SEMs. The
positions of these galaxies have been indicated in Fig. 21.
It seems that the best candidate of the starburst host galaxy in our BCGs
is a galaxy of early morphological type.
We know that dEs have the highest fraction of dark matter of all galaxy types
and
that the DM density is extremely high, approximately 1000 times higher than
in large ellipticals. Here we have the preconditions needed for creating
dynamical instabilities in an infalling LSB disk, followed by inflows and a
starburst. But there is also another alternative. Massive ellipticals may form
in the gravitational wells of large amplitude dark matter
fluctuations. In the early formation phase they consequently were much more
dark matter dominated than they are today. In sparse regions the buildup of the
stellar
component of the galaxies would proceed with a lower tempo and maybe there
we could find DM dominated massive Es that occasionally would be involved
in
mergers. A massive DM halo would be more efficient in retaining metals
produced in a burst than a low mass one, thus explaining the red colours.
Support for mergers or infall taking place in isolated
early type galaxies of L* luminosities (
![]() )
comes from e.g.
Colbert et al. (2001). They found evidence of recent mergers in
about 40% of the cases and in higher proportions than found in richer groups.
)
comes from e.g.
Colbert et al. (2001). They found evidence of recent mergers in
about 40% of the cases and in higher proportions than found in richer groups.
Early type galaxies follow a colour-magnitude relationship that may be used to estimate the predicted luminosity of the host, provided it is a normal early-type galaxy. We can for instance use the relationship based on cluster ellipticals or compare to V-K colours derived from models including effects of infall of gas and SN generated outflows (e.g. Gibson 1997; Ferreras & Silk 2000; Fioc & Rocca-Volmerange 2000). The luminosity we would expect for a galaxy with colours similar to the halo colours of our BCG sample is much higher than what we obtain from the photometry. There are at least two possible ways to explain this difference. One is related to the mechanism behind the metallicity-colour-luminosity relationship. This relationship is mostly thought to be caused by the mass dependency of loss of metals through stellar winds. According to the models by Mc Low & Ferrara (1999) and Ferreras & Silk (2000) mass loss from galaxies during a starburst phase is strongly dependent on the mass of the galaxy and dwarfs may, depending on the morphology, lose most of the metals produced in the starburst to the environment. If galaxy formation is biased towards high density regions, it would mean that the field ellipticals contain less baryons per dark matter mass unit, i.e. there would be an anticorrelation between mass-to-luminosity and mean density of the environment. The critical luminosity for mass loss would therefore decrease and we might find low luminosity, metal-rich galaxies in sparse regions. From time to time a gas-rich galaxy would fall into this potential well and start a starburst similar to what we would expect to see at high redshifts. It is interesting to note that the fit to the Sersic equation of the halo luminosity profile that was described in Sect. 4.5, resulted in very high values of the n parameter. Although individually these are quite uncertain values, these data collectively also indicate that the mass of the host is large. If ther merger hypothesis is valid, further support for massive halos comes from n-body simulations of mergers. Dubinski et al. (1999) found that tidal tails do not develope in disk galaxies where the mass is stongly dominated by the halo. Although we see some morphological signatures of the aftermaths of mergers, we do not see tails.
One may also consider the possibility of an abnormal IMF, which drastically
could change the interpretation of the colours. More and more evidence is
accumulating however in the direction of a universal IMF. While local
variations may occur, the global properties closely agree with the classical
Salpeter IMF (Scalo 1998). On the other hand there are strong biases
in IMF studies since they normally deal with star forming regions that are
luminous and the star formation efficiency is high. The low surface brightness
makes it problematic to investigate star formation regions in which the mean
density is low, as in e.g. low surface brightness galaxies. Dynamical
estimates of the mass and the ![]() /L ratio are more reliable but also have their
limitations because of the uncertainties in inclination, contribution from
dark matter and due to distorsions in the velocity field, both in the central
area and in the HI distribution. A possible contribution from population III
stars with peculiar IMF cannot be excluded as an exotic candidate to explain
the red excess.
/L ratio are more reliable but also have their
limitations because of the uncertainties in inclination, contribution from
dark matter and due to distorsions in the velocity field, both in the central
area and in the HI distribution. A possible contribution from population III
stars with peculiar IMF cannot be excluded as an exotic candidate to explain
the red excess.
We present the result of an optical/near-IR photometric/spectroscopic investigation of four luminous blue compact galaxies and their companions. The chemical abundances of the BCG starbursts are low, typically 10% of the solar values. The star formation is intense, corresponding to gas consumption timescales of the order of 100 Myr only. We show that the main body is embedded in a huge halo of ionised gas, possibly ionised by the central burst. The galaxies thus have properties we normally associate with young galaxies and one of our targets, ESO 400-G43, is in the list of young galaxy candidates. We conclude however that all galaxies discussed here contain a significant population of old stars.
We demonstrate that is is possible to disentangle a separate "halo population'' from the burst population. This very red component has colours and structural properties typical of elliptical galaxies with metallicities considerably in excess of that of those derived from the starburst H II-regions. From this we conclude that the starburst is not an internal affair but is caused by a galaxy merger or infall of gas from the intergalactic space.
In the optical region the galaxy type that dominates the light is typical of gas-rich low surface brightness galaxies. The luminosity of the halo, as derived from the empirical metallicity-luminosity relationship of normal galaxies, is much in excess of what is observed. A possible scenario is that we witness mergers between gas-rich LSB galaxies or massive HI clouds and massive and metal-rich, but extraordinary faint ellipticals. Such galaxies may exist in low density regions as a consequence of a different distribution of baryons and dark matter (the classical bias), causing the field ellipticals to contain relatively more dark matter than the cluster ellipticals. Alternatively the host may have a very peculiar IMF.
The deep dark matter potential field of the Es may be necessary conditions for the burst to start. Our findings may be typical of luminous blue compact galaxies in general and may prove to be important in the early formation of galaxies. Similar starbursts occurring in more luminous ellipticals may be rare because such galaxies have experienced sufficiently many starbursts to build up an extended hot corona of ionised gas that will shield the galaxy from infall of neutral gas by thermal conduction.
Acknowledgements
We thank Saga Dagnesjö, Steven Jörsäter, Kjell Olofsson, Jari Rönnback and Erik Zackrisson for their contributions to this work and for stimulating discussions. This work was partly supported by the Swedish Natural Science Research Council.