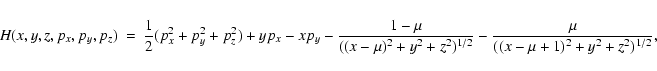
A&A 390, 733-749 (2002)
DOI: 10.1051/0004-6361:20020625
G. Gómez1,3 - J. J. Masdemont2,3 - J. M. Mondelo2
1 - Departament de Matemàtica Aplicada i Anàlisi,
Universitat de Barcelona, Gran Via 585, 08007 Barcelona, Spain
2 -
Departament de Matemàtica Aplicada I, Universitat Politècnica de
Catalunya, E.T.S.E.I.B., Diagonal 647, 08028 Barcelona, Spain
3 -
Institut d'Estudis Espacials de Catalunya, Edifici Nexus,
Gran Capità 2-4, 08034 Barcelona, Spain
Received 4 March 2002 / Accepted 19 April 2002
Abstract
The purpose of this paper is to develop a methodology to generate
simplified models suitable for the analysis of the motion of a small particle,
such as a spacecraft or an asteroid, in the Solar System. The procedure is
based on applying refined Fourier analysis methods to the time-dependent
functions that appear in the differential equations of the problem. The
equations of the models obtained are quasi-periodic perturbations of the
Restricted Three Body Problem that depend explicitly on natural frequencies of
the Solar System. Some examples of these new models are given and compared
with other ones found in the literature. For one of these new models, close to
the Earth-Moon system, we have computed the dynamical substitutes of the
collinear libration points.
The methodology developed in this paper can also be used for the analytical construction of simplified models of systems governed by differential equations which have a quasi-periodic (in time) external excitation and such that the form of the equations is rather cumbersome.
Key words: celestial mechanics - Solar System - reference systems - ephemerides
The main goal of this paper is the construction of quasi-periodic analytic models suitable for the study of the motion of a small particle in the Solar System. Without any simplification, the equations of the general problem form a set of 60 first order differential equations difficult to analyze. It is well known that very simple models, such as the Two Body Problem or the Restricted Three Body Problem (RTBP), are suitable for many purposes, since they give a good insight of dynamics in large regions of the phase space of the problem. Some of these models are restricted, which means that the small particle does not have any influence in the motion of the remaining bodies. The models introduced in this paper will be also restricted but not so simple as the ones already mentioned. We will try to keep within them the behavior of the dynamics related to the resonances between natural and excitation frequencies.
Most of the well known restricted problems take as starting point the RTBP.
We recall that it models the motion of a particle under the gravitational
attraction of two primaries which are assumed to be point masses revolving
in circular orbits around their center of mass. The Hamilton function of
this system is, in a coordinate system that revolves with the
primaries (such a system is called synodic, see Szebehely 1967),
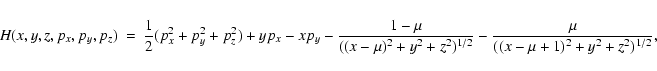
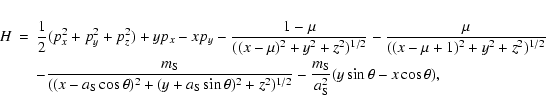
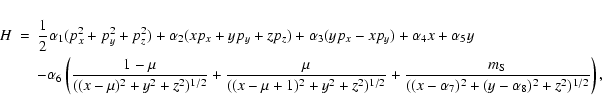
In our approach, instead of taking as starting equations those of the RTBP,
we will consider Newton's equation for the motion of an infinitesimal body
in the force field created by the bodies of the Solar System
Following the ideas of Gómez et al. (2001b), in Sect. 2 we introduce suitable reference systems and units such that, after selecting two bodies of the Solar System as primaries, the above equations are set as a perturbation of the RTBP. These new equations will be a generalization of the ones that we have already introduced for the intermediate models just discussed. In Sect. 3, and for two particular choices of primaries, we will perform the Fourier analysis of all the time periodic functions that appear in the new equations. In this way we are able to introduce a graded set of models with an increasing number of frequencies, that can be considered between the RTBP and the true equations. This is done in Sect. 4. Finally, in the last section we compute the dynamical substitutes of the collinear equilibrium points for one of the intermediate models introduced, close to the Earth-Moon system.
Through the full paper, the set of bodies of the Solar System will be
denoted by
In an inertial reference system, the Lagrangian related to Newton's
equations of motion (Eq. (1)) of an infinitesimal body Q under the
gravitational action of the bodies in ![]() ,
is
,
is
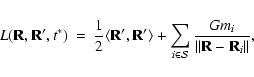
Since we are interested in writing the equations of motion for Q as a
perturbation of the RTBP equations, we must select two bodies
![]() with mI>mJ, which will play the role of primaries.
In this way, the mass
parameter,
with mI>mJ, which will play the role of primaries.
In this way, the mass
parameter, ![]() ,
is defined as
,
is defined as
![]() ,
and so
,
and so
![]() .
Next, we must introduce the synodic reference frame.
Recall that the origin of this system is set at the barycenter of I, Jand that the positions of the primaries are fixed at
.
Next, we must introduce the synodic reference frame.
Recall that the origin of this system is set at the barycenter of I, Jand that the positions of the primaries are fixed at ![]() and
and
![]() (see Szebehely 1967).
(see Szebehely 1967).
Following Gómez et al. (2001b), the transformation from synodical coordinates,
![]() ,
to sidereal ones,
,
to sidereal ones, ![]() ,
is defined by
,
is defined by
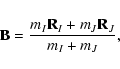
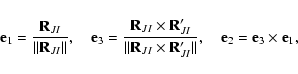
The change of coordinates given by Eq. (3) is checked to preserve the Lagrangian form of the
equations and the new Lagrangian becomes
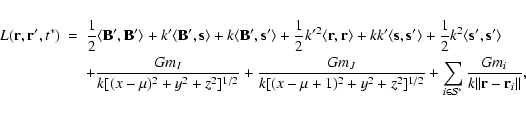
Finally, we want to use the same time units as those usual for the RTBP,
where ![]() time units correspond to one revolution of the primaries. If
t* is some dynamical time and n is the mean motion of J with respect
to I, then we perform the change of independent variable through
time units correspond to one revolution of the primaries. If
t* is some dynamical time and n is the mean motion of J with respect
to I, then we perform the change of independent variable through
| Earth-Moon | Sun-(Earth+Moon) | |
| n | 0.22997154619514 | 0.01720209883844 |
| a | 384 601.25606767 | 149 598 058.09228115 |
If we denote with a dot the derivative with respect to t, then the new
Lagrangian can be written as
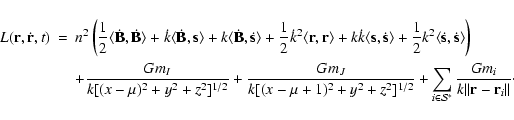
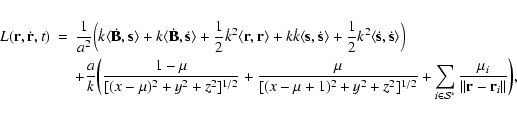
Since
![]() form an orthogonal basis, we
have that
form an orthogonal basis, we
have that
![]() ,
,
![]() and
and
![]() for
i,j=1,2,3. It can be further shown that
for
i,j=1,2,3. It can be further shown that
![]() ,
,
![]() and
and
![]() .
Recalling that
.
Recalling that
![]() ,
writing
,
writing
![]() and
using the previous relations, we get
and
using the previous relations, we get
![\begin{eqnarray*}L({\bf r},\dot{\bf r},t) &=& a_1(\dot x^2+\dot y^2+\dot z^2)
+...
...S}^*}\frac{\mu_i}{[(x-x_i)^2+(y-y_i)^2+(z-z_i)^2]^{1/2}}\biggr),
\end{eqnarray*}](/articles/aa/full/2002/29/aah3524/img77.gif)
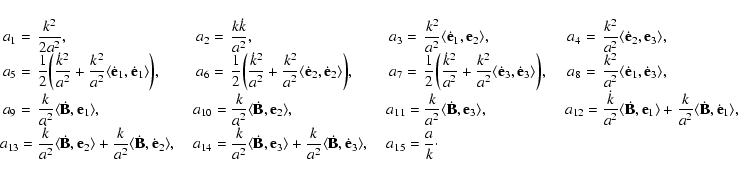
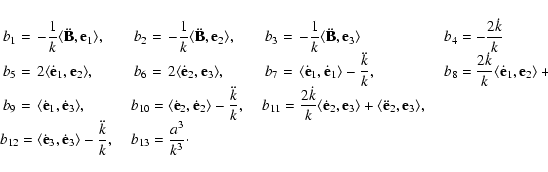
We note that setting bi=0 for
![]() ,
b5=2,
b7=b10=b13=1 and skipping the sum over
,
b5=2,
b7=b10=b13=1 and skipping the sum over
![]() in
Eq. (6), the Eqs. (5) become the usual RTBP
equations with mass parameter
in
Eq. (6), the Eqs. (5) become the usual RTBP
equations with mass parameter ![]() .
Therefore, we can see
Eqs. (5) as a perturbation of the RTBP equations. Once the
primaries have been fixed, we will get an idea of the order of magnitude of
the perturbation, by looking at the first coefficient of the Fourier
expansions of the bi functions. The Fourier analysis of this functions
will be done in the next sections for two different systems.
.
Therefore, we can see
Eqs. (5) as a perturbation of the RTBP equations. Once the
primaries have been fixed, we will get an idea of the order of magnitude of
the perturbation, by looking at the first coefficient of the Fourier
expansions of the bi functions. The Fourier analysis of this functions
will be done in the next sections for two different systems.
This section is devoted to the results of the Fourier analysis applied to
all the time-dependent functions appearing in Eqs. (5), this
is: the bj functions and the coordinates,
xi, yi, zi, of the bodies of
the Solar System included in
![]() .
The Fourier analysis follows the
methodology developed in Gómez et al. (2001c), which is a refined
procedure that allows a very accurate determination of frequencies and
amplitudes for analytic quasi-periodic functions. Here we will discuss the
selection of the main parameters used in the method as well as the results
obtained. Although the analysis can be done for any set of primaries, we have
selected two different couples - the Earth and the Moon and the Sun and the
Earth-Moon barycenter - because of their relevance in many spacecraft mission
analysis simulations.
.
The Fourier analysis follows the
methodology developed in Gómez et al. (2001c), which is a refined
procedure that allows a very accurate determination of frequencies and
amplitudes for analytic quasi-periodic functions. Here we will discuss the
selection of the main parameters used in the method as well as the results
obtained. Although the analysis can be done for any set of primaries, we have
selected two different couples - the Earth and the Moon and the Sun and the
Earth-Moon barycenter - because of their relevance in many spacecraft mission
analysis simulations.
Using the algorithm described in Gómez et al. (2001c), we have performed Fourier
analysis of the
![]() functions, both for the Earth-Moon
case and the Sun-(Earth+Moon) case. This means that for each bifunction we have obtained a set of frequencies and amplitudes that define
its quasi-periodic approximation as a trigonometric polynomial,
Qbi(t). As for any Fourier procedure, the most relevant parameters
to be specified are the size, T, of the time (sampling) interval and the
number, N, of equally spaced sampling points chosen in the interval.
These parameters define, for instance, the Nyquist critical frequency,
functions, both for the Earth-Moon
case and the Sun-(Earth+Moon) case. This means that for each bifunction we have obtained a set of frequencies and amplitudes that define
its quasi-periodic approximation as a trigonometric polynomial,
Qbi(t). As for any Fourier procedure, the most relevant parameters
to be specified are the size, T, of the time (sampling) interval and the
number, N, of equally spaced sampling points chosen in the interval.
These parameters define, for instance, the Nyquist critical frequency,
![]() ,
that fixes the window within we will find all the
frequencies (true or aliased) of our time series. So, the first thing that
we need is some criteria to choose properly T and N.
,
that fixes the window within we will find all the
frequencies (true or aliased) of our time series. So, the first thing that
we need is some criteria to choose properly T and N.
Due to our implementation of the Fourier analysis procedure, the parameter
N must range over powers of two. For consistency, the length, T, of the
time-interval has also been chosen to range over a geometric progression,
and the time-interval has always started at January 1st, 2001. The
smallest time-interval length,
![]() ,
has been taken of 95 years
(34698.75 Julian days) and the greatest time-interval length,
,
has been taken of 95 years
(34698.75 Julian days) and the greatest time-interval length,
![]() ,
has been chosen as the maximum time-interval covered by the JPL
DE406 ephemerides after Jan 1st 2001, which is 364938 Julian days (999.15
years). Therefore, we have let T range over the set
,
has been chosen as the maximum time-interval covered by the JPL
DE406 ephemerides after Jan 1st 2001, which is 364938 Julian days (999.15
years). Therefore, we have let T range over the set
![]() where
where
![]() .
The
time units used are revolutions of the secondary (J) around the primary
(I) or, equivalently, dimensionless time divided by
.
The
time units used are revolutions of the secondary (J) around the primary
(I) or, equivalently, dimensionless time divided by ![]() .
The reason for
this is that, in this way, the frequency 1.0 corresponds to one
revolution of J around I, which has a more intuitive meaning (one lunar
month in the Earth-Moon case, one sidereal year in the Sun-(Earth+Moon)
case) that will help in the elaboration of the intermediate models of
motion. Moreover, in order to evaluate the trigonometric approximations of
the bi functions, we only have to multiply the frequencies found by the
dimensionless time, without the need of an additional
.
The reason for
this is that, in this way, the frequency 1.0 corresponds to one
revolution of J around I, which has a more intuitive meaning (one lunar
month in the Earth-Moon case, one sidereal year in the Sun-(Earth+Moon)
case) that will help in the elaboration of the intermediate models of
motion. Moreover, in order to evaluate the trigonometric approximations of
the bi functions, we only have to multiply the frequencies found by the
dimensionless time, without the need of an additional ![]() factor.
factor.
The maximum number of samples
![]() has been chosen to be 220,
in order to allow for "comfortable'' runs on machines with 64MB of memory
(or, equivalently, bi-processor machines with 128MB). For each value of
T, the minimum number of samples has been chosen such that
has been chosen to be 220,
in order to allow for "comfortable'' runs on machines with 64MB of memory
(or, equivalently, bi-processor machines with 128MB). For each value of
T, the minimum number of samples has been chosen such that
![]() ,
in order to make the maximum detectable frequency to be at
least 1.5.
,
in order to make the maximum detectable frequency to be at
least 1.5.
Assume that, for certain fixed values of T and N, we have performed
Fourier analysis of a given function bi(t) obtaining the trigonometric
polynomial
Qbi(t). Then, we can easily compute the maximum
difference between the analyzed function and its quasi-periodic
approximation at the sampling points, that is,
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{H3524F01.eps}\hspace*{5mm}...
...m} \includegraphics[width=4.3cm,clip]{H3524F13.eps}\hspace*{5.8mm}\end{figure}](/articles/aa/full/2002/29/aah3524/Timg95.gif) |
Figure 1:
Error results of the Fourier analysis of
the bi functions in the Earth-Moon case. For each
value of T explored, we have represented the minimum value of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{H3524F14.eps}\hspace*{5mm}...
...3mm]
\hspace*{5.8mm} \includegraphics{H3524F26.eps}\hspace*{5.8mm}\end{figure}](/articles/aa/full/2002/29/aah3524/Timg96.gif) |
Figure 2: Same as Fig. 1 but for the Sun-(Earth+Moon) case. The values of T are given in revolutions of the Earth+Moon barycenter around the Sun. |
| Open with DEXTER | |
To reduce the leakage effect, in all the computations we have multiplied
our data by a Hanning function of order two
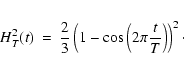
In order to control aliasing, two different strategies have been followed.
The first one is based on time-domain, and consists in computing the
maximum difference between the initial function and its quasi-periodic
approximation, over a refinement of the initial grid of data used for the
Fourier analysis. This difference will be denoted as ![]() .
If it
increases significantly when increasing the number of points of the grid,
then aliasing is very likely to occur. For this test, we have used a refinement
with 16N equally spaced points in [0,T].
.
If it
increases significantly when increasing the number of points of the grid,
then aliasing is very likely to occur. For this test, we have used a refinement
with 16N equally spaced points in [0,T].
The second anti-aliasing strategy is based on frequency-domain. It
consists in computing the number of rightmost consecutive harmonics of the
residual Discrete Fourier Transform (DFT) that have modulus less than a
fraction of the maximum modulus of the residual DFT. Then, we divide this
number by N/2, the total number of harmonics, and this defines the
parameter ![]() .
That is, if
Ei(t) = bi(t)-Qbi(t) is the error
of the trigonometric approximation of bi(t) and
cEi,T,N(j),
sEi,T,N(j),
.
That is, if
Ei(t) = bi(t)-Qbi(t) is the error
of the trigonometric approximation of bi(t) and
cEi,T,N(j),
sEi,T,N(j),
![]() ,
are the cosine and sine coefficients of
its DFT, we compute
,
are the cosine and sine coefficients of
its DFT, we compute
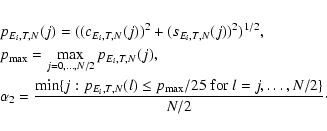
As an example of aliasing and how the two previously-described strategies
detect it, we have represented in Fig. 3 the residual DFT of
some of the Fourier analysis of the b1 function in the Earth-Moon case.
Some numerical values of these analysis are given in Table 2. In the
left plot, we see that for N=16384 there are frequencies of high amplitude
near
![]() .
As we increase N, the amplitude of the
frequencies near
.
As we increase N, the amplitude of the
frequencies near
![]() decrease and the values of
decrease and the values of
![]() as
well as the parameter
as
well as the parameter ![]() of the first anti-aliasing strategy
become closer.
of the first anti-aliasing strategy
become closer.
According to this, for the results displayed in Figs. 1
and
![]() only those analyses with
only those analyses with
![]() and
and
![]() have
been taken into account.
have
been taken into account.
For the generation of simplified models for the Solar System, among
all the analysis performed we have selected the best ones in terms of
minimum
![]() .
The corresponding parameters of these "best'' analysis are
given in Tables 3 (Earth-Moon) and 4
(Sun-(Earth+Moon)).
.
The corresponding parameters of these "best'' analysis are
given in Tables 3 (Earth-Moon) and 4
(Sun-(Earth+Moon)).
In order to complete the quasi-periodic approximation of all the
time-dependent part in the vector-field given by Eqs. (5),
we give in this
section the results of the Fourier analysis of the positions of the Solar
System bodies in dimensionless coordinates. For each coordinate xi,
yi, zi, we have performed Fourier analysis using the same
procedure as for the analysis of the bi functions. The minimum value of
![]() with respect to N, for fixed values of T, is plotted in
Fig. 4 for the Earth-Moon system. The values of the
parameters for the best analysis are given in Table 5.
In the electronic version of the paper the reader can find the results for
the Sun-(Earth+Moon)system, which can be also provided by the authors.
with respect to N, for fixed values of T, is plotted in
Fig. 4 for the Earth-Moon system. The values of the
parameters for the best analysis are given in Table 5.
In the electronic version of the paper the reader can find the results for
the Sun-(Earth+Moon)system, which can be also provided by the authors.
| |
Figure 3: Modulus of the residual DFT some of the Fourier analysis of the b1 function in the Earth-Moon case. The values of the parameters of these analysis are given in Table 2. |
| Open with DEXTER | |
| day0 | day |
T | N |
|
|
|
||
| 366 | 55 917.4 | 2033.24 | 16 384 | 4.02903 | 2.66E-05 | 4.90E-04 | 2.29E-03 | 0.0007 |
| 366 | 55 917.4 | 2033.24 | 32 768 | 8.05806 | 2.66E-05 | 5.30E-04 | 5.67E-04 | 0.1633 |
| 366 | 55 917.4 | 2033.24 | 65 536 | 16.1161 | 2.66E-05 | 5.63E-04 | 5.67E-04 | 0.5816 |
| function | T (days) | T (J-rev.) | N |
|
|
| b1 | 55 551.4 | 2033.24 | 65 536 | 2.66E-05 | 5.63E-04 |
| b2 | 55 551.4 | 2033.24 | 65 536 | 2.67E-05 | 5.49E-04 |
| b3 | 55 551.4 | 2033.24 | 32 768 | 3.30E-06 | 5.58E-05 |
| b4 | 55 551.4 | 2033.24 | 65 536 | 2.31E-06 | 5.01E-05 |
| b5 | 43 904.0 | 1606.94 | 32 768 | 4.85E-06 | 9.16E-05 |
| b6 | 70 288.7 | 2572.64 | 32 768 | 3.92E-08 | 1.13E-06 |
| b7 | 55 551.4 | 2033.24 | 65 536 | 3.51E-06 | 7.81E-05 |
| b8 | 55 551.4 | 2033.24 | 524 288 | 1.96E-07 | 5.94E-06 |
| b9 | 70 288.7 | 2572.64 | 65 536 | 1.97E-08 | 5.69E-07 |
| b10 | 55 551.4 | 2033.24 | 65 536 | 3.51E-06 | 7.83E-05 |
| b11 | 70 288.7 | 2572.64 | 65 536 | 1.67E-08 | 5.05E-07 |
| b12 | 43 904.0 | 1606.94 | 32 768 | 1.58E-06 | 3.29E-05 |
| b13 | 55 551.4 | 2033.24 | 65 536 | 3.51E-06 | 7.99E-05 |
| function | T (days) | T (J-rev) | N |
|
|
| b1 | 142 382.6 | 389.815 | 65 536 | 4.95E-08 | 4.40E-07 |
| b2 | 142 382.6 | 389.815 | 65 536 | 4.95E-08 | 4.33E-07 |
| b3 | 112 529.5 | 308.083 | 131 072 | 2.28E-09 | 2.68E-08 |
| b4 | 34 698.8 | 94.998 | 4096 | 8.34E-06 | 6.74E-05 |
| b5 | 34 698.8 | 94.998 | 4096 | 1.75E-05 | 1.26E-04 |
| b6 | 88 935.7 | 243.488 | 262 144 | 1.76E-08 | 5.71E-07 |
| b7 | 34 698.8 | 94.998 | 4096 | 1.36E-05 | 9.17E-05 |
| b8 | 288 422.1 | 789.642 | 524 288 | 9.65E-08 | 1.67E-06 |
| b9 | 88 935.7 | 243.488 | 131 072 | 9.71E-09 | 3.19E-07 |
| b10 | 34 698.8 | 94.998 | 4096 | 1.36E-05 | 9.17E-05 |
| b11 | 70 288.7 | 192.436 | 524 288 | 2.35E-08 | 2.38E-06 |
| b12 | 34 698.8 | 94.998 | 4096 | 3.92E-06 | 4.06E-05 |
| b13 | 34 698.8 | 94.998 | 4096 | 1.34E-05 | 9.47E-05 |
| body | coord. | T (days) | T (years) | T (J-rev) | N |
|
|
| Mercury | x | 70 288.7 | 192.440 | 2572.64 | 65 536 | 1.37E-02 | 3.41E-01 |
| Mercury | y | 70 288.7 | 192.440 | 2572.64 | 65 536 | 1.08E-02 | 2.89E-01 |
| Mercury | z | 70 288.7 | 192.440 | 2572.64 | 32 768 | 3.18E-03 | 9.99E-02 |
| Venus | x | 55 551.4 | 152.091 | 2033.24 | 65 536 | 5.13E-03 | 1.53E-01 |
| Venus | y | 55 551.4 | 152.091 | 2033.24 | 65 536 | 5.60E-03 | 1.65E-01 |
| Venus | z | 88 935.7 | 243.493 | 3255.14 | 65 536 | 1.25E-03 | 4.10E-02 |
| Mars | x | 55 551.4 | 152.091 | 2033.24 | 65 536 | 3.61E-02 | 8.43E-01 |
| Mars | y | 180 155.5 | 493.239 | 6593.89 | 131 072 | 3.21E-02 | 7.53E-01 |
| Mars | z | 180 155.5 | 493.239 | 6593.89 | 131 072 | 3.26E-03 | 1.38E-01 |
| Jupiter | x | 55 551.4 | 152.091 | 2033.24 | 32 768 | 1.40E+00 | 1.53E+01 |
| Jupiter | y | 112 529.5 | 308.089 | 4118.71 | 65 536 | 5.39E-01 | 1.31E+01 |
| Jupiter | z | 70 288.7 | 192.440 | 2572.64 | 32 768 | 1.37E-01 | 1.31E+00 |
| Saturn | x | 70 288.7 | 192.440 | 2572.64 | 32 768 | 6.07E+00 | 6.19E+01 |
| Saturn | y | 142 382.6 | 389.822 | 5211.36 | 65 536 | 2.53E+00 | 6.46E+01 |
| Saturn | z | 180 155.5 | 493.239 | 6593.89 | 65 536 | 3.87E-01 | 1.04E+01 |
| Uranus | x | 142 382.6 | 389.822 | 5211.36 | 131 072 | 2.33E+00 | 3.75E+01 |
| Uranus | y | 142 382.6 | 389.822 | 5211.36 | 131 072 | 2.33E+00 | 3.76E+01 |
| Uranus | z | 364 938.0 | 999.146 | 13 357.14 | 131 072 | 2.42E-01 | 4.14E+00 |
| Neptune | x | 288 422.1 | 789.657 | 10 556.57 | 262 144 | 3.12E+00 | 4.52E+01 |
| Neptune | y | 364 938.0 | 999.146 | 13 357.14 | 262 144 | 2.37E+00 | 4.51E+01 |
| Neptune | z | 364 938.0 | 999.146 | 13 357.14 | 131 072 | 1.80E+00 | 2.72E+01 |
| Pluto | x | 364 938.0 | 999.146 | 13 357.14 | 262 144 | 4.15E+00 | 1.69E+02 |
| Pluto | y | 364 938.0 | 999.146 | 13 357.14 | 262 144 | 2.08E+01 | 2.93E+02 |
| Pluto | z | 364 938.0 | 999.146 | 13 357.14 | 131 072 | 2.42E+00 | 5.16E+01 |
| Sun | x | 55 551.4 | 152.091 | 2033.24 | 65 536 | 4.41E-03 | 9.73E-02 |
| Sun | y | 55 551.4 | 152.091 | 2033.24 | 65 536 | 4.41E-03 | 9.21E-02 |
| Sun | z | 34 698.8 | 95.000 | 1270.01 | 16 384 | 8.49E-04 | 8.65E-03 |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{H3524F30.eps}\hspace*{5mm}...
....eps}\hspace*{5mm} \includegraphics[width=4.3cm,clip]{H3524F44.eps}
\end{figure}](/articles/aa/full/2002/29/aah3524/Timg106.gif) |
Figure 4:
Error results of the Fourier analysis of
the coordinates of the Solar System bodies (in dimensionless
coordinates) for the Earth-Moon case. For each value of T explored,
we have represented the minimum value of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{H3524F45.eps}\hspace*{5mm}...
....eps}\hspace*{5mm} \includegraphics[width=4.3cm,clip]{H3524F56.eps}
\end{figure}](/articles/aa/full/2002/29/aah3524/Timg107.gif) |
Figure 5: Continuation of Fig. 4. |
| Open with DEXTER | |
In this section we will generate several simplified Solar System models using the Fourier approximations computed according to the previous section. The models obtained will be compared with other ones through the computation of residual accelerations.
In order to give a more physical meaning to the results obtained from the Fourier analysis, we will write the computed frequencies as linear combinations, with integer coefficients, of basic ones. These basic frequencies can be identified as "natural'' frequencies of the planetary and lunar theories. The introduction in the Fourier expansions of the basic frequencies will be the key point for the construction of models of motion with increasing dynamical complexity.
In principle, the basic frequencies will be extracted from the list of frequencies computed in the Fourier analysis and using the procedure explained below. Nevertheless, in some cases it can be convenient to introduce a fixed set of basic frequencies obtained by other means, for instance from an analytical lunar theory, and then write all the computed frequencies as linear combinations of the ones in this fixed set. Both approaches will be considered in what follows.
To set up the algorithms we need two definitions. Assume that
![]() is a set of basic frequencies and that a frequency f can be
written as
is a set of basic frequencies and that a frequency f can be
written as
![]() with
with
![]() integer numbers, then we say that f is a linear combination of
integer numbers, then we say that f is a linear combination of
![]() of order
of order
![]() .
We say that fis a linear combination of
.
We say that fis a linear combination of
![]() of order kwithin tolerance
of order kwithin tolerance
![]() if, for some
if, for some
![]() such that
such that
![]() ,
we have
,
we have
A simple approach for the determination of the basic frequencies is:
These considerations lead to the following procedure for the determination of a basic set of frequencies:
In this formulation, we have introduced two functions,
,
for
if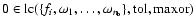
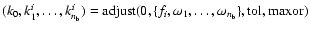
for
if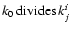
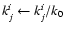
else
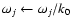
for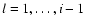
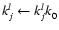
else
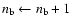
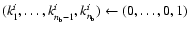
for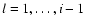
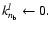
In the second case, in which the basic frequencies
![]() are known, we can just take the best
linear combination for each frequency. This can be stated as
are known, we can just take the best
linear combination for each frequency. This can be stated as
for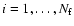
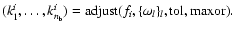
In a rather accurate theory for the lunar motion, as the simplified Brown theory given in Escobal (1968), the fundamental parameters can be expressed in terms of five basic frequencies. In terms of cycles per lunar revolution, their numerical values are
For the Earth-Moon models to be developed in this section, and leaving
aside the two primaries - Earth and Moon - the Sun will be the only
perturbing body in
![]() .
As it will be shown, this provides rather
accurate models and, at the same time, avoids the introduction of additional
basic frequencies. In this way, in the equations of motion (5)
we will only use the Fourier expansions of
.
As it will be shown, this provides rather
accurate models and, at the same time, avoids the introduction of additional
basic frequencies. In this way, in the equations of motion (5)
we will only use the Fourier expansions of
![]() and
and
![]() and its general expression for the equations of motion will
be
and its general expression for the equations of motion will
be
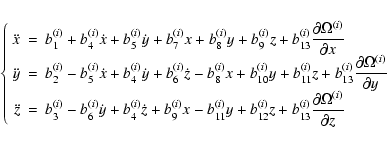
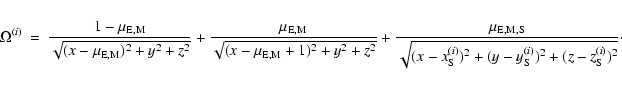
In Tables 6 and 7 we give partial results
relative to the Fourier analyses of ![]() ,
,
![]() ,
,
![]() and the bifunctions. The full trigonometric expansions can be found in
Mondelo (2001). For these tables we have used Algorithm 2 of the
preceding section to adjust the frequencies, found by the Fourier method, as
linear combinations of the
and the bifunctions. The full trigonometric expansions can be found in
Mondelo (2001). For these tables we have used Algorithm 2 of the
preceding section to adjust the frequencies, found by the Fourier method, as
linear combinations of the
![]() .
The values of the
parameters used for the adjustment are:
.
The values of the
parameters used for the adjustment are:
![]() and
and
![]() .
Only the frequencies associated to the five largest amplitudes are
given in the tables.
.
Only the frequencies associated to the five largest amplitudes are
given in the tables.
| Func | Frequency | Amplitude | Error | k1 | k2 | k3 | k4 | k5 | k |
| 0.00000000000 | -6.27023E-02 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.92519578630 | 3.86480E+02 | -2.11130E-07 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 1.91674083000 | 3.17140E+01 | -3.88890E-07 | 1 | 1 | -1 | 0 | 0 | 3 | |
| 0.06634926280 | 1.32180E+01 | 3.87440E-08 | 1 | -1 | -1 | 0 | 0 | 3 | |
| 0.99999608230 | 1.03360E+01 | -3.43580E-07 | 1 | 0 | 0 | 0 | -1 | 2 | |
| 0.00000000000 | 1.60785E-05 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.92519578630 | 3.87760E+02 | -2.11130E-07 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 1.91674083000 | 3.17800E+01 | -3.88890E-07 | 1 | 1 | -1 | 0 | 0 | 3 | |
| 0.99999608230 | 1.03360E+01 | -3.43590E-07 | 1 | 0 | 0 | 0 | -1 | 2 | |
| 0.06634926280 | 8.30700E+00 | 3.87360E-08 | 1 | -1 | -1 | 0 | 0 | 3 | |
| 0.00000000000 | 4.24394E-04 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.07882283000 | 3.40520E+01 | -1.09480E-08 | 1 | -1 | 0 | 1 | 0 | 3 | |
| 0.91272219540 | 9.30940E-01 | -1.85070E-07 | 0 | 1 | -1 | -1 | 0 | 3 | |
| 0.00402231670 | 9.11850E-01 | -9.57650E-08 | 0 | 0 | 0 | 1 | 1 | 2 | |
| 1.07036785680 | 9.31450E-01 | -2.05600E-07 | 2 | -1 | -1 | 1 | 0 | 5 |
| Func | Frequency | Amplitude | Error | k1 | k2 | k3 | k4 | k5 | k |
| b1 | 0.00000000000 | 3.49728E-04 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.92519578630 | 2.16240E+00 | -2.11120E-07 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 1.91674083000 | 1.77450E-01 | -3.88880E-07 | 1 | 1 | -1 | 0 | 0 | 3 | |
| 0.85039537680 | 7.53250E-02 | -1.92240E-07 | -1 | 2 | 0 | 0 | 1 | 4 | |
| 0.06634926290 | 7.39730E-02 | 3.88600E-08 | 1 | -1 | -1 | 0 | 0 | 3 | |
| b2 | 0.00000000000 | -6.70000E-09 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.92519578630 | 2.16960E+00 | -2.11120E-07 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 1.91674083000 | 1.77820E-01 | -3.88890E-07 | 1 | 1 | -1 | 0 | 0 | 3 | |
| 0.85039537680 | 7.58320E-02 | -1.92220E-07 | -1 | 2 | 0 | 0 | 1 | 4 | |
| 0.06634926260 | 4.64680E-02 | 3.85950E-08 | 1 | -1 | -1 | 0 | 0 | 3 | |
| b3 | 0.00000000000 | -1.41400E-07 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.07882283210 | 1.90520E-01 | -8.87040E-09 | 1 | -1 | 0 | 1 | 0 | 3 | |
| 0.15362345870 | 6.56920E-03 | 1.89270E-07 | 2 | -2 | 0 | 1 | -1 | 6 | |
| 0.91272221270 | 5.20890E-03 | -1.67780E-07 | 0 | 1 | -1 | -1 | 0 | 3 | |
| 1.07036787670 | 5.21170E-03 | -1.85760E-07 | 2 | -1 | -1 | 1 | 0 | 5 | |
| b4 | 0.00000000000 | 0.00000E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.99154505160 | 1.07920E-01 | -1.69890E-07 | 1 | 0 | -1 | 0 | 0 | 2 | |
| 1.85039157300 | 2.94710E-02 | -4.21940E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 0.85884652970 | 1.68610E-02 | -2.43690E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.98309009370 | 8.82140E-03 | -3.49210E-07 | 2 | 0 | -2 | 0 | 0 | 4 | |
| b5 | 0.00000000000 | 2.00003E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.99154503470 | 2.17650E-01 | -1.86770E-07 | 1 | 0 | -1 | 0 | 0 | 2 | |
| 1.85039156830 | 4.29420E-02 | -4.26650E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 0.85884653190 | 3.81670E-02 | -2.41550E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.98309007300 | 1.48070E-02 | -3.69960E-07 | 2 | 0 | -2 | 0 | 0 | 4 | |
| b6 | 0.00000000000 | 0.00000E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.84637295300 | 1.44550E-03 | -2.03520E-07 | -1 | 2 | 0 | -1 | 0 | 4 | |
| 1.00401861550 | 1.44530E-03 | -2.22890E-07 | 1 | 0 | 0 | 1 | 0 | 2 | |
| 0.01247357960 | 1.89340E-04 | -3.72940E-08 | 0 | 0 | 1 | 1 | 0 | 2 | |
| 0.14517208260 | 1.88980E-04 | 1.76520E-08 | 2 | -2 | -1 | 1 | 0 | 6 | |
| b7 | 0.00000000000 | 1.00478E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.99154504270 | 1.65040E-01 | -1.78730E-07 | 1 | 0 | -1 | 0 | 0 | 2 | |
| 0.85884652970 | 3.24780E-02 | -2.43700E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.85039157280 | 1.84070E-02 | -4.22070E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 1.98309009370 | 1.35090E-02 | -3.49200E-07 | 2 | 0 | -2 | 0 | 0 | 4 |
| Func | Frequency | Amplitude | Error | k1 | k2 | k3 | k4 | k5 | k |
| b8 | 0.00000000000 | -7.00000E-10 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1.85039159880 | 8.24730E-03 | -3.96070E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 2.84193667480 | 9.04550E-04 | -5.41620E-07 | 1 | 2 | -1 | 0 | 0 | 4 | |
| 0.85884652020 | 9.17510E-04 | -2.53210E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.77559103310 | 5.07100E-04 | -5.33340E-07 | -1 | 3 | 0 | 0 | 1 | 5 | |
| b9 | 0.00000000000 | -0.00000E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.84637295300 | 7.24530E-04 | -2.03520E-07 | -1 | 2 | 0 | -1 | 0 | 4 | |
| 1.00401861550 | 7.24450E-04 | -2.22890E-07 | 1 | 0 | 0 | 1 | 0 | 2 | |
| 0.01247357980 | 4.82170E-05 | -3.71330E-08 | 0 | 0 | 1 | 1 | 0 | 2 | |
| 0.14517208260 | 4.80940E-05 | 1.76380E-08 | 2 | -2 | -1 | 1 | 0 | 6 | |
| b10 | 0.00000000000 | 1.00478E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.99154504270 | 1.65030E-01 | -1.78730E-07 | 1 | 0 | -1 | 0 | 0 | 2 | |
| 0.85884652970 | 3.24780E-02 | -2.43700E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.85039157280 | 1.84070E-02 | -4.22070E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 1.98309009370 | 1.35090E-02 | -3.49200E-07 | 2 | 0 | -2 | 0 | 0 | 4 | |
| b11 | 0.00000000000 | -0.00000E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1.00401861560 | 7.20820E-04 | -2.22850E-07 | 1 | 0 | 0 | 1 | 0 | 2 | |
| 0.84637295300 | 6.06950E-04 | -2.03500E-07 | -1 | 2 | 0 | -1 | 0 | 4 | |
| 0.14517208280 | 4.66020E-05 | 1.78760E-08 | 2 | -2 | -1 | 1 | 0 | 6 | |
| 1.99556364910 | 3.64300E-05 | -4.10800E-07 | 2 | 0 | -1 | 1 | 0 | 4 | |
| b12 | 0.00000000000 | -1.61183E-03 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.99154502640 | 5.38970E-02 | -1.95110E-07 | 1 | 0 | -1 | 0 | 0 | 2 | |
| 1.85039157030 | 2.69200E-02 | -4.24600E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 0.85884654110 | 8.04870E-03 | -2.32340E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.98309004860 | 7.32970E-03 | -3.94350E-07 | 2 | 0 | -2 | 0 | 0 | 4 | |
| b13 | 0.00000000000 | 1.00747E+00 | 0.00000E+00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.99154504270 | 1.64840E-01 | -1.78730E-07 | 1 | 0 | -1 | 0 | 0 | 2 | |
| 0.85884652970 | 3.15620E-02 | -2.43700E-07 | -1 | 2 | 1 | 0 | 0 | 4 | |
| 1.85039157290 | 2.66550E-02 | -4.22010E-07 | 0 | 2 | 0 | 0 | 0 | 2 | |
| 1.98309009370 | 1.34800E-02 | -3.49210E-07 | 2 | 0 | -2 | 0 | 0 | 4 |
| z-a. | RTBP | BCP | QBCP | |||||
| 0.020 | 0.140126 | 0.146459 | 0.138580 | 0.365299 | 0.095769 | 0.010674 | 0.001374 | 0.000727 |
| 0.025 | 0.136603 | 0.142856 | 0.135174 | 0.353302 | 0.093293 | 0.010388 | 0.001346 | 0.000720 |
| 0.031 | 0.132882 | 0.139025 | 0.131578 | 0.340305 | 0.090590 | 0.010076 | 0.001315 | 0.000711 |
| 0.038 | 0.129087 | 0.135080 | 0.127914 | 0.326550 | 0.087699 | 0.009744 | 0.001282 | 0.000702 |
| 0.048 | 0.125352 | 0.131141 | 0.124312 | 0.312235 | 0.084643 | 0.009393 | 0.001247 | 0.000691 |
| 0.059 | 0.121813 | 0.127324 | 0.120905 | 0.297505 | 0.081429 | 0.009024 | 0.001210 | 0.000678 |
| 0.073 | 0.118614 | 0.123757 | 0.117835 | 0.282462 | 0.078045 | 0.008637 | 0.001171 | 0.000664 |
| 0.091 | 0.115905 | 0.120571 | 0.115249 | 0.267173 | 0.074461 | 0.008229 | 0.001128 | 0.000646 |
| 0.113 | 0.113823 | 0.117895 | 0.113283 | 0.251690 | 0.070634 | 0.007796 | 0.001081 | 0.000625 |
| 0.141 | 0.112471 | 0.115836 | 0.112037 | 0.236056 | 0.066510 | 0.007331 | 0.001030 | 0.000598 |
| 0.175 | 0.111872 | 0.114443 | 0.111533 | 0.220325 | 0.062042 | 0.006831 | 0.000973 | 0.000566 |
| 0.217 | 0.111928 | 0.113663 | 0.111672 | 0.204551 | 0.057196 | 0.006292 | 0.000910 | 0.000526 |
| 0.269 | 0.112400 | 0.113311 | 0.112201 | 0.188782 | 0.051978 | 0.005716 | 0.000840 | 0.000481 |
| 0.300 | 0.112678 | 0.113200 | 0.112492 | 0.180899 | 0.049240 | 0.005417 | 0.000802 | 0.000456 |
From the preceding tables it is clear that the largest bi functions are: b2, whose Fourier expansion has an independent term close to 2, as could be expected from the RTBP equations and b1, b2, which are the "independent terms'' of the planar (z=0) equations of motion (5). We will use these in what follows.
Starting from the frequency basis
![]() ,
we will look
for a new basis
,
we will look
for a new basis
![]() ,
in terms of which we will generate
5 models, that will be labeled as
,
in terms of which we will generate
5 models, that will be labeled as ![]() ,
,
![]() .
The index i will
indicate the number of frequencies,
.
The index i will
indicate the number of frequencies, ![]() ,
retained in the model. We take
,
retained in the model. We take
![]() as the first frequency of the new basis. The reason for
that is that it is the main frequency of b1, b2,
as the first frequency of the new basis. The reason for
that is that it is the main frequency of b1, b2, ![]() and
and ![]() ,
and, in this way, it can be considered the main "planar frequency''.
According to this, for the first model,
,
and, in this way, it can be considered the main "planar frequency''.
According to this, for the first model, ![]() ,
we only keep in the
Fourier expansions, the independent terms and those harmonics with the
,
we only keep in the
Fourier expansions, the independent terms and those harmonics with the
![]() frequency. This is coherent with the fact that
frequency. This is coherent with the fact that ![]() is also
the frequency of the BCP and QBCP models.
is also
the frequency of the BCP and QBCP models.
The second model, ![]() ,
will depend on two frequencies:
,
will depend on two frequencies: ![]() and
and
![]() .
We observe that, except for b3, b6, b9, b11 and
.
We observe that, except for b3, b6, b9, b11 and
![]() ,
the main frequencies of the remaining functions can be expressed as
linear combinations of
,
the main frequencies of the remaining functions can be expressed as
linear combinations of ![]() and
and
![]() .
Thus, we will
take
.
Thus, we will
take
![]() .
Note that, in this way, bi for
i=3,6,9,11 and
.
Note that, in this way, bi for
i=3,6,9,11 and ![]() will be poorly approximated in
will be poorly approximated in ![]() ,
but this
will not give a too bad global approximation, because bi for
i=3,6,9,11are smaller than the remaining bi, and
,
but this
will not give a too bad global approximation, because bi for
i=3,6,9,11are smaller than the remaining bi, and ![]() is also smaller than
is also smaller than
![]() .
.
The remaining ![]() have been taken in order to make the sequence of
models
have been taken in order to make the sequence of
models ![]() ,
,
![]() ,
,
![]() decreasing in error in the residual
accelerations test that will be discussed below. After some trials,
we have set
decreasing in error in the residual
accelerations test that will be discussed below. After some trials,
we have set
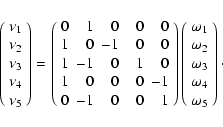
Once the different models have been produced, it is desirable to see if they
are close or not the the "real'' one, that is: the full equations of motion
in which the time periodic functions, bi and
xi,yi,zi, are computed
using the JPL ephemeris files. We will also compare these intermediate
models with more standard simplifications, such as the RTBP, the Bicircular
Problem and the Quasi-Bicircular Problem, with the Earth-Moon mass ratio.
For these purposes we first select a set of trajectories,
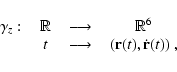
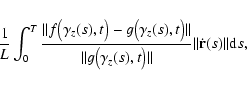 |
(8) |
For the second test the computations are similar except that we have taken
instead of
![]() a set of points uniformly distributed around a large
neighborhood of the equilibrium points. We have also required to their
energy (Jacobi constant) to be in a certain interval around the value
associated to the equilibrium points. The results obtained are analogous to
the ones obtained for the halo orbits, and will not be given here.
a set of points uniformly distributed around a large
neighborhood of the equilibrium points. We have also required to their
energy (Jacobi constant) to be in a certain interval around the value
associated to the equilibrium points. The results obtained are analogous to
the ones obtained for the halo orbits, and will not be given here.
It must be noted that the BCP and the QBCP, as stated in the Introduction,
assume that for t=0 the Moon and the Sun are in opposition with respect
to the Earth. Therefore, we must set the origin of dimensionless time, both
in the ![]() models and the real Solar System, such that Earth, Moon and
Sun are in a configuration close to the one of the BCP and the QBCP for
t=0. We have chosen as t=0 the first epoch after Jan. 1st, 2001 at which
this happens, this is the Julian day 2451919.3489 (Jan. 9th, 2001).
models and the real Solar System, such that Earth, Moon and
Sun are in a configuration close to the one of the BCP and the QBCP for
t=0. We have chosen as t=0 the first epoch after Jan. 1st, 2001 at which
this happens, this is the Julian day 2451919.3489 (Jan. 9th, 2001).
The results for the residual accelerations are given in Table 8, using as test paths several halo orbits around the collinear equilibrium point L2. As it has already been mentioned, the results with other trajectories, or other equilibrium points, give the same qualitative information. From this table, it becomes clear that the best one-frequency models that we can be used, according to the residual acceleration criteria, are the BCP and the QBCP. But, when we allow two or more frequencies, the models we get fit the JPL one much better. As it has been said, only the Sun has been taken into account in all the intermediate models. By adding additional Solar System bodies, the residual accelerations are of the same order of magnitude than the ones obtained just using the Sun. It is also clear that, from this point of view, there is not a significant improvement between the RTBP and the non-autonomous Bicircular and Quasi Bicircular models.
In this case, we proceed as in the Earth-Moon system, except that the basic frequencies will be obtained using the results of the Fourier analysis of Sect. 3 and Algorithm 1 for their determination.
From the numerical data obtained (see the electronic version of the paper), we first observe that the maximum modulus of the highest Fourier coefficient of b1, b2, b3, b6, b8, b9, b11 is 3.521E-05, whereas the minimum modulus of the highest Fourier coefficient of the remaining bi is 1.669E-02. Therefore, in order to detect basic frequencies, we will only take into consideration the b4, b5, b7, b10, b12 and b13 functions. In addition to this simplification, we will not consider any Solar System body in Eq. (6), since, just using the bi, we are already taking the Sun into account.
Applying Algorithm 1 to the b13function, setting
![]() ,
,
![]() ,
we get the following four basic frequencies:
,
we get the following four basic frequencies:
| z-a. | RTBP | ||
| 0.020000 | 3.446497E-02 | 9.901526E-05 | 8.905454E-04 |
| 0.024838 | 3.411184E-02 | 9.779360E-05 | 8.768670E-04 |
| 0.030846 | 3.366579E-02 | 9.616913E-05 | 8.589500E-04 |
| 0.038308 | 3.313580E-02 | 9.416327E-05 | 8.364166E-04 |
| 0.047575 | 3.254789E-02 | 9.175134E-05 | 8.092527E-04 |
| 0.059084 | 3.194355E-02 | 8.895610E-05 | 7.776813E-04 |
| 0.073376 | 3.137381E-02 | 8.582841E-05 | 7.420444E-04 |
| 0.091126 | 3.089082E-02 | 8.236183E-05 | 7.026421E-04 |
| 0.113169 | 3.053770E-02 | 7.859979E-05 | 6.597243E-04 |
| 0.140545 | 3.033772E-02 | 7.450252E-05 | 6.135638E-04 |
| 0.174543 | 3.028516E-02 | 7.020714E-05 | 5.643885E-04 |
| 0.216766 | 3.034115E-02 | 6.579492E-05 | 5.127031E-04 |
| 0.300000 | 3.047577E-02 | 5.898080E-05 | 4.323859E-04 |
In Table 9, we compare the models RTBP, ![]() and
and
![]() with the real Solar System using the same residual
acceleration tests that we used in the Earth-Moon case. We note that
the
with the real Solar System using the same residual
acceleration tests that we used in the Earth-Moon case. We note that
the ![]() model gives worse results than
model gives worse results than ![]() .
This is not a
contradiction.
In the electronic version of the paper
we can see that the maximum amplitude of the frequencies of b4,
b5, b7, b10 and b12 that are not multiple of
.
This is not a
contradiction.
In the electronic version of the paper
we can see that the maximum amplitude of the frequencies of b4,
b5, b7, b10 and b12 that are not multiple of ![]() is 6.695E-05. Because of that, adding frequencies does not improve
significantly the approximation of the bi functions, and in this
way the structure of Eqs. (5) takes over the
fact that the bi terms of
is 6.695E-05. Because of that, adding frequencies does not improve
significantly the approximation of the bi functions, and in this
way the structure of Eqs. (5) takes over the
fact that the bi terms of ![]() are closer to the ones of the
real Solar System than the corresponding terms of
are closer to the ones of the
real Solar System than the corresponding terms of ![]() .
.
Therefore, for the Sun-(Earth+Moon) case, we will give ![]() as
simplified Solar System model. Note that this is a model with very
few frequencies that significantly improves the RTBP.
as
simplified Solar System model. Note that this is a model with very
few frequencies that significantly improves the RTBP.
As it is well known, the RTBP has five equilibrium points: three of them
(L1, L2, L3) are collinear with the primaries and the other two
(L4 and L5) form an equilateral triangle with them. Although the
intermediate models introduced in the preceding section are
close to the RTBP, they are non autonomous, so they do not have any
critical point. If we consider the ![]() model, since it depends on only
one frequency, it can be seen as a periodic perturbation of the RTBP so,
under very general non-resonance conditions between the natural modes
around the equilibrium points and the perturbing frequency, the libration
points can be continued to periodic orbits of the model. These periodic
orbits, which have the same period as the perturbation, are the dynamical
substitutes of the equilibrium points. In this section we will show these
substitutes for the three collinear equilibrium points for
model, since it depends on only
one frequency, it can be seen as a periodic perturbation of the RTBP so,
under very general non-resonance conditions between the natural modes
around the equilibrium points and the perturbing frequency, the libration
points can be continued to periodic orbits of the model. These periodic
orbits, which have the same period as the perturbation, are the dynamical
substitutes of the equilibrium points. In this section we will show these
substitutes for the three collinear equilibrium points for ![]() ,
in the
Earth-Moon system. For the other models,
,
in the
Earth-Moon system. For the other models, ![]() ,...,
,..., ![]() ,
as the
perturbation is quasi-periodic, the corresponding substitutes will be also
quasi-periodic solutions. The methodology for their efficient computation,
as well as the results obtained, will appear elsewhere. The dynamical
substitutes of the triangular points in the Earth-Moon system, for models
close to the ones of this paper, have been studied in
Gómez et al. (2001a), Simó et al. (1995)
and Jorba (2000) and will not be considered here.
,
as the
perturbation is quasi-periodic, the corresponding substitutes will be also
quasi-periodic solutions. The methodology for their efficient computation,
as well as the results obtained, will appear elsewhere. The dynamical
substitutes of the triangular points in the Earth-Moon system, for models
close to the ones of this paper, have been studied in
Gómez et al. (2001a), Simó et al. (1995)
and Jorba (2000) and will not be considered here.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{H3524F57.eps}\hspace*{7mm}...
...24F58.eps}\\ [5mm]
\includegraphics[width=6.3cm,clip]{H3524F59.eps}
\end{figure}](/articles/aa/full/2002/29/aah3524/Timg197.gif) |
Figure 6:
Dynamical substitutes for the |
| Open with DEXTER | |
The numerical computation of the periodic orbits of ![]() that
substitute L1 and L3 has no problem and the results obtained are
shown in Fig. 6. We can see that L1 is replaced by a
very small size periodic orbit and that the substitute of L3 is also
almost planar but rather large in the (x,y)-plane. The computation of
the substitute of L2, also displayed in Fig. 6,
requires more care. Mainly, we need to introduce a continuation parameter
between the RTBP and
that
substitute L1 and L3 has no problem and the results obtained are
shown in Fig. 6. We can see that L1 is replaced by a
very small size periodic orbit and that the substitute of L3 is also
almost planar but rather large in the (x,y)-plane. The computation of
the substitute of L2, also displayed in Fig. 6,
requires more care. Mainly, we need to introduce a continuation parameter
between the RTBP and ![]() ,
so we consider the 1-parameter family of
vector-fields which can be formally written as
,
so we consider the 1-parameter family of
vector-fields which can be formally written as
| |
Figure 7:
a) Evolution with the continuation parameter
|
| Open with DEXTER | |
The evolution with the continuation parameter
![]() of the family
of isoperiodic orbits that start at the libration point L2 is shown in
Fig. 7a. In this figure, the point O represents the
equilibrium point for
of the family
of isoperiodic orbits that start at the libration point L2 is shown in
Fig. 7a. In this figure, the point O represents the
equilibrium point for
![]() .
When the continuation is done
starting at O with increasing positive values of
.
When the continuation is done
starting at O with increasing positive values of
![]() ,
we never
reach
,
we never
reach
![]() .
The continuation of this branch has been stopped,
for the representation, at the point A, where the value
.
The continuation of this branch has been stopped,
for the representation, at the point A, where the value
![]() has been reached again. This point corresponds to a planar Lyapunov orbit
of the RTBP with frequency equal to the double of the frequency of the model and
displayed in Fig. 7b. The other branch, starting for
decreasing values of
has been reached again. This point corresponds to a planar Lyapunov orbit
of the RTBP with frequency equal to the double of the frequency of the model and
displayed in Fig. 7b. The other branch, starting for
decreasing values of
![]() ,
reaches the value
,
reaches the value
![]() at
the point C. In fact, this curve goes through
at
the point C. In fact, this curve goes through
![]() at the
point B, which again corresponds to the previously mentioned planar
Lyapunov orbit. In the diagram, both points, A and B have y=0 and the
different x coordinates correspond to the two orthogonal crossings with
y=0 of the planar periodic orbit.
at the
point B, which again corresponds to the previously mentioned planar
Lyapunov orbit. In the diagram, both points, A and B have y=0 and the
different x coordinates correspond to the two orthogonal crossings with
y=0 of the planar periodic orbit.
Acknowledgements
The research has been supported by DGICYT grant PB94-0215. Partial support of the Catalan grants CIRIT 1998S0GR-00042 and 2000 SGR-27 is also acknowledged. The numerical explorations have been carried out on HIDRA. We are grateful to CIRIT, DGICYT and the University of Barcelona who are providing funds for this array. J. M. M. wishes also to acknowledge the support of the doctoral research grant 1997FI00136PG from the Generalitat de Catalunya.