

Up: The nature of the
3 Broad band spectrum
The flux was fairly stable during the NFI observation; on a time scale
of an hour the variability of the source did not exceed the 5%
level. The shape of the 1 to 200 keV spectrum can be characterized by
an absorbed power law, with a photon index of 1.7, which is moderately
cut off above 60 keV by an exponential with an e-folding energy of
130 keV. There is no strong soft component which is typical of many
bright X-ray transients. We tested the spectrum against various
continuum models that are applicable to X-ray binaries, for instance a
(cut-off) power law, a Comptonized spectrum, bremsstrahlung radiation,
and disk black-body radiation. Data were restricted to 1-4 keV for
LECS, 1.6-10.5 keV for MECS, 7-34 keV for HP-GSPC, and 15-200 keV for
PDS. None of the continuum models adequately describe the data (see
cases in Table 2 for which
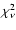 exceeds 2). The
primary reason for this is a narrow-band spectral component between 4
and 9 keV which is not represented in these models. In
Fig. 5, we present the residuals with respect to the
best-fit model when excluding the 4-9 keV range from the fitting. A
narrow-band emission feature is apparent, with a peak that is near the
energy expected for the Fe-K line complex. The feature is seen in its
entirety with the MECS, and is partly confirmed by HP-GSPC data. To
accommodate the emission feature, we tested two models in combination
with a variety of continuum models. The emission-feature models
include a broad Gaussian line, optionally supplemented by an
absorption edge, and an emission line that is relativistically
broadened by Doppler shifts due to orbital motion of the emitting
material around a compact object and to gravitational redshift. For
the latter, the model as formulated by Laor (1991) for a rotating
compact object was employed. In this model, we fixed the outer radius
at 400
exceeds 2). The
primary reason for this is a narrow-band spectral component between 4
and 9 keV which is not represented in these models. In
Fig. 5, we present the residuals with respect to the
best-fit model when excluding the 4-9 keV range from the fitting. A
narrow-band emission feature is apparent, with a peak that is near the
energy expected for the Fe-K line complex. The feature is seen in its
entirety with the MECS, and is partly confirmed by HP-GSPC data. To
accommodate the emission feature, we tested two models in combination
with a variety of continuum models. The emission-feature models
include a broad Gaussian line, optionally supplemented by an
absorption edge, and an emission line that is relativistically
broadened by Doppler shifts due to orbital motion of the emitting
material around a compact object and to gravitational redshift. For
the latter, the model as formulated by Laor (1991) for a rotating
compact object was employed. In this model, we fixed the outer radius
at 400 and the power-law index of the emissivity-radius
dependence at -3. None of the fixed parameters are in fact
constrained by the data.
and the power-law index of the emissivity-radius
dependence at -3. None of the fixed parameters are in fact
constrained by the data.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{h3518f5.ps}
\end{figure}](/articles/aa/full/2002/29/aah3518/Timg47.gif) |
Figure 5:
2-11 keV NFI data of SAX J1711.6-3808 divided by the best-fit Comptonized
model, excluding 4-9 keV in the fit. |
The continuum models consist of a disk black
body (according to Mitsuda et al. 1984) plus either a (high-energy cut
off) power law plus, a Comptonized thermal spectrum (Titarchuk 1994;
Titarchuk & Lyubarskij 1995; Hua & Titarchuk 1995) or a power-law
model reflected off cold or ionized material (following Magdziarz &
Zdziarski 1995). The results for the goodness of fit are presented in
Table 2. Formally, the values for
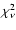 are not
acceptable. For the best fit, the chance probability is as small as
about 1%. We attribute this to calibration uncertainties. With the
introduction of a reasonable systematic flux uncertainty of 1% per
channel,
are not
acceptable. For the best fit, the chance probability is as small as
about 1%. We attribute this to calibration uncertainties. With the
introduction of a reasonable systematic flux uncertainty of 1% per
channel,
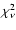 decreases to 1.0. In Table 3, we
present the parameter values for four of the best-fit models. We chose
to not consider absorption edges because the evidence for their
existence is not convincing. Also we chose the disk black body model
for the soft excess because single-temperature black body radiation
does not fit PCA data (see Sect. 4). Although one of the
four is the best fit, the other 3 are consistent at the 1 sigma level.
We conclude that 1) the fitted line width is very broad, much larger
than the spectral resolution of the MECS (33% versus 8% FWHM); 2)
the emission line is consistent with being symmetric with a shape that
can either be modeled with a broadened Gauss function or a
relativistically broadened emission line with a fairly high
inclination angle; 3) the absorption edge is not mandated by the data;
4) reflection models are inconsistent with the data (they particularly
have a problem with explaining the high-energy cutoff); 5) both
non-reflected continuum models give nearly equally as good a
description of the data and 6) the data do not discriminate between
single-temperature or multi-temperature black body models.
decreases to 1.0. In Table 3, we
present the parameter values for four of the best-fit models. We chose
to not consider absorption edges because the evidence for their
existence is not convincing. Also we chose the disk black body model
for the soft excess because single-temperature black body radiation
does not fit PCA data (see Sect. 4). Although one of the
four is the best fit, the other 3 are consistent at the 1 sigma level.
We conclude that 1) the fitted line width is very broad, much larger
than the spectral resolution of the MECS (33% versus 8% FWHM); 2)
the emission line is consistent with being symmetric with a shape that
can either be modeled with a broadened Gauss function or a
relativistically broadened emission line with a fairly high
inclination angle; 3) the absorption edge is not mandated by the data;
4) reflection models are inconsistent with the data (they particularly
have a problem with explaining the high-energy cutoff); 5) both
non-reflected continuum models give nearly equally as good a
description of the data and 6) the data do not discriminate between
single-temperature or multi-temperature black body models.
The disk black body accounts for 9% of the 1-10 keV unabsorbed flux
or 3% in the 1-200 keV band. The absorbed flux in 3 to 20 keV is
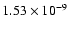 erg cm-2 s-1; the unabsorbed flux in the 1 to 200 keV band is
erg cm-2 s-1; the unabsorbed flux in the 1 to 200 keV band is
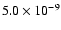 erg cm-2 s-1. The equivalent width of the broad emission feature
is between 0.35 and 0.50 keV, depending on the model.
erg cm-2 s-1. The equivalent width of the broad emission feature
is between 0.35 and 0.50 keV, depending on the model.


Up: The nature of the
Copyright ESO 2002
![]() wa = interstellar absorption following Morrison
& McCammon (1983), comptt = Comptonized spectrum,
gauss = Gauss function, edge = 1 for
wa = interstellar absorption following Morrison
& McCammon (1983), comptt = Comptonized spectrum,
gauss = Gauss function, edge = 1 for
![]() and 1 - exp(
and 1 - exp(![]() )
for
)
for
![]() ,
po = power law, highecut = 1 for
,
po = power law, highecut = 1 for
![]() and
exp(
and
exp(
![]() )
for
)
for
![]() ,
bbody = single-temperature black
body radiation, diskbb = disk
black body (Mitsuda et al. 1984); pexriv = Compton reflection against
an ionized medium (Magdziarz & Zdziarski 1995); pexrav = Compton
reflection off a neutral medium (Magdziarz & Zdziarski 1995).
,
bbody = single-temperature black
body radiation, diskbb = disk
black body (Mitsuda et al. 1984); pexriv = Compton reflection against
an ionized medium (Magdziarz & Zdziarski 1995); pexrav = Compton
reflection off a neutral medium (Magdziarz & Zdziarski 1995).
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{h3518f5.ps}
\end{figure}](/articles/aa/full/2002/29/aah3518/Timg47.gif)